| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 10 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201323003 | |
| Published online | 11 June 2014 | |
Planck intermediate results
XVI. Profile likelihoods for cosmological parameters
1
APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3,
CEA/lrfu, Observatoire de Paris,
Sorbonne Paris Cité, 10 rue Alice Domon et Léonie
Duquet,
75205
Paris Cedex 13,
France
2
Aalto University Metsähovi Radio Observatory and Dept of Radio
Science and Engineering, PO Box
13000, 00076
Aalto,
Finland
3
African Institute for Mathematical Sciences,
6-8 Melrose Road,
Muizenberg, Cape
Town, South Africa
4
Agenzia Spaziale Italiana Science Data Center, via del Politecnico
snc, 00133
Roma,
Italy
5
Agenzia Spaziale Italiana, Viale Liegi 26,
Roma,
Italy
6
Astrophysics Group, Cavendish Laboratory, University of Cambridge,
J J Thomson Avenue,
Cambridge
CB3 0HE,
UK
7
Astrophysics & Cosmology Research Unit, School of
Mathematics, Statistics & Computer Science, University of KwaZulu-Natal,
Westville Campus, Private Bag
X54001, 4000
Durban, South
Africa
8
Atacama Large Millimeter/submillimeter Array, ALMA Santiago
Central Offices, Alonso de Cordova 3107, Vitacura, Casilla 763 0355,
Santiago,
Chile
9
CITA, University of Toronto, 60 St. George St., Toronto, ON
M5S 3H8,
Canada
10
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
11
California Institute of Technology, Pasadena, California, USA
12
Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Plaza
San Juan 1, planta 2, 44001
Teruel,
Spain
13
Computational Cosmology Center, Lawrence Berkeley National
Laboratory, Berkeley,
California,
USA
14
Consejo Superior de Investigaciones Científicas (CSIC),
Madrid,
Spain
15
DSM/Irfu/SPP, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
16
DTU Space, National Space Institute, Technical University of
Denmark, Elektrovej
327, 2800
Kgs. Lyngby,
Denmark
17
Département de Physique Théorique, Université de Genève,
24 Quai E.
Ansermet, 1211
Genève 4,
Switzerland
18
Departamento de Física, Universidad de Oviedo,
Avda. Calvo Sotelo s/n,
Oviedo,
Spain
19
Department of Astrophysics/IMAPP, Radboud University
Nijmegen, PO Box
9010, 6500 GL
Nijmegen, The
Netherlands
20
Department of Physics and Astronomy, Dana and David Dornsife
College of Letter, Arts and Sciences, University of Southern California,
Los Angeles
CA
90089,
USA
21
Department of Physics and Astronomy, University College
London, London
WC1E 6BT,
UK
22
Department of Physics and Astronomy, University of
Sussex, Brighton
BN1 9QH,
UK
23
Department of Physics, Florida State University,
Keen Physics Building, 77 Chieftan
Way, Tallahassee,
Florida,
USA
24
Department of Physics, Gustaf Hällströmin katu 2a, University of
Helsinki, Helsinki,
Finland
25
Department of Physics, Princeton University,
Princeton, New Jersey, USA
26
Department of Physics, University of California,
Berkeley, California, USA
27
Department of Physics, University of California,
One Shields Avenue,
Davis, California, USA
28
Department of Physics, University of California,
Santa Barbara, California, USA
29
Department of Physics, University of Illinois at
Urbana-Champaign, 1110 West Green
Street, Urbana,
Illinois,
USA
30
Dipartimento di Fisica e Astronomia G. Galilei, Università degli
Studi diPadova, via Marzolo
8, 35131
Padova,
Italy
31
Dipartimento di Fisica e Scienze della Terra, Università di
Ferrara, via Saragat
1, 44122
Ferrara,
Italy
32
Dipartimento di Fisica, Università La Sapienza,
P.le A. Moro 2, Roma, Italy
33
Dipartimento di Fisica, Università degli Studi di
Milano, via Celoria,
16, Milano,
Italy
34
Dipartimento di Fisica, Università degli Studi di
Trieste, via A. Valerio
2, Trieste,
Italy
35
Dipartimento di Fisica, Università di Roma Tor
Vergata, via della Ricerca
Scientifica 1, Roma, Italy
36
Discovery Center, Niels Bohr Institute,
Blegdamsvej 17,
Copenhagen,
Denmark
37
Dpto. Astrofísica, Universidad de La Laguna (ULL),
38206,
La Laguna, Tenerife,
Spain
38
European Southern Observatory, ESO Vitacura, Alonso de Cordova 3107, Vitacura, Casilla
19001, Santiago,
Chile
39
European Space Agency, ESAC, Planck Science Office, Camino bajo
del Castillo s/n, Urbanización Villafranca del Castillo, Villanueva de la Cañada,
Madrid,
Spain
40
European Space Agency, ESTEC, Keplerlaan 1,
2201 AZ
Noordwijk, The
Netherlands
41
Helsinki Institute of Physics, Gustaf Hällströmin katu 2,
University of Helsinki, Helsinki, Finland
42
INAF – Osservatorio Astrofisico di Catania, via S. Sofia 78,
Catania,
Italy
43
INAF – Osservatorio Astronomico di Padova, Vicolo
dell’Osservatorio 5, Padova, Italy
44
INAF – Osservatorio Astronomico di Roma, via di Frascati 33,
Monte Porzio Catone,
Italy
45
INAF – Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11,
Trieste,
Italy
46
INAF Istituto di Radioastronomia, via P. Gobetti 101,
40129
Bologna,
Italy
47
INAF/IASF Bologna, via Gobetti 101, Bologna, Italy
48
INAF/IASF Milano, via E. Bassini 15, Milano, Italy
49
INFN, Sezione di Bologna, via Irnerio 46,
40126,
Bologna,
Italy
50
INFN, Sezione di Roma 1, Università di Roma Sapienza,
Piazzale Aldo Moro
2, 00185
Roma,
Italy
51
INFN/National Institute for Nuclear Physics,
via Valerio 2,
34127
Trieste,
Italy
52
IUCAA, Post Bag 4, Ganeshkhind, Pune University Campus,
411 007
Pune,
India
53
Imperial College London, Astrophysics group, Blackett Laboratory,
Prince Consort
Road, London,
SW7 2AZ,
UK
54
Infrared Processing and Analysis Center, California Institute of
Technology, Pasadena
CA
91125,
USA
55
Institut Universitaire de France, 103 bd Saint-Michel, 75005
Paris,
France
56
Institut d’Astrophysique Spatiale, CNRS (UMR 8617) Université
Paris-Sud 11, Bâtiment
121, Orsay,
France
57
Institut d’Astrophysique de Paris, CNRS (UMR 7095),
98bis Boulevard
Arago, 75014
Paris,
France
58
Institute for Space Sciences, Bucharest-Magurale,
Romania
59
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA,
UK
60 Institute of Theoretical Astrophysics, University of Oslo,
Blindern, Oslo, Norway
61
Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, La Laguna, Tenerife, Spain
62
Instituto de Física de Cantabria (CSIC-Universidad de Cantabria),
Avda. de los Castros
s/n, Santander,
Spain
63
Jet Propulsion Laboratory, California Institute of Technology,
4800 Oak Grove
Drive, Pasadena,
California,
USA
64
Jodrell Bank Centre for Astrophysics, Alan Turing Building, School
of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester, M13
9PL, UK
65
Kavli Institute for Cosmology Cambridge,
Madingley Road,
Cambridge, CB3 0HA, UK
66
LAL, Université Paris-Sud, CNRS/IN2P3,
Orsay,
France
67
LERMA, CNRS, Observatoire de Paris, 61 Avenue de l’Observatoire,
Paris,
France
68
Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DSM – CNRS –
Université Paris Diderot, Bât. 709, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
69
Laboratoire Traitement et Communication de l’Information, CNRS
(UMR 5141) and Télécom ParisTech, 46 rue Barrault, 75634
Paris Cedex 13,
France
70
Laboratoire de Physique Subatomique et de Cosmologie, Université
Joseph Fourier Grenoble I, CNRS/IN2P3, Institut National Polytechnique de Grenoble,
53 rue des Martyrs,
38026
Grenoble Cedex,
France
71
Laboratoire de Physique Théorique, Université Paris-Sud 11
& CNRS, Bâtiment
210, 91405
Orsay,
France
72
Lawrence Berkeley National Laboratory,
Berkeley,
California,
USA
73
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741
Garching,
Germany
74
National University of Ireland, Department of Experimental
Physics, Maynooth,
Co. Kildare,
Ireland
75
Niels Bohr Institute, Blegdamsvej 17, Copenhagen, Denmark
76
Optical Science Laboratory, University College London,
Gower Street,
London,
UK
77
SISSA, Astrophysics Sector, via Bonomea 265,
34136
Trieste,
Italy
78
SUPA, Institute for Astronomy, University of Edinburgh, Royal
Observatory, Blackford
Hill, Edinburgh
EH9 3HJ,
UK
79
School of Physics and Astronomy, Cardiff University,
Queens Buildings, The
Parade, Cardiff,
CF24 3AA,
UK
80
UPMC Univ. Paris 06, UMR 7095, 98bis BoulevardArago, 75014
Paris,
France
81
Université de Toulouse, UPS-OMP, IRAP, 31028
Toulouse Cedex 4,
France
82
University of Granada, Departamento de Física Teórica y del
Cosmos, Facultad de Ciencias, Granada, Spain
83
University of Granada, Instituto Carlos I de Física Teórica y
Computacional, Granada, Spain
84
Warsaw University Observatory, Aleje Ujazdowskie 4, 00-478
Warszawa,
Poland
Received:
7
November
2013
Accepted:
2
May
2014
We explore the 2013 Planck likelihood function with a high-precision multi-dimensional minimizer (Minuit). This allows a refinement of the ΛCDM best-fit solution with respect to previously-released results, and the construction of frequentist confidence intervals using profile likelihoods. The agreement with the cosmological results from the Bayesian framework is excellent, demonstrating the robustness of the Planck results to the statistical methodology. We investigate the inclusion of neutrino masses, where more significant differences may appear due to the non-Gaussian nature of the posterior mass distribution. By applying the Feldman-Cousins prescription, we again obtain results very similar to those of the Bayesian methodology. However, the profile-likelihood analysis of the cosmic microwave background (CMB) combination (Planck+WP+highL) reveals a minimum well within the unphysical negative-mass region. We show that inclusion of the Planck CMB-lensing information regularizes this issue, and provide a robust frequentist upper limit ∑ mν ≤ 0.26 eV (95% confidence) from the CMB+lensing+BAO data combination.
Key words: cosmic background radiation / cosmology: observations / cosmology: theory / cosmological parameters / methods: statistical
© ESO, 2014
1. Introduction
This paper, one of a set associated with the 2013 release of data from the Planck1 mission (Planck Collaboration I 2014), describes a frequentist estimation of cosmological parameters using profile likelihoods.
Parameter estimation in cosmology is predominantly performed using Bayesian inference, particularly following the introduction of Markov chain Monte Carlo (MCMC) techniques (Christensen et al. 2001). Many scientists in the field use the sophisticated CosmoMC2 software (Lewis & Bridle 2002) to study cosmological parameters, and several experiments provide ready-to-use plugins for it. The Planck satellite mission has recently released high-quality data on the cosmic microwave background (CMB) temperature anisotropies3. The analysis of the cosmological parameters (Planck Collaboration XVI 2014) is based on Bayesian inference using a dedicated version of CosmoMC.
In this methodology, the likelihood leads to the posterior distribution of the parameters once it has been multiplied by some prior distribution that encompasses our knowledge before the measurement is performed. For Planck, wide bounds on uniform distributions have typically been used. However the choice of a particular set of parameters for MCMC sampling, such as the efficient “physical basis” (Kosowsky et al. 2002) used in CosmoMC, may also be viewed as an implicit prior choice.
Frequentist methods do not need priors, other than that some limits on the explored domain
are used in practice and can be seen as the bounds of some “uniform priors”. The maximum
likelihood estimate (MLE) does not depend on the choice of the set of parameters, since it
possesses the property of invariance: if 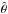 represents the MLE of the parameter θ, then the MLE of any function τ(θ) is
represents the MLE of the parameter θ, then the MLE of any function τ(θ) is
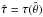 .
This means that one can compute the MLE with any set of parameters. As we will see in Sect.
2.3, this property is powerful and can be used to
obtain asymmetric confidence intervals.
.
This means that one can compute the MLE with any set of parameters. As we will see in Sect.
2.3, this property is powerful and can be used to
obtain asymmetric confidence intervals.
The multi-dimensional solution is only one aspect of parameter estimation and we are also interested in statements on individual parameters. In the MCMC procedure, once the chains have converged this is obtained through marginalization, which is performed by a simple projection of the samples onto one or sometimes two axes. This may however lead to so-called “volume effects”, where the mean of the projected distribution can become incompatible with the multi-dimensional MLE (e.g., Hamann et al. 2007). In the frequentist framework, one instead builds profile likelihoods (Wilks 1938) for individual variables and, by construction, the individual parameter estimates match (up to numerical accuracy) the MLE values.
Such a method has already been used by Yèche et al. (2006) with Wilkinson Microwave Anisotropy Probe (WMAP) data for a nine-parameter fit. The high sensitivity of data from Planck and from the ground-based South Pole Telescope (SPT) and Atacama Cosmology Telescope (ACT) projects requires the simultaneous fit of a larger number of parameters, up to about 40, with some nuisance ones being poorly constrained. We therefore need to precisely tune a high-quality minimizer, as will be described in this paper.
MCMC sampling is sometimes used to perform a “poor-man’s” determination of the maximum likelihood (e.g., Reid et al. 2010): one bins a given parameter and reports the sample of maximum likelihood in other dimensions. As pointed out in Hamann (2012), in many dimensions it is most likely that the real maximum was never reached in any reasonably-sized chain. The authors suggest changing the temperature of the chain, but this still requires running lengthy evaluations of the likelihood and is less straightforward than directly using a multi-dimensional minimization algorithm.
In this article, we investigate whether the use of priors or marginalization can affect the determination of the cosmological parameters by comparing the published Bayesian results to a frequentist method. For the base ΛCDM model, it happens that the cosmological parameter posteriors are essentially Gaussian, so it is expected that frequentist and Bayesian methods will lead to similar results. In extensions to the standard ΛCDM model this is however not true for some parameters (e.g., the sum of neutrino masses), and priors have been shown to play some role in parameter determination (Hamann et al. 2007; Gonzalez-Morales et al. 2011; Hamann 2012). Given the sensitivity of the Planck data, statistical methodologies may matter, and this issue is scrutinized in this work.
In order to build precise profile likelihoods in a high-dimensional space (up to about 40 dimensions), we need a powerful minimizer. We use the mature and widely-used Minuit software (James & Roos 1975). We interfaced it to the modular class Boltzmann solver (Blas et al. 2011) which, from a set of input cosmological parameters, computes the corresponding temperature and polarization power spectra that are tested against the Planck likelihood. This required that we tune the class precision parameters to a level where the numerical noise can be handled by our minimizer, as is described in Sect. 2.1. In Sect. 2.2, we describe our Minuit minimization strategy, and cover in Sect. 2.3 the basics of the frequentist methodology to estimate unknown parameters based on the properties of profile likelihoods. The data sets we use are then discussed in Sect. 3. We give results for the ΛCDM parameters in Sect. 4.1 and finally investigate, in Sect. 4.2, a case where the posterior distribution is far from Gaussian, namely the neutrino mass case. Additionally, the Appendix gathers some comments on the overall computation time of the method.
2. Method
2.1. The Boltzmann solver: class
To compute the relevant CMB power spectra from a cosmological model, we need a “Boltzmann solver” that numerically evolves the coupled perturbation equations in an expanding universe. While camb is used in the CosmoMC sampler, we prefer to use the class (v1.6) software (Blas et al. 2011). It offers a rigorous way to control the accuracy of output quantities through a comprehensive list of precision parameters (Lesgourgues 2011a). While one can use some high-speed/low-quality settings to perform MCMC sampling because the random nature of the algorithm smooths out discontinuities, this is no longer the case here when searching for an extremum, which requires precise computation of numerical derivatives. Equally, due to computation time, one cannot use precision settings that are too extreme, so a trade-off with Minuit convergence has to be found.
As we will see in Sect. 2.3, 68% confidence intervals are obtained by cutting χ2 ≡ −2lnℒ values at one. We therefore need the numerical noise to be much less than unity.
Starting from the Planck likelihood code, described in Sect. 3, we fix all parameters to their published best-fit values (Planck Collaboration XVI 2014) and scan a given parameter θ. We compute the χ2(θ) curves and subtract a smooth component to estimate the amplitude of the numerical noise. According to the precision settings, trade-off between the amplitude of this noise and the computation time can then be found. An example with two precision settings is shown in Fig. 1 for θ = ωb = Ωbh2 which is used as our benchmark.
We have determined a set of high-precision settings which achieves sufficient smoothness of the Planck likelihood for the fits to converge, with an increase of only about a factor two in the code computation speed with respect to the default “fast” settings. The values of the settings are reported in Table 1.
We also found that working with the Thomson scattering optical depth τ is numerically less stable than using the reionization redshift zre, which defines where the reionization fraction is half of its maximum. We therefore use zre as a primary parameter. The relation to τ, for a tanh-based ionization profile and a fixed Δzre = 0.5 width, is given in Lewis (2008).
Since we will compare our results to the previously-published ones, we need to ensure our class configuration reproduces the camb-based results of Planck Collaboration XVI (2014). For this purpose, we use the Planck ΛCDM best-fit solution and compute its χ2 value and compare with the published results in Table 2. The agreement is good. The slight discrepancy is typical of the differences between class and camb implementations (Lesgourgues 2011b), so we consider our setup to be properly calibrated. From now on, we perform consistent comparisons using only class.
 |
Fig. 1 Upper panel: the ωb parameter is scanned (keeping all other parameters fixed to their best-fit values) and the Planck χ2 values are shown on the vertical axis. Blue points are obtained with the class default settings, and red ones with our high-precision ones. A smooth parabola is fit and shown in black. Lower panel: residuals with respect to the parabola. The rms of this noise is improved from 0.02 for the default settings to 0.005 for the high-precision ones. |
Values of the non-default precision parameters for class used for the Minuit minimization.
2.2. Minimizing with Minuit
We chose to work with the powerful Minuit package (James & Roos 1975), a well-known minimizer originally developed for high-energy physics and used recently for the Higgs mass determination with a simultaneous fit of 354 parameters (ATLAS Collaboration 2013). While its roots trace back to the 1970s, it has been continually improved and rewritten in C++ as Minuit2, which is the version we use. Minuit is a toolbox including several algorithms that can be deployed depending on the problem under consideration. We refer the reader to the user guide4 for a detailed description of the procedures we used.
For cosmological parameter estimation with the Planck data, we executed the following strategy
-
1.
Starting from the Planck Collaboration published values and using the high-precision class settings described in Sect. 2.1, we minimize the χ2 function using the MIGRAD algorithm, which is based on Fletcher’s switching algorithm (Fletcher 1970). All parameters are bounded by large (or physical) limits during this exploration.
-
2.
Once a minimum is found, we release all cosmological parameter limits and again perform the MIGRAD minimization. The limits on nuisance parameters are kept in order to avoid exploring unphysical regions.
-
3.
Finally, we use the HESSIAN procedure which refines the local covariance matrix.
Comparison of the χ2 values of the Planck best-fit solution from Planck Collaboration XVI (2014), based on camb, to our class-based implementation, for the CMB and CMB+BAO data sets.
The outcome of this procedure is the minimum χ2 solution together with its Hessian matrix. This solution represents the MLE, but, since the problem is highly non-linear (in particular in H0), the Hessian is only a crude approximation to the parameter uncertainties5. The complete treatment is through the construction of profile likelihoods.
2.3. Profile likelihoods
The MLE (or “best-fit” or 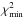 ) is the
global maximum likelihood estimate given the entire set of parameters (cosmological and
nuisance). One can choose to isolate one parameter (hereafter called θ) and for fixed values of
it look for the maximum of the likelihood function in all other dimensions. One scans
θ within
some range and, for each fixed value, runs a minimization with respect to all the other
parameters. The minimum χ2 value is reported for this parameter
θ, which
allows one to build the profile likelihood χ2(θ). The procedure
ensures the minimum of χ2(θ) appears at the
same value as the MLE, avoiding the potential volume effects mentioned in the
introduction.
) is the
global maximum likelihood estimate given the entire set of parameters (cosmological and
nuisance). One can choose to isolate one parameter (hereafter called θ) and for fixed values of
it look for the maximum of the likelihood function in all other dimensions. One scans
θ within
some range and, for each fixed value, runs a minimization with respect to all the other
parameters. The minimum χ2 value is reported for this parameter
θ, which
allows one to build the profile likelihood χ2(θ). The procedure
ensures the minimum of χ2(θ) appears at the
same value as the MLE, avoiding the potential volume effects mentioned in the
introduction.
A confidence region, which has the correct frequentist coverage properties, can then be
extracted from the likelihood ratio statistic, or equivalently the
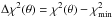 distribution.
For a parabolic χ2(θ) shape (i.e.
Gaussian estimator distribution), a 1 −
α level confidence interval is obtained by the set
of values
distribution.
For a parabolic χ2(θ) shape (i.e.
Gaussian estimator distribution), a 1 −
α level confidence interval is obtained by the set
of values 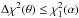 , where
, where
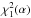 denotes the 1 − α quantile of the
chi-square distribution with one degree of freedom, and is 1, 2.7, and 3.84 for 1 − α = 68,
90 and 95%
respectively (e.g., James 2007).
denotes the 1 − α quantile of the
chi-square distribution with one degree of freedom, and is 1, 2.7, and 3.84 for 1 − α = 68,
90 and 95%
respectively (e.g., James 2007).
It is less well known that if the profile likelihood is non-parabolic, one can still
build an approximate confidence interval using the same recipe, because the full
likelihood ratio has the invariance property mentioned in the introduction: one can
estimate any monotonic function of θ and make the same inference not only on the MLE
but on any likelihood ratio. For example, one can build the Δχ2(As)
distribution from the Δχ2(ln(1010 As))
profile by simply switching the ln(1010 As) → As axis. Formally,
when the profile likelihood is non-parabolic, one can still imagine a transformation that
would make it quadratic in the new variable. One would then apply the parabolic cuts
described previously and, by the invariance property, the same inference on the original
variable would be obtained. Therefore we can find an (asymmetric) confidence interval by
cutting the non-parabolic Δχ2 curve at the same χ2(α) values. This
method, sometimes called MINOS (the name of the routine that first
implemented it in Minuit), is long known in the statistics field
(Wilks 1938). It is exact up to order
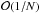 (James 2007), N being the number of
samples, and is in practice excellent unless N is very small.
(James 2007), N being the number of
samples, and is in practice excellent unless N is very small.
Nevertheless, the profile-likelihood-based confidence intervals must be revisited in the case where the estimate lies near a physical boundary. This will be performed in Sect. 4.2 for the neutrino mass case.
3. Data sets
As our purpose is to compare the frequentist methodology to the Bayesian one, we focus on exactly the same data and parameters as in Planck Collaboration XVI (2014) and refer the reader to Planck Collaboration XV (2014) for their exact definitions. Since the CMB, baryon acoustic oscillation (BAO), and CMB-lensing data were found to be in excellent agreement, we will consider the following likelihood combinations.
The CMB data set consists of the following likelihoods:
-
the Planck 2013 data in both low and high ℓ ranges;
-
the WMAP low-ℓ polarization data (referred to as WP in the Planck papers);
-
the SPT (Reichardt et al. 2012)+ACT (Das et al. 2014) high-ℓ data, referred to as highL.
The combined likelihood, obtained by multiplying the three, includes 31 nuisance parameters, related to the characterization of the unresolved foregrounds, the effective beam, and to the inter-calibration of the Planck and highL power spectra.
The BAO data set consists of a Gaussian likelihood based on the scale measurements from the 6dF (Beutler et al. 2011), SDSS (Padmanabhan et al. 2012), and BOSS (Anderson et al. 2012) experiments, combined as in Planck Collaboration XVI (2014).
For the neutrino mass case, we will also use the Planck lensing likelihood (Planck Collaboration XVII 2014), based on the measurement of the deflection power spectrum.
Best-fit comparison.
4. Results
4.1. The base ΛCDM model
We begin by revisiting the global best-fit solution (MLE) using this new minimizer, over all 37 parameters, on the CMB and CMB+BAO data sets. We use the Hubble constant (H0) instead of the CMB acoustic scale (θMC), which is not available within class, and zre instead of τ since it is more stable as discussed in Sect. 2.1. The new minimum is given in Table 3 and compared to the results previously released in Planck Collaboration XVI (2014), which were obtained with another minimizer6. In both cases we find a slightly lower χ2. On the cosmological side we find very similar parameters, except for zre which is slightly shifted. On the nuisance parameters side, results are also similar, but we are now sensitive to the SZ–CIB cross-correlation parameter ξtSZ−CIB while the Planck Collaboration minimum was not shifted from its zero initial value. Additionally the estimated kinetic SZ amplitude AkSZ is more stable when including the BAO data set.
We then build the profile likelihoods by scanning each cosmological parameter and computing the χ2 minimum in the remaining 36 dimensions at each point. Figure 2 shows the reconstructed profiles. They are found to be mostly parabolic, but we still fit them with a third-order polynomial in order to measure any deviation from a symmetric error, and threshold them at unity in order to obtain the 68% frequentist confidence level interval as explained in Sect. 2.3. Results are reported in Table 4 and compared there to the Planck Collaboration posterior distributions. In most cases the values and errors we obtain are in good agreement with the Bayesian posteriors, demonstrating that the Planck Collaboration results, for the ΛCDM model, are not biased by a particular choice of parameters (implicit priors) or by the marginalization process (volume effects).
 |
Fig. 2 Profile likelihoods (Δχ2) reconstructed for each ΛCDM cosmological parameter, from the CMB (blue) and CMB+BAO (red) data sets. Each point is the result of a 36-parameter minimization. We reject the points that are outliers of the expected distance to minimum (EDM, Sect. 2.2) distribution. Curves are fits to a third-order polynomial. 68% confidence intervals are obtained by thresholding these curves at unity, and their projections onto the parameter axis are shown. |
 |
Fig. 3 Neutrino mass profile likelihood for the CMB (red), CMB+lensing (blue), and CMB+lensing+BAO (green) data sets. Each point is the result of a 37-parameter fit which can only be computed in the positive region. The points are fit by a parabola and extrapolated into the negative region. For the CMB only case, the parabolic fit agreement is poor and is only shown for discussion. The coloured green/blue lines are used to set 95% confidence upper limits according to the Feldman-Cousins prescription, as described in the text. |
Results of the profile-likelihood analysis (i.e., this work) for the cosmological parameters, using the CMB and CMB+BAO data sets.
By comparing the mean values of Table 4 to the best-fit ones (Table 3) we observe that the minima coincide at the percent level, as expected for this frequentist method.
Since we observe some difference in the reionization parameter zre, we also
perform the profile-likelihood analysis with the Planck data alone and
obtain 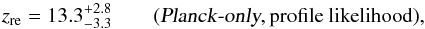 (1)while the Planck
Collaboration reports
(1)while the Planck
Collaboration reports 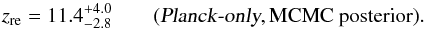 (2)The results, using
exactly the same data, are different. We believe that these new results are robust since
the profile-likelihood method is particularly well suited for this case. Indeed
zre is fixed in each step so that the
minimization does not suffer from the classical (As,zre)
degeneracy due to the normalization of the temperature-only power spectrum. In contrast,
the MCMC method relies strongly on the priors used on both As and
zre. We find that it is the inclusion of
the WMAP polarization data that pulls down this value to zre = 11.0 ±
1.1, as reported in Table 4.
(2)The results, using
exactly the same data, are different. We believe that these new results are robust since
the profile-likelihood method is particularly well suited for this case. Indeed
zre is fixed in each step so that the
minimization does not suffer from the classical (As,zre)
degeneracy due to the normalization of the temperature-only power spectrum. In contrast,
the MCMC method relies strongly on the priors used on both As and
zre. We find that it is the inclusion of
the WMAP polarization data that pulls down this value to zre = 11.0 ±
1.1, as reported in Table 4.
4.2. Mass of standard neutrinos
Since the cosmological parameter posterior distributions for the ΛCDM model are mostly Gaussian (parabolic χ2), the Bayesian and frequentist approaches lead to similar results. However, we may expect greater differences when including neutrino masses in the model, for which the marginalized posterior distribution is peaked towards zero.
CMB measurements are sensitive to the sum of neutrino mass eigenstates ∑
mν through several effects
reviewed in detail in Lesgourgues et al. (2013).
For large values ∑
mν ≳ 1.3 eV, the
neutrinos’ non-relativistic transition happens before decoupling and the integrated
Sachs–Wolfe effect reduces the amplitude of the first acoustic peak. For lower mass
values, neutrino free-streaming erases small-scale matter fluctuations and accordingly
reduces the CMB lensing power. This in turn affects the lensed Cℓ spectrum, especially
its high-ℓ
part, and explains the gain when including SPT/ACT data. Furthermore, since according to
oscillation experiments at least two neutrinos are non-relativistic today (Beringer et al. 2012), the matter–radiation equality
scale factor, which is strongly constrained by the Planck data, reads:
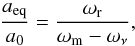 (3)where ωr,
ωm, and ων are the physical
densities of radiation, matter, and massive neutrinos respectively, i.e. ωr =
Ωrh2, ωm =
Ωmh2, and ων =
Ωνh2 ≃ 10-3 ∑
mν/0.1
eV. The quantities ων and ωm are clearly
degenerate, and so any data set that helps in reducing the CMB geometrical degeneracies by
providing a measurement at another scale indirectly benefits ∑
mν. Robust observables,
compatible with the Planck ΛCDM cosmology, are the BAO scale measurement around z ≃ 0.5 and/or the
CMB-lensing trispectrum that probes matter structures around z ≃ 2.
(3)where ωr,
ωm, and ων are the physical
densities of radiation, matter, and massive neutrinos respectively, i.e. ωr =
Ωrh2, ωm =
Ωmh2, and ων =
Ωνh2 ≃ 10-3 ∑
mν/0.1
eV. The quantities ων and ωm are clearly
degenerate, and so any data set that helps in reducing the CMB geometrical degeneracies by
providing a measurement at another scale indirectly benefits ∑
mν. Robust observables,
compatible with the Planck ΛCDM cosmology, are the BAO scale measurement around z ≃ 0.5 and/or the
CMB-lensing trispectrum that probes matter structures around z ≃ 2.
An unexpected result found by Planck Collaboration XVI (2014) is that the 95% confidence upper limit on ∑ mν obtained from Planck data is worsened when including the lensing trispectrum information (the 95% upper limit goes from 0.66 to 0.84). How can the addition of new information weaken the limit? Is this an effect of the Bayesian methodology, which computes credible intervals and where such effects may arise when combining incompatible data? Naively, in a frequentist analysis adding some information (in the Fisher sense, see James 2007) can only lower the size of confidence interval, since the profile-likelihood “error” (its curvature at the minimum) can only decrease and thresholding it at a constant value should only lead to a smaller region.
We construct the profile likelihood for ∑ mν. It is shown in Fig. 3 for the CMB, CMB+lensing and CMB+lensing+BAO data sets. We observe an intriguing feature with the CMB data set. Even though the parabolic fit of the profile likelihood is poor, the minimum lies at about −2.5σ into the unphysical negative region. When adding the lensing trispectrum information, it shifts back to a value compatible with zero. We do not yet have a proper understanding of why this is happening, but note a possible connection to the AL issue discussed in Planck Collaboration XVI (2014), where this phenomenological parameter is discrepant from unity by about 2σ using the CMB data set, but lowered to 1σ when adding the lensing information.
We can then understand why our previous argument on reducing the confidence interval by adding information is invalid near a physical boundary, even in a frequentist sense. If we consider a constant threshold of the profile likelihood (for instance around 8 in Fig. 3) we may end up with an upper limit that is smaller (even though the curvature is larger) when omitting the lensing information, because of the shift of the minimum into the unphysical region. This resembles the Bayesian result.
However the methodologies shows their differences in this situation. In the Bayesian case, when combining somewhat incompatible data sets within a model the credible region enlarges to account for it. In the frequentist case, thresholding the profile likelihood is incorrect and we apply instead the Feldman & Cousins (1998) prescription. Within this classical framework, there is a decoupling of the confidence level of the goodness of fit probability from the one used in building the confidence interval. Unlike in the Bayesian case, one first tests the consistency of the data with the model, and then constructs the confidence interval (at some given level) only for the candidates that fulfil it. In our case, a minimum at −2.5σ is very unlikely (below 1% probability) and we will therefore not consider it in the following.
We give in Table 5 the parameters of the parabolic
fits ![\hbox{$\chi^2(\mnu)=\chi^2_{\rm min}+\left[ (\mnu-m_0)/\sigma_\nu\right]^2$}](/articles/aa/full_html/2014/06/aa23003-13/aa23003-13-eq99.png) . We only use
points within 2σν from zero, since
the function is not necessarily quadratic far from its minimum. In the following we will
vary this cut. We report here the numbers that lead to the largest final limit.
. We only use
points within 2σν from zero, since
the function is not necessarily quadratic far from its minimum. In the following we will
vary this cut. We report here the numbers that lead to the largest final limit.
The classical Neyman construction of a confidence interval has some inherent degree of
freedom in it (e.g., Beringer et al. 2012). The
Feldman–Cousins prescription, that is most powerfull near a physical a boundary, is to
introduce an ordering based upon the likelihood ratios R: 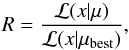 (4)where x is the measured value of
the sum of neutrino masses ∑
mν, μ is the true value, and
μbest is the best-fit value of
∑
mν, given the data and
the physically-allowed region for μ. Hence we have μbest =
x if x ≥ 0, but μbest = 0 if
x<
0, and the ratio R is given by (Feldman & Cousins 1998):
(4)where x is the measured value of
the sum of neutrino masses ∑
mν, μ is the true value, and
μbest is the best-fit value of
∑
mν, given the data and
the physically-allowed region for μ. Hence we have μbest =
x if x ≥ 0, but μbest = 0 if
x<
0, and the ratio R is given by (Feldman & Cousins 1998): 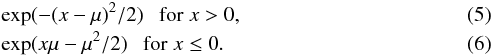 We
then search for an interval [x1,x2] such that R(x1) =
R(x2) and
We
then search for an interval [x1,x2] such that R(x1) =
R(x2) and
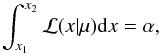 (7)with α = 0.95 as the confidence
level. These intervals are tabulated in Feldman &
Cousins (1998).
(7)with α = 0.95 as the confidence
level. These intervals are tabulated in Feldman &
Cousins (1998).
We obtain the confidence interval [μ1,μ2] for each x = m0/σν extracted from the parabolic fit to the χ2 profile as given in Table 5. The upper limits are then simply μ2 × σν.
We give our final results in Table 6 and compare them to the Planck Bayesian ones of Planck Collaboration XVI (2014). The agreement is impressive, despite the use of two very different statistical techniques. Finally, we varied the range of points used in the parabolic fit and the limits we obtain are always lower than the one reported in Table 6, meaning that our results are conservative.
Upper limit (95% confidence) on the neutrino mass (in eV) in the Planck Bayesian framework and in the frequentist one based on Feldman–Cousins prescription.
5. Conclusion
The use of Bayesian methodology in cosmology is partly motivated by the fact that one observes a single realization of the Universe, while, in particle physics, one accumulates a number of events which leads more naturally to using frequentist methods. This argument is of a sociological rather than scientific nature, and nothing prevents us from using one or the other methodology in these fields.
We demonstrated that a purely frequentist method is tractable with the recent Planck-led high-precision cosmology data. It required lowering the numerical noise of the Boltzmann solver code and we have provided a set of precision parameters for the class software that, in conjunction with a proper Minuit minimization strategy, allowed us to perform the roughly 40 parameter optimization efficiently. We re-determined the maximum likelihood solution, obtaining essentially consistent results but with a slightly better χ2 value.
We built profile likelihoods for each of the cosmological parameters of the ΛCDM model, using the CMB and CMB+BAO data sets, and obtained results very similar to those from the Bayesian methodology. This confirmed, in this model, that the Planck results do not depend on the choice of base parameters (implicit priors) and are free of volume effects in the likelihood projection during the marginalization process.
When including the neutrino mass as a free parameter, the profile likelihood helped us to understand why the computed upper limit increases when including the extra information from CMB lensing. This is not due to the Bayesian methodology, but is related to the physical boundary ∑ mν > 0. The profile likelihood analysis showed that neutrino mass limits obtained without using the lensing information were pulled down to unphysical negative values. Including the extra CMB lensing information allowed us to obtain consistent frequentist results.
Using the Feldman–Cousins prescription, we obtained a 95% confidence upper limit of ∑ mν ≤ 0.26 eV for the CMB+lensing+BAO combination, again in excellent agreement with the Bayesian result.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.
Available from http://cosmologist.info/cosmomc/readme_planck.html
As discussed in http://seal.cern.ch/documents/minuit/mnerror.pdf
Named BOBYQUA and described in http://www.damtp.cam.ac.uk/user/na/NA_papers/NA2009_06.pdf
Acknowledgments
We thank F. Le Diberder for discussions about the Feldman–Cousins method. We gratefully acknowledge IN2P3 Computer Center (http://cc.in2p3.fr) for providing the computing resources and services needed to this work. The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). A description of the Planck Collaboration and a list of its members, including the technical or scientific activities in which they have been involved, can be found at http://www.sciops.esa.int/index.php?project=planck&page=Planck_Collaboration.
References
- Anderson, L., Aubourg, E., Bailey, S., et al. 2012, MNRAS, 427, 3435 [Google Scholar]
- ATLAS Collaboration. 2013, Combined measurements of the mass and signal strength of the Higgs-like boson with the ATLAS detector using up to 25 fb-1 of proton-proton collision data, Tech. Rep. ATLAS-CONF-2013-014, CERN, Geneva [Google Scholar]
- Beringer, J., Arguin, J. F., Barnett, R. M., et al. 2012, Phys. Rev. D, 86, 010001 [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2011, MNRAS, 416, 3017 [NASA ADS] [CrossRef] [Google Scholar]
- Blas, D., Lesgourgues, J., & Tram, T. 2011, J. Cosmol. Astropart. Phys., 7, 34 [Google Scholar]
- Christensen, N., Meyer, R., Knox, L., & Luey, B. 2001, Class. Quant. Grav., 18, 2677 [Google Scholar]
- Das, S., Louis, T., Nolta, M. R., et al. 2014, JCAP, 04, 014 [Google Scholar]
- Davidon, W., & Laboratory, A. N. 1959, Variable metric method for minimization, AEC research and development report (Argonne National Laboratory) [Google Scholar]
- Feldman, G. J., & Cousins, R. D. 1998, Phys. Rev. D, 57, 3873 [Google Scholar]
- Fletcher, R. 1970, Comput. J., 317 [Google Scholar]
- Gonzalez-Morales, A. X., Poltis, R., Sherwin, B. D., & Verde, L. 2011, unpublished [arXiv:1106.5052] [Google Scholar]
- Hamann, J. 2012, J. Cosmol. Astropart., 3, 21 [Google Scholar]
- Hamann, J., Hannestad, S., Raffelt, G. G., & Wong, Y. Y. Y. 2007, J. Cosmol. Astropart. Phys., 8, 21 [Google Scholar]
- James, F. 2007, Statistical Methods in Experimental Physics (World Scientific) [Google Scholar]
- James, F., & Roos, M. 1975, Comput. Phys. Commun., 10, 343 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kosowsky, A., Milosavljevic, M., & Jimenez, R. 2002, Phys. Rev. D, 66, 063007 [NASA ADS] [CrossRef] [Google Scholar]
- Lesgourgues, J. 2011a, unpublished [arXiv:1104.2932] [Google Scholar]
- Lesgourgues, J. 2011b, unpublished [arXiv:1104.2934] [Google Scholar]
- Lesgourgues, J., Mangano, G., Miele, G., & Pastor, S. 2013, Neutrino Cosmology (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Lewis, A. 2008, Phys. Rev. D, 78, 023002 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Padmanabhan, N., Xu, X., Eisenstein, D. J., et al. 2012, MNRAS, 427, 2132 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Planck Collaboration I. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321529 [Google Scholar]
- Planck Collaboration XV. 2014, A&A, in press, DOI: 10.1051/004-6361/201321573 [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321591 [Google Scholar]
- Planck Collaboration XVII. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321543 [Google Scholar]
- Reichardt, C. L., de Putter, R., Zahn, O., & Hou, Z. 2012, ApJ, 749, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, B. A., Verde, L., Jimenez, R., & Mena, O. 2010, J. Cosmol. Astropart. Phys., 1, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Wilks, A. S. S. 1938, Ann. Math. Statist., 1, 60 [Google Scholar]
- Yèche, C., Ealet, A., Réfrégier, A., et al. 2006, A&A, 448, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Note on CPU time
It it sometimes stated that multi-dimensional minimization in high-dimension space is inefficient (or intractable) while MCMC methods scale linearly. Both statements need clarification.
Standard MCMC methods (e.g., Metropolis–Hastings or Gibbs sampling as in
CosmoMC) are extremely CPU-intensive. They require the lengthy
computation of a multi-variate proposal before running a final Markov chain, which by
essence is sequential and therefore cannot scale on multiple processors. In the
Planck case about 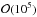 iterations (i.e., computations of the likelihood) were needed for this final stage.
iterations (i.e., computations of the likelihood) were needed for this final stage.
One Minuit minimization in our scheme is obtained in about
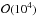 iterations. It, however, requires a higher precision tuning of the Boltzmann solver, which
enhances the computation time of each likelihood by about a factor two. In practice the
minimum, in the D =
40 case, is found in about 10 h, and is limited by the Boltzmann
computation speed. The profile likelihood approach requires many minimizations but these
are independent of one another. The problem now scales with the number of computers, so
that the total wall-clock time is still of the same order of magnitude on a reasonable
computer cluster.
iterations. It, however, requires a higher precision tuning of the Boltzmann solver, which
enhances the computation time of each likelihood by about a factor two. In practice the
minimum, in the D =
40 case, is found in about 10 h, and is limited by the Boltzmann
computation speed. The profile likelihood approach requires many minimizations but these
are independent of one another. The problem now scales with the number of computers, so
that the total wall-clock time is still of the same order of magnitude on a reasonable
computer cluster.
All Tables
Values of the non-default precision parameters for class used for the Minuit minimization.
Comparison of the χ2 values of the Planck best-fit solution from Planck Collaboration XVI (2014), based on camb, to our class-based implementation, for the CMB and CMB+BAO data sets.
Results of the profile-likelihood analysis (i.e., this work) for the cosmological parameters, using the CMB and CMB+BAO data sets.
Upper limit (95% confidence) on the neutrino mass (in eV) in the Planck Bayesian framework and in the frequentist one based on Feldman–Cousins prescription.
All Figures
 |
Fig. 1 Upper panel: the ωb parameter is scanned (keeping all other parameters fixed to their best-fit values) and the Planck χ2 values are shown on the vertical axis. Blue points are obtained with the class default settings, and red ones with our high-precision ones. A smooth parabola is fit and shown in black. Lower panel: residuals with respect to the parabola. The rms of this noise is improved from 0.02 for the default settings to 0.005 for the high-precision ones. |
| In the text | |
 |
Fig. 2 Profile likelihoods (Δχ2) reconstructed for each ΛCDM cosmological parameter, from the CMB (blue) and CMB+BAO (red) data sets. Each point is the result of a 36-parameter minimization. We reject the points that are outliers of the expected distance to minimum (EDM, Sect. 2.2) distribution. Curves are fits to a third-order polynomial. 68% confidence intervals are obtained by thresholding these curves at unity, and their projections onto the parameter axis are shown. |
| In the text | |
 |
Fig. 3 Neutrino mass profile likelihood for the CMB (red), CMB+lensing (blue), and CMB+lensing+BAO (green) data sets. Each point is the result of a 37-parameter fit which can only be computed in the positive region. The points are fit by a parabola and extrapolated into the negative region. For the CMB only case, the parabolic fit agreement is poor and is only shown for discussion. The coloured green/blue lines are used to set 95% confidence upper limits according to the Feldman-Cousins prescription, as described in the text. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


