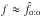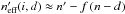Probabilistic positional association of catalogs of astrophysical sources: the Aspects code

Michel Fioc

doi:10.1051/0004-6361/201220021

Home

All issues

Volume 566 (June 2014)

A&A, 566 (2014) A8

Full HTML

Free Access

Issue		A&A Volume 566, June 2014


Article Number		A8
Number of page(s)		16
Section		Numerical methods and codes
DOI		https://doi.org/10.1051/0004-6361/201220021
Published online		29 May 2014

A&A 566, A8 (2014)

Probabilistic positional association of catalogs of astrophysical sources: the Aspects code ^⋆,^⋆⋆

Michel Fioc

Institut d’Astrophysique de Paris, UPMC – Univ. Paris 6, CNRS, UMR 7095, 98bis boulevard Arago, 75014 Paris, France
e-mail: Michel.Fioc@iap.fr

Received: 16 July 2012
Accepted: 1 November 2013

Abstract

We describe a probabilistic method of cross-identifying astrophysical sources in two catalogs from their positions and positional uncertainties. The probability that an object is associated with a source from the other catalog, or that it has no counterpart, is derived under two exclusive assumptions: first, the classical case of several-to-one associations, and then the more realistic but more difficult problem of one-to-one associations. In either case, the likelihood of observing the objects in the two catalogs at their effective positions is computed and a maximum likelihood estimator of the fraction of sources with a counterpart – a quantity needed to compute the probabilities of association – is built. When the positional uncertainty in one or both catalogs is unknown, this method may be used to estimate its typical value and even to study its dependence on the size of objects. It may also be applied when the true centers of a source and of its counterpart at another wavelength do not coincide. To compute the likelihood and association probabilities under the different assumptions, we developed a Fortran 95 code called Aspects ([aspε], “Association positionnelle/probabiliste de catalogues de sources” in French); its source files are made freely available. To test Aspects, all-sky mock catalogs containing up to 10⁵ objects were created, forcing either several-to-one or one-to-one associations. The analysis of these simulations confirms that, in both cases, the assumption with the highest likelihood is the right one and that estimators of unknown parameters built for the appropriate association model are reliable.

Key words: methods: statistical / catalogs / galaxies: statistics / stars: statistics / astrometry

^⋆

Available at www2.iap.fr/users/fioc/Aspects/

^⋆⋆

The Aspects code is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/566/A8

© ESO, 2014

1. Introduction

The most basic method of cross-identifying two catalogs K and K′ with known circular positional uncertainties is to consider that a K′-source M′ is the same as an object M of K if it falls within a disk centered on M and having a radius equal to a few times their combined positional uncertainty; if the disk is void, M has no counterpart, and if it contains several K′-sources, the nearest one is identified to M. This solution is defective for several reasons: it does not take the density of sources into account; positional uncertainty ellipses are not properly treated; the radius of the disk is arbitrary; positional uncertainties are not always known; K and K′ do not play symmetrical roles; the identification is ambiguous if a K′-source may be associated to several objects of K. Worst of all, it does not provide a probability of association.

Beyond this naïve method, the cross-identification problem has been studied by Condon et al. (1975), de Ruiter et al. (1977), Prestage & Peacock (1983), Sutherland & Saunders (1992), Bauer et al. (2000), and Rutledge et al. (2000), among others. As shown by the recent papers of Budavári & Szalay (2008), Brand et al. (2006), Rohde et al. (2006), Roseboom et al. (2009), and Pineau et al. (2011), this field is still very active and will be more so with the wealth of forthcoming multiwavelength data and the virtual observatory (Vignali et al. 2009). In these papers, the identification is performed using a “likelihood ratio”. For two objects (M,M′) ∈ K × K′ with known coordinates and positional uncertainties, and given the local surface density of K′-sources, this ratio is typically computed as 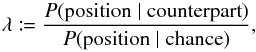$λ := \frac{P (position | counterpart)}{P (position | chance)},$ $\begin{equation} \label{def_LR} \lambda \coloneqq \frac{ \Prob(\text{position} \mid \text{counterpart}) }{ \Prob(\text{position} \mid \text{chance}) }, \end{equation}$ (1)where P(position | counterpart) is the probability of finding M′ at some position relative to M if M′ is a counterpart of M, and P(position | chance) is the probability that M′ is there by chance. As noticed by Sutherland & Saunders (1992), there has been some confusion when defining and interpreting λ, and, more importantly, in deriving the probability ¹ that M and M′ are the same.

To associate sources from catalogs at different wavelengths, some authors include some a priori information on the spectral energy distribution (SED) of the objects in this likelihood ratio. When this work started, our primary goal was to build template observational SEDs from the optical to the far-infrared for different types of galaxies. We initially intended to cross-identify the Iras Faint Source Survey (Moshir et al. 1992, 1993) with the Leda database (Paturel et al. 1995). Because of the high positional inaccuracy of Iras data, special care was needed to identify optical sources with infrared ones. While Iras data are by now quite outdated and have been superseded by Spitzer and Herschel observations, we think that the procedure we began to develop at that time may be valuable for other studies. Because we aimed to fit synthetic SEDs to the template observational ones, we could not and did not want to make assumptions on the SED of objects based on their type, since this would have biased the procedure. We therefore rely only on positions in what follows.

The method we use is in essence similar to that of Sutherland & Saunders (1992). Because thinking in terms of probabilities rather than of likelihood ratios highlights some implicit assumptions, we found it however useful for the sake of clarity to detail hereafter our calculations. This allows us moreover to propose a systematic way to estimate the unknown parameters required to compute the probabilities of association and to extend our work to a case not covered by the papers cited above (see Sect. 4).

After some preliminaries (Sect. 2), we compute in Sect. 3 the probability of association under the hypothesis that a K-source has at most one counterpart in K′ but that several objects of K may share the same one (“several-to-one” associations). We also compute the likelihood to observe all the sources at their effective positions and use it to estimate the fraction of objects with a counterpart and, if unknown, the positional uncertainty in one or both catalogs. In Sect. 4, we do the same calculations under the assumption that a K-source has at most one counterpart in K′ and that no other object of K has the same counterpart (“one-to-one” associations). In Sect. 5, we present a code, Aspects, implementing the results of Sects. 3 and 4, and with which we compute the likelihoods and probabilities of association under the aforementioned assumptions. We test it on simulations in Sect. 6. The probability distribution of the relative positions of associated sources is modeled in Appendix A.

2. Preliminaries

2.1. Notations

We consider two catalogs K and K′ defined on a common surface of the sky, of area S, and containing respectively n sources (M_i)_{i ∈ [[1,n]]} and 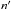$n^{'}$ $\hbox{$\np$}$ sources $(M_{j}^{'})_{j \in [[1, n^{'}]]}$ $\hbox{$(\Mp_j)^{}_{\smash[t]{j\in\integinterv{1}{\np}}}$}$ . We define the following events:

c_i: M_i is in the infinitesimal surface element d²r_i located at r_i;
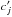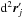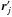$c_{j}^{'}$ $\hbox{$\coordpj$}$ : $M_{j}^{'}$ $\hbox{$\Mp_j$}$ is in the infinitesimal surface element $d^{2} r_{j}^{'}$ $\hbox{$\df^2\vrpj$}$ located at $r_{j}^{'}$ $\hbox{$\vrpj$}$ ;
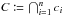$C := {^{􏽔}}_{i = 1}^{n} c_{i}$ $\hbox{$C \coloneqq \bigcap_{i=1}^n c_i$}$ : the coordinates of all K-sources are known;
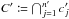$C^{'} := {^{􏽔}}_{j = 1}^{n^{'}} c_{j}^{'}$ $\hbox{$C' \coloneqq \bigcap_{j=1}^\np \coordpj$}$ : the coordinates of all K′-sources are known;
A_i,j, with i ≠ 0 and j ≠ 0: $M_{j}^{'}$ $\hbox{$\Mp_j$}$ is a counterpart of M_i;
A_{i, 0}: M_i has no counterpart in K′, i.e. 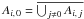$A_{i, 0} = {^{􏽓}}_{j \neq 0} A_{i, j}$ $\hbox{$A_{i\comma 0} = \overline{\bigcup_{j\neq0}A_{i\comma j}}$}$ , where 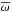$ω$ $\hbox{$\overline{\omega}$}$ is the negation of an event ω;
A_0,j: $M_{j}^{'}$ $\hbox{$\Mp_j$}$ has no counterpart in K.

We denote by f (resp. f′) the unknown a priori (i.e., not knowing the coordinates) probability that any element of K (resp. K′) has a counterpart in K′ (resp. K). In terms of the events (A_i,j), for any 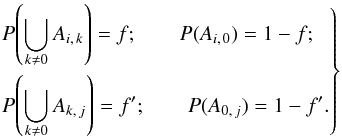$(M_{i}, M_{j}^{'}) \in K \times K^{'}$ $\hbox{$(M_i, \Mp_j) \in K \times K'$}$ , $\begin{matrix} \begin{matrix} \end{matrix} P (\underset{k \neq 0}{􏽛} A_{i, k}) = f; P (A_{i, 0}) = 1 - f; \begin{matrix} \end{matrix} \\ \begin{matrix} \end{matrix} P (\underset{k \neq 0}{􏽛} A_{k, j}) = f^{'}; P (A_{0, j}) = 1 - f^{'} . \end{matrix} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix}$ $\begin{equation} \label{def_f} \Left. \begin{aligned} &\Prob\Left(\bigcup_{k\neq0} A_{i\comma k}\Right) = f; \qquad \Prob(A_{i\comma 0}) = 1-f; \\ &\Prob\Left(\bigcup_{k\neq0} A_{k\comma j}\Right) = f'; \qquad \Prob(A_{0\comma j}) = 1-f'. \end{aligned} \Right\} \end{equation}$ (2)We see in Sects. 3.2 and 4.2 how to estimate f and f′.

The angular distance between two points Y and Z is written ψ(Y,Z). More specifically, we put 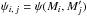$ψ_{i, j} = ψ (M_{i}, M_{j}^{'})$ $\hbox{$\psi_{i\comma j} = \psi(M_i, \Mp_j)$}$ .

2.2. Assumptions

Calculations are carried out under one of three exclusive assumptions:

Several-to-one hypothesis: 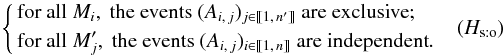$\begin{matrix} {\begin{matrix} \begin{matrix} \end{matrix} forall M_{i}, theevents (A_{i, j})_{j \in [[1, n^{'}]]} areexclusive; \begin{matrix} \end{matrix} \\ \begin{matrix} \end{matrix} forall M_{j}^{'}, theevents (A_{i, j})_{i \in [[1, n]]} areindependent . \end{matrix} (H_{s:o}) \end{matrix}$ $\begin{eqnarray*} \Left\{ \begin{aligned} &\text{for all }M_i,\text{ the events }(A_{i\comma j})_{j\in\integinterv{1}{\np}} \text{ are exclusive}; \\ &\text{for all }\Mp_j,\text{ the events }(A_{i\comma j})_{i\in\integinterv{1}{n}} \text{ are independent}. \end{aligned} \Right. \quad({H_\sto}) \end{eqnarray*}$ Therefore, a K-source has at most one counterpart in K′, but a K′-source may have several counterparts in K. Since more K-sources have a counterpart in K′ than the converse, 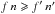$f n ⩾ f^{'} n^{'}$ $\hbox{$f\multspace n \geqslant f'\multspace \np$}$ . This assumption is reasonable if the angular resolution in K′ (e.g. Iras) is much poorer than in K (e.g. Leda), since several distinct objects of K may then be confused in K′.
One-to-several hypothesis: the symmetric of assumption (H_s:o), i.e., 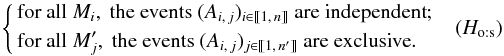$\begin{matrix} {\begin{matrix} \begin{matrix} \end{matrix} forall M_{i}, theevents (A_{i, j})_{i \in [[1, n]]} areindependent; \begin{matrix} \end{matrix} \\ \begin{matrix} \end{matrix} forall M_{j}^{'}, theevents (A_{i, j})_{j \in [[1, n^{'}]]} areexclusive . \end{matrix} (H_{o:s}) \end{matrix}$ $\begin{eqnarray*} \Left\{ \begin{aligned} &\text{for all }M_i,\text{ the events }(A_{i\comma j})_{i\in\integinterv{1}{n}} \text{ are independent}; \\ &\text{for all }\Mp_j,\text{ the events }(A_{i\comma j})_{j\in\integinterv{1}{\np}} \text{ are exclusive}. \end{aligned} \Right. \quad({H_\ots}) \end{eqnarray*}$ In that case, 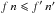$f n ⩽ f^{'} n^{'}$ $\hbox{$f\multspace n \leqslant f'\multspace \np$}$ . This assumption is appropriate for catalogs of extended sources that, although observed as single at the wavelength of K, may look broken up at the wavelength of K′.
One-to-one hypothesis: any K-source has at most one counterpart in K′ and reciprocally, i.e. 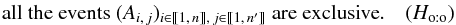$\begin{matrix} alltheevents (A_{i, j})_{i \in [[1, n]], j \in [[1, n^{'}]]} areexclusive . (H_{o:o}) \end{matrix}$ $\begin{eqnarray*} \text{all the events } (A_{i\comma j})_{i\in\integinterv{1}{n}\comma j\in\integinterv{1}{\np}} \text{ are exclusive}. 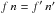\quad({H_\oto}) \end{eqnarray*}$ Then, $f n = f^{'} n^{'}$ $\hbox{$f\multspace n = f'\multspace \np$}$ . This assumption is the most relevant one for high-resolution catalogs of point sources or of well-defined extended sources.

Probabilities, likelihoods, and estimators specifically derived under either assumption (H_s:o), (H_o:s), or (H_o:o) are written with the subscript “s:o”, “o:s”, or “o:o”, respectively; the subscript “:o” is used for results valid for both (H_s:o) and (H_o:o). The “several-to-several” hypothesis where all the events 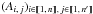$(A_{i, j})_{i \in [[1, n]], j \in [[1, n^{'}]]}$ $\hbox{$(A_{i\comma j})_{i\in\integinterv{1}{n}\comma j\in\integinterv{1}{\np}}$}$ are independent is not considered here.

We make two other assumptions: all the associations A_i,j with i ≠ 0 and j ≠ 0 are considered a priori as equally likely, and the effect of clustering is negligible.

2.3. Approach

Our approach is the following. For each of the assumptions (H_s:o), (H_o:o), and (H_o:s), we

find an expression for the probabilities of association,
build estimators of the unknown parameters needed to compute these probabilities, and
compute the likelihood of the assumption from the data.

Then, we compute the probabilities of association for the best estimators of unknown parameters and the most likely assumption.

Although (H_s:o) is less symmetrical and neutral than (H_o:o), we begin our study with this assumption: first, because computations are much simpler under (H_s:o) than under (H_o:o) and serve as a guide for the latter; second, because they provide initial values for the iterative procedure (Sect. 5.4.3) used to effectively compute probabilities under (H_o:o).

3. Several-to-one associations

In this section, we assume that hypothesis (H_s:o) holds. As shown in Sect. 3.3, this is also the assumption implicitly made by the authors cited in the introduction.

3.1. Probability of association: global computation

We want to compute² the probability P(A_i,j | C ∩ C′) of association between sources M_i and $M_{j}^{'}$ $\hbox{$\Mp_j$}$ (j ≠ 0) or the probability that M_i has no counterpart (j = 0), knowing the coordinates of all the objects in K and K′. 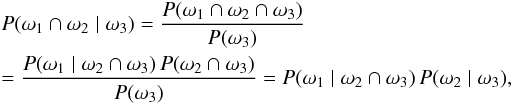Remembering that, for any events ω₁, ω₂, and ω₃, P(ω₁ | ω₂) = P(ω₁ ∩ ω₂) /P(ω₂) and thus $\begin{matrix} P (ω_{1} \cap ω_{2} | ω_{3}) = \frac{P (ω_{1} \cap ω_{2} \cap ω_{3})}{P (ω_{3})} \end{matrix}$ $\begin{eqnarray} && \Prob(\omega_1 \cap \omega_2 \mid \omega_3) = \frac{\Prob(\omega_1 \cap \omega_2 \cap \omega_3)}{\Prob(\omega_3)} \nonumber\\&&= \frac{\Prob(\omega_1 \mid \omega_2 \cap \omega_3)\multspace \Prob(\omega_2 \cap \omega_3)}{\Prob(\omega_3)} = \Prob(\omega_1 \mid \omega_2 \cap \omega_3) \multspace \Prob(\omega_2 \mid \omega_3), \label{Bayes2} \end{eqnarray}$ (3)we have, with ω₁ = A_i,j, ω₂ = C, and ω₃ = C′, 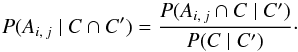$P (A_{i, j} | C \cap C^{'}) = \frac{P (A_{i, j} \cap C | C^{'})}{P (C | C^{'})} \cdot$ $\begin{equation} \label{P(Aij|C,C)_gen} \Prob(A_{i\comma j} \mid C \cap C') = \frac{ \Prob(A_{i\comma j} \cap C \mid C') }{ \Prob(C \mid C') }\cdot \end{equation}$ (4)

3.1.1. Computation of P_s:o(C | C′)

We first compute the denominator of Eq. (4)³. The event 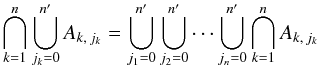$􏽜_{k = 1}^{n} 􏽛_{j_{k} = 0}^{n^{'}} A_{k, j_{k}} = 􏽛_{j_{1} = 0}^{n^{'}} 􏽛_{j_{2} = 0}^{n^{'}} \cdot \cdot \cdot 􏽛_{j_{n} = 0}^{n^{'}} 􏽜_{k = 1}^{n} A_{k, j_{k}}$ $\begin{equation} \bigcap_{k=1}^n\bigcup_{j_k=0}^\np A_{k\comma j_k} = \bigcup_{j_1=0}^\np\bigcup_{j_2=0}^\np\cdots\bigcup_{j_n=0}^\np \bigcap_{k=1}^n A_{k\comma j_k} \end{equation}$ (5)is certain by definition of the A_{k,j_k} and, under either assumption (H_s:o) or (H_o:o), A_k,ℓ ∩ A_k,m =? for all M_k if ℓ ≠ m. Consequently, using the symbol ^􏽕 for mutually exclusive events instead of ^􏽓, we obtain 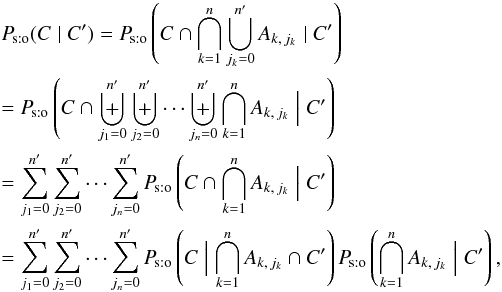$\begin{matrix} P_{s:o} (C | C^{'}) = P_{s:o} (C \cap 􏽜_{k = 1}^{n} 􏽛_{j_{k} = 0}^{n^{'}} A_{k, j_{k}} | C^{'}) \\ = P_{s:o} (C \cap 􏽝_{j_{1} = 0}^{n^{'}} 􏽝_{j_{2} = 0}^{n^{'}} \cdot \cdot \cdot 􏽝_{j_{n} = 0}^{n^{'}} 􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}) \\ = \sum_{j_{1} = 0}^{n^{'}} \sum_{j_{2} = 0}^{n^{'}} \cdot \cdot \cdot \sum_{j_{n} = 0}^{n^{'}} P_{s:o} (C \cap 􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}) \end{matrix}$ $\begin{eqnarray} &&\Psto(C \mid C') = \Psto\left(C \cap \bigcap_{k=1}^n\bigcup_{j_k=0}^\np A_{k\comma j_k} \mid C'\right) \nonumber \\&&= \Psto\left(C \cap \biguplus_{j_1=0}^\np\biguplus_{j_2=0}^\np\cdots\biguplus_{j_n=0}^\np \bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C' \right) \nonumber \\&&= \sum_{j_1=0}^\np \sum_{j_2=0}^\np \cdots \sum_{j_n=0}^\np \Psto\left(C \cap \bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C' \right) \nonumber \\&&= \sum_{j_1=0}^\np \sum_{j_2=0}^\np \cdots \sum_{j_n=0}^\np \Psto\left(C \Bigm| \bigcap_{k=1}^n A_{k\comma j_k} \cap C' \right) \multspace \Psto\left(\bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C' \right), \label{P_sto(C|C)_gen} \end{eqnarray}$ (6)with ω₁ = C, $ω_{2} = {^{􏽔}}_{k = 1}^{n} A_{k, j_{k}}$ $\hbox{$\omega_2 = \bigcap_{\smash[t]{k=1}}^n A_{k\comma j_k}$}$ , and ω₃ = C′ in Eq. (3).

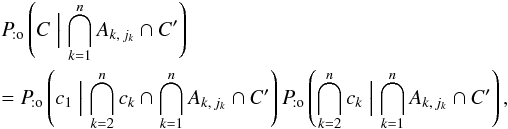Since $C = {^{􏽔}}_{k = 1}^{n} c_{k}$ $\hbox{$C = \bigcap_{\smash[t]{k=1}}^n c_k$}$ , the first factor in the product of Eq. (6)is $\begin{matrix} P_{:o} (C | 􏽜_{k = 1}^{n} A_{k, j_{k}} \cap C^{'}) \\ = P_{:o} (c_{1} | 􏽜_{k = 2}^{n} c_{k} \cap 􏽜_{k = 1}^{n} A_{k, j_{k}} \cap C^{'}) P_{:o} (􏽜_{k = 2}^{n} c_{k} | 􏽜_{k = 1}^{n} A_{k, j_{k}} \cap C^{'}), \end{matrix}$ $\begin{eqnarray} && \Pato\left(C \Bigm| \bigcap_{k=1}^n A_{k\comma j_k} \cap C'\right) \nonumber \\&&= \Pato\left(c_1 \Bigm| \bigcap_{k=2}^n c_k \cap \bigcap_{k=1}^n A_{k\comma j_k} \cap C'\right) \multspace \Pato\left(\bigcap_{k=2}^n c_k \Bigm| \bigcap_{k=1}^n A_{k\comma j_k} \cap C' \right), \end{eqnarray}$ (7)with ω₁ = c₁, $ω_{2} = {^{􏽔}}_{k = 2}^{n} c_{k}$ $\hbox{$\omega_2 = \bigcap_{\smash[t]{k=2}}^n c_k$}$ , and ω₃ = A_{k,j_k} ∩ C′ in Eq. (3). 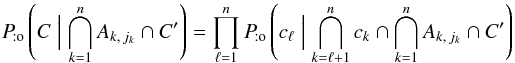Doing the same with ${^{􏽔}}_{k = 2}^{n} c_{k}$ $\hbox{$\bigcap_{\smash[t]{k=2}}^n c_k$}$ instead of C, we obtain $P_{:o} (C | 􏽜_{k = 1}^{n} A_{k, j_{k}} \cap C^{'}) = 􏽙_{ℓ = 1}^{n} P_{:o} (c_{ℓ} | 􏽜_{k = ℓ + 1}^{n} c_{k} \cap 􏽜_{k = 1}^{n} A_{k, j_{k}} \cap C^{'})$ $\begin{equation} \Pato\left(C \Bigm| \bigcap_{k=1}^n A_{k\comma j_k} \cap C'\right) = \prod_{\ell=1}^n \Pato\left(c_\ell \Bigm| \bigcap_{k=\ell+1}^n c_k \cap \bigcap_{k=1}^n A_{k\comma j_k} \cap C'\right) \label{P_sto(C|A,C)_gen} \end{equation}$ (8)by iteration.

If j_ℓ ≠ 0, M_ℓ is only associated with 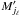$M_{j_{ℓ}}^{'}$ $\hbox{$\Mp_{j_\ell}$}$ . Consequently, $\begin{matrix} P_{:o} (c_{ℓ} | 􏽜_{k = ℓ + 1}^{n} c_{k} \cap 􏽜_{k = 1}^{n} A_{k, j_{k}} \cap C^{'}) & = & P_{:o} (c_{ℓ} | A_{ℓ, j_{ℓ}} \cap c_{j_{ℓ}}^{'}) \\ = \end{matrix}$ $\begin{eqnarray} \Pato\Left(c_\ell \Bigm| \bigcap_{k=\ell+1}^n c_k \cap \bigcap_{k=1}^n A_{k\comma j_k} \cap C'\Right) &=& \Pato(c_\ell \mid A_{\ell\comma j_\ell} \cap c'_{\smash[t]{j_\ell}}) \notag \\ &=& \xi_{\ell\comma j_\ell} \multspace \df^2\vec r_\ell, \label{jl_non_nul} \end{eqnarray}$ (9)where, denoting by $r_{ℓ, j_{ℓ}} := r_{j_{ℓ}}^{'} - r_{ℓ}$ $\hbox{$\vec r_{\ell\comma j_\ell} \coloneqq \vec r'_{\smash[t]{j_\ell}} - \vec r_\ell$}$ the position vector of $M_{j_{ℓ}}^{'}$ $\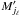hbox{$\Mp_{j_\ell}$}$ relative to M_ℓ and by Γ_{ℓ,j_ℓ} the covariance matrix of r_{ℓ,j_ℓ} (cf. Appendix A.2), $ξ_{ℓ, j_{ℓ}} = \frac{\exp (- \frac{1}{2} r_{ℓ, j_{ℓ}}^{t} \cdot Γ_{ℓ, j_{ℓ}}^{-1} \cdot r_{ℓ, j_{ℓ}})}{2 ß \sqrt{\det Γ_{ℓ, j_{ℓ}}}} \cdot$ $\begin{equation} \xi_{\ell\comma j_\ell} = \frac{ \exp\left( -\frac{1}{2}\multspace \transpose{\vec r}_{\smash[t]{\ell\comma j_\ell}} \cdot \Gamma_{\smash[t]{\ell\comma j_\ell}}^{-1} \cdot \vec r_{\ell\comma j_\ell} \right) }{ 2\multspace \piup\multspace \!\sqrt{\det \Gamma_{\ell\comma j_\ell}} }\cdot \end{equation}$ (10)If j_ℓ = 0, M_ℓ is not associated with any source in K′. Since clustering is neglected, $P_{:o} (c_{ℓ} | 􏽜_{k = ℓ + 1}^{n} c_{k} \cap 􏽜_{k = 1}^{n^{'}} c_{k}^{'} \cap 􏽜_{k = 1}^{n} A_{k, j_{k}}) = P_{:o} (c_{ℓ} | A_{ℓ, 0}) = ξ_{ℓ, 0} d^{2} r_{ℓ},$ $\begin{equation} \Pato\left(c_\ell \Bigm| \bigcap_{k=\ell+1}^n c_k \cap \bigcap_{k=1}^\np c'_{\smash[t]{k}} \cap \bigcap_{k=1}^n A_{k\comma j_k}\right) = \Pato(c_\ell \mid A_{\ell\comma 0}) = \xi_{\ell\comma 0}\multspace \df^2\vec r_\ell, \label{jl_nul} \end{equation}$ (11)where the last equality defines the spatial probability density ξ_{ℓ, 0}; for the uninformative prior of a uniform a priori probability distribution of K-sources without counterpart, ξ_{ℓ, 0} = 1 /S. From Eqs. 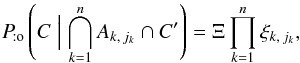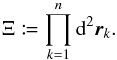(8), (9), and (11), it follows that $P_{:o} (C | 􏽜_{k = 1}^{n} A_{k, j_{k}} \cap C^{'}) = Ξ 􏽙_{k = 1}^{n} ξ_{k, j_{k}},$ $\begin{equation} \label{prod_xi} \Pato\left(C \Bigm| \bigcap_{k=1}^n A_{k\comma j_k} \cap C' \right) = \Xi \multspace \prod_{k=1}^n \xi_{k\comma j_k}, \end{equation}$ (12)where $Ξ := 􏽙_{k = 1}^{n} d^{2} r_{k} .$ $\begin{equation} \label{lambda} \Xi \coloneqq \prod_{k=1}^n \df^2\vec r_k. \end{equation}$ (13)

We now compute the second factor in the product of Eq. (6). Knowing the coordinates of K′-sources alone, without those of any in K, does not change the likelihood of the associations (A_{k,j_k}); in other words, C′ and ${^{􏽔}}_{k = 1}^{n} A_{k, j_{k}}$ $\hbox{$\bigcap_{\smash[t]{k=1}}^n A_{k\comma j_k}$}$ are mutually unconditionally independent (but conditionally dependent on C). 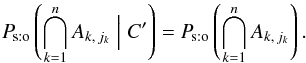Therefore, $P_{s:o} (􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}) = P_{s:o} (􏽜_{k = 1}^{n} A_{k, j_{k}}) .$ $\begin{equation} \Psto\left(\bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C'\right) = \Psto\left(\bigcap_{k=1}^n A_{k\comma j_k}\right). \end{equation}$ (14)Let q := # { k ∈ [[1,n]] | j_k ≠ 0 }, where #E denotes the number of elements of any set E. Since the events (A_{k,j_k})_{k ∈ [[1,n]]} are independent by assumption (H_s:o), 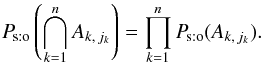$P_{s:o} (􏽜_{k = 1}^{n} A_{k, j_{k}}) = 􏽙_{k = 1}^{n} P_{s:o} (A_{k, j_{k}}) .$ $\begin{equation} \Psto\left(\bigcap_{k=1}^n A_{k\comma j_k}\right) = \prod_{k=1}^n \Psto(A_{k\comma j_k}). \end{equation}$ (15)Using definition (2), and on the hypothesis that all associations 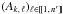$(A_{k, ℓ})_{ℓ \in [[1, n^{'}]]}$ $\hbox{$(A_{k\comma\ell})_{\ell\in\integinterv{1}{\np}}$}$ are a priori equally likely if k ≠ 0 (Sect. 2.2), we get 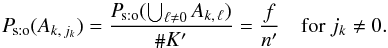$P_{s:o} (A_{k, j_{k}}) = \frac{P_{s:o} (^{􏽓} ℓ \neq 0 A_{k, ℓ})}{# K^{'}} = \frac{f}{n^{'}} for j_{k} \neq 0.$ $\begin{equation} \Psto(A_{k\comma j_k}) = \frac{\Psto(\bigcup_{\ell\neq0} A_{k\comma\ell})}{\card K'} = \frac{f}\np \quad\text{for } j_k \neq 0. \end{equation}$ (16)Since P_s:o(A_{k, 0}) = 1 − f, we have 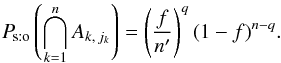$P_{s:o} (􏽜_{k = 1}^{n} A_{k, j_{k}}) = (\frac{f}{n^{'}})^{q} (1 - f)^{n - q} .$ $\begin{equation} \label{P_sto(A)} \Psto\left(\bigcap_{k=1}^n A_{k\comma j_k}\right) = \Biggl(\frac{f}\np\Biggr)^q\multspace (1-f)^{n-q}. \end{equation}$ (17)Hence, from Eqs. (6), (12)and (17), 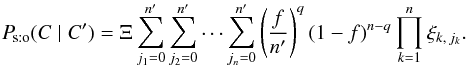$P_{s:o} (C | C^{'}) = Ξ \sum_{j_{1} = 0}^{n^{'}} \sum_{j_{2} = 0}^{n^{'}} \cdot \cdot \cdot \sum_{j_{n} = 0}^{n^{'}} (\frac{f}{n^{'}})^{q} (1 - f)^{n - q} 􏽙_{k = 1}^{n} ξ_{k, j_{k}} .$ $\begin{equation} \Psto(C \mid C') = \Xi\multspace \sum_{j_1=0}^\np \sum_{j_2=0}^\np \cdots \sum_{j_n=0}^\np {\Biggl(\frac{f}\np\Biggr)^q \multspace (1-f)^{n-q} \multspace \prod_{k=1}^n \xi_{k\comma j_k}}. \label{P_sto(C|C)_xi} \end{equation}$ (18)By the definition of q, there are q strictly positive indices j_k (as many as the factors “ 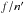$f / n^{'}$ $\hbox{$f/\np$}$ ” in Eq. (18)) and n − q null ones (as many as the factors “(1 − f)”). Therefore, with 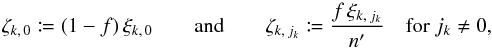$ζ_{k, 0} := (1 - f) ξ_{k, 0} and ζ_{k, j_{k}} := \frac{f ξ_{k, j_{k}}}{n^{'}} for j_{k} \neq 0,$ $\begin{equation} \label{def_zeta} \zeta_{k\comma 0} \coloneqq (1-f)\multspace \xi_{k\comma 0} \qquad\text{and}\qquad \zeta_{k\comma j_k} \coloneqq \frac{f\multspace \xi_{k\comma j_k}}{\np} \quad\text{for }j_k \neq 0, \end{equation}$ (19)Eq. (18)reduces to 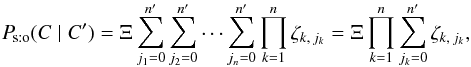$P_{s:o} (C | C^{'}) = Ξ \sum_{j_{1} = 0}^{n^{'}} \sum_{j_{2} = 0}^{n^{'}} \cdot \cdot \cdot \sum_{j_{n} = 0}^{n^{'}} 􏽙_{k = 1}^{n} ζ_{k, j_{k}} = Ξ 􏽙_{k = 1}^{n} \sum_{j_{k} = 0}^{n^{'}} ζ_{k, j_{k}},$ $\begin{equation} \Psto(C \mid C') = \Xi\multspace \sum_{j_1=0}^\np\sum_{j_2=0}^\np \cdots \sum_{j_n=0}^\np\prod_{k=1}^n\zeta_{k\comma j_k} = \Xi\multspace \prod_{k=1}^n\sum_{j_k=0}^\np\zeta_{k\comma j_k}, \label{P_sto(C|C)_res} \end{equation}$ (20)where the last equality is derived by induction from the distributivity of multiplication over addition.

3.1.2. Computation of P_s:o(A_i, j∩ C | C′)

The computation of the numerator of Eq. (4)is similar to that of P_s:o(C | C′): 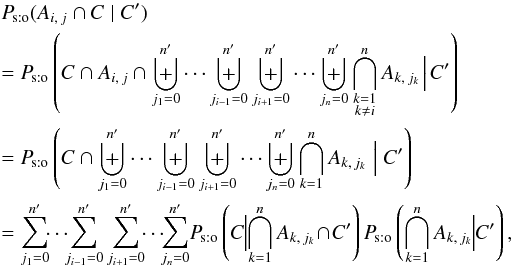$\begin{matrix} P_{s:o} (A_{i, j} \cap C | C^{'}) \\ = P_{s:o} (C \cap A_{i, j} \cap 􏽝_{j_{1} = 0}^{n^{'}} \cdot \cdot \cdot 􏽝_{j_{i - 1} = 0}^{n^{'}} 􏽝_{j_{i + 1} = 0}^{n^{'}} \cdot \cdot \cdot 􏽝_{j_{n} = 0}^{n^{'}} 􏽜_{\begin{matrix} k = 1 \\ k \neq i \end{matrix}}^{n} A_{k, j_{k}} | C^{'}) \\ = P_{s:o} (C \cap 􏽝_{j_{1} = 0}^{n^{'}} \cdot \cdot \cdot 􏽝_{j_{i - 1} = 0}^{n^{'}} 􏽝_{j_{i + 1} = 0}^{n^{'}} \cdot \cdot \cdot 􏽝_{j_{n} = 0}^{n^{'}} 􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}) \\ = \sum_{j_{1} = 0}^{n^{'}} \cdot \cdot \cdot \sum_{j_{i - 1} = 0}^{n^{'}} \sum_{j_{i + 1} = 0}^{n^{'}} \cdot \cdot \cdot \sum_{j_{n} = 0}^{n^{'}} P_{s:o} (C | 􏽜_{k = 1}^{n} A_{k, j_{k}} \cap C^{'}) P_{s:o} (􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}), \end{matrix}$ $\begin{eqnarray} \label{P_sto(Aij,C|C)_gen} &&\Psto(A_{i\comma j} \cap C \mid C') \nonumber\\&&= \Psto\left(C \cap A_{i\comma j} \cap \biguplus_{j_1=0}^\np \cdots \biguplus_{j_{i-1}=0}^\np \biguplus_{j_{i+1}=0}^\np \cdots \biguplus_{j_n=0}^\np \bigcap_{\substack{k=1\\ k\neq i}}^n A_{k\comma j_k}\! \Bigm|\! C' \right) \nonumber\\&&= \Psto\left(C \cap \biguplus_{j_1=0}^\np \cdots \biguplus_{j_{i-1}=0}^\np \biguplus_{j_{i+1}=0}^\np \cdots \biguplus_{j_n=0}^\np \bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C' \right) \nonumber \\&&= \sum_{j_1=0}^\np\!\! \cdots\!\! \sum_{j_{i-1}=0}^\np \sum_{j_{i+1}=0}^\np \!\!\cdots\!\! \sum_{j_n=0}^\np\! \Psto\left(C \!\!\Bigm|\!\! \bigcap_{k=1}^n A_{k\comma j_k} \! \cap\! C' \right) \multspace \Psto\left(\bigcap_{k=1}^n A_{k\comma j_k} \!\!\Bigm|\!\! C' \right),\!\! \end{eqnarray}$ (21)where we put j_i := j.

Let q^⋆ := # { k ∈ [[1,n]] | j_k ≠ 0 } (indices j_k are now those of Eq. (21)). As for P_s:o(C | C′), 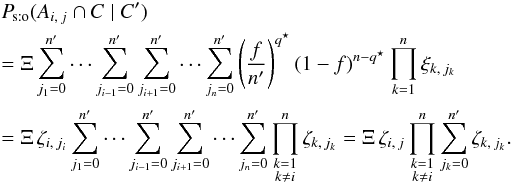$\begin{matrix} P_{s:o} (A_{i, j} \cap C | C^{'}) \\ = Ξ \sum_{j_{1} = 0}^{n^{'}} \cdot \cdot \cdot \sum_{j_{i - 1} = 0}^{n^{'}} \sum_{j_{i + 1} = 0}^{n^{'}} \cdot \cdot \cdot \sum_{j_{n} = 0}^{n^{'}} (\frac{f}{n^{'}})^{q^{⋆}} (1 - f)^{n - q^{⋆}} 􏽙_{k = 1}^{n} ξ_{k, j_{k}} \end{matrix}$ $\begin{eqnarray} && \Psto(A_{i\comma j} \cap C \mid C') \nonumber \\&&= \Xi\multspace \sum_{j_1=0}^\np \cdots \sum_{j_{i-1}=0}^\np \sum_{j_{i+1}=0}^\np \cdots \sum_{j_n=0}^\np {\Biggl(\frac{f}\np\Biggr)^{q^\star}\multspace (1-f)^{n-q^\star} \prod_{k=1}^n \xi_{k\comma j_k}} \nonumber\\&&= \Xi\multspace \zeta_{i\comma j_i}\multspace \sum_{j_1=0}^\np\cdots \sum_{j_{i-1}=0}^\np\sum_{j_{i+1}=0}^\np\cdots \sum_{j_n=0}^\np\prod_{\substack{k=1\\ k\neq i}}^n \zeta_{k\comma j_k} = \Xi\multspace \zeta_{i\comma j}\multspace \prod_{\substack{k=1\\ k\neq i}}^n \sum_{j_k=0}^\np\zeta_{k\comma j_k}. \label{P_sto(Aij,C|C)_res} \end{eqnarray}$ (22)

3.1.3. Final results

Finally, from Eqs. (4), (20), and (22), fori ≠ 0, 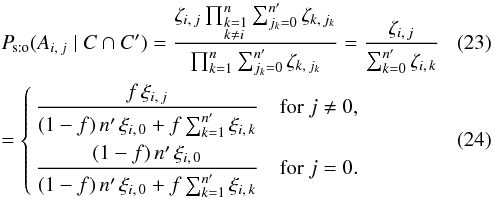$\begin{matrix} P_{s:o} (A_{i, j} | C \cap C^{'}) = \frac{ζ_{i, j}^{􏽑} \begin{matrix} n \\ k = 1 k \neq i \end{matrix} \sum_{j_{k} = 0}^{n^{'}} ζ_{k, j_{k}}}{􏽑_{k = 1}^{n} \sum_{j_{k} = 0}^{n^{'}} ζ_{k, j_{k}}} = \frac{ζ_{i, j}}{\sum_{k = 0}^{n^{'}} ζ_{i, k}} \\ = {\begin{matrix} \begin{matrix} \end{matrix} \frac{f ξ_{i, j}}{(1 - f) n^{'} ξ_{i, 0} + f \sum_{k = 1}^{n^{'}} ξ_{i, k}} for j \neq 0, \begin{matrix} \end{matrix} \\ \begin{matrix} \end{matrix} \frac{(1 - f) n^{'} ξ_{i, 0}}{(1 - f) n^{'} ξ_{i, 0} + f \sum_{k = 1}^{n^{'}} ξ_{i, k}} for j = 0. \end{matrix} \end{matrix}$ $\begin{eqnarray} \label{P_sto(Aij|C,C)_res1} && \Psto(A_{i\comma j} \mid C \cap C') = \frac{ \zeta_{i\comma j}\multspace \prod_{\leftsubstack{k=1\\ k\neq i}}^n \sum_{j_k=0}^\np\zeta_{k\comma j_k} }{ \prod_{k=1}^n\sum_{j_k=0}^\np\zeta_{k\comma j_k} } = \frac{\zeta_{i\comma j}}{\sum_{k=0}^\np\zeta_{i\comma k}} \\ \label{P_sto(Aij|C,C)_res2} &&= \Left\{ \begin{aligned} \frac{f\multspace \xi_{i\comma j}}{ (1-f)\multspace \np\multspace \xi_{i\comma 0} + f\multspace \sum_{k=1}^\np\xi_{i\comma k}} & \quad \text{for } j \neq 0, \\ \frac{(1-f)\multspace \np\multspace \xi_{i\comma 0}}{ (1-f)\multspace \np\multspace \xi_{i\comma 0} + f\multspace \sum_{k=1}^\np\xi_{i\comma k}} & \quad \text{for } j = 0. \end{aligned} \Right. \end{eqnarray}$

As to the probability P_s:o(A_0,j | C ∩ C′) that $M_{j}^{'}$ $\hbox{$\Mp_j$}$ has no counterpart in K, it can be computed in this way: $\begin{matrix} P_{s:o} (A_{0, j} \cap C | C^{'}) = P_{s:o} (C \cap A_{0, j} \cap 􏽝_{j_{1} = 0}^{n^{'}} 􏽝_{j_{2} = 0}^{n^{'}} \cdot \cdot \cdot 􏽝_{j_{n} = 0}^{n^{'}} 􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}) \\ = P_{s:o} (C \cap \begin{matrix} n^{'} \\ 􏽝 \\ j_{1} = 0 j_{1} \neq j \end{matrix} \begin{matrix} n^{'} \\ 􏽝 \\ j_{2} = 0 j_{2} \neq j \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ 􏽝 \\ j_{n} = 0 j_{n} \neq j \end{matrix} 􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}) \\ = \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \neq j \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{2} = 0 j_{2} \neq j \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \neq j \end{matrix} P_{s:o} (C \cap 􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}) \\ = Ξ \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \neq j \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{2} = 0 j_{2} \neq j \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \neq j \end{matrix} 􏽙_{k = 1}^{n} ζ_{k, j_{k}} = Ξ 􏽙_{k = 1}^{n} \begin{matrix} n^{'} \\ \sum \\ j_{k} = 0 j_{k} \neq j \end{matrix} ζ_{k, j_{k}} \end{matrix}$ $\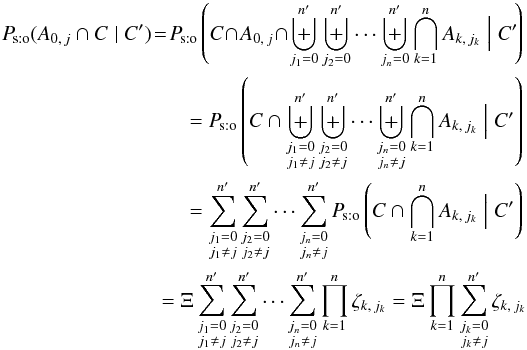begin{eqnarray} \Psto(A_{0\comma j} \cap C \mid C') \! =\! \Psto\left(C\! \cap\! A_{0\comma j} \!\cap\! \biguplus_{j_1=0}^\np \biguplus_{j_2=0}^\np \cdots \biguplus_{j_n=0}^\np \bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C'\!\right) \nonumber \\= \Psto\left(C \cap \biguplus_{\substack{j_1=0\\ j_1\neq j}}^\np \biguplus_{\substack{j_2=0\\ j_2\neq j}}^\np \cdots \biguplus_{\substack{j_n=0\\ j_n\neq j}}^\np \bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C'\right) \nonumber\\= \sum_{\substack{j_1=0\\ j_1\neq j}}^\np \sum_{\substack{j_2=0\\ j_2\neq j}}^\np \cdots \sum_{\substack{j_n=0\\ j_n\neq j}}^\np \Psto\left(C \cap \bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C'\right) \nonumber\\= \Xi\multspace \sum_{\substack{j_1=0\\ j_1\neq j}}^\np \sum_{\substack{j_2=0\\ j_2\neq j}}^\np \cdots \sum_{\substack{j_n=0\\ j_n\neq j}}^\np \prod_{k=1}^n\zeta_{k\comma j_k} = \Xi\multspace \prod_{k=1}^n\sum_{\substack{j_k=0\\ j_k\neq j}}^\np\zeta_{k\comma j_k} \end{eqnarray}$ (25)and, using Eqs. (20), (23), and (3), $\begin{matrix} P_{s:o} (A_{0, j} | C \cap C^{'}) = \frac{P_{s:o} (A_{0, j} \cap C | C^{'})}{P_{s:o} (C | C^{'})} = \frac{Ξ 􏽑_{k = 1}^{n} \sum \begin{matrix} n^{'} \\ j_{k} = 0 j_{k} \neq j \end{matrix} ζ_{k, j_{k}}}{Ξ 􏽑_{k = 1}^{n} \sum_{j_{k} = 0}^{n^{'}} ζ_{k, j_{k}}} \\ = 􏽙_{k = 1}^{n} \frac{\sum_{j_{k} = 0}^{n^{'}} ζ_{k, j_{k}} - ζ_{k, j}}{\sum_{j_{k} = 0}^{n^{'}} ζ_{k, j_{k}}} = 􏽙_{k = 1}^{n} (1 - \frac{ζ_{k, j_{k}}}{\sum_{j_{k} = 0}^{n^{'}} ζ_{k, j_{k}}}) \\ = 􏽙_{k = 1}^{n} (1 - P_{s:o} [A_{k, j} | C \cap C^{'}]^{)} for j \neq 0. \end{matrix}$ $\begin{eqnarray} \Psto(A_{0\comma j} \mid C \cap C') = \frac{ \Psto(A_{0\comma j} \cap C \mid C') }{ \Psto(C \mid C') } = \frac{\Xi\multspace \prod_{k=1}^n\sum_{\leftsubstack{j_k=0\\ j_k\neq j}}^\np \zeta_{k\comma j_k}}{\Xi\multspace \prod_{k=1}^n\sum_{j_k=0}^\np\zeta_{k\comma j_k}} \nonumber\\ = \prod_{k=1}^n\frac{\sum_{j_k=0}^\np\zeta_{k\comma j_k} - \zeta_{k\comma j}}{ \sum_{j_k=0}^\np\zeta_{k\comma j_k}} = \prod_{k=1}^n{\Biggl( 1-\frac{\zeta_{k\comma j_k}}{\sum_{j_k=0}^\np\zeta_{k\comma j_k}} \Biggr)} \nonumber\\= \prod_{k=1}^n{\left(1 - \Psto[A_{k\comma j} \mid C \cap C']\right)} \quad \text{for } j \neq 0. \label{P_sto(A0j|C,C)}\!\! \end{eqnarray}$ (26)

3.2. Likelihood and estimation of unknown parameters

3.2.1. General results

Various methods have been proposed for estimating the fraction of sources with a counterpart (Kim et al. 2012; Fleuren et al. 2012; McAlpine et al. 2012; Haakonsen & Rutledge 2009). Pineau et al. (2011), for instance, fit f to the overall distribution of the likelihood ratios. We propose a more convenient and systematic method in this section.

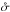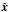Besides f, the probabilities P(A_i,j | C ∩ C′) may depend on other unknowns, such as the parameters $\begin{matrix} ˚ \\ σ \end{matrix}$ $\hbox{$\sigmatot$}$ and $\begin{matrix} ˚ \\ ν \end{matrix}$ $\hbox{$\nutot$}$ modeling the positional uncertainties (cf. Appendices A.2.2 and A.2.3). We write here x₁, x₂, etc., for all these parameters, and put x := (x₁,x₂,...). An estimate $\hat{x}$ $\hbox{$\hat{\vec x}$}$ of x may be obtained by maximizing with respect to x (and with the constraint $\hbox{$\hat f \in[0, 1]$}$ ) the overall likelihood $L := \frac{P (C \cap C^{'})}{(􏽑_{i = 1}^{n} d^{2} r_{i}) 􏽑_{j = 1}^{n^{'}} d^{2} r_{j}^{'}}$ $\begin{equation} \label{def_Lh} \Lh \coloneqq \frac{\Prob(C \cap C')}{ (\prod_{i=1}^n \df^2\vec r_i)\multspace \prod_{j=1}^\np\df^2\vec r'_{\smash[t]{j}}} \end{equation}$ (27)to observe all the K- and K′-sources at their effective positions. 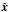Unless the result is outside the possible domain for x (i.e., if L reaches its maximum on the boundary of this domain), the maximum likelihood estimator $\hat{x}$ $\hbox{$\hat{\vec x}$}$ is a solution to 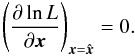$(\frac{\partial \ln L}{\partial x})_{x = \hat{x}} = 0.$ $\begin{equation} \label{max_Lh} \Biggl(\frac{\partial\ln\Lh}{\partial\vec x}\Biggr)_{\vec x=\hat{\vec x}} = 0. \end{equation}$ (28)From now on, all quantities calculated at 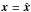$x = \hat{x}$ $\hbox{$\vec x = \hat{\vec x}$}$ bear a circumflex.

We have 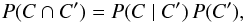$P (C \cap C^{'}) = P (C | C^{'}) P (C^{'}),$ $\begin{equation} \label{P(C,C)} \Prob(C \cap C') = \Prob(C \mid C')\multspace \Prob(C'), \end{equation}$ (29)and, since clustering is neglected, $P (C^{'}) = 􏽙_{j = 1}^{n^{'}} P (c_{j}^{'}) = 􏽙_{j = 1}^{n^{'}} ξ_{0, j} d^{2} r_{j}^{'},$ $\begin{equation} \label{P(C)} \Prob(C') = \prod_{j=1}^\np \Prob(\coordpj) = \prod_{j=1}^\np \xi_{0\comma j}\multspace \df^2\vec r'_{\smash[t]{j}}, \end{equation}$ (30)where ξ_0,j is the spatial probability density defined by $P (c_{j}^{'}) = ξ_{0, j} d^{2} r_{j}^{'}$ $\hbox{$\Prob(\coordpj) = \xi_{0\comma j}\multspace \df^2\vec r'_{\smash[t]{j}}$}$ ; for the uninformative prior of a uniform a priori probability distribution of K′-sources, ξ_0,j = 1 /S. From Eqs. 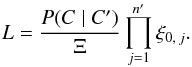(27), (29), (30), and (13), we obtain $L = \frac{P (C | C^{'})}{Ξ} 􏽙_{j = 1}^{n^{'}} ξ_{0, j} .$ $\begin{equation} \label{Lh_gen} \Lh = \frac{\Prob(C \mid C')}{\Xi}\multspace \prod_{j=1}^\np \xi_{0\comma j}. \end{equation}$ (31)

In particular, under assumption (H_s:o), Eqs. (31), (20), and (13)give 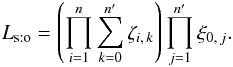$L_{s:o} = (􏽙_{i = 1}^{n} \sum_{k = 0}^{n^{'}} ζ_{i, k}) 􏽙_{j = 1}^{n^{'}} ξ_{0, j} .$ $\begin{equation} \label{Lh_sto} \Lhsto = \left(\prod_{i=1}^n\sum_{k=0}^\np\zeta_{i\comma k}\right)\multspace \prod_{j=1}^\np \xi_{0\comma j}. \end{equation}$ (32)Therefore, for any parameter x_p and because the ξ_0,j are independent of x, 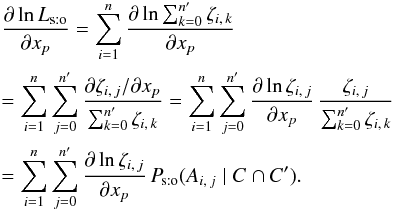$\begin{matrix} \frac{\partial \ln L_{s:o}}{\partial x_{p}} = \sum_{i = 1}^{n} \frac{\partial \ln \sum_{k = 0}^{n^{'}} ζ_{i, k}}{\partial x_{p}} \\ = \sum_{i = 1}^{n} \sum_{j = 0}^{n^{'}} \frac{\partial ζ_{i, j} / \partial x_{p}}{\sum_{k = 0}^{n^{'}} ζ_{i, k}} = \sum_{i = 1}^{n} \sum_{j = 0}^{n^{'}} \frac{\partial \ln ζ_{i, j}}{\partial x_{p}} \frac{ζ_{i, j}}{\sum_{k = 0}^{n^{'}} ζ_{i, k}} \end{matrix}$ $\begin{eqnarray} && \frac{\partial\ln\Lhsto}{\partial x_p} = \sum_{i=1}^n\frac{\partial\ln\sum_{k=0}^\np\zeta_{i\comma k}}{\partial x_p} \nonumber \\&&= \sum_{i=1}^n\sum_{j=0}^\np\frac{\partial\zeta_{i\comma j}/\partial x_p}{ \sum_{k=0}^\np\zeta_{i\comma k}} = \sum_{i=1}^n\sum_{j=0}^\np\frac{\partial\ln\zeta_{i\comma j}}{\partial x_p} \multspace \frac{\zeta_{i\comma j}}{\sum_{k=0}^\np\zeta_{i\comma k}} \nonumber \\&&= \sum_{i=1}^n\sum_{j=0}^\np\frac{\partial\ln\zeta_{i\comma j}}{\partial x_p} \multspace \Psto(A_{i\comma j} \mid C \cap C'). \label{der(Lh_sto)/x} \end{eqnarray}$ (33)(For reasons highlighted just after Eq. (73), it is convenient to express most results as a function of the probabilities P(A_i,j | C ∩ C′).)

Uncertainties on the unknown parameters may be computed from the covariance matrix V of 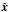$\hat{x}$ $\hbox{$\hat{\vec x}$}$ . For large numbers of sources, V is asymptotically given (Kendall & Stuart 1979) by 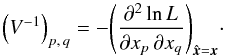${(V^{-1})}_{p, q} = - {(\frac{\partial^{2} \ln L}{\partial x_{p} \partial x_{q}})}_{\hat{x} = x} \cdot$ $\begin{equation} \label{cov_x} \left(V^{-1}\right)_{p\comma q} = -\Left( \frac{\partial^2\ln\Lh}{\partial x_p\multspace \partial x_q} \Right)_{\hat{\vec x} = \vec x}\cdot \end{equation}$ (34)

3.2.2. Fraction of sources with a counterpart

Consider, in particular, the case x_p = f. We note that 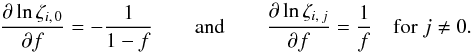$\frac{\partial \ln ζ_{i, 0}}{∂f} = - \frac{1}{1 - f} and \frac{\partial \ln ζ_{i, j}}{∂f} = \frac{1}{f} for j \neq 0.$ $\begin{equation} \label{der(zeta)} \frac{\partial\ln\zeta_{i\comma 0}}{\partial f} = -\frac{1}{1-f} \qquad\text{and}\qquad \frac{\partial\ln\zeta_{i\comma j}}{\partial f} = \frac{1}{f} \quad\text{for } j \neq 0. \end{equation}$ (35)Under the assumption (H_s:o) or (H_o:o) (but not under (H_o:s)), 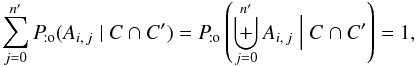$\sum_{j = 0}^{n^{'}} P_{:o} (A_{i, j} | C \cap C^{'}) = P_{:o} (􏽝_{j = 0}^{n^{'}} A_{i, j} | C \cap C^{'}) = 1,$ $\begin{equation} \label{somme_prob} \sum_{j=0}^\np \Pato(A_{i\comma j} \mid C \cap C') = \Pato\left(\biguplus_{j=0}^\np A_{i\comma j} \Bigm| C \cap C'\right) = 1, \end{equation}$ (36)so, using Eq. (35), 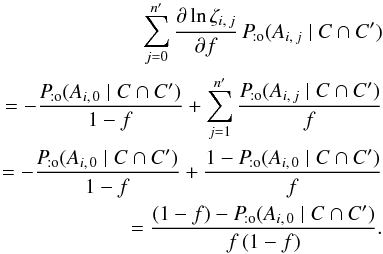$\begin{matrix} \sum_{j = 0}^{n^{'}} \frac{\partial \ln ζ_{i, j}}{∂f} P_{:o} (A_{i, j} | C \cap C^{'}) \\ = - \frac{P_{:o} (A_{i, 0} | C \cap C^{'})}{1 - f} + \sum_{j = 1}^{n^{'}} \frac{P_{:o} (A_{i, j} | C \cap C^{'})}{f} \\ = - \frac{P_{:o} (A_{i, 0} | C \cap C^{'})}{1 - f} + \frac{1 - P_{:o} (A_{i, 0} | C \cap C^{'})}{f} \\ = \frac{(1 - f) - P_{:o} (A_{i, 0} | C \cap C^{'})}{f (1 - f)} . \end{matrix}$ $\begin{eqnarray} \sum_{j=0}^\np\frac{\partial\ln\zeta_{i\comma j}}{\partial f}\multspace \Pato(A_{i\comma j} \mid C \cap C') \nonumber \\= -\frac{\Pato(A_{i\comma 0} \mid C \cap C')}{1-f} + \sum_{j=1}^\np \frac{\Pato(A_{i\comma j} \mid C \cap C')}{f} \nonumber\\= -\frac{\Pato(A_{i\comma 0} \mid C \cap C')}{1-f} + \frac{1-\Pato(A_{i\comma 0} \mid C \cap C')}{f} \nonumber \\= \frac{(1-f) - \Pato(A_{i\comma 0} \mid C \cap C') }{ f\multspace (1-f)}. \label{somme_j} \end{eqnarray}$ (37)Summing Eq. (37)on i, we obtain from Eq. (33)that 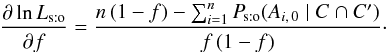$\frac{\partial \ln L_{s:o}}{∂f} = \frac{n (1 - f) - \sum_{i = 1}^{n} P_{s:o} (A_{i, 0} | C \cap C^{'})}{f (1 - f)} \cdot$ $\begin{equation} \label{der(Lh_sto)/f} \frac{\partial\ln\Lhsto}{\partial f} = \frac{ n\multspace (1-f) - \sum_{i=1}^n\Psto(A_{i\comma 0} \mid C \cap C') }{ f\multspace (1-f) }\cdot \end{equation}$ (38)Consequently, the maximum likelihood estimator of the fraction f of K-sources with a counterpart in K′ is 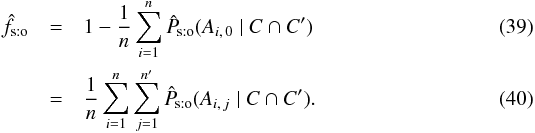$\begin{matrix} f̂ s:o & = \\ = \end{matrix}$ $\begin{eqnarray} \hat f_\sto &=& 1 - \frac{1}{n}\multspace \sum_{i=1}^n\expandafter\hat\Psto(A_{i\comma 0} \mid C \cap C') \label{f_est_sto1} \\ &=& \frac{1}{n}\multspace \sum_{i=1}^n\sum_{j=1}^\np\expandafter\hat\Psto(A_{i\comma j} \mid C \cap C'). \label{f_est_sto2} \end{eqnarray}$ After some tedious calculations, it can be shown that $\frac{\partial^{2} \ln L_{s:o}}{\partial f^{2}} = - \frac{\sum_{i = 1}^{n} {([1 - f] - P_{s:o} [A_{i, 0} | C \cap C^{'}])}^{2}}{f^{2} (1 - f)^{2}} < 0$ $\begin{equation} \label{concave} \frac{\partial^2\ln\Lhsto}{\partial f^2} = -\frac{ \sum_{i=1}^n{\left([1-f] - \Psto[A_{i\comma 0} \mid C \cap C']\right)^2} }{ f^2\multspace (1-f)^2 } < 0 \end{equation}$ (41)for all f, so ∂lnL_s:o/∂f has at most one zero in [0,1]: $\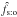hbox{$\hat f_\sto$}$ is unique.

Since 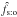$\hbox{$\hat f_\sto$}$ appears on the two sides of Eq. (39)(remember that 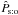$\hbox{$\expandafter\hat\Psto$}$ is the value of P_s:o at 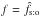$\hbox{$f = \hat f_\sto$}$ ), we may try to determine it through an iterative back and forth computation between the lefthand and the righthand sides of this equation. (A similar idea was also proposed by Benn 1983.) We prove in Sect. 5.3 that this procedure converges for any starting value f ∈] 0,1 [.

An estimate 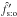$f̂ \begin{matrix} ' \\ s:o \end{matrix}$ $\hbox{$\hat f'_\sto$}$ of the fraction f′ of K′-sources with a counterpart is given by 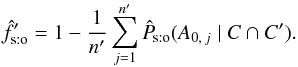$f̂ \begin{matrix} ' \\ s:o \end{matrix} = 1 - \frac{1}{n^{'}} \sum_{j = 1}^{n^{'}} P̂ s:o (A_{0, j} | C \cap C^{'}) .$ $\begin{equation} \hat f'_\sto = 1 - \frac{1}{\np}\multspace \sum_{j=1}^\np\expandafter\hat\Psto(A_{0\comma j} \mid C \cap C'). \label{f_est_sto} \end{equation}$ (42)It can be checked from Eqs. (40), (42), and (26)that, as expected if assumption (H_s:o) is valid (cf. Sect. 2.2), 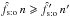$f̂_{s:o} n ⩾ f̂ \begin{matrix} ' \\ s:o \end{matrix} n^{'}$ $\hbox{$\hat f_\sto\multspace n \geqslant \hat f'_\sto\multspace \np$}$ . (Just notice that, for any numbers y_i ∈ [0,1], 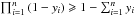${^{􏽑}}_{i = 1}^{n} (1 - y_{i}) ⩾ 1 - \sum_{i = 1}^{n} y_{i}$ $\hbox{$\prod_{i=1}^n {(1 - y_i)} \geqslant 1 - \sum_{i=1}^n y_i$}$ , which is obvious by induction; apply this to 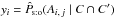$\hbox{$y_i = \expandafter\hat\Psto(A_{i\comma j} \mid C \cap C')$}$ and then sum on j.)

3.3. Probability of association: local computation

Under assumption (H_s:o), a purely local computation (subscript “loc” hereafter) of the probabilities of association is also possible. Consider a region U_i of area 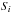$S i$ $\hbox{$\Si$}$ containing the position of M_i, and such that we can safely hypothesize that the counterpart in K′ of M_i, if any, is inside. We assume that the local surface density 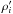$ρ_{i}^{'}$ $\hbox{$\rhopi$}$ of K′-sources unrelated to M_i is uniform on U_i. To avoid biasing the estimate if M_i has a counterpart, 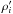$ρ_{i}^{'}$ $\hbox{$\rhopi$}$ may be evaluated from the number of K′-sources in a region surrounding U_i, but not overlapping it (an annulus around a disk U_i centered on M_i, for instance).

Besides the A_i,j, we consider the following events:

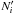$N_{i}^{'}$ $\hbox{$\Npi$}$ : U_i contains 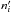$n_{i}^{'}$ $\hbox{$\npi$}$ sources;
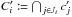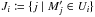$C_{i}^{'} := {^{􏽔}}_{j \in J_{i}} c_{j}^{'}$ $\hbox{$\COORDpi \coloneqq \bigcap_{j \in J_i} \coordpj$}$ , where $J_{i} := {j | M_{j}^{'} \in U_{i}}$ $\hbox{$J_i \coloneqq \{j \mid \Mp_j \in U_i\}$}$ .

We want to compute the probability that a source $M_{j}^{'}$ $\hbox{$\Mp_j$}$ in U_i is the counterpart of M_i, given the positions relative to M_i of all its possible counterparts $(M_{k}^{'})_{k \in J_{i}}$ $\hbox{$(\Mp_k)^{}_{\smash[t]{k\in J_i}}$}$ , i.e. $P_{loc} (A_{i, j} | C_{i}^{'} \cap N_{i}^{'})$ $\hbox{$\Ploc(A_{i\comma j} \mid \COORDpi\cap \Npi)$}$ . Using Eq. 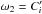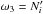(3)with ω₁ = A_i,j, $ω_{2} = C_{i}^{'}$ $\hbox{$\omega_2 = \COORDpi$}$ , and $ω_{3} = N_{i}^{'}$ $\hbox{$\omega_3 = \Npi$}$ in the first equality below, and then with 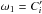$ω_{1} = C_{i}^{'}$ $\hbox{$\omega_1 = \COORDpi$}$ , ω₂ = A_i,k, and ω₃ unchanged in the last one, we obtain $\begin{matrix} P_{loc} (A_{i, j} | C_{i}^{'} \cap N_{i}^{'}) = \frac{P_{loc} (A_{i, j} \cap C_{i}^{'} | N_{i}^{'})}{P_{loc} (C_{i}^{'} | N_{i}^{'})} \\ = \frac{P_{loc} (C_{i}^{'} \cap A_{i, j} | N_{i}^{'})}{P_{loc} (C_{i}^{'} \cap 􏽕_{k \in J_{i} \cup {0}} A_{i, k} | N_{i}^{'})} = \frac{P_{loc} (C_{i}^{'} \cap A_{i, j} | N_{i}^{'})}{\sum_{k \in J_{i} \cup {0}} P_{loc} (C_{i}^{'} \cap A_{i, k} | N_{i}^{'})} \\ = \frac{P_{loc} (C_{i}^{'} | A_{i, j} \cap N_{i}^{'}) P_{loc} (A_{i, j} | N_{i}^{'})}{\sum_{k \in J_{i} \cup {0}} P_{loc} (C_{i}^{'} | A_{i, k} \cap N_{i}^{'}) P_{loc} (A_{i, k} | N_{i}^{'})} \cdot \end{matrix}$ $\begin{eqnarray} \Ploc(A_{i\comma j} \mid \COORDpi\cap \Npi) = \frac{\Ploc(A_{i\comma j} \cap \COORDpi \mid \Npi)}{ \Ploc(\COORDpi \mid \Npi)} \nonumber\\[1mm] = \frac{\Ploc(\COORDpi \cap A_{i\comma j} \mid \Npi)}{ \Ploc(\COORDpi \cap \biguplus_{k\in J_i\cup\{0\}} A_{i\comma k} \mid \Npi)} = \frac{\Ploc(\COORDpi \cap A_{i\comma j} \mid \Npi)}{ \sum_{k\in J_i\cup\{0\}} \Ploc(\COORDpi \cap A_{i\comma k} \mid \Npi)} \nonumber\\[1mm]= \frac{\Ploc(\COORDpi\mid A_{i\comma j} \cap \Npi)\multspace \Ploc(A_{i\comma j} \mid \Npi)}{ \sum_{k\in J_i\cup\{0\}} \Ploc(\COORDpi\mid A_{i\comma k} \cap \Npi) \multspace \Ploc(A_{i\comma k} \mid \Npi)}\cdot \label{P_loc(Aij|C,N)} \end{eqnarray}$ (43)Now, $\begin{matrix} P_{loc} (A_{i, 0} | N_{i}^{'}) = \frac{P_{loc} (N_{i}^{'} \cap A_{i, 0})}{P_{loc} (N_{i}^{'})} \\ = \frac{P_{loc} (N_{i}^{'} | A_{i, 0}) P_{loc} (A_{i, 0})}{P_{loc} (N_{i}^{'} | A_{i, 0}) P_{loc} (A_{i, 0}) + P_{loc} (N_{i}^{'} | A_{i, 0}) P_{loc} (A_{i, 0})} \end{matrix}$ $\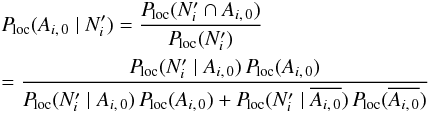begin{eqnarray} \label{P_loc(Ai0|N)} &&\Ploc(A_{i\comma 0} \mid \Npi) = \frac{\Ploc( \Npi \cap A_{i\comma 0})}{\Ploc(\Npi)} \nonumber\\&&= \frac{\Ploc(\Npi\mid A_{i\comma 0})\multspace \Ploc(A_{i\comma 0})}{ \Ploc(\Npi\mid A_{i\comma 0})\multspace \Ploc(A_{i\comma 0}) + \Ploc(\Npi\mid \overline{A_{i\comma 0}})\multspace \Ploc(\overline{A_{i\comma 0}})} \end{eqnarray}$ (44)and $P_{loc} (A_{i, j} | N_{i}^{'}) = \frac{P_{loc} (A_{i, 0} | N_{i}^{'})}{n_{i}^{'}} = \frac{1 - P_{loc} (A_{i, 0} | N_{i}^{'})}{n_{i}^{'}} for j \neq 0.$ $\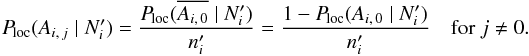begin{equation} \label{P_loc(Aij|N)} \Ploc(A_{i\comma j} \mid \Npi) = \frac{\Ploc(\overline{A_{i\comma 0}} \mid \Npi)}{\npi} = \frac{1-\Ploc(A_{i\comma 0} \mid \Npi)}{\npi} \quad \text{for } j \neq 0. \end{equation}$ (45)(The probability P_loc(A_i,j) itself could not have been computed as 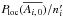$P_{loc} (A_{i, 0}) / n_{i}^{'}$ $\hbox{$\Ploc(\overline{A_{i\comma 0}})/\npi$}$ because 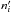$n_{i}^{'}$ $\hbox{$\npi$}$ would be undefined, which is why event 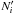$N_{i}^{'}$ $\hbox{$\Npi$}$ was introduced.) If clustering is negligible, the number of K′-sources randomly distributed with a mean surface density 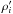$ρ_{i}^{'}$ $\hbox{$\rhopi$}$ in an area 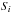$S i$ $\hbox{$\Si$}$ follows a Poissonian distribution, so 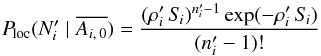$P_{loc} (N_{i}^{'} | A_{i, 0}) = \frac{(ρ_{i}^{'} S i)^{n_{i}^{'} - 1} \exp (- ρ_{i}^{'} S i)}{(n_{i}^{'} - 1)!}$ $\begin{equation} \label{P_loc(N|nonAi0)} \Ploc(\Npi \mid \overline{A_{i\comma 0}}) = \frac{(\rhopi\multspace \Si)^{\npi-1}\multspace \exp(-\rhopi\multspace \Si)}{ (\npi-1)!} \end{equation}$ (46)(one counterpart and 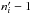$n_{i}^{'} - 1$ $\hbox{$\npi-1$}$ sources by chance in 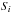$S i$ $\hbox{$\Si$}$ ) and $P_{loc} (N_{i}^{'} | A_{i, 0}) = \frac{(ρ_{i}^{'} S i)^{n_{i}^{'}} \exp (- ρ_{i}^{'} S i)}{n_{i}^{'}!}$ $\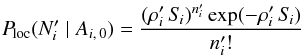begin{equation} \label{P_loc(N|Ai0)} \Ploc(\Npi\mid A_{i\comma 0}) = \frac{(\rhopi\multspace \Si)^{\npi}\multspace \exp(-\rhopi\multspace \Si)}{ \npi!} \end{equation}$ (47)(no counterpart and 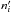$n_{i}^{'}$ $\hbox{$\npi$}$ sources by chance in 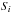$S i$ $\hbox{$\Si$}$ ). Thus, from Eqs. (45)–(47), and (2), 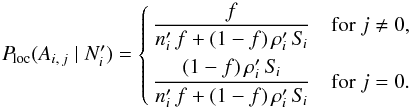$P_{loc} (A_{i, j} | N_{i}^{'}) = {\begin{matrix} \begin{matrix} \end{matrix} \frac{f}{n_{i}^{'} f + (1 - f) ρ_{i}^{'} S_{i}} for j \neq 0, \begin{matrix} \end{matrix} \\ \begin{matrix} \end{matrix} \frac{(1 - f) ρ_{i}^{'} S_{i}}{n_{i}^{'} f + (1 - f) ρ_{i}^{'} S_{i}} for j = 0. \end{matrix}$ $\begin{equation} \label{P_loc(Aij|N)_res} \Ploc(A_{i\comma j} \mid \Npi) = \Left\{ \begin{aligned} \frac{f}{\npi\multspace f+(1-f)\multspace \rhopi\multspace \Si} & \quad \text{for } j \neq 0, \\ \frac{(1-f)\multspace \rhopi\multspace \Si}{ \npi\multspace f+(1-f)\multspace \rhopi\multspace \Si} & \quad \text{for } j = 0. \end{aligned} \Right. \end{equation}$ (48)We have $\begin{matrix} P_{loc} (C_{i}^{'} | A_{i, 0} \cap N_{i}^{'}) = \underset{k \in J_{i}}{􏽙} \frac{d^{2} r_{k}^{'}}{S_{i}} and \\ P_{loc} (C_{i}^{'} | A_{i, j} \cap N_{i}^{'}) = ξ_{i, j} d^{2} r_{j}^{'} \underset{\begin{matrix} k \in J_{i} \\ k \neq j \end{matrix}}{􏽙} \frac{d^{2} r_{k}^{'}}{S_{i}} for j \neq 0 \end{matrix}$ $\begin{eqnarray} \label{P_loc(C|Aij,N)} \Ploc(\COORDpi\mid A_{i\comma 0}\cap \Npi) = \prod_{k\in J_i} \frac{\df^2\vec r'_{\smash[t]{k}}}{\Si} \qquad\text{and}\qquad\nonumber\\ \Ploc(\COORDpi\mid A_{i\comma j} \cap \Npi) = \xi_{i\comma j}\multspace \df^2\vrpj\multspace \prod_{\substack{k\in J_i\\ k\neq j}} \frac{\df^2\vec r'_{\smash[t]{k}}}{\Si} \quad\text{for } j \neq 0 \end{eqnarray}$ (49)(rigorously, ξ_i,j should be replaced by 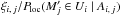$ξ_{i, j} / P_{loc} (M_{j}^{'} \in U_{i} | A_{i, j})$ $\hbox{$\xi_{i\comma j}/\Ploc(\Mp_j\in U_i\mid A_{i\comma j})$}$ , but $P_{loc} (M_{j}^{'} \notin U_{i} | A_{i, j})$ $\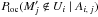hbox{$\Ploc(\Mp_j\not\in U_i \mid A_{i\comma j})$}$ is negligible by definition of U_i), so, using Eqs. (43), (48), and (49), we obtain 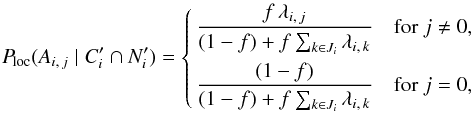$P_{loc} (A_{i, j} | C_{i}^{'} \cap N_{i}^{'}) = {\begin{matrix} \begin{matrix} \end{matrix} \frac{f λ_{i, j}}{(1 - f) + f \sum_{k \in J_{i}} λ_{i, k}} for j \neq 0, \begin{matrix} \end{matrix} \\ \begin{matrix} \end{matrix} \frac{(1 - f)}{(1 - f) + f \sum_{k \in J_{i}} λ_{i, k}} for j = 0, \end{matrix}$ $\begin{equation} \label{P_loc} \Ploc(A_{i\comma j}\mid \COORDpi\cap \Npi) = \Left\{ \begin{aligned} \frac{f\multspace \lambda_{i\comma j}}{ (1-f)+f\multspace \sum_{k\in J_i}\lambda_{i\comma k}} & \quad \text{for } j \neq 0, \\ \frac{(1-f)}{(1-f)+f\multspace \sum_{k\in J_i}\lambda_{i\comma k}} & \quad \text{for } j = 0, \end{aligned} \Right. \end{equation}$ (50)where 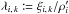$λ_{i, k} := ξ_{i, k} / ρ_{i}^{'}$ $\hbox{$\lambda_{i\comma k} \coloneqq \xi_{i\comma k}/\rhopi$}$ is the likelihood ratio (cf. Eq. (1)). Mutatis mutandis, we obtain the same result as Eq. (14) of Pineau et al. (2011) and the aforementioned authors. When the computation is extended from U_i to the whole surface covered by K′, 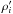$ρ_{i}^{'}$ $\hbox{$\rhopi$}$ is replaced by 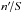$n^{'} / S$ $\hbox{$\np\!/\Stot$}$ in Eq. (50), ∑ _{k ∈ J_i} by 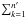$\sum_{k = 1}^{n^{'}}$ $\hbox{$\sum_{k=1}^\np$}$ , and we recover Eq. (24)since ξ_{i, 0} = 1 /S for a uniform distribution.

The index j_MLC(i) of the most likely counterpart 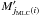$M_{j_{MLC} (i)}^{'}$ $\hbox{$\Mp_{\jMLC(i)}$}$ of M_i is the value of j ≠ 0 maximizing λ_i,j. Very often, λ_{i,j_MLC(i)} ≫ ∑ _{k ∈ J_i; k ≠ j_MLC(i)}λ_i,k, so 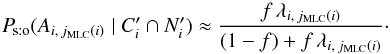$P_{s:o} (A_{i, j_{MLC} (i)} | C_{i}^{'} \cap N_{i}^{'}) \approx \frac{f λ_{i, j_{MLC} (i)}}{(1 - f) + f λ_{i, j_{MLC} (i)}} \cdot$ $\begin{equation} \Psto(A_{i\comma \jMLC(i)}\mid \COORDpi\cap \Npi) \approx \frac{f\multspace \lambda_{i\comma \jMLC(i)}}{ (1-f)+f\multspace \lambda_{i\comma \jMLC(i)}}\cdot \end{equation}$ (51)As a “poor man’s” recipe, if the value of f is unknown and not too close to either 0 or 1, an association may be considered as true if λ_{i,j_MLC(i)} ≫ 1 and as false if λ_{i,j_MLC(i)} ≪ 1. Where to set the boundary between true associations and false ones is somewhat arbitrary (Wolstencroft et al. 1986). For a large sample, however, f can be estimated from the distribution of the positions of all sources, as shown in Sect. 3.2.

4. One-to-one associations

Under (H_s:o) (Sect. 3), a given $M_{j}^{'}$ $\hbox{$\Mp_j$}$ can be associated with several M_i: there is no symmetry between K and K′ under this assumption and, while $\sum_{j = 0}^{n^{'}} P_{s:o} (A_{i, j} | C \cap C^{'}) = 1$ $\hbox{$\sum_{\smash[t]{j=0}}^{\smash[t]{\np}} \Psto(A_{i\comma j}\mid C \cap C') = 1$}$ for all M_i, $\sum_{i = 1}^{n} P_{s:o} (A_{i, j} | C \cap C^{'})$ $\hbox{$\sum_{\smash[t]{i=1}}^n \Psto(A_{i\comma j}\mid C \cap C')$}$ could be strictly larger than 1 for some sources $M_{j}^{'}$ $\hbox{$\Mp_j$}$ . We assume here that the much more constraining assumption (H_o:o) holds. As far as we know and despite some attempt by Rutledge et al. (2000), this problem has not been solved previously (see also Bartlett & Egret 1998 for a simple statement of the question).

Since a K′-potential counterpart $M_{j}^{'}$ $\hbox{$\Mp_j$}$ of M_i within some neighborhood U_i of M_i might in fact be the true counterpart of another source M_koutside of U_i, there is no obvious way to adapt the exact local several-to-one computation of Sect. 3.3 to the case of the one-to-one assumption. We therefore have to consider all the K- and K′-sources, as in Sect. 3.1.

Under assumption (H_o:o), catalogs K and K′ play symmetrical roles; in particular, 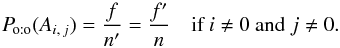$P_{o:o} (A_{i, j}) = \frac{f}{n^{'}} = \frac{f^{'}}{n} if i \neq 0 and j \neq 0.$ $\begin{equation} \label{f_f_oto} \Poto(A_{i\comma j}) = \frac{f}\np = \frac{f'}n \quad \text{if }i \neq 0\text{ and }j \neq 0. \end{equation}$ (52)For practical reasons (cf. Eq. (61)), we nonetheless name K the catalog with the fewer objects and K′ the other one, so 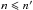$n ⩽ n^{'}$ $\hbox{$n \leqslant \np$}$ in the following.

4.1. Probability of association

4.1.1. Computation of P_o:o(C | C′)

The denominator of Eq. (4)is 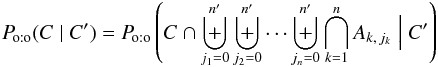$P_{o:o} (C | C^{'}) = P_{o:o} (C \cap 􏽝_{j_{1} = 0}^{n^{'}} 􏽝_{j_{2} = 0}^{n^{'}} \cdot \cdot \cdot 􏽝_{j_{n} = 0}^{n^{'}} 􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'})$ $\begin{equation} \Poto(C \mid C') = \Poto\left(C \cap \biguplus_{j_1=0}^\np\biguplus_{j_2=0}^\np\cdots\biguplus_{j_n=0}^\np \bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C' \right) \end{equation}$ (53)(same reasons as for Eq. (6)). Because A_k,m ∩ A_ℓ,m =? if k ≠ ℓ and m ≠ 0 by assumption (H_o:o), this reduces to 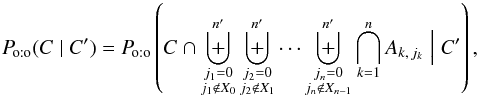$P_{o:o} (C | C^{'}) = P_{o:o} (C \cap \begin{matrix} n^{'} \\ 􏽝 \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \begin{matrix} n^{'} \\ 􏽝 \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ 􏽝 \\ j_{n} = 0 j_{n} \notin X_{n - 1} \end{matrix} 􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}),$ $\begin{equation} \label{P_oto(C|C)_union} \Poto(C \mid C') = \Poto\left(C \cap \biguplus_{\substack{j_1=0\\ j_1\not\in X_0}}^\np \biguplus_{\substack{j_2=0\\ j_2\not\in X_1}}^\np \cdots \biguplus_{\substack{j_n=0\\ j_n\not\in X_{n-1}}}^\np \bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C' \right), \end{equation}$ (54)where, to ensure that each K′-source is associated with at most one of K, the sets X_k of excluded counterparts are defined iteratively by 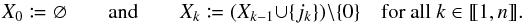$X_{0} := ? and X_{k} := (X_{k - 1} \cup {j_{k}}) \ {0} forall k \in [[1, n]] .$ $\begin{equation} \label{def_J} X_0 \coloneqq \varnothing \qquad \text{and}\qquad X_k \coloneqq (X_{k-1} \cup \{j_k\}) \setminus \{0\} \quad\text{for all } k \in \integinterv{1}{n}. \end{equation}$ (55)As a result, 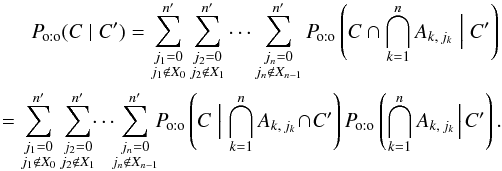$\begin{matrix} P_{o:o} (C | C^{'}) = \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \notin X_{n - 1} \end{matrix} P_{o:o} (C \cap 􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}) \\ = \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \notin X_{n - 1} \end{matrix} P_{o:o} (C | 􏽜_{k = 1}^{n} A_{k, j_{k}} \cap C^{'}) P_{o:o} (􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}) . \end{matrix}$ $\begin{eqnarray} \Poto(C \mid C') = \sum_{\substack{j_1=0\\ j_1\not\in X_0}}^\np \sum_{\substack{j_2=0\\ j_2\not\in X_1}}^\np \cdots \sum_{\substack{j_n=0\\ j_n\not\in X_{n-1}}}^\np \Poto\left(C \cap \bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C' \right) \nonumber \\= \sum_{\substack{j_1=0\\ j_1\not\in X_0}}^\np \sum_{\substack{j_2=0\\ j_2\not\in X_1}}^\np \!\! \cdots\!\! \sum_{\substack{j_n=0\\ j_n\not\in X_{n-1}}}^\np \!\! \Poto\left(C \Bigm| \bigcap_{k=1}^n A_{k\comma j_k}\! \cap\! C' \right) \multspace \Poto\left(\bigcap_{k=1}^n A_{k\comma j_k} \!\Bigm|\! C' \right). \label{P_oto(C|C)_gen} \end{eqnarray}$ (56)The first factor in the product of Eq. (56)is still given by Eq. (12), so we just have to compute the second factor, 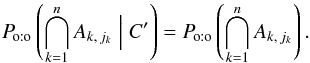$P_{o:o} (􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}) = P_{o:o} (􏽜_{k = 1}^{n} A_{k, j_{k}}) .$ $\begin{equation} \Poto\left(\bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C'\right) = \Poto\left(\bigcap_{k=1}^n A_{k\comma j_k}\right). \end{equation}$ (57)Let 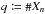$q := {}_{#}X_{n}$ $\hbox{$q \coloneqq \card X_n$}$ and Q be a random variable describing the number of associations between K and K′: $\begin{matrix} P_{o:o} (􏽜_{k = 1}^{n} A_{k, j_{k}}) = P_{o:o} (􏽜_{k = 1}^{n} A_{k, j_{k}} | Q = q) P_{o:o} (Q = q) \\ + P_{o:o} (􏽜_{k = 1}^{n} A_{k, j_{k}} | Q \neq q) P_{o:o} (Q \neq q) . 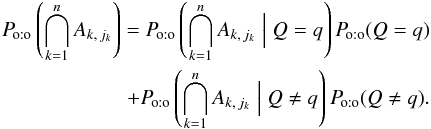\end{matrix}$ $\begin{eqnarray} \Poto\left(\bigcap_{k=1}^n A_{k\comma j_k}\right) = \Poto\left(\bigcap_{k=1}^n A_{k\comma j_k} \Bigm| Q = q\right) \multspace \Poto(Q = q) \nonumber\\+ \Poto\left(\bigcap_{k=1}^n A_{k\comma j_k} \Bigm| Q \neq q\right) \multspace \Poto(Q \neq q). 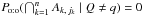\end{eqnarray}$ (58)Since $P_{o:o} ({^{􏽔}}_{k = 1}^{n} A_{k, j_{k}} | Q \neq q) = 0$ $\hbox{$\Poto(\bigcap_{k=1}^n A_{k\comma j_k} \mid Q \neq q) = 0$}$ by definition of q, we only have to compute 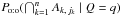$P_{o:o} ({^{􏽔}}_{k = 1}^{n} A_{k, j_{k}} | Q = q)$ $\hbox{$\Poto(\bigcap_{k=1}^n A_{k\comma j_k} \mid Q = q)$}$ and P_o:o(Q = q).

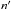There are n ! /(q ! [n − q] !) choices of q elements among n in K, and $n^{'}! / (q! [n^{'} - q]!)$ $\hbox{$\np!/(q!\multspace [\np-q]!)$}$ choices of q elements among $n^{'}$ $\hbox{$\np$}$ in K′. The number of permutations of q elements is q !, so the total number of one-to-one associations of q elements from K to q elements of K′ is 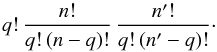$q! \frac{n!}{q! (n - q)!} \frac{n^{'}!}{q! (n^{'} - q)!} \cdot$ $\begin{equation} q!\multspace \frac{n!}{q!\multspace (n-q)!}\multspace \frac{\np!}{q!\multspace (\np-q)!}\cdot \end{equation}$ (59)The inverse of this number is 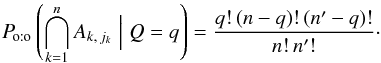$P_{o:o} (􏽜_{k = 1}^{n} A_{k, j_{k}} | Q = q) = \frac{q! (n - q)! (n^{'} - q)!}{n! n^{'}!} \cdot$ $\begin{equation} \label{P_oto(A|m)} \Poto\left(\bigcap_{k=1}^n A_{k\comma j_k} \Bigm| Q = q\right) = \frac{q!\multspace (n-q)!\multspace (\np-q)!}{n!\multspace \np!}\cdot \end{equation}$ (60)With our definition of K and K′, 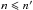$n ⩽ n^{'}$ $\hbox{$n \leqslant \np$}$ , so all the elements of K may have a counterpart in K′ jointly. Therefore, P_o:o(Q = q) is given by the binomial law: 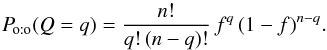$P_{o:o} (Q = q) = \frac{n!}{q! (n - q)!} f^{q} (1 - f)^{n - q} .$ $\begin{equation} \label{binom} \Poto(Q = q) = \frac{n!}{q!\multspace (n-q)!}\multspace f^q\multspace (1-f)^{n-q}. \end{equation}$ (61)From Eqs. (56), (12), (60), and (61), we obtain $\begin{matrix} P_{o:o} (C | C^{'}) \\ = Ξ \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \notin X_{n - 1} \end{matrix} \frac{(n^{'} - q)!}{n^{'}!} f^{q} (1 - f)^{n - q} 􏽙_{k = 1}^{n} ξ_{k, j_{k}} \end{matrix}$ $\begin{eqnarray} &&\Poto(C \mid C') \notag\\ &&= \Xi\multspace \sum_{\substack{j_1=0\\ j_1\not\in X_0}}^\np \sum_{\substack{j_2=0\\ j_2\not\in X_1}}^\np \cdots \sum_{\substack{j_n=0\\ j_n\not\in X_{n-1}}}^\np {\frac{(\np-q)!}{\np!} \multspace f^q \multspace (1-f)^{n-q}\multspace \prod_{k=1}^n \xi_{k\comma j_k}} ~~~~~~~~~~~~~~~~~ \\ &&= \Xi\multspace \sum_{\substack{j_1=0\\ j_1\not\in X_0}}^\np \sum_{\substack{j_2=0\\ j_2\not\in X_1}}^\np \cdots \sum_{\substack{j_n=0\\ j_n\not\in X_{n-1}}}^\np {\Left(\prod_{\ell=1}^q\frac{f}{\np-\ell+1}\Right)\multspace \Left(\prod_{\ell=1}^{n-q}[1-f]\Right)\multspace \prod_{k=1}^n \xi_{k\comma j_k}}.~~~~~~~~~~~~~~~~~ \label{P_oto(C|C)_eta} \end{eqnarray}$ There are q factors “ $f / (n^{'} - ℓ + 1)$ $\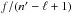hbox{$f/(\np-\ell+1)$}$ ” in the above equation, one for each index j_k ≠ 0. There are also n − q factors “(1 − f)”, one for each null j_k. For every j_k ≠ 0, 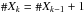${}_{#}X_{k} = {}_{#}X_{k - 1} + 1$ $\hbox{$\card X_k = \card X_{k-1} + 1$}$ ; and, since 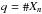$q = {}_{#}X_{n}$ $\hbox{$q = \card X_n$}$ , a different j_k corresponds to each ℓ ∈ [[1,q]], so 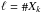$ℓ = {}_{#}X_{k}$ $\hbox{$\ell = \card X_k$}$ . With 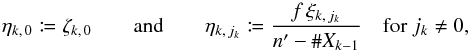$η_{k, 0} := ζ_{k, 0} and η_{k, j_{k}} := \frac{f ξ_{k, j_{k}}}{n^{'} - # X_{k - 1}} for j_{k} \neq 0,$ $\begin{equation} \label{def_eta} \eta_{k\comma 0} \coloneqq \zeta_{k\comma 0} \qquad \text{and} \qquad \eta_{k\comma j_k} \coloneqq \frac{f\multspace \xi_{k\comma j_k}}{\np-\card X_{k-1}} \quad\text{for } j_k \neq 0, \end{equation}$ (64)Eq. (63)therefore simplifies to 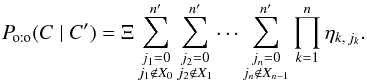$P_{o:o} (C | C^{'}) = Ξ \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \notin X_{n - 1} \end{matrix} 􏽙_{k = 1}^{n} η_{k, j_{k}} .$ $\begin{equation} \Poto(C \mid C') = \Xi\multspace \sum_{\substack{j_1=0\\ j_1\not\in X_0}}^\np \sum_{\substack{j_2=0\\ j_2\not\in X_1}}^\np\cdots \sum_{\substack{j_n=0\\ j_n\not\in X_{n-1}}}^\np \prod_{k=1}^n \eta_{k\comma j_k}. \label{P_oto(C|C)_res} \end{equation}$ (65)

4.1.2. Computation of P_o:o(A_i, j∩ C | C′)

The denominator of Eq. (4)is computed in the same way as P_o:o(C | C′): 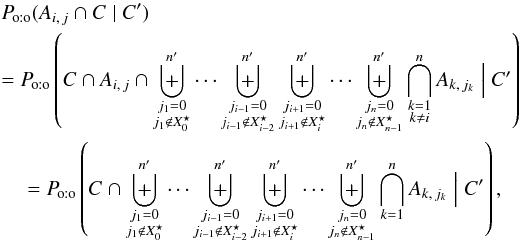$\begin{matrix} P_{o:o} (A_{i, j} \cap C | C^{'}) \\ = P_{o:o} (C \cap A_{i, j} \cap \begin{matrix} n^{'} \\ 􏽝 \\ j_{1} = 0 j_{1} \notin X_{0}^{⋆} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ 􏽝 \\ j_{i - 1} = 0 j_{i - 1} \notin X_{i - 2}^{⋆} \end{matrix} \begin{matrix} n^{'} \\ 􏽝 \\ j_{i + 1} = 0 j_{i + 1} \notin X_{i}^{⋆} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ 􏽝 \\ j_{n} = 0 j_{n} \notin X_{n - 1}^{⋆} \end{matrix} 􏽜_{\begin{matrix} k = 1 \\ k \neq i \end{matrix}}^{n} A_{k, j_{k}} | C^{'}) \\ = P_{o:o} (C \cap \begin{matrix} n^{'} \\ 􏽝 \\ j_{1} = 0 j_{1} \notin X_{0}^{⋆} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ 􏽝 \\ j_{i - 1} = 0 j_{i - 1} \notin X_{i - 2}^{⋆} \end{matrix} \begin{matrix} n^{'} \\ 􏽝 \\ j_{i + 1} = 0 j_{i + 1} \notin X_{i}^{⋆} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ 􏽝 \\ j_{n} = 0 j_{n} \notin X_{n - 1}^{⋆} \end{matrix} 􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}), \end{matrix}$ $\begin{eqnarray} && \Poto(A_{i\comma j} \cap C \mid C') \nonumber\\&&= \Poto\left(C \cap A_{i\comma j} \cap \biguplus_{\substack{j_1=0\\ j_1\not\in X^\star_0}}^\np \cdots \biguplus_{\substack{j_{i-1}=0\\ j_{i-1}\not\in X^\star_{i-2}}}^\np \biguplus_{\substack{j_{i+1}=0\\ j_{i+1}\not\in X^\star_{i}}}^\np \cdots \biguplus_{\substack{j_n=0\\ j_n\not\in X^\star_{n-1}}}^\np \bigcap_{\substack{k=1\\ k\neq i}}^n A_{k\comma j_k} \Bigm| C' \right) \nonumber \\&&~~~~~= \Poto\left(C \cap \biguplus_{\substack{j_1=0\\ j_1\not\in X^\star_0}}^\np \cdots \biguplus_{\substack{j_{i-1}=0\\ j_{i-1}\not\in X^\star_{i-2}}}^\np \biguplus_{\substack{j_{i+1}=0\\ j_{i+1}\not\in X^\star_{i}}}^\np \cdots \biguplus_{\substack{j_n=0\\ j_n\not\in X^\star_{n-1}}}^\np \bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C' \right), \end{eqnarray}$ (66)where $\begin{matrix} X_{0}^{⋆} := {j} \ {0}, j_{i} := j and \\ X_{k}^{⋆} := (X_{k - 1}^{⋆} \cup {j_{k}}) \ {0} forall k \in [[1, n]], \end{matrix}$ $\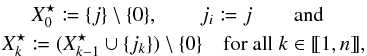begin{eqnarray} \label{def_J*} X^\star_0 \coloneqq \{j\} \setminus \{0\}, \qquad j_i \coloneqq j \qquad\text{and}\qquad \nonumber\\ X^\star_{k} \coloneqq (X^\star_{k-1} \cup \{j_k\}) \setminus \{0\} \quad\text{for all } k\in \integinterv{1}{n}, \end{eqnarray}$ (67)so $\begin{matrix} P_{o:o} (A_{i, j} \cap C | C^{'}) \\ = \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \notin X_{0}^{⋆} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{i - 1} = 0 j_{i - 1} \notin X_{i - 2}^{⋆} \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{i + 1} = 0 j_{i + 1} \notin X_{i}^{⋆} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \notin X_{n - 1}^{⋆} \end{matrix} P_{o:o} (C | 􏽜_{k = 1}^{n} A_{k, j_{k}} \cap C^{'}) \\ \times P_{o:o} (􏽜_{k = 1}^{n} A_{k, j_{k}} | C^{'}) . 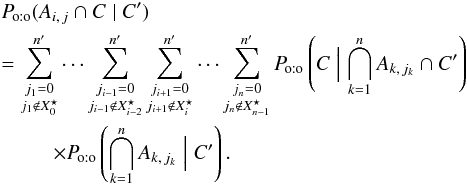\end{matrix}$ $\begin{eqnarray} &&\Poto(A_{i\comma j} \cap C \mid C') \nonumber \\&&= \sum_{\substack{j_1=0\\ j_1\not\in X^\star_0}}^\np \cdots\sum_{\substack{j_{i-1}=0\\ j_{i-1}\not\in X^\star_{i-2}}}^\np \sum_{\substack{j_{i+1}=0\\ j_{i+1}\not\in X^\star_{i}}}^\np \cdots \sum_{\substack{j_n=0\\ j_n\not\in X^\star_{n-1}}}^\np \Poto\left(C \Bigm| \bigcap_{k=1}^n A_{k\comma j_k} \cap C' \right) \nonumber\\&&~~~~~~~~~~\times \Poto\left(\bigcap_{k=1}^n A_{k\comma j_k} \Bigm| C' \right). 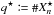\end{eqnarray}$ (68)Let $q^{⋆} := {}_{#}X_{n}^{⋆}$ $\hbox{$q^\star \coloneqq \card X^\star_n$}$ . As for P_o:o(C | C′), $\begin{matrix} P_{o:o} (A_{i, j} \cap C | C^{'}) \\ = Ξ \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \notin X_{0}^{⋆} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{i - 1} = 0 j_{i - 1} \notin X_{i - 2}^{⋆} \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{i + 1} = 0 j_{i + 1} \notin X_{i}^{⋆} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \notin X_{n - 1}^{⋆} \end{matrix} \frac{(n^{'} - q^{⋆})!}{n^{'}!} f^{q^{⋆}} (1 - f)^{n - q^{⋆}} 􏽙_{k = 1}^{n} ξ_{k, j_{k}} \end{matrix}$ $\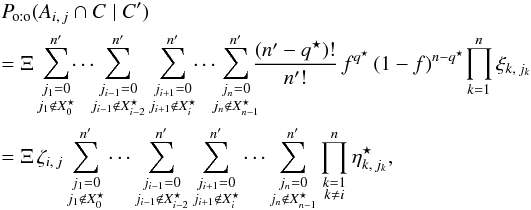begin{eqnarray} && \Poto(A_{i\comma j} \cap C \mid C') \nonumber\\&&= \Xi\multspace \sum_{\substack{j_1=0\\ j_1\not\in X^\star_0}}^\np \!\!\cdots\!\! \sum_{\substack{j_{i-1}=0\\ j_{i-1}\not\in X^\star_{i-2}}}^\np \sum_{\substack{j_{i+1}=0\\ j_{i+1}\not\in X^\star_{i}}}^\np \! \!\cdots\! \!\sum_{\substack{j_n=0\\ j_n\not\in X^\star_{n-1}}}^\np \!\!\! {\frac{(\np-q^\star)!}{\np!} \multspace f^{q^\star} \multspace (1-f)^{n-q^\star}\multspace \!\prod_{k=1}^n \xi_{k\comma j_k}} \! \nonumber \\&&= \Xi\multspace \zeta_{i\comma j}\multspace \sum_{\substack{j_1=0\\ j_1\not\in X^\star_0}}^\np \cdots \sum_{\substack{j_{i-1}=0\\ j_{i-1}\not\in X^\star_{i-2}}}^\np \sum_{\substack{j_{i+1}=0\\ j_{i+1}\not\in X^\star_{i}}}^\np \cdots \sum_{\substack{j_n=0\\ j_n\not\in X^\star_{n-1}}}^\np \prod_{\substack{k=1\\ k\neq i}}^n \eta^\star_{k\comma j_k}, \label{P_oto(Aij,C|C)_res} \end{eqnarray}$ (69)where $η_{k, 0}^{⋆} := ζ_{k, 0} and η_{k, j_{k}}^{⋆} := \frac{f ξ_{k, j_{k}}}{n^{'} - # X_{k - 1}^{⋆}} for j_{k} \neq 0.$ $\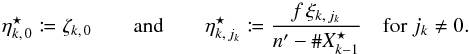begin{equation} \label{def_eta*} \eta^\star_{k\comma 0} \coloneqq \zeta_{k\comma 0} \qquad\text{and}\qquad \eta^\star_{k\comma j_k} \coloneqq \frac{f\multspace \xi_{k\comma j_k}}{\np-\card X^\star_{k-1}} \quad \text{for } j_k \neq 0. \end{equation}$ (70)

4.1.3. Final results

Finally, from Eqs. (4), (65), and (69), fori ≠ 0, 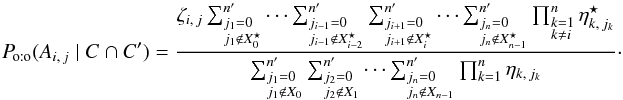$\begin{matrix} P_{o:o} (A_{i, j} | C \cap C^{'}) = \frac{ζ_{i, j} \sum \begin{matrix} n^{'} \\ j_{1} = 0 j_{1} \notin X_{0}^{⋆} \end{matrix} \cdot \cdot \cdot \sum \begin{matrix} n^{'} \\ j_{i - 1} = 0 j_{i - 1} \notin X_{i - 2}^{⋆} \end{matrix} \sum \begin{matrix} n^{'} \\ j_{i + 1} = 0 j_{i + 1} \notin X_{i}^{⋆} \end{matrix} \cdot \cdot \cdot \sum \begin{matrix} n^{'} \\ j_{n} = 0 j_{n} \notin X_{n - 1}^{⋆} \end{matrix} 􏽑 \begin{matrix} n \\ k = 1 k \neq i \end{matrix} η_{k, j_{k}}^{⋆}}{\sum \begin{matrix} n^{'} \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \sum \begin{matrix} n^{'} \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \sum \begin{matrix} n^{'} \\ j_{n} = 0 j_{n} \notin X_{n - 1} \end{matrix} 􏽑_{k = 1}^{n} η_{k, j_{k}}} \cdot \end{matrix}$ $\begin{eqnarray} \label{P_oto(Aij|C,C)_res} \Poto(A_{i\comma j} \mid C \cap C') = \frac{ \zeta_{i\comma j}\multspace \sum_{\leftsubstack{j_1=0\\ j_1\not\in X^\star_0}}^\np \cdots \sum_{\leftsubstack{j_{i-1}=0\\ j_{i-1}\not\in X^\star_{i-2}}}^\np \sum_{\leftsubstack{j_{i+1}=0\\ j_{i+1}\not\in X^\star_{i}}}^\np \cdots \sum_{\leftsubstack{j_n=0\\ j_n\not\in X^\star_{n-1}}}^\np \prod_{\leftsubstack{k=1\\ k\neq i}}^n \eta^\star_{k\comma j_k} }{ \sum_{\leftsubstack{j_1=0\\ j_1\not\in X_0}}^\np \sum_{\leftsubstack{j_2=0\\ j_2\not\in X_1}}^\np \cdots \sum_{\leftsubstack{j_n=0\\ j_n\not\in X_{n-1}}}^\np \prod_{k=1}^n \eta_{k\comma j_k} }\cdot \end{eqnarray}$ (71)

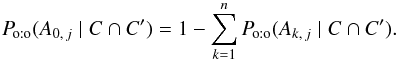The probability that a source $M_{j}^{'}$ $\hbox{$\Mp_j$}$ has no counterpart in K is simply given by $P_{o:o} (A_{0, j} | C \cap C^{'}) = 1 - \sum_{k = 1}^{n} P_{o:o} (A_{k, j} | C \cap C^{'}) .$ $\begin{equation} \Poto(A_{0\comma j} \mid C \cap C') = 1-\sum_{k=1}^n \Poto(A_{k\comma j}\mid C \cap C'). \end{equation}$ (72)

4.2. Likelihood and estimation of unknown parameters

As in Sect. 3.2, an estimate 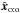$\hat{x}_{o:o}$ $\hbox{$\hat{\vec x}_\oto$}$ of the set x of unknown parameters may be obtained by solving Eq. (28). Under assumption (H_o:o), we obtain from Eqs. (65), (31), and (13)that 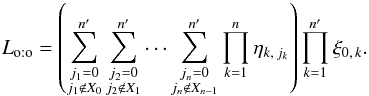$L_{o:o} = (\begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \notin X_{n - 1} \end{matrix} 􏽙_{k = 1}^{n} η_{k, j_{k}}) 􏽙_{k = 1}^{n^{'}} ξ_{0, k} .$ $\begin{equation} \label{Lh_oto_brut} \Lhoto = \left(\sum_{\substack{j_1=0\\ j_1\not\in X_0}}^\np \sum_{\substack{j_2=0\\ j_2\not\in X_1}}^\np\cdots \sum_{\substack{j_n=0\\ j_n\not\in X_{n-1}}}^\np \prod_{k=1}^n \eta_{k\comma j_k}\right)\multspace \prod_{k=1}^\np\xi_{0\comma k}. \end{equation}$ (73)Because the number of terms in Eq. (73)grows exponentially with n and 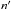$n^{'}$ $\hbox{$\np$}$ , this equation seems useless. In fact, the prior computation of L_o:o is not necessary if the probabilities P_o:o(A_i,j | C ∩ C′) are calculable (we see how to evaluate these in Sect. 5.4).

Indeed, for any parameter x_p, we get the same result (Eq. (33)) as under assumption (H_s:o). First, we note that, since the ξ_0,j are independent of x, we obtain from Eq. (31)that 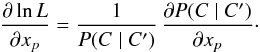$\frac{\partial \ln L}{\partial x_{p}} = \frac{1}{P (C | C^{'})} \frac{∂P (C | C^{'})}{\partial x_{p}} \cdot$ $\begin{equation} \label{der(Lh)} \frac{\partial\ln\Lh}{\partial x_p} = \frac{1}{\Prob(C \mid C')}\multspace \frac{\partial\Prob(C \mid C')}{\partial x_p}\cdot \end{equation}$ (74)Now, for any set Υ of indices and any product of strictly positive functions h_k of some variable y, 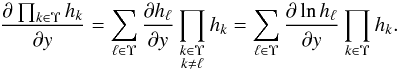$\frac{\partial 􏽑_{k \in Υ} h_{k}}{∂y} = \sum_{ℓ \in Υ} \frac{\partial h_{ℓ}}{∂y} \underset{\begin{matrix} k \in Υ \\ k \neq ℓ \end{matrix}}{􏽙} h_{k} = \sum_{ℓ \in Υ} \frac{\partial \ln h_{ℓ}}{∂y} \underset{k \in Υ}{􏽙} h_{k} .$ $\begin{equation} \label{der(prod_g)} \frac{\partial\prod_{k\in \Upsilon} h_k}{\partial y} = \sum_{\ell\in \Upsilon}{\frac{\partial h_\ell}{\partial y}\multspace \prod_{\substack{k\in \Upsilon\\ k\neq\ell}} h_k} = \sum_{\ell\in \Upsilon}{\frac{\partial\ln h_\ell}{\partial y}\multspace \prod_{k\in \Upsilon} h_k}. \end{equation}$ (75)With h_k = η_{k,j_k}, y = x_p and Υ = [[1,n]], we therefore obtain from Eq. (65)that 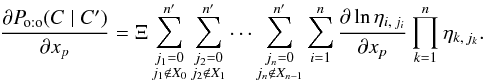$\frac{\partial P_{o:o} (C | C^{'})}{\partial x_{p}} = Ξ \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \notin X_{n - 1} \end{matrix} \sum_{i = 1}^{n} \frac{\partial \ln η_{i, j_{i}}}{\partial x_{p}} 􏽙_{k = 1}^{n} η_{k, j_{k}} .$ $\begin{equation} \label{der(P_oto)_gauche} \frac{\partial \Poto(C \mid C')}{\partial x_p} = \Xi \multspace \sum_{\substack{j_1=0\\j_1\notin X_0}}^\np\sum_{\substack{j_2=0\\j_2\notin X_1}}^\np \cdots\sum_{\substack{j_n=0\\j_n\notin X_{n-1}}}^\np\sum_{i=1}^n{ \frac{\partial\ln\eta_{i\comma j_i}}{\partial x_p}\multspace \prod_{k=1}^n\eta_{k\comma j_k}}. \end{equation}$ (76)The expression of P_o:o(A_i,j ∩ C | C′) (Eq. (69)) may also be written 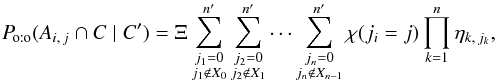$P_{o:o} (A_{i, j} \cap C | C^{'}) = Ξ \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \notin X_{n - 1} \end{matrix} χ (j_{i} = j) 􏽙_{k = 1}^{n} η_{k, j_{k}},$ $\begin{equation} \Poto(A_{i\comma j} \cap C \mid C') = \Xi \multspace \sum_{\substack{j_1=0\\j_1\notin X_0}}^\np\sum_{\substack{j_2=0\\j_2\notin X_1}}^\np \cdots\sum_{\substack{j_n=0\\j_n\notin X_{n-1}}}^\np {\chi(j_i = j)\multspace \prod_{k=1}^n \eta_{k\comma j_k}}, \end{equation}$ (77)where χ is the indicator function (i.e. χ(j_i = j) = 1 if proposition “j_i = j” is true and χ(j_i = j) = 0 otherwise), so 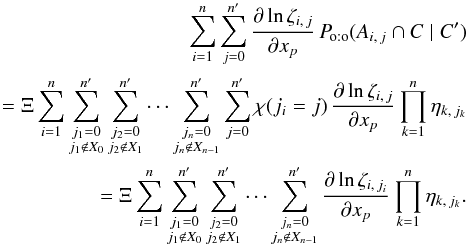$\begin{matrix} \sum_{i = 1}^{n} \sum_{j = 0}^{n^{'}} \frac{\partial \ln ζ_{i, j}}{\partial x_{p}} P_{o:o} (A_{i, j} \cap C | C^{'}) \\ = Ξ \sum_{i = 1}^{n} \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \notin X_{n - 1} \end{matrix} \sum_{j = 0}^{n^{'}} χ (j_{i} = j) \frac{\partial \ln ζ_{i, j}}{\partial x_{p}} 􏽙_{k = 1}^{n} η_{k, j_{k}} \\ = Ξ \sum_{i = 1}^{n} \begin{matrix} n^{'} \\ \sum \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \begin{matrix} n^{'} \\ \sum \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \begin{matrix} n^{'} \\ \sum \\ j_{n} = 0 j_{n} \notin X_{n - 1} \end{matrix} \frac{\partial \ln ζ_{i, j_{i}}}{\partial x_{p}} 􏽙_{k = 1}^{n} η_{k, j_{k}} . \end{matrix}$ $\begin{eqnarray} \label{der(P_oto)_droite} \sum_{i=1}^n\sum_{j=0}^\np{\frac{\partial\ln\zeta_{i\comma j}}{\partial x_p} \multspace \Poto(A_{i\comma j} \cap C \mid C')} \nonumber \\= \Xi\multspace \sum_{i=1}^n\sum_{\substack{j_1=0\\j_1\notin X_0}}^\np \sum_{\substack{j_2=0\\j_2\notin X_1}}^\np \cdots\sum_{\substack{j_n=0\\j_n\notin X_{n-1}}}^\np\sum_{j=0}^\np {\chi(j_i = j)\multspace \frac{\partial\ln\zeta_{i\comma j}}{ \partial x_p}\multspace \prod_{k=1}^n\eta_{k\comma j_k}} \nonumber \\= \Xi\multspace \sum_{i=1}^n\sum_{\substack{j_1=0\\j_1\notin X_0}}^\np \sum_{\substack{j_2=0\\j_2\notin X_1}}^\np \cdots\sum_{\substack{j_n=0\\j_n\notin X_{n-1}}}^\np {\frac{\partial\ln\zeta_{i\comma j_i}}{\partial x_p}\multspace \prod_{k=1}^n\eta_{k\comma j_k}}. \end{eqnarray}$ (78)If j_i = 0, then η_{i,j_i} = ζ_{i,j_i}; and if j_i ≠ 0, the numerators of η_{i,j_i} and ζ_{i,j_i} are the same and their denominators do not depend on x_p: in all cases, ∂lnη_{i,j_i}/∂x_p = ∂lnζ_{i,j_i}/∂x_p. The righthand sides of Eqs. (76)and (78)are therefore identical. Dividing their lefthand sides by P_o:o(C | C′) and using Eqs. (74)and (4), we obtain, as announced, 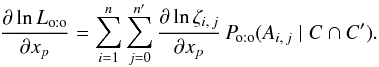$\frac{\partial \ln L_{o:o}}{\partial x_{p}} = \sum_{i = 1}^{n} \sum_{j = 0}^{n^{'}} \frac{\partial \ln ζ_{i, j}}{\partial x_{p}} P_{o:o} (A_{i, j} | C \cap C^{'}) .$ $\begin{equation} \label{der(Lh_oto)/x} \frac{\partial\ln\Lhoto}{\partial x_p} = \sum_{i=1}^n\sum_{j=0}^\np{\frac{\partial\ln\zeta_{i\comma j}}{ \partial x_p}\multspace \Poto(A_{i\comma j} \mid C \cap C')}. \end{equation}$ (79)

For x_p = f in particular, because of Eq. (37), and as under assumption (H_s:o), Eq. (79)reduces to 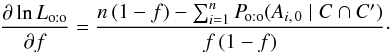$\frac{\partial \ln L_{o:o}}{∂f} = \frac{n (1 - f) - \sum_{i = 1}^{n} P_{o:o} (A_{i, 0} | C \cap C^{'})}{f (1 - f)} \cdot$ $\begin{equation} \label{der(Lh_oto)/f} \frac{\partial\ln\Lhoto}{\partial f} = \frac{ n\multspace (1-f) - \sum_{i=1}^n \Poto(A_{i\comma 0} \mid C \cap C') }{ f\multspace (1-f) }\cdot \end{equation}$ (80)From Eq. 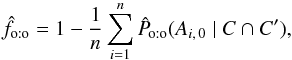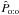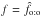(28), a maximum likelihood estimator of f is thus $f̂ o:o = 1 - \frac{1}{n} \sum_{i = 1}^{n} P̂ o:o (A_{i, 0} | C \cap C^{'}),$ $\begin{equation} \hat f_\oto = 1 - \frac{1}{n}\multspace \sum_{i=1}^n\expandafter\hat\Poto(A_{i\comma 0} \mid C \cap C'), \label{f_est_oto} \end{equation}$ (81)where $\hbox{$\expandafter\hat\Poto$}$ is the value of P_o:o at $\hbox{$f = \hat f_\oto$}$ .

To compare assumptions (H_s:o), (H_o:o), and (H_s:o) and to select the most appropriate one to compute P(A_i,j | C ∩ C′), an expression is needed for L_o:o. If probabilities P_o:o(A_{i, 0} | C ∩ C′) are calculable, L_o:o may be obtained for any f by integrating Eq. (80)with respect to f. Since all K- and K′-sources are unrelated and randomly distributed for f = 0, the integration constant is (cf. Eq. (73)) 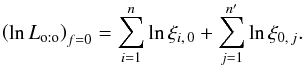${(\ln L_{o:o})}_{f = 0} = \sum_{i = 1}^{n} \ln ξ_{i, 0} + \sum_{j = 1}^{n^{'}} \ln ξ_{0, j} .$ $\begin{equation} \label{Lh_oto(0)} {\left(\ln\Lhoto\right)}^{}_{f=0} = \sum_{i=1}^n \ln\xi_{i\comma0} + \sum_{j=1}^\np \ln\xi_{0\comma j}. \end{equation}$ (82)

5. Practical implementation: the Aspects code

5.1. Overview

To implement the results established in Sects. 3.1, 3.2, 4.1, and 4.2, we have built a Fortran 95 code, Aspects – a French acronym (pronounced [aspε] in International Phonetic Alphabet, not [æspekts]) for “Association positionnelle/probabiliste de catalogues de sources”, or “probabilistic positional association of source catalogs” in English. The source files are freely available ⁴ at www2.iap.fr/users/fioc/Aspects/ . The code compiles with IFort and GFortran.

Given two catalogs of sources with their positions and the uncertainties on these, Aspects computes, under assumptions (H_s:o), (H_o:o), and (H_o:s), the overall likelihood L, estimates of f and f′, and the probabilities P(A_i,j | C ∩ C′). It may also simulate all-sky catalogs for various association models (cf. Sect. 6.1).

We provide hereafter explanations of general interest for the practical implementation in Aspects of Eqs. (23), (39), (32), (71), (81), and (73). Some more technical points (such as the procedures used to search for nearby objects, simulate the positions of associated sources and integrate Eq. (80)) are only addressed in appendices to the documentation of the code (Fioc 2014). The latter also contains the following complements: another (but equivalent) expression for L_o:o, formulae derived under H_o:s, computations under H_o:o for 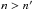$n > n^{'}$ $\hbox{$n > \np$}$ , a calculation of the uncertainties on unknown parameters under H_s:o, and a proof of Eq. (41).

5.2. Elimination of unlikely counterparts

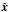Under assumption (H_s:o), computing the probability of association P_s:o(A_i,j | C ∩ C′) between M_i and $M_{j}^{'}$ $\hbox{$\Mp_j$}$ from Eq. (23)is straightforward if f and the positional uncertainties are known. However, the number of calculations for the whole sample or for determining $\hat{x}$ $\hbox{$\hat{\vec x}$}$ is on the order of 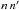$n n^{'}$ $\hbox{$n\multspace \np$}$ , a huge number for the catalogs available nowadays. We must therefore try to eliminate all unnecessary computations.

Since ξ_i,k is given by a normal law if i ≠ 0 and k ≠ 0, it rapidly drops to almost 0 when we consider sources 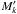$M_{k}^{'}$ $\hbox{$\Mp_k$}$ at increasing angular distance ψ_i,k from M_i. Therefore, there is no need to compute P_s:o(A_i,j | C ∩ C′) for all couples 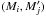$(M_{i}, M_{j}^{'})$ $\hbox{$(M_i, \Mp_j)$}$ or to sum on all k from 1 to 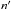$n^{'}$ $\hbox{$\np$}$ in Eq. (24). 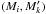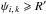More explicitly, let R′ be some angular distance such that, for all $(M_{i}, M_{k}^{'})$ $\hbox{$(M_i, \Mp_k)$}$ , if $\hbox{$\psi_{i\comma k} \geqslant R'$}$ then ξ_i,k ≈ 0, say $R^{'} ≳ 5 \sqrt{\max_{ℓ \in [[1, n]]} a_{ℓ}^{2} + \max_{ℓ \in [[1, n^{'}]]} a_{ℓ}^{' 2}},$ $\begin{equation} \label{def_R} R' \ga 5\multspace \!\sqrt{ \smash[b]{ \max_{\ell\in\integinterv{1}{n}} a_\ell^2 + \max_{\ell\in\integinterv{1}{\np}} a_{\ell}'^2 } }, \vphantom{ \max_{\ell\in\integinterv{1}{n}} a_\ell^2 + \max_{\ell\in\integinterv{1}{\np}} a_{\ell}'^2 } \end{equation}$ (83)where the a_ℓ and $a_{ℓ}^{'}$ $\hbox{$a'_{\smash[t]{\ell}}$}$ are the semi-major axes of the positional uncertainty ellipses of K- and K′-sources (cf. Appendix A.2.1; the square root in Eq. (83)is thus the maximal possible uncertainty on the relative position of associated sources). We may set P_s:o(A_i,j | C ∩ C′) to 0 if ψ_i,j>R′, and replace the sums $\sum_{k = 1}^{n^{'}}$ $\hbox{$\smash[t]{\sum_{\smash[t]{k=1}}^\np}$}$ by $\sum_{k = 1; ψ_{i, k} ⩽ R^{'}}^{n^{'}}$ $\hbox{$\smash[t]{\sum_{\smash[t]{k=1{;}\, \psi_{i\comma k}\leqslant R'}}^\np}$}$ in Eq. (24): only nearby K′-sources matter.

5.3. Fraction of sources with a counterpart

All the probabilities depend on f and, possibly, on other unknown parameters like 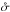$\begin{matrix} ˚ \\ σ \end{matrix}$ $\hbox{$\sigmatot$}$ and $\begin{matrix} ˚ \\ ν \end{matrix}$ $\hbox{$\nutot$}$ (cf. Appendices A.2.2 and A.2.3). Under assumption (H_s:o), estimates of these parameters may be found by solving Eq. (28)using Eq. (33).

If the fraction of sources with a counterpart is the only unknown, the ξ_i,j need to be computed only once and 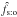$\hbox{$\hat f_\sto$}$ may easily be determined from Eq. (39)by an iterative procedure. 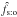Denoting by g the function $g : f \in [0, 1] - \to 1 - \frac{1}{n} \sum_{i = 1}^{n} P_{s:o} (A_{i, 0} | C \cap C^{'}),$ $\begin{equation} \label{fonction_g} g\colon f \in [0, 1] \longmapsto 1-\frac{1}{n}\multspace \sum_{i=1}^n\Psto(A_{i\comma 0} \mid C \cap C'), \end{equation}$ (84)we now prove that, for any f₀ ∈] 0,1 [, the sequence (f_k)_{k ∈?} defined by f_{k + 1} := g(f_k) tends to $\hbox{$\hat f_\sto$}$ .

As is obvious from Eq. (24b), P_s:o(A_{i, 0} | C ∩ C′) decreases for all i when f increases: g is consequently an increasing function. Note also that, from Eqs. (38)and (84), 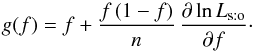$g (f) = f + \frac{f (1 - f)}{n} \frac{\partial \ln L_{s:o}}{∂f} \cdot$ $\begin{equation} \label{expression_g} g(f) = f + \frac{f\multspace (1-f)}n \multspace \frac{\partial\ln\Lhsto}{\partial f}\cdot \end{equation}$ (85)The only fixed points of g are thus 0, 1 and the unique solution 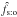$\hbox{$\hat f_\sto$}$ to ∂lnL_s:o/∂f = 0. Because ∂²lnL_s:o/∂f²< 0 (cf. Eq. 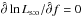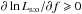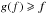(41)) and $\hbox{$\hat\partial\ln\Lhsto/\hat\partial f = 0$}$ , we have $\hbox{$\partial\ln\Lhsto/\partial f \geqslant 0$}$ if $\hbox{$f \in [0, \hat f_\sto]$}$ , so $\hbox{$g(f) \geqslant f$}$ in this interval by Eq. (85). 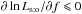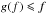Similarly, if $\hbox{$f \in [\hat f_\sto, 1]$}$ , then $\hbox{$\partial\ln\Lhsto/\partial f \leqslant 0$}$ and thus $\hbox{$g(f) \leqslant f$}$ .

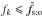Consider the case $\hbox{$f_0 \in \mathopen{]}0, \hat f_\sto]$}$ . If $\hbox{$f_k \leqslant \hat f_\sto$}$ , then as just shown, 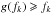$\hbox{$g(f_k) \geqslant f_k$}$ ; we also have 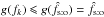$\hbox{$g(f_k) \leqslant g(\hat f_\sto) = \hat f_\sto$}$ , because g is an increasing function and 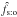$\hbox{$\hat f_\sto$}$ is a fixed point of it. Since g(f_k) = f_{k + 1}, the sequence (f_k)_{k ∈?} is increasing and bounded from above by 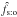$\hbox{$\hat f_\sto$}$ : it therefore converges in $\hbox{$[f_0, \hat f_\sto]$}$ . 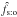Because g is continuous and $\hbox{$\hat f_\sto$}$ is the only fixed point in this interval, (f_k)_{k ∈?} tends to 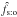$\hbox{$\hat f_\sto$}$ . 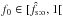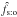Similarly, if $\hbox{$f_0 \in [\hat f_\sto, 1\mathclose{[}$}$ , then (f_k)_{k ∈?} is a decreasing sequence converging to $\hbox{$\hat f_\sto$}$ .

Because of Eq. (81), this procedure also works in practice under assumption (H_o:o) (with P_s:o replaced by P_o:o in Eq. (84)), although it is not obvious that P_o:o(A_{i, 0} | C ∩ C′) decreases for all i when f increases, nor that ∂²lnL_o:o/∂f²< 0. A good starting value f₀ may be 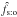$\hbox{$\hat f_\sto$}$ .

5.4. Computation of one-to-one probabilities of association

What was said in Sect. 5.2 about eliminating unlikely counterparts in the calculation of probabilities under H_s:o still holds under H_o:o. However, because of the combinatorial explosion of the number of terms in Eq. (71), computing P_o:o(A_i,j | C ∩ C′) exactly is still clearly hopeless. Yet, after some wandering (Sects. 5.4.1 and 5.4.2), we found a working solution (Sect. 5.4.3).

5.4.1. A first try

Our first try was inspired by the (partially wrong) idea that, although all K-sources are involved in the numerator and denominator of Eq. (71), only those close to M_i should matter in their ratio. A sequence of approximations converging to the true value of P_o:o(A_i,j | C ∩ C′) might then be built as follows (all quantities defined or produced in this first try are written with the superscript “w” for “wrong”).

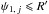To make things clear, consider M₁ and some possible counterpart $M_{j}^{'}$ $\hbox{$\Mp_j$}$ within its neighborhood ( $\hbox{$\psi_{1\comma j} \leqslant R'$}$ ) and assume that M₂ is the first nearest neighbor of M₁ in K, M₃ its second nearest neighbor, etc. For any d ∈ [[1,n]], define $p_{d}^{w} (1,j) := \frac{ζ_{1, j} \sum \begin{matrix} n^{'} \\ j_{2} = 0 j_{2} \notin X_{1}^{⋆} \end{matrix} \cdot \cdot \cdot \sum \begin{matrix} n^{'} \\ j_{d} = 0 j_{d} \notin X_{d - 1}^{⋆} \end{matrix} 􏽑_{k = 2}^{d} η_{k, j_{k}}^{⋆}}{\sum \begin{matrix} n^{'} \\ j_{1} = 0 j_{1} \notin X_{0} \end{matrix} \sum \begin{matrix} n^{'} \\ j_{2} = 0 j_{2} \notin X_{1} \end{matrix} \cdot \cdot \cdot \sum \begin{matrix} n^{'} \\ j_{d} = 0 j_{d} \notin X_{d - 1} \end{matrix} 􏽑_{k = 1}^{d} η_{k, j_{k}}} \cdot$ $\begin{equation} p^\wrong_{\smash[t]{d}}(1, j) \coloneqq \frac{ \zeta_{1\comma j}\multspace \sum_{\leftsubstack{j_2=0\\ j_2\not\in X^{\star}_1}}^\np \cdots \sum_{\leftsubstack{j_d=0\\ j_d\not\in X^{\star}_{d-1}}}^\np \prod_{k=2}^d \eta^{\star}_{k\comma j_k} }{ \sum_{\leftsubstack{j_1=0\\ j_1\not\in X_0}}^\np \sum_{\leftsubstack{j_2=0\\ j_2\not\in X_1}}^\np \cdots \sum_{\leftsubstack{j_d=0\\ j_d\not\in X_{d-1}}}^\np \prod_{k=1}^d \eta_{k\comma j_k} }\cdot \end{equation}$ (86)The quantity $p_{d}^{w} (1,j)$ $\hbox{$p^\wrong_{\smash[t]{d}}(1, j)$}$ thus depends only on M₁ and its d − 1 nearest neighbors in K. 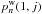As $p_{n}^{w} (1,j)$ $\hbox{$p^\wrong_n(1, j)$}$ is the one-to-one probability of association between M₁ and $M_{j}^{'}$ $\hbox{$\Mp_j$}$ (cf. Eq. (71)), the sequence $(p_{d}^{w} [1,j])$ $\hbox{$(p^\wrong_{\smash[t]{d}}[1, j])$}$ tends to P_o:o(A_1,j | C ∩ C′) when the depth d of the recursive sums tends to n. After some initial fluctuations, $p_{d}^{w} (1,j)$ $\hbox{$p^\wrong_{\smash[t]{d}}(1, j)$}$ enters a steady state. This occurs when ψ(M₁,M_{d + 1}) exceeds a distance R equal to a few times R′ (at least 2 R′). We may therefore think that the convergence is then achieved and stop the recursion at this d. 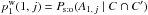It is all the more tempting that $p_{1}^{w} (1,j) = P_{s:o} (A_{1, j} | C \cap C^{'})$ $\hbox{$p^\wrong_1(1, j) = \Psto(A_{1\comma j} \mid C \cap C')$}$ and that the several-to-one probability looks like a first-order approximation to P_o:o...

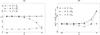Fig. 1

One-to-one simulations for f = 1/2, $n^{'} = 10^{5}$ $\hbox{$\np = 10^5$}$ , and circular positional uncertainty ellipses with $\begin{matrix} _{˚} \\ σ \end{matrix} = 10^{-3} rad$ $\hbox{$\sigmatot = 10^{-3}\,\radian$}$ (see Sects. 6.1 and 6.2 for details). a) Mean value of different estimators $\hbox{$\hat f$}$ of f as a function of n. The dotted line indicates the input value of f. b) Normalized average maximum value $\hbox{$\hat\Lh$}$ of different likelihoods as a function of n, compared to $L̂ \begin{matrix} w \\ o:o \end{matrix}$ $\hbox{$\expandafter\hat\Lhoto^\wrong$}$ .

More formally and generally, for any M_i, let φ be a permutation on K ordering the elements M_φ(1), M_φ(2), ..., M_φ(n) by increasing angular distance to M_i (in particular, M_φ(1) = M_i). For j = 0 or $M_{j}^{'}$ $\hbox{$\Mp_j$}$ within a distance R′ (cf. Sect. 5.2) from M_i, and for any d ∈ [[1,n]], define $p_{d}^{w} (i,j) := \frac{ζ_{i, j} \sum \begin{matrix} n^{'} \\ j_{2} = 0 j_{2} \notin \begin{matrix} 􏽥 \\ X_{1}^{⋆} \end{matrix} \end{matrix} \cdot \cdot \cdot \sum \begin{matrix} n^{'} \\ j_{d} = 0 j_{d} \notin \begin{matrix} 􏽥 \\ X_{d - 1}^{⋆} \end{matrix} \end{matrix} 􏽑_{k = 2}^{d} {η_{k, j_{k}}^{⋆ w}}^{􏽥}}{\sum \begin{matrix} n^{'} \\ j_{1} = 0 j_{1} \notin \begin{matrix} 􏽥 \\ X_{0} \end{matrix} \end{matrix} \sum \begin{matrix} n^{'} \\ j_{2} = 0 j_{2} \notin \begin{matrix} 􏽥 \\ X_{1} \end{matrix} \end{matrix} \cdot \cdot \cdot \sum \begin{matrix} n^{'} \\ j_{d} = 0 j_{d} \notin \begin{matrix} 􏽥 \\ X_{d - 1} \end{matrix} \end{matrix} 􏽑_{k = 1}^{d} \begin{matrix} 􏽥 \\ η_{k, j_{k}}^{w} \end{matrix}},$ $\begin{equation} \label{P_oto_iter_w} p^\wrong_{\smash[t]{d}}(i, j) \coloneqq \frac{ \zeta_{i\comma j}\multspace\sum_{\leftsubstack{j_2=0\\ j_2\not\in \widetilde X^{\star}_1}}^\np \cdots \sum_{\leftsubstack{j_d=0\\ j_d\not\in \widetilde X^{\star}_{d-1}}}^\np \prod_{k=2}^d \widetilde\eta^{\,\star\,\wrong}_{k\comma j_k} }{ \sum_{\leftsubstack{j_1=0\\ j_1\not\in \widetilde X_0}}^\np \sum_{\leftsubstack{j_2=0\\ j_2\not\in \widetilde X_1}}^\np \cdots \sum_{\leftsubstack{j_d=0\\ j_d\not\in \widetilde X_{d-1}}}^\np \prod_{k=1}^d \widetilde\eta^{\,\wrong}_{k\comma j_k} }, \vspace*{3mm} \end{equation}$ (87)where, as in Eqs. (55), (67), (64), and (70),

$\begin{matrix} \begin{matrix} \end{matrix} \begin{matrix} 􏽥 \\ X_{k} \end{matrix} := X_{k} forall k \in [[0, n]]; \begin{matrix} 􏽥 \\ X_{1}^{⋆} \end{matrix} := {j} \ {0}; \begin{matrix} \end{matrix} \begin{matrix} \end{matrix} \\ \begin{matrix} \end{matrix} \begin{matrix} 􏽥 \\ X_{k}^{⋆} \end{matrix} := (\begin{matrix} 􏽥 \\ X_{k - 1}^{⋆} \end{matrix} \cup {j_{k}}) \ {0} forall k \in [[2, n]]; \begin{matrix} \end{matrix} \end{matrix} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix}$ $\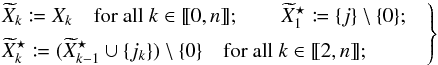begin{equation} \Left. \begin{aligned} &\widetilde X_k \coloneqq X_k \quad \text{for all } k \in \integinterv{0}{n}; \qquad \widetilde X^{\star}_1 \coloneqq \{j\} \setminus \{0\}; && \\ &\widetilde X^{\star}_k \coloneqq (\widetilde X^{\star}_{k-1} \cup \{j_k\}) \setminus \{0\} \quad\text{for all } k \in \integinterv{2}{n}; && \end{aligned} \Right\} \end{equation}$ (88) $\begin{matrix} \begin{matrix} \end{matrix} \begin{matrix} 􏽥 \\ η_{k, 0}^{w} \end{matrix} := {η_{k, 0}^{⋆ w}}^{􏽥} := ζ_{φ (k), 0}; \begin{matrix} 􏽥 \\ η_{k, j_{k}}^{w} \end{matrix} := \frac{f ξ_{φ (k), j_{k}}}{n^{'} - # \begin{matrix} 􏽥 \\ X_{k - 1} \end{matrix}} \\ \begin{matrix} \end{matrix} and {η_{k, j_{k}}^{⋆ w}}^{􏽥} := \frac{f ξ_{φ (k), j_{k}}}{n^{'} - # \begin{matrix} 􏽥 \\ X_{k - 1}^{⋆} \end{matrix}} for j_{k} \neq 0. 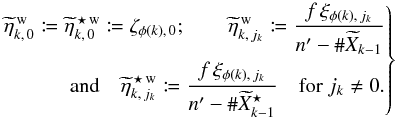\end{matrix} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix}$ $\begin{equation} \label{tilde} \Left. \begin{aligned} \widetilde\eta^{\,\wrong}_{k\comma 0} \coloneqq \widetilde\eta^{\,\star\,\wrong}_{k\comma 0} \coloneqq \zeta_{\phi(k)\comma 0}; \qquad \widetilde\eta^{\,\wrong}_{k\comma j_k} \coloneqq \frac{f\multspace \xi_{\phi(k)\comma j_k}}{ \np-\card \widetilde X_{k-1}} \\ \text{and}\quad \widetilde\eta^{\,\star\,\wrong}_{k\comma j_k} \coloneqq \frac{f\multspace \xi_{\phi(k)\comma j_k}}{ \np-\card \widetilde X^{\star}_{k-1}} \quad \text{for } j_k \neq 0. \end{aligned} \Right\} \end{equation}$ (89)Let $d_{\min} (i) := \begin{matrix} \min \end{matrix} (d \in [[1, n]] | ψ [M_{i}, M_{φ (d + 1)}] > R^{)} .$ $\begin{equation} \label{min_prof} \depthmin(i) \coloneqq \min\left(d \in \integinterv{1}{n} \bigm| \psi[M_i, M_{\phi(d+1)}] > R\right). \end{equation}$ (90)Given above considerations, P_o:o(A_i,j | C ∩ C′) can be evaluated as $p_{o:o}^{w} (i,j) := p_{d_{\min} (i)}^{w} (i,j)$ $\hbox{$p^\wrong_\oto(i, j) \coloneqq p^\wrong_{\smash[t]{\depthmin(i)}}(i, j)$}$ .

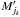The computation of $p_{d}^{w} (i,j)$ $\hbox{$p^\wrong_{\smash[t]{d}}(i, j)$}$ may be further restricted (and in practice, because of the recursive sums in Eq. (87), must be) to sources $M_{j_{k}}^{'}$ $\hbox{$\Mp_{j_k}$}$ in the neighborhood of the objects (M_φ(k))_{k ∈ [[1,d]]}, as explained in Sect. 5.2.

5.4.2. Failure of the first try

To test the reliability of the evaluation of P_o:o(A_i,j | C ∩ C′) by 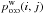$p_{o:o}^{w} (i,j)$ $\hbox{$p^\wrong_\oto(i, j)$}$ , we simulated all-sky mock catalogs for one-to-one associations and analyzed them with a first version of Aspects. Simulations were run for f = 1/2, 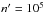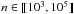$n^{'} = 10^{5}$ $\hbox{$\np = \cramped{10^5}$}$ , $n \in [[10^{3}, 10^{5}]]$ $\hbox{$n \in \integinterv{\cramped{10^3}}{\cramped{10^5}}$}$ , and known circular positional uncertainties with 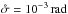$\begin{matrix} _{˚} \\ σ \end{matrix} = 10^{-3} rad$ $\hbox{$\sigmatot = 10^{-3}\,\radian$}$ (see Sects. 6.1 and 6.2 for a detailed description).

Three estimators of f were compared to the input value:

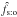$\hbox{$\hat f_\sto$}$ , the value maximizing L_s:o (Eq. (39));
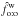$f̂ \begin{matrix} w \\ o:o \end{matrix}$ $\hbox{$\hat f_\oto^\wrong$}$ , the value maximizing the one-to-one likelihood 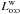$L_{o:o}^{w}$ $\hbox{$\Lhoto^\wrong$}$ derived from the 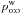$p_{o:o}^{w}$ $\hbox{$p^\wrong_\oto$}$ . This estimator is computed from Eq. (81)with 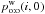$p_{o:o}^{w} (i, 0)$ $\hbox{$p^\wrong_\oto(i, 0)$}$ instead of P_o:o(A_{i, 0} | C ∩ C′);
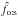$\hbox{$\hat f_\ots$}$ , an estimator built from the one-to-several assumption in the following way: because (H_o:s) is fully symmetric to (H_s:o), we just need to swap K and K′ (i.e., swap f and f′, n and 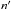$n^{'}$ $\hbox{$\np$}$ , etc.) in Eqs. (24), (26), and (39)to obtain 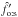$f̂ \begin{matrix} ' \\ o:s \end{matrix}$ $\hbox{$\hat f'_\ots$}$ instead of 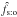$\hbox{$\hat f_\sto$}$ , and then, from Eq. (42), 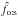$\hbox{$\hat f_\ots$}$ instead of 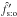$f̂ \begin{matrix} ' \\ s:o \end{matrix}$ $\hbox{$\hat f'_\sto$}$ . The one-to-several likelihood L_o:s is computed from Eq. (32)in the same way.

The mean values of these estimators are plotted as a function of n in Fig. 1a (error bars are smaller than the size of the points). As is obvious, the ad hoc estimator 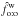$f̂ \begin{matrix} w \\ o:o \end{matrix}$ $\hbox{$\hat f_\oto^\wrong$}$ diverges from f when n increases. This statistical inconsistency ⁵ seems surprising for a maximum likelihood estimator since the model on which it is based is correct by construction. However, all the demonstrations of consistency of maximum likelihood estimators we found in the literature (e.g., in Kendall & Stuart 1979) rest on the assumption that the overall likelihood is the product of the probabilities of each datum, which is not the case for L_o:o (cf. Eq. (73)). Since 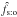$\hbox{$\hat f_\sto$}$ is a good estimator of f, it might be used to compute P_o:o(A_i,j | C ∩ C′) from 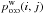$p_{o:o}^{w} (i,j)$ $\hbox{$p^\wrong_\oto(i, j)$}$ – if the latter correctly approximates the former. By itself, the inconsistency of 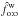$f̂ \begin{matrix} w \\ o:o \end{matrix}$ $\hbox{$\hat f^\wrong_\oto$}$ is therefore not a problem.

More embarrassing is that (H_o:o) is not the most likely assumption (see Fig. 1b): the mean value of 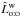$L̂ \begin{matrix} w \\ o:o \end{matrix}$ $\hbox{$\expandafter\hat\Lhoto^\wrong$}$ is less than that of 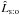$\hbox{$\expandafter\hat\Lhsto$}$ over the full interval of n ! These two failures hint that the sequence $(p_{d}^{w} [i,j])$ $\hbox{$(p^\wrong_{\smash[t]{d}}[i, j])$}$ has not yet converged to P_o:o(A_i,j | C ∩ C′) at d = d_min(i).

To check this, we ran simulations with small numbers of sources (n and 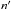$n^{'}$ $\hbox{$\np$}$ less than 10), so that we could compute 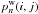$p_{n}^{w} (i,j)$ $\hbox{$p^\wrong_n(i, j)$}$ exactly and study how $(p_{d}^{w} [i,j])$ $\hbox{$(p^\wrong_{\smash[b]d}[i, j])$}$ tends to it. 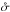To test whether source confusion might be the reason for the problem, we created mock catalogs with very large positional uncertainties ⁶ $\begin{matrix} ˚ \\ σ \end{matrix}$ $\hbox{$\sigmatot$}$ , comparable to the distance between unrelated sources. Because the expressions given in Appendix A for ξ_i,j are for planar normal laws and become wrong when the distance between M_i and $M_{j}^{'}$ $\hbox{$\Mp_j$}$ is more than a few degrees because of the curvature, we ran simulations on a whole circle instead of a sphere; nevertheless, we took 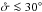$\begin{matrix} _{˚} \\ σ \end{matrix} ≲ 30^{◦}$ $\hbox{$\sigmatot \la 30^\circ$}$ because the linear normal law is inappropriate on a circle for higher values, due to its finite extent. What we found is that, after the transient phase where it oscillates, $(p_{d}^{w} [i,j])$ $\hbox{$(p^\wrong_{\smash[t]{d}}[i, j])$}$ slowly drifts to P_o:o(A_i,j | C ∩ C′) and only converges at d = n ! 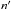This drift was imperceptible for the high values of n and $n^{'}$ $\hbox{$\np$}$ used in Sect. 5.4.1.

5.4.3. Reconsideration and solution

To understand where the problem comes from, we consider the simplest case of interest: 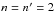$n = n^{'} = 2$ $\hbox{$n = \np = 2$}$ . We assume moreover that ξ_{1, 2} ≈ ξ_{2, 1} ≈ 0. We then have $\begin{matrix} P_{o:o} (C | C^{'}) \approx ([1 - f]^{2} ξ_{1, 0} ξ_{2, 0} + \frac{[1 - f] f}{2} [ξ_{1, 0} ξ_{2, 2} + ξ_{1, 1} ξ_{2, 0}] \\ + \frac{f^{2}}{2} ξ_{1, 1} ξ_{2, 2}) d^{2} r_{1} d^{2} r_{2}, \end{matrix}$ $\begin{eqnarray} \Poto(C \mid C') \approx \Biggl([1-f]^2\multspace \xi_{1\comma 0}\multspace \xi_{2\comma 0} + \frac{[1-f]\multspace f}{2}\multspace [\xi_{1\comma 0}\multspace \xi_{2\comma 2} + \xi_{1\comma 1}\multspace \xi_{2\comma 0}] \nonumber \\ +\frac{f^2}{2}\multspace \xi_{1\comma 1}\multspace \xi_{2\comma 2}\Biggr) \multspace \df^2\vec r_1\multspace \df^2\vec r_2, \end{eqnarray}$ (91) $\begin{matrix} P_{o:o} (A_{1, 0} \cap C | C^{'}) \approx (1 - f) ξ_{1, 0} ([1 - f] ξ_{2, 0} + \frac{f}{2} ξ_{2, 2}) d^{2} r_{1} d^{2} r_{2}, \\ P_{o:o} (A_{1, 1} \cap C | C^{'}) \approx \frac{f}{2} ξ_{1, 1} ([1 - f] ξ_{2, 0} + f ξ_{2, 2}) d^{2} r_{1} d^{2} r_{2} . \end{matrix}$ $\begin{eqnarray} && \Poto(A_{1\comma 0} \cap C \mid C') \approx (1\!-\!f)\multspace \xi_{1\comma 0}\multspace \Biggl([1\!-\!f]\multspace \xi_{2\comma 0} + \frac{f}{2}\multspace \xi_{2\comma 2}\Biggr) \multspace \df^2\vec r_1\multspace \df^2\vec r_2, ~~~~~~~~~~~~~~~~~~~~~~~\\ &&\Poto(A_{1\comma 1} \cap C \mid C') \approx \frac{f}{2}\multspace \xi_{1\comma 1}\multspace \left([1-f]\multspace \xi_{2\comma 0} + f\multspace \xi_{2\comma 2}\right)\multspace \df^2\vec r_1 \multspace \df^2\vec r_2.~~~~~~~~~~~~~~~~~~~~~~~ \end{eqnarray}$ The probabilities P_o:o(A_1,j | C ∩ C′) = P_o:o(A_1,j ∩ C | C′) /P_o:o(C | C′) obviously depend on ξ_{2, 2}. In particular, ifξ_{2, 2} ≪ ξ_{2, 0}, $\begin{matrix} \begin{matrix} \end{matrix} P_{o:o} (A_{1, 0} | C \cap C^{'}) \approx \frac{(1 - f) ξ_{1, 0}}{(1 - f) ξ_{1, 0} + f ξ_{1, 1} / 2}, \begin{matrix} \end{matrix} \\ \begin{matrix} \end{matrix} P_{o:o} (A_{1, 1} | C \cap C^{'}) \approx \frac{f ξ_{1, 1} / 2}{(1 - f) ξ_{1, 0} + f ξ_{1, 1} / 2}; \end{matrix} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix}$ $\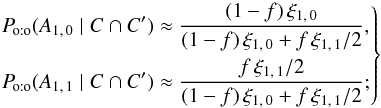begin{equation} \label{<<} \Left. \begin{aligned} \Poto(A_{1\comma 0} \mid C \cap C') &\approx \frac{(1-f)\multspace \xi_{1\comma 0}}{ (1-f)\multspace \xi_{1\comma 0} + f\multspace \xi_{1\comma 1}/2}, \\ \Poto(A_{1\comma 1} \mid C \cap C') &\approx \frac{f\multspace \xi_{1\comma 1}/2}{ (1-f)\multspace \xi_{1\comma 0} + f\multspace \xi_{1\comma 1}/2}; \end{aligned} \Right\} \end{equation}$ (94)in that case, P_o:o(A_{2, 2} | C ∩ C′) ≈ 0, and both $M_{1}^{'}$ $\hbox{$\Mp_1$}$ and $M_{2}^{'}$ $\hbox{$\Mp_2$}$ are free for M₁. On the other hand, ifξ_{2, 2} ≫ ξ_{2, 0}, $\begin{matrix} \begin{matrix} \end{matrix} P_{o:o} (A_{1, 0} | C \cap C^{'}) \approx \frac{(1 - f) ξ_{1, 0}}{(1 - f) ξ_{1, 0} + f ξ_{1, 1} / 1}, \begin{matrix} \end{matrix} \\ \begin{matrix} \end{matrix} P_{o:o} (A_{1, 1} | C \cap C^{'}) \approx \frac{f ξ_{1, 1} / 1}{(1 - f) ξ_{1, 0} + f ξ_{1, 1} / 1}; \end{matrix} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix}$ $\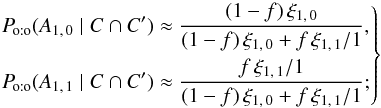begin{equation} \label{>>} \Left. \begin{aligned} \Poto(A_{1\comma 0} \mid C \cap C') &\approx \frac{(1-f)\multspace \xi_{1\comma 0}}{ (1-f)\multspace \xi_{1\comma 0} + f\multspace \xi_{1\comma 1}/1}, \\ \Poto(A_{1\comma 1} \mid C \cap C') &\approx \frac{f\multspace \xi_{1\comma 1}/1}{ (1-f)\multspace \xi_{1\comma 0} + f\multspace \xi_{1\comma 1}/1}; \end{aligned} \Right\} \end{equation}$ (95)in that case, P_o:o(A_{2, 2} | C ∩ C′) ≈ 1: M₂ and 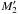$M_{2}^{'}$ $\hbox{$\Mp_{2}$}$ are almost certainly bound, so 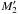$M_{2}^{'}$ $\hbox{$\Mp_{2}$}$ may not be associated to M₁, and 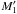$M_{1}^{'}$ $\hbox{$\Mp_{1}$}$ is the only possible counterpart of M₁.

Fig. 2

Mean value of different estimators $\hbox{$\hat f$}$ of f as a function of n for f = 1/2 (dotted line), $n^{'} = 10^{5}$ $\hbox{$\np = 10^5$}$ , and circular positional uncertainty ellipses with $\begin{matrix} _{˚} \\ σ \end{matrix} = 10^{-3} rad$ $\hbox{$\sigmatot = 10^{-3}\,\radian$}$ (see Sects. 6.1 and 6.2 for details). a) Several-to-one simulations. b) One-to-one simulations ( $\hbox{$\hat f_\sto$}$ and $\hbox{$\hat f_\oto$}$ overlap).

The difference between the results obtained for ξ_{2, 2} ≪ ξ_{2, 0} and ξ_{2, 2} ≫ ξ_{2, 0} shows that probabilities P_o:o(A_1,j | C ∩ C′) depend on the relative positions of M₂ and 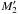$M_{2}^{'}$ $\hbox{$\Mp_{2}$}$ , even when both M₂ and 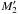$M_{2}^{'}$ $\hbox{$\Mp_{2}$}$ are distant from M₁ and 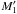$M_{1}^{'}$ $\hbox{$\Mp_{1}$}$ : unlike the idea stated in Sect. 5.4.1, distant K-sources do matter for P_o:o probabilities! However, as highlighted by the “/ 2” and “/ 1” factors in Eqs. (94)and (95), the distant K-source M₂ only changes the number of K′-sources (two for ξ_{2, 2} ≪ ξ_{2, 0}, one for ξ_{2, 2} ≫ ξ_{2, 0}) that may be identified to M₁: its exact position is unimportant.

This suggests the following solution: replace 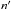$n^{'}$ $\hbox{$\np$}$ in Eq. (89)by the number 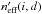$n_{eff}^{'} (i,d)$ $\hbox{$\npeff(i,d)$}$ of K′-sources that may effectively be associated to M_i and its d − 1 nearest neighbors in K; i.e., dropping the superscript “w”, define $p_{d} (i,j) := \frac{ζ_{i, j} \sum \begin{matrix} n^{'} \\ j_{2} = 0 j_{2} \notin \begin{matrix} 􏽥 \\ X_{1}^{⋆} \end{matrix} \end{matrix} \cdot \cdot \cdot \sum \begin{matrix} n^{'} \\ j_{d} = 0 j_{d} \notin \begin{matrix} 􏽥 \\ X_{d - 1}^{⋆} \end{matrix} \end{matrix} 􏽑_{k = 2}^{d} {η_{k, j_{k}}^{⋆}}^{􏽥}}{\sum \begin{matrix} n^{'} \\ j_{1} = 0 j_{1} \notin \begin{matrix} 􏽥 \\ X_{0} \end{matrix} \end{matrix} \sum \begin{matrix} n^{'} \\ j_{2} = 0 j_{2} \notin \begin{matrix} 􏽥 \\ X_{1} \end{matrix} \end{matrix} \cdot \cdot \cdot \sum \begin{matrix} n^{'} \\ j_{d} = 0 j_{d} \notin \begin{matrix} 􏽥 \\ X_{d - 1} \end{matrix} \end{matrix} 􏽑_{k = 1}^{d} \begin{matrix} 􏽥 \\ η_{k, j_{k}} \end{matrix}},$ $\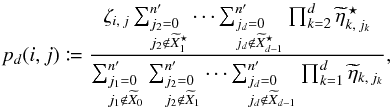begin{equation} \label{P_oto_iter} p_d(i, j) \coloneqq \frac{\zeta_{i\comma j}\multspace \sum_{\leftsubstack{j_2=0\\ j_2\not\in \widetilde X^{\star}_1}}^\np \cdots \sum_{\leftsubstack{j_d=0\\ j_d\not\in \widetilde X^{\star}_{d-1}}}^\np \prod_{k=2}^d \widetilde\eta^{\,\star}_{k\comma j_k} }{ \sum_{\leftsubstack{j_1=0\\ j_1\not\in \widetilde X_0}}^\np \sum_{\leftsubstack{j_2=0\\ j_2\not\in \widetilde X_1}}^\np \cdots \sum_{\leftsubstack{j_d=0\\ j_d\not\in \widetilde X_{d-1}}}^\np \prod_{k=1}^d \widetilde\eta_{k\comma j_k} }, \end{equation}$ (96)where $\begin{matrix} \begin{matrix} \end{matrix} \begin{matrix} 􏽥 \\ η_{k, 0} \end{matrix} := {η_{k, 0}^{⋆}}^{􏽥} := ζ_{φ (k), 0}; {η_{k, j_{k}}^{⋆}}^{􏽥} := \frac{f ξ_{φ (k), j_{k}}}{n_{eff}^{'} (i, d) - # \begin{matrix} 􏽥 \\ X_{k - 1}^{⋆} \end{matrix}} \\ \begin{matrix} \end{matrix} and \begin{matrix} 􏽥 \\ η_{k, j_{k}} \end{matrix} := \frac{f ξ_{φ (k), j_{k}}}{n_{eff}^{'} (i, d) - # \begin{matrix} 􏽥 \\ X_{k - 1} \end{matrix}} for j_{k} \neq 0, \end{matrix} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix}$ $\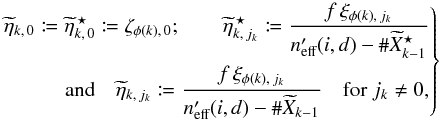begin{equation} \Left. \begin{aligned} \widetilde\eta_{k\comma 0} \coloneqq \widetilde\eta^{\,\star}_{k\comma 0} \coloneqq \zeta_{\phi(k)\comma 0}; \qquad \widetilde\eta^{\,\star}_{k\comma j_k} \coloneqq \frac{f\multspace \xi_{\phi(k)\comma j_k}}{ \npeff(i{,}\,d)-\card \widetilde X^{\star}_{k-1}} \\ \text{and}\quad \widetilde\eta_{k\comma j_k} \coloneqq \frac{f\multspace \xi_{\phi(k)\comma j_k}}{ \npeff(i{,}\,d)-\card \widetilde X_{k-1}} \quad\text{for } j_k \neq 0, \end{aligned}\Right\} \end{equation}$ (97)and use p_o:o(i,j) := p_{d_min(i)}(i,j), where d_min(i) is defined by Eq. (90), to evaluate P_o:o(A_i,j | C ∩ C′).

An estimate of 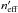$n_{eff}^{'}$ $\hbox{$\npeff$}$ is given by ⁷ $n_{eff}^{'} (i,d) = n^{'} - \sum_{k = d + 1}^{n} (1 - P_{o:o} [A_{φ (k), 0} | C \cap C^{'}]^{)} .$ $\begin{equation} \label{n_eff} \npeff(i,d) = \np - \sum_{k=d+1}^n{\left(1 - \Poto[A_{\phi(k)\comma0} \mid C \cap C']\right)}. \end{equation}$ (98)The sum in Eq. (98)is nothing but the typical number of counterparts in K′ associated to distant K-sources. 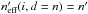Note that $n_{eff}^{'} (i,d = n) = n^{'}$ $\hbox{$\npeff(i, d = n) = \np$}$ , so we recover the theoretical result for P_o:o(A_i,j | C ∩ C′) when all sources are considered. As P_o:o depends on 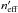$n_{eff}^{'}$ $\hbox{$\npeff$}$ which in turn depends on P_o:o, both may be computed with a back and forth iteration; this procedure converges in a few steps if, instead of P_o:o, the value of P_s:o is taken to initiate the sequence.

5.5. Tests of Aspects

As computations made under assumption (H_o:o) are complex (they involve recursive sums for instance), we made several consistency checks of the code. In particular, we swapped K and K′ for 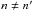$n \neq n^{'}$ $\hbox{$n \neq \np$}$ and compared quantities resulting from this swap (written with the superscript “↔”) to original ones: within numerical errors, 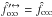$f̂ \begin{matrix} ' \leftrightarrow \\ o:o \end{matrix} = f̂_{o:o}$ $\hbox{$\hat f'^\leftrightarrow_\oto = \hat f_\oto$}$ and, for f^{′ ↔} = f, we get 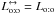$L_{o:o}^{\leftrightarrow} = L_{o:o}$ $\hbox{$\Lhoto^\leftrightarrow = \Lhoto$}$ and $P_{o:o}^{\leftrightarrow} (A_{j, i} | C^{'} \cap C) = P_{o:o} (A_{i, j} | C \cap C^{'})$ $\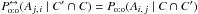hbox{$\Poto^\leftrightarrow(A_{j\comma i} \mid C' \cap C) = \Poto(A_{i\comma j} \mid C \cap C')$}$ for all $(M_{i}, M_{j}^{'})$ $\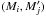hbox{$(M_i, \Mp_j)$}$ .

We moreover numerically checked for small n and 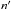$n^{'}$ $\hbox{$\np$}$ (≲5) that Eq. (73)and the integral of Eq. (80)with respect to f are consistent and that Aspects returns the same value as Mathematica (Wolfram 1996). For even smaller n and 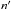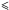$n^{'}$ $\hbox{$\np$}$ ( $\hbox{$\leqslant $}$ 3), we confirmed that manual analytical expressions, obtained from the enumeration of all possible associations between K and K′, are identical to Mathematica’s symbolic calculations. For the large n and 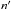$n^{'}$ $\hbox{$\np$}$ of practical interest, although we did not give a formal proof of the solution of Sect. 5.4.3, the analysis of simulations (Sect. 6) makes us confident in the code.

6. Simulations

In this section, we analyze various estimators of the unknown parameters. Because of the complexity of the expressions we obtained, we did not try to do it analytically but used simulations. We also compare the likelihood of the assumptions (H_s:o), (H_o:o), and (H_o:s), given the data.

6.1. Creation of mock catalogs

We have built all-sky mock catalogs with Aspects in the cases of several- and one-to-one associations. To do this, we first selected the indices of fn objects in K, and associated randomly the index of a counterpart in K′ to each of them; for one-to-one simulations, a given K′-source was associated at most once. We then drew the true positions of K′-sources uniformly on the sky. The true positions of K-sources without counterpart were also drawn in the same way; for sources with a counterpart, we took the true position of their counterpart. The observed positions of K- and K′-sources were finally computed from the true positions for given parameters (a_i,b_i,β_i) and $(a_{j}^{'}, b_{j}^{'}, β_{j}^{'})$ $\hbox{$(a'_{\smash[t]{j}}, b'_{\smash[t]{j}}, \betapj)$}$ of the positional uncertainty ellipses (see Appendix A.2.1).

6.2. Estimation of f if positional uncertainty ellipses are known and circular

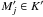Mock catalogs were created with a_i = b_i = σ (see notations in Appendix A.2.1) for all M_i ∈ K and with $a_{j}^{'} = b_{j}^{'} = σ^{'}$ $\hbox{$a'_{\smash[t]{j}} = b'_{\smash[t]{j}} = \sigma'$}$ for all $M_{j}^{'} \in K^{'}$ $\hbox{$\Mp_j \in K'$}$ . Positional uncertainty ellipses are therefore circular here. Only two parameters matter in that case: f and 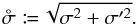$\begin{matrix} ˚ \\ σ \end{matrix} := \sqrt{σ^{2} + σ^{' 2}} .$ $\begin{equation} \sigmatot \coloneqq \!\sqrt{\sigma^2+\sigma'^2}. \end{equation}$ (99)Hundreds of simulations were run for f = 1/2, 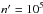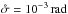$n^{'} = 10^{5}$ $\hbox{$\np = 10^5$}$ , $\begin{matrix} _{˚} \\ σ \end{matrix} = 10^{-3} rad$ $\hbox{$\sigmatot = 10^{-3}\,\radian$}$ , and n ∈ [[10³, 10⁵]]. We analyzed them with Aspects, knowing positional uncertainties, and plot the mean value of the estimators of f listed in Sect. 5.4.2 as a function of n in Fig. 2. This time, however, we replaced 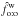$f̂ \begin{matrix} w \\ o:o \end{matrix}$ $\hbox{$\hat f_\oto^\wrong$}$ by the estimator 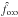$\hbox{$\hat f_\oto$}$ computed from the p_o:o.

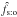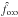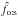For several-to-one simulations, $\hbox{$\hat f_\sto$}$ is by far the best estimator of f and does not show any significant bias, whatever the value of n. 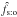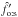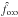Estimators $\hbox{$\hat f_\oto$}$ and $\hbox{$\hat f_\ots$}$ do not recover the input value of f, which is not surprising since they are not built from the right assumption here; moreover, while $\hbox{$\hat f_\sto$}$ , $f̂ \begin{matrix} ' \\ o:s \end{matrix}$ $\hbox{$\hat f'_\ots$}$ , and $\hbox{$\hat f_\oto$}$ are obtained by maximizing L_s:o, L_o:s, and L_o:o, respectively, 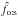$\hbox{$\hat f_\ots$}$ is not directly fitted to the data.

For one-to-one simulations, and unlike 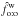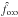$f̂ \begin{matrix} w \\ o:o \end{matrix}$ $\hbox{$\hat f_\oto^\wrong$}$ , $\hbox{$\hat f_\oto$}$ is a consistent estimator of f, as expected. Puzzlingly, 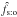$\hbox{$\hat f_\sto$}$ also works very well, maybe because (H_s:o) is a more relaxed assumption than (H_o:o); whatever the reason, this is not a problem.

6.3. Simultaneous estimation of f and 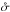$\begin{matrix} ˚ \\ σ \end{matrix}$ $\hbox{$\sigmatot$}$

6.3.1. Circular positional uncertainty ellipses

How do different estimators of f and $\begin{matrix} ˚ \\ σ \end{matrix}$ $\hbox{$\sigmatot$}$ behave when the true values of positional uncertainties are also ignored? We show in Fig. 3 the result of simulations with the same input as in Sect. 6.2, except that $n = n^{'} = 2 \times 10^{4}$ $\hbox{$n = \np = 2\times10^4$}$ . The likelihood L_s:o peaks very close to the input value of $x := (f, \begin{matrix} _{˚} \\ σ \end{matrix})$ $\hbox{$\vec x \coloneqq (f, \sigmatot)$}$ for both types of simulations: $\hat{x}_{s:o}$ $\hbox{$\hat{\vec x}_\sto$}$ is still an unbiased estimator of x. For one-to-one simulations, L_o:o is also maximal near the input value of x, so 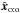$\hat{x}_{o:o}$ $\hbox{$\hat{\vec x}_\oto$}$ is unbiased, too.

Fig. 3

Contour lines of L_s:o (solid) and L_o:o (dashed) in the $(f, \begin{matrix} _{˚} \\ σ \end{matrix})$ $\hbox{$(f, \sigmatot)$}$ plane. Input parameters are the same as in Fig. 2, except that $n = n^{'} = 2 \times 10^{4}$ $\hbox{$n = \np = 2\times10^4$}$ ; the input values of f and $\begin{matrix} ˚ \\ σ \end{matrix}$ $\hbox{$\sigmatot$}$ are indicated by dotted lines (see Sect. 6.3.1 for details). a) Several-to-one simulations. b) One-to-one simulations.

Fig. 4

Contour lines of L_s:o (solid) and L_o:o (dashed) in the $(f, \begin{matrix} _{˚} \\ σ \end{matrix})$ $\hbox{$(f, \sigmatot)$}$ plane. Input parameters are the same as in Fig. 2, except that positional uncertainty ellipses are elongated and randomly oriented (see Sect. 6.3.2 for details); the input value of f is indicated by a dotted line. a) Several-to-one simulations. b) One-to-one simulations.

6.3.2. Elongated positional uncertainty ellipses

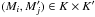To test the robustness of estimators of f, we ran simulations with the same parameters, but with elongated positional uncertainty ellipses: we took $a_{i} = a_{j}^{'} = 1.5 \times 10^{-3} rad$ $\hbox{$a_i = a'_{\smash[t]{j}} = 1.5\times10^{-3}\,\radian$}$ and $b_{i} = b_{j}^{'} = a_{i} / 3$ $\hbox{$b_i = b'_{\smash[t]{j}} = a_i/3$}$ for all $(M_{i}, M_{j}^{'}) \in K \times K^{'}$ $\hbox{$(M_i, \Mp_j) \in K \times K'$}$ . These ellipses were randomly oriented; i.e., position angles (cf. Appendix A.2.1) β_i and 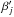$β_{j}^{'}$ $\hbox{$\betapj$}$ have uniform random values in [0,ß [. We then estimated f, but ignoring these positional uncertainties (see Fig. 4).

Although the model from which the parameters are fitted is inaccurate here (the ξ_i,j are computed assuming circular positional uncertainties instead of the unknown elliptical ones), the input value of f is still recovered by 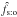$\hbox{$\hat f_\sto$}$ for both types of simulations and by 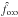$\hbox{$\hat f_\oto$}$ for one-to-one simulations. The fitting also provides the typical positional uncertainty 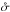$\begin{matrix} ˚ \\ σ \end{matrix}$ $\hbox{$\sigmatot$}$ on the relative positions of associated sources.

6.4. Choice of association model

Now, given the two catalogs, which assumption should we adopt to compute the probabilities P(A_i,j | C ∩ C′): several-to-one, one-to-one or one-to-several? As shown in Fig. 5, for known positional uncertainties and a given 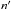$n^{'}$ $\hbox{$\np$}$ , source confusion is rare at low values of n (there is typically at most one possible counterpart) and all assumptions are equally likely. 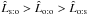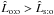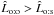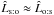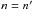At larger n, $\hbox{$\expandafter\hat\Lhsto > \expandafter\hat\Lhoto > \expandafter\hat\Lhots$}$ for several-to-one simulations; as expected, for one-to-one simulations, $\hbox{$\expandafter\hat\Lhoto > \expandafter\hat\Lhsto$}$ and $\hbox{$\expandafter\hat\Lhoto > \expandafter\hat\Lhots$}$ , with $\hbox{$\expandafter\hat\Lhsto \approx \expandafter\hat\Lhots$}$ for $n = n^{'}$ $\hbox{$n = \np$}$ . In all cases, on average, the right assumption is the most likely. This is also true when positional uncertainties are ignored (Sect. 6.3).

The calculation of L_o:o is lengthy, and as a substitute to the comparison of the likelihoods, the following procedure may be applied to select the most appropriate assumption to compute the probabilities of association: if 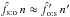$f̂_{s:o} n \approx f̂ \begin{matrix} ' \\ o:s \end{matrix} n^{'}$ $\hbox{$\hat f_\sto\multspace n \approx \hat f'_\ots\multspace \np$}$ , use (H_o:o); if 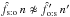$f̂_{s:o} n ≉ f̂ \begin{matrix} ' \\ o:s \end{matrix} n^{'}$ $\hbox{$\hat f_\sto\multspace n \not\approx \hat f'_\ots\multspace \np$}$ , then use (H_s:o) if 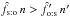$f̂_{s:o} n > f̂ \begin{matrix} ' \\ o:s \end{matrix} n^{'}$ $\hbox{$\hat f_\sto\multspace n > \hat f'_\ots\multspace \np$}$ , and (H_o:s) otherwise.

Fig. 5

Normalized average maximum value $\hbox{$\hat\Lh$}$ of different likelihoods as a function of n, compared to $\hbox{$\expandafter\hat\Lhoto$}$ . Simulations are the same as in Fig. 2. a) Several-to-one simulations. b) One-to-one simulations.

7. Conclusion

In this paper, we computed the probabilities of positional association of sources between two catalogs K and K′ under two different assumptions: first, the easy case where several K-objects may share the same counterpart in K′, then the more natural but numerically intensive case of one-to-one associations only between K and K′.

These probabilities depend on at least one unknown parameter: the fraction of sources with a counterpart. If the positional uncertainties are unknown, other parameters are required to compute the probabilities. We calculated the likelihood of observing all the K- and K′-sources at their effective positions under each of the two assumptions described above, and estimated the unknown parameters by maximizing these likelihoods. The latter are also used to select the best association model.

These relations were implemented in a code, Aspects, which we make public and with which we analyzed all-sky several-to-one and one-to-one simulations. In all cases, the assumption with the highest likelihood is the right one, and estimators of unknown parameters obtained for it do not show any bias.

In the simulations, we assumed that the density of K- and K′-sources was uniform on the sky area S: the quantities ξ_{i, 0} and ξ_0,j used to compute the probabilities are then equal to 1 /S. If the density of objects is not uniform, we might take ξ_{i, 0} = ρ(M_i) /n and 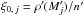$ξ_{0, j} = ρ^{'} (M_{j}^{'}) / n^{'}$ $\hbox{$\xi_{0\comma j} = \rho'\mkern-1mu(\Mp_j)/\np$}$ , where ρ and ρ′ are, respectively, the local surface densities of K- and K′-sources; but if the ρ′rho ratio varies on the sky, so will the fraction of sources with a counterpart – something we did not try to model. Considering clustering or the side effects ⁸ due to a small S, as well as taking priors on the SED of objects into account was also beyond the scope of this paper.

In spite of these limitations, Aspects is a robust tool that should help astronomers cross-identify astrophysical sources automatically, efficiently and reliably.

¹

For instance, de Ruiter et al. (1977) wrongly state that, if there is a counterpart, the closest object is always the right one.

²

For the sake of clarity, we mention that we adopt the same decreasing order of precedence for operators as in Mathematica (Wolfram 1996): × and /; Π; ∑; + and −.

³

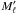Computing P_s:o(C | C′) is easier than for P_s:o(C′ | C): the latter would require calculating $P_{s:o} (c_{ℓ}^{'} | {^{􏽔}}_{k = 1; j_{k} = ℓ}^{n} [c_{k} \cap A_{k, j_{k}}])$ $\hbox{$\Psto(c'_{\smash[t]{\ell}} \mid \bigcap_{\smash[t]{k=1{;}\, j_k=\ell}}^n {[c_k \cap A_{k\comma j_k}]})$}$ (cf. Eq. (9)) because several M_k might be associated with the same $M_{ℓ}^{'}$ $\hbox{$\Mp_\ell$}$ . This does not matter for computations made under assumption (H_o:o).

⁴

Fortran 90 routines from Numerical Recipes (Press et al. 1992) are used to sort arrays and locate a value in an ordered table. Because of license constraints, we cannot provide them, but they may easily be replaced by free equivalents.

⁵

A consistent estimator is a statistic converging to the true value of a parameter when the size of the sample from which it is derived increases. The concept of consistency is not very clear in the context of this paper, since there are two sample sizes, n and $n^{'}$ $\hbox{$\np$}$ .

⁶

Small positional uncertainties could also be used if sources were distributed on a small fraction of the sky, but there might be side effects.

⁷

Equation (98)is valid for any f ∈ [0,1]. When $\hbox{$f \approx \hat f_\oto$}$ , it is more efficient to make the approximation $n_{eff}^{'} (i,d) \approx n^{'} - f (n - d)$ $\hbox{$\npeff(i,d) \approx \np -f\multspace (n-d)$}$ : this expression accelerates the convergence to $\hbox{$\hat f_\oto$}$ of the sequence (f_k) defined in Sect. 5.3.

⁸

The impact of clustering or of side effects on estimators of unknown parameters might however easily be tested through simulations.

⁹

None of the results established outside of Appendix A depends on this assumption.

¹⁰

If it were not the case, the probability of and might be modeled using Kent (1982) distributions (an adaptation to the sphere of the planar normal law), but no result like Eq. (A.8)would then hold: unlike Gaussians, Kent distributions are not stable.

¹¹

We seize this opportunity to correct Eqs. (A.8) to (A.11) of Pineau et al. (2011): and should be replaced by their squares in these formulae.

¹²

However, as noticed by de Vaucouleurs & Head (1978) in a different context, if three samples with unknown uncertainties σ_i (i ∈ [[1, 3]]) are available and if the combined uncertainties 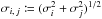$σ_{i, j} := (σ_{i}^{2} + σ_{j}^{2})^{1 / 2}$ $\hbox{$\sigma_{i\comma j} \coloneqq (\sigma_i^2+\sigma^2_j)^{1/2}$}$ may be estimated for all the pairs (i,j)_{j ≠ i} ∈ [[1, 3]]², as in our case, then σ_i may be determined for each sample. Paturel & Petit (1999) used this technique to compute the accuracy of galaxy coordinates.

Acknowledgments

The initial phase of this work took place at the NASA/ Goddard Space Flight Center, under the supervision of Eli Dwek, and was supported by the National Research Council through the Resident Research Associateship Program. We acknowledge them sincerely. We also thank Stéphane Colombi for the discussions we had on the properties of maximum likelihood estimators.

References

Bartlett, J. G., & Egret, D. 1998, in New Horizons from Multi-Wavelength Sky Surveys, eds. B. J. McLean, D. A. Golombek, J. J. E. Hayes, & H. E. Payne, IAU Symp., 179, 437 [Google Scholar]
Bauer, F. E., Condon, J. J., Thuan, T. X., & Broderick, J. J. 2000, ApJS, 129, 547 [NASA ADS] [CrossRef] [Google Scholar]
Benn, C. R. 1983, The Observatory, 103, 150 [NASA ADS] [Google Scholar]
Brand, K., Brown, M. J. I., Dey, A., et al. 2006, ApJ, 641, 140 [NASA ADS] [CrossRef] [Google Scholar]
Budavári, T., & Szalay, A. S. 2008, ApJ, 679, 301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Condon, J. J., Balonek, T. J., & Jauncey, D. L. 1975, AJ, 80, 887 [NASA ADS] [CrossRef] [Google Scholar]
Condon, J. J., Anderson, E., & Broderick, J. J. 1995, AJ, 109, 2318 [NASA ADS] [CrossRef] [Google Scholar]
de Ruiter, H. R., Arp, H. C., & Willis, A. G. 1977, A&AS, 28, 211 [NASA ADS] [Google Scholar]
de Vaucouleurs, G., & Head, C. 1978, ApJS, 36, 439 [NASA ADS] [CrossRef] [Google Scholar]
de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies (New York: Springer) [Google Scholar]
Fioc, M. 2014, Aspects: code documentation and complements [arXiv:1404.4224] [Google Scholar]
Fleuren, S., Sutherland, W., Dunne, L., et al. 2012, MNRAS, 423, 2407 [NASA ADS] [CrossRef] [Google Scholar]
Haakonsen, C. B., & Rutledge, R. E. 2009, ApJS, 184, 138 [NASA ADS] [CrossRef] [Google Scholar]
Kendall, M., & Stuart, A. 1979, The advanced theory of statistics. Vol. 2: Inference and relationship (London: Griffin) [Google Scholar]
Kent, J. T. 1982, J. Roy. Stat. Soc. Ser. B, Stat. Methodol., 44, 71 [Google Scholar]
Kim, S., Wardlow, J. L., Cooray, A., et al. 2012, ApJ, 756, 28 [NASA ADS] [CrossRef] [Google Scholar]
Kuchinski, L. E., Freedman, W. L., Madore, B. F., et al. 2000, ApJS, 131, 441 [NASA ADS] [CrossRef] [Google Scholar]
McAlpine, K., Smith, D. J. B., Jarvis, M. J., Bonfield, D. G., & Fleuren, S. 2012, MNRAS, 423, 132 [NASA ADS] [CrossRef] [Google Scholar]
Moshir, M., Kopman, G., & Conrow, T. A. O. 1992, IRAS Faint Source Survey, Explanatory supplement version 2 (IPAC) [Google Scholar]
Moshir, M., Copan, G., Conrow, T., et al. 1993, VizieR Online Data Catalog: II/156 [Google Scholar]
Paturel, G., & Petit, C. 1999, A&A, 352, 431 [NASA ADS] [Google Scholar]
Paturel, G., Bottinelli, L., & Gouguenheim, L. 1995, Astrophys. Lett. Commun., 31, 13 [Google Scholar]
Paturel, G., Petit, C., Prugniel, P., et al. 2003, VizieR Online Data Catalog: VII/237 [Google Scholar]
Pineau, F.-X., Motch, C., Carrera, F., et al. 2011, A&A, 527, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in Fortran. The art of scientific computing (Cambridge: University press) [Google Scholar]
Prestage, R. M., & Peacock, J. A. 1983, MNRAS, 204, 355 [NASA ADS] [Google Scholar]
Rohde, D. J., Gallagher, M. R., Drinkwater, M. J., & Pimbblet, K. A. 2006, MNRAS, 369, 2 [NASA ADS] [CrossRef] [Google Scholar]
Roseboom, I. G., Oliver, S., Parkinson, D., & Vaccari, M. 2009, MNRAS, 400, 1062 [NASA ADS] [CrossRef] [Google Scholar]
Rutledge, R. E., Brunner, R. J., Prince, T. A., & Lonsdale, C. 2000, ApJS, 131, 335 [NASA ADS] [CrossRef] [Google Scholar]
Sutherland, W., & Saunders, W. 1992, MNRAS, 259, 413 [NASA ADS] [CrossRef] [Google Scholar]
Vignali, C., Fiore, F., Comastri, A., et al. 2009, in Multi-wavelength Astronomy and Virtual Observatory (European Space Agency), eds. D. Baines, & P. Osuna, 53 [Google Scholar]
Wolfram, S. 1996, The Mathematica book (Cambridge University Press) [Google Scholar]
Wolstencroft, R. D., Savage, A., Clowes, R. G., et al. 1986, MNRAS, 223, 279 [NASA ADS] [Google Scholar]

Appendix A: Probability distribution of the observed relative positions of associated sources

Appendix A.1: Properties of normal laws

We first recall a few standard results. The probability that an m-dimensional normally distributed random vector W of mean μ and variance Γ falls in some domain Ω is $P (W \in Ω) = \int_{w \in Ω} \frac{\exp (- \frac{1}{2} [w - μ]_{B}^{t} \cdot Γ_{B}^{-1} \cdot [w - μ]_{B})}{(2 ß)^{m / 2} \sqrt{\det Γ_{B}}} d^{m} w_{B},$ $\appendix \setcounter{section}{1} \begin{equation} \Prob(\vec W \in \Omega) = \int_{\vec w \in \Omega} \frac{ \exp\left(-\frac{1}{2}\multspace \transpose{[\vec w-\vec\mu]_B} \cdot \Gamma_B^{-1} \cdot [\vec w-\vec\mu]_B\right) }{ (2\multspace \piup)^{m/2} \multspace \!\sqrt{\det\Gamma_B} } \multspace \df^m\vec w_B, \end{equation}$ (A.1)where B := (u₁,...,u_m) is a basis, w is a vector, w_B = (w₁,...,w_m)^t (resp. μ_B) is the column vector expression of w (resp. 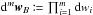μ) in B, $d^{m} w_{B} := {^{􏽑}}_{i = 1}^{m} d w_{i}$ $\hbox{$\df^m\vec w_B \coloneqq \prod_{i=1}^m \df w_i$}$ , and Γ_B is the covariance matrix of W (i.e. the matrix representation of Γ) in B. We denote this by W ~ G_m(μ,Γ).

In another basis $B^{'} := (u_{1}^{'}, ..., u_{m}^{'})$ $\hbox{$B' \coloneqq (\vec u'_{\smash[t]{1}}, \ldots, \vec u'_{\smash[t]{m}})$}$ , we have w_B = T_{B → B′}·w_B′, where T_{B → B′} is the transformation matrix from B to B′ (i.e. $u_{j}^{'} = \sum_{i = 1}^{m} (T_{B \to B^{'}})_{i, j} u_{i}$ $\hbox{$\vec u'_{\smash[t]{j}} = \sum_{i=1}^m {(T_{B\rightarrow B'})_{i\comma j}\multspace \vec u_i}$}$ ). Since d^mw_B = | detT_{B → B′} | d^mw_B′ and $\begin{matrix} (w - μ)_{B}^{t} \cdot Γ_{B}^{-1} \cdot (w - μ)_{B} \\ = (w - μ)_{B^{'}}^{t} \cdot {(T_{B \to B^{'}}^{-1} \cdot Γ_{B} \cdot [T_{B \to B^{'}}^{-1}]^{t})}^{-1} \cdot (w - μ)_{B^{'}}, \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} \transpose{(\vec w-\vec\mu)_B} \cdot \Gamma_B^{-1} \cdot (\vec w-\vec\mu)_B \nonumber\\ = \transpose{(\vec w-\vec\mu)_{B'}} \cdot \left(T_{B\rightarrow B'}^{-1} \cdot \Gamma_B \cdot \transpose{[T_{B\rightarrow B'}^{-1}]}\right)^{-1} \cdot (\vec w-\vec\mu)_{B'}, \end{eqnarray}$ (A.2)we still obtain $P (W \in Ω) = \int_{w \in Ω} \frac{\exp (- \frac{1}{2} [w - μ]_{B^{'}}^{t} \cdot Γ_{B^{'}}^{-1} \cdot [w - μ]_{B^{'}})}{(2 ß)^{m / 2} \sqrt{\det Γ_{B^{'}}}} d^{m} w_{B^{'}},$ $\appendix \setcounter{section}{1} \begin{equation} \Prob(\vec W \in \Omega) = \int_{\vec w \in \Omega}\!\!\!\!\! 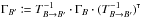\frac{ \exp\left(-\frac{1}{2}\multspace \transpose{[\vec w\!-\!\vec\mu]_{B'}} \cdot \Gamma_{B'}^{-1} \cdot [\vec w\!-\!\vec\mu]_{B'}\right) }{ (2\multspace \piup)^{m/2} \multspace \!\sqrt{\det\Gamma_{B'}} } \multspace \df^m\vec w_{B'}, \end{equation}$ (A.3)where $Γ_{B^{'}} := T_{B \to B^{'}}^{-1} \cdot Γ_{B} \cdot (T_{B \to B^{'}}^{-1})^{t}$ $\hbox{$\Gamma_{B'} \coloneqq T_{B\rightarrow B'}^{-1} \cdot \Gamma_B \cdot \transpose{(T_{B\rightarrow B'}^{-1})}$}$ is the covariance matrix of W in B′. In the following, B and B′ are orthonormal bases, so T_{B → B′} is a rotation matrix. From 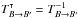$T_{B \to B^{'}}^{t} = T_{B \to B^{'}}^{-1}$ $\hbox{$\transpose{T_{B\rightarrow B'}} = T_{B\rightarrow B'}^{-1}$}$ , we get 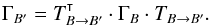$Γ_{B^{'}} = T_{B \to B^{'}}^{t} \cdot Γ_{B} \cdot T_{B \to B^{'}} .$ $\appendix \setcounter{section}{1} \begin{equation} \Gamma_{B'} = \transpose{T_{B\rightarrow B'}} \cdot \Gamma_B \cdot T_{B\rightarrow B'}. \end{equation}$ (A.4)

For independent random vectors W₁ ~ G_m(μ₁,Γ₁) and W₂ ~ G_m(μ₂,Γ₂), we have 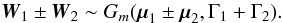$W_{1} \pm W_{2} ~ G_{m} (μ_{1} \pm μ_{2}, Γ_{1} + Γ_{2}) .$ $\appendix \setcounter{section}{1} \begin{equation} \label{somme_gaussiennes} \vec W_1 \pm \vec W_2 \sim G_m(\vec\mu_1 \pm \vec\mu_2, \Gamma_1+\Gamma_2). \end{equation}$ (A.5)

Appendix A.2: Covariance matrix of the probability distribution of relative positions

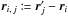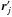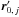We now use these results to derive the probability distribution of vector $r_{i, j} := r_{j}^{'} - r_{i}$ $\hbox{$\vec r_{i\comma j} \coloneqq \vrpj-\vec r_i$}$ , where r_i and $r_{j}^{'}$ $\hbox{$\vrpj$}$ are, respectively, the observed positions of source M_i of K and of its counterpart $M_{j}^{'}$ $\hbox{$\Mp_j$}$ in K′. 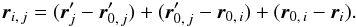Introducing the true positions r_0,i and $r_{0, j}^{'}$ $\hbox{$\vrpzj$}$ of M_i and $M_{j}^{'}$ $\hbox{$\Mp_j$}$ , we have $r_{i, j} = (r_{j}^{'} - r_{0, j}^{'}) + (r_{0, j}^{'} - r_{0, i}) + (r_{0, i} - r_{i}) .$ $\appendix \setcounter{section}{1} \begin{equation} \label{rel_pos} \vec r_{i\comma j} = (\vrpj - \vrpzj) + (\vrpzj - \vrzi) + (\vrzi -\vec r_i). \end{equation}$ (A.6)

Appendix A.2.1: Covariance matrix for identical true positions and known positional uncertainties

Assume⁹, as is usual, that $r_{i} - r_{0, i} ~ G_{2} (0, Γ_{i}) and r_{j}^{'} - r_{0, j}^{'} ~ G_{2} (0, Γ_{j}^{'}) .$ $\appendix \setcounter{section}{1} \begin{equation} \label{r_i,r_j} \vec r_i - \vrzi \sim G_2(\vec 0,\Gamma_i) \qquad\text{and}\qquad \vrpj - \vrpzj \sim G_2(\vec 0,\Gammapj). \end{equation}$ (A.7)If the true positions of M_i and $M_{j}^{'}$ $\hbox{$\Mp_j$}$ are identical (case of point sources), then, from Eqs. (A.5)–(A.7), $r_{i, j} ~ G_{2} (0, Γ_{i, j}), where Γ_{i, j} := Γ_{i} + Γ_{j}^{'} .$ $\appendix \setcounter{section}{1} \begin{equation} \label{rel_pos_ident} \vec r_{i\comma j} \sim G_2(\vec 0, \Gamma_{i\comma j}), \quad\text{where } \Gamma_{i\comma j} \coloneqq \Gamma_i + \Gammapj. \end{equation}$ (A.8)(See also Condon et al. 1995.) In Eqs. (A.7), r_i − r_0,i and $r_{j}^{'} - r_{0, j}^{'}$ $\hbox{$\vrpj - \vrpzj$}$ must be considered as the projections (gnomonic ones, for instance) of these vectors on the planes tangent to the sphere at M_i and $M_{j}^{'}$ $\hbox{$\Mp_j$}$ , respectively; Eqs. (A.7)are approximations, valid only because positional uncertainties are small ¹⁰. Equation (A.8)is also an approximation: it is appropriate because the observed positions of associated sources M_i and $M_{j}^{'}$ $\hbox{$\Mp_j$}$ are close, so the tangent planes to the sphere at both points nearly coincide.

To use Eq. (A.8), we now compute the column vector expression of r_i,j and the covariance matrices associated to Γ_i, $Γ_{j}^{'}$ $\hbox{$\Gammapj$}$ , and Γ_i,j in some common basis. For convenience, we drop the subscript and the “prime” symbol in the following whenever an expression only depends on either M_i or $M_{j}^{'}$ $\hbox{$\Mp_j$}$ .

Let (u_x,u_y,u_z) be a direct orthonormal basis, with u_z oriented from the Earth’s center O to the North Celestial Pole and u_x from O to the Vernal Point. At a point M of right ascension α and declination δ, a direct orthonormal basis (u_r,u_α,u_δ) is defined by $\begin{matrix} u_{r} \\ u_{α} \\ u_{δ} \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} \vec u_r &&\coloneqq \frac{\vec{OM}}{\lVert\vec{OM}\rVert} = \cos\delta\multspace \cos\alpha\multspace \vec u_x + \cos\delta\multspace \sin\alpha\multspace \vec u_y + \sin\delta\multspace \vec u_z,~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \label{u_r} \\[2mm] \vec u_\alpha &&\coloneqq \frac{\partial\vec u_r/\partial\alpha}{ \lVert\partial\vec u_r/\partial\alpha\rVert} = -\!\sin\alpha\multspace \vec u_x + \cos\alpha\multspace \vec u_y,~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \label{u_alpha} \\[2mm] \vec u_\delta &&\coloneqq \frac{\partial\vec u_r/\partial\delta}{ \lVert\partial\vec u_r/\partial\delta\rVert} = -\!\sin\delta\multspace \cos\alpha\multspace \vec u_x - \sin\delta\multspace \sin\alpha\multspace \vec u_y + \cos\delta\multspace \vec u_z.~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \label{u_delta} \end{eqnarray}$ The uncertainty ellipse on the position of M is characterized by the lengths a and b of its semi-major and semi-minor axes, and by the position angle β between the north and the semi-major axis. Let u_a and u_b be unit vectors directed along the major and the minor axes, respectively, and such that (u_r,u_a,u_b) is a direct orthonormal basis and that β := ∠(u_δ,u_a) is in [0,ß [ when counted eastward. 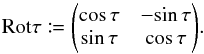Since (u_α,u_δ) is obtained from (u_a,u_b) by a (β − ß/2)-counterclockwise rotation in the plane oriented by + u_r, we have T_{(u_a,u_b) → (u_α,u_δ)} = Rot(β − ß/2), where, for any angle τ, $Rot τ := (\begin{matrix} \cos τ & - \sin τ \\ \sin τ & \cos τ \end{matrix}) .$ $\appendix \setcounter{section}{1} \begin{equation} \Rot\tau \coloneqq \Left(\begin{matrix} \cos\tau & -\!\sin\tau \\ \sin\tau & \cos\tau \end{matrix}\Right). \end{equation}$ (A.12)Using notation 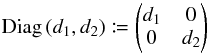$Diag (d_{1}, d_{2}) := (\begin{matrix} d_{1} & 0 \\ 0 & d_{2} \end{matrix})$ $\appendix \setcounter{section}{1} \begin{equation} \Diag\left(d_1, d_2\right) \coloneqq \Left(\begin{matrix} d_1 & 0 \\ 0 & d_2 \end{matrix}\Right) \end{equation}$ (A.13)for diagonal matrices, we have ¹¹ 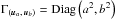$Γ_{(u_{a}, u_{b})} = Diag {}^{(}a^{2}, b^{2}^{)}$ $\hbox{$\Gamma_{(\vec u_a{,}\, \vec u_b)} = \Diag\left(a^2, b^2\right)$}$ and $Γ_{(u_{α}, u_{δ})} = {Rot}^{t} (β - ß / 2) \cdot Diag (a^{2}, b^{2}) \cdot Rot (β - ß / 2) .$ $\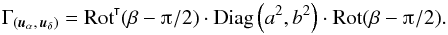appendix \setcounter{section}{1} \begin{equation} \Gamma_{(\vec u_\alpha{,}\, \vec u_\delta)} = \transpose{\Rot}(\beta-\piup/2) \cdot \Diag\left(a^2, b^2\right) \cdot \Rot(\beta-\piup/2). \end{equation}$ (A.14)As noticed by Pineau et al. 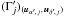(2011), around the Poles, even for sources M_i and $M_{j}^{'}$ $\hbox{$\Mp_j$}$ close to each other, we may have (u_α,i,u_δ,i) ≉ (u_α′,j,u_δ′,j): the covariance matrices (Γ_i)_{(u_α,i,u_δ,i)} and $(Γ_{j}^{'})_{(u_{α^{'}, j}, u_{δ^{'}, j})}$ $\hbox{$(\Gammapj)_{(\uapj,\,\udpj)}$}$ must therefore be first converted to a common basis before their summation in Eq. (A.8). We use the same basis as Pineau et al. (2011), denoted by (t,n) below. While the results we get are intrinsically the same, some people may find our expressions more convenient.

Denote by n := u_r,i × u_r′,j/ ∥ u_r,i × u_r′,j ∥ a unit vector perpendicular to the plane 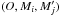$(O, M_{i}, M_{j}^{'})$ $\hbox{$(O, M_i, \Mp_j)$}$ . Because ψ_i,j := ∠(u_r,i,u_r′,j) ∈ [0,ß], we have u_r,i·u_r′,j = cosψ_i,j and ∥ u_r,i × u_r′,j ∥ = sinψ_i,j, so $ψ_{i, j} = \arccos (\cos δ_{i} \cos δ_{j}^{'} \cos [α_{j}^{'} - α_{i}] + \sin δ_{i} \sin {δ_{j}^{'}}^{)},$ $\appendix \setcounter{section}{1} \begin{equation} \label{psi_arccos} \psi_{i\comma j} = \arccos\left( \cos\delta_i\multspace \cos\deltapj\multspace \cos[\alphapj-\alpha_i] + \sin\delta_i\multspace \sin\deltapj \right), \end{equation}$ (A.15)and $n = \frac{u_{r, i} \times u_{r^{'}, j}}{\sin ψ_{i, j}} \cdot$ $\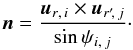appendix \setcounter{section}{1} \begin{equation} \label{vec_n} \vec n = \frac{\uri \times \urpj}{\sin\psi_{i\comma j}}\cdot \end{equation}$ (A.16)Let γ_i := ∠(n,u_δ,i) and 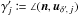$γ_{j}^{'} := ∠ (n, u_{δ^{'}, j})$ $\hbox{$\gammapj \coloneqq \angle(\vec n, \udpj)$}$ be angles oriented clockwise around + u_r,i and + u_r′,j, respectively. Angle γ_i is fully determined by the following expressions (cf. Eqs. (A.16)and (A.9)–(A.11)): 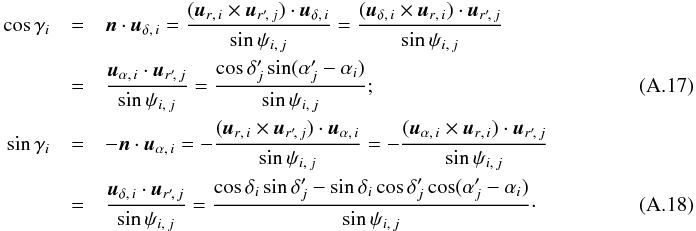$\begin{matrix} \cos γ_{i} & = & n \cdot u_{δ, i} = \frac{(u_{r, i} \times u_{r^{'}, j}) \cdot u_{δ, i}}{\sin ψ_{i, j}} = \frac{(u_{δ, i} \times u_{r, i}) \cdot u_{r^{'}, j}}{\sin ψ_{i, j}} \\ = & \frac{u_{α, i} \cdot u_{r^{'}, j}}{\sin ψ_{i, j}} = \frac{\cos δ_{j}^{'} \sin (α_{j}^{'} - α_{i})}{\sin ψ_{i, j}}; \\ \sin γ_{i} & = & - n \cdot u_{α, i} = - \frac{(u_{r, i} \times u_{r^{'}, j}) \cdot u_{α, i}}{\sin ψ_{i, j}} = - \frac{(u_{α, i} \times u_{r, i}) \cdot u_{r^{'}, j}}{\sin ψ_{i, j}} \\ = & \frac{u_{δ, i} \cdot u_{r^{'}, j}}{\sin ψ_{i, j}} = \frac{\cos δ_{i} \sin δ_{j}^{'} - \sin δ_{i} \cos δ_{j}^{'} \cos (α_{j}^{'} - α_{i})}{\sin ψ_{i, j}} \cdot \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} \cos\gamma_i &=& \vec n\cdot \udi = \frac{(\uri \times \urpj) \cdot \udi}{\sin\psi_{i\comma j}} = \frac{(\udi \times \uri) \cdot \urpj}{\sin\psi_{i\comma j}}~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \notag \\& =& \frac{\uai\cdot \urpj}{\sin\psi_{i\comma j}} = \frac{\cos\deltapj\multspace \sin(\alphapj-\alpha_i)}{\sin\psi_{i\comma j}};~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ \sin\gamma_i &=& -\vec n\cdot \uai = -\frac{(\uri \times \urpj) \cdot \uai}{\sin\psi_{i\comma j}} = -\frac{(\uai \times \uri) \cdot \urpj}{\sin\psi_{i\comma j}}~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \notag \\& =& \frac{\udi\cdot \urpj}{\sin\psi_{i\comma j}} = \frac{\cos\delta_i\multspace \sin\deltapj - \sin\delta_i\multspace \cos\deltapj\cos(\alphapj-\alpha_i)}{ \sin\psi_{i\comma j}}\cdot~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{eqnarray}$ Similarly, $\begin{matrix} \cos γ_{j}^{'} = \frac{\cos δ_{i} \sin (α_{j}^{'} - α_{i})}{\sin ψ_{i, j}} and \\ \sin γ_{j}^{'} = \frac{\cos δ_{i} \sin δ_{j}^{'} \cos (α_{j}^{'} - α_{i}) - \sin δ_{i} \cos δ_{j}^{'}}{\sin ψ_{i, j}} \cdot \end{matrix}$ $\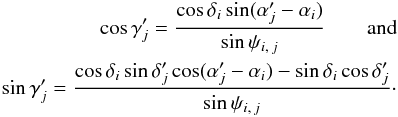appendix \setcounter{section}{1} \begin{eqnarray} \cos\gammapj = \frac{\cos\delta_i\multspace \sin(\alphapj-\alpha_i)}{\sin\psi_{i\comma j}} \qquad \text{and}\nonumber \\ \sin\gammapj = \frac{\cos\delta_i\multspace \sin\deltapj\cos(\alphapj-\alpha_i) - \sin\delta_i\multspace \cos\deltapj}{\sin\psi_{i\comma j}}\cdot \end{eqnarray}$ (A.19)Let $t := n \times u_{r, i}$ $\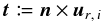appendix \setcounter{section}{1} \begin{equation} \vec t \coloneqq \vec n \times \uri \end{equation}$ (A.20)(≈n × u_r′,j since M_i and $M_{j}^{'}$ $\hbox{$\Mp_j$}$ are close): vector t is a unit vector tangent in M_i to the minor arc of great circle going from M_i to $M_{j}^{'}$ $\hbox{$\Mp_j$}$ . Project the sphere on the plane (M_i,t,n) tangent to the sphere in M_i (the specific projection does not matter since we consider only K′-sources in the neighborhood of M_i). 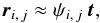We have $r_{i, j} \approx ψ_{i, j} t,$ $\appendix \setcounter{section}{1} \begin{equation} \vec r_{i\comma j} \approx \psi_{i\comma j}\multspace \vec t, \end{equation}$ (A.21)and the basis (t,n) is obtained from (u_a,u_b) by a (β + γ − ß/2)-counterclockwise rotation around + u_r, so, $\begin{matrix} (Γ_{i})_{(t, n)} & = & {Rot}^{t} (β_{i} + γ_{i} - ß / 2) \cdot Diag (a_{i}^{2}, {b_{i}^{2}}^{)} \cdot Rot (β_{i} + γ_{i} - ß / 2), \\ (Γ_{j}^{'})_{(t, n)} & = & {Rot}^{t} (β_{j}^{'} + γ_{j}^{'} - ß / 2) \cdot Diag (a_{j}^{' 2}, {b_{j}^{' 2}}^{)} \cdot Rot (β_{j}^{'} + γ_{j}^{'} - ß / 2) . \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} (\Gamma_i)_{(\vec t,\,\vec n)} &=& \transpose{\Rot}(\beta_i+\gamma_i-\piup/2) \!\cdot\! \Diag\left(a_i^2, b_i^2\right) \! \cdot\! \Rot(\beta_i+\gamma_i-\piup/2), ~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ (\Gammapj)_{(\vec t,\,\vec n)} &=& \transpose{\Rot}(\betapj+\gammapj-\piup/2)\! \cdot\! \Diag\left(a_{\smash[t]{j}}'^2, b_{\smash[t]{j}}'^2\right) \! \cdot\! \Rot(\betapj+\gammapj\!-\!\piup/2).~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{eqnarray}$

Appendix A.2.2: Case of unknown positional uncertainties

If the positional uncertainty on M_i is unknown, we may model it with (Γ_i)_(t,n) = σ² Diag(1,1), using the same σ for all K-sources, and derive an estimate of 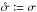$\begin{matrix} _{˚} \\ σ \end{matrix} := σ$ $\hbox{$\sigmatot \coloneqq \sigma$}$ by maximizing the likelihood to observe the distribution of K- and K′-sources (see Sects. 3.2 and 4.2). For a galaxy, however, the positional uncertainty on its center is likely to increase with its size. If the position angle θ_i (counted eastward from the north) and the major and minor diameters D_i and d_i of the best-fitting ellipse of some isophote are known for M_i (for instance, parameters PA, D₂₅ and d₂₅ := D₂₅/R₂₅ taken from the RC3 catalog (de Vaucouleurs et al. 1991) or HyperLeda (Paturel et al. 2003)), we may model the positional uncertainty with $\begin{matrix} (Γ_{i})_{(t, n)} & = & {Rot}^{t} (θ_{i} + γ_{i} - ß / 2) \cdot Diag (σ^{2} + [ν D_{i}]^{2}, σ^{2} + [ν d_{i}]^{2}) \\ \cdot Rot (θ_{i} + γ_{i} - ß / 2) \\ = & σ^{2} Diag (1, 1) + ν^{2} {Rot}^{t} (θ_{i} + γ_{i} - ß / 2) \\ \cdot Diag (D_{i}^{2}, {d_{i}^{2}}^{)} \cdot Rot (θ_{i} + γ_{i} - ß / 2), \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} (\Gamma_i)_{(\vec t,\,\vec n)} &=& \transpose{\Rot}(\theta_i+\gamma_i-\piup/2) \cdot \Diag\left(\sigma^2 + [\nu\multspace D_i]^2, \sigma^2 + [\nu\multspace d_i]^2\right) \notag \\&&\quad\cdot \Rot(\theta_i+\gamma_i-\piup/2) \notag \\ &=& \sigma^2\multspace \Diag(1, 1) + \nu^2\multspace \transpose{\Rot}(\theta_i+\gamma_i-\piup/2) \notag \\&&\quad\cdot \Diag\left(D_i^2, d_i^2\right) \cdot \Rot(\theta_i+\gamma_i-\piup/2), \end{eqnarray}$ (A.24)and derive estimates of $\begin{matrix} _{˚} \\ σ \end{matrix} := σ$ $\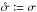hbox{$\sigmatot \coloneqq \sigma$}$ and $\begin{matrix} _{˚} \\ ν \end{matrix} := ν$ $\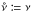hbox{$\nutot \coloneqq \nu$}$ from the likelihood. Such a technique might indeed be used to estimate the accuracy of coordinates in some catalog (see Paturel & Petit 1999 for another method).

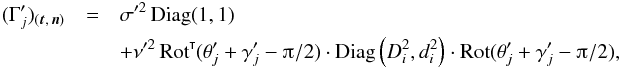If the positional uncertainty on $M_{j}^{'}$ $\hbox{$\Mp_j$}$ is unknown too, we can also put $\begin{matrix} (Γ_{j}^{'})_{(t, n)} & = & σ^{' 2} Diag (1, 1) \\ + ν^{' 2} {Rot}^{t} (θ_{j}^{'} + γ_{j}^{'} - ß / 2) \cdot Diag (D_{i}^{2}, {d_{i}^{2}}^{)} \cdot Rot (θ_{j}^{'} + γ_{j}^{'} - ß / 2), \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} (\Gammapj)_{(\vec t,\,\vec n)} &=& \sigma'^2\multspace \Diag(1, 1) \nonumber \\&&+ \nu'^2\multspace \transpose{\Rot}(\thetapj+\gammapj-\piup/2) \cdot \Diag\left(D_i^2, d_i^2\right) \cdot \Rot(\thetapj+\gammapj-\piup/2), \end{eqnarray}$ (A.25)with the same σ′ and ν′ for all K′-sources. 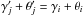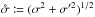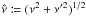As $γ_{j}^{'} + θ_{j}^{'} = γ_{i} + θ_{i}$ $\hbox{$\gammapj + \thetapj = \gamma_i + \theta_i$}$ , only estimates of $\begin{matrix} _{˚} \\ σ \end{matrix} := (σ^{2} + σ^{' 2})^{1 / 2}$ $\hbox{$\sigmatot \coloneqq (\sigma^2+\sigma'^2)^{1/2}$}$ and $\begin{matrix} _{˚} \\ ν \end{matrix} := (ν^{2} + ν^{' 2})^{1 / 2}$ $\hbox{$\nutot \coloneqq (\nu^2+\nu'^2)^{1/2}$}$ may be obtained ¹² by maximizing the likelihood, not the values of σ, σ′, ν or ν′ themselves.

Appendix A.2.3: Possibly different true positions

A similar technique can be applied if the true centers of K-sources and of their counterparts in K′ sometimes differ. This might be useful in particular when associating galaxies from an optical catalog and from a ultraviolet or far-infrared one, because, while the optical is dominated by smoothly-distributed evolved stellar populations, the ultraviolet and the far-infrared mainly trace star-forming regions. Observations of galaxies (e.g., Kuchinski et al. 2000) have indeed shown that galaxies are very patchy in the ultraviolet, and the same has been observed in the far-infrared.

Since the angular distance between the true centers should increase with the size of the galaxy, we might model this as 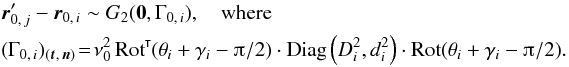$\begin{matrix} r_{0, j}^{'} - r_{0, i} ~ G_{2} (0, Γ_{0, i}), where \\ (Γ_{0, i})_{(t, n)} = ν_{0}^{2} {Rot}^{t} (θ_{i} + γ_{i} - ß / 2) \cdot Diag (D_{i}^{2}, {d_{i}^{2}}^{)} \cdot Rot (θ_{i} + γ_{i} - ß / 2) . \end{matrix}$ $\appendix \setcounter{section}{1} \begin{eqnarray} && \vrpzj-\vrzi\sim G_2(\vec 0, \Gammazi), \quad\text{where } \nonumber\\&& (\Gammazi)_{(\vec t,\,\vec n)} \! =\! \nu_0^2\multspace \transpose{\Rot}(\theta_i+\gamma_i-\piup/2) \cdot \Diag\left(D_i^2, d_i^2\right) \cdot \Rot(\theta_i+\gamma_i-\piup/2). \end{eqnarray}$ (A.26)We then have 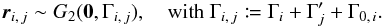$r_{i, j} ~ G_{2} (0, Γ_{i, j}), with Γ_{i, j} := Γ_{i} + Γ_{j}^{'} + Γ_{0, i} .$ $\appendix \setcounter{section}{1} \begin{equation} \vec r_{i\comma j} \sim G_2(\vec 0, \Gamma_{i\comma j}), \quad \text{with } \Gamma_{i\comma j} \coloneqq \Gamma_i+\Gammapj+\Gammazi. \end{equation}$ (A.27)

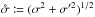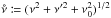Once again, if σ, σ′, ν, ν′ and ν₀ are unknown, only $\begin{matrix} _{˚} \\ σ \end{matrix} := (σ^{2} + σ^{' 2})^{1 / 2}$ $\hbox{$\sigmatot \coloneqq (\sigma^2+\sigma'^2)^{1/2}$}$ and $\begin{matrix} _{˚} \\ ν \end{matrix} := (ν^{2} + ν^{' 2} + ν_{0}^{2})^{1 / 2}$ $\hbox{$\nutot \coloneqq (\nu^2+\nu'^2+\nu_0^2)^{1/2}$}$ may be estimated through likelihood maximization.

All Figures

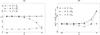Fig. 1

One-to-one simulations for f = 1/2, $n^{'} = 10^{5}$ $\hbox{$\np = 10^5$}$ , and circular positional uncertainty ellipses with $\begin{matrix} _{˚} \\ σ \end{matrix} = 10^{-3} rad$ $\hbox{$\sigmatot = 10^{-3}\,\radian$}$ (see Sects. 6.1 and 6.2 for details). a) Mean value of different estimators $\hbox{$\hat f$}$ of f as a function of n. The dotted line indicates the input value of f. b) Normalized average maximum value $\hbox{$\hat\Lh$}$ of different likelihoods as a function of n, compared to $L̂ \begin{matrix} w \\ o:o \end{matrix}$ $\hbox{$\expandafter\hat\Lhoto^\wrong$}$ .

In the text

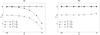Fig. 2

Mean value of different estimators $\hbox{$\hat f$}$ of f as a function of n for f = 1/2 (dotted line), $n^{'} = 10^{5}$ $\hbox{$\np = 10^5$}$ , and circular positional uncertainty ellipses with $\begin{matrix} _{˚} \\ σ \end{matrix} = 10^{-3} rad$ $\hbox{$\sigmatot = 10^{-3}\,\radian$}$ (see Sects. 6.1 and 6.2 for details). a) Several-to-one simulations. b) One-to-one simulations ( $\hbox{$\hat f_\sto$}$ and $\hbox{$\hat f_\oto$}$ overlap).

In the text

Fig. 3

Contour lines of L_s:o (solid) and L_o:o (dashed) in the $(f, \begin{matrix} _{˚} \\ σ \end{matrix})$ $\hbox{$(f, \sigmatot)$}$ plane. Input parameters are the same as in Fig. 2, except that $n = n^{'} = 2 \times 10^{4}$ $\hbox{$n = \np = 2\times10^4$}$ ; the input values of f and $\begin{matrix} ˚ \\ σ \end{matrix}$ $\hbox{$\sigmatot$}$ are indicated by dotted lines (see Sect. 6.3.1 for details). a) Several-to-one simulations. b) One-to-one simulations.

In the text

Fig. 4

Contour lines of L_s:o (solid) and L_o:o (dashed) in the $(f, \begin{matrix} _{˚} \\ σ \end{matrix})$ $\hbox{$(f, \sigmatot)$}$ plane. Input parameters are the same as in Fig. 2, except that positional uncertainty ellipses are elongated and randomly oriented (see Sect. 6.3.2 for details); the input value of f is indicated by a dotted line. a) Several-to-one simulations. b) One-to-one simulations.

In the text

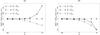	Fig. 5 Normalized average maximum value $\hbox{$\hat\Lh$}$ of different likelihoods as a function of n, compared to $\hbox{$\expandafter\hat\Lhoto$}$ . Simulations are the same as in Fig. 2. a) Several-to-one simulations. b) One-to-one simulations.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Bartlett, J. G., & Egret, D. 1998, in New Horizons from Multi-Wavelength Sky Surveys, eds. B. J. McLean, D. A. Golombek, J. J. E. Hayes, & H. E. Payne, IAU Symp., 179, 437 [Google Scholar]

[2] Bauer, F. E., Condon, J. J., Thuan, T. X., & Broderick, J. J. 2000, ApJS, 129, 547 [NASA ADS] [CrossRef] [Google Scholar]

[3] Benn, C. R. 1983, The Observatory, 103, 150 [NASA ADS] [Google Scholar]

[4] Brand, K., Brown, M. J. I., Dey, A., et al. 2006, ApJ, 641, 140 [NASA ADS] [CrossRef] [Google Scholar]

[5] Budavári, T., & Szalay, A. S. 2008, ApJ, 679, 301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

[6] Condon, J. J., Balonek, T. J., & Jauncey, D. L. 1975, AJ, 80, 887 [NASA ADS] [CrossRef] [Google Scholar]

[7] Condon, J. J., Anderson, E., & Broderick, J. J. 1995, AJ, 109, 2318 [NASA ADS] [CrossRef] [Google Scholar]

[8] de Ruiter, H. R., Arp, H. C., & Willis, A. G. 1977, A&AS, 28, 211 [NASA ADS] [Google Scholar]

[9] de Vaucouleurs, G., & Head, C. 1978, ApJS, 36, 439 [NASA ADS] [CrossRef] [Google Scholar]

[10] de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies (New York: Springer) [Google Scholar]

[11] Fioc, M. 2014, Aspects: code documentation and complements [arXiv:1404.4224] [Google Scholar]

[12] Fleuren, S., Sutherland, W., Dunne, L., et al. 2012, MNRAS, 423, 2407 [NASA ADS] [CrossRef] [Google Scholar]

[13] Haakonsen, C. B., & Rutledge, R. E. 2009, ApJS, 184, 138 [NASA ADS] [CrossRef] [Google Scholar]

[14] Kendall, M., & Stuart, A. 1979, The advanced theory of statistics. Vol. 2: Inference and relationship (London: Griffin) [Google Scholar]

[15] Kent, J. T. 1982, J. Roy. Stat. Soc. Ser. B, Stat. Methodol., 44, 71 [Google Scholar]

[16] Kim, S., Wardlow, J. L., Cooray, A., et al. 2012, ApJ, 756, 28 [NASA ADS] [CrossRef] [Google Scholar]

[17] Kuchinski, L. E., Freedman, W. L., Madore, B. F., et al. 2000, ApJS, 131, 441 [NASA ADS] [CrossRef] [Google Scholar]

[18] McAlpine, K., Smith, D. J. B., Jarvis, M. J., Bonfield, D. G., & Fleuren, S. 2012, MNRAS, 423, 132 [NASA ADS] [CrossRef] [Google Scholar]

[19] Moshir, M., Kopman, G., & Conrow, T. A. O. 1992, IRAS Faint Source Survey, Explanatory supplement version 2 (IPAC) [Google Scholar]

[20] Moshir, M., Copan, G., Conrow, T., et al. 1993, VizieR Online Data Catalog: II/156 [Google Scholar]

[21] Paturel, G., & Petit, C. 1999, A&A, 352, 431 [NASA ADS] [Google Scholar]

[22] Paturel, G., Bottinelli, L., & Gouguenheim, L. 1995, Astrophys. Lett. Commun., 31, 13 [Google Scholar]

[23] Paturel, G., Petit, C., Prugniel, P., et al. 2003, VizieR Online Data Catalog: VII/237 [Google Scholar]

[24] Pineau, F.-X., Motch, C., Carrera, F., et al. 2011, A&A, 527, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[25] Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in Fortran. The art of scientific computing (Cambridge: University press) [Google Scholar]

[26] Prestage, R. M., & Peacock, J. A. 1983, MNRAS, 204, 355 [NASA ADS] [Google Scholar]

[27] Rohde, D. J., Gallagher, M. R., Drinkwater, M. J., & Pimbblet, K. A. 2006, MNRAS, 369, 2 [NASA ADS] [CrossRef] [Google Scholar]

[28] Roseboom, I. G., Oliver, S., Parkinson, D., & Vaccari, M. 2009, MNRAS, 400, 1062 [NASA ADS] [CrossRef] [Google Scholar]

[29] Rutledge, R. E., Brunner, R. J., Prince, T. A., & Lonsdale, C. 2000, ApJS, 131, 335 [NASA ADS] [CrossRef] [Google Scholar]

[30] Sutherland, W., & Saunders, W. 1992, MNRAS, 259, 413 [NASA ADS] [CrossRef] [Google Scholar]

[31] Vignali, C., Fiore, F., Comastri, A., et al. 2009, in Multi-wavelength Astronomy and Virtual Observatory (European Space Agency), eds. D. Baines, & P. Osuna, 53 [Google Scholar]

[32] Wolfram, S. 1996, The Mathematica book (Cambridge University Press) [Google Scholar]

[33] Wolstencroft, R. D., Savage, A., Clowes, R. G., et al. 1986, MNRAS, 223, 279 [NASA ADS] [Google Scholar]

Probabilistic positional association of catalogs of astrophysical sources: the Aspects code ⋆,⋆⋆

1. Introduction

2. Preliminaries

2.1. Notations

2.2. Assumptions

2.3. Approach

3. Several-to-one associations

3.1. Probability of association: global computation

3.1.1. Computation of Ps:o(C | C′)

3.1.2. Computation of Ps:o(Ai, j∩ C | C′)

3.1.3. Final results

3.2. Likelihood and estimation of unknown parameters

3.2.1. General results

3.2.2. Fraction of sources with a counterpart

3.3. Probability of association: local computation

4. One-to-one associations

4.1. Probability of association

4.1.1. Computation of Po:o(C | C′)

4.1.2. Computation of Po:o(Ai, j∩ C | C′)

4.1.3. Final results

4.2. Likelihood and estimation of unknown parameters

5. Practical implementation: the Aspects code

5.1. Overview

5.2. Elimination of unlikely counterparts

5.3. Fraction of sources with a counterpart

5.4. Computation of one-to-one probabilities of association

5.4.1. A first try

5.4.2. Failure of the first try

5.4.3. Reconsideration and solution

5.5. Tests of Aspects

6. Simulations

6.1. Creation of mock catalogs

6.2. Estimation of f if positional uncertainty ellipses are known and circular

6.3. Simultaneous estimation of f and ˚σ

6.3.1. Circular positional uncertainty ellipses

6.3.2. Elongated positional uncertainty ellipses

6.4. Choice of association model

7. Conclusion

Acknowledgments

References

Appendix A: Probability distribution of the observed relative positions of associated sources

Appendix A.1: Properties of normal laws

Appendix A.2: Covariance matrix of the probability distribution of relative positions

Appendix A.2.1: Covariance matrix for identical true positions and known positional uncertainties

Appendix A.2.2: Case of unknown positional uncertainties

Appendix A.2.3: Possibly different true positions

All Figures

Probabilistic positional association of catalogs of astrophysical sources: the Aspects code ^⋆,^⋆⋆

3.1.1. Computation of P_s:o(C | C′)

3.1.2. Computation of P_s:o(A_i, j∩ C | C′)

4.1.1. Computation of P_o:o(C | C′)

4.1.2. Computation of P_o:o(A_i, j∩ C | C′)

6.3. Simultaneous estimation of f and $\begin{matrix} ˚ \\ σ \end{matrix}$ $\hbox{$\sigmatot$}$