| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 4 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201423806 | |
| Published online | 06 May 2014 | |
Research Note
A fast version of the k-means classification algorithm for astronomical applications
1
Instituto de Física de Cantabria,
Avenida de los Castros, s/n,
39005
Santander,
Spain
e-mail:
ordovas@ifca.unican.es
2
Departamento de Astrofísica, Universidad de La
Laguna, 38205, La
Laguna, Tenerife,
Spain
3
Instituto de Astrofísica de Canarias, 38205, La Laguna, Tenerife, Spain
e-mail:
jos@iac.es
Received:
14
March
2014
Accepted:
28
March
2014
Context. K-means is a clustering algorithm that has been used to classify large datasets in astronomical databases. It is an unsupervised method, able to cope very different types of problems.
Aims. We check whether a variant of the algorithm called single pass k-means can be used as a fast alternative to the traditional k-means.
Methods. The execution time of the two algorithms are compared when classifying subsets drawn from the SDSS-DR7 catalog of galaxy spectra.
Results. Single-pass k-means turn out to be between 20% and 40% faster than k-means and provide statistically equivalent classifications. This conclusion can be scaled up to other larger databases because the execution time of both algorithms increases linearly with the number of objects.
Conclusions. Single-pass k-means can be safely used as a fast alternative to k-means.
Key words: astronomical databases: miscellaneous / methods: data analysis / methods: statistical
© ESO, 2014
1. Rationale
The volume of many existing and forthcoming astronomical databases is simply too large to use traditional techniques of analysis. Objects cannot be inspected individually by astronomers, and decisions about whether downloading observations from a satellite or about following up interesting targets will be taken by numerical algorithms. Two examples of observations that must be handled using automatic methods are the datasets gathered by the satellite Gaia1 (Prusti2012) and the images to be provided by the Large Synoptic Survey Telescope2 (LSST, Ivezic et al.2008). Gaia can only download a minuscule fraction of the observed frames, and onboard software decides what is sent back to earth. LSST will image the full southern sky every few days, requiring that more than 30 terabytes are processed and stored every day during ten years. Thus new automated techniques of analysis must be developed. Regardless of the details, the methods to be chosen are bound to be central to future astronomy.
In this context, our group has been using the algorithm k-means as an automated tool to classify large astronomical data sets. It has been shown to be fast and robust in different contexts, for example, to improve the signal-to-noise ratio by stacking similar spectra (Sánchez Almeida et al. 2009), to identity unusual objects in large datasets of galaxies and stars (Sánchez Almeida & Allende Prieto 2013; Sánchez Almeida et al. 2013), to search for rare targets that are particularly telling from a physical point of view (Morales-Luis et al. 2011), to select alike targets to speed up complex modeling of spectro-polarimetric data (Sánchez Almeida & Lites 2000), to identify and discard noisy spectra (Sánchez Almeida et al. 2013), or to classify large astronomical datasets (Sánchez Almeida et al. 2010; Sánchez Almeida & Allende Prieto 2013).
Many other applications can be found in the literature, e.g., clustering analysis of stars (Simpson et al. 2012), spectroscopy of Hα objects in IC 1396 star-forming region (Balazs et al. 1996), study of formation of ultracompact dwarf galaxies (Chattopadhyay et al. 2012), detection of anomalous objects among periodic variable stars (Rebbapragada et al. 2009) and description of galaxy diversification (Fraix-Burnet et al. 2012).
So far we have used the traditional version of k-means, which requires finding cluster centers and assigning the objects to them in a sequential way. There is another version of the algorithm called single-pass k-means that does the finding of the clusters and the assignation simultaneously (e.g., Bishop 2006). Because of this unification of two steps in only one, single-pass k-means is expected to be faster (and so more efficient) than the traditional approach.
In this Research Note we compare the performance of the two variants of algorithms to see whether single pass k-means can be reliably used as a fast alternative to the traditional k-means for astronomy applications. Both algorithms are described in Sect. 2. The comparison is worked out in Sect. 3, and it is based on the SDSS-DR7 spectra database. We use this dataset because it has been thoroughly tested with the original k-means (Sánchez Almeida et al. 2010). Single pass k-means is indeed faster than the original algorithm and provides statistically equivalent results, as we conclude in Sect. 4.
2. K-means and single-pass k-means
In the context of classification algorithms, objects are points in a high-dimensional space with as many dimensions as the number of parameters used to describe the objects. (For example, the dimension of the space is the number of wavelengths of the spectra used for testing in Sect. 3.) The catalog to be classified is a set of points in this space, and so the (Euclidean) distance between any pair of them is well defined. Points (i.e., objects) are assumed to be clustered around a number of cluster centers. The classification problem consists in (1) finding the number of clusters; (2) finding the cluster centers; and (3) assigning each object to one of these centers; In the standard formulation, k-means begins by selecting a number k of objects at random from the full dataset. They are assumed to be the centers of the clusters, and then each object in the catalog is assigned to the closest cluster center (i.e., that of minimum distance). Once all objects have been classified, the cluster center is recomputed as the centroid of the objects in the cluster. This procedure is iterated with the new cluster centers, and it finishes when no object is reclassified in two consecutive steps. The number of clusters k is arbitrarily chosen, but in practice, the results are insensitive to this selection since only a few clusters possess a significant number of members, so that the rest can be discarded. On exiting, the algorithm provides a number of clusters, their corresponding cluster centers, as well as the classification of all the original objects now assigned to one of the clusters.
As a result, the standard k-mean method is divided into two steps; the first one
is the assignation step. The ith object xi is assigned to the
cluster k if
the distance between xi and the
kth cluster
center μk is less than the
distances to all other cluster centers,
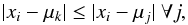 (1)where the index
j labels all
possible cluster centers. The assignation is quantified in terms of the matrix
J(i,j) defined as
(1)where the index
j labels all
possible cluster centers. The assignation is quantified in terms of the matrix
J(i,j) defined as 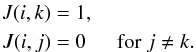 (2)Once
the n objects
in the catalog have been assigned, the second step consists of computing new cluster centers
as the centroids of all the objects in the classes, i.e.,
(2)Once
the n objects
in the catalog have been assigned, the second step consists of computing new cluster centers
as the centroids of all the objects in the classes, i.e., 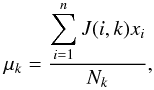 (3)with
Nk the number of objects
assigned to class k,
(3)with
Nk the number of objects
assigned to class k, 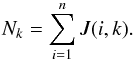 (4)The two steps are
iterated until there are negligible reassignments between successiveiterations. In other
words, when repeated until the assignation matrix J(i,j) has negligible variation
between two iterations.
(4)The two steps are
iterated until there are negligible reassignments between successiveiterations. In other
words, when repeated until the assignation matrix J(i,j) has negligible variation
between two iterations.
The objective of the alternative single-pass k-means
method is to update the centroids on-the-fly immediately after the assignation of
each data vector, without having to finish assignating all the vectors in the database. This
algorithm is expected to be faster because we do not have to wait to update the cluster
centroids until all data are reassigned. As in the case of k-means, this new method
begins by choosing the initial centroids randomly in the database, and then assigns each
data vector to the closest centroid. Then the loop that combines Steps 1 and 2 begins.
Object number i
is assigned to the nearest cluster centroid. If that data element does not change its class,
then the algorithm goes to the next element i + 1. If it changes, the centroids of the initial
class and the final class are recalculated immediately after the assignation. Assume that
the ith object
previously in class k is now assigned to class m,
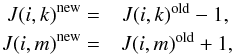 (5)where
the superscripts old and new refer to the value before and after the
reassignment, respectively. Then the centroids of the clusters are updated as Bishop (2006, Sect. 9.1),
(5)where
the superscripts old and new refer to the value before and after the
reassignment, respectively. Then the centroids of the clusters are updated as Bishop (2006, Sect. 9.1), 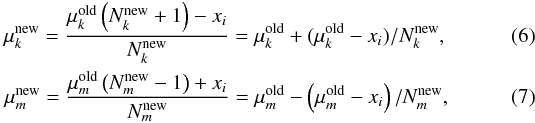 which
are just renderings of Eq. (3) with the new
assignation of the ith object. After those two centroids are updated, the
algorithm continues with the next data vector until completion of the catalog. As in the
regular k-means, the catalog is classified repeatedly until no
further reassignment in needed.
which
are just renderings of Eq. (3) with the new
assignation of the ith object. After those two centroids are updated, the
algorithm continues with the next data vector until completion of the catalog. As in the
regular k-means, the catalog is classified repeatedly until no
further reassignment in needed.
3. Tests
We carried out two sets of tests to verify whether, on the one hand, single-pass k-means are faster than k-means and, on the other hand, if the classifications resulting from both methods are equivalents. We explain these two tests and their results in the following sections.
The tests are based on the SDSS-DR7 spectroscopic galaxy catalog (Abazajian et al. 2009), which we choose because it has already been classified using k-means (Sánchez Almeida et al. 2010). The resulting classes are known in quite some detail (Ascasibar & Sánchez Almeida 2011; Sánchez Almeida et al. 2012), so we do not show and discuss them here. This selection implies that the classification space has 1637 dimensions set by the number of wavelengths in the spectra.
The tests have been carried out in two rather modest computers: a laptop3 (hereafter laptop) and a desktop4 (hereafter FORD). Laptop and FORD have RAM memory of 3 Gb and 4 Gb, respectively, so the datasets cannot be very large. This fact sets the number of objects used in the tests to a range between 1000 and 20 000 galaxy spectra.
3.1. Time per classification
First of all, we measure the relative speed of k-means and single pass k-means by classifying different subsets of galaxy spectra from SDSS-DR7 and comparing the time needed for completion. We choose random subsets of the full SDSS-DR7 catalog having between 1000 and 20 000 galaxy spectra.
For each subset and each algorithm, we repeat the classification ten times to separate
systematic differences between the algorithms from time differences due to the random
initial conditions. If the randomly chosen initial centroids are very similar to the final
centroids, it takes much less time for any algorithm to converge. The time differences are
quantified in terms of the gain G,
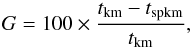 (8)where the symbols
tkm and tspkm denote the
time per classification for k-means and single pass k-means, respectively.
Since classifications are repeated several times, we compute the average and the
dispersion of the gain.
(8)where the symbols
tkm and tspkm denote the
time per classification for k-means and single pass k-means, respectively.
Since classifications are repeated several times, we compute the average and the
dispersion of the gain.
The results of our test are shown in Figs. 1 and 2. The time for classification depends strongly on the initialization, and this leads to a large dispersion of the time per classification. For example, for 20 000 spectra FORD’s computer time varies from 40 and 80 min (Fig. 1). On top of this significant scatter, there is a systematic difference between the two methods, where single pass k-means between 20% and 40% faster than k-means – the mean gain spans from 20% to 40% independently of the size of the dataset and the computer (see Figs. 1 and 2; bottom panels). This systematic gain when using single pass k-means is the main result of our RN, provided that the two algorithms yield equivalent classifications. This equivalence is indeed proven in Sect. 3.2.
 |
Fig. 1 Top: computer time required for FORD to classify subsets of the SDSS-DR7 galaxy spectrum catalog. Given the number of galaxies to be classified (in abscissa), the time when using k-means (the solid line) is systematically longer than the time for the alternative single pass k-means (the dashed line). The computer time increases linearly with the number of galaxies in the catalog. Error bars code the dispersion produced by the random initialization of the algorithms. Bottom: gain when using single pass k-means, which saves between 20% and 40% of the time. |
 |
Fig. 2 Time for the classification (top) and gain (bottom) when using the laptop. For symbols and further details, see Fig. 1. |
The tests described above required approximately seven CPU days to run. This limited the size of the largest subset, since the required time increases linearly with the number of objects in the catalog (Figs. 1 and 2). However, single pass k-means would outperform k-mean even for other larger datasets. That the computer time employed by the two alternative algorithms increases linearly with time implies that the gain should be constant even for significantly larger datasets. Moreover, k-means is a workhorse proven to converge in many very different contexts. The datasets we use are not special, therefore the properties inferred for them can be probably extrapolated to many other datasets.
3.2. Equivalence of the classifications provided by the two algorithms
K-means and single pass k-means render different classifications of a catalog even if they start from the very same initial cluster centers. However, the two classifications are equivalent for practical applications. With a given a dataset, k-means does not provide a single classification but a number of them generated by the random initialization of the algorithm (see Sect. 2). This is a well known downside of k-means, whose impact must be evaluated in actual applications of the algorithm (see, e.g., Sánchez Almeida et al. 2010, Sect. 4). There is an intrinsic uncertainty of the classification ensuing from the random initialization, therefore the classes resulting from single pass k-means and k-means are equivalent so far as they are within this uncertainty. Consequently, to study whether single pass k-means is statistically equivalent to k-means, we test that the differences between classifications carried out using the two methods are similar to the differences when comparing various initializations of the same method.
To carry out this test, we choose a subset of 20 000 galaxy spectra randomly drawn from SDSS-DR7 and then 50 different initializations. We proceed by classifying the 20 000 spectra using those 50 initializations and the two algorithms, so as to obtain 100 classifications of that dataset. It took approximately four days for FORD to complete the task. The idea is to compare these classifications pairwise, and we do it by employing the parameter coincidence defined by Sánchez Almeida et al. (2010, Sect. 2.1). In essence, the classes in two classifications are paired so that they contain the most objects in common. The percentage of objects in these equivalent classes is the coincidence, which would be 100% if the two classifications were identical.
 |
Fig. 3 Top: histogram of coincidence for pairs of classifications, one inferred with k-means and the other with single pass k-means. The mean coincidence, around 70%, is characteristic of the SDSS-DR7 galaxy spectrum catalog (Sánchez Almeida et al. 2010). Bottom: same as avobe, except that only classifications using k-means are compared. It shows the intrinsic dispersion in possible classifications due to the random initialization of the algorithm. |
The 100 classifications can be paired in 5050 different ways with some combining only k-means classifications, some combining only single pass k-means classifications, and some mixing them up. They can be divided into four groups:
-
1.
50 pairs of classifications where each member of the pair hasbeen treated with a different algorithm but both with the sameinitialization,
-
2.
2450 pairs of classifications where each member has been treated with a different algorithm and a different initialization,
-
3.
1275 pairs, all of them treated with k-means but with different initializations,
-
4.
1275 pairs, all of them treated with single pass k-means but with different initializations.
The histograms with the values of coincidence for the groups # 2 and 3 are represented in Fig. 3. Both are very similar, including their means and standard deviations (67.9 ± 9.4% and 68.3 ± 9.5%, respectively). The lower histogram compares classifications derived using k-means alone, and so it quantifies the intrinsic scatter due to the random initialization. The upper histogram compares classifications from single pass k-means and k-means, so it includes the intrinsic scatter plus the systematic differences that k-means and single pass k-means may have. Since the two distributions are so similar, we conclude that there are no systematic differences, and the classifications inferred from k-means and single pass k-means are equivalent. The distributions corresponding to groups # 1 and # 4 are not shown, but they are very similar to those in Fig. 3, and from them it also follows that the classes inferred from k-means and single pass k-means are equivalent for practical applications.
The discussion above is purely qualitative. We have gone a step further to show that the histograms of coincidence corresponding to the four groups are statistically equivalent. The Kolmogorov-Smirnov (KS) test allows determining the probability that two observed distributions are drawn from the
same parent distribution (e.g., Massey 1951). Using the KS test, the probability that the histograms in Fig. 3 represent the same distribution is more than 99.9%. Using all possible pairs of the histograms from the four groups, the KS conclude that the probability of being the same distribution is between 97% and 100%. Our claim that single pass k-means and k-means provide statistically equivalent classifications relies on this result.
4. Conclusions
The classification algorithm k-means has the potential to classify huge astronomical databases, such as those to be expected with the advent of new instruments and catalogs (see Sect. 1). We tested a variant of the original algorithm, called single pass k-means, which unifies the two main steps of k-means (Sect. 2). Single pass k-means turns out to be between 20 % and 40 % faster than k-means (Sect. 3.1), and it provides statistically equivalent classifications (Sect. 3.2).
Saving 20% to 40% of the time may not look like a lot, however the actual gain when using single pass k-means depends very much on the specific application. Keep in mind that k-means (and so single pass k-means) is a tool with the potential of classifying gigantic datasets by brute force. The foreseeable applications may require long execution times and, therefore a 40% saving may actually represent days or weeks of work.
The tests were carried out using a particular catalog of galaxy spectra with limited data volumes (up to 20 000 objects in 1637 dimensions). However, single pass k-means would outperform k-mean even for other larger datasets. That the computer time employed by the two alternative algorithms increases linearly with time implies that the gain should be constant even for significantly larger datasets. Moreover, k-means is a workhorse proven to converge in many very different contexts. The datasets we use are not special, therefore the properties inferred for them can probably be extrapolated to many other datasets.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Ascasibar, Y., & Sánchez Almeida, J. 2011, MNRAS, 415, 2417 [NASA ADS] [CrossRef] [Google Scholar]
- Balazs, L. G., Garibjanyan, A. T., Mirzoyan, L. V., et al. 1996, A&A, 311, 145 [NASA ADS] [Google Scholar]
- Bishop, C. M. 2006, Pattern Recognition and Machine Learning (Springer), 424 [Google Scholar]
- Chattopadhyay, T., Sharina, M., Davoust, E., De, T., & Chattopadhyay, A. K. 2012, ApJ, 750, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Fraix-Burnet, D., Chattopadhyay, T., Chattopadhyay, A. K., Davoust, E., & Thuillard, M. 2012, A&A, 545, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivezic, Z., Tyson, J. A., Acosta, E., et al. 2008 [arXiv:0805.2366] [Google Scholar]
- Massey, F. J. 1951, J. Am. Stat. Assoc., 46, 68 [CrossRef] [Google Scholar]
- Morales-Luis, A. B., Sánchez Almeida, J., Aguerri, J. A. L., & Muñoz-Tuñón, C. 2011, ApJ, 743, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Prusti, T. 2012, Astron. Nachr., 333, 453 [NASA ADS] [Google Scholar]
- Rebbapragada, U., Protopapas, P., Brodley, C. E., & Alcock, C. 2009, Mach. Learn., 74, 281 [CrossRef] [Google Scholar]
- Sánchez Almeida, J., & Allen de Prieto, C. 2013, ApJ, 763, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., & Lites, B. W. 2000, ApJ, 532, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Aguerri, J. A. L., Muñoz-Tuñón, C., & Vazdekis, A. 2009, ApJ, 698, 1497 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Aguerri, J. A. L., Muñoz-Tuñón, C., & de Vicente, A. 2010, ApJ, 714, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Terlevich, R., Terlevich, E., Cid Fernandes, R., & Morales-Luis, A. B. 2012, ApJ, 756, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Aguerri, J. A. L., & Muñoz-Tuñón, C. 2013, in Rev. Mex. Astron. Astrofis. Conf. Ser., 42, 111 [Google Scholar]
- Simpson, J. D., Cottrell, P. L., & Worley, C. C. 2012, MNRAS, 427, 1153 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Top: computer time required for FORD to classify subsets of the SDSS-DR7 galaxy spectrum catalog. Given the number of galaxies to be classified (in abscissa), the time when using k-means (the solid line) is systematically longer than the time for the alternative single pass k-means (the dashed line). The computer time increases linearly with the number of galaxies in the catalog. Error bars code the dispersion produced by the random initialization of the algorithms. Bottom: gain when using single pass k-means, which saves between 20% and 40% of the time. |
| In the text | |
 |
Fig. 2 Time for the classification (top) and gain (bottom) when using the laptop. For symbols and further details, see Fig. 1. |
| In the text | |
 |
Fig. 3 Top: histogram of coincidence for pairs of classifications, one inferred with k-means and the other with single pass k-means. The mean coincidence, around 70%, is characteristic of the SDSS-DR7 galaxy spectrum catalog (Sánchez Almeida et al. 2010). Bottom: same as avobe, except that only classifications using k-means are compared. It shows the intrinsic dispersion in possible classifications due to the random initialization of the algorithm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


