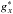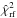| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 18 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201323271 | |
| Published online | 28 April 2014 | |
Astrometric planet search around southern ultracool dwarfs
II. Astrometric reduction methods and a deep astrometric catalogue⋆,⋆⋆,⋆⋆⋆
1 Main Astronomical Observatory, National Academy of Sciences of the Ukraine, Zabolotnogo 27, 03680 Kyiv, Ukraine
e-mail: laz@mao.kiev.ua
2 European Space Agency, European Space Astronomy Centre, P.O. Box 78, Villanueva de la Cañada, 28691 Madrid, Spain
3 Observatoire de Genève, Université de Genève, 51 Chemin Des Maillettes, 1290 Versoix, Switzerland
4 INTA-CSIC Centro de Astrobiología, 28850 Torrejón de Ardoz, Madrid, Spain
5 University of Cambridge, Cavendish Laboratory, J J Thomson Avenue, Cambridge, CB3 0HE, UK
Received: 18 December 2013
Accepted: 14 March 2014
Aims. We describe the astrometric reduction of images obtained with the FORS2/VLT camera in the framework of an astrometric planet search around 20 M/L-transition dwarfs. We present the correction of systematic errors, the achieved astrometric performance, and a new astrometric catalogue containing the faint reference stars in 20 fields located close to the Galactic plane.
Methods. Remote reference stars were used both to determine the astrometric trajectories of the nearby planet search targets and to identify and correct systematic errors.
Results. We detected three types of systematic errors in the FORS2 astrometry: the relative motion of the camera’s two CCD chips, errors that are correlated in space, and an error contribution of as yet unexplained origin. The relative CCD motion probably has a thermal origin and typically is 0.001–0.010 px (~0.1–1 mas), but sometimes amounts to 0.02–0.05 px (3–6 mas). This instability and space-correlated errors are detected and mitigated using reference stars. The third component of unknown origin has an amplitude of 0.03–0.14 mas and is independent of the observing conditions. We find that a consecutive sequence of 32 images of a well-exposed star over 40 min at 0.6′′ seeing results in a median rms of the epoch residuals of 0.126 mas. Overall, the epoch residuals are distributed according to a normal law with a χ2 value near unity. We compiled a catalogue of 12 000 stars with I-band magnitudes of 16–22 located in 20 fields, each covering ~ 2′ × 2′. It contains I-band magnitudes, ICRF positions with 40–70 mas precision, and relative proper motions and absolute trigonometric parallaxes with a precision of 0.1 mas/yr and 0.1 mas at the bright end, respectively.
Conclusions. This work shows that an astrometric accuracy of ~100 micro-arcseconds over two years can be achieved with a large optical telescope in a survey covering several targets and varying observing conditions.
Key words: astrometry / techniques: high angular resolution / atmospheric effects / parallaxes / brown dwarfs
Based on observations made with ESO telescopes at the La Silla Paranal Observatory under programme IDs 086.C-0680, 087.C-0567, 088.C-0679, 089.C-0397, and 090.C-0786.
Appendices are available in electronic form at http://www.aanda.org
The catalogue is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/565/A21
© ESO, 2014
1. Introduction
Extrasolar planets around stars can be discovered and characterised by a variety of observation techniques (Seager 2011). Different methods give access to different observables of a given exoplanetary system and are subject to different practical limitations. To obtain a complete picture of extrasolar planets, we therefore depend on having access to the widest possible range of observing techniques.
Astrometry consists in measuring the photocentre positions of stellar objects and can be used for indirect exoplanet detection by revealing a star’s orbital reflex motion (Sozzetti 2005). However, this relies on a measurement accuracy better than one milli-arcsecond (mas) over time-scales of several years, which requires specialised instruments and methods. Dedicated space missions such as Hipparcos (ESA 1997) and, in particular, its successor Gaia (Perryman et al. 2001; de Bruijne 2012) can meet these requirements, and instruments on-board Hubble have been used for this purpose, too (Benedict et al. 2010). On the ground, the main practical limitation is turbulence in the Earth’s atmosphere (Sahlmann et al. 2013a), which can be overcome with the use of large-aperture telescopes, interferometry, or adaptive optics.
For observations of dense stellar fields with the optical camera FORS2 of ESO’s Very Large Telescope (VLT), we have achieved astrometric precisions of 0.05 mas for well-exposed star images at the field centre when the seeing is restricted to the optimal range (Lazorenko et al. 2009, hereafter PL09). Because this performance is sufficient for exoplanet detection, we initiated an astrometric search targeting ultracool dwarfs (UCD) at the M/L transition in 2010, a survey that is described in detail in the first paper in our series (Sahlmann et al. 2014, hereafter Paper I).
The detection of planetary signals at or close to the noise level requires high-quality astrometric data, that is, precise position measurements ideally free of systematic errors, and adequate precision estimates that correspond to the measurement accuracy. In this paper, we present the latest optimisations of the astrometric methods for the reduction of FORS2 observations described in PL09. These methods were already successfully used for the detection of a close 28 Jupiter-mass (MJ) companion of an L1.5 dwarf (Sahlmann et al. 2013b) and are implemented for the planet search survey (Paper I).
The paper is structured as follows: the observations are described in Sect. 2, the astrometric model is outlined in Sect. 3, and the single-frame precision of the measurements is characterised in Sect. 4.1. The epoch residuals and precision of these residuals are introduced in Sect. 4.2, and in Sect. 4.3 we demonstrate the method of the detection and reduction of systematic errors. The observed χ2 statistic for the epoch residuals and its comparison with the theoretical χ2 distribution law is analysed in Sect. 4.4. In Sect. 5, we describe the catalogue of astrometric and photometric data obtained for field stars in the observed fields. We conclude in Sect. 6.
2. Observations and initial data reduction
Observations were obtained at ESO’s VLT with the 4.2′ × 4.2′-field imaging camera FORS2 (Appenzeller et al. 1998), whose detector is composed of two CCD chips and has a high-resolution collimator, yielding an image scale of 0.126 ′′ px-1 with 2 × 2 pixel binning. The target list (Paper I) contains 20 southern M/L dwarfs, which were monitored for two years starting in November 2010, each with approximately 4–6 epochs per year with one-month spacing in the visibility period. In the third year, a few more follow-up observations were obtained for some targets, for example the binary DE0823−49 (Sahlmann et al. 2013b). Because the targets are red dwarfs, we observed with the I-Bessel filter with a central wavelength at 768 nm. We obtained 9–16 epochs, each consisting of a series of 20 to 60 exposures in I band, for every target. The target list with short identifiers (ID) from Paper I, which refer to approximate field sky position, the I-band magnitudes (see Sect. 5.3), and the number of observing epochs Ne are given in Table 1. A more detailed description of the observations is given in Paper I.
Target list.
The ESO archive contains 7970 exposures of our programme collected during five semesters. Of these, we effectively used 6813 exposures, meaning that there is a nominal overhead of ~14%. This is mostly attributable to observations taken in poor conditions that were repeated, but nevertheless appear in the archive. In general, they did not pass the reduction process, which rejects frames with image FWHM larger than 0.9′′. The overhead also includes the 4% of exposures for each target that were rejected to remove outliers and the data with lowest precision.
The raw images were de-biased and flat-fielded using the standard calibration files. The computation of photocentres is based on fitting the stellar image profiles with a model composed of three centred Gaussian components. Due to the complex shape of the measured point spread function (PSF), deviations from the analytic model often exceed the fluctuations expected from the Poisson statistics of photoelectrons and contain a systematic component common to all star images within a frame. A model of these deviations was compiled for each exposure and subtracted from the measured images of stars, ensuring a significantly better fit and a higher precision of the photocentre determination (Lazorenko 2006).
This procedure was improved for crowded fields, where close pairs of star images were processed iteratively with mutual subtraction of light coming from the nearby image component. This required modelling the PSF variation over each of the two CCD chips, which were processed separately. For this purpose, we divided the detector field into a grid of 16 × 16 square areas. In each area, we selected a few dozen isolated bright stars to create two-dimensional PSFs by co-adding these images with a resolution of 1/2 px and assigning a weight to each star that decreased with increasing distance from the grid node. In this way, we obtained a set of average PSFs that are evenly spaced over the CCD. For each CCD chip, a polynomial fit was used to derive the final calibration PSF with a size of 30 × 30 px (3.8 × 3.8′′) at 1/2 px resolution and a model of its deformation across the CCD. The PSF estimate is good up to 15 px from the star centre, but becomes too noisy at larger distances, where we applied a simple axially symmetric approximation up to 40 px. This calibration of the PSF allowed us to process crowded fields with stellar densities of 300 stars/arcmin2.
2.1. Saturated target images
At the start of the survey and in very good seeing conditions (≲0.5′′), the central pixels of bright star images were saturated, which increased the photocentre uncertainties and, even worse, introduced systematic displacements. Only a few percent of the exposures were affected, but it produced strongly biased solutions when the processing was made with a simple rejection of saturated pixels. For instance, with four saturated pixels, the bias in the photocentre position was about 1 mas, significantly higher than the epoch precision of 0.1 mas. To remove this effect, we modelled it by artificially saturating field-star images with the same saturation pattern as for the target. The difference in photocentre position between the original and modified images, averaged over all field stars, yields the bias value for the target. This method, applied to the target alone, reduced the systematic epoch-averaged image displacements to 0.1 mas for one saturated pixel, which is similar to the epoch precision. However, for four saturated pixels, the residual bias of 0.2–0.3 mas was just at the tolerance limit. Therefore, images with five or more saturated pixels in the target image were rejected. Saturated images of reference stars were always rejected to exclude possible systematic errors, at the expense of a slight increase in the reference frame noise.
After recognising these problems caused by saturation, we shortened the exposure T durations in the survey observations to prevent saturation in very good seeing1. We selected exposure durations that resulted in 0.5–0.7 × 106 photoelectrons per target image, which corresponds to the light collected in a fully exposed image at best seeing. For average seeing of 0.6′′, this results in only one third of the maximum flux, but it ensures a low probability of saturation, thus preventing the appearance of systematic errors.
3. Astrometric model
The astrometric reduction is based on the symmetrising method applied to reduce atmospheric image motion (Lazorenko & Lazorenko 2004; PL09). The implementation of the method, however, has significantly changed and several crucial improvements were made. Figure 1 shows a typical configuration of stars in the focal plane of FORS2 and illustrates some of the concepts and conventions discussed in the next sections.
 |
Fig. 1 Stars in the DE1756−48 field that are used for the astrometric reduction and are included in the catalogue. The UCD is marked with a star, bright stars with magnitudes within ±0.5 mag of the target are shown with solid circles, and open circles show all other reference stars. The footprints of the FORS2 chips and the axes orientations are indicated. Only catalogue stars within 1′50′′around the target are shown, and concentric circles with increasing radii of Ropt(k) mark reference fields used for for the reduction with k = 4,6,8,10,12,14,16. See text for details. |
3.1. Atmospheric image motion
The atmospheric image motion has a continuous spectrum of spatial frequencies, that can be represented by an infinite expansion in series of even integer powers k = 2,4,..., where k is the modal index, and the mode amplitude decreases rapidly with increasing k. Over the CCD space (x,y), image motion causes deformations of the frame of reference stars that for each frame exposure m are modelled by the expansion Φm(x,y) = ∑ wcw,mfw(x,y) into a series of basic functions fw(x,y), whose number w = 1...k(k + 2)/8 depends on k. The functions fw(x,y) are full polynomials in x,y of all powers from zero to the highest power k∗ = k/ 2 − 1, and cw,m are the expansion coefficients. The centre of the reference frame is aligned with a star called the target, therefore the solution is only valid for this star.
In practice, we realised a sequence of independent solutions with all modes k = 4,6...16, which corresponds to the power k∗ taking values between unity (a linear model) and k∗ = 7. For each solution, the field of reference stars is restricted to the optimal radius R = Ropt(k) (e.g. Fig. 1), whose value depends on k and corresponds to the field size where the image motion variance 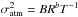 (which increases with R) equals the reference frame noise
(which increases with R) equals the reference frame noise 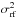 (which decreases with R)
(which decreases with R) 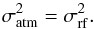 (1)The values of the coefficients B and b for each k are given in Lazorenko (2006) and PL09, but they are approximate and allow us to derive only the first approximation of Ropt by numerical solution of Eq. (1). Its determination can be improved as detailed in Sect. 3.3.3. For targets near the field centre, Ropt is typically between 1′ and 2′, when the intermediate mode k = 10 is applied, whereas for the highest mode k = 16, the reference frame covers most of the FoV (Fig. 1). Solutions obtained with different k are highly correlated and are eventually merged to obtain the final solution.
(1)The values of the coefficients B and b for each k are given in Lazorenko (2006) and PL09, but they are approximate and allow us to derive only the first approximation of Ropt by numerical solution of Eq. (1). Its determination can be improved as detailed in Sect. 3.3.3. For targets near the field centre, Ropt is typically between 1′ and 2′, when the intermediate mode k = 10 is applied, whereas for the highest mode k = 16, the reference frame covers most of the FoV (Fig. 1). Solutions obtained with different k are highly correlated and are eventually merged to obtain the final solution.
3.2. Differential chromatic refraction
Positional observations through the atmosphere are affected by the refraction that deflects the light rays to zenith depending on the effective wavelength and zenith distance ζ. The measured effect is known as differential chromatic refraction (DCR), because it shifts images of blue and red stars differently by ρtanζ, where ρ is the difference of refraction indexes of the target and reference stars. The value of ρ can be computed if the spectral energy distribution is known (Monet et al. 1992; Pravdo & Shaklan 1996).
FORS2 observations are obtained with an atmospheric dispersion compensator LADC (Avila et al. 1997), which produces inverse deflection of light rays on dtanζLADC, where d is a constant dependent on the star color and ζLADC is the effective zenith angle of the LADC. In the current programme, we derive ρ and d as free model parameters for each star (Pravdo et al. 2004; PL09).
3.3. Computational layout of the model
The reduction is run in a sequence of repeating steps, starting from the computation of the positional residuals (Sects. 3.3.1, 3.3.2) for a single UCD or a set of field stars. This is followed by the computation of Ropt, which implies multiple repetitions of the preceding steps (Sect. 3.3.3). The complete sequence is repeated again in the course of improving determination of the systematic corrections (Sect. 4), because the value of Ropt changes.
3.3.1. Deriving field deformations Φ(x,y)
Let Xi,m be the measured two-dimensional CCD positions of the reference star i in the frame (=exposure) m = 1...M, which we assume to include the measurements in both x and y unless the other (one-dimensional case) is evident from the context. The astrometric reduction of these data is performed within a field of the radius Ropt and reveals the deformations Φm(x,y) of the field geometry in frame m. The motion of each of i = 1...Nrf reference star in time is described by the model motion 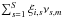 with S astrometric parameters ξi,s and known factors νs,m, for instance the parallax factor, time, etc. The set of parameters ξi,s contains two zero points, two proper motions, the parallax, DCR parameter ρ, and the LADC parameter d, thus, S = 7 and s = 1..S. The solution for S × Nrf astrometric parameters ξi,s and 2 × M × k(k + 2)/8 coefficients cw,m is derived by the least-squares fit of 2 × M × Nrf displacements ΔXi,m = Xi,m − Xi,0 of reference stars relative to the grid of stars within R<Ropt in a reference image m = 0. The reference star sample and solution of the model is unique for each target.
with S astrometric parameters ξi,s and known factors νs,m, for instance the parallax factor, time, etc. The set of parameters ξi,s contains two zero points, two proper motions, the parallax, DCR parameter ρ, and the LADC parameter d, thus, S = 7 and s = 1..S. The solution for S × Nrf astrometric parameters ξi,s and 2 × M × k(k + 2)/8 coefficients cw,m is derived by the least-squares fit of 2 × M × Nrf displacements ΔXi,m = Xi,m − Xi,0 of reference stars relative to the grid of stars within R<Ropt in a reference image m = 0. The reference star sample and solution of the model is unique for each target.
It follows from the procedures introduced in Sect. 4.3 that the measurements X made in the frames m and m′ of the same epoch e (i.e. taken in the same night) are correlated. Therefore, the covariance matrix D of X (or ΔX) has a block structure with the block-diagonal elements 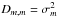 , where σm is the precision of a single frame measurement, non-zero off-diagonal elements Dm,m′ if m,m′ ∈ e, and Dm,m′ = 0 if m and m′ were taken in different epochs (Appendix B).
, where σm is the precision of a single frame measurement, non-zero off-diagonal elements Dm,m′ if m,m′ ∈ e, and Dm,m′ = 0 if m and m′ were taken in different epochs (Appendix B).
The astrometric parameters ξi,s are relative because the solution only converges if the k(k + 2)/8 additional restrictions ∑ iξi,sPifw(xi,yi) = 0 are set, where Pi are optional weighting factors. In particular, we require 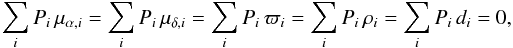 (2)which implies that approximately half of the relative parallaxes ϖ of reference stars are negative and that the average of all proper motions is zero.
(2)which implies that approximately half of the relative parallaxes ϖ of reference stars are negative and that the average of all proper motions is zero.
3.3.2. Deriving astrometric parameters for the target star
Using the solution of the astrometric model, we computed 2 × M displacements ΔXm = Xm − X0 − Φm(Xm,Ym) of the target in frame m relative to its position X0 in the reference frame. and used them to recover S astrometric parameters ξs of the target by fitting their change in time t with the model νξ + Ψ(t) = ΔX (Lazorenko et al. 2011), which, in the general case, includes the orbital motion Ψ(t) of the target and is solved as described by Sahlmann et al. (2013b). For the field stars with Ψ(t) = 0, the solution of this model provides the residuals xm and parameters ξs which refer to the system of reference stars set by Eq. (2). The correction terms to obtain their absolute values have to be determined using external data.
3.3.3. Deriving Ropt
Equation (1) is solved numerically for Ropt, provided that the coefficients B and b of the model expression for σatm are known. These values, given in Lazorenko (2006), are approximate because of the differing observing conditions, and the measured image motion σatm can contain additional components of instrumental origin (PL09). Therefore we assumed that the actual image motion is zσatm, where z is an amplitude factor. To find the value of z, we varied it in the range of 0.5...2.5, and derived Ropt by numerical solution of Eq. (1). Then we performed the astrometric reduction for the target star (Sects. 3.3.1, 3.3.2) and computed the estimator Υ(z), whose minimum indicates the best value of z (typically 0.8–1.5). As suitable estimator, we used the index Υ(z) = ∑ m(xm/σm − xm − 1/σm − 1)2 of high-frequency noise in the positional residuals of individual frames. For the final steps of the reduction, we used a similar expression but based on the high-frequency noise in the epoch residuals, where any orbital motion (if detected) was removed.
4. Results and mitigation of systematic errors
4.1. Single-frame precision
The precision of a single frame measurement σm depends on the photocentre measurement uncertainty, the atmospheric image motion, and uncertainties in the transformation to the reference frame. Our model of σm (PL09) describes the measured dispersion of residuals xm well, which we verified again by processing field stars as if they were the target, followed by the comparison of σm and the measured rms of xm.
 |
Fig. 2 Single-frame precision as a function of magnitude for stars in the FoV with DE0716−06. Measured (dots) and model σm (open circles) values are shown, and the solid line indicates the dominant photocentre uncertainty component for a) the average of a full set of frames; b) an epoch with excellent 0.38′′ seeing. Magnitudes are given relative to DE0716−06 (mI = 17.5). |
We illustrate this and the next reduction steps with the help of the target Nr. 5 in Table 1 (Paper I), whose Simbad identifier is DENIS-P J0716478-063037 and hereafter is referred to as DE0716−06. For reference stars close to DE0716−06, the comparison is shown in Fig. 2a, where only observations obtained in 0.4–0.8′′ seeing are plotted. This figure looks similar for all targets. The component that corresponds to the uncertainty of the photocentre measurement (solid line) is dominant except at the bright end, where the contribution from atmospheric image motion and reference frame noise become significant. Evidently, the model values σm match the observed rms of xm well over a range of the six magnitudes.
At the bright end, the single-frame precision is about 0.6 mas, which is higher than σm = 0.3 mas obtained in the test study of the FORS2 astrometric performance (Lazorenko 2006), but this is a consequence of a different observation strategy. In the current programme, we specifically restricted the exposure duration to avoid systematic errors caused by saturation in very good seeing (Sect. 2), whereas Lazorenko (2006) aimed at determining the best astrometric precision with a single series of frames in stable seeing and with non-saturated target images with 1.5–2 × 106 electrons. The threefold gain in flux and a slightly better seeing (0.55′′ in Lazorenko 2006 compared with 0.6′′here) are responsible for the difference in precision, which becomes negligible when scaled to similar conditions. Consequently, another investigation of the FORS2 astrometric precision during the timespan of five month (PL09) yielded the same σm = 0.6 mas precision for stars wi th 0.5–0.7 × 106 electrons in the image. For extremely bright stars in that study, the precision improved to 0.3–0.4 mas, but such stars are not measured here because of the saturation problem.
For a single series of images obtained in very good seeing of 0.37–0.42′′ (shown in Fig. 2b), the model prediction also matches well except for the brightest stars, again, because of saturation. The impact of good seeing on the precision is evident with a twofold decrease of random uncertainty to 0.35 mas for bright stars. We conclude that the model value of σm adequately represents the random uncertainty. This is an important prerequisite for separating noise and systematic components in the epoch residuals, because the random part decreases inversely to the square root of the number of exposures, and its value is well predicted by our model of σm.
4.2. Epoch residuals
By taking the averages of ne individual frame residuals xm available for each epoch e, we derived the epoch-averaged residuals xe. These quantities are not directly used in the standard astrometric reduction (Sect. 3.3), for example, to compute the astrometric parameters ξ. However, they are critical to search for and eliminate systematic errors with an inter-epoch variability. The epoch residuals take into account the individual measurement precisions 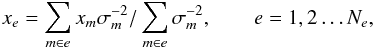 (3)where Ne is number of epochs. They correspond to the usual weighted average of ne random normal values Xm,Ym that have precisions of
(3)where Ne is number of epochs. They correspond to the usual weighted average of ne random normal values Xm,Ym that have precisions of 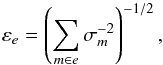 (4)which we call the nominal precision of the epoch residuals. This formal precision of the measured epoch data does not depend on the reduction that follows, in contrast to σe, which specifies the rms of the model-dependent fit residuals xe
(4)which we call the nominal precision of the epoch residuals. This formal precision of the measured epoch data does not depend on the reduction that follows, in contrast to σe, which specifies the rms of the model-dependent fit residuals xe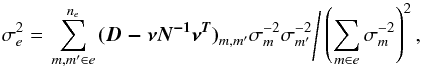 (5)where N is the normal matrix (PL09). The least-squares fit absorbs some noise from the measurements and induces correlations between the residuals xm, therefore we have σe<εe. The equality is reached in the limit Ne → ∞, where Eq. (5) equals Eq. (4). Using expression E [(xe/σe)2] = 1, where the operator E [] denotes the mathematical expectation, we can introduce the reduced χ2 value
(5)where N is the normal matrix (PL09). The least-squares fit absorbs some noise from the measurements and induces correlations between the residuals xm, therefore we have σe<εe. The equality is reached in the limit Ne → ∞, where Eq. (5) equals Eq. (4). Using expression E [(xe/σe)2] = 1, where the operator E [] denotes the mathematical expectation, we can introduce the reduced χ2 value 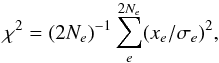 (6)whose deviation from unity indicates systematic errors or the signature of a companion. For the following statistical analysis, we have to know the degree of freedom (DoF) of χ2. By numerical simulations, where we used the actual observing conditions and added random noise to the measured data, we found that
(6)whose deviation from unity indicates systematic errors or the signature of a companion. For the following statistical analysis, we have to know the degree of freedom (DoF) of χ2. By numerical simulations, where we used the actual observing conditions and added random noise to the measured data, we found that 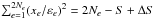 (the sum involves Ne data points both in RA and Dec) with ΔS = 0.39...0.44. This sum evaluates the effective number of DoF when all in-frame information is compressed to 2×Ne epoch residuals. For our observations, Ne = 10.8 on average, therefore DoF ≃ 15 if S = 7. Another convenient representation is DoF = 2 θ2Ne, where the value θ2 ≈ 0.70 is typical for our programme.
(the sum involves Ne data points both in RA and Dec) with ΔS = 0.39...0.44. This sum evaluates the effective number of DoF when all in-frame information is compressed to 2×Ne epoch residuals. For our observations, Ne = 10.8 on average, therefore DoF ≃ 15 if S = 7. Another convenient representation is DoF = 2 θ2Ne, where the value θ2 ≈ 0.70 is typical for our programme.
When the data are free of systematic errors, the expectation of the rms of xe is σe = θεe, thus 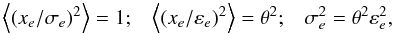 (7)where the angle brackets indicate averaging over epochs.
(7)where the angle brackets indicate averaging over epochs.
 |
Fig. 3 Reduced χ2 for bright stars in the DE0716−06 field (asterisks) as a function of brightness. The solid line corresponds to the best linear fit, and the target itself is marked with a filled circle. Data were reduced with k = 10 and the chip’s instability (Sect. 4.3.2) was corrected. |
Systematic errors become apparent primarily by a substantial increase of χ2 for bright stars. We illustrate this in Fig. 3 with stars in the DE0716−06 field, which was observed in a wide range of seeing conditions. The preliminary reduction of reference stars processed as targets produced large epoch residuals characterised by χ2 ≫ 1, showing a general tendency of increasing χ2 with the star brightness.
 |
Fig. 4 Dependence of the reduced |
Systematic errors also give rise to a seeing-dependence of the quantity 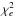 , which is the mean of (xe/σe)2 for bright stars at the epoch e. As shown in Fig. 4a, the
, which is the mean of (xe/σe)2 for bright stars at the epoch e. As shown in Fig. 4a, the 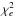 -values tend to be higher in good seeing. This dependence is less pronounced for stars about one magnitude fainter (Fig. 4b). This indicates that the amplitude of systematic errors is similar to σe for bright stars, that is 0.05–0.2 mas. Therefore, the excess in
-values tend to be higher in good seeing. This dependence is less pronounced for stars about one magnitude fainter (Fig. 4b). This indicates that the amplitude of systematic errors is similar to σe for bright stars, that is 0.05–0.2 mas. Therefore, the excess in 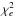 is registered primarily for these stars and only in good seeing.
is registered primarily for these stars and only in good seeing.
4.3. Systematic errors in the epoch residuals
4.3.1. Calibration files
To investigate the origin of the systematic errors, we used the information provided by the positions of reference stars and performed a special calibration computation for each star near the field centre. These stars were processed as targets with k = 10 and the actually targeted UCD was excluded from the reference objects. This provided us with a calibration file that has two important applications.
First, because the majority of reference stars in our sample are very distant (there are only 20 reference stars that have a measured trigonometric parallax larger than 10 mas) and any companion signature would be negligibly small, we can use the epoch residuals xe,rf and ye,rf of these stars for the detection, modelling, and mitigation of systematic errors. Second, it becomes possible to evaluate and consequently minimise the statistical difference between the scatter of epoch residuals for reference stars and the target, which is necessary to find traces of a weak orbital signal in the latter.
4.3.2. Instability of the relative CCD-chip position
The inspection of the epoch residuals xe,rf and ye,rf of stars in the calibration files sometimes revealed unexpected distribution patterns close to the border between the two chips making up the CCD detector of FORS2. A typical case is presented in Fig. 5a. A discontinuity between the residuals in chip 1 (y> 1000 px) and chip 2 (y< 1000 px) is present at the location of the inter-chip gap (y = 1000). We described this systematic trend with a smooth function G(y) that is anti-symmetric about the gap position. The discontinuity amplitude was usually registered at the noise level, but in many cases it was detected with a significance of 5–10 sigma, and could reach a peak-to-peak amplitude of g = 0.007–0.010 px, either in RA or Dec or in both dimensions. The occurrences of large amplitudes appears randomly distributed over the programme calendar, except for the time interval of November 19–24, 2011, when unusually large discontinuities of equal sign in RA (g = 0.02–0.05 px) were registered in five out of six epochs taken during this period. Surprisingly, the discontinuity was not seen in the epoch residuals of DENIS-P J0615493-010041 (hereafter DE0615−01) observed on 19 November 2011 only one hour before another target for which a large discontinuity amplitude was detected. This riddle will be resolved later in this section.
 |
Fig. 5 Positional residuals in RA on 24.11.2011 for stars in the DE0716−06 field computed with k = 10 and Ropt = 815 px. a) The original two-chip data showing the discontinuity at the chip edge with a full amplitude of gx = 0.0376 px, which is approximated by the function Gx(y) (solid line); b) only data of chip 1; c) after offset of chip 2 photocentre positions in RA by |
One of the extreme examples detected on 24 November 2011 in RA for DE0716−06 is shown in Fig. 5a and has a peak-to-peak amplitude of g = 0.0376 ± 0.0030 px = 4.74 ± 0.38 mas. We found that the systematic behaviour of the epoch residuals as a function of y disappears when discarding the data of one chip in the processing, see Fig. 5b which shows chip 1 residuals obtained without using data from chip 2.
 |
Fig. 6 Systematic change of star parallaxes in the DE0615−01 field. a) Measured values with the bias pattern caused by the chip displacement; b) the corrected data. The chip border is at y = 1000 px and the dot size is proportional to the star brightness. |
We investigated the origin of this behaviour and found that it is not an artefact of the PSF modelling at the chip edges. Instead, it must be caused by the relative shift of either of the CCD chips (as solid-body motion) along the x or y axis with the corresponding effect in RA or Dec. The effect can be understood as follows: consider a target star imaged on chip 1 just above the gap between the chips and let all images in chip 2 be shifted by + g along the x-axis. Because half of the reference stars are displaced, this results in the change of the RA zero-point by + g/ 2, and we see a −g/ 2 change in the positional residuals of the target. In the same way, the positional residuals of a target imaged on chip 2 close to the gap are biased by + g/ 2. The effect amplitude decreases with increasing distance from the gap, because of the decreasing relative weight of the reference stars from the other chip. A piecewise linear function describes this systematic effect sufficiently well: 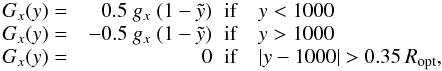 (8)where
(8)where 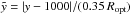 is a normalised distance. The function (8) is valid in RA and involves one free parameter gx, and a corresponding function depending on gy describes the effect of chip motion along the Dec axis, that is orthogonal to the chip gap. By fitting the calibration file data with the model (8), we derived the parameters gx and gy for every epoch and moved all chip 2 photocentre positions by constant offsets
is a normalised distance. The function (8) is valid in RA and involves one free parameter gx, and a corresponding function depending on gy describes the effect of chip motion along the Dec axis, that is orthogonal to the chip gap. By fitting the calibration file data with the model (8), we derived the parameters gx and gy for every epoch and moved all chip 2 photocentre positions by constant offsets 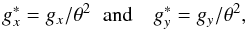 (9)which are slightly larger than gx, gy. Here we considered that the values of g are determined relative to the average chip position (i.e. including the epoch with a large shift), thus are biased. Using the term 1 /θ2, we approximately removed this bias in the zero-points, obtaining accurate shifts g∗. The dataset
(9)which are slightly larger than gx, gy. Here we considered that the values of g are determined relative to the average chip position (i.e. including the epoch with a large shift), thus are biased. Using the term 1 /θ2, we approximately removed this bias in the zero-points, obtaining accurate shifts g∗. The dataset  (10)where the chip 2 motion was corrected (e.g. Fig. 5c) is free of the systematic pattern.
(10)where the chip 2 motion was corrected (e.g. Fig. 5c) is free of the systematic pattern.
A potential origin of the chip motion was proposed by the ESO User Support Department (van den Ancker 2013, priv. comm.). The FORS2 camera has two interchangeable CCDs (red- and blue-optimised) of which only one is mounted at a given time. To exchange the CCD, the cryostat is warmed up and subsequently cooled down and the associated thermal shock can cause the instability in relative chip position at sub-micrometer level. This hypothesis is supported by that fact that we recorded epochs with large amplitudes of gx around times when the red CCD, which was used for our observations, was temporarily replaced, requiring cryostat interventions on November 4 and 25, 2011.
As we noted above, the observations of DE0615−01 on 19 November 2011 do not show the signature of a large relative chip shift, although this might be expected. Instead, we discovered a systematic change of the relative parallax values of field stars along the y-axis, that is similar in shape to the function G with a peak-to-peak amplitude of 8 mas, see Fig. 6a. The chip instability is evidently the reason of this effect. Due to differential nature of the measurements, a chip displacement that changes in time proportional to the parallax factor cannot be distinguished from the parallax motion, and the measured parallaxes of field stars are biased with an amplitude that depends on y (Fig. 6a). Consequently, the discontinuity in the epoch residuals disappears. To correct for the bias, we fitted the distribution of field star parallaxes with a function of the type (8) and then removed the systematic component, which yielded a bias-free distribution of parallaxes (Fig. 6b). Finally, a similar correlation can cause biases in the proper motions if g changes linearly in time, and a corresponding correction procedure was applied to the proper motions, too.
 |
Fig. 7 Correlation between the measured motion of chips gx and the telescope pointing error in Dec (filled circles); between gy and the pointing error in RA (open circles). Lines show the expected image shift due to the rotated mounting of chips. |
In addition to actual chip instability, the discontinuity in measured positions between chips can be caused by the slightly inclined mounting of chip 2 relative to chip 1 by the angle 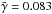 ° (see ESO documentation2). If the telescope pointing is not perfect and deviates by Δx, Δy from its “normal” pointing, the star field in chip 1 is also moved by Δx and Δy, but in chip 2 the images are moved by
° (see ESO documentation2). If the telescope pointing is not perfect and deviates by Δx, Δy from its “normal” pointing, the star field in chip 1 is also moved by Δx and Δy, but in chip 2 the images are moved by 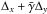 and
and 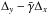 . This is equivalent to a chip 2 pseudo-displacement by
. This is equivalent to a chip 2 pseudo-displacement by 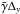 and
and 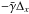 . For the VLT Unit Telescope 1, the pointing error Δ exceeded 1′′ in observations of seven targets for at least one epoch. In Fig. 7, we compare the induced image shifts
. For the VLT Unit Telescope 1, the pointing error Δ exceeded 1′′ in observations of seven targets for at least one epoch. In Fig. 7, we compare the induced image shifts 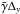 (dashed line) and
(dashed line) and 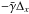 (straight line) with gx and gy derived from the calibration files for all available epochs of the seven targets. Considering that the precision of g is 0.0005–0.002 px (depending on the star density and seeing), we found a considerable but incomplete correlation between the induced and measured shift of chips. Thus, the measured relative motion of chips can be in part only caused by the telescope pointing error. In the problematic period of November 19–24, 2011, illustrated in Fig. 5, the telescope pointing was almost perfect, and the detected motion along the chip gap is real with an amplitude of ~0.3–0.7 micrometer. Its absolute value, however, cannot be determined because of the relative nature of the astrometric reduction.
(straight line) with gx and gy derived from the calibration files for all available epochs of the seven targets. Considering that the precision of g is 0.0005–0.002 px (depending on the star density and seeing), we found a considerable but incomplete correlation between the induced and measured shift of chips. Thus, the measured relative motion of chips can be in part only caused by the telescope pointing error. In the problematic period of November 19–24, 2011, illustrated in Fig. 5, the telescope pointing was almost perfect, and the detected motion along the chip gap is real with an amplitude of ~0.3–0.7 micrometer. Its absolute value, however, cannot be determined because of the relative nature of the astrometric reduction.
The chip instability can be very small but well-determined in good observing conditions (Fig. 5d corresponds to gx = 0.0044 ± 0.0008 px = 0.55 ± 0.10 mas). Therefore, we corrected all chip 2 positions irrespective of the effect amplitude g by moving X and Y in chip 2 by g∗x and g∗y, respectively. The uncertainty of individual corrections according to Eq. (8) for most field stars is smaller than 0.01–0.03 mas and hardly affects the final astrometric precision. In poor seeing, as displayed in Fig. 5a, the correction uncertainty can degrade to 0.1–0.5 mas for objects near the chip gap.
4.3.3. Correlation between epoch residuals
The epoch residuals xe,rf,ye,rf in calibration files were corrected for the chip instability (previous section), thus the largest deviations were filtered out before the following analysis of systematic errors. We found no significant correlation between the epoch residuals and the star colour, magnitude, proper motion, parallax, or seeing in the calibration file data.
To investigate the error distribution over the CCD, we introduced the value 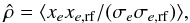 (11)which expresses the correlation between the epoch residuals xe and xe,rf of the target and of a field star at distance r. The brackets denote the average over epochs.
(11)which expresses the correlation between the epoch residuals xe and xe,rf of the target and of a field star at distance r. The brackets denote the average over epochs.
 |
Fig. 8 Individual |
Figure 8 presents a typical distribution of  . By averaging the
. By averaging the  values, we obtained the function
values, we obtained the function 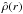 , whose shape does not significantly depend on the choice of the star treated as the ’target’. We found that
, whose shape does not significantly depend on the choice of the star treated as the ’target’. We found that  is usually positive on small scales from r = 0 to r ≃ 0.05 − 0.08 Ropt and negative at larger distances r ≃ 0.1 Ropt − 0.5 Ropt.
is usually positive on small scales from r = 0 to r ≃ 0.05 − 0.08 Ropt and negative at larger distances r ≃ 0.1 Ropt − 0.5 Ropt.
A similar correlation is often seen in experimental data when the random signal limited in space (or time) is fitted by a polynomial. By numerical simulation, Andronov (1994) and Lazorenko (1997) have shown that the remainders of the fitting (in our case, the epoch residuals obtained after polynomial fitting in CCD space) usually exhibit an oscillating autocorrelation function, whose shape depends on the polynomial order and, to a minor extent, on the power spectrum of the signal. Generally, the autocorrelation function of detrended measurements is positive at small scales before turning to zero at 0.1–0.15 times the “normalised series length”. In one-dimensional space, this quantity is defined as a twice the series length (2 Ropt for the present instance of reduction) divided by the polynomial order divided by two (k∗/ 2 in our case). Because k∗ = k/ 2–1, the normalised series length is simply Ropt for the calibration file that was generated with k = 10. The general properties of time series therefore predict the existence of the positive correlation at r< (0.1–0.15)Ropt, and the negative correlation at larger r up to 0.6Ropt. The autocorrelation minimum occurs at (0.25 − 0.35) Ropt. The two-dimensional astrometric data (Fig. 8) match the theoretical predictions for the autocorrelation shape, scales, and signs of de-trended measurements well. Therefore, this correlation pattern is not specific to FORS2 astrometry.
Correlations can also originate from high-order optical distortions and PSF changes across the CCD. Because they are related to the actual telescope alignment, these factors cause complicated image displacements that are not modelled by the basic functions f(x,y), but they tend to be stable during one epoch. The difference αe between the real and the modelled photocentre positions is the uncompensated systematic position error, that produces the spatial correlation  in the epoch residuals.
in the epoch residuals.
4.3.4. Detection and inhibition of systematic errors
The elimination of αe for individual frames is problematic because of the low signal-to-noise ratio (S/N) of αe/σm, but it becomes possible for an epoch, because of the higher S/N of αe/σe in the epoch residuals. For the computations, we used the sample estimates  , but the direct estimates of αe are inapplicable, because they are too noisy (Fig. 8). Instead of αe, we calculated the quantities Δe, which were defined to ensure minimum variance and low correlation in the corrected residuals xe. We applied two different types of space-dependent corrections:
, but the direct estimates of αe are inapplicable, because they are too noisy (Fig. 8). Instead of αe, we calculated the quantities Δe, which were defined to ensure minimum variance and low correlation in the corrected residuals xe. We applied two different types of space-dependent corrections: 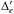 for small-scale and
for small-scale and 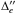 for large-scale systematic errors.
for large-scale systematic errors.
For each epoch e, we averaged the values of xe,rf for the reference stars in the calibration file encircled within the small radius rsmall = β′Ropt from the target star, which produced the averaged residuals xe, ∗ and their precision σe, ∗. Using these values instead of xe,rf and σe,rf in Eq. (11), we computed  , which now represents the correlation between the target and the nearby star group residuals. We searched for the strongest positive correlation
, which now represents the correlation between the target and the nearby star group residuals. We searched for the strongest positive correlation  by varying β′, usually reached at β′ = 0.05 − 0.15. For DE0716−06, the maximum is at rsmall = 128 px ≃16″, which is marked by a solid vertical line in Fig. 8. Using these data and the optimal subtraction of the common component in correlated values described in Appendix A, we computed the corrections
by varying β′, usually reached at β′ = 0.05 − 0.15. For DE0716−06, the maximum is at rsmall = 128 px ≃16″, which is marked by a solid vertical line in Fig. 8. Using these data and the optimal subtraction of the common component in correlated values described in Appendix A, we computed the corrections 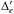 and applied them to target positions Xm at each frame of the epoch e. Typical values of
and applied them to target positions Xm at each frame of the epoch e. Typical values of 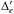 are 0.05–0.2 mas.
are 0.05–0.2 mas.
The precision φsmall(e) of the correction 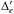 depends on the number of nearby field stars and on the seeing. For low values rsmall = 0.1...0.2′, the number of encircled stars is low and for some field stars,
depends on the number of nearby field stars and on the seeing. For low values rsmall = 0.1...0.2′, the number of encircled stars is low and for some field stars, 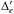 cannot be found. It is important to recognise that despite apparently introducing additional noise due to the sometimes low nearby star number, the actual uncertainty of the corrected residuals does not increase, because of the optimal subtraction of the systematic error component. The method of removing the spatial correlation (Appendix A) is a tool of decomposing the observed variance De of xe into a sum (Eq. (A.1)) of the model variance
cannot be found. It is important to recognise that despite apparently introducing additional noise due to the sometimes low nearby star number, the actual uncertainty of the corrected residuals does not increase, because of the optimal subtraction of the systematic error component. The method of removing the spatial correlation (Appendix A) is a tool of decomposing the observed variance De of xe into a sum (Eq. (A.1)) of the model variance 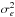 and the mean square of the systematic error α2. The systematic component is removed only partially to ensure the best final precision (Eq. (A.5)).
and the mean square of the systematic error α2. The systematic component is removed only partially to ensure the best final precision (Eq. (A.5)).
To search for systematic errors at large scales, we averaged the values of xe for reference stars in the calibration file within the annular area around the target between r = 0.6 βRopt and r = 1.6 βRopt, where β is a variable. The obtained values, which we denote as 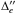 , have opposite sign to
, have opposite sign to 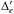 because
because  is negative at large scales. Numerically, we found that the best convergence of the output epoch residuals is reached when
is negative at large scales. Numerically, we found that the best convergence of the output epoch residuals is reached when 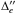 is added to Xm for m ∈ e.
is added to Xm for m ∈ e.
While varying β, we processed each of ~30 bright stars in the field centre as targets and applied the correction 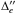 to the photocentre positions Xm. The optimal value of β is found when the sum of
to the photocentre positions Xm. The optimal value of β is found when the sum of 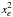 , computed over the star sample, is minimum. For DE0716−06, this value is β = 0.28 and corresponds to the minimum of the function
, computed over the star sample, is minimum. For DE0716−06, this value is β = 0.28 and corresponds to the minimum of the function  at 0.28 Ropt, which agrees with its theoretical location at 0.25–0.35 times the ’normalised series length’ (Lazorenko 1997). Because β is defined on large scales, it is applicable across the entire field, but β′ varies in space and therefore is specific to each target.
at 0.28 Ropt, which agrees with its theoretical location at 0.25–0.35 times the ’normalised series length’ (Lazorenko 1997). Because β is defined on large scales, it is applicable across the entire field, but β′ varies in space and therefore is specific to each target.
 |
Fig. 9 Dependence of the total uncertainty φspace(e) of spatial corrections on seeing for the brightest stars in all fields and for all epochs. |
The astrometric reduction includes the complete computation of many bright field stars as targets and the application of the corrections 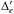 and
and 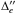 with precisions φsmall(e) and φlarge(e), respectively, determined for each star individually. The sum
with precisions φsmall(e) and φlarge(e), respectively, determined for each star individually. The sum 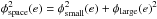 is the total variance of space-correlated errors in the reduced FORS2 astrometry. The value of φspace(e) depends on seeing, as shown in Fig. 9, because the systematic errors are better determined in good observing conditions (~0.06 mas at average seeing). The variance
is the total variance of space-correlated errors in the reduced FORS2 astrometry. The value of φspace(e) depends on seeing, as shown in Fig. 9, because the systematic errors are better determined in good observing conditions (~0.06 mas at average seeing). The variance 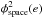 is added to the nominal variance
is added to the nominal variance 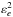 and appears in the covariance matrix D as the residual covariance of measurements in the frames m and m′ of an epoch e. The related specificities in the reduction of correlated measurements are discussed in Appendix B.
and appears in the covariance matrix D as the residual covariance of measurements in the frames m and m′ of an epoch e. The related specificities in the reduction of correlated measurements are discussed in Appendix B.
4.3.5. Residual systematic errors
Despite the mitigation of systematic errors correlated in space, the χ2-value continues to depend on seeing (Fig. 4c). Compared with the initial values (Fig. 4a), the updated χ2-values are lower, but still unacceptably high in good seeing. One possible reason is the presence of an unknown systematic error ϕ in the observations, which is not removed by the reduction and not revealed by the dependence of the residuals xe on observing conditions or model parameters. We modelled the corresponding effect in χ2 by the expression 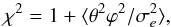 (12)where the brackets denote the average over epochs,
(12)where the brackets denote the average over epochs, 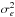 is computed taking into account the uncertainties of space-dependent corrections
is computed taking into account the uncertainties of space-dependent corrections 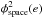 , and θ2 reflects the decrease of uncertainty by the least-squares fit.
, and θ2 reflects the decrease of uncertainty by the least-squares fit.
By adjusting the χ2-values with the model Eq. (12) for bright stars in the field centre, we derived ϕ, whose value is 0.08 mas for DE0716−06 and 0.03–0.14 mas for other targets with a median of 0.09 mas. The ϕ estimate was derived assuming that its value does not depend on epoch and location in the FoV. Because of its typical magnitude of 0.1 mas (Table 2), ϕ dominates the space-dependent components and limits the precision of bright star observations, for which εe is of similar amplitude. No clear dependence of ϕ on observing conditions or field star density was found, except a weak upward trend for crowded fields (Nr. 17 and 18), where photocentres are biased by nearby star images, and in fields with low star density.
Data related to the computation of 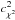 , the residual systematic error ϕ, the rms of the epoch residuals xe and the epoch precision σe for bright stars.
, the residual systematic error ϕ, the rms of the epoch residuals xe and the epoch precision σe for bright stars.
The revised variance of systematic errors is now 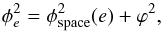 (13)therefore the nominal variance of epoch measurements is
(13)therefore the nominal variance of epoch measurements is 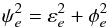 (14)instead of
(14)instead of 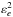 . Consequently, Eq. (7) is updated to
. Consequently, Eq. (7) is updated to 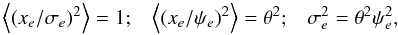 (15)where
(15)where 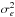 is defined by Eq. (5), provided that computations are made while allowing for all systematic errors.
is defined by Eq. (5), provided that computations are made while allowing for all systematic errors.
The quantity ϕ is used to adjust the model expectation of epoch residuals to their measured rms. The efficiency of including ϕ in the reduction model is illustrated by Fig. 4d, where 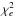 is independent of seeing. In addition, it allows us to update the covariance matrix D (Appendix B).
is independent of seeing. In addition, it allows us to update the covariance matrix D (Appendix B).
4.3.6. Seeing variability and systematic errors
Finally, we inspect the relation between seeing and intrinsic systematic space-dependent errors in the epoch residuals, which were not corrected with the approach of Sect. 4.3.4. The definition of their magnitude αsyst is somewhat ambiguous but it seems natural to specify it as the average squared sum of the small- and large-scale components αe and 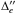 .
.
The characteristics of αsyst for FORS2 were already analysed in PL09, following a slightly different definition, for a single sky field and five epoch observations with monthly spacing. There, the typical amplitude of αsyst was found to be 0.16 mas within 1′ from the field centre. For observations in a more restrictive 0.47–0.78′′seeing range, which included 80% of all images, they decreased to about 0.05 mas at the field centre and to 0.1 mas in the periphery.
 |
Fig. 10 Space-dependent errors in RA for each epoch: αe (open circles) and |
Here, a similar estimate αsyst ≃ 0.15 mas was obtained for a few sky fields with roughly the same 20% ratio of non-standard seeing. By simulating restricted observing conditions and artificially rejecting frames obtained outside of 0.47–0.78′′seeing, this value decreased to 0.09–0.11 mas. In both cases, the current estimates are close to those obtained in PL09.
The effect of seeing restriction is illustrated by Fig. 10, which shows the components αe and 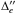 separately for bright stars in the DE1253−57 field. The observations of this target stand out because of the high percentage (34%) of non-standard seeing and the large systematic errors (Fig. 10 top). When the astrometric reduction is made with the restriction 0.47″ <FWHM< 0.78″, the error components become smaller (Fig. 10 bottom, where only sufficiently well measured systematic errors are shown). When averaged over the complete target sample, however, the overall improvement by restricting the seeing is small (~10%).
separately for bright stars in the DE1253−57 field. The observations of this target stand out because of the high percentage (34%) of non-standard seeing and the large systematic errors (Fig. 10 top). When the astrometric reduction is made with the restriction 0.47″ <FWHM< 0.78″, the error components become smaller (Fig. 10 bottom, where only sufficiently well measured systematic errors are shown). When averaged over the complete target sample, however, the overall improvement by restricting the seeing is small (~10%).
A substantial 20% fraction of the exposures taken for our programme was obtained outside the optimal seeing domain (Fig. 11). In 45 epochs, most images were obtained with FWHM outside of the best 0.47–0.78′′range, and in 12 epochs, all images were obtained out of that restriction. For six targets, substantial (>50%) occurrence of non-optimal seeing was registered in three or more epochs. Discarding data using the seeing criterion is thus unacceptable, because leads to a dramatic loss in number of observations that is not compensated for by a gain in precision.
 |
Fig. 11 Distribution of actual seeing in 7442 frames collected for our programme between 26 November 2010 and 15 March 2013, and for which we measured the star photocentres. |
4.4. Adjusting χ2 of epoch residuals for field stars
After removing the systematic errors, the 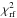 -values of epoch residuals (Eq. (6)) for reference stars hardly depend on seeing anymore and are close to unity in most fields. Their dependence on brightness is also negligible, therefore our model of observational errors is now adequate. The following analyses revealed minor deviations of the
-values of epoch residuals (Eq. (6)) for reference stars hardly depend on seeing anymore and are close to unity in most fields. Their dependence on brightness is also negligible, therefore our model of observational errors is now adequate. The following analyses revealed minor deviations of the 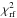 -distribution from the theoretical χ2-distribution, however.
-distribution from the theoretical χ2-distribution, however.
4.4.1. Statistics of χ2
A typical 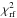 -distribution for field stars (each processed as a target object with k = 10) is illustrated by Fig. 12. The individual
-distribution for field stars (each processed as a target object with k = 10) is illustrated by Fig. 12. The individual 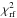 -values are concentrated around the average value
-values are concentrated around the average value 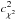 close to unity with a scatter, which ideally should match the theoretical χ2 distribution with DoF = 15 on average (Sect. 4.2). The residuals
close to unity with a scatter, which ideally should match the theoretical χ2 distribution with DoF = 15 on average (Sect. 4.2). The residuals 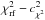 are expected to show an rms scatter of
are expected to show an rms scatter of 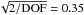 and the probability of detecting deviations above three sigma, i.e.
and the probability of detecting deviations above three sigma, i.e. 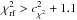 , should be low.
, should be low.
The observed distribution of 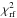 , however, has a long non-Gaussian tail extending to extremely high values of 3–20 (one deviation in Fig. 12), which is incompatible with the statistical prediction. We verified that most outliers are related to non-standard cases such as elongated images, apparent binarity of the object, a close background star, CCD defects, and too large or too small FWHM, and those were rejected by requiring
, however, has a long non-Gaussian tail extending to extremely high values of 3–20 (one deviation in Fig. 12), which is incompatible with the statistical prediction. We verified that most outliers are related to non-standard cases such as elongated images, apparent binarity of the object, a close background star, CCD defects, and too large or too small FWHM, and those were rejected by requiring 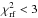 .
.
 |
Fig. 12
|
The data show that 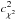 can be described by first a constant and then, above a threshold brightness I>I0, by a linear function:
can be described by first a constant and then, above a threshold brightness I>I0, by a linear function: 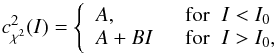 (16)with a small positive or, in most cases, insignificant slope B. The data is listed in Table 2 with
(16)with a small positive or, in most cases, insignificant slope B. The data is listed in Table 2 with 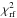 given for the fainter (Col. 2) and brighter (Col. 3) half of ~35 of the brightest stars near the field centre,
given for the fainter (Col. 2) and brighter (Col. 3) half of ~35 of the brightest stars near the field centre, 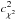 at the target brightness computed with Eq. (16), and the measured
at the target brightness computed with Eq. (16), and the measured 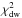 for the targets. While these data refer to the reduction mode k = 10,
for the targets. While these data refer to the reduction mode k = 10, 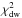 for targets are given for the reduction that incorporates all modes k from 4 to 16, because it better serves the purpose of the analysis. For the brightest stars,
for targets are given for the reduction that incorporates all modes k from 4 to 16, because it better serves the purpose of the analysis. For the brightest stars, 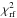 is normally within 1.0 and 1.3, but in dense fields (Nr. 17 and 20), it increases to 1.6–1.9. In the example of Fig. 12, the distribution of
is normally within 1.0 and 1.3, but in dense fields (Nr. 17 and 20), it increases to 1.6–1.9. In the example of Fig. 12, the distribution of 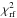 for reference stars is fitted by a constant
for reference stars is fitted by a constant 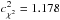 . For DE0716−06,
. For DE0716−06, 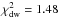 , which is well within an rms of 0.49 of the data points (in Table 2,
, which is well within an rms of 0.49 of the data points (in Table 2, 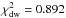 refers to the mean of k = 4...16 reduction modes; it also lies within the statistical scatter).
refers to the mean of k = 4...16 reduction modes; it also lies within the statistical scatter).
Distant reference stars have no or a negligible orbital signature and the expected value of 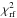 is exactly 1.0. Therefore, the reference stars provide the calibration
is exactly 1.0. Therefore, the reference stars provide the calibration 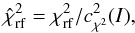 (17)which leads to a better estimate of
(17)which leads to a better estimate of 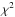 .
.
 |
Fig. 13 Histogram of the absolute values of epoch residuals (open histogram), the best-fit normal function (solid curve), and the histogram of the epoch precision σe (filled histogram) for epochs with 32 exposures and 0.6′′ seeing: for bright stars (lower panel) and UCDs only (upper panel). |
Considering that 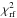 is the mean ratio of
is the mean ratio of 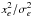 , one might suggest that the excess in
, one might suggest that the excess in 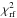 detected for most fields (Table 2) is due to systematically underestimated model values of σe. However, for stars whose brightnesses are similar to the target within ± 0.5 mag, the measured rms of xe does not exceed σe on average. This conclusion is based on the estimates given in the last two columns of Table 2, which correspond to observations in standard conditions with median seeing (expressed by FWHM) of 0.6′′ and 32 frames. These estimates were obtained by scaling the measured rms of xe and σe with the factor 0.6′′/FWHM
detected for most fields (Table 2) is due to systematically underestimated model values of σe. However, for stars whose brightnesses are similar to the target within ± 0.5 mag, the measured rms of xe does not exceed σe on average. This conclusion is based on the estimates given in the last two columns of Table 2, which correspond to observations in standard conditions with median seeing (expressed by FWHM) of 0.6′′ and 32 frames. These estimates were obtained by scaling the measured rms of xe and σe with the factor 0.6′′/FWHM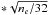 , which makes the data more homogeneous. Evidently, xe ≈ σe on average.
, which makes the data more homogeneous. Evidently, xe ≈ σe on average.
The histogram of the epoch residuals (normalised to the standard seeing and frame number) for bright stars within 50′′ from the target is shown in lower panel of Fig. 13 and is fitted by a normal distribution with sigma parameter 0.125 ± 0.003 mas, which is close to the independently computed mean-square value of 0.126 mas for xe. For σe, whose histogram is also shown in the lower panel of Fig. 13, we obtained the median of 0.126 mas and the mean-square value of 0.128 mas. We conclude that the model value 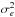 matches the observed
matches the observed 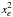 well, therefore the excess in
well, therefore the excess in 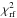 has to have another origin. Note that while
has to have another origin. Note that while 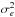 refers to the epoch fit residuals, the nominal precision of epoch measurements ψe is a factor 1 /θ = 1.20 higher, that is, 0.15 mas.
refers to the epoch fit residuals, the nominal precision of epoch measurements ψe is a factor 1 /θ = 1.20 higher, that is, 0.15 mas.
The interpretation of the excess in 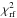 is difficult because of its low value. Considering the above analysis, we relate it to the uncertain determination of
is difficult because of its low value. Considering the above analysis, we relate it to the uncertain determination of 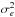 . In other words, while we verified that the real and model
. In other words, while we verified that the real and model 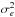 values are equal on average, the predictions for individual epochs can deviate from their actual values. This systematically biases the ratio
values are equal on average, the predictions for individual epochs can deviate from their actual values. This systematically biases the ratio 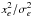 towards higher values, while
towards higher values, while 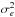 matches
matches 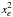 on average. Therefore, Eq. (17) leads to better estimates of χ2, but a similar correction is not applicable to
on average. Therefore, Eq. (17) leads to better estimates of χ2, but a similar correction is not applicable to 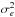 .
.
Finally, we estimated the precision of the epoch residuals for the data filtered by the seeing criterion, that is, using images with 0.47′′< FWHM < 0.78′′ only, and obtained 0.11 mas for an rms of epoch residuals and 0.13 mas for the nominal epoch precision, with only 10% improvement compared with the complete data set.
4.4.2. Cumulative distribution of χ2 for epoch residuals.
 |
Fig. 14 Normalised cumulative distribution of the measured |
In Fig. 14a, the measured cumulative distribution of 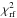 for epoch residuals of field stars is compared with the theoretical χ2-distribution with DoF = 15. The measured distribution significantly deviates from its theoretical expectation, but after the correction Eq. (17) (filled circles), they become compatible. The same quantities but for targets only are displayed in Fig. 14b. In summary, we showed that the statistics of the epoch residuals expressed in terms of χ2 follows the expected normal distribution sufficiently well.
for epoch residuals of field stars is compared with the theoretical χ2-distribution with DoF = 15. The measured distribution significantly deviates from its theoretical expectation, but after the correction Eq. (17) (filled circles), they become compatible. The same quantities but for targets only are displayed in Fig. 14b. In summary, we showed that the statistics of the epoch residuals expressed in terms of χ2 follows the expected normal distribution sufficiently well.
4.5. Astrometric precision for UCDs
The histogram of the epoch residuals for bright stars can be compared with that for UCDs only (upper panel of Fig. 13), which is fitted by a normal distribution with sigma parameter 0.128 ± 0.009 mas, close to the mean-square value of 0.137 mas for xe. For σe, we obtained the median of 0.122 mas and the mean-square value of 0.127 mas. The derived values are very near to the corresponding estimates for bright stars; the precision characteristic of UCDs and bright stars is therefore identical. Note that these estimates correspond to FWHM = 0.6′′and ne = 32 frames. If the precision parameters are not normalised to these standard conditions (e.g. frame series with small and large frame number are used with equal weights), the rms dispersion of the epoch residuals increases to 0.146 mas, which is the global astrometric precision of the programme (Paper I).
Figure 15 illustrates that the precision of the epoch residuals for UCDs (normalised to ne = 32 exposures) changes from 0.1 to 0.2 mas almost linearly with FWHM.
 |
Fig. 15 Precision of the epoch residuals for UCDs for a frame series with 32 exposures. |
Catalogue characteristics.
5. Catalogue of field stars
The FORS2 data collected for our project contain rich information on the kinematics and distances of a large number of faint field stars. We make this data available by publishing a catalogue containing 12 000 stars with I = 16–21 mag in 20 fields. The catalogue includes all stars within 1′50′′ distance from the respective target (1′30′′ for targets Nr. 17 and 18, which have a high star density) whose photocentres were measured with acceptable precision. Elongated images (e.g. galaxies) and images of close star pairs were rejected. Computations were restricted to the reduction mode k = 10 only and reproduce those made for the calibration file (Sect. 4.3.1), but for a much larger star sample and with all systematic corrections applied. This produced a complete set of astrometric parameters, including CCD coordinates at the MJD = 55 700 epoch adopted for all reference frames. Positions were determined with precisions of ~0.05–0.07 mas for bright stars. However, because they are given in the local system of reference frames with uncertain orientation and deformation caused by the telescope optics, they are not directly available for external use. In our catalogue, these coordinates are transformed to ICRF and J2000.0 using external catalogues, unfortunately, with a loss of three orders of magnitude in precision.
5.1. Transformation to the ICRF system
The conversion from relative FORS2 positions to the ICRF system was made by aligning field star coordinates with positions in the USNO-B catalogue (Monet et al. 2003). In each field, we selected 50–200 stars that are well identified in USNO-B. The residuals “FORS2”–“USNO-B” were found to have distributions with long non-Gaussian tails, therefore the identification window size was set to the value that minimised the residuals ofthe coordinate systems fit. Considering that the uncertainties of FORS2 positions and proper motions are very small, we temporarily converted our data to the average epoch of each USNO-B star observation, which improved the precision of the coordinate systems alignment. Then we applied the least-squares fit with a model that included full quadratic and cubic polynomials. The typical rms of individual “FORS2”–“USNO-B” residuals was ~0.2′′ and allowed us to transform FORS2 positions to the ICRF system with a precision of 0.05–0.10′′ for most fields, and with an accuracy maintained by “USNO-B”. Using the future Gaia (Perryman et al. 2001) astrometric catalogue, we plan to better tie the FORS2 local fields to the ICRF and to maintain the high precision of ~0.05–0.07 mas for stars of I = 15–17 mag in an absolute sense.
5.2. Pixel scale
An accurate pixel scale value is necessary to convert astrometric parameters from pixel to the arc metric with no loss of accuracy. The approximate value of 0.126′′ px-1 given in the FORS2 documentation is not sufficient, as we need to know it with a relative precision of at least 10-3 ≃ 0.0001′′ px-1 to match the precision of the parallax measurements. At this level of precision, it should also be known individually for each sky field, because the fields have reference frames composed in unique ways, they were observed in different temperature conditions with varying fine alignment of the telescope optics, and they are based on approximate star positions.
The pixel-scale values listed in Table 3 were determined from the derivatives of the transformation fit function along the coordinate axes at the target’s position, with a subsequent average of these two values. The scale variation across target fields is slightly larger then the uncertainties and possibly displays a real variation between the reference frames formed in different ways. To convert the astrometric parameters we applied individual pixel scale values for each field.
We ascertained also that the median difference between scales for x and y axes is −0.37 ± 0.06 mas/px. Because this is only 3 × 10-3 of the average scale, the corresponding effect for the conversion of astrometric parameters is negligible for the catalogue stars, but it has to be accounted for the UCDs.
5.3. Photometric system
Because the observations were not necessarily obtained in photometric conditions, we estimated the star fluxes approximately by computing the sum of counts within the central 11 × 11 pixel area of the star images, and the magnitude zero-point was determined for each epoch using external catalogues. The best reference photometry is provided by the DENIS catalogue (DENIS Consortium 2005), which contains I-band magnitudes obtained with a Gunn-I filter at 820 nm for stars brighter than 18.5 mag. For most fields, this yielded corrections to FORS2 photometry with a precision of ±0.01–0.02 mag. For fields Nr. 2, 8, and 15, however, none or very few common stars were found. In these cases, we used the average value of the corrections determined for other fields and assumed that the zero-point precision is equal to the scatter of individual field corrections (±0.08 mag).
 |
Fig. 16 Distribution of proper motion and absolute parallaxes on DCR parameter ρ for bright stars of the catalogue. Dot size marks the star magnitude. |
5.4. Colour–dependent systematic errors
To control possible colour-dependent systematic errors, we used DCR parameter ρ (Sect. 3.2), which is +10...+20 mas for UCDs and ρ = 0 corresponds to the average colour of field stars, probably of K–M spectral classes. Parameters ρ are not included in the catalogue because of the large uncertainty of determination, which is of acceptable ~1–2 mas precision for bright stars alone. Using them as equivalent of the colour, we found no clear systematic dependence of the proper motion and absolute parallaxes on ρ (Fig. 16) for stars of 15–17.5 mag I, that is, of the UCDs brightness.
5.5. Catalogue characteristics
The overall catalogue characteristic are given in Table 3 for each target listed with its DENIS identifier: the catalogue star number, number of stars within ± 0.5 mag from the target, which indicates the sky density of bright stars, the size of the reference field Ropt for stars in the field centre, the magnitude limits I1 and I2, the precision of ICRF positions, proper motions, parallaxes, the number of stars in common with “USNO-B”, the pixel scale, and the rms of differences FORS2–“USNO-B”.
 |
Fig. 17 Distribution of absolute parallaxes and relative proper motions of catalogue stars as a function of magnitude in target fields 2, 5, and 9. The sequence number is shown in the upper left corner of the panels and 1σ uncertainty ranges are shown as dashed lines. |
The catalogue table, available at the CDS, contains the field number (Col. 1), the sequential star number n in the field (Col. 2), the I-band magnitude and its precision σI (Cols. 3, 4), RA and Dec for the equinox and epoch J2000.0 (Cols. 5, 6), the precisions in RA and Dec (Cols. 7, 8), the relative proper motion 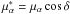 and μδ per Julian year (Cols. 9, 10), the absolute parallax (Col. 11), the precisions of these data (Cols. 12–14), the mean epoch T of observations in Julian years since J2000.0 (Col. 15), and the χ2-value for the epoch residuals to flag the quality of the data (Col. 16). An excerpt from the catalogue is given in Table 4.
and μδ per Julian year (Cols. 9, 10), the absolute parallax (Col. 11), the precisions of these data (Cols. 12–14), the mean epoch T of observations in Julian years since J2000.0 (Col. 15), and the χ2-value for the epoch residuals to flag the quality of the data (Col. 16). An excerpt from the catalogue is given in Table 4.
The catalogue proper motions are relative and given in the system of distant field stars. As explained in Sect. 3.3.1, approximately half of the proper motions are thus negative. The conversion to absolute parallaxes was made using the corrections Δϖgalax derived from the comparison of relative FORS2 parallaxes with a Galaxy model (Robin et al. 2003), which are given in Table 5 of Paper I. For bright stars, typical precisions are σμ = 0.1 mas/yr and σϖ = 0.1 mas (Table 3), which for stars 5 mag fainter degrades by a factor of ten. For illustration, the distribution of relative proper motions and absolute parallaxes on magnitude is shown in Fig. 17. For our example field Nr. 5 of DE0716−06, the parallaxes of relatively bright I ≤ 20 stars are ~ 0.5 mas on average, that is, they are located at about 2 kpc, but some of them with ϖ =1–1.5 mas (statistically well over the 3σ margin) are nearby objects at distances of 0.7–1 kpc. From this bright star subsample, one star with I = 19.5 is located at 250 pc distance. The scatter of proper motions of bright stars is ±3–4 mas/yr, which is intrinsic because it significantly exceeds the random uncertainties. A few stars have high proper motions of about ~10 mas/yr.
 |
Fig. 18 Distribution of distances, with 1σ uncertainty ranges, and I-band magnitudes of catalogue stars with well-measured parallaxes. Theoretical curves correspond to M5, M0, and K0 main-sequence stars. |
 |
Fig. 19 Nominal single-epoch precision σe/θe as a function of I-band magnitude for catalogue stars in fields Nr. 2, 5, and 20 at any seeing (dots) and for best-seeing epoch (open circles). The target magnitude is marked by an arrow and the precision floor set by systematic errors ⟨ φe ⟩ is shown with a dashed line. |
Like the distribution of χ2 for the epoch residuals, the distribution of the ratio ϖ/σϖ has a long non-Gaussian tail. In some instances, parallaxes have negative values much higher than −3σϖ. For bright magnitudes, this is caused by reasons similar to those related to large χ2 in the epoch residuals (elongated images, etc.) and already discussed in Sect. 4.4. For high star densities (e.g. target fields Nr.17, 18, and 20), where star images overlap frequently, the percentage of large negative parallaxes increases for faint stars. Figure 18 shows distances and I-band magnitudes of 720 reference stars that have acceptable astrometric solutions (χ2< 6) and well-determined parallaxes (ϖ/σϖ> 5). For reference, the theoretical curves corresponding to M5, M0, and K0 main-sequence stars are shown as well. We thus are able to determine reliable distances to I = 15–18 stars out to a distance of ~1–3.5 kpc.
6. Conclusion and discussion
The FORS2/VLT observations made for our planet search programme necessitated a detailed analysis of the systematic errors in the epoch residuals. We analysed three types of errors: the instability in the relative position of the two CCD chips, systematic errors correlated in space, and errors not correlated in space. The chip motion instability and space-dependent errors are relatively well modelled and suppressed to ~0.05 mas. The residual error ϕ of uncertain origin, however, could not be removed. We only found its rms value and added it quadratically to the model precision. This component largely determines the single-epoch precision for bright field and dwarf stars, which in the field centre is 0.12–0.17 mas with a median of 0.15 mas. The median rms of the epoch residuals is a factor θ smaller because of the noise absorption by the least squares fitting and is 0.126 mas (0.10–0.15 mas for different fields). These estimates refer to the median seeing of 0.6′′and 32 exposures in one epoch.
The single-epoch precision for bright stars depends on the field and varies by a factor of two from the best (densely populated but not crowded field Nr. 20) to typical (Nr. 5, which is DE0716−06), and the worst-case (relatively poor populated star field Nr. 2) precision. This is shown in Fig. 19, which presents the nominal precision σe/θe corresponding to an infinite number of epochs. The vertical-strip structure of the data points in the plot (each strip corresponds to a separate epoch) is due to the difference in epoch seeing, which varies from 0.4 to 0.9′′. The epochs with best seeing of about 0.40–0.45′′are shown separately by open circles for each field where they form the lower bound with the best precision. In these cases, the nominal FORS2 precision is 0.07–0.15 mas at I =16–17 mag. This demonstrates that the nominal epoch precision improves almost proportionally with seeing, and good seeing is favourable for astrometry. In these epochs, however, bright reference star images were often saturated and, even with a single saturated pixel, rejected (Sect. 2). The number of suitable images within these epochs decreases, and the epoch precision degrades. Moreover, the rejection of equally bright nearby reference stars increases the reference star noise, which deteriorates the precision even more. The result is an upward trend in precision, most distinct for stars brighter than I =17 mag in field Nr. 2. For field Nr. 20, the images of selected bright stars never saturate because of stable seeing conditions and the precision improves with brightness.
The precision floor due to systematic errors is set by 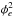 , which is the squared sum of ϕ and the space-correlated error φspace(e) (Eq. (13)). After averaging over all epochs and stars, we obtained the limiting precision ⟨ φe ⟩ marked by the horizontal dashed line in Fig. 19. However, for stars with small space-correlated errors, the precision is better, and the same is true when the small-scale corrections are not measurable due to insufficient number of nearby reference stars and therefore were set to zero.
, which is the squared sum of ϕ and the space-correlated error φspace(e) (Eq. (13)). After averaging over all epochs and stars, we obtained the limiting precision ⟨ φe ⟩ marked by the horizontal dashed line in Fig. 19. However, for stars with small space-correlated errors, the precision is better, and the same is true when the small-scale corrections are not measurable due to insufficient number of nearby reference stars and therefore were set to zero.
The current 0.15 mas estimate of the nominal epoch precision for bright field stars and UCDs specifies the astrometric precision of VLT/FORS2 routine observations under variable observing conditions, with a restriction of 0.9′′ on seeing alone. Not surprisingly, this precision exceeds the 0.05 mas value obtained in PL09 for observations in optimal conditions. Here, because of problems with saturation (Sect. 2.1), we restricted the exposure duration, and therefore the light flux for a single image of a bright star is 0.5–0.7 × 106 photoelectrons, while the peak flux in the pilot study in PL09 was 1.5–2.0 × 106 photoelectrons. Thus, the label ’bright star’ really refers to objects with threefold difference in brightness between both studies. For this reason, the median uncertainty of the photocentre determination increases from 0.23 mas in PL09 to 0.49 mas in the current programme, and the reference frame noise increases respectively from 0.15 mas to 0.30 mas. With this two-fold difference, the pilot study estimates scaled to the current observing conditions leads to 0.10 mas epoch precision, in agreement with Fig. 16 in PL09, and which is similar to the 0.13 mas precision for observations restricted to the optimal seeing (Sect. 4.4.1).
We compared the astrometric performance of the VLT and the Gaia predictions, which illuminates effects related to differences in the entrance apertures and consequently in the light collecting power. Astrometry of bright objects is surely much better from dedicated space satellites, but the precision for very faint stars favours the use of large ground-based facilities. We illustrated this by comparing the Gaia single-epoch precision (Mignard 2011; de Bruijne 2012) with the precision for VLT/FORS2 catalogue stars shown in Fig. 19, given by the estimator σe/θe that does not depend on the number of epochs. For bright stars, Gaia can achieve ~0.01 mas single-epoch precision, while at the faint end of G = 20, this value is expected to be ~0.7–1.1 mas. With the relation G−I ~ 0.8−1.8, valid for spectral classes F8...L2 (Jordi et al. 2010a,b), this limit corresponds to the range I = 18.2–19.2 where FORS2 provides us with an epoch precision of 0.2–0.3 mas. For UCDs with I-band magnitudes of 16–18, the FORS2 precision is thus up to five times better than the expected Gaia precision. This can be reformulated differently: for faint stars, the expected Gaia single-measurement precision can be reached with FORS2 for stars that are approximately 4 magnitudes fainter.
The main motivations of this study was to provide data with well-predicted statistics, which is critically needed for the detection of low-mass companions to UCDs. We achieved this goal, because the obtained epoch residuals are distributed according to a normal law with a scatter parameter equal to the model value σe. In addition, the χ2-values for the epoch residuals corrected with the factor 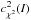 follow the theoretical χ2-statistic.
follow the theoretical χ2-statistic.
The immediate scientific result of FORS2 high precision astrometry is the discovery of two tight binaries, which is discussed in Paper I, and the measurements of trigonometric parallaxes of 20 UCDs and hundreds of I = 16–17.5 stars with precision of ~ 0.1 mas. This is an excellent performance for ground-based optical astrometry and comes close to the best precisions obtained in the optical with HST/WFC3-scanning (Riess et al. 2014) and for radio sources with VLBI (Reid & Honma 2013).
Online material
Appendix A: Small-scale correlation in epoch residuals
Let xe and xe, ∗ be the residual values for the epochs e = 1...Ne introduced in Sect. 4.3.4. These values are correlated due to space-dependent errors, thus they contain some common component αe. Formally, this is expressed by 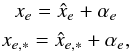 (A.1)where
(A.1)where 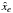 and
and 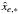 are uncorrelated random values with zero expectation and with variances equal to the model epoch variances
are uncorrelated random values with zero expectation and with variances equal to the model epoch variances 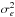 and
and 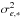 , respectively. We also assume that
, respectively. We also assume that 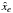 ,
, 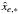 , and αe are not correlated. The model (A.1) implies that the measured variances
, and αe are not correlated. The model (A.1) implies that the measured variances 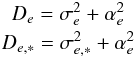 (A.2)for xe and xe, ∗, respectively, are larger than the model predictions. We want to combine xe and xe, ∗ in a term
(A.2)for xe and xe, ∗, respectively, are larger than the model predictions. We want to combine xe and xe, ∗ in a term 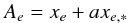 (A.3)that has minimum variance
(A.3)that has minimum variance ![\hbox{$\sigma^2(A_e)=E[A_e^2]$}](/articles/aa/full_html/2014/05/aa23271-13/aa23271-13-eq355.png) reached for some a (here E denotes mathematical expectation substituted by the average over epochs). This is equivalent to the condition
reached for some a (here E denotes mathematical expectation substituted by the average over epochs). This is equivalent to the condition ![\hbox{$ \partial E[A_e^2]/\partial a=0$}](/articles/aa/full_html/2014/05/aa23271-13/aa23271-13-eq358.png) , which has the solution
, which has the solution 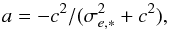 (A.4)yielding the best variance of Ae
(A.4)yielding the best variance of Ae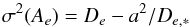 (A.5)or
(A.5)or 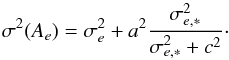 (A.6)Here, c2 = E [xexe, ∗] corresponds to the covariance between xe and xe, ∗ in the calibration file data. Note that c2 and the solution a in Eq. (A.4) depend on rsmall (the radial size containing the calibration stars), therefore σ2(Ae) has the lowest value for a rsmall that ensures maximum a2 or c2. Thus, the optimal rsmall is defined by the condition on the highest measured correlation
(A.6)Here, c2 = E [xexe, ∗] corresponds to the covariance between xe and xe, ∗ in the calibration file data. Note that c2 and the solution a in Eq. (A.4) depend on rsmall (the radial size containing the calibration stars), therefore σ2(Ae) has the lowest value for a rsmall that ensures maximum a2 or c2. Thus, the optimal rsmall is defined by the condition on the highest measured correlation 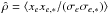 , where the average is taken over epochs. For this specific value of rsmall, and using the measured value of
, where the average is taken over epochs. For this specific value of rsmall, and using the measured value of  , we recover the variance
, we recover the variance 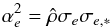 (A.7)of the systematic component between epochs.
(A.7)of the systematic component between epochs.
The relation σ2(Ae) <De, which follows from Eq. (A.5), means that the correction never degrades the precision of the result, even for very large σe, ∗. For σe, ∗ → ∞, no improvement is expected, because a → 0.
We conclude that the best correction for the small-scale space errors to the measured values of xe is not αe but 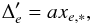 (A.8)which is determined with the precision σ(Ae) (in Sect. 4.3.4 denoted as φsmall(e)). It is important that the correction Eq. (A.8) efficiently mitigates the common systematic component αe. Taking into consideration Eq. (A.1), we find that the initial expectation of xe is E [xe] = αe. Following Eq. (A.3), we find that after the correction
(A.8)which is determined with the precision σ(Ae) (in Sect. 4.3.4 denoted as φsmall(e)). It is important that the correction Eq. (A.8) efficiently mitigates the common systematic component αe. Taking into consideration Eq. (A.1), we find that the initial expectation of xe is E [xe] = αe. Following Eq. (A.3), we find that after the correction ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:apB_6b} E[A_e]=\alpha_e (1+a). \end{equation}](/articles/aa/full_html/2014/05/aa23271-13/aa23271-13-eq378.png) (A.9)The systematic error thus vanishes either in the trivial case of αe = 0 (no error) or if a = −1. The complete subtraction of systematic errors (the case of a = −1) is never possible, because
(A.9)The systematic error thus vanishes either in the trivial case of αe = 0 (no error) or if a = −1. The complete subtraction of systematic errors (the case of a = −1) is never possible, because 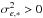 . For stars in the field centre, a is usually −0.2... − 0.7. For DE0716−06, for example, a ≈ − 0.6, which means that the systematic errors in this case are reduced by half.
. For stars in the field centre, a is usually −0.2... − 0.7. For DE0716−06, for example, a ≈ − 0.6, which means that the systematic errors in this case are reduced by half.
The computation of 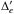 should be based on the calibration files related for the current mode k, and ideally, these files should be generated for each k. However, this is time consuming and, in practice, we computed the calibration file with k = 10 alone. In addition, instead of adding
should be based on the calibration files related for the current mode k, and ideally, these files should be generated for each k. However, this is time consuming and, in practice, we computed the calibration file with k = 10 alone. In addition, instead of adding 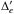 to xe, whose value depend on k, we added it to Xm for each m ∈ e. In the limit Ne → ∞, both procedures are equivalent. We verified numerically that with the limited number of epochs given in our project, the differences between the two procedures are negligible.
to xe, whose value depend on k, we added it to Xm for each m ∈ e. In the limit Ne → ∞, both procedures are equivalent. We verified numerically that with the limited number of epochs given in our project, the differences between the two procedures are negligible.
Appendix B: Correlation of individual frame measurements
Because E [xe] = αe (see Appendix A), each frame measurement is biased by this constant value, thus E [xm] = αe. The systematic errors therefore induce the covariance ![\hbox{$E[x_m,x_m']=\alpha_e^2$}](/articles/aa/full_html/2014/05/aa23271-13/aa23271-13-eq387.png) between the frames m,m′ ∈ e. After the correction Eq. (A.3), the covariance between frame measurements within the epoch e is decreased to
between the frames m,m′ ∈ e. After the correction Eq. (A.3), the covariance between frame measurements within the epoch e is decreased to ![\hbox{${\rm cov}(m,m')=E[(x_m+a x_{e,\ast} )(x_{m'}+a x_{e,\ast} )] = \alpha_e^2 (1+a)^2$}](/articles/aa/full_html/2014/05/aa23271-13/aa23271-13-eq388.png) , hence
, hence 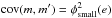 , due to small-scale systematic errors. The effect of large-scale systematic errors is similar, because they are removed incompletely. The uncertainty φlong(e) of that correction gives the measure of the bias in the frame measurements, which results in the covariance cov(m,m′) = φlong(e)2. Taking into account the contribution from ϕ, the complete covariance is
, due to small-scale systematic errors. The effect of large-scale systematic errors is similar, because they are removed incompletely. The uncertainty φlong(e) of that correction gives the measure of the bias in the frame measurements, which results in the covariance cov(m,m′) = φlong(e)2. Taking into account the contribution from ϕ, the complete covariance is 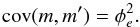 (B.1)The covariance matrix D (Sect. 3.3) is therefore non-diagonal and has a simple block structure with equal non-diagonal elements
(B.1)The covariance matrix D (Sect. 3.3) is therefore non-diagonal and has a simple block structure with equal non-diagonal elements 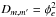 for m,m′ ∈ e and Dm,m′ = 0 for m,m′ ∉ e. The diagonal elements are
for m,m′ ∈ e and Dm,m′ = 0 for m,m′ ∉ e. The diagonal elements are 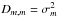 . For instance, for a two-epoch data set with three frames each, the covariance matrix would be
. For instance, for a two-epoch data set with three frames each, the covariance matrix would be
![$$ {\bf D} = \begin{pmatrix} \sigma_1^2 & \phi_1^2 & \phi_1^2 & 0 & 0 & 0 \\[1mm] \phi_1^2 & \sigma_2^2 & \phi_1^2 & 0 & 0 & 0 \\[1mm] \phi_1^2 & \phi_1^2 & \sigma_3^2 & 0 & 0 & 0 \\[1mm] 0 & 0 & 0 & \sigma_4^2 & \phi_2^2 & \phi_2^2 \\[1mm] 0 & 0 & 0 & \phi_2^2 & \sigma_5^2 & \phi_2^2 \\[1mm] 0 & 0 & 0 & \phi_2^2 & \phi_2^2 & \sigma_6^2 \\ \end{pmatrix}. $$](/articles/aa/full_html/2014/05/aa23271-13/aa23271-13-eq399.png) The non-diagonal structure increases the computation time when many field stars are computed as targets (each one computed with reference to all other stars using its own matrix D). It introduces several nested loops and the computation using the direct inversion of D becomes too slow. Therefore we proceed differently when fitting data of the target and reference stars. The target is processed nominally, that is, using the generalised least-squares fit and the direct computation of the inverse matrix D-1. For reference stars, we used the approximate analytic expression for the inverse matrix
The non-diagonal structure increases the computation time when many field stars are computed as targets (each one computed with reference to all other stars using its own matrix D). It introduces several nested loops and the computation using the direct inversion of D becomes too slow. Therefore we proceed differently when fitting data of the target and reference stars. The target is processed nominally, that is, using the generalised least-squares fit and the direct computation of the inverse matrix D-1. For reference stars, we used the approximate analytic expression for the inverse matrix ![\appendix \setcounter{section}{2} \begin{equation} \label{eq:t_1} \begin{array}{l} D^{-1}_{m,m'}= \dfrac{-\phi_e^2 \sigma_e''^{-4}} {1+\phi_e^2 \sigma_e''^{-2}(n_e-2) -\phi_e^4 \sigma_e''^{-4}(n_e-1) } \\[4mm] D^{-1}_{m,m}= \sigma_e''^{-2} \dfrac{1+\phi_e^2 \sigma_e''^{-2}(n_e-2)} {1+\phi_e^2 \sigma_e''^{-2}(n_e-2) -\phi_e^4 \sigma_e''^{-4}(n_e-1) } \!+\! \sigma_m^{-2} \! - \! \sigma_e''^{-2}, \end{array} \end{equation}](/articles/aa/full_html/2014/05/aa23271-13/aa23271-13-eq401.png) (B.2)where
(B.2)where 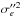 is the weighted average of
is the weighted average of 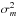 within the epoch e. The correcting term
within the epoch e. The correcting term 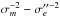 added to
added to 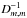 partially accounts for the change of precision between the frames. This approximation leads to equal non-diagonal elements in the inverse matrix and increases the computation speed. The expression (B.2) is used while running the reduction iterations, whereas the last cycle is performed with the direct inversion of D.
partially accounts for the change of precision between the frames. This approximation leads to equal non-diagonal elements in the inverse matrix and increases the computation speed. The expression (B.2) is used while running the reduction iterations, whereas the last cycle is performed with the direct inversion of D.
In this paper, seeing refers to the image FWHM, which are usually considered to be different quantities (Martinez et al. 2010).
References
- Andronov, I. L. 1994, Astron. Nachr., 315, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
- Avila, G., Rupprecht, G., & Beckers, J. M. 1997, in SPIE Conf. Ser., 2871, ed. A. L. Ardeberg, 1135 [Google Scholar]
- Benedict, G. F., McArthur, B. E., Bean, J. L., et al. 2010, AJ, 139, 1844 [NASA ADS] [CrossRef] [Google Scholar]
- de Bruijne, J. H. J. 2012, Ap&SS, 341, 31 [NASA ADS] [CrossRef] [Google Scholar]
- DENIS Consortium 2005, VizieR Online Data Catalog: II/263 [Google Scholar]
- ESA 1997, VizieR Online Data Catalog: I/239 [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010a, A&A, 523, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010b, VizieR Online Data Catalog, J/A+A/523/A48 [Google Scholar]
- Lazorenko, P. F. 1997, Kinem. Phys. Celest. Bodies, 13, 63 [NASA ADS] [Google Scholar]
- Lazorenko, P. F. 2006, A&A, 449, 1271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazorenko, P. F., & Lazorenko, G. A. 2004, A&A, 427, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazorenko, P. F., Mayor, M., Dominik, M., et al. 2009, A&A, 505, 903 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazorenko, P. F., Sahlmann, J., Ségransan, D., et al. 2011, A&A, 527, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinez, P., Kolb, J., Sarazin, M., & Tokovinin, A. 2010, The Messenger, 141, 5 [NASA ADS] [Google Scholar]
- Mignard, F. 2011, Advances in Space Research, 47, 356 [Google Scholar]
- Monet, D. G., Dahn, C. C., Vrba, F. J., et al. 1992, AJ, 103, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pravdo, S. H., & Shaklan, S. B. 1996, ApJ, 465, 264 [Google Scholar]
- Pravdo, S. H., Shaklan, S. B., Henry, T., & Benedict, G. F. 2004, ApJ, 617, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., & Honma, M. 2013, ARA&A, submitted [arXiv:1312.2871] [Google Scholar]
- Riess, A. G., Casertano, S., Anderson, J., Mackenty, J., & Filippenko, A. V. 2014, ApJ, submitted [arXiv:1401.0484] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Lazorenko, P. F., Mérand, A., et al. 2013a, in SPIE Conf. Ser., 8864 [Google Scholar]
- Sahlmann, J., Lazorenko, P. F., Ségransan, D., et al. 2013b, A&A, 556, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Lazorenko, P. F., Ségransan, D., et al. 2014, A&A, 565, A20 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S. 2011, Exoplanets (University of Arizona Press) [Google Scholar]
- Sozzetti, A. 2005, PASP, 117, 1021 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Data related to the computation of 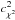 , the residual systematic error ϕ, the rms of the epoch residuals xe and the epoch precision σe for bright stars.
, the residual systematic error ϕ, the rms of the epoch residuals xe and the epoch precision σe for bright stars.
All Figures
 |
Fig. 1 Stars in the DE1756−48 field that are used for the astrometric reduction and are included in the catalogue. The UCD is marked with a star, bright stars with magnitudes within ±0.5 mag of the target are shown with solid circles, and open circles show all other reference stars. The footprints of the FORS2 chips and the axes orientations are indicated. Only catalogue stars within 1′50′′around the target are shown, and concentric circles with increasing radii of Ropt(k) mark reference fields used for for the reduction with k = 4,6,8,10,12,14,16. See text for details. |
| In the text | |
 |
Fig. 2 Single-frame precision as a function of magnitude for stars in the FoV with DE0716−06. Measured (dots) and model σm (open circles) values are shown, and the solid line indicates the dominant photocentre uncertainty component for a) the average of a full set of frames; b) an epoch with excellent 0.38′′ seeing. Magnitudes are given relative to DE0716−06 (mI = 17.5). |
| In the text | |
 |
Fig. 3 Reduced χ2 for bright stars in the DE0716−06 field (asterisks) as a function of brightness. The solid line corresponds to the best linear fit, and the target itself is marked with a filled circle. Data were reduced with k = 10 and the chip’s instability (Sect. 4.3.2) was corrected. |
| In the text | |
 |
Fig. 4 Dependence of the reduced |
| In the text | |
 |
Fig. 5 Positional residuals in RA on 24.11.2011 for stars in the DE0716−06 field computed with k = 10 and Ropt = 815 px. a) The original two-chip data showing the discontinuity at the chip edge with a full amplitude of gx = 0.0376 px, which is approximated by the function Gx(y) (solid line); b) only data of chip 1; c) after offset of chip 2 photocentre positions in RA by |
| In the text | |
 |
Fig. 6 Systematic change of star parallaxes in the DE0615−01 field. a) Measured values with the bias pattern caused by the chip displacement; b) the corrected data. The chip border is at y = 1000 px and the dot size is proportional to the star brightness. |
| In the text | |
 |
Fig. 7 Correlation between the measured motion of chips gx and the telescope pointing error in Dec (filled circles); between gy and the pointing error in RA (open circles). Lines show the expected image shift due to the rotated mounting of chips. |
| In the text | |
 |
Fig. 8 Individual |
| In the text | |
 |
Fig. 9 Dependence of the total uncertainty φspace(e) of spatial corrections on seeing for the brightest stars in all fields and for all epochs. |
| In the text | |
 |
Fig. 10 Space-dependent errors in RA for each epoch: αe (open circles) and |
| In the text | |
 |
Fig. 11 Distribution of actual seeing in 7442 frames collected for our programme between 26 November 2010 and 15 March 2013, and for which we measured the star photocentres. |
| In the text | |
 |
Fig. 12
|
| In the text | |
 |
Fig. 13 Histogram of the absolute values of epoch residuals (open histogram), the best-fit normal function (solid curve), and the histogram of the epoch precision σe (filled histogram) for epochs with 32 exposures and 0.6′′ seeing: for bright stars (lower panel) and UCDs only (upper panel). |
| In the text | |
 |
Fig. 14 Normalised cumulative distribution of the measured |
| In the text | |
 |
Fig. 15 Precision of the epoch residuals for UCDs for a frame series with 32 exposures. |
| In the text | |
 |
Fig. 16 Distribution of proper motion and absolute parallaxes on DCR parameter ρ for bright stars of the catalogue. Dot size marks the star magnitude. |
| In the text | |
 |
Fig. 17 Distribution of absolute parallaxes and relative proper motions of catalogue stars as a function of magnitude in target fields 2, 5, and 9. The sequence number is shown in the upper left corner of the panels and 1σ uncertainty ranges are shown as dashed lines. |
| In the text | |
 |
Fig. 18 Distribution of distances, with 1σ uncertainty ranges, and I-band magnitudes of catalogue stars with well-measured parallaxes. Theoretical curves correspond to M5, M0, and K0 main-sequence stars. |
| In the text | |
 |
Fig. 19 Nominal single-epoch precision σe/θe as a function of I-band magnitude for catalogue stars in fields Nr. 2, 5, and 20 at any seeing (dots) and for best-seeing epoch (open circles). The target magnitude is marked by an arrow and the precision floor set by systematic errors ⟨ φe ⟩ is shown with a dashed line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.