| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | L13 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201423735 | |
| Published online | 14 April 2014 | |
The GAPS Programme with HARPS-N at TNG ⋆,⋆⋆
III: The retrograde orbit of HAT-P-18b
1 Instituto de Astrofísica de Canarias, C/ Vía Láctea s/n, 38205 – La Laguna, Tenerife, Spain
e-mail: mesposito@iac.es
2 Dep. de Astrofísica, Universidad de La Laguna, Avda. Astrofísico Francisco Sánchez s/n, 38206 La Laguna, Tenerife, Spain
3 INAF – Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Naples, Italy
4 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
5 Fundación Galileo Galilei - INAF, Rambla José Ana Fernandez Pérez, 738712 Breña Baja, Tenerife, Spain
6 Astrophysics Group, Keele University, Keele ST5 5BG, UK
7 INAF – Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
8 Dipartimento di Fisica e Astronomia Galileo Galilei, Università di Padova, Vicolo dell’Osservatorio 2, 35122 Padova, Italy
9 INAF – Osservatorio Astrofisico di Torino, via Osservatorio 20, 10025 Pino Torinese, Italy
10 INAF – Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate (Lecco), Italy
11 INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
12 INAF – Osservatorio Astronomico di Palermo, Piazza del Parlamento, 90134 Palermo, Italy
13 INAF – IASF Milano, via Bassini 15, 20133 Milano, Italy
14 INAF – Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143 Trieste, Italy
Received: 28 February 2014
Accepted: 20 March 2014
The measurement of the Rossiter-McLaughlin effect for transiting exoplanets places constraints on the orientation of the orbital axis with respect to the stellar spin axis, which can shed light on the mechanisms shaping the orbital configuration of planetary systems. Here we present the interesting case of the Saturn-mass planet HAT-P-18b, which orbits one of the coolest stars for which the Rossiter-McLaughlin effect has been measured so far. We acquired a spectroscopic time-series, spanning a full transit, with the HARPS-N spectrograph mounted at the TNG telescope. The very precise radial velocity measurements delivered by the HARPS-N pipeline were used to measure the Rossiter-McLaughlin effect. Complementary new photometric observations of another full transit were also analysed to obtain an independent determination of the star and planet parameters. We find that HAT-P-18b lies on a counter-rotating orbit, the sky-projected angle between the stellar spin axis and the planet orbital axis being λ = 132 ± 15 deg. By joint modelling of the radial velocity and photometric data we obtain new determinations of the star (M⋆ = 0.770 ± 0.027 M⊙; R⋆ = 0.717 ± 0.026 R⊙; VsinI⋆ = 1.58 ± 0.18 km s-1) and planet (Mp = 0.196 ± 0.008 MJ; Rp = 0.947 ± 0.044 RJ) parameters. Our spectra provide for the host star an effective temperature Teff = 4870 ± 50 K, a surface gravity of log g⋆ = 4.57 ± 0.07 cm s-2, and an iron abundance of [Fe/H] = 0.10 ± 0.06. HAT-P-18b is one of the few planets known to transit a star with Teff ≲ 6250 K on a retrograde orbit. Objects such as HAT-P-18b (low planet mass and/or relatively long orbital period) most likely have a weak tidal coupling with their parent stars, therefore their orbits preserve any original misalignment. As such, they are ideal targets to study the causes of orbital evolution in cool main-sequence stars.
Key words: planetary systems / techniques: spectroscopic / techniques: radial velocities / stars: fundamental parameters / stars: individual: HAT-P-18
Based on observations collected at the Italian Telescopio Nazionale Galileo (TNG), operated on the island of La Palma by the Fundación Galileo Galilei of the Istituto Nazionale di Astrofisica (INAF) at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, in the frame of the programme Global Architecture of Planetary Systems (GAPS).
Table 1 is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
The number of known extrasolar planets has recently passed the milestone of one thousand. While many discovery surveys are still ongoing, the characterization of known extrasolar planetary systems is gaining ever more attention. Transiting extrasolar planets (TEPs) are especially interesting as they allow for the direct determination of fundamental parameters such as planetary mass and radius (Southworth 2012). Moreover, observations of secondary eclipses put constraints on the planet albedo and brightness temperature, while transmission spectroscopy can be used to probe molecular and atomic features in the planet atmospheres.
Another possibility offered by TEPs is to study the Rossiter-McLaughlin (RM) effect, which is an anomaly in the radial velocity orbital trend that occurs when the planet moves across the stellar photospheric disc (see Hirano et al. 2011 and references therein). The measurement of the RM effect permits the determination of the angle λ, the projection on the sky plane of the misalignment angle Θ between the stellar spin axis and the planet orbital axis. The knowledge of λ can give insight into the mechanisms of formation and orbital migration of exoplanets (Naoz et al. 2011; Nagasawa et al. 2008; Wu & Lithwick 2011).
In the context of GAPS, a long-term observational programme with HARPS-N at TNG (Covino et al. 2013, hereafter Paper I; Desidera et al. 2013), we are carrying out a sub-programme aimed at measuring the RM effect in a sample of TEP host stars. We plan to explore a wide assortment of stellar temperatures, ages, and masses, as well as diverse orbital (period, eccentricity) and physical (mass, radius) planet properties.
In this paper, we report on the measurement of the RM effect for the HAT-P-18 transiting system (Hartman et al. 2011). HAT-P-18b is a Saturn-mass planet orbiting a K2 dwarf star with a period P ~ 5.5 days. Hartman et al. (2011, hereafter H11) pointed out that with a density ρp ~ 0.25 g cm-3, HAT-P-18b is not expected to have a significant heavy element core, according to the planetary models by Fortney et al. (2007).
2. Observations and data reduction
A time series of 20 spectra of HAT-P-18 was acquired with HARPS-N at TNG (Cosentino et al. 2012) in 2013 June 11–12, bracketing a full transit of HAT-P-18b. The exposure time was of 15 min, resulting in spectra with an S/N ~ 20 (per extracted pixel at 5500 Å), degrading to ~15 for the last three spectra due to worsening seeing conditions (see Table 1). In the following months, three additional spectra were taken, two of which at phases nearly corresponding to the expected minimum and maximum of the radial velocity curve.
HARPS-N spectra were reduced using the standard pipeline. Radial velocities (RVs) were derived using the weighted cross-correlation function (CCF) method (Baranne et al. 1996; Pepe et al. 2002); for HAT-P-18 we used the K5 mask. The pipeline also provided rebinned 1D spectra that were used for the stellar atmosphere characterization (see Sect. 3.1).
A complete transit event of HAT-P-18b was observed on 2011 May 24, with the Bologna Faint Object Spectrograph & Camera (BFOSC) imager mounted on the 1.52-m Cassini Telescope at the Astronomical Observatory of Bologna in Loiano, Italy (Mancini et al. 2013; Ciceri et al. 2013). The night was not photometric and some data before ingress were rejected as they were affected by clouds. The CCD was used unbinned, giving a plate scale of 0.58′′/ pixel for a total field-of-view of 13′ × 12.6′, and the transit was observed through a Gunn r filter. The telescope was autoguided and defocussed to increase the exposure time to 140 s, which minimises the effects of systematic noises. The photometric data were derived using an upgraded version of the defot package (Southworth et al. 2009a,b).
3. Results
3.1. Spectroscopic determination of stellar parameters
We derived the photospheric parameters of the planet-hosting star HAT-P-18 by applying two different methods on the mean of all the available HARPS-N spectra.
The first method relies on the use of the spectral analysis package MOOG (Sneden 1973, version 2013). As in Paper I, we measured the equivalent widths (EWs) of iron lines chosen from the list by Biazzo et al. (2012) and adopted the abfind driver within MOOG. We hence determined the effective temperature (Teff) by imposing that the Fe i abundance does not depend on the excitation potential of the lines, the microturbulence velocity (vmic) by imposing that the Fe i abundance is independent on the EW of the lines, and the surface gravity (log g∗) by the Fe i/Fe ii ionization equilibrium condition. The projected rotational velocity V sin I⋆ was measured following the procedure described in D’Orazi et al. (2011).
The second method compares the composite HARPS-N spectrum with a grid of theoretical model spectra using spectral features that are sensitive to different photospheric parameters (Castelli & Kurucz 2004; Coelho et al. 2005; Gustafsson et al. 2008). Briefly, we used the wings of the Balmer lines to estimate the Teff of the star, and the Mg i 5167, 5173, and 5184 Å, the Ca i 6162 and 6439 Å, and the Na i D lines to determine its log g∗. The iron abundance [Fe/H] and vmic were derived by applying the method described in Blackwell & Shallis (1979) on isolated Fe i and Fe ii lines. The V sin I⋆ and macroturbulence velocity (vmac) were measured by fitting the profiles of several clean and isolated metal lines.
The two methods provided consistent results, well within the error bars. The final adopted values, obtained as the weighted mean of the two independent determinations, agree very well with the values by H11 (see Table 2). We note that the V sin I⋆ and log g∗ are consistent within the errors with the values obtained by modelling the RM- and light-curve (see Sect. 3.2), thereby validating our global analysis.
3.2. RV and photometric data analysis
The RV and photometric data sets were analysed jointly. To this purpose we developed a MATLAB code that implements a global model and a data-fitting algorithm.
code that implements a global model and a data-fitting algorithm.
The model considers the parameters necessary to describe the planet and star position and velocity vectors at any given time, that is, the masses of the star M⋆ and of the planet Mp, the orbital period P and eccentricity e, the epoch τ and argument ω of periastron, the systemic RV γ; the orbital space orientation is described by the inclination angle ip and the misalignment angle λ1. Other parameters necessary to model the RM effect and the light curve are the stellar R⋆ and planetary Rp radius, the stellar projected rotational velocity VsinI⋆, and the limb-darkening coefficients. Our model can implement each of the five equations proposed by Claret & Bloemen (2011) to describe the limb-darkening law. Other effects that can affect the measurements, such as stellar surface inhomogeneities, stellar differential rotation and convective blue-shift, are not included in the model. We refer to Paper I for the details of the method used to determine the RV anomaly when the planet is transiting the stellar disc.
The best-fit values of the parameters are obtained by a least-squares minimization algorithm. The region of the parameters space to be explored can be limited providing upper and lower limits to the parameter values. Most importantly, any number of linear and non-linear constraints can be set: this allows placing limits on other parameters (such as K, T14, b, see Table 2 for their definition), even though they are not direct parameters of the fit. The mass of the star, (M⋆ = 0.770 ± 0.027M⊙), is preliminarily determined from evolutionary track models (Yi et al. 2001), adopting the values of the atmospheric parameters determined previously and using the a/R⋆ value derived from the light curve. Evolutionary tracks also provide an estimate of the stellar age of 7.0 ± 3.6 Gyr.
Together with our data sets, the global fit also considers the RVs presented in H11. We show in the top panel of Fig. 1 the phase-folded RV data, with superimposed the best-fit RV curve. We find the eccentricity to be 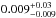 , consistent with a circular orbit (Zakamska et al. 2011). The middle panel displays an expanded view of the phases around the transit. During the transit the RVs are first blue- and then red-shifted with respect to the orbital trend, indicating that the planet is moving on a retrograde orbit. The best-fit value for the sky-projected spin-orbit misalignment angle is λ = 132 ± 15 deg. To evaluate the significance of the detection of the RM effect, we used the transit RV data alone (− 0.050< phase <− 0.024) and compared the
, consistent with a circular orbit (Zakamska et al. 2011). The middle panel displays an expanded view of the phases around the transit. During the transit the RVs are first blue- and then red-shifted with respect to the orbital trend, indicating that the planet is moving on a retrograde orbit. The best-fit value for the sky-projected spin-orbit misalignment angle is λ = 132 ± 15 deg. To evaluate the significance of the detection of the RM effect, we used the transit RV data alone (− 0.050< phase <− 0.024) and compared the 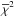 values obtained by modelling the effect,
values obtained by modelling the effect, 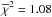 , and by just fitting the orbital trend,
, and by just fitting the orbital trend, 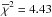 . The bottom panel of Fig. 1 shows the phase-folded r-band photometric data set and the best-fit light curve. We adopted the simple linear law to describe the stellar limb-darkening, as no significant improvement on the light curves fit is obtained by using a quadratic law.
. The bottom panel of Fig. 1 shows the phase-folded r-band photometric data set and the best-fit light curve. We adopted the simple linear law to describe the stellar limb-darkening, as no significant improvement on the light curves fit is obtained by using a quadratic law.
The best-fit values for all the parameters are listed in Table 2, together with the errors that were determined by means of a Monte Carlo method. Our results agree well with those reported in H11.
 |
Fig. 1 Upper panel: phase-folded RV data set. Blue open circles are the HARPS-N data, black asterisks are the RVs from Hartman et al. (2011). Superimposed is the best-fit RV curve. Middle panel: zoom in the RV measurements spanning the transit. Lower panel: r-band photometric time-series and best-fit light curve. |
Star and planet parameters of the system HAT-P-18.
4. Discussion
Winn et al. (2010a) first noticed, and later Albrecht et al. (2012, hereafter A12) confirmed, an empirical correlation between the spin-orbit relative orientation and the effective temperature of the host star: planets hosted by stars with Teff≳ 6250 K display a wide distribution of λ values, while planets around cooler stars are almost always well aligned (see Fig. 2).
This fact has been interpreted as supporting evidence of a scenario in which giant planets approach closely their parent stars following planet-planet gravitational scattering, Kozai-Lidov cycles, or secular chaotic orbital evolution, as opposed to gentle migration in a protoplanetary disc (Dawson & Murray-Clay 2013; Wu & Lithwick 2011; Baruteau et al. 2013). Initially, planets can have large misalignments around both cool and hot stars. Later on, because of their convective envelopes, tidal interactions are effective in cool stars to realign the systems on relatively short time-scales.
 |
Fig. 2 Compilation of the values of λ, measured via the RM effect, as a function of the host star effective temperature (see: http://www.astro.keele.ac.uk/jkt/tepcat/rossiter.html). HAT-P-18b is shown as a filled blue dot. For the two objects marked with red squares, the determination of λ is doubtful (see text for details). The dashed red line at Teff = 6250 K marks the limit above which the mass of the convective shell becomes negligible (Winn et al. 2010a). |
HAT-P-18, with a Teff = 4870 ± 50 K and a very large misalignment angle λ = 132 ± 15 deg, seems to represent an exception in this scheme. However, as already argued by A12, the realignment time-scale also depends on other parameters such as the planet/star mass ratio and the scaled semi-major axis a/R⋆. In fact, using the equation (2) in A12 to estimate the alignment timescale τCE, for HAT-P-18 we find τCE ⋍ 1015 yr, adopting the equilibrium tide theory of Zahn (1977). Given the present uncertainty of the tidal theory, rather than the absolute value of τCE, it is interesting how it compares with the values for other TEPs. HAT-P-18b has one of the highest values of τCE among the TEPs that orbit cool stars, inferior only to HAT-P-11b and HD 80606b, which are also both significantly misaligned (see Fig. 24 in A12). Therefore, HAT-P-18b confirms that planets around cool stars can also have misaligned orbits, provided that they have a longer tidal realignment time-scale due to smaller mass (HAT-P-11b, Winn et al. 2010b; Kepler-63b, Sanchis-Ojeda et al. 2013) and/or larger orbital semi-major axis (WASP-8b, Queloz et al. 2010; HD 80606b, Hébrard et al. 2010; Kepler-63b). The high misalignment angle λ = 153 deg of WASP-2b (Triaud et al. 2010) is at odds with its mass and separation (Mp = 0.9 MJ, a = 0.03 AU), but the reliability of the measure was confuted by Albrecht et al. (2011), based on new observations. The value of λ for WASP-80b (Triaud et al. 2013) is strongly dependent on the value assumed for VsinI⋆, because of the nearly zero impact parameter.
The circularization of the orbit proceeds on a much shorter time-scale because of tidal dissipation inside the planet. Adopting a modified tidal quality factor of 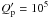 , corresponding to the value measured in Jupiter (Lainey et al. 2009), we obtain a damping time-scale of about 90 Myr for the eccentricity.
, corresponding to the value measured in Jupiter (Lainey et al. 2009), we obtain a damping time-scale of about 90 Myr for the eccentricity.
Rogers & Lin (2013) challenged the interpretation of A12 of the λ–Teff correlation. They advocated migration in the protoplanetary disc that produces aligned hot-Jupiters, and invoked a mechanism based on stellar internal gravity waves to explain the high obliquities found in hot stars. We point out that this mechanism is not applicable to stars such as HAT-P-18, which have a convective envelope.
5. Conclusions
We have found that the Saturn-mass planet hosted by HAT-P-18, a K2 dwarf star with Teff = 4870 ± 50 K, lies on a retrograde orbit. We discussed how the existence of such object fits in the context of the current alternative theories of giant planet orbital migration. HAT-P-18b scores a point in favour of gravitational N-body (N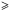 3) interactions, while migration in the proto-planetary disc seems unable to explain its existence. HAT-P-18b, which is one of the very few planets around cool stars found to be on a retrograde orbit, also allows setting constraints on the efficiency of tidal interactions in obliquity damping.
3) interactions, while migration in the proto-planetary disc seems unable to explain its existence. HAT-P-18b, which is one of the very few planets around cool stars found to be on a retrograde orbit, also allows setting constraints on the efficiency of tidal interactions in obliquity damping.
Online material
HARPS-N RV measurements of HAT-P-18.
Acknowledgments
M.E. acknowledges financial support from the Spanish Ministry project MINECO AYA2011-26244. We thank the TNG staff for help in the observations and with data retrieval from the TNG archive. The GAPS project in Italy acknowledges support from INAF through the “Progetti Premiali” funding scheme of the Italian Ministry of Education, University, and Research. D.G. acknowledges funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement No. 267251.
References
- Albrecht, S., Winn, J. N., Johnson, J. A., et al. 2011, ApJ, 738, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Albrecht, S., Winn, J. N., Johnson, J. A., et al. 2012, ApJ, 757, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baruteau, C., Crida, A., Paardekooper, S.-J., et al. 2013 [arXiv:1312.4293] [Google Scholar]
- Biazzo, K., D’Orazi, V., Desidera, S., et al. 2012, MNRAS, 427, 2905 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., & Shallis, M. J. 1979, MNRAS, 186, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004 [arXiv:astro-ph/0405087] [Google Scholar]
- Ciceri, S., Mancini, L., Southworth, J., et al. 2013, A&A, 557, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, in Proc. SPIE, 8446, 1V [Google Scholar]
- Covino, E., Esposito, M., Barbieri, M., et al. 2013, A&A, 554, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Orazi, V., Biazzo, K., & Randich, S. 2011, A&A, 526, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, R. I., & Murray-Clay, R. A. 2013, ApJ, 767, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Desidera, S., Sozzetti, A., Bonomo, A. S., et al. 2013, A&A, 554, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Sato, B., et al. 2011, ApJ, 726, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, G., Désert, J.-M., Díaz, R. F., et al. 2010, A&A, 516, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirano, T., Suto, Y., Winn, J. N., et al. 2011, ApJ, 742, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V., Arlot, J.-E., Karatekin, Ö., & van Hoolst, T. 2009, Nature, 459, 957 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mancini, L., Southworth, J., Ciceri, S., et al. 2013, A&A, 551, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagasawa, M., Ida, S., & Bessho, T. 2008, ApJ, 678, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Naoz, S., Farr, W. M., Lithwick, Y., Rasio, F. A., & Teyssandier, J. 2011, Nature, 473, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Anderson, D. R., Collier Cameron, A., et al. 2010, A&A, 517, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogers, T. M., & Lin, D. N. C. 2013, ApJ, 769, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., Winn, J. N., Marcy, G. W., et al. 2013, ApJ, 775, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. 1973, ApJ, 184, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2012, MNRAS, 426, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Hinse, T. C., Burgdorf, M. J., et al. 2009a, MNRAS, 399, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Hinse, T. C., Jørgensen, U. G., et al. 2009b, MNRAS, 396, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Triaud, A. H. M. J., Collier Cameron, A., Queloz, D., et al. 2010, A&A, 524, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Triaud, A. H. M. J., Anderson, D. R., Collier Cameron, A., et al. 2013, A&A, 551, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winn, J. N., Fabrycky, D., Albrecht, S., & Johnson, J. A. 2010a, ApJ, 718, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Howard, A. W., et al. 2010b, ApJ, 723, L223 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., & Lithwick, Y. 2011, ApJ, 735, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S., Demarque, P., Kim, Y.-C., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
- Zakamska, N. L., Pan, M., & Ford, E. B. 2011, MNRAS, 410, 1895 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Upper panel: phase-folded RV data set. Blue open circles are the HARPS-N data, black asterisks are the RVs from Hartman et al. (2011). Superimposed is the best-fit RV curve. Middle panel: zoom in the RV measurements spanning the transit. Lower panel: r-band photometric time-series and best-fit light curve. |
| In the text | |
 |
Fig. 2 Compilation of the values of λ, measured via the RM effect, as a function of the host star effective temperature (see: http://www.astro.keele.ac.uk/jkt/tepcat/rossiter.html). HAT-P-18b is shown as a filled blue dot. For the two objects marked with red squares, the determination of λ is doubtful (see text for details). The dashed red line at Teff = 6250 K marks the limit above which the mass of the convective shell becomes negligible (Winn et al. 2010a). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


