| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201323035 | |
| Published online | 11 April 2014 | |
On the shape of the mass-function of dense clumps in the Hi-GAL fields
II. Using Bayesian inference to study the clump mass function
1
INAF, Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125
Firenze, Italy
e-mail: olmi.luca@gmail.com
2
University of Puerto Rico, Rio Piedras Campus, Physics
Dept., Box 23343, UPR
station, San Juan,
Puerto Rico,
USA
3
Department of Physics, University of Arizona,
1118 E. 4th Street,
Tucson
AZ
85721,
USA
4
INAF, Istituto di Astrofisica e Planetologia
Spaziali, via Fosso del Cavaliere
100, 00133
Roma,
Italy
5
Infrared Processing and Analysis Center, California Institute of
Technology, Pasadena
CA
91125,
USA
6
ESO, Karl-Schwarzschild-Str. 2, 85748
Garching bei Munchen,
Germany
7
Centre for Astrophysics Research, University of
Hertfordshire, College
Lane, Hatfield,
AL10 9AB,
UK
Received:
12
November
2013
Accepted:
18
February
2014
Context. Stars form in dense, dusty clumps of molecular clouds, but little is known about their origin, their evolution, and their detailed physical properties. In particular, the relationship between the mass distribution of these clumps (also known as the “clump mass function”, or CMF) and the stellar initial mass function (IMF) is still poorly understood.
Aims. To better understand how the CMF evolve toward the IMF and to discern the “true” shape of the CMF, large samples of bona-fide pre- and proto-stellar clumps are required. Two such datasets obtained from the Herschel infrared GALactic Plane Survey (Hi-GAL) have been described in Paper I. Robust statistical methods are needed to infer the parameters describing the models used to fit the CMF and to compare the competing models themselves.
Methods. In this paper, we apply Bayesian inference to the analysis of the CMF of the two regions discussed in Paper I. First, we determine the posterior probability distribution for each of the fitted parameters. Then, we carry out a quantitative comparison of the models used to fit the CMF.
Results. We have compared several methods of sampling posterior distributions and calculating global likelihoods, and we have also analyzed the impact of the choice of priors and the influence of various constraints on the statistical conclusions for the values of model parameters. We find that both parameter estimation and model comparison depend on the choice of parameter priors.
Conclusions. Our results confirm our earlier conclusion that the CMFs of the two Hi-GAL regions studied here have very similar shapes but different mass scales. Furthermore, the lognormal model appears to better describe the CMF measured in the two Hi-GAL regions studied here. However, this preliminary conclusion is dependent on the choice of parameter priors.
Key words: stars: formation / ISM: clouds / methods: data analysis / methods: statistical
© ESO, 2014
1. Introduction
Stars form in dense, dusty cores, or clumps1, of molecular clouds, but the physical processes that regulate the transition from molecular clouds/clumps to (proto)stars are still being debated. In particular, the relationship between the mass distribution of molecular clumps (also known as the clump mass function, or CMF2) and the stellar initial mass function (IMF) is poorly understood (McKee & Ostriker 2007). To improve our understanding of this relationship, it is necessary to undertake the study of statistically significant samples of pre- and proto-stellar clumps.
The Herschel infrared GALactic Plane Survey (Hi-GAL), a key program of the Herschel Space Observatory (HSO) that has been carrying out a 5-band photometric imaging survey at 70, 160, 250, 350, and 500 μm of a |b|≤ 1°-wide strip of the Milky Way Galactic plane (Molinari et al. 2010), is now providing us with large samples of starless and proto-stellar clumps in a variety of star-forming environments. In the first paper (Olmi et al. 2013, Paper I, hereafter), we gave a general description of the Hi-GAL data and described the source extraction and photometry techniques. We also determined the spectral energy distributions and performed a statistical analysis of the CMF in the two regions mapped by HSO during its science demonstration phase (SDP). The two SDP fields were centered at ℓ = 59° and ℓ = 30°, and the final maps spanned ≃2° in both Galactic longitude and latitude.
The goal of this second paper is twofold. On one side, we build on the premises of Paper I, and apply a Bayesian analysis to the CMF of the two SDP fields. First, we determine the posterior probability distribution of the parameters specific to each of the CMF models analyzed in this work, i.e., powerlaw and lognormal. Next, we carry out a quantitative comparison of these models by using the given data and an explicit set of assumptions.
The other major aim of our paper is to compare the results of several popular methods, which sample posterior probability distributions and compute global likelihoods, to highlight the effects that different algorithms may have on the results. In particular, we are interested in analyzing the impact of the choice of priors and the influence of various constraints on the statistical conclusions for the values of model parameters.
The outline of the paper is thus as follows: in Sect. 2, we summarize the models used to describe the mass distribution. In Sect. 3, we give a general description of Bayesian inference and how it is applied to the analysis of the CMF. We describe the algorithms used in Sect. 4 and discuss our results in Sect. 5. We finally draw our conclusions in Sect. 6.
2. Description of models used to fit the CMF
In the following sub-sections we give a short description of the mathematical functions used in this analysis, but the reader should refer to Paper I for more details.
2.1. Definitions
We start by defining the CMF, ξ(M), in the general case of a
continuous distribution. If dN represents the number of objects of mass
M lying
between M and
M +
dM, then we can define the number density distribution
per mass interval, dN/dM with the relation (Chabrier 2003):  (1)thus, ξ(M)dM represents
the number of objects with mass M lying in the interval [M, M +
dM]. The probability of a mass
falling in the interval [M, M
+ dM] can be written for a continuous distribution as
p(M)dM, where
p(M) represents the mass probability
density function (or distribution, PDF). For the case of discrete data,
p(M) can be written as
(1)thus, ξ(M)dM represents
the number of objects with mass M lying in the interval [M, M +
dM]. The probability of a mass
falling in the interval [M, M
+ dM] can be written for a continuous distribution as
p(M)dM, where
p(M) represents the mass probability
density function (or distribution, PDF). For the case of discrete data,
p(M) can be written as  (2)where Ntot represents
the total number of objects being considered in the sample. The PDF and CMF must obey the
following normalization conditions (which we write here for continuous data):
(2)where Ntot represents
the total number of objects being considered in the sample. The PDF and CMF must obey the
following normalization conditions (which we write here for continuous data):
 (3)where Minf and
Msup denote, respectively, the inferior
and superior limits of the mass range for the objects in the sample beyond which the
distribution does not follow the specified behavior.
(3)where Minf and
Msup denote, respectively, the inferior
and superior limits of the mass range for the objects in the sample beyond which the
distribution does not follow the specified behavior.
2.2. Powerlaw form
The most widely used functional form for the CMF is the powerlaw:  where Apw is the
normalization constant. The original Salpeter value for the IMF is α = 1.35 (Salpeter 1955).
where Apw is the
normalization constant. The original Salpeter value for the IMF is α = 1.35 (Salpeter 1955).
The PDF of a powerlaw (continuous) distribution is given by (Clauset et al. 2009):  (6)where the normalization constant can be
approximated as
(6)where the normalization constant can be
approximated as 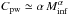 , if α> 0 and Msup ≫
Minf (see Paper I and references
therein). As described later in Sect. 3, Bayesian
inference provides a technique to estimate the probability distribution of the model
parameters α
and Minf.
, if α> 0 and Msup ≫
Minf (see Paper I and references
therein). As described later in Sect. 3, Bayesian
inference provides a technique to estimate the probability distribution of the model
parameters α
and Minf.
2.3. Lognormal form
The continuous lognormal CMF can be written (e.g., Chabrier 2003) as ![\begin{eqnarray} \xi_{\rm ln}(\ln\,M) = \frac{A_{\rm ln}}{\sqrt{2\pi} \, \sigma} \, \exp \left[ - \frac{(\ln M - \mu)^2}{2 \sigma^2} \right] , \label{eq:logn} \end{eqnarray}](/articles/aa/full_html/2014/04/aa23035-13/aa23035-13-eq30.png) (7)where μ and σ2 = ⟨ (lnM − ⟨
lnM ⟩)2 ⟩ denote, respectively, the mean
mass and the variance in units of ln
M and Aln represents a normalization constant
(see Paper I).
(7)where μ and σ2 = ⟨ (lnM − ⟨
lnM ⟩)2 ⟩ denote, respectively, the mean
mass and the variance in units of ln
M and Aln represents a normalization constant
(see Paper I).
The PDF of a continuous lognormal distribution can be written as (e.g., Clauset et al. 2009) ![\begin{eqnarray} p_{\rm ln}(M) = \frac{C_{\rm ln}}{M} \, \exp \left[ - x^2 \right] \, , \label{eq:PDFln} \end{eqnarray}](/articles/aa/full_html/2014/04/aa23035-13/aa23035-13-eq35.png) (8)where we have defined the variable
(8)where we have defined the variable
 . If the condition Msup ≫
Minf holds, the normalization constant,
Cln, can be approximated as (see Paper I)
. If the condition Msup ≫
Minf holds, the normalization constant,
Cln, can be approximated as (see Paper I)
![\begin{eqnarray} C_{\rm ln} \simeq \sqrt{\frac{2}{\pi \sigma^2} } \, \times \left[ {\rm erfc}(x_{\rm inf}) \right]^{-1}, \label{eq:PDFCln2} \end{eqnarray}](/articles/aa/full_html/2014/04/aa23035-13/aa23035-13-eq38.png) (9)where xinf =
x(Minf). As already
mentioned for the powerlaw case, the Bayesian inference allows us to estimate the
probability distribution of the three model parameters μ, σ and Minf.
(9)where xinf =
x(Minf). As already
mentioned for the powerlaw case, the Bayesian inference allows us to estimate the
probability distribution of the three model parameters μ, σ and Minf.
3. Bayesian Inference
3.1. Overview of Bayesian methodology and prior information
Our main goal is to confront theories for the origin of the IMF using an analysis of the CMF data that provides information on the processes responsible for cloud fragmentation and clump formation. Bayesian inference allows the quantitative comparison of alternative models by using the data and an explicit set of assumptions. This last topic is known as model selection, or the problem of distinguishing competing models, which generally feature different numbers of free parameters.
Bayesian statistics also provides a mathematically well-defined framework that allows one to determine the posterior probability distribution of the parameters of a given model. As we have already seen in Sect. 2, the powerlaw model for the CMF depends on two parameters, α and Minf, while the lognormal model contains three parameters, μ, σ, and Minf (unless Minf is considered a fixed parameter, see Sect. 5.1.2).
A very distinctive feature of Bayesian inference is that it deals quite naturally with prior information (for example, on the parameters of a given model), which is highly relevant in many cases, such as when the parameters of interest have a physical meaning that restricts their possible values (e.g., masses or positive quantities in general). The prior choice in Bayesian statistics has been regarded both as a weakness and as a strength. In principle, prior assignment becomes less important as better and better data make the posterior distribution of the parameters dominated by the likelihood of the data (see, e.g., Trotta 2008). However, more often the data are not strong enough to override the prior, in which case the final inference may depend on the prior choice. If different prior choices lead to different posteriors one should conclude that the data are not informative enough to completely override our prior state of knowledge. An analysis of the role of priors in cosmological parameter extraction and Bayesian cosmological model building has already been presented by Trotta et al. (2008).
The situation is even more critical in model selection. In this case, the impact of the prior choice is much stronger, and care should be exercised in assessing how much the outcome would change for physically reasonable changes in the prior (see Berger & Pericchi 2001; Pericchi 2005). In addition to being nonrobust with respect to the choice of parameter priors, Bayesian model selection also suffers from another deep difficulty, specifically with the computation of a quantity, known as the global likelihood, which is difficult to calculate to the required accuracy.
In this section, we first give a short introduction to Bayesian inference by reviewing the basic terminology and describing the most common prior types. We also briefly discuss model comparison and define global likelihood. The mathematical tools required to efficiently evaluate the global likelihood and their limitations are then discussed in the subsequent sections.
3.2. Definitions
Here we give a short list of defintions that are used later.
-
1.
We denote a particular model by the letterℳ. This particular model is characterized by Q parameters, which we denote by θq, q = 1, ..., Q (with size Q dependent on the model). The set of θq constitutes the parameter vector θ. In this paper we consider two models for the CMF: the powerlaw (Q = 2, θ = [α, Minf]) and the lognormal (Q = 3, θ = [μ, σ, Minf]) models.
-
2.
We denote the data by the letter D. In this work, the data consist of the observed CMF for the ℓ = 59° and ℓ = 30° Hi-GAL SDP fields (see Paper I). More restrictive selection criteria have been applied to ensure that all methods described in Sect. 4 did converge. Individual clump masses are denoted by Mi (not to be confused with the model, ℳ).
-
3.
In the following, we use the likelihood of a given set of data D, or the combined probability that D would be obtained from model ℳ and its set of parameters θq, which we denote by P(D|θ, ℳ) or ℒ. For the present case and for a set of data D = { Mi }, the likelihood can be written as
 (10)where it is assumed that the data are
drawn from the PDF associated with model ℳ, as denoted by p(Mi|θ)
(see Sect. 2).
(10)where it is assumed that the data are
drawn from the PDF associated with model ℳ, as denoted by p(Mi|θ)
(see Sect. 2). -
4.
In principle, the model parameters θq can take any value, unless we have some information limiting their range. We can constrain the expected ranges of parameter values by assigning the probability distributions of the unknown parameters θq. These are called the parameters prior probability distribution (often called simply the parameters prior and are denoted by P(θq|ℳ). Hence:
 (11)
(11) -
5.
In contrast to traditional point estimation methods (e.g., maximum-likelihood estimation, or MLE) Bayesian inference does not provide specific estimates for the parameters. Rather, it provides a technique to estimate the probability distribution (assumed to be continuous) of each model parameter θq, also known as the posterior PDF, or simply the posterior distribution, P(θ|D,ℳ). In Bayesian statistics, the posterior distribution encodes the full information coming from the data and the prior, and it is given by the Bayes theorem:
 (12)where
(12)where
 is a normalization factor
and is often called global likelihood or evidence
for the model,
is a normalization factor
and is often called global likelihood or evidence
for the model, 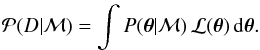 (13)Thus, the global likelihood of a model
is equal to the weighted (by the parameters prior, P(θ|ℳ); also
known as marginalization over the parameter space) average
likelihood for its parameters, which is why it is also often called the
total marginalized likelihood. We work mostly with logarithmic
probabilities; thus Eq. (12) becomes
(13)Thus, the global likelihood of a model
is equal to the weighted (by the parameters prior, P(θ|ℳ); also
known as marginalization over the parameter space) average
likelihood for its parameters, which is why it is also often called the
total marginalized likelihood. We work mostly with logarithmic
probabilities; thus Eq. (12) becomes
 (14)where
(14)where  (15)
(15)
3.3. Specifying the parameter priors
If we have some expectation of the ranges in which the parameter values lie, then we can incorporate this information in the parameter priors P(θ|ℳ). Even when parameters in a given range of values are equally probable, we can specify plausible bounds on parameters.
Here, we briefly introduce the two forms of priors most commonly used, the uniform and Jeffreys’ priors. In Sect. 4, we then discuss the priors actually used in our computations.
-
1.
When dealing with scale parameters3, the preferred formis the Jeffreys’ priors, which assign an equal probabilityper decade interval (appropriate for quantities that are scaleinvariant), and are given by (see Gregory 2005):
 (16)where
(16)where
![\hbox{$ [\theta_{q}^{\rm min}, \theta_{q}^{\rm max}]$}](/articles/aa/full_html/2014/04/aa23035-13/aa23035-13-eq67.png) represents the range allowed for
parameter θq to vary.
represents the range allowed for
parameter θq to vary.
-
2.
On the other hand, when dealing with location parameters4, the preferred form is the uniform priors, which give uniform probability per arithmetic interval:
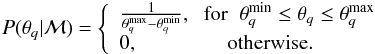 (17)
(17)
3.4. Model comparison
In many cases, such as the present one, more than one parameterized model is available to
explain a given set of data, and it is thus of interest to compare them. The models may
differ in form and/or in number of parameters. Use of Bayes’ theorem allows one to compare
competing models by calculating the probability of each model as a whole. The equivalent
form of Eq. (12) to calculate the
posterior probability of a model ℳ, P(ℳ|D, I), which represents the
probability that model ℳ has
actually generated the data D, is the following (Gregory 2005):  (18)where I represents our prior
information that one of the models under consideration is true. One can recognize
(18)where I represents our prior
information that one of the models under consideration is true. One can recognize
 as the
global likelihood for model ℳ,
which can be calculated according to Eq. (13). The function P(ℳ|I) represents the
prior probability for model ℳ, while the term at the denominator P(D|I) is again a
normalization constant, which is obtained by summing the products of the priors and the
global likelihoods of all models being considered.
as the
global likelihood for model ℳ,
which can be calculated according to Eq. (13). The function P(ℳ|I) represents the
prior probability for model ℳ, while the term at the denominator P(D|I) is again a
normalization constant, which is obtained by summing the products of the priors and the
global likelihoods of all models being considered.
Then, the plausibility of two different models ℳ1 and ℳ2, parameterized by the model parameters vectors
θ1 and θ2,
can be assessed by the odds ratio: 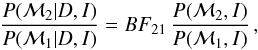 (19)which can be interpreted as the “odds
provided by the data for model ℳ2 versus ℳ1”. In Eq. (19) we have also introduced the Bayes factor (e.g., Gelfand & Dey 1994; Gregory 2005):
(19)which can be interpreted as the “odds
provided by the data for model ℳ2 versus ℳ1”. In Eq. (19) we have also introduced the Bayes factor (e.g., Gelfand & Dey 1994; Gregory 2005):  (20)In general, it is also assumed that
P(ℳ2,I) =
P(ℳ1,I) (i.e., no model
is favored over the other); thus, the odds ratio becomes equal to the Bayes factor. A
value of BF21 > 1 would
indicate that the data provide evidence in favor of model ℳ2 vs. the alternative model
ℳ1. Usually, the
Bayes factor is quoted in ln
units; that is, we change to ln(BF):
(20)In general, it is also assumed that
P(ℳ2,I) =
P(ℳ1,I) (i.e., no model
is favored over the other); thus, the odds ratio becomes equal to the Bayes factor. A
value of BF21 > 1 would
indicate that the data provide evidence in favor of model ℳ2 vs. the alternative model
ℳ1. Usually, the
Bayes factor is quoted in ln
units; that is, we change to ln(BF):  (21)Then, sgn(ℬℱ) indicates the most
probable model with positive values of ℬℱ favoring model ℳ2 and negative values favoring model ℳ1.
(21)Then, sgn(ℬℱ) indicates the most
probable model with positive values of ℬℱ favoring model ℳ2 and negative values favoring model ℳ1.
Thus, for each model, we must compute the global likelihoods, which means evaluating the
integrals in Eq. (20), which can be
written in general as5![\begin{eqnarray} \label{eq:MargLike} {\mathcal P}( D|{\mathcal M_j}, I) &=& \int {\mathcal L}(\vec{\theta}_j) P( \vec{\theta}_j|{\mathcal M_j}) \, {\rm d}\vec{\theta}_j \nonumber \\ & = &\int \left [ \prod_{i\,=\,1}^{N_{\rm tot}} \, p_{\rm j}(M_i|\vec{\theta}_{\rm j}) \right ] \left [ \prod_{q\,=\,1}^{Q} \, P( \theta_{\rm jq}|{\mathcal M_j} ) \right ] \, {\rm d}\vec{\theta}_j \\ j&=&1,2 \hspace{5mm} q=1,...,Q_j. \nonumber \end{eqnarray}](/articles/aa/full_html/2014/04/aa23035-13/aa23035-13-eq88.png) (22)The above equation can be written more
explicitly, for example, in the powerlaw case and using Jeffreys priors for both
parameters as
(22)The above equation can be written more
explicitly, for example, in the powerlaw case and using Jeffreys priors for both
parameters as ![\begin{eqnarray} \label{eq:MargLikePW1} & & {\mathcal P}( D|{\mathcal M_{\rm pw}}, I) = \nonumber \\ & & \int \left [ \prod_{i\,=\,1}^{N_{\rm tot}} \, C_{\rm pw} \, M_i^{-\alpha} \right ] \, P( \vec{\theta}_{\rm pw}|{\mathcal M_{\rm pw}}) \, {\rm d}\alpha \,\, {\rm d}M_{\rm inf}, \hspace{3mm} {\rm with} \\ & & P( \vec{\theta}_{\rm pw}|{\mathcal M_{\rm pw}}) = \frac{1}{M_{\rm inf} \, \ln(M_{\rm inf}^{\rm max}/M_{\rm inf}^{\rm min} )} \times \frac{1}{\alpha \, \ln(\alpha_{\rm max}/ \alpha_{\rm min} ) }, \nonumber \end{eqnarray}](/articles/aa/full_html/2014/04/aa23035-13/aa23035-13-eq89.png) (23)where we have used Eq. (6) and Cpw has been
given in Sect. 2.2.
(23)where we have used Eq. (6) and Cpw has been
given in Sect. 2.2.
4. Computation of model parameters and global likelihood
4.1. General constraints
We now turn to the description of various methods that allow the computation of the posterior distributions of the model parameters which, in some cases, also allow to estimate the global likelihood as a by-product. Several open software resources exist that can perform the computation of model parameters. However, estimating the multidimensional integrals in equations of the type (22) and (23) is impossible when done analytically in most cases, and is otherwise computationally very intensive when done numerically. Therefore, popular statistical packages (e.g., WinBUGS6, ℛ7) are usually not able to compute the global likelihood directly, and more specialized programs or dedicated procedures must be used.
 |
Fig. 1 Distribution of ln(M) for the selected subset of clumps in the ℓ = 30° (top) and ℓ = 59° (bottom) fields. Vertical bars show Poisson errors. The solid lines show one realization of the posterior distributions (corresponding to the mean values obtained with the Metropolis-Hastings method, see Sect. 4.3) discussed in Sect. 5. The vertical dashed lines represent the completeness limits as described in Paper I. |
As discussed in greater detail in Sect. 5, we note that all methods described below have proved to be sensitive, to various degrees, to both the priors type and range, as well as to other parameters specific to each algorithm. In addition, some of these algorithms would either crash, if, for example, the prior range was too wide, or some of the model parameters (e.g., α, μ) would converge toward one end of the prior range. Therefore, to have meaningful comparisons of various methods, and to avoid software problems, we selected the same type of priors and range, as well as an even more restrictive subset of our data, as compared to those used in Paper I. As shown in Fig. 1, both datasets have been imposed M ≥ 1 M⊙, which resulted in masses below the completeness limit in the ℓ = 30° region. This allowed us to test how this may affect the final posterior distributions. For the case of the ℓ = 59° field, Fig. 1 shows that ignoring sources with mass below the completeness limit may lead to deviations at the low-mass end.
Ranges for uniform priors used toward the ℓ = 30° and ℓ = 59° fields.
Since WinBUGS only supports a small set of proper8 priors, we have selected uniform priors (see Table 1) as they are non-informative (which supposedly provide “minimal” influence on the inference) compared to, for example, Gaussian priors. The ranges for all parameters, except Minf, have been selected around the values originally estimated in Paper I and have then been somewhat enlarged while maintaining convergence of all methods used here. The parameter Minf has proved to be more critical and its range has been selected to achieve convergence with all methods (see Sect. 5).
4.2. Laplace approximation and harmonic mean estimator
Mean values and standard deviations estimated from the posterior distributions of the parameters, obtained using the methods described in the text (WinBUGS, MHPT, and MultiNest), for the powerlaw distribution.
In this section we describe two methods to implement the computation of the global likelihood that use open software resources (e.g., WinBUGS in this work) and, thus, do not require users to develop their own software.
4.2.1. Laplace approximation
One of the most popular approximations of the global likelihood is the so-called
Laplace approximation. In this method, the product of prior and
likelihood in Eq. (13) is approximated
by a multivariate Gaussian. The integral then becomes the volume of a Gaussian
distribution, and thus the accuracy of this method depends on how well the posterior is
approximated by a Gaussian. The Laplace approximation for Eq. (13) results in (e.g., Gregory 2005, Ntzoufras 2009):
 (24)where Q represents the number
of parameters (see Sect. 3.2, item 1),
(24)where Q represents the number
of parameters (see Sect. 3.2, item 1),
 is the posterior mode of the parameters
of model ℳ, and
H is equal to the minus of the second
derivative matrix (with respect to the parameters, or the Hessian) of
the posterior PDF, which is P(θ|D,ℳ) (see
Sect. 3.2, item 5), evaluated at the posterior mode
is the posterior mode of the parameters
of model ℳ, and
H is equal to the minus of the second
derivative matrix (with respect to the parameters, or the Hessian) of
the posterior PDF, which is P(θ|D,ℳ) (see
Sect. 3.2, item 5), evaluated at the posterior mode
 .
.
As described by Ntzoufras (2009), the
Laplace-Metropolis estimator can be used to evaluate Eq. (24), where  and H can be
estimated from the output of a Markov chain Monte Carlo (MCMC) algorithm (see Sect.
4.3.1). Thus, Eq. (24) becomes
and H can be
estimated from the output of a Markov chain Monte Carlo (MCMC) algorithm (see Sect.
4.3.1). Thus, Eq. (24) becomes  (25)where the posterior means (replacing the
posterior modes) of the parameters of interest are denoted by
(25)where the posterior means (replacing the
posterior modes) of the parameters of interest are denoted by
 , Rθ
represents the posterior correlation between the parameters of interest, sq are the posterior
standard deviations of the θq parameters of
model ℳ, and
, Rθ
represents the posterior correlation between the parameters of interest, sq are the posterior
standard deviations of the θq parameters of
model ℳ, and
 is the PDF associated to model
ℳ and evaluated at data
point i
(see Sect. 3.2, item 3).
is the PDF associated to model
ℳ and evaluated at data
point i
(see Sect. 3.2, item 3).
Following Ntzoufras (2009), we estimate the posterior means, standard deviations, and correlation matrix from a MCMC run in WinBUGS, and then we calculate the global likelihood from Eq. (25). The results are listed in Tables 2 and 3, while the Bayes factors are listed in Table 4 and are discussed later in Sect. 5.
4.2.2. Harmonic mean estimator
The harmonic mean estimator (HME) is also based on a MCMC run and provides the
following estimate for the global likelihood (Ntzoufras
2009): 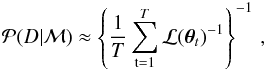 (26)where ℒ(θt)
represents the likelihood of the data corresponding to the t-th sample of the MCMC
simulation, which has a total of T samples. Although very simple, this estimator
is quite unstable and sensitive to small likelihood values; hence, it is not
recommended. However, we present the HME values obtained by us with WinBUGS in Table
4 as a comparison for the Laplace-Metropolis
method.
(26)where ℒ(θt)
represents the likelihood of the data corresponding to the t-th sample of the MCMC
simulation, which has a total of T samples. Although very simple, this estimator
is quite unstable and sensitive to small likelihood values; hence, it is not
recommended. However, we present the HME values obtained by us with WinBUGS in Table
4 as a comparison for the Laplace-Metropolis
method.
4.3. Computation of the global likelihood with the Metropolis-Hastings algorithm
In this section, we describe how the global likelihood and the Bayes factor can also be estimated by implementing our own MCMC procedure.
4.3.1. Markov chain Monte Carlo
As we previously mentioned in Sect. 3.2, the Bayesian inference parameter estimation consists of calculating the posterior PDF, or density, P(θ|D,ℳ), given by Eq. (12). However, since we must vary all θq parameters, we need a method for exploring the parameter space because gridding in each parameter direction would lead to an unmanageably large number of sampling points. The Q-dimensional parameter space can be explored with the aid of MCMC techniques, which are able to draw samples from the unknown posterior density (also called the target distribution) by constructing a pseudo-random walk in model parameter space, such that the number of samples drawn from a particular region is proportional to its posterior density. Such a pseudo-random walk is achieved by generating a Markov chain, which we create using the Metropolis-Hastings (MH) algorithm (Metropolis et al. 1953; Hastings 1970).
Briefly, the MH algorithm proceeds as follows. Given the posterior density
P(θ|D,ℳ)
and any starting position θt in
the parameter space, the step to the next position θt+1 in the random walk is obtained from a proposal
distribution (for example, a normal distribution) g(θt+1|θt).
Assuming g
to be symmetric in θt and
θt+1, the requirement of detailed balance leads to the following
rule: accept the proposed move to θt+1
if the Metropolis ratio r ≥ u, where r =
P(θt+1|D,ℳ)/P(θt
|D,ℳ), and u is a random variable
drawn from a uniform distribution in the interval 0 to 1. If r<u,
remain at θt.
This sequence of proposing new steps and accepting or rejecting these steps is then
iterated until the samples (after a burn-in phase) have converged to the target
distribution. Since the factor at the denominator of Eq. (12) in the Metropolis ratio cancels out, the evaluation of
r
requires only the calculation of the parameter priors and of the likelihoods but
not of the global likelihood,  .
.
A modified version of the MH algorithm to fully explore all regions in the parameter
space with significant probability employs the so-called parallel tempering
(MHPT; Gregory 2005, see also Handberg & Campante 2011). In the MHPT method,
several versions, or chains (nβ in total), of the
MH algorithm are launched in parallel. Each of these nβ chains is
characterized by a different tempering parameter, β, and the new target
distribution can be written by modifying Eq. (12):  (27)Thus, by modifying the chains according to
Eq. (27) a discrete set of progressively
flatter versions of the target distribution, also known as tempered
distributions, are generated. For β = 1, we recover the target distribution. The
MHPT method allows one to visit regions of parameter space containing significant
probability, which are not accessible to the basic algorithm. The main steps in the MHPT
algorithm are described in Appendix A.
(27)Thus, by modifying the chains according to
Eq. (27) a discrete set of progressively
flatter versions of the target distribution, also known as tempered
distributions, are generated. For β = 1, we recover the target distribution. The
MHPT method allows one to visit regions of parameter space containing significant
probability, which are not accessible to the basic algorithm. The main steps in the MHPT
algorithm are described in Appendix A.
4.3.2. Application of MHPT method to model comparison
Going back, now, to the issue of model comparison, an important property of the MHPT
method is that the samples drawn from the tempered distributions can be used to compute
the global likelihood,  , of a given model
ℳ. It can be shown that
the global log-likelihood of a model is given by (for a derivation see Gregory 2005)
, of a given model
ℳ. It can be shown that
the global log-likelihood of a model is given by (for a derivation see Gregory 2005)  (28)where
(28)where  (29)where T is the number of
samples in each set after the burn-in period. The log-likelihoods in Eq. (29), lnℒ(θtβ),
can be evaluated from Eq. (10) and MHPT
results, which consist of sets of {θt}
samples with one set (i.e., Markov chain, θ1 →
θ2 → ... →
θt →
...) for each value of the tempering parameter
β.
(29)where T is the number of
samples in each set after the burn-in period. The log-likelihoods in Eq. (29), lnℒ(θtβ),
can be evaluated from Eq. (10) and MHPT
results, which consist of sets of {θt}
samples with one set (i.e., Markov chain, θ1 →
θ2 → ... →
θt →
...) for each value of the tempering parameter
β.
As a by-product of the computation of the global likelihood, the MHPT method can also be used to determine the posteriors of the parameters. With both the posterior summaries and the global likelihoods, the results are also listed in Tables 2 and 3.
4.4. Computation of the global likelihood using the nested sampling method
The main problem of the methods outlined in Sect. 4.2 is the approximations involved, whereas the MCMC sampling methods, such as the MHPT technique described in Sect. 4.3, may have problems in estimating the parameters of some model, if the resulting posterior distribution is, for example, multimodal. In addition, calculation of the Bayesian evidence for each model is still computationally expensive using MCMC sampling methods.
The nested sampling method introduced by Skilling
(2004) is supposed to greatly reduce the computational expense of calculating
evidence and also produces posterior inferences as a by-product. This method replaces the
multidimensional integral in Eq. (13) with
a one-dimensional integral over an unit range:
 (30)where dX =
P(θ|ℳ)
dθ is the element of “prior volume”. A
sequence of values Xj
can then be generated and the evidence is approximated numerically using standard
quadrature methods (see Skilling 2004; and Feroz & Hobson 2008). Here, we use the “multimodal
nested sampling algorithm” (MultiNest9, Feroz & Hobson 2008; Feroz et al. 2009) to calculate both global likelihood and posterior
distributions. The results are summarized in Tables 2 and 3.
(30)where dX =
P(θ|ℳ)
dθ is the element of “prior volume”. A
sequence of values Xj
can then be generated and the evidence is approximated numerically using standard
quadrature methods (see Skilling 2004; and Feroz & Hobson 2008). Here, we use the “multimodal
nested sampling algorithm” (MultiNest9, Feroz & Hobson 2008; Feroz et al. 2009) to calculate both global likelihood and posterior
distributions. The results are summarized in Tables 2 and 3.
5. Discussion
We now turn to the discussion of the effects of priors and different algorithms on the CMF parameter inference and model comparison using Bayesian statistics. As it was mentioned in Sect. 4, our comparison is limited to uniform priors only, because they are non-informative and also because of other software constraints.
Our purpose is not to perform a general analysis of the impact of priors type and range on Bayesian inference, since, as previously discussed in Sect. 3.1, this is a very complex topic that goes well beyond the scope of the present work. Instead, we are interested in the two distributions considered here for analyzing the sensitivity of our results to variations in the bounds of our uniform priors. In particular, we are interested in the role of the parameter Minf, which is clearly critical for both powerlaw and lognormal distributions, as discussed below.
5.1. Powerlaw results
5.1.1. Non-regular likelihood: Consideration of Minf as a free parameter
We start our discussion by analyzing the results of the posterior distributions for the powerlaw model, when the parameter Minf is free to vary. Then, Table 2 shows that the three methods described in Sect. 4 deliver remarkably similar values of the α parameter, which are separate for the two SDP fields and with the prior ranges shown in Table 1. However, the powerlaw slope estimated for the two fields is different and is also different from the values quoted in Paper I (α ≃ 1.1 and ≃1.2, for the ℓ = 30° and ℓ = 59° fields, respectively).
 |
Fig. 2 Comparison of results obtained for the mean value of the parameter α (powerlaw case) in the ℓ = 30° field using the MHPT (green plus signs), MultiNest (red triangles), and WinBUGS (blue asterisks) methods, as a function of fM = (Minf2 − Minf1)/(Minf1 + Minf2), where Minf1 and Minf2 are the extremes of the prior range for Minf (see text). The larger symbols correspond to the values listed in Table 2. |
This discrepancy, however, is less significant compared to the sensitivity of the posteriors on the priors range and, in particular, on the range [Minf1, Minf2] for the uniform prior on the parameter Minf. We checked this sensitivity toward one of the two SDP fields, the ℓ = 30° region. Thus, in Fig. 2, we plot the values of α obtained with the three methods discussed above, as a function of the parameter fM = (Minf2 − Minf1)/(Minf1 + Minf2). The parameter fM, thus, represents a measure of the amplitude of the prior range, and the scatter in Fig. 2 is due either to different Minf ranges (which we have varied between 0 and 200 M⊙), which may have the same value of fM, or to the variation of other parameters specific to the method used. Despite their sensitivity to the parameter fM, the values of α are much less sensitive to the range of its own uniform prior, that is, [α1,α2] (which we have varied between 0 and 4; see also Sect. 5.1.2).
Looking at Fig. 2 it is not surprising that the values listed in Table 2 are somewhat different from those quoted in Paper I (Table 4). The values listed in Paper I could be easily reproduced with the proper choice of fM. In addition, it should be noted that the values of α and Minf listed in Paper I were determined using the PLFIT method (Clauset et al. 2009). Even with this method, the result for these parameters depends on whether an upper limit for Minf is selected or not.
We also note that all of the methods used were unable to deliver a well-defined value for the Minf parameter, unless Gaussian (i.e., informative) priors were used. In all cases considered, this parameter tends to converge toward the higher end of the prior range. However, this is not an effect caused by the specific data samples used. To test this issue, we generated a set of power-law distributed data, using the method described in Clauset et al. (2009) and applied to it the MHPT and MultiNest methods. In both cases, Minf tended to converge toward the higher end of the prior range. Therefore, it is more likely that the convergence problems of Minf arise because it is this unknown parameter that determines the range of the distribution. The likelihoods associated to such probability distributions are known as non-regular (see Smith 1985) and both likelihood and Bayesian estimators may be affected, requiring alternative techniques (see Atkinson et al. 1991; Nadal & Pericchi 1998) whose discussion is outside the scope of the present work.
 |
Fig. 3 Comparison of results obtained for the mean value of the parameter α (powerlaw case) in the ℓ = 30° field keeping Minf fixed. Symbols and colors are as in Fig. 2. The points representing the MHPT and WinBUGS results overlap almost exactly, and the error bars on α are not shown because they are typically contained within the symbol size (see text). |
In conclusion, the bayesian estimators considered here cannot constrain the value of the Minf parameter, and it also appears that our data are not yet strong enough to override the prior of the powerlaw slope. Therefore, the value of α is sensitive to the choice of priors, and their range (mostly on Minf) and the present data do not allow us to draw statistically robust conclusions on possible differences between the two SDP fields, if we allow Minf to be a free parameter. The uncertainty on the estimated value of α should be that derived from scatter plots like the one shown in Fig. 2 rather than the formal errors estimated by a specific method.
5.1.2. Regular likelihood: Keeping the value of Minf fixed
To remove the potential problems associated with non-regular likelihoods, we carried out some tests to determine whether the sensitivity to the prior range would be the same even when the value of the Minf parameter is kept fixed. We therefore modified the MHPT, MultiNest, and WinBUGS procedures to have only one free parameter, or α in the case of the powerlaw model. Minf was kept fixed, but the range of the uniform prior on α was allowed to vary.
In Fig. 3, we show the results obtained for the ℓ = 30° field. We selected a series of values for Minf, and then we ran the three methods discussed above for each of these values, repeating each procedure several times using a different range [α1, α2] for the uniform prior on α. The figure shows three main features: (i) the two MCMC methods (MHPT and WinBUGS) yield almost identical results for α (In Fig. 3 their corresponding symbols almost exactly overlap.), which is independent of the selected value of Minf, whereas MultiNest progressively diverges from the other two methods. (ii) Then, the estimated values of α become larger for all methods, when Minf is increased. (iii) Finally, for each specific value of Minf all three methods are rather insensitive to variations of the prior range [α1, α2]. (In Fig. 3, the error bars representing the variations of α when using a different prior range are not shown because they are typically contained within the symbol size.)
Therefore, the sensitivity to the uniform priors range, which has been discussed in Sect. 5.1.1 and graphically shown in Fig. 2, disappears when Minf is fixed, and the only free parameter left is α. This result would appear to confirm that the effects discussed in Sect. 5.1.1 are indeed a special consequence of the non-regularity of the likelihood.
5.2. Lognormal results
5.2.1. Non-regular likelihood: Consideration of Minf as a free parameter
The results from the posterior distribution of the parameters are listed in Table 3, and they are also shown graphically in Figs. 4 and 5. Although we do not show a scatter plot similar to Fig. 2 for the lognormal case, we have equally noted a high sensitivity of all methods to the range of the uniform priors on Minf. This must be taken into account when comparing the results of Table 3 to those quoted in Paper I (Table 5). Further differences with respect to Paper I may also be caused by the different samples selected, particularly for the ℓ = 59° field, where the selection of sources with mass above the completeness limit may lead, for example, to overestimate parameter μ compared to the value reported in Paper I (see Fig. 1)
 |
Fig. 4 Results on the posterior distributions of the μ and σ parameters for the lognormal PDF shown simultaneously in the μ − σ plane (Minf is the third model parameter, see text) for the MHPT (top panel), MultiNest (middle panel), and WinBUGS (bottom panel) methods. The results refer to the ℓ = 30° field. |
Similar to what happens for the powerlaw PDF (Sect. 5.1.1), even in the lognormal case, all methods considered here are unable to constrain the Minf parameter, which makes the likelihood non-regular. Our comparison is thus limited to the μ and σ parameters. By comparing their values in Table 3 then, we note again that the three methods discussed in Sect. 4 deliver similar values for the μ and σ parameters. This is also clearly visible in Fig. 4, where it can be seen that the two MCMC-based methods deliver somewhat higher values of the μ parameter, compared to MultiNest. In both SDP fields, we also note the different shape of the posteriors distribution with the MHPT and MultiNest distribution having a similar shape, that is, with comparable widths in μ and σ (although with a different scale), while WinBUGS tends to have a more symmetrical distribution.
Therefore, if the parameter Minf is allowed to vary even for the lognormal case, the data are not constraining enough to allow one to reliably predict the absolute values of some key parameters discussed here. However, our estimates are still good enough to allow a relative comparison between the two SDP regions. Even accounting for the different posterior distributions obtained with the various methods and the different choice of priors, the parameter μ is substantially higher in the ℓ = 30° field than in the ℓ = 59° region. On the other hand, the values of the parameter σ are much more alike between the two SDP fields. This result appears to confirm our earlier conclusion from Paper I. That is, the CMFs of the two SDP fields have very similar shapes but different mass scales, which, according to the simulations discussed in Paper I, cannot be explained by distance effects alone.
5.2.2. Regular likelihood: Keeping the value of Minf fixed
As already done in Sect. 5.1.2 for the powerlaw model, we have also run similar tests in the case of the lognormal distribution. Thus, we have selected some specific values of the Minf parameter, and then we ran the three methods discussed above for each of these values, repeating each procedure several times using different ranges, [μ1,μ2] and [σ1,σ2], for the uniform priors on the μ and σ parameters. The results for the ℓ = 30° field are shown in Fig. 6. As with the powerlaw case, the two MCMC methods yield similar values, although to a lesser extent when compared to Fig. 3. The MultiNest algorithm converges toward one end of the [μ1,μ2] prior range when Minf ≥ 40 M⊙, and this may also be the reason for the fluctuations seen in the parameter σ. We also note that the parameter μ tends to increase with larger values of Minf, while σ appears to be more stable at least in the case of the MCMC methods.
As with the powerlaw model, when the parameter Minf is fixed, the posteriors of the remaining parameters, μ and σ, are not very sensitive to the ranges of the uniform priors for all three methods. For the distributions analyzed here, it would thus appear that the extreme sensitivity to the range of the uniform prior for the parameter Minf is directly linked to the non-regularity of the likelihood, as described in Sect. 5.1.1, rather than being related to the more general sensitivity of Bayesian inference to the choice of priors type and range. As an additional comparison, we plot the posterior distributions in the μ − σ plane when Minf is held fixed in Figs. 7 and 8. Compared to Figs. 4 and 5 one can note a better agreement among all algorithms. One can also note that the WinBUGS distributions (with a variable and fixed parameter Minf) look very much the same.
 |
Fig. 6 Comparison of results obtained for the mean value of the parameters μ and σ (lognormal case) in the ℓ = 30° field, which keeps Minf fixed. For Minf ≥ 40 M⊙, no convergence is obtained for parameter μ with MultiNest. Symbols and colors are as in Fig. 2. |
5.3. Model comparison
We have previously seen how the posterior distributions can depend on the type of the parameter priors used and on their range, as well as depend on the specific algorithm and software used to estimate the posteriors. As we mentioned in Sect. 3.1, the situation is even more critical in model comparison, where the global likelihood, a priors-weighted average likelihood, and the Bayes factor also depend on the choice of priors. Even more so, given we usually wish to compare models with different number of parameters.
Therefore, the results listed in Table 4 should be regarded with some caution. In the table, we show the resulting Bayes factors (in logarithmic units) as estimated using the global likelihoods reported in Tables 2 and 3. According to our discussion in Sect. 3.4, the Bayes factors estimated by our analysis support the lognormal vs. the powerlaw model. In Table 4, we can note several features. (i) All methods result in the same conclusion for both SDP regions. (ii) However, the values of ln(BF)ln/pw are quite large: In the so-called “Jeffreys scale”, a value of ln(BF)21> 5 should be interpreted as “strong” support in favor of model 2 over model 1. The values that we find are suspiciously large and suggest that they may be a consequence of the choice of priors. (iii) With the exception of MultiNest, all other methods show a substantial difference in the Bayes factors estimated for the two SDP fields.
We have also estimated the Bayes factors for the case of the parameter Minf fixed to check for any significant difference. The results are shown in Table 5, and we can note that the values of ln(BF)ln/pw are still positive and still quite large. The values ln(BF)ln/pw are also strongly dependent on the selected value of the Minf parameter and are typically lower for higher values of Minf. Therefore, our preliminary conclusion is that the lognormal model appears to better describe the CMF measured in the two SDP regions. However, we caution that this conclusion may be affected by different choices of priors and their ranges.
6. Conclusions
Following our study (Paper I) of the two Hi-GAL, SDP fields centered at ℓ = 59° and ℓ = 30°, we have applied a Bayesian analysis to the CMF of these two regions to determine how well powerlaw and lognormal models describe the data. First, we have determined the posterior probability distribution of the model parameters. Next, we have carried out a quantitative comparison of these models by using the data and an explicit set of assumptions. This analysis has highlighted the peculiarities of Bayesian inference compared to more commonly used MLE methods. In parameter estimation, the Bayesian inference allows one to estimate the probability distribution of each parameter, making it easier in principle to obtain realistic error bars on the results and, in addition, to include prior information on the parameters. However, Bayesian inference may be computationally intensive, and we have also shown that the results may be quite sensitive to the priors type and range, particularly if the parameters limit the range of the distribution (such as the Minf parameter).
In terms of the powerlaw model, we found that the three Bayesian methods described here deliver remarkably similar values of the powerlaw slope for both SDP fields. Likewise, for the lognormal model of the CMF, we have found that the three computational methods deliver similar values for the μ (center of the lognormal distribution) and σ (width of the lognormal distribution) parameters, which are separate for the two SDP fields. In addition, the parameter μ is substantially higher in the ℓ = 30° field than in the ℓ = 59° region, while the values of the parameter σ are much more alike between the two SDP fields. This result confirms our earlier conclusion from Paper I, that is, the CMFs of the two SDP fields have very similar shapes but different mass scales. We have also shown that the difference with respect to the values of the parameters determined in Paper I may be due to the sensitivity of the posterior distributions to the specific choice of the parameter priors, and, in particular, of the Minf parameter.
As far as model comparison is concerned, we have discussed and compared several methods to compute the global likelihood, which, in general, cannot be calculated analytically and is fundamental to estimate the Bayes factor. All methods tested here show that the lognormal model appears to better describe the CMF measured in the two SDP regions. However, this preliminary conclusion is dependent on the choice of parameter priors and needs to be confirmed using more constraining data.
Acknowledgments
L.O. would like to thank L. Pericchi for fruitful discussions on various issues related to Bayesian inference and parameter priors.
References
- Berger, J. O., & Pericchi, L. R. 2001, in Model selection, ed. P. Lahiri, IMS-Lecture Notes, Institute of Mathematical Statistics, Beachwood (OH), 38, 135 [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Clauset, A., Shalizi, C. R., & Newman, M. E. J. 2009, SIAM Rev., 51, 661 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Feroz, F., & Hobson, M. P. 2008, MNRAS, 384, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Gelfand, A. E., & Dey, D. K. 1994, J. Roy. Stat. Soc. Ser. B Methodol., 56, 501 [Google Scholar]
- Gregory, P. C. 2005, Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with ‘Mathematica’ Support (Cambridge University Press) [Google Scholar]
- Handberg, R., & Campante, T. L. 2011, A&A, 527, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hastings, W. K. 1970, Biometrika, 57, 97 [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, PASP, 122, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Ntzoufras, I. 2009, Bayesian Modeling Using WinBUGS (Wiley) [Google Scholar]
- Olmi, L., Anglés-Alcázar, D., Elia, D., et al. 2013, A&A, 551, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pericchi, L. R. 2005, in Bayesian thinking: modeling and computation, eds. D.K. Dey, & C.R. Rao, Handbook of Statistics (Elsevier), 25, 115 [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Skilling, J. 2004, in AIP Conf. Ser. 735, eds. R. Fischer, R. Preuss, & U. V. Toussaint, 395 [Google Scholar]
- Trotta, R. 2008, Contemp. Phys., 49, 71 [Google Scholar]
- Trotta, R., Feroz, F., Hobson, M., Roszkowski, L., & Ruiz de Austri, R. 2008, J. High Energy Phys., 12, 24 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Procedure to implement the Metropolis-Hastings algorithm with parallel tempering (MHPT)
We briefly list here the main steps of the Metropolis-Hastings algorithm with the inclusion of parallel tempering (see Sects. 2.1 and 4.3 for defintions).
1: Initialize the parameters vector for all tempered distributions θ0, i = θ0,1 ≤ i ≤ nβ 2: Start MCMC loop for t = 1, ..., (T − 1) 3:Start parallel tempering loop for i = 0, 1, ..., (nβ − 1) 4:Propose a new sample drawn from, e.g., a Normal distribution with a mean equal to current parameters values and standard deviation fixed θprop ~ N(θt, i; σ) 5:Compute the Metropolis ratio using Eq. (27) lnr = lnP(θprop|D,ℳ, βi) − lnP(θt, i|D, ℳ, βi) 6:Sample a uniform random variable u1 ~ Uniform(0, 1) 7:if lnu1 ≤ lnr then θt + 1, i = θprop else θt + 1, i = θt, i end if 8:end forEnd parallel tempering loop 9:Sample another uniform random variable u2 ~ Uniform(0,1) 10:Do swap between chains? (nswap = N. of swaps between chains) 11:if u2 ≤ 1/nswap then 12:Select random chain: j ~ UniformInt(1, nβ−1) 13:Compute rswaplnrswap = lnP(θt, j + 1|D, ℳ, βj) + lnP(θt, j|D, ℳ, βj + 1)− lnP(θt, j|D, ℳ, βj) − lnP(θt, j + 1|D, ℳ, βj + 1) 14:u3 ~ Uniform(0, 1) 15:if lnu3 ≤ lnrswap then Swap parameters states of chains j and j + 1θt, j ↔ θt, j+1 15:end if 16:end if 17:end forEnd MCMC loop
All Tables
Mean values and standard deviations estimated from the posterior distributions of the parameters, obtained using the methods described in the text (WinBUGS, MHPT, and MultiNest), for the powerlaw distribution.
All Figures
 |
Fig. 1 Distribution of ln(M) for the selected subset of clumps in the ℓ = 30° (top) and ℓ = 59° (bottom) fields. Vertical bars show Poisson errors. The solid lines show one realization of the posterior distributions (corresponding to the mean values obtained with the Metropolis-Hastings method, see Sect. 4.3) discussed in Sect. 5. The vertical dashed lines represent the completeness limits as described in Paper I. |
| In the text | |
 |
Fig. 2 Comparison of results obtained for the mean value of the parameter α (powerlaw case) in the ℓ = 30° field using the MHPT (green plus signs), MultiNest (red triangles), and WinBUGS (blue asterisks) methods, as a function of fM = (Minf2 − Minf1)/(Minf1 + Minf2), where Minf1 and Minf2 are the extremes of the prior range for Minf (see text). The larger symbols correspond to the values listed in Table 2. |
| In the text | |
 |
Fig. 3 Comparison of results obtained for the mean value of the parameter α (powerlaw case) in the ℓ = 30° field keeping Minf fixed. Symbols and colors are as in Fig. 2. The points representing the MHPT and WinBUGS results overlap almost exactly, and the error bars on α are not shown because they are typically contained within the symbol size (see text). |
| In the text | |
 |
Fig. 4 Results on the posterior distributions of the μ and σ parameters for the lognormal PDF shown simultaneously in the μ − σ plane (Minf is the third model parameter, see text) for the MHPT (top panel), MultiNest (middle panel), and WinBUGS (bottom panel) methods. The results refer to the ℓ = 30° field. |
| In the text | |
 |
Fig. 5 Same as Fig. 4 for the ℓ = 59° field. |
| In the text | |
 |
Fig. 6 Comparison of results obtained for the mean value of the parameters μ and σ (lognormal case) in the ℓ = 30° field, which keeps Minf fixed. For Minf ≥ 40 M⊙, no convergence is obtained for parameter μ with MultiNest. Symbols and colors are as in Fig. 2. |
| In the text | |
 |
Fig. 7 Same as Fig. 4 for the case Minf fixed (Minf = 20 M⊙). |
| In the text | |
 |
Fig. 8 Same as Fig. 5 for the case Minf fixed (Minf = 0.5 M⊙). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


