| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 13 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322801 | |
| Published online | 10 April 2014 | |
Topology and field strength in spherical, anelastic dynamo simulations⋆
MAG (ENS/IPGP), LRA/LERMA, Département de Physique, École Normale
Supérieure, 24 rue Lhomond,
75252
Paris Cedex 5,
France
e-mail:
martin@schrinner.eu
Received:
4
October
2013
Accepted:
30
December
2013
Context. Numerical modelling of convection driven dynamos in the Boussinesq approximation revealed fundamental characteristics of the dynamo-generated magnetic fields and the fluid flow. Because these results were obtained for an incompressible fluid of constant density, their validity for gas planets and stars remains to be assessed. A common approach is to take some density stratification into account with the so-called anelastic approximation.
Aims. The validity of previous results obtained in the Boussinesq approximation is tested for anelastic models. We point out and explain specific differences between both types of models, in particular, with respect to the field geometry and the field strength, but we also compare scaling laws for the velocity amplitude, the magnetic dissipation time, and the convective heat flux.
Methods. Our investigation is based on a systematic parameter study of spherical dynamo models in the anelastic approximation. We make use of a recently developed numerical solver and provide results for the test cases of the anelastic dynamo benchmark.
Results. The dichotomy of dipolar and multipolar dynamos identified in Boussinesq simulations is also present in our sample of anelastic models. Dipolar models require that the typical length scale of convection is an order of magnitude larger than the Rossby radius. However, the distinction between both classes of models is somewhat less explicit than in previous studies. This is mainly due to two reasons: we found a number of models with a considerable equatorial dipole contribution and an intermediate overall dipole field strength. Furthermore, a large density stratification may hamper the generation of dipole dominated magnetic fields. Previously proposed scaling laws, such as those for the field strength, are similarly applicable to anelastic models. It is not clear, however, if this consistency necessarily implies similar dynamo processes in both settings.
Key words: convection / magnetohydrodynamics (MHD) / dynamo / methods: numerical / stars: magnetic field
Appendices B and C are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Magnetic fields of low-mass stars and planets are maintained by currents resulting from the motion of a conducting fluid (or gas) in their interiors. Because the magnetic field acts back on the flow via the Lorentz force, the hydrodynamic dynamo problem is intrinsically non-linear. Moreover, a sufficiently complex flow and magnetic field geometry has to be assumed in order to enable dynamo action. Further complications result from tiny diffusivities, such as small kinematic viscosities, which introduce small dynamic length scales compared to stellar or planetary radii. Thus, self-consistent simulations of natural dynamos are not only three-dimensional, but a vast range of spatial and temporal scales has to be resolved. These difficulties prevented a direct numerical treatment of the dynamo problem for a significant time. Only for the past 20 years, increasing computer power made global, direct numerical simulations feasible, in particular for the geodynamo problem (e.g., Glatzmaier & Roberts 1995; Kageyama & Sato 1997; Kuang & Bloxham 1997; Christensen et al. 1998; Sarson et al. 1998; Katayama et al. 1999; Buffett 2000; Dormy et al. 2000); for an early cylindrical annulus model of the geodynamo see Busse (1975). In these simulations, an incompressible conducting fluid was considered, and the Boussinesq approximation was applied. Intensive and systematic parameter studies revealed fundamental properties of these models related to their field and flow topologies, their field strength, their velocity amplitudes, their advective heat transport, or their time dependence (e.g. Christensen et al. 1999; Grote et al. 2000; Kutzner & Christensen 2002; Busse & Simitev 2006; Christensen & Aubert 2006; Sreenivasan & Jones 2006; Busse & Simitev 2010; Hori et al. 2010; Landeau & Aubert 2011; Schrinner et al. 2012; Yadav et al. 2013a). The simplifying assumption of constant density in Boussinesq models, however, is probably not justified for gas planets or stars, in which the density typically varies over many scale heights. An alternative approach, which takes compressibility into account, is the so-called anelastic approximation (Ogura & Phillips 1962; Gough 1969; Gilman & Glatzmaier 1981). In anelastic models, the density varies with radius, but its time derivative is neglected in the continuity equation and the mass flux is solenoidal (e.g., Glatzmaier 1984; Braginsky & Roberts 1995; Lantz & Fan 1999; Miesch et al. 2000; Brun et al. 2004; Browning et al. 2004). Consequently, fast travelling sound waves are filtered out and, compared to fully compressible models, larger time steps in the discretisation scheme may be reached. In this article, we carry out a systematic parameter study of global dynamo simulations in the anelastic approximation guided by well known results of Boussinesq models. In this way, we intend to point out specific differences between anelastic and Boussinesq models and assess the validity of previous findings obtained in the Boussinesq approximation. A similar approach was followed by Gastine et al. (2012) and Yadav et al. (2013b). We compare our results with their findings and discuss some differences we obtained for our varied sample of models. The conditions for the generation of large-scale, dipolar fields (Sect. 3) and the test of the flux-based scalinglaw for the magnetic field strength (Sect. 4), originally proposed by Christensen & Aubert (2006) for Boussinesq models, are revisited . We argue that the typical length scale of convection relative to the Rossby radius is of crucial importance for the resulting field topology (see also Schrinner et al. 2012) and show that larger magnetic Prandtl numbers are required to obtain dipolar solutions with increasing density contrast. Furthermore, the flux-based scaling laws derived for Boussinesq models seem to hold in the anelastic approximation as well. However, because of their general validity, the flux-based scaling laws might not be appropriate to distinguish between different conditions for magnetic field generation.
The paper is organised as follows: Sect. 2 introduces the anelastic models considered here and the recently developed numerical solver; results for a numerical benchmark are given in Appendix A. In Sect. 3, we present new evidence of the existence of a class of dynamos dominated by an axial dipole and a class of models with a more variable magnetic field geometry. Various scaling laws originally derived for Boussinesq models are tested and discussed in Sect. 4, and we give some conclusions in Sect. 5.
2. Dynamo calculations
2.1. The anelastic approximation
Convection of a gas or a compressible fluid in the interior of planets and stars takes
place on a vast range of spatial and temporal scales. Sound waves excited in convection
zones, for example, have very short oscillation periods compared to the turnover time of
convection or the magnetic diffusion time relevant for the generation of magnetic fields.
Thus, extremely small timesteps would be required to resolve these waves in numerical
dynamo models. To avoid this problem, simplifications of the governing equations are often
applied. The anelastic approximation used in this study advantageously filters out sound
waves (Ogura & Phillips 1962; Gough 1969; Gilman
& Glatzmaier 1981); it is motivated by the idea that the superadiabatic
temperature gradient driving convection in planetary or stellar convection zones is tiny.
The thermodynamic variables are then decomposed into the sum of (close to adiabatic)
reference values, denoted here by an overbar, and perturbations, denoted by a prime,
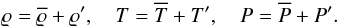 (1)Subsequently, the
anelastic equations result from the “thermodynamic linearization” around the reference
state. It should be stressed that a number of different formulations of the anelastic
problem can be found in the literature (e.g., Glatzmaier
1984; Braginsky & Roberts 1995;
Lantz & Fan 1999; Miesch et al. 2000; Brun et al.
2004; Rogers & Glatzmaier 2005;
Jones & Kuzanyan 2009; Alboussière & Ricard 2013). We follow here the
approach introduced by Lantz & Fan (1999)
and Braginsky & Roberts (1995), also known
as LBR-approximation. They noticed that the only relevant thermodynamic variable in the
equation of motion is the entropy, if the reference state is assumed to be close to
adiabatic. Further advantages of the LBR-equations over others are that they give a
mathematically consistent, asymptotic limit of the full, general equations (Jones et al. 2011) and guarantee the conservation of
energy (Brown et al. 2012). Moreover, the
LBR-equations were used to formulate anelastic dynamo benchmarks (Jones et al. 2011). The presentation of the equations given here
follows the benchmark paper and Jones et al.
(2009).
(1)Subsequently, the
anelastic equations result from the “thermodynamic linearization” around the reference
state. It should be stressed that a number of different formulations of the anelastic
problem can be found in the literature (e.g., Glatzmaier
1984; Braginsky & Roberts 1995;
Lantz & Fan 1999; Miesch et al. 2000; Brun et al.
2004; Rogers & Glatzmaier 2005;
Jones & Kuzanyan 2009; Alboussière & Ricard 2013). We follow here the
approach introduced by Lantz & Fan (1999)
and Braginsky & Roberts (1995), also known
as LBR-approximation. They noticed that the only relevant thermodynamic variable in the
equation of motion is the entropy, if the reference state is assumed to be close to
adiabatic. Further advantages of the LBR-equations over others are that they give a
mathematically consistent, asymptotic limit of the full, general equations (Jones et al. 2011) and guarantee the conservation of
energy (Brown et al. 2012). Moreover, the
LBR-equations were used to formulate anelastic dynamo benchmarks (Jones et al. 2011). The presentation of the equations given here
follows the benchmark paper and Jones et al.
(2009).
2.2. Basic assumptions
We consider a perfect, electrically conducting gas in a rotating spherical shell with an inner boundary at r = ri and an outer boundary at r = ro. The aspect ratio of the shell is then defined by χ = ri/ro. Convection in our simulations is driven by an imposed entropy difference, Δs, between the inner and the outer boundary. As discussed above, Δs is assumed to be small. This implies small convective velocities compared to the speed of sound. For consistency, we also require that the Alfvén velocity of the magnetic field is small. Moreover, the kinematic viscosity ν, the thermal diffusivity κ, and the magnetic diffusivity η are constants throughout in this paper. Following Jones et al. (2011), we represent the heat flux in our models in terms of the entropy gradient instead of the temperature gradient. This assumption relies on wide-spread ideas about turbulent mixing (Braginsky & Roberts 1995) but does not follow from first principles. Applying this simplification allows us to consider the entropy as the only relevant thermodynamic variable in the formulation of the anelastic problem.
2.3. The reference state
The reference state of our models is a solution of the hydrostatic equations for an
adiabatic atmosphere. Moreover, the centrifugal acceleration is neglected and we assume
that gravity varies radially,  ,
with G being
the gravitational constant and M the central mass of the star or the planet. This
admits a polytropic solution for the reference atmosphere,
,
with G being
the gravitational constant and M the central mass of the star or the planet. This
admits a polytropic solution for the reference atmosphere, 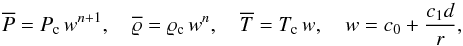 (2)with the polytropic
index n and
d =
ro − ri. We
note that n
defines the value of the adiabatic exponent γ, or the ratio of specific heats cp/cv
via γ = (n +
1)/n. The values Pc,
ϱc, and Tc are taken
midway between the inner and the outer boundary and serve as units for the reference-state
variables. Moreover, the constants c0 and c1 in (2) are defined as
(2)with the polytropic
index n and
d =
ro − ri. We
note that n
defines the value of the adiabatic exponent γ, or the ratio of specific heats cp/cv
via γ = (n +
1)/n. The values Pc,
ϱc, and Tc are taken
midway between the inner and the outer boundary and serve as units for the reference-state
variables. Moreover, the constants c0 and c1 in (2) are defined as 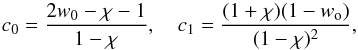 (3)with
(3)with 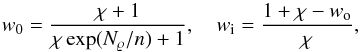 (4)and Nϱ =
ln(ϱi/ϱo),
where ϱi and ϱo denote the
reference state density at the inner and outer boundary, respectively. We emphasise again
that convection in our models is not driven by the reference state, or by the choice of a
particular polytropic index n, but by an imposed entropy difference
Δs between
the boundaries.
(4)and Nϱ =
ln(ϱi/ϱo),
where ϱi and ϱo denote the
reference state density at the inner and outer boundary, respectively. We emphasise again
that convection in our models is not driven by the reference state, or by the choice of a
particular polytropic index n, but by an imposed entropy difference
Δs between
the boundaries.
2.4. The non-dimensional equations
The use of non-dimensional equations minimizes the number of free parameters and is a
prerequisite for a systematic parameter study. We choose the shell width d as the fundamental length
scale of our models, time is measured in units of d2/η,
and Δs is the
unit of entropy. The magnetic field is then measured in units of
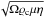 ,
where Ω is the rotation rate
and μ the
magnetic permeability. Finally, our dynamo models are solutions for the velocity
v, the magnetic field B, and the
entropy s of
the following, non-dimensional equations,
,
where Ω is the rotation rate
and μ the
magnetic permeability. Finally, our dynamo models are solutions for the velocity
v, the magnetic field B, and the
entropy s of
the following, non-dimensional equations, ![\begin{eqnarray} \label{mhd1}\frac{\partial\bv}{\partial t}+\bv\cdot\nabla\bv & = & P{\rm m}\,\left[-\frac{1}{E}\nabla\frac{P'}{w^n} +\frac{P{\rm m}}{Pr}Ra\frac{s}{r^2}\vec{\hat{r}}-\frac{2}{E}\,\vec{\hat{z}} \times\bv\right.\nonumber\\ &&\left.+\vec{F}_\nu+\frac{1}{E\,w^n}(\nabla\times\bb)\times\bb\right] ,\\ \label{mhd2} \frac{\partial\bb}{\partial t} & = &\nabla\times(\bv\times\bb)+\nabla^2\bb,\\ \frac{\partial s}{\partial t}+\bv\cdot\nabla s&=& w^{-n-1}\frac{P{\rm m}}{Pr}\nabla\cdot\left(w^{n+1}\,\nabla s\right)\nonumber\\ \label{mhd3}&&+\frac{Di}{w}\left[E^{-1}w^{-n}(\nabla\times \bb)^2+Q_\nu\right] ,\\ \label{mhd4}\nabla\cdot \left(w^n\bv \right)& = & 0 ,\\ \label{mhd5}\nabla\cdot\bb & = & 0 . \end{eqnarray}](/articles/aa/full_html/2014/04/aa22801-13/aa22801-13-eq36.png) In
(5), we used the viscous force
Fν =
w−n∇S with the rate
of strain tensor
In
(5), we used the viscous force
Fν =
w−n∇S with the rate
of strain tensor  (10)Moreover, the dissipation
parameter Di
and the viscous heating Qν in (7) are given by
(10)Moreover, the dissipation
parameter Di
and the viscous heating Qν in (7) are given by
 (11)and
(11)and
![\begin{equation} Q_\nu=2\left[e_{ij}e_{ij}-\frac{1}{3}(\nabla\cdot\bv)^2\right] . \end{equation}](/articles/aa/full_html/2014/04/aa22801-13/aa22801-13-eq42.png) (12)The system of
Eqs. (5)−(9) is governed by a number of dimensionless parameters. These are the Rayleigh
number Ra,
the Ekman number E, the Prandtl number Pr, and the magnetic
Prandtl number Pm. With the aspect ratio χ, the polytropic index
n, and the
number of density scale heights Nϱ defining the
reference state, our models are therefore fully determined by seven dimensionless
parameters:
(12)The system of
Eqs. (5)−(9) is governed by a number of dimensionless parameters. These are the Rayleigh
number Ra,
the Ekman number E, the Prandtl number Pr, and the magnetic
Prandtl number Pm. With the aspect ratio χ, the polytropic index
n, and the
number of density scale heights Nϱ defining the
reference state, our models are therefore fully determined by seven dimensionless
parameters:  (13)Following
Jones et al. (2009), we also considered a
linearized form of Eqs. (5) and (7) to calculate some critical Rayleigh numbers
for the onset of convection. These are listed in Table A.1.
(13)Following
Jones et al. (2009), we also considered a
linearized form of Eqs. (5) and (7) to calculate some critical Rayleigh numbers
for the onset of convection. These are listed in Table A.1.
2.5. Boundary conditions
The mechanical boundary conditions are impenetrable and stress free on both boundaries,
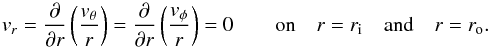 (14)Furthermore, the magnetic
field matches a potential field outside the fluid shell. The choice of these boundary
conditions requires that the total angular momentum is conserved (Jones et al. 2011). Finally, the entropy is fixed on the inner and the
outer boundary with
(14)Furthermore, the magnetic
field matches a potential field outside the fluid shell. The choice of these boundary
conditions requires that the total angular momentum is conserved (Jones et al. 2011). Finally, the entropy is fixed on the inner and the
outer boundary with 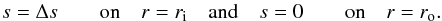 (15)
(15)
2.6. Output parameters
We use a number of non-dimensional output parameters to characterize our numerical dynamo
models. These are mostly based on the kinetic and magnetic energy densities,  (16)where the integrals
are taken over the volume of the fluid shell V. A non-dimensional measure for the velocity
amplitude is then the magnetic Reynolds number,
(16)where the integrals
are taken over the volume of the fluid shell V. A non-dimensional measure for the velocity
amplitude is then the magnetic Reynolds number, 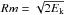 ,
or the Rossby number,
,
or the Rossby number, 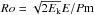 . To distinguish models with
different field geometries, it turned out to be useful to introduce also a local Rossby
number, Roℓ =
Rocℓc/π.
Here, ℓc stands for the mean harmonic degree of
the velocity component vc from which the mean
zonal flow has been subtracted (Schrinner et al.
2012),
. To distinguish models with
different field geometries, it turned out to be useful to introduce also a local Rossby
number, Roℓ =
Rocℓc/π.
Here, ℓc stands for the mean harmonic degree of
the velocity component vc from which the mean
zonal flow has been subtracted (Schrinner et al.
2012),  (17)The brackets in
(17) denote an average over time and
radii. Also, Roc is adapted
consistently and stands for the Rossby number based on the kinetic energy density without
the contribution from the mean zonal flow. The definition of Roℓ
given here is different from Christensen & Aubert
(2006), as it is not based on the total velocity and tries to avoid any
dependence on the mean zonal flow.
(17)The brackets in
(17) denote an average over time and
radii. Also, Roc is adapted
consistently and stands for the Rossby number based on the kinetic energy density without
the contribution from the mean zonal flow. The definition of Roℓ
given here is different from Christensen & Aubert
(2006), as it is not based on the total velocity and tries to avoid any
dependence on the mean zonal flow.
The amplitude of the average magnetic field in our simulations is measured in terms of
the Lorentz number, 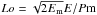 , which was previously used to
derive a power law for the field strength in Boussinesq simulations (Christensen & Aubert 2006). The topology of the field is
characterized by the relative dipole field strength, fdip, defined as
the time-average ratio on the outer shell boundary of the dipole field strength to the
total field strength.
, which was previously used to
derive a power law for the field strength in Boussinesq simulations (Christensen & Aubert 2006). The topology of the field is
characterized by the relative dipole field strength, fdip, defined as
the time-average ratio on the outer shell boundary of the dipole field strength to the
total field strength.
The total amount of heat transported in and out of the fluid shell relative to the
conductive heat flux is quantified by the Nusselt number, 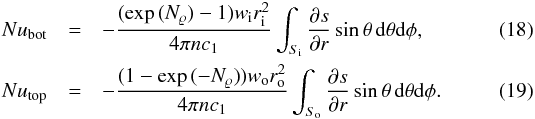 The
integrals are taken here over the spherical surface at radius ri and radius
ro, respectively. For a steady equilibrium
state, Nubot and
Nutop are identical if
time averaged. For later use, we also define a Nusselt number based on the advective heat
flux alone,
The
integrals are taken here over the spherical surface at radius ri and radius
ro, respectively. For a steady equilibrium
state, Nubot and
Nutop are identical if
time averaged. For later use, we also define a Nusselt number based on the advective heat
flux alone,  (20)and accordingly a
quantity usually referred as the flux based Rayleigh number,
(20)and accordingly a
quantity usually referred as the flux based Rayleigh number,  (21)The energy balance plays
a crucial role in the classical derivation of scaling laws for the saturation level of the
magnetic field. In particular, the fraction of ohmic to total dissipation, fohm =
D/P, is introduced
because it determines the available power used for the magnetic field generation. In an
equilibrium state, the total dissipation equals the power released by buoyancy,
(21)The energy balance plays
a crucial role in the classical derivation of scaling laws for the saturation level of the
magnetic field. In particular, the fraction of ohmic to total dissipation, fohm =
D/P, is introduced
because it determines the available power used for the magnetic field generation. In an
equilibrium state, the total dissipation equals the power released by buoyancy,
 (22)and the ohmic
dissipation is given by
(22)and the ohmic
dissipation is given by  (23)In (22) and (23), we scaled P and D by ϱcΩ3d5.
(23)In (22) and (23), we scaled P and D by ϱcΩ3d5.
2.7. Equation for a tracer field
For some of our models, we calculated the evolution of a magnetic tracer field
simultaneously with (5)−(9),  (24)In the above
equation, BTr is a passive vector
field, which was advanced at each time step kinematically with the quenched velocity
field, but BTr did not contribute to
the Lorentz force (Cattaneo & Tobias 2009;
Tilgner & Brandenburg 2008; Schrinner et al. 2010). Schrinner et al. (2010) found that BTr grows exponentially
for multipolar dynamos but stays stable for models dominated by a dipole field. The
stability of BTr also serves in this
study to distinguish between different classes of dynamos (Schrinner et al. 2012).
(24)In the above
equation, BTr is a passive vector
field, which was advanced at each time step kinematically with the quenched velocity
field, but BTr did not contribute to
the Lorentz force (Cattaneo & Tobias 2009;
Tilgner & Brandenburg 2008; Schrinner et al. 2010). Schrinner et al. (2010) found that BTr grows exponentially
for multipolar dynamos but stays stable for models dominated by a dipole field. The
stability of BTr also serves in this
study to distinguish between different classes of dynamos (Schrinner et al. 2012).
2.8. Numerical implementation
The numerical solver used to compute solutions of Eqs. (5)−(9) is a recently developed anelastic version of PaRoDy (Dormy et al. 1998 and further developments). The code uses a poloidal-toroidal expansion and a pseudo-spectral spherical harmonic expansion. The numerical method is similar in these aspects to the one originally introduced in Glatzmaier (1984). The radial discretisation, however, is based on finite differences on a stretched grid (allowing for a parallelization by a radial domain decomposition). Moreover, the pressure term has been eliminated by taking twice the curl of the momentum equation. The anelastic benchmark results obtained with PaRoDy are presented in Appendix A.
3. Field topology
3.1. Dipolar and multipolar dynamos
Parameter studies for Boussinesq simulations revealed two distinct classes of dynamo models. They can be distinguished by their field geometry and are therefore referred to as “dipolar” and “multipolar” models (Kutzner & Christensen 2002; Christensen & Aubert 2006). The spatial variability of multipolar dynamos is a direct consequence of dynamo action in a turbulent environment and has to be expected. The class of dipolar dynamos, however, is more peculiar. Schrinner et al. (2011b) showed that these models are single-mode dynamos, that is, except for the fundamental mode, all more structured magnetic eigenmodes are highly damped. The single-mode property leads to further characteristic differences between both classes of dynamos apart from their different field geometries. Whereas the dipole axis is stable for models with a dominant axial dipole field, multipolar models show frequent polarity reversals (Kutzner & Christensen 2002) or oscillations (Goudard & Dormy 2008; Schrinner et al. 2012). A third fundamental difference between dipolar and multipolar models is related to their saturation mechanism. If a magnetic tracer field is advanced kinematically with the self-consistent, quenched velocity field stemming from the full dynamo simulation, the tracer field grows exponentially for multipolar but not for dipolar models. Dipolar dynamos are “kinematically stable” and in this numerical experiment, the tracer field becomes aligned with the actual, self-consistent magnetic field after some initial transition period (Schrinner et al. 2010). Finally, dipolar and multipolar dynamos follow slightly different scaling laws for the magnetic field (Christensen 2010; Schrinner et al. 2012; Yadav et al. 2013a). This aspect is further discussed in Sect. 4.1.
Christensen & Aubert (2006) proposed a criterion based on a local Rossby number to separate dipolar from multipolar dynamos. We adopt this criterion in a slightly altered form (Schrinner et al. 2012). It says that dipolar dynamos may be found if the typical length scale of convection, ℓ, is at least an order of magnitude larger than the Rossby radius, or, Roℓ = v/(Ωℓ) < 0.12 (in which v is a typical rms velocity). Our criterion is different from Christensen & Aubert (2006), and entirely based on convection and not influenced by the mean zonal flow. This helped to generalize the Rossby number rule to models with different aspect ratios and mechanical boundary conditions (Schrinner et al. 2012). Moreover, our reinterpretation assumes that the magnetic field is generated only by convection and therefore explains why the Rossby number criterion is not applicable to models for which differential rotation plays an essential role.
 |
Fig. 1 Relative dipole field-strength versus the local Rossby number for our sample of models. Filled symbols stand for dipolar, open symbols for multipolar dynamos. The symbol shape indicates the number of density scale heights: Nϱ = 0.5: circle; Nϱ = 1: upward triangle; Nϱ = 1.5: downward triangle; Nϱ = 2: diamond; Nϱ = 2.5: square; Nϱ = 3,3.5,4: star. A cross inscribed in some open symbols means that the field of these models exhibits a strong equatorial dipole component. |
Figure 1 shows the relative dipole field strength versus the local Rossby number for all anelastic models considered here. Gastine et al. (2012) presented a similar plot but with fdip based on the magnetic energy density instead of the field strength. This leads to considerably lower values of fdip for multipolar dynamos. As for Boussinesq simulations, only multipolar models are found for Roℓ> 0.12 (Christensen & Aubert 2006), and the multipolar branch extends into the dipolar regime in the form of a bistable region, where both solutions are possible, depending on the initial conditions (Schrinner et al. 2012). However, in contrast to comparable parameter studies of Boussinesq models (Christensen & Aubert 2006; Schrinner et al. 2012), dipolar and multipolar dynamos are hardly distinguishable from each other in terms of their relative dipole field strength. Contrary to previous results, models with an intermediate dipolarity (fdip ≈ 0.5) lead to a fairly smooth transition of fdip in Fig. 1. These are in particular those models with a high equatorial dipole contribution denoted by a cross that is inscribed in the plotting symbol. Because the dipole field strength alone is not conclusive to classify our models in Fig. 1, their time-dependence, their kinematic stability, and their scaling behaviour (see Sect. 4.1) were additionally considered to assign them to one of both classes.
As in the case of Boussinesq simulations, only multipolar models were found to exhibit polarity reversals or oscillatory dynamo solutions. An example of a coherent dynamo wave for model3m (Nϱ = 3) is given in Fig. 2. The period of these oscillatory dynamo modes and the poleward propagation direction of the resulting wave can be surprisingly well explained by Parker’s plane layer formalism (Parker 1955; Busse & Simitev 2006; Goudard & Dormy 2008; Schrinner et al. 2011a; Gastine et al. 2012). However, the recent claim that dynamo waves could migrate towards the equator if there is a considerable density stratification (Käpylä et al. 2013) was not confirmed by our simulations.
 |
Fig. 2 Contour plot of the azimuthally averaged radial magnetic field of model3m versus time and colatitude. The contour plot was normalised by the maximum absolute value at each time step. The grey-scale coding ranges from −1, white, to +1, black. |
Moreover, we tested 13 arbitrarily chosen models (see the caption of Table B.1) for kinematic stability and found the dipolar models to be kinematically stable, whereas all multipolar models considered exhibited at least periods of instability. Figure 3 shows as an example the evolution of the kinematically advanced tracer field for model2m and model54d. For the first, the tracer field grows exponentially but it stays stable for the latter although it has been permanently perturbed during the simulation.
 |
Fig. 3 Evolution of the energy of the tracer field normalised by the energy of the actual magnetic field for model2m (dashed line) and model54d (solid line). |
 |
Fig. 4 Relative dipole field strength versus Roℓ for a sequence of models with E = 3 × 10-4, Ra = 4Rac, Pm = 3, and Pr = 1. The meaning of the symbols is defined in the caption of Fig. 1. |
A transition from the dipolar to the multipolar regime can be triggered by a decrease in the rotation rate or the dynamical length scale (possibly associated with a change in the aspect ratio), or an increase in the velocity amplitude. These three quantities influence the local Rossby number directly. In Fig. 4, we show that a transition towards the multipolar regime may also be forced by increasing Nϱ. A higher density stratification with all the other parameters fixed causes smaller length scales and larger velocity amplitudes. This leads to an increase of Roℓ and to a decrease of fdip at Roℓ ≈ 0.12 in Fig. 4.
 |
Fig. 5 Contour plot (equatorial cut) of the radial magnetic field of model2m at a given time. |
3.2. Equatorial dipole
An example of a model strongly influenced by an equatorial dipole mode is presented in Fig. 5. A strong mean zonal flow often present in these models seems to be in conflict with the generation of non-axisymmetric fields. Figure 6 demonstrates that the strong equatorial dipole mode of model5m is indeed maintained and rebuilt by the columnar convection and damped by the differential rotation. In Fig. 6 the mean zonal kinetic energy normalised by an arbitrary value (dotted line) and the ratio of the axisymmetric magnetic energy to the total magnetic energy (solid line) are displayed. The action of the mean zonal flow, or more precisely the differential rotation, tends to damp non-axisymmetric components of the magnetic field. Thus, a burst of the mean zonal kinetic energy is followed by a maximum of the axisymmetric and a dip in the non-axisymmetric magnetic energy. Subsequently, the mean zonal flow is quenched by the axisymmetric field, the axisymmetric field decays and the non-axisymmetric field is rebuilt. The interaction between the mean zonal flow and the magnetic field observed in this model is still fairly weak, although the mean zonal flow contributes already 58% to the total kinetic energy. Therefore, the magnetic field of model5m stays on average highly non-axisymmetric. We note that this is very different from the Sun, for instance, where probably an even more efficient differential rotation causes a predominantly axisymmetric large-scale magnetic field (Charbonneau 2010), but also non-axisymmetric stellar magnetic fields were reported (Donati & Landstreet 2009).
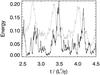 |
Fig. 6 Dotted line: axisymmetric kinetic energy of model5m normalised by an arbitrary value. Solid line: ratio of axisymmetric to total magnetic energy. |
3.3. Discussion
The fundamental cause of the high dipolarity of dynamo models in the low Rossby number regime is an outstanding question. Schrinner et al. (2012) argued that cylindrical convection in a spherical fluid domain leads to a characteristic pattern of the axisymmetric toroidal field for Boussinesq models, which eventually results in the clear preference of only one, dipolar eigenmode. The argument relies on the idea that a line of fluid elements moving towards the outer spherical boundary has to shorten and causes a converging flow towards the equatorial plane. The toroidal field is then advected and markedly shaped by this flow component (see also Olson et al. 1999). This advection process could be rigorously identified and quantified as a strong γ-effect in a corresponding mean-field description (Schrinner et al. 2007, 2012). In addition, the recent finding that the dichotomy of dipolar and multipolar dynamos seems to be absent in convective dynamo simulations in Cartesian geometry (Tilgner 2012) is consistent with this argument and points again to the significance of the underlying symmetry constraints.
What has been said above about Boussinesq models largely applies to anelastic models, too. However, geometrical constraints are somewhat relaxed for a compressible fluid. Therefore, compressibility might damp the advection of the mean toroidal field towards the equatorial plane (γ-effect), and we hypothesize that this results in at least two specific differences.
First, depending on the density contrast applied, it is more difficult to obtain dipolar solutions for anelastic models than for Boussinesq ones, even if Roℓ < 0.12. However, unlike Gastine et al. (2012), we did not find that dipolar solutions become impossible if Nϱ exceeds a certain threshold. Instead, we observe that for a given Nϱ, Ekman and Prandtl number, there seems to exist a critical magnetic Prandtl number for dipolar dynamos. For E = 10-4, Pr = 1, and Nϱ ≥ 1.5, we found Pmcrit = 2Nϱ − 2, as apparent from Fig. 7. We emphasize again that the results of Fig. 7 depend of course on E and Pr; the data of our numerical study indicate that decreasing E and increasing Pr is favorable to dipolar dynamo models.
Second, magnetic field configurations dominated by an equatorial dipole seem to be more easily realized in anelastic than in Boussinesq simulations. For the latter, only a few examples under very specific conditions were reported (Aubert & Wicht 2004; Gissinger et al. 2012). The preference of non-axisymmetric modes is well known from dynamo models based on columnar convection (e.g. Ruediger 1980; Tilgner 1997), it is also the case of the Karlsruhe dynamo experiment (Müller & Stieglitz 2002). This agrees with our reasoning on the importance of the γ-effect in the axial dipole generation mechanisms (see also Schrinner et al. 2012). Indeed, the γ-effect vanishes in the above examples, as the geometrical constraints are relaxed.
 |
Fig. 7 Magnetic Prandtl number versus Nϱ for models with E = 10-4 and Pr = 1 and variable Rayleigh numbers. Filled circles stand for parameters for which dipolar solutions were obtained. |
4. Scaling laws
Because of computational limitations, very small length scales and time scales associated with extreme parameter values that are relevant for planets and stars cannot be resolved in global direct numerical dynamo simulations. Therefore, numerical models are in general not directly comparable to planetary or stellar dynamos. Instead, scaling laws, in particular for the field strength, have been derived from theory and simulations and then extrapolated to realistic parameter regimes (see Christensen 2010, and references therein).
Subsequently, their predictions may be compared with planetary or stellar magnetic-field data obtained from observations (Christensen et al. 2009; Christensen 2010; Davidson 2013). By this consistency test, scaling laws may provide some evidence about the reliability of numerical dynamo models.
Moreover, different scaling laws typically represent different force balances or dynamo mechanisms, and their investigation might enable us to better distinguish between different types of dynamo models. It is this second aspect in particular, which is of interest in the following. We adopt here the approach by Christensen & Aubert (2006) and derive scaling laws for the field strength, the velocity, the magnetic dissipation time, and the convective heat transport and compare them with previous results from Boussinesq simulations. A similar study was recently published by Yadav et al. (2013b) based on a somewhat different sample of models. Similarities and differences with their findings are discussed.
Most of the proposed scaling laws are independent of diffusivities, which are thought to be negligible under astrophysical conditions (Christensen 2010). However, present global dynamo simulations run in parameter regimes where diffusivities still influence the overall dynamics and weak dependencies on the magnetic Prandtl number seem to persist in purely empirically derived scalings (Christensen & Tilgner 2004; Christensen & Aubert 2006; Christensen 2010; Yadav et al. 2013a; Stelzer & Jackson 2013). In this study we do not attempt to resolve this secondary dependence on Pm because the magnetic Prandtl number varies only between 1 and 5 in our sample of models.
4.1. Magnetic field scaling
The magnetic field strength measured in terms of the Lorentz number scales with the
available energy flux to the power of approximately 1/3. For the dipolar
dynamos of our sample we find 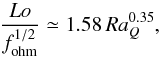 (25)and for the
multipolar models,
(25)and for the
multipolar models,  (26)Except for somewhat
larger exponential prefactors, this is in good agreement with previous results from
Boussinesq simulations (Christensen 2010; Schrinner et al. 2012; Yadav et al. 2013a) and very similar to the magnetic field scaling given by
Yadav et al. (2013b). Unlike Yadav et al. (2013b), we note, however, that we scale
the Lorentz number with the flux-based Rayleigh number RaQ
and not directly with the power released by buoyancy forces. Of course, both should be
closely related to each other. The same remark applies for the velocity scaling discussed
below.
(26)Except for somewhat
larger exponential prefactors, this is in good agreement with previous results from
Boussinesq simulations (Christensen 2010; Schrinner et al. 2012; Yadav et al. 2013a) and very similar to the magnetic field scaling given by
Yadav et al. (2013b). Unlike Yadav et al. (2013b), we note, however, that we scale
the Lorentz number with the flux-based Rayleigh number RaQ
and not directly with the power released by buoyancy forces. Of course, both should be
closely related to each other. The same remark applies for the velocity scaling discussed
below.
Models on the multipolar branch exhibit lower field strengths compared to their dipolar counterparts. This is not only apparent by the smaller prefactor in the multipolar scaling, but also the dynamo efficiency fohm for multipolar models is systematically lower than for the corresponding dipolar ones. The latter indicates that the bistable behaviour for models at Roℓ ≤ 0.12 is caused by different dynamo mechanisms. This was already seen in Boussinesq simulations (Schrinner et al. 2012) and later confirmed by Gastine et al. (2012) for anelastic models.
Apart from a few exceptions, the shift between the two scalings in Fig. 8 may serve to separate dipolar from multipolar dynamos. In agreement with Yadav et al. (2013b), we obtained several models with dipole field strengths up to fdip ≈ 0.5, which, nevertheless, clearly follow the multipolar scaling and belong to the multipolar class of dynamos.
 |
Fig. 8 Lorentz number compensated by fohm versus the flux-based Rayleigh number for our sample of models. Filled symbols correspond to dipolar models, open symbols are multipolar models and the symbol shape indicates Nρ as explained in the caption of Fig. 1. |
4.2. Velocity scaling
There is an ongoing discussion about the velocity scaling in dynamo models (Christensen 2010; Davidson 2013; Yadav et al. 2013b). It is
probably not surprising that the velocity measured in terms of the Rossby number scales
with the flux based Rayleigh number, but the correct exponent and its theoretical
justification is debated. The lower bound is set by the assumption of a balance between
inertia and buoyancy forces (mixing length balance), which leads to an exponent of
1/3
(Christensen 2010). If, however, the predominant
force balance is assumed to be between the Lorentz force, the buoyancy, and the Coriolis
force (MAC-balance) the exponent is closer to 1
/2 (Christensen
2010; Davidson 2013). As most previous
studies (Christensen & Aubert 2006; Christensen 2010; Yadav
et al. 2013a; Stelzer & Jackson
2013; Yadav et al. 2013b), we obtained an
exponent in between these two values for our sample of models, 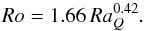 (27)The scatter in Fig.
9 is considerable, but the standard error is of the
same order as for Boussinesq models with stress-free mechanical boundary conditions (Yadav et al. 2013a). Compressible effects do not seem
to deteriorate the scaling.
(27)The scatter in Fig.
9 is considerable, but the standard error is of the
same order as for Boussinesq models with stress-free mechanical boundary conditions (Yadav et al. 2013a). Compressible effects do not seem
to deteriorate the scaling.
 |
Fig. 9 Rossby number versus the flux-based Rayleigh number for our sample of models. |
However, as in Yadav et al. (2013b), we are not able to distinguish between dipolar and multipolar models in our velocity scaling, which is contrary to what has been previously reported by Yadav et al. (2013a) for Boussinesq models.
Scaling laws for anelastic and Boussinesq models.
4.3. Scaling of Ohmic dissipation time
The scaling of magnetic dissipation time,  (28)is used to evaluate the
characteristic length scale ℓB of the magnetic
field. Christensen & Tilgner (2004)
originally identified a linear dependence of τdiss on the inverse Rossby number
provided that time is measured in units of Ω-1. Their finding was supported by dipole-dominated
Boussinesq models with no-slip mechanical boundary conditions and the evaluation of the
Ohmic dissipation time in the Karlsruhe dynamo experiment. The best fit for our data
points in Fig. 10, however, gives an exponent with a
significantly lower absolute value,
(28)is used to evaluate the
characteristic length scale ℓB of the magnetic
field. Christensen & Tilgner (2004)
originally identified a linear dependence of τdiss on the inverse Rossby number
provided that time is measured in units of Ω-1. Their finding was supported by dipole-dominated
Boussinesq models with no-slip mechanical boundary conditions and the evaluation of the
Ohmic dissipation time in the Karlsruhe dynamo experiment. The best fit for our data
points in Fig. 10, however, gives an exponent with a
significantly lower absolute value, 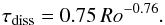 (29)An almost
identical result was found by Yadav et al. (2013b)
from their somewhat more diverse and scattered data set. Apparently, the application of
stress-free boundary conditions and possibly the compressible effects flatten the slope of
τdiss as a function of the Rossby number.
Moreover, it would seem plausible that τdiss followed different scaling
relations for dipolar and multipolar models. Indeed, the dissipation time for bistable
pairs is systematically larger for dipolar than for multipolar models. However, separate
least square fits for all dipolar and all multipolar models of our sample lead to very
similar results.
(29)An almost
identical result was found by Yadav et al. (2013b)
from their somewhat more diverse and scattered data set. Apparently, the application of
stress-free boundary conditions and possibly the compressible effects flatten the slope of
τdiss as a function of the Rossby number.
Moreover, it would seem plausible that τdiss followed different scaling
relations for dipolar and multipolar models. Indeed, the dissipation time for bistable
pairs is systematically larger for dipolar than for multipolar models. However, separate
least square fits for all dipolar and all multipolar models of our sample lead to very
similar results.
 |
Fig. 10 Ohmic dissipation time versus Rossby number for all models considered in this study. |
4.4. Nusselt number scaling
The convective heat transport in dynamo models is very sensitive to rotation and depends
on the magnetic field, boundary conditions, or the geometry of the fluid domain to a much
lower degree (Christensen 2002; Christensen & Aubert 2006; Aurnou 2007; Schmitz
& Tilgner 2009; Busse & Simitev
2011; Gastine & Wicht 2012; Yadav et al. 2013a; Stelzer & Jackson 2013). The power law for the Nusselt number inferred
from Fig. 11,
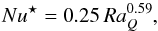 (30)is consistent with
previous results and also confirms this finding for anelastic dynamo models; the exponent
of 0.59 is very close to the
value of 5/9 established by the above mentioned references. However, the scaling
is somewhat more scattered than for Boussinesq models (Yadav et al. 2013a). We excluded in a test all models for which convection is
only marginaly above the onset (Nu⋆ <
2), but this reselection of models did not improve the quality of the
fit.
(30)is consistent with
previous results and also confirms this finding for anelastic dynamo models; the exponent
of 0.59 is very close to the
value of 5/9 established by the above mentioned references. However, the scaling
is somewhat more scattered than for Boussinesq models (Yadav et al. 2013a). We excluded in a test all models for which convection is
only marginaly above the onset (Nu⋆ <
2), but this reselection of models did not improve the quality of the
fit.
 |
Fig. 11 Nusselt number versus the flux-based Rayleigh number for our sample of models. |
4.5. Discussion
In an overall view, the scaling relations for Boussinesq and anelastic models are very similar (see Table 1). Beyond that, there is no obvious effect of compressibility on the scaling results and they might be even considered as consistent irrespective of the density stratification of the underlying models (Yadav et al. 2013b). However, the reason for the good agreement could be that the flux-based scaling laws are insensitive to different physical conditions. Using the example of the magnetic field scaling, we argue in the following that differences in the dynamo processes might not be visible in the scaling relation, and some caution is needed in generalizing results from Boussinesq simulations.
If the magnetic energy density follows a simple power law in terms of the convective energy flux, an exponent of 2 /3 is already required for dimensional reasons (e.g., Christensen 2010). Moreover, the flux-based scaling law for the magnetic field is composed of the scalings for the velocity and the magnetic dissipation time. By definition, we have EM ~ fohmτdissP, and with Ro ~ Pα and τdiss ~ Roβ, we find EM ~ fohmPPαβ. Dimensional arguments require αβ = −1/3, which establishes relations (25) and (26). Whereas the exponent in the flux-based scaling law for the magnetic field is fix, α and β are to some extend variable and may change according to the specific physical conditions. This reflects the outcome of more and more extended parameter studies: The exponent of 1/3 in the magnetic-field scaling is reliably reproduced, but the values for α and β seem to be less certain and are under debate.
In addition, scaling relations (25) and (26) require that the field strength, measured by Lo, is compensated by the square root of fohm (interpreted as dynamo efficiency in Schrinner 2013). However, fohm is probably a complicated function of several control parameters and might depend strongly on the specific physical conditions. The often made assumption that fohm → 1 for Pm ≪ 1 (e.g. Davidson 2013) is probably too simple. For example, Schrinner (2013) recently demonstrated that fohm in dynamo models might depend strongly on the rotation rate. The dynamo efficiency dropped by two orders of magnitude as the rotation rate of these models was decreased. A further counterexample could be the solar dynamo. Independent estimates result in fohm ~ O(10-3), (Schrinner 2013; Rempel 2006) although the magnetic Prandtl number is thought to be much smaller than one in the solar interior.1 In other words, the flux based scaling laws probably do not distinguish between different types of dynamos because differences in the field strength are absorbed by changes in fohm.
5. Conclusions
Our study revealed a number of similarities between Boussinesq and anelastic dynamo models. The dichotomy between dipolar and multipolar models seems to extend to anelastic models, and the flux-based scaling laws originally proposed for Boussineq models appear to hold similarly for models in the anelastic approximation. Thus, large scale, dipolar magnetic fields for both types of models can only be produced if rotation is important (as measured by the local Rossby number), and the magnetic field strength is directly related to the energy flux via (25) and (26) (see Fig. 8).
However, we also pointed out some significant differences between Boussinesq and anelastic dynamo simulations. Magnetic field configurations with a significant equatorial dipole contribution are less typical for Boussinesq than for anelastic models. Moreover, a large density stratification in anelastic models may inhibit the generation of magnetic fields dominated by an axial dipole. The above claimed consistency of the scalings for Boussinesq and anelastic simulations partly relies on the very general formulation of the flux-based scaling laws and does not necessarily imply similar dynamo processes. We also stress that the assumption of a radially varying conductivity may introduce additional effects, which were not examined here. Whereas Yadav et al. (2013b) obtained very similar scaling laws for models with variable conductivities, Duarte et al. (2013) reported that the field topology of some models depends on the radial conductivity profile. A mean-field analysis (Schrinner et al. 2007; Schrinner 2011) of numerical dynamo models in the anelastic approximation might give more detailed insight in relevant dynamo processes and is envisaged for a future study.
Online material
Appendix A: Critical Rayleigh numbers for the onset of convection
Overview of the critical Rayleigh numbers and the corresponding critical azimuthal wavenumbers for the onset of convection determined, as explained in Jones et al. (2009).
Appendix B: Numerical models
Overview of the simulations carried out, ordered with respect to their local Rossby number.
In Schrinner (2013), a wrong mean solar density has been used to estimate fohm which lead to fohm ≈ 10-2. We correct this error here.
Acknowledgments
M.S. is grateful for financial support from the DFG fellowship SCHR 1299/1-1. Computations were performed at CINES, CEMAG, and GWDG computing centres. Moreover, this work was granted access to the HPC resources of MesoPSL financed by the Région Ile de France and the project Equip@Meso (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche.
References
- Alboussière, T., & Ricard, Y. 2013, J. Fluid Mech., 725, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Aubert, J., & Wicht, J. 2004, Earth Planetary Sci. Lett., 221, 409 [Google Scholar]
- Aurnou, J. M. 2007, Geophys. Astrophys. Fluid Dyn., 101, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Braginsky, S. I., & Roberts, P. H. 1995, Geophysical and Astrophysical Fluid Dynamics, 79, 1 [Google Scholar]
- Brown, B. P., Vasil, G. M., & Zweibel, E. G. 2012, ApJ, 756, 109 [Google Scholar]
- Browning, M. K., Brun, A. S., & Toomre, J. 2004, ApJ, 601, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., Miesch, M. S., & Toomre, J. 2004, ApJ, 614, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Buffett, B. A. 2000, Science, 288, 2007 [NASA ADS] [CrossRef] [Google Scholar]
- Busse, F. H. 1975, Geophys. J. Int., 42, 437 [Google Scholar]
- Busse, F. H., & Simitev, R. D. 2006, Geophys. Astrophys. Fluid Dyn., 100, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Busse, F. H., & Simitev, R. D. 2010, in Turbulence in the Atmosphere and Oceans, IUTAM Bookseries (Springer), 28, 181 [Google Scholar]
- Busse, F., & Simitev, R. 2011, Geophys. Astrophys. Fluid Dyn., 105, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, F., & Tobias, S. M. 2009, J. Fluid Mech., 621, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, P. 2010, Liv. Rev. Sol. Phys., 7 [Google Scholar]
- Christensen, U. R. 2002, J. Fluid Mech., 470, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, U. R. 2010, Space Sci. Rev., 152, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, U. R., & Aubert, J. 2006, Geophy. J. Int., 166, 97 [Google Scholar]
- Christensen, U. R., & Tilgner, A. 2004, Nature, 429, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, U., Olson, P., & Glatzmaier, G. A. 1998, Geophys. Res. Lett., 25, 1565 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, U., Olson, P., & Glatzmaier, G. A. 1999, Geophys. J. Int., 138, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, U. R., Holzwarth, V., & Reiners, A. 2009, Nature, 457, 167 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Davidson, P. A. 2013, Geophys. J. Int., 195, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dormy, E., Cardin, P., & Jault, D. 1998, Earth Planet. Sci. Lett., 160, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Dormy, E., Valet, J.-P., & Courtillot, V. 2000, Geochem. Geophys. Geosyst., 1, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Duarte, L. D. V., Gastine, T., & Wicht, J. 2013, Phys. Earth Planet. Inter., 222, 22 [Google Scholar]
- Gastine, T., & Wicht, J. 2012, Icarus, 219, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Gastine, T., Duarte, L., & Wicht, J. 2012, A&A, 546, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilman, P. A., & Glatzmaier, G. A. 1981, ApJS, 45, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Gissinger, C., Petitdemange, L., Schrinner, M., & Dormy, E. 2012, Phys. Rev. Lett., 108, 234501 [NASA ADS] [CrossRef] [Google Scholar]
- Glatzmaier, G. A. 1984, J. Comput. Phys., 55, 461 [Google Scholar]
- Glatzmaier, G. A., & Roberts, P. H. 1995, Nature, 377, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Goudard, L., & Dormy, E. 2008, Europhys. Lett., 83, 59001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gough, D. O. 1969, J. Atmos. Sci., 26, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Grote, E., Busse, F. H., & Tilgner, A. 2000, Phys. Earth Planet. Inter., 117, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Hori, K., Wicht, J., & Christensen, U. R. 2010, Phys. Earth Planet. Inter., 182, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, C. A., & Kuzanyan, K. M. 2009, Icarus, 204, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, C. A., Kuzanyan, K. M., & Mitchell, R. H. 2009, J. Fluid Mech., 634, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, C. A., Boronski, P., Brun, A. S., et al. 2011, Icarus, 216, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Kageyama, A., & Sato, T. 1997, Phys. Rev. E, 55, 4617 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., Cole, E., Warnecke, J., & Brandenburg, A. 2013, ApJ, 778, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Katayama, J. S., Matsushima, M., & Honkura, Y. 1999, Phys. Earth Planet. Inter., 111, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Kuang, W., & Bloxham, J. 1997, Nature, 389, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Kutzner, C., & Christensen, U. R. 2002, Phys. Earth Planet. Inter., 131, 29 [Google Scholar]
- Landeau, M., & Aubert, J. 2011, Phys. Earth Planet. Inter., 185, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Lantz, S. R., & Fan, Y. 1999, ApJS, 121, 247 [Google Scholar]
- Miesch, M. S., Elliott, J. R., Toomre, J., et al. 2000, ApJ, 532, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, U., & Stieglitz, R. 2002, Nonlinear Processes in Geophysics, 9, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Ogura, Y., & Phillips, N. A. 1962, J. Atmos. Sci., 19, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Olson, P., Christensen, U. R., & Glatzmaier, G. A. 1999, J. Geophys. Res., 104, 10383 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1955, ApJ, 122, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2006, ApJ, 647, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, T. M., & Glatzmaier, G. A. 2005, ApJ, 620, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Ruediger, G. 1980, Astron. Nachr., 301, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Sarson, G. R., Jones, C. A., & Longbottom, A. W. 1998, Geophys. Astrophys. Fluid Dyn., 88, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitz, S., & Tilgner, A. 2009, Phys. Rev. E, 80, 015305 [NASA ADS] [CrossRef] [Google Scholar]
- Schrinner, M. 2011, A&A, 533, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrinner, M. 2013, MNRAS, 431, L78 [NASA ADS] [CrossRef] [Google Scholar]
- Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M., & Christensen, U. R. 2007, Geophys. Astrophys. Fluid Dyn., 101, 81 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Schrinner, M., Schmitt, D., Cameron, R., & Hoyng, P. 2010, Geophys. J. Int., 182, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Schrinner, M., Petitdemange, L., & Dormy, E. 2011a, A&A, 530, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrinner, M., Schmitt, D., & Hoyng, P. 2011b, Phys. Earth Planet. Inter., 188, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Schrinner, M., Petitdemange, L., & Dormy, E. 2012, ApJ, 752, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Sreenivasan, B., & Jones, C. A. 2006, Geophys. J. Int., 164, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Stelzer, Z., & Jackson, A. 2013, Geophys. J. Int., 193, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Tilgner, A. 1997, Phys. Lett. A, 226, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Tilgner, A. 2012, Phys. Rev. Lett., 109, 248501 [NASA ADS] [CrossRef] [Google Scholar]
- Tilgner, A., & Brandenburg, A. 2008, MNRAS, 391, 1477 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, R. K., Gastine, T., & Christensen, U. R. 2013a, Icarus, 225, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, R. K., Gastine, T., Christensen, U. R., & Duarte, L. D. V. 2013b, ApJ, 774, 6 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Benchmark results
Hydrodynamic benchmark (E = 10-3,Nϱ = 5,χ = 0.35,Ra = 3.52 × 105,Pr = 1,n = 2).
Steady dynamo benchmark ( E = 2 × 10-3,Nϱ = 3,χ = 0.35,Ra = 8.00 × 104,Pr = 1,Pm = 50,n = 2).
Unsteady dynamo benchmark (E = 5 × 10-5,Nϱ = 3,χ = 0.35,Ra = 2.50 × 107,Pr = 2,Pm = 2,n = 2).
All Tables
Overview of the critical Rayleigh numbers and the corresponding critical azimuthal wavenumbers for the onset of convection determined, as explained in Jones et al. (2009).
Overview of the simulations carried out, ordered with respect to their local Rossby number.
Hydrodynamic benchmark (E = 10-3,Nϱ = 5,χ = 0.35,Ra = 3.52 × 105,Pr = 1,n = 2).
Steady dynamo benchmark ( E = 2 × 10-3,Nϱ = 3,χ = 0.35,Ra = 8.00 × 104,Pr = 1,Pm = 50,n = 2).
Unsteady dynamo benchmark (E = 5 × 10-5,Nϱ = 3,χ = 0.35,Ra = 2.50 × 107,Pr = 2,Pm = 2,n = 2).
All Figures
 |
Fig. 1 Relative dipole field-strength versus the local Rossby number for our sample of models. Filled symbols stand for dipolar, open symbols for multipolar dynamos. The symbol shape indicates the number of density scale heights: Nϱ = 0.5: circle; Nϱ = 1: upward triangle; Nϱ = 1.5: downward triangle; Nϱ = 2: diamond; Nϱ = 2.5: square; Nϱ = 3,3.5,4: star. A cross inscribed in some open symbols means that the field of these models exhibits a strong equatorial dipole component. |
| In the text | |
 |
Fig. 2 Contour plot of the azimuthally averaged radial magnetic field of model3m versus time and colatitude. The contour plot was normalised by the maximum absolute value at each time step. The grey-scale coding ranges from −1, white, to +1, black. |
| In the text | |
 |
Fig. 3 Evolution of the energy of the tracer field normalised by the energy of the actual magnetic field for model2m (dashed line) and model54d (solid line). |
| In the text | |
 |
Fig. 4 Relative dipole field strength versus Roℓ for a sequence of models with E = 3 × 10-4, Ra = 4Rac, Pm = 3, and Pr = 1. The meaning of the symbols is defined in the caption of Fig. 1. |
| In the text | |
 |
Fig. 5 Contour plot (equatorial cut) of the radial magnetic field of model2m at a given time. |
| In the text | |
 |
Fig. 6 Dotted line: axisymmetric kinetic energy of model5m normalised by an arbitrary value. Solid line: ratio of axisymmetric to total magnetic energy. |
| In the text | |
 |
Fig. 7 Magnetic Prandtl number versus Nϱ for models with E = 10-4 and Pr = 1 and variable Rayleigh numbers. Filled circles stand for parameters for which dipolar solutions were obtained. |
| In the text | |
 |
Fig. 8 Lorentz number compensated by fohm versus the flux-based Rayleigh number for our sample of models. Filled symbols correspond to dipolar models, open symbols are multipolar models and the symbol shape indicates Nρ as explained in the caption of Fig. 1. |
| In the text | |
 |
Fig. 9 Rossby number versus the flux-based Rayleigh number for our sample of models. |
| In the text | |
 |
Fig. 10 Ohmic dissipation time versus Rossby number for all models considered in this study. |
| In the text | |
 |
Fig. 11 Nusselt number versus the flux-based Rayleigh number for our sample of models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


