| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201323363 | |
| Published online | 04 March 2014 | |
Spectroscopic mapping of the planetary nebula NGC 6302⋆
1
Laboratório de Análise Numérica e Astrofísica, Departamento de
MatemáticaUniversidade Federal de Santa Maria, Av. Roraima 1000, CEP 97119-900, Santa Maria
RS, Brazil
e-mail: alinerauber@gmail.com
2
Universidade do Vale do Paraíba, Av. Shishima Hifumi 2911, CEP 12244-000
São José dos Campos, SP, Brazil
Received:
31
December
2013
Accepted:
17
January
2014
Context. Most spectroscopic studies of planetary nebulae (PNe) are based on data from specific parts of the objects. Considering the high complexity of their morphological structures, integrated or average values across an observed region can only provide limited information of their ionic, density, and temperature structures.
Aims. We investigate the spatial variation of the physical and chemical properties of NGC 6302, a high-ionization PNe, with a complex bipolar structure.
Methods. Spatially resolved long-slit spectroscopic data were obtained from 11 parallel and equally spaced directions over the nebula. Maps of emission line fluxes, line ratios, electron temperature Te, electron density Ne, and ionic abundances (He+, He2+, N0, N+, O0, O+, O2+, S+, S2+, Ne2+, Ar2+, Ar3+, and Ar4+ relative to H+) were constructed with a spatial resolution of 1.45″ × 1″ for a large portion of the nebula over an area of 11″ × 250″. Electron densities were estimated from the [S ii] λ 6716/λ 6731 and [Ar iv] λ 4711/λ 4740 line ratios, and electron temperatures were estimated from the [O iii] (λ 4959 + λ 5007)/λ 4363 and [N ii] (λ 6548 + λ 6584)/λ 5755 ratios. Integrated spectra were also obtained and 142 lines were identified.
Results. The electron density maps show a peaked distribution, with the
densest area at the circumstellar region, reaching Ne ≈ 40 000 cm-3, and
decreasing to Ne ≤ 1000 cm-3 at the
lobes. Knots were observed in the Ne(S ii) map, with
2000 cm-3 < Ne < 3000 cm-3.
The Ne(Ar iv) map suggests the
presence of an inner region with Ne ≈ 20 000 cm-3 that
extends from the center through the east lobe. A homogeneous temperature distribution was
found for both Te(O iii) and Te(N ii). Small temperature
fluctuations on the plane of the sky of 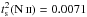 and
and
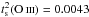 were estimated.
were estimated.
Conclusions. In general, the total abundances obtained are similar to the maximum found in the ionic abundance maps of the dominant ionic species. This demonstrates the potential of spatially resolved abundance studies for establishing lower limits of the total abundances based on ionic abundances, for checking the ionization correlation factors, and in some cases, for determining the total abundances directly from maps of ionic abundances.
Key words: planetary nebulae: individual: NGC 6302 / ISM: abundances
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
The bipolar planetary nebula (PN) NGC 6302 has been classified as Type I (Peimbert & Torres-Peimbert 1983; Kingsburgh & Barlow 1994) with high helium and nitrogen abundances. Narrow band images in different emission lines obtained with the Hubble Space Telescope show the conspicuous bipolar morphology and the complex small-scale structures of the nebula (see Matsuura et al. 2005, Fig. 7). The lobes and the innermost parts of the nebula are expanding with a velocity increasing with the radial distance (Szyszka et al. 2011). At the center, there is a high extinction molecular torus, oriented north-south, roughly perpendicular to the axis of the lobes, and expanding slowly with a velocity of 8 km s-1 (Peretto et al. 2007). Within it, there is an ionized torus whose nature and evolution is not completely understood.
Because of the high extinction of its circumstellar region, the central star of NGC 6302 has only recently been identified at the position
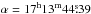 ,
, 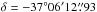 (J2000) (Szyszka et al. 2009). It is among the
hottest central stars of PNe with an effective temperature higher than 250 000 K, as
indicated by the detection of emission lines from very high-ionization species (Ashley & Hyland 1988; Casassus et al. 2000; Feibelman 2001).
(J2000) (Szyszka et al. 2009). It is among the
hottest central stars of PNe with an effective temperature higher than 250 000 K, as
indicated by the detection of emission lines from very high-ionization species (Ashley & Hyland 1988; Casassus et al. 2000; Feibelman 2001).
In the literature, there are a number of studies of the physical conditions of NGC 6302 based on spectroscopic observations in the optical, ultraviolet, and mid- and near-infrared ranges (Aller et al. 1981; Pottasch & Beintema 1999; Casassus et al. 2000; Groves et al. 2002; Tsamis et al. 2003; Krabbe & Copetti 2005). Different regions of the nebula were observed with different telescopes, also using different slit configurations and aperture sizes. Although these works give a reliable overview of the object, they do not provide detailed information of different morphological structures. Wright et al. (2011) presented a 3D photoionization model of NGC 6302 based on data compiled from these studies. The best-fitting model was obtained using a homogeneous elemental abundance distribution and three principal components for the density: a very dense circumstellar disk, a pair of lobes with a constant density, and a higher density component at the inner region of the lobes. Knots were also introduced to simulate density inhomogeneities. Most of the emission line ratios in the literature were reproduced, but some could not be matched. Significant differences were found between some model ionic abundances and those reported by Tsamis et al. (2003).
Krabbe & Copetti (2005) published a spatially resolved spectroscopic study of NGC 6302. However, they only studied the spatial variation in the physical conditions along a single projected line on this nebula, based on long-slit spectroscopic data obtained at one slit position. Richer 2D spatially resolved data can be obtained by using integral field units or from multiple parallel long-slit spectroscopic observations. The derived 2D maps of line ratios and physical properties provide better constraints for the 3D modeling of photoionized nebulae. However, only a small number of PNe have been studied using a spectroscopic mapping technique. Some examples are NGC 6369 (Monteiro et al. 2004), NGC 40 (Leal-Ferreira et al. 2011), NGC 5882 (Tsamis et al. 2008), NGC 6153 (Tsamis et al. 2008), and NGC 7009 (Tsamis et al. 2008; Phillips et al. 2010).
This paper reports the results of a spectroscopic mapping of the PN NCG 6302. Two-dimensional spectral maps and spatial profiles of emission line fluxes, relative line intensities, and physical properties, such as electron density, electron temperature, and ionic and total abundances, were produced with a spatial resolution of approximately 1.45″ × 1″. In Sect. 2, we describe the observations and the data reduction procedure. The results are presented and discussed in Sect. 3, and a summary of our conclusions is presented in Sect. 4.
2. Observations and data reduction
Long-slit spectra of NGC 6302 were obtained on 29, 30, and 31 August 2008 with the Goodman spectrograph at the 4.1 m Southern Astrophysical Research Telescope (SOAR), Cerro Pachón, Chile. A 4096 × 4096 pixels Fairchild CCD was used. The spatial scale was approximately 0.15″pixel-1. The slit was 3.7′ long and 1′′ wide. The 300 l mm-1 and the 600 l mm-1 gratings were used. The 300 l mm-1 spectra covered the range from 3600 Å to 9150 Å, with a reciprocal dispersion of 1.3 Å pixel-1 and a spectral resolution of 8.9 Å, and the 600 l mm-1 spectra from 3550 Å to 6300 Å, with 0.65 Å pixel-1 and resolution of 4.5 Å. The slit was oriented east-west and centered at 11 different equally spaced declinations. The declination offsets relative to the adopted reference star 2MASS J17134915-3706075 (α = 17h13m49s, δ = −37°06′08″, J2000) ranged from 6′′ S to 4′′ N, with steps of 1′′. The exposure times at each slit position were 3 × 300 s for the 600 l mm-1 grating and 3 × 250 s for the 300 l mm-1 grating. Figure 1 shows the slit positions on an R-band image of NGC 6302 from the ESO survey, obtained with the Aladin software made available by the Centre de Données astronomiques de Strasbourg.
The spectra were reduced using the IRAF1 standard procedures for bias subtraction, flat-fielding, and cosmic-ray rejection. From each 2D spectrum we extracted a series of 150 1D spectra from contiguous sectors with 1.45′′ (10 pixels) length along the slit axis using the apall task. On each 2D spectrum, we identified and measured the positions along the slit of the detected field star to assure the extraction of the 1D spectra from the same bands in different exposures and slit positions. After adding together the 1D spectra from different exposures, 1650 1D spectra were obtained for each grating. Spectra of an Hg-Ar lamp were taken for the wavelength calibration, but in some parts of the spectra, their emission lines were too sparse or weak. Thus, the wavelength calibration was refined using the main emission lines observed in the spectra of NGC 6302 itself. Spectra of the standard stars LTT 9491 and LTT 7379 were obtained for flux calibration.
 |
Fig. 1 Positions of the slit on an R-band image of NGC 6302 from the ESO survey, obtained with the ALADIN software made available by the Centre de Données astronomiques de Strasbourg. The slit positions are represented by the red and blue lines. The red line indicates the offset 0′′. |
Emission lines selected for the maps.
The line fluxes were obtained from a single or multiple Gaussian profiles fitting between
two given limits and over a local continuum. These measurements were made with the
splot routine of the IRAF package. The error associated with the line
flux was estimated by 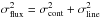 , where σcont and
σline are the errors due to the continuum
baseline determination and the Poisson error of the line, respectively.
, where σcont and
σline are the errors due to the continuum
baseline determination and the Poisson error of the line, respectively.
3. Results
 |
Fig. 2 Logarithmic maps of the observed fluxes (in units of erg cm-2 s-1) in [O ii] λ3727, [Ne iii] λ3869, He ii λ4686, [Ar iv] λ4740, Hβ, [O iii] λ5007, He i λ5876, Hα, [N ii] λ6584, and [S ii] λ6717. In all maps, north is up and east to the left and the coordinates are offset with respect to the position of the central star. |
 |
Fig. 3 Map of the logarithmic extinction coefficient c(Hβ). |
Emission-line flux maps of NGC 6302 with a spatial resolution of 1.45″ × 1″ were constructed for each of the lines listed in Table 1. These are the main recombination lines of H i, He i, and He ii lines, as well as the collisional excitation lines (CELs) used to compute the physical conditions in the nebula. To avoid spurious measurements of any specific line at a position where it was too weak and to define the boundaries of the nebula in different emission lines, we discarded the measurements in the pixels where the line had an intensity peak below 2.5 times the root-mean-square deviation of the continuum. The observed flux maps in [O ii] λ3727, [Ne iii] λ3869, He ii λ4686, [Ar iv] λ4740, Hβ, [O iii] λ5007, He i λ5876, Hα, [N ii] λ6584, and [S ii] λ6717 are shown in Fig. 2.
3.1. Extinction
The observed emission line fluxes with respect to Hβ were corrected for the effects of the interstellar extinction. The logarithmic extinction coefficient c(Hβ) was estimated by comparing the Hγ/Hβ and Hα/Hβ flux ratios measured in each aperture with the case B theoretical ratios computed by Storey & Hummer (1995) for Te = 10 000 K and Ne = 1000 cm-3. The Galactic reddening function of Savage & Mathis (1979) was used.
The c(Hβ) map presented in Fig. 3 clearly depicts the dust lane crossing the nebula along the north-south direction associated with the molecular disk or torus that gives NGC 6302 its bipolar morphology. The amount of extinction across the nebula is fairly homogeneous in the lobes (Hα/Hβ = 5.01 ± 0.34 and c(Hβ) = 0.78 ± 0.10), but is much higher in the direction of the circumstellar torus (Hα/Hβ = 6.94 ± 0.91 and c(Hβ) = 1.23 ± 0.18). We do not confirm previous reports (Rodríguez et al. 1985; Bohigas 1994) that the extinction would be substantially lower in the eastern lobe than in the wertern lobe. We only found a marginal difference in the Balmer ratio with Hα/Hβ = 4.87 ± 0.42 (c(Hβ) = 0.74 ± 0.11) in the eastern lobe and Hα/Hβ = 5.11 ± 0.34 (c(Hβ) = 0.81 ± 0.09) in the western lobe.
The area of higher extinction is near the central star position, but displaced to the west. A maximum of c(Hβ) = 1.69 (Hα/Hβ = 9.51,AHα = 2.9) is measured at the position 6′′ W and 5′′ N of the central star. This is consistent with the fact that the torus is not seen exactly edge-on, but with a small inclination of ≈15° (Meaburn et al. 2005; Dinh-V-Trung et al. 2008). Matsuura et al. (2005) mapped the extinction in the central area of NGC 6302 based on the comparison between Hα and Brα images and a 6 cm radio continuum map. They found an extinction of AHα = 3.5−7, with the highest values towards the disk. These values are higher than those found from the optical Balmer decrement (see, e.g., Tsamis et al. 2003; Groves et al. 2002; Bohigas 1994), indicating that a considerable fraction of the extinction is caused by internal dust.
3.2. Integrated spectra
Integrated spectra were obtained by summing the flux contributions in all apertures within the boundary of the Hβ map. Table A.1 presents the observed and reddening-corrected intensities of the 142 emission lines detected in the integrated spectra. We used a preliminary version of the emission nebula spectral synthesis code X-SSN (Péquignot et al. 2012) to identify faint lines. From the observed Balmer ratios Hγ/Hβ and Hα/Hβ, we obtained a mean extinction coefficient of c(Hβ) = 1.00 ± 0.10. The total observed flux in Hβ of 2.21 × 10-11 erg cm-2 s-1 corresponds to 75% of the integrated flux obtained by Copetti (1990) using narrow-band filter photometry. Thus, although our observations did not cover the whole nebula, a preponderant fraction of 3/4 of the total nebular line emission was included.
3.3. Excitation properties
 |
Fig. 4 [N ii] /Hα, [S ii] /Hα, [O ii] /Hβ, and [O iii] /Hβ maps. |
Line ratio maps can provide information about the excitation conditions of the nebula. In Fig. 4, we show the [N ii] (λ6548 + λ6584)/Hα, [S ii] (λ6717 + λ6731)/Hα, [O ii] (λ3726 + λ3729)/Hβ and [O iii] (λ4959 + λ5007)/Hβ maps. To avoid restricting the maps to pixels where c(Hβ) was measured, the line ratios are not reddening corrected, with the exception of [O ii] /Hβ. These and other similar maps reflect the stratified structure of photoionized nebulae. Lame & Ferland (1991) proposed that NGC 6302 might be partially shock-excited by stellar wind. However, Casassus et al. (2000) and Oliva et al. (1996) did not find any indication of shock ionization in this nebula. From the comparison of different line ratios, we tend to conclude that NGC 6302 is essentially a photoionized nebula. To illustrate this, we show in Fig. 5 that the data from NGC 6302 and from supernova remnants occupy separate areas on the plot of Hα/[S ii] vs. Hα/[N ii]. However, the effects of possible abundance differences among the objects are not taken into account in this analysis. Furthermore, the presence of very small regions excited by shocks is not discarded. As an example, Phillips et al. (2010) concluded from high spatial resolution data that a small fraction of the emission from some specific regions of NGC 7009 might be due to shock.
3.4. Electron temperature and density
Electron temperatures Te and electron densities Ne were derived from collisional excitation line ratios by numerically solving the equilibrium equations for an n-level atom using the IRAF routine temden of the nebular package (Shaw & Dufour 1995) of STSDAS2 with the same atomic parameters used by Krabbe & Copetti (2005). We determined Te from [O iii] (λ4959 + λ5007)/λ4363 and [N ii] (λ6548 + λ6584)/λ5755 intensity ratios, and Ne from [S ii] λ6717/λ6731 and [Ar iv] λ4711/λ4740. We detected the [Cl iii] doublet in some apertures, but we did not use these lines to map the electron density because of large errors associated.
The [O iii] temperature sensor is practically independent of the density assumed. Thus, we derived the electron temperatures Te(O iii) assuming a constant density of 1000 cm-3. The electron densities Ne(Ar iv) were obtained assuming a constant electron temperature of 15 000 K. Errors of less than 5% are expected if the actual temperature differs by less than 2000 K of the assumed value. As the lines He I λ4713 and [Ar IV] λ4711 were not resolved, the contribution of He I λ4713 to the flux measured for [Ar IV] λ4711 was estimated as one tenth of the line intensity of He I λ4471 (Benjamin et al. 1999).
For the wide range of densities found in NGC 6302, Te(N ii) shows a significant dependence on the assumed density and so to derive the [N ii] temperatures and the [S ii] densities, we followed an interactive procedure. Initially, we calculated the electron densities Ne(S ii) assuming a constant electron temperature of 10 000 K. Then, the density values were used to compute Te(N ii) in each aperture. We iterated until convergence, which was observed after the fifth iteration, to obtain the adopted Ne(S ii) and Te(N ii).
Figure 6 shows the Ne(S ii), Ne(Ar iv), Te(O iii), and Te(N ii) maps. Table 2 presents some non-parametric statistics of the electron density and temperature distributions, including the minimum (min) and maximum (max), the median, the first quartile (Q1, upper limit of the 25% lower values), the third quartile (Q3, lower limit of the 25% highest values), and the number N of different nebular sections. Table 3 presents the physical conditions determined from the integrated spectra and a comparison with the mean values (weighted by the Hβ flux) from the temperature maps and with previous values found in the literature.
 |
Fig. 5 Hα/[S ii] vs. Hα/[N ii] for NGC 6302 (this paper) and supernova remnants (data from the literature). |
 |
Fig. 6 Maps of the densities Ne(S ii) and Ne(Ar iv) (in units of cm-3) and temperatures Te(N ii) and Te(O iii) (in units of K). |
Statistics of the electron density and temperature maps.
Physical conditions from the integrated spectra, the mean from the temperature maps (weighted by the Hβ flux) and a comparison with previous works.
A wide range of values of density is observed with 70 cm-3 ≲ Ne ≲ 41 400 cm-3. The density maps of Ne(S ii) and Ne(Ar iv) show a similar behavior. The central area of the nebula presents densities above 30 000 cm-3. At these high densities, the [S ii] line ratio is near saturation, and consequently the derived density values may be uncertain. The maximum values of Ne(S ii) = 41 600 ± 4700 cm-3 and Ne(Ar iv) = 31 400 ± 420 cm-3 were found at positions less than 2′′ from the central star. Both density sensors indicate that the density decreases from the central to the outer regions, but there are some differences that can be seen in the density profiles shown in Fig. 7. The Ne(S ii) density falls towards the edges faster than Ne(Ar iv). At the lobes, a uniform low density of less than 1000 cm-3 is observed in the Ne(S ii) map, with the exception of a few knots with 2000−3000 cm-3. Much higher Ne(Ar iv) densities are observed in the lobes. On average, the values of Ne(Ar iv) are 2.6 greater than those of Ne(S ii) at the same position. There is an extended area of 20′′ to the east of the central star that shows Ne(Ar iv)/Ne(S ii) ≈ 5−7. From the integrated spectra, this ratio is about 3, and Ne(S ii) < Ne(Cl iii) < Ne(Ar iv), i.e., the density estimated is increasing with the ionization potential of the ion. Thus, all these observations are consistent with the presence of a general internal gradient of the density that decreases towards the outskirts of the nebula. The only area with Ne(S ii) > Ne(Ar iv) is the densest central region, what may be understood as the consequence of the hampering of the expansion of the nebula towards the molecular torus.
The [N ii] and [O iii] electron temperature maps (Fig. 6) are almost uniform. Slightly higher (≈10%) temperatures are found near the central star and at the outskirts of the nebula. The values of the [O iii] temperatures are everywhere higher than the [N ii] temperatures, with a mean ratio of Te(O iii)/Te(N ii) = 1.47 ± 0.15. This 50% difference between the two temperature estimates indicates that there is a significant internal variation of temperature despite the uniformity of the temperature distribution obtained from each sensor. The N+ zone is more external than the O++ zone, which would indicate a decrease of temperature outwards.
The temperatures derived from the integrated spectra Te(N ii) = 14 140 K and Te(O iii) = 17 730 K differ by only 25% and are in good agreement with the values found in the literature (see Table 3). The weighted mean value of temperature obtained from the maps are Te(N ii) = 12 304 K (with a dispersion of 1045 K or 8.5%), and Te(O iii) = 17 390 K (with a dispersion of 1158 K or 6.7%). While the mean estimate of Te(O iii) obtained from the temperature map is similar to that computed from the integrated spectra, a 15% higher value of Te(N ii) was obtained from the integrated spectra. This discrepancy may be explained by the dependence of Te(N ii) on the assumed density.
 |
Fig. 7 Spatial profiles of F(Hβ) (in units of 10-14erg cm-2 s-1), of the densities Ne(S ii) and Ne(Ar iv) (in units of 104cm-3), and of the ratio Ne(Ar iv)/Ne(S ii) along the declination line of the central star. |
3.4.1. Magnitude of the electron temperature fluctuations
Peimbert (1967) suggested the presence of
spatial electron temperature fluctuations to explain the fact that the derived Balmer
jump temperatures were significantly lower than the temperatures obtained from forbidden
lines. He introduced two parameters to describe the temperature fluctuation over the
observed volume of a nebula: the average temperature T0 and the
mean-square electron temperature fluctuation t2 defined as 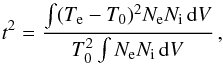 (1)with
(1)with 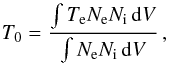 (2)where Ni is the
density of the ion used to measure the temperature. The integrations are computed over
the entire volume V of the nebula.
(2)where Ni is the
density of the ion used to measure the temperature. The integrations are computed over
the entire volume V of the nebula.
Estimates of t2 were obtained assuming that the differences between abundances derived from collisionally excited (CEL) and recombination (RL) lines are due to the presence of these temperature variations. In PNe, these estimatives show high values. As examples, Liu et al. (2006) found t2 ≈ 0.14 for Hf 2-2, and Krabbe & Copetti (2006) found t2 ≈ 0.09 for NGC 3242 and NGC 7009 to obtain consistent O++/H+ estimates derived from RLs and CELs.
A discrete estimation of t2 on the plane of the sky can be
computed from point-to-point measurements of temperature, following the procedure
proposed by Liu (1998). A surface temperature
fluctuation parameter 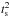 is given by
is given by 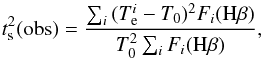 (3)where
(3)where
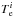 and Fi(Hβ)
are the temperature and Hβ flux at the ith aperture,
respectively. The summation is over all the observed apertures where the temperature is
determined. As part of the temperature variance comes from the measurement errors, a
corrected estimate of
and Fi(Hβ)
are the temperature and Hβ flux at the ith aperture,
respectively. The summation is over all the observed apertures where the temperature is
determined. As part of the temperature variance comes from the measurement errors, a
corrected estimate of 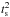 can be obtained by
can be obtained by
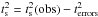 , where
, where
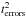 is the quadratic mean of the relative
errors of the temperature estimates.
is the quadratic mean of the relative
errors of the temperature estimates.
We obtained 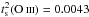 and
and
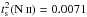 , which are equivalent to the dispersions
of 6.6% and 8.4%, respectively. From long-slit spectra obtained along a single
direction, Krabbe & Copetti (2005) found the
similar values of
, which are equivalent to the dispersions
of 6.6% and 8.4%, respectively. From long-slit spectra obtained along a single
direction, Krabbe & Copetti (2005) found the
similar values of 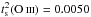 and
and
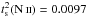 for NGC 6302 and
for NGC 6302 and 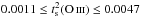 and
and
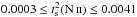 in nine other PNe. Low values of
in nine other PNe. Low values of
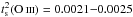 were also found in the H ii
regions NGC 346 and 30 Doradus (Krabbe
& Copetti 2005; Oliveira et al.
2008).
were also found in the H ii
regions NGC 346 and 30 Doradus (Krabbe
& Copetti 2005; Oliveira et al.
2008).
The values of 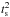 only provide a lower limit for
t2, because the temperature calculated
for each aperture is an average of the temperatures found along the line of sight.
Through numerical simulations, Copetti (2006)
found that typically
only provide a lower limit for
t2, because the temperature calculated
for each aperture is an average of the temperatures found along the line of sight.
Through numerical simulations, Copetti (2006)
found that typically 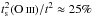 . Thus, we can estimate that
t2 ≈ 0.017 in NGC 6302, a value compatible with the predictions of
the photoionization models. This level of temperature fluctuation is too low to have any
significant impact on the abundance determination from CELs.
. Thus, we can estimate that
t2 ≈ 0.017 in NGC 6302, a value compatible with the predictions of
the photoionization models. This level of temperature fluctuation is too low to have any
significant impact on the abundance determination from CELs.
 |
Fig. 8 Maps of ionic abundances. |
Mean ionic and total abundances and comparison with other works.
 |
Fig. 9 Maps of ionic abundances. |
 |
Fig. 10 Maps of ionic abundances. |
 |
Fig. 11 Maps of ionic abundances. |
3.5. Nebular abundances
We constructed maps of the ionic abundances of N0, N+, O0, O+, O2+, S+, S2+, Ne2+, Ar2+, Ar3+, and Ar4+ from CELs using the IRAF task ionic of the package nebular. We adopted a two-zone scheme: Te(N ii) and Ne(S ii) were used for ions with a low ionization potential (N0, N+, O0, O+, and S+), and Te(O iii) and Ne(Ar iv) for ions with a high ionization potential (S2+, O2+, Ne2+, Ar2+, Ar3+, and Ar4+). The temperature and density obtained for each aperture were used wherever possible. Otherwise, the mean values for the whole nebula were assumed. We also mapped the He+ and He2+ abundances. The He+ abundances were determined from the intensities of the He i λ5876 line, using the effective recombination coefficients for Hβ taken from Storey & Hummer (1995) and for the helium line calculated from the interpolation formula given by Porter et al. (2007). A correction for the collisional contribution to He i λ5876 was carried out based on Porter et al. (2007). The He2+ abundances were obtained from the intensities of He ii λ4686, using the effective recombination coefficients from Storey & Hummer (1995). The Te(O iii) temperatures were adopted in these calculations. The maps of ionic abundances are shown in Figs. 10 and 11. These maps manifest the stratified ionic structure of the nebula. As expected, the abundance maps of ions with similar ionization potential are very similar to each other (e.g., N+ and O0, He2+ and Ar4+) and the high ionization potential ions are concentrated around the central star.
We calculated the total abundances using the ionization correction factors ICFs to compensate for the undetected ionic stages for a given element from Kwitter & Henry (2001) (for Cl) and Kingsburgh & Barlow (1994) (for the other elements). For Ne and K, we assume that Ne/H = 1.35 × (Ne+/H++ Ne2+/H+) (or Ne/H = 2.87 × Ne+/H+ when Ne2+/H+ is lacking) and K/H = 10.8 × (K3+/H+ + K4+/H+) based on the ionic fractions for Ne+, Ne2+, and Ne3+ obtained for NGC 6302 by Tsamis et al. (2003) and the model for this object by Wright et al. (2011). We also obtained the ionic and the total abundances from the integrated spectra. Table 4 presents some statistics of the ionic abundance maps, including the minimum (“min”) and maximum (“max”) values, the mean and the standard deviation (σ) weighted by the Hβ flux, the total abundances from the maps, the ionic and total abundances obtained from the integrated spectra, and a comparison with previous abundance determinations found in the literature. The PN NGC 6302 is an extreme case of nitrogen enrichment and the oxygen seems to be depleted by a factor of 2–3 compared to the solar value. The discrepancies between our mean ionic and total abundances and the results reported by other authors can be largely explained by the fact that we considered a much larger portion of the nebula in our analysis.
 |
Fig. 12 Maps of the ionic abundances (He+ + He2+)/H+ and N+/O+. |
The total abundances of He, N, O, and Ar obtained from the integrated spectra are similar to those derived from the ionic abundance maps within less than 10% (see the columns labeled “integrated” and “mean” columns in Table 4) despite the different approaches for defining the electron temperature. To calculate the integrated abundances, we adopted a two-zone temperature scheme, while the mean ionic abundances are the average of the values obtained point-to-point. Interestingly, these abundances are also similar to the maximum values of the dominant ionic species of each of these elements. For instance, the maximum ionic abundances O+/H+ = 1.36 × 10-4 and O2+/H+ = 1.67 × 10-4 are similar to the mean and the integrated total oxygen abundances of O/H = 1.66 × 10-4 and O/H = 1.44 × 10-4, respectively. This demonstrates the potential of the spatially resolved abundance studies for establishing lower limits of the total abundances based on ionic abundances, for checking the ionization correlation factors, and, in some cases, for determining the total abundances directly from the ionic abundances.
For sulfur, the abundances of the two dominant ions, S+ and S2+, are similar to each other,
but are 50% higher than the total abundance, indicating that the ionization correction
factor used, 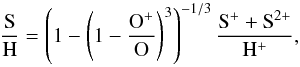 (4)was not entirely appropriate for this nebula.
For neon, using the usual ICF (Kingsburgh & Barlow
1994),
(4)was not entirely appropriate for this nebula.
For neon, using the usual ICF (Kingsburgh & Barlow
1994), 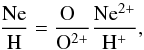 (5)the total abundance would be significantly
(~65%) lower than maximum Ne2+. Therefore, we used instead
the fractional ionic abundances of Ne+, Ne2+, and Ne3+ obtained for NGC 6302 by Tsamis et al. (2003).
(5)the total abundance would be significantly
(~65%) lower than maximum Ne2+. Therefore, we used instead
the fractional ionic abundances of Ne+, Ne2+, and Ne3+ obtained for NGC 6302 by Tsamis et al. (2003).
3.6. Apparent overabundances
We might question whether or not spatial variation of the total abundance of any element can be detected. This is difficult because the observed spectra correspond to the light integrated along the line of sight. For this task, the helium abundance can be considered a good candidate, because the He abundance determination is less sensitive to the electron density and temperature, and the emission lines are strong. The total helium abundance map was obtained by summing the He+/H+ and He2+/H+ abundance maps and is shown in Fig. 12. As expected, areas near the edges of the nebula tend to show lower values of this abundance ratio, because these are the regions where the contribution of neutral He may be significant. Excluding these areas, the dispersion of (He+ + He2+)/H+ is only 8%. The individual maps of He+/H+ and He2+/H+ show much higher variations, which were mostly canceled out by summing the two maps. The remaining systematic variation of (He+ + He2+)/H+ is probably a meaningless residual of this sum.
The ratio of ionic abundances N+/O+, also shown in Fig. 12, is often taken as an estimate of the total abundance N/O. In the south of the nebula, there is an extended area where values 30% to 60% higher than the mean are observed. Gonçalves et al. (2003) obtained homogeneous elemental abundances along NGC 7009. However, they found some outer structures with an apparent overabundance of N (by a factor of ≲2). They attributed this difference to possible errors in the ICFs. Alexander & Balick (1997) showed that, in spatially resolved analysis, the errors due to the ICFs can be high, mainly for N, Ne, and Ar, and can lead to overestimated N/O variations in bipolar nebulae. To investigate this, Gonçalves et al. (2006) used three-dimensional photoionization models, whose constraints were the observational data of Gonçalves et al. (2003). They predicted ratios of (N+/N)/(O+/O) significantly lower than unity (up to 40%). Thus, the usual assumption that N+/N = O+/O may not be appropriate for all parts of the nebula. A similar problem with the ICFs could be the cause of the apparent overabundances found in some regions of NGC 6302.
3.7. Comparison with the 3D model of Wright et al. (2011)
Wright et al. (2011) presented a 3D photoionization model of NGC 6302 based on data compiled from the literature. The final best-fitting model was achieved with a characteristic density for the circumstellar disk of 80 000 cm-3. This was the most influential parameter of the model. The lobes were modeled with a constant density of 2000 cm-3, and an uncertainty of ±50% was estimated for this value. To improve the fitting of some line ratios sensitive to the electron density and temperature, they assumed the presence in the inner parts of the lobes of a ~12″ area with a high density of 20 000 cm-3 and other inhomogeneous densities, which were simulated using 5–50 knots distributed randomly across the nebula with overdensities up to a factor of 3. Although based on limited spatially resolved information, the model density structure reproduces remarkably well the main characteristics of the electron density maps of Ne(S ii) and Ne(Ar iv) (Fig. 2).
With regard to the thermal structure of the nebula, the model predicts a monotonic radial decrease in electron temperature away from the center. The temperature estimates from integrated line ratios of different ions shown in Table 3 indicate that the temperature tends to increase with ionization potential of the ions, in agreement with the temperature gradient predicted by the model. The maps of Te(O iii) and Te(N ii) (Fig. 6) show higher temperatures near the central star, as predicted by the model, but also at the outskirts of the nebula. Moreover, Wright et al. (2011) found average temperatures of 12 000 K over the entire nebula, 19 400 K in the lobes, and 3800 K in the circumstellar disk. The mean electron temperatures weighted by the N+ and O2+ ions were, respectively, 4800 K and 10 900 K for the circumstellar disk, and 8480 K and 10 360 K for the bipolar lobes. These values are much lower than those found in our temperature maps and also lower than the temperatures estimated via the integrated spectra. Consequently, some ionic abundance ratios derived from the model differ greatly from our results (Table 4), especially those of low ionization ions. For instance, Wright et al. (2011) obtained a ratio O+/H+ about 8 times higher than our mean value, while the estimates for O2+/H+ differ by less than 10%. For the total abundances used by Wright et al. (2011) as model parameters, the highest discrepancies are verified for Ar/H, Ne/H, and O/H, which are higher than our values by factors of about 10, 6, and 3, respectively.
4. Conclusions
Through spatially resolved long-slit spectroscopy, we studied the physical and chemical conditions of the PN NGC 6302. Data from 11 parallel and equally spaced directions were obtained, allowing the construction of maps of line fluxes, line ratios, electron density and temperature, and ionic abundances with a spatial resolution of 1.45″ × 1″ over an area of 11″ × 250″. Integrated spectra were also obtained and 142 lines were identified. The main results are the following.
-
1.
The c(Hβ) extinction map shows a dust lane crossing the nebula along the north-south direction associated with the molecular disk or torus that gives NGC 6302 its bipolar morphology. The extinction is fairly homogeneous in the lobes (c(Hβ) = 0.78 ± 0.10), but it is much higher in the direction of the circumstellar torus (c(Hβ) = 1.23 ± 0.18). The area of higher extinction is near, but displaced to the west, of the central star position. This is consistent with the fact that the torus is not seen exactly edge-on, but with a small inclination angle.
-
2.
The [S ii] and [Ar iv] electron density maps indicate the presence of a steep internal gradient with the density decreasing towards the outskirts of the nebula. The density peaks above 40 000 cm-3 at the central area and drops below 100 cm-3 at the edges of the nebula.
-
3.
The [N ii] and [O iii] electron temperature maps are almost uniform. Slightly higher (≈10%) temperatures are found near the central star and at the outskirts of the nebula. The [O iii] temperature is everywhere higher than the [N ii] temperature, with a mean ratio of Te(O iii)/Te(N ii) = 1.47 ± 0.15, indicating that there is a significant internal variation of temperature despite the uniformity of the temperature distribution obtained from each sensor. Among the five different temperature estimates obtained from the integrated spectra, we observed a correlation between the temperature estimate and the ionization potential of the ion, which indicates the presence of an internal radial decrease in electron temperature.
-
4.
From the distributions of the [N ii] and [O iii] electron temperatures on the plane of the sky, we obtained the surface temperature fluctuation parameters
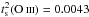 and
and
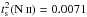 , which are equivalent to dispersions
of 6.6% and 8.4%, respectively. Based on numerical simulations, we estimate a 3D
temperature fluctuation parameter of t2 ≈ 0.017 in NGC 6302, a value compatible with the predictions of
the photoionization models and too small to have any significant impact on the
abundance determination from collisionally excited lines.
, which are equivalent to dispersions
of 6.6% and 8.4%, respectively. Based on numerical simulations, we estimate a 3D
temperature fluctuation parameter of t2 ≈ 0.017 in NGC 6302, a value compatible with the predictions of
the photoionization models and too small to have any significant impact on the
abundance determination from collisionally excited lines. -
5.
We constructed maps of the ionic abundances of He+, He2+, N0, N+, O0, O+, O2+, S+, S2+, Ne2+, Ar2+, Ar3+, and Ar4+ and derived the total abundances. We also obtained the ionic and the total abundances from the integrated spectra. For many elements, the total abundances obtained from the integrated spectra are similar to those derived from the ionic abundance maps and are also similar to the maximum abundances of the dominant ionic species of each of these elements. This demonstrates the potential of the spatially resolved abundance studies for establishing lower limits of the total abundances based on ionic abundances, for checking the ionization correlation factors, and, in some cases, for determining the total abundances directly from the ionic abundances.
Online material
Appendix A
Observed F(λ) and dereddened I(λ) line intensities (on a scale F(Hβ) = 100) and the reddening function f(λ).
Acknowledgments
This work was supported by the Brazilian agencies CAPES and CNPq. A. C. Krabbe thanks for the support of FAPESP, process 2010/01490-3.
References
- Alexander, J., & Balick, B. 1997, ApJ, 114, 713 [Google Scholar]
- Aller, L. H., Ross, J. E., Omara, B. J., & Keyes, C. D. 1981, MNRAS, 197, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Ashley, M. C. B., & Hyland, A. R. 1988, ApJ, 331, 532 [Google Scholar]
- Benjamin, R. A., Skillman, E. D., & Smits, D. P. 1999, ApJ, 514, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Bohigas, J. 1994, A&A, 288, 617 [NASA ADS] [Google Scholar]
- Casassus, S., Roche, P. F., & Barlow, M. J. 2000, MNRAS, 314, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Copetti, M. V. F. 1990, PASP, 102, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Copetti, M. V. F. 2006, A&A, 453, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dinh-V-Trung, Bujarrabal, V., Castro-Carrizo, A., Lim, J., & Kwok, S. 2008, ApJ, 673, 934 [NASA ADS] [CrossRef] [Google Scholar]
- Feibelman, W. A. 2001, ApJ, 550, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Gonçalves, D. R., Corradi, R. L. M., Mampaso, A., & Perinotto, M. 2003, ApJ, 597, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Gonçalves, D. R., Ercolano, B., Carnero, A., Mampaso, A., & Corradi, R. L. M. 2006, MNRAS, 365, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B., Dopita, M. A., Williams, R. E., & Hua, C. 2002, PASA, 19, 425 [Google Scholar]
- Kingdon, J., & Ferland, G. J. 1995, AJ, 442, 714 [Google Scholar]
- Kingsburgh, R. L., & Barlow, M. J. 1994, MNRAS, 271, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Krabbe, A. C., & Copetti, M. V. F. 2005, A&A, 443, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krabbe, A. C., & Copetti, M. V. F. 2006, A&A, 450, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kwitter, K. B., & Henry, R. B. C. 2001, ApJ, 562, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X.-W. 1998, MNRAS, 295, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X.-W., Storey, P. J., Barlow, M. J., et al. 2000, MNRAS, 312, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X.-W., Barlow, M. J., Zhang, Y., Bastin, R. J., & Storey, P. J. 2006, MNRAS, 368, 1959 [NASA ADS] [CrossRef] [Google Scholar]
- Leal-Ferreira, M. L., Gonçalves, D. R., Monteiro, H., & Richards, J. W. 2011, MNRAS, 411, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- Lame, N. J., & Ferland, G. J. 1991, ApJ, 367, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuura, M., Zijlstra, A. A., Molster, F. J., et al. 2005, MNRAS, 359, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Meaburn, J., López, J. A., Steffen, W., Graham, M. F., & Holloway, A. J. 2005, AJ, 130, 2303 [NASA ADS] [CrossRef] [Google Scholar]
- Monteiro, H., Schwarz, H. E., Gruenwald, R., & Heathcote, S. 2004, AJ, 609, 194 [Google Scholar]
- Oliveira, V. A., Copetti, M. V. F., & Krabbe, A. C. 2008, A&A, 492, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peimbert, M. 1967, ApJ, 150, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., & Torres-Peimbert, S. 1983, in Type I Planetary Nebulae, ed., D. R. Flower, IAU Symp., 103, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Péquignot, D., Morisset, C., & Casassus, S. 2012, IAU Symp., 283, 470 [NASA ADS] [Google Scholar]
- Peretto, N., Fuller, G., Zijlstra, A., Patel, N. 2007, A&A, 473, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottasch, S. R., & Beintema, D. A. 1999, A&A, 347, 975 [NASA ADS] [Google Scholar]
- Rodriguez, L. F., Garcia-Barreto, J. A., Canto, J., et al. 1985, MNRAS, 215, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbadin, F., Minello, S., & Bianchini, A. 1977, A&A, 60, 147 [NASA ADS] [Google Scholar]
- Savage, B. D., & Mathis, J. S. 1979, ARA&A, 17, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, R. A., & Dufour, R. J. 1995, PASP, 107, 896 [NASA ADS] [CrossRef] [Google Scholar]
- Storey, P. J., & Hummer, D. G. 1995, MNRAS, 272, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Szyszka, C., Zijlstra, A. A., & Walsh, J. R. 2011, MNRAS, 416, 715 [NASA ADS] [Google Scholar]
- Szyszka, C., Walsh, J. R., Zijlstra, A. A., & Tsamis, Y. G. 2009, AJ, 707, 32 [Google Scholar]
- Oliva, E., Pasquali, A., Reconditi, M. 1996, A&A, 305, 21 [Google Scholar]
- Phillips, J. P., Cuesta, L. C., & Ramos-Larios, G. 2010, MNRAS, 409, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, R. L., Ferland, G. J., MacAdam, K. B. 2007, AJ, 657, 327 [Google Scholar]
- Tsamis, Y. G., Barlow, M. J., Liu, X.-W, Danziger, I. J., & Storey, P. J. 2003, MNRAS, 345, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Tsamis, Y. G., Walsh, J. R., Péquignot, D., Barlow, M. J., & Danziger, I. J. 2008, MNRAS, 386, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., Barlow, M. J., Ercolano, B., & Rauch, T. 2011, MNRAS, 418, 370 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Physical conditions from the integrated spectra, the mean from the temperature maps (weighted by the Hβ flux) and a comparison with previous works.
Observed F(λ) and dereddened I(λ) line intensities (on a scale F(Hβ) = 100) and the reddening function f(λ).
All Figures
 |
Fig. 1 Positions of the slit on an R-band image of NGC 6302 from the ESO survey, obtained with the ALADIN software made available by the Centre de Données astronomiques de Strasbourg. The slit positions are represented by the red and blue lines. The red line indicates the offset 0′′. |
| In the text | |
 |
Fig. 2 Logarithmic maps of the observed fluxes (in units of erg cm-2 s-1) in [O ii] λ3727, [Ne iii] λ3869, He ii λ4686, [Ar iv] λ4740, Hβ, [O iii] λ5007, He i λ5876, Hα, [N ii] λ6584, and [S ii] λ6717. In all maps, north is up and east to the left and the coordinates are offset with respect to the position of the central star. |
| In the text | |
 |
Fig. 3 Map of the logarithmic extinction coefficient c(Hβ). |
| In the text | |
 |
Fig. 4 [N ii] /Hα, [S ii] /Hα, [O ii] /Hβ, and [O iii] /Hβ maps. |
| In the text | |
 |
Fig. 5 Hα/[S ii] vs. Hα/[N ii] for NGC 6302 (this paper) and supernova remnants (data from the literature). |
| In the text | |
 |
Fig. 6 Maps of the densities Ne(S ii) and Ne(Ar iv) (in units of cm-3) and temperatures Te(N ii) and Te(O iii) (in units of K). |
| In the text | |
 |
Fig. 7 Spatial profiles of F(Hβ) (in units of 10-14erg cm-2 s-1), of the densities Ne(S ii) and Ne(Ar iv) (in units of 104cm-3), and of the ratio Ne(Ar iv)/Ne(S ii) along the declination line of the central star. |
| In the text | |
 |
Fig. 8 Maps of ionic abundances. |
| In the text | |
 |
Fig. 9 Maps of ionic abundances. |
| In the text | |
 |
Fig. 10 Maps of ionic abundances. |
| In the text | |
 |
Fig. 11 Maps of ionic abundances. |
| In the text | |
 |
Fig. 12 Maps of the ionic abundances (He+ + He2+)/H+ and N+/O+. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


