| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201323204 | |
| Published online | 25 March 2014 | |
Transiting planets from WASP-South, Euler, and TRAPPIST
WASP-68 b, WASP-73 b, and WASP-88 b, three hot Jupiters transiting evolved solar-type stars⋆,⋆⋆
1
Institut d’Astrophysique et Géophysique, Université de Liège,
allée du 6 Août 17,
4000
Liège,
Belgium
e-mail:
ldelrez@ulg.ac.be
2
Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK
3
SUPA, School of Physics and Astronomy, University of St. Andrews, North Haugh,
Fife, KY16 9SS, UK
4
Observatoire de Genève, Université de Genève,
51 Chemin des
Maillettes, 1290
Sauverny,
Switzerland
5
Department of Physics, University of Warwick,
Coventry
CV4 7AL,
UK
6
Cavendish Laboratory, Department of Physics, University of
Cambridge, JJ Thomson
Avenue, Cambridge,
CB3 0HE,
UK
7
N. Copernicus Astronomical Centre, Polish Academy of Sciences,
Bartycka 18,
00-716
Warsaw,
Poland
8
Department of Physics and Kavli Institute for Astrophysics
& Space Research, Massachusetts Institute of Technology,
Cambridge
MA
02139,
USA
Received:
6
December
2013
Accepted:
18
January
2014
Using the WASP transit survey, we report the discovery of three new hot Jupiters, WASP-68 b, WASP-73 b and WASP-88 b. The planet WASP-68 bhas a mass of 0.95 ± 0.03 MJup, a radius of 1.24-0.06+0.10 RJup, and orbits a V = 10.7 G0-type star (1.24 ± 0.03 M⊙ 1.69-0.06+0.11 R⊙, Teff = 5911 ± 60 K) with a period of 5.084298 ± 0.000015 days. Its size is typical of hot Jupiters with similar masses. The planet WASP-73 bis significantly more massive (1.88-0.06+0.07 MJup) and slightly larger (1.16-0.08+0.12 RJup) than Jupiter. It orbits a V = 10.5 F9-type star (1.34-0.04+0.05 M⊙, 2.07-0.08+0.19 R⊙, Teff = 6036 ± 120 K) every 4.08722 ± 0.00022 days. Despite its high irradiation (~2.3 × 109 erg s-1 cm-2), WASP-73 b has a high mean density (1.20-0.30+0.26 ρJup) that suggests an enrichment of the planet in heavy elements. The planet WASP-88 bis a 0.56 ± 0.08 MJuphot Jupiter orbiting a V = 11.4 F6-type star (1.45 ± 0.05 M⊙, 2.08-0.06+0.12 R⊙, Teff = 6431 ± 130 K) with a period of 4.954000 ± 0.000019 days. With a radius of 1.70-0.07+0.13 RJup, it joins the handful of planets with super-inflated radii. The ranges of ages we determine through stellar evolution modeling are 4.5–7.0 Gyr for WASP-68, 2.8-5.7 Gyr for WASP-73 and 1.8–4.3 Gyr for WASP-88. The star WASP-73 appears to be significantly evolved, close to or already in the subgiant phase. The stars WASP-68 and WASP-88 are less evolved, although in an advanced stage of core H-burning.
Key words: planetary systems / techniques: photometric / techniques: radial velocities / techniques: spectroscopic
Tables 1–3 are available in electronic form at http://www.aanda.org
The photometric time-series used in this work are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/563/A143
© ESO, 2014
1. Introduction
Since the discovery of the first extrasolar planet around a solar-type star by Mayor & Queloz (1995), more than 1000 planets have been detected outside our solar system1. Among this large harvest, the sub-sample of planets that transit the disc of their host star is extremely valuable. Indeed, transiting exoplanets allow parameters such as mass, radius, and density to be accurately determined (e.g. Charbonneau et al. 2000), and their atmospheric properties to be studied during their transits and occultations (e.g. Seager & Deming 2010). At the time of writing, over 400 transiting planets have been discovered1; a significant fraction of them are Jovian-type planets orbiting within 0.1 AU of their host star. Most of these so-called “hot Jupiters” were detected by ground-based transit surveys, among which the Wide Angle Search for Planets (WASP) survey (Pollacco et al. 2006) has been the most successful with now more than 100 planets discovered (Hellier et al. 2013). Ongoing WASP discoveries are important for the field of exoplanetology, as these systems tend to be particularly prone to thorough characterizations, owing to their bright host stars (9 < V < 13), short orbits, and favorable planet-to-star area ratios. Therefore, they will be prime targets for thorough characterizations with future facilities, such as CHaracterising ExOPlanets Satellite (CHEOPS, Broeg et al. 2013) and James Webb Space Telescope (JWST, Gardner et al. 2006).
In this paper, we report the discovery of three additional transiting planets by the WASP survey. The planet WASP-68 b is a 0.95 MJuphot Jupiter in a 5 days orbit around a G0-type star; WASP-73 b is a dense 1.88 MJup planet that orbits an F9-type star every 4.1 days, while WASP-88 bis a super-bloated 0.56 MJupplanet in a 4.9 daysorbit around an F6-type star. All three host stars appear to be significantly evolved. Consequently, they have relatively large radii (R⋆ = 1.7−2.1 R⊙), translating into long (5–6 h)and low-amplitude transits for the three planets: ~0.6% for WASP-68 b, ~0.3% for WASP-73 b (the shallowest transits yet for a WASP planet), and ~0.7% for WASP-88 b. Their detection demonstrates, therefore, the excellent photometric potential of the WASP survey.
Section 2 presents the WASP discovery photometry, as well as the follow-up photometric and spectroscopic observations that we used to confirm and characterize the three systems. In Sect. 3, we describe the spectroscopic determination of the stellar atmospheric properties and the derivation of the systems’ parameters through combined analyses of our photometric and spectroscopic data. Finally, we discuss and summarize our results in Sect. 4.
2. Observations
2.1. WASP transit detection photometry
The WASP transit survey is operated from two sites with one for each hemisphere: the Observatorio del Roque de los Muchachos in the Canary Islands in the North and the Sutherland Station of the South African Astronomical Observatory (SAAO) in the South. Each facility consists of eight Canon 200 mm f/1.8 focal lenses coupled to e2v 2048 × 2048 pixels CCDs, which yields a field of view of 450 deg2 for each site with a corresponding pixel scale of 13.7′′/pixel. Further details of the instruments, survey, and data reduction procedures can be found in Pollacco et al. (2006), while details of the candidate selection process can be found in Collier Cameron et al. (2006, 2007). The three targets presented here, WASP-68 (1SWASPJ202022.98-191852.9 = 2MASS20202298-1918528, V = 10.7, K = 8.9), WASP-73 (1SWASPJ211947.91-580856.0 = 2MASS21194790-5808559, V = 10.5, K = 9.0), and WASP-88 (1SWASPJ203802.70-482743.2 = 2MASS20380268-4827434, V = 11.4, K = 10.3), were observed exclusively from the southern WASP site. In total, 20 804 data points were obtained for WASP-68 between May 2006 and October 2011, 50 588 measurements were gathered for WASP-73 between June 2008 and November 2011, while 39 906 data points were obtained for WASP-88 between June 2008 and October 2011. For each target, the WASP data were processed and searched for transit signals, as described in Collier Cameron et al. (2006), leading to the detection of periodic dimmings in the light curves of WASP-68, –73 and –88 with periods of 5.084 d, 4.087 d and 4.954 d, respectively. For the three objects, Fig. 1 presents the WASP photometry folded on the deduced transit ephemeris.
The method described in Maxted et al. (2011) was used to search for rotational modulation in the photometry of each object. The analysis was performed over the frequency interval 0–1.5 cycles/dayat 8192 evenly spaced frequencies. No periodic signal was found above the mmag amplitude.
 |
Fig. 1 WASP photometry for WASP-68 (top), WASP-73 (middle), and WASP-88 (bottom) folded on the best-fitting transit ephemeris from the transit search algorithm presented in Collier Cameron et al. (2006), and binned per 0.01 d intervals. |
2.2. Spectroscopy and radial velocities
Spectroscopic measurements of each star were obtained using the CORALIE spectrograph mounted on the 1.2 m Euler-Swiss telescope at the La Silla site (Chile). A total of 43 spectra were gathered for WASP-68 between May 2011 and August 2013; 20 spectra were obtained for WASP-73 from October 2011 to September 2013, while 23 spectra were gathered for WASP-88 between September 2011 and October 2013. For all spectroscopic observations, radial velocities (RVs) were computed using the weighted cross-correlation technique described in Pepe et al. (2002). These RVs are presented in Tables 1–3. For each star, RV variations were detected with periods similar to those found in the WASP photometry and with semi-amplitudes consistent with planetary-mass companions (see Figs. 2, 4, and 6, upper panels).
 |
Fig. 2 Top: CORALIE RVs for WASP-68 phase-folded on the best-fit orbital period with the best-fit Keplerian model over-imposed in red. Bottom: correlation diagram CCF bisector span vs. RV. |
 |
Fig. 3 Top: individual follow-up transit light curves for WASP-68 b. Bottom: combined follow-up photometry for WASP-68 b. The observations are shown as red points (bin width =2min) and are period-folded on the best-fit transit ephemeris. Each light curve has been divided by the respective photometric baseline model (see Sect. 3.2). For each filter, the superimposed, solid black line is our best-fit transit model. The light curves are shifted along the y-axis for clarity. |
 |
Fig. 4 Top: CORALIE RVs for WASP-73 phase-folded on the best-fit orbital period with the best-fit Keplerian model over-imposed in red. Bottom: correlation diagram CCF bisector span vs. RV. |
 |
Fig. 5 Top: individual follow-up transit light curves for WASP-73 b. Bottom: combined follow-up photometry for WASP-73 b. The observations are shown as red points (bin width =2 min) and are period-folded on the best-fit transit ephemeris. Each light curve has been divided by the respective photometric baseline model (see Sect. 3.2). For each filter, the superimposed, solid black line is our best-fit transit model. The light curves are shifted along the y-axis for clarity. |
To discard any false-positive scenarios that could create RV variations that mimic planetary signatures, we checked the CORALIE cross-correlation functions (CCF) bisector spans, according to the technique described by Queloz et al. (2001). Indeed, false positives, such as blended eclipsing binaries or starspots, would also induce spectral-line distortions, resulting in correlated variations of RVs and bisector spans. This effect was, for example, observed for the HD 41004 system (Santos et al. 2002), which consists of a K-dwarf blended with an M-dwarf companion (separation of ~0.5′′) that is orbited itself by a short-period brown dwarf. For this extreme system, the RVs showed a clear signal at the period of the brown dwarf orbit (1.3 d) and with an amplitude ~50 m s-1 that could have been interpreted as the signal of a sub-Saturn mass planet orbiting the K-dwarf. However, the 0.67 ± 0.03 slope of the RV-bisector relation clearly revealed that the observed signal did not originate from the K-dwarf and shed light on the blended nature of the system.
For our three systems, the bisector spans revealed to be stable; their standard deviation are close to their average error (15 vs. 12 m s-1 for WASP-68, 27 vs. 18 m s-1 for WASP-73 and 48 vs. 45 m s-1 for WASP-88). No correlation between the RVs and the bisector spans was found (see Figs. 2, 4, and 6, lower panels); the slopes deduced from linear regressions were −0.01 ± 0.03 (WASP-68), 0.04 ± 0.05 (WASP-73), and 0.10 ± 0.21 (WASP-88). These values and errors support our conclusion that the periodic dimming and RV variation of each system are caused by a transiting planet. This conclusion is also strengthened by the consistency of the solutions derived from the global analysis of our spectroscopic and photometric data (see Sect. 3.2).
2.3. Follow-up photometry
To refine the systems’ parameters, high-quality transit observations were obtained using the 0.6 m TRAPPIST robotic telescope (TRAnsiting Planets and PlanetesImals Small Telescope) and the EulerCam CCD camera that is mounted on the 1.2 m Euler-Swiss telescope, which are both located at ESO La Silla Observatory. These follow-up light curves are summarized in Table 4 and presented in Figs. 3, 5, and 7.
2.3.1. TRAPPIST observations
TRAPPIST is a 60 cm robotic telescope dedicated to the detection and characterization of transiting exoplanets and to the photometric monitoring of bright comets and other small bodies. It is equipped with a thermoelectrically-cooled 2K × 2K CCD, which has a pixel scale of 0.65′′ that translates into a 22′ × 22′ field of view. For details of TRAPPIST, see Gillon et al. (2011b) and Jehin et al. (2011). The TRAPPIST photometry was obtained using a readout mode of 2 × 2 MHz with 1 × 1 binning, which results in a readout + overhead time of 6.1 s and a readout noise of 13.5 e−. A slight defocus was applied to the telescope to improve the duty cycle, spread the light over more pixels, and, thereby, improve the sampling of the PSF. Three transits of WASP-68 b and two transits of WASP-88 b were observed through a special “I + z” filter that has a transmittance >90% from 750 nm to beyond 1100 nm2. For WASP-73b, two transits were observed in a Sloan z′ filter (λeff = 915.9 ± 0.5 nm). During the runs, the positions of the stars on the chip were maintained to within a few pixels thanks to a “software guiding” system that regularly derives an astrometric solution for the most recently acquired image and sends pointing corrections to the mount if needed. After a standard pre-reduction (bias, dark, and flatfield correction), the stellar fluxes were extracted from the images using the IRAF/DAOPHOT3 aperture photometry software (Stetson 1987). For each light curve, we tested several sets of reduction parameters and kept the one giving the most precise photometry for the stars of similar brightness as the target. After a careful selection of reference stars, the transit light curves were finally obtained using differential photometry.
2.3.2. EulerCam observations
EulerCam is an E2V 4K × 4K back-illuminated, deep-depletion CCD detector installed at the Cassegrain focus of the 1.2 m Euler-Swiss telescope. The field of view of EulerCam is 15.7′ × 15.7′, producing a pixel scale of 0.23′′. To keep the stars on the same locations on the detector during the observations, EulerCam employs an “Absolute Tracking” system that is very similar to the one of TRAPPIST, which matches the point sources in each image with a catalog, and if needed, adjusts the telescope pointing between exposures to compensate for drifts. Two transits of WASP-73 b and three transits of WASP-88 b were observed with EulerCam through Gunn-r′ filter (λeff = 620.4 ± 0.5 nm), while two transits of WASP-68 b were observed in an Ic filter (λeff = 806 ± 0.5 nm). A slight defocus was applied to the telescope to optimize the observation efficiency and to minimize pixel-to-pixel effects. The reduction procedure used to extract the transit light curves was similar to that performed on TRAPPIST data. Further details of the EulerCam instrument and data reduction procedures can be found in Lendl et al. (2012).
3. Analysis
3.1. Spectroscopic analysis: Stellar atmospheric properties
For each star, the individual CORALIE spectra were co-added to produce a single spectrum with a typical S/N of around 100:1. The stellar atmospheric parameters were then derived using the methods given in Doyle et al. (2013). These parameters are listed in Tables 6–8 for WASP-68, WASP-73, and WASP-88, respectively. The excitation balance of the Fe i lines was used to determine the effective temperature Teff. The surface gravity log g⋆ was determined from the ionisation balance of Fe i and Fe ii. The Ca i line at 6439 Å and the Na i D lines were also used as log g⋆ diagnostics. The elemental abundances were determined from equivalent width measurements of several unblended lines. Iron abundances are relative to the solar values obtained by Asplund et al. (2009). Values for microturbulence (ξt) were determined from Fe i using the method of Magain (1984). The quoted error estimates include that given by the uncertainties in Teff and log g⋆, as well as the scatter due to measurement and atomic data uncertainties. The projected stellar rotation velocity v sin i⋆ was determined by fitting the profiles of several unblended Fe i lines. An instrumental FWHM of 0.11 ± 0.01 Å was determined for the three stars from the telluric lines around 6300 Å. Macroturbulence (vmac) values were obtained from the calibration of Bruntt et al. (2010). Spectral types were estimated from Teff using the table in Gray (2008). Finally, we also used the Torres et al. (2010) calibration to obtain first stellar mass estimates: 1.24 ± 0.10 M⊙ for WASP-68, 1.40 ± 0.12 M⊙ for WASP-73, and 1.38 ± 0.12 M⊙ for WASP-88.
Summary of follow-up photometry obtained for WASP-68, WASP-73, and WASP-88.
 |
Fig. 6 Top: CORALIE RVs for WASP-88 phase-folded on the best-fit orbital period with the best-fit Keplerian model over-imposed in red. Bottom: correlation diagram CCF bisector span vs. RV. |
 |
Fig. 7 Top: individual follow-up transit light curves for WASP-88 b. Bottom: combined follow-up photometry for WASP-88 b. The observations are shown as red points (bin width =2min) and are period-folded on the best-fit transit ephemeris. Each light curve has been divided by the respective photometric baseline model (see Sect. 3.2). For each filter, the superimposed, solid black line is our best-fit transit model. The light curves are shifted along the y-axis for clarity. |
3.2. Global analysis
To determine the parameters of each system, we performed a combined analysis of the follow-up photometry and the RV data, using for this purpose the adaptive Markov chain Monte-Carlo (MCMC) code described in Gillon et al. (2012) and references therein. The algorithm simultaneously models the data, using for the photometry, the transit model by Mandel & Agol (2002) multiplied by a different baseline model for each light curve, and a classical Keplerian model for the RVs (e.g. Murray & Correia 2010).
The photometric baseline models aim to represent astrophysical, instrumental, or environmental effects, which are able to produce photometric variations and can, therefore, affect the transit light curves. They are made up of different first to fourth-order polynomials with respect to time or other variables, such as airmass, PSF full-width at half maximum, background, or stellar position on the detector. To find the optimal baseline function for each light curve, i.e. the model minimizing the number of parameters and the level of noise in the best-fit residuals, the Bayes factor, as estimated from the Bayesian Information Criterion (Schwarz 1978), was used. The best photometric model functions are listed in Table 4. For six TRAPPIST light curves (see Table 4), a normalization offset was also part of the baseline model to represent the effect of the meridian flip; that is, the 180° rotation that the German equatorial mount telescope has to undergo when the meridian is reached. This movement results in different positions of the stellar images on the detector before and after the flip, and the normalization offset allows to take into account a possible consecutive jump in the differential photometry at the time of the flip.
Concerning the RVs, a model with a trend was tested for each system. Such a trend would be indicative of the presence of an additional massive body in the system. A model with a slope was slightly favored in the case of WASP-68 with a Bayes factor ~90. We thus adopted this model for this system but the Bayes factor value is not high enough to be decisive (Jeffreys 1961) and more RVs are needed to confirm this possible trend.
The basic jump parameters in our MCMC analyses, i.e. the parameters that are randomly
perturbed at each step of the MCMC, were: the planet/star area ratio (Rp/R⋆)2;
the transit impact parameter in the case of a circular orbit b′ = acosip/R⋆
where a is
the orbital semi-major axis and ip is the orbital inclination; the
transit width (from 1st to 4th contact) W; the time of mid-transit T0; the orbital
period P; the
parameter 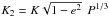 where
K is the RV
orbital semi-amplitude and e is the orbital eccentricity; and the two parameters
where
K is the RV
orbital semi-amplitude and e is the orbital eccentricity; and the two parameters
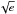 cos ωand
cos ωand
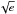 sin ω, where
ω is the
argument of the periastron. The reasons to use
sin ω, where
ω is the
argument of the periastron. The reasons to use 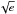 cos ωand
cos ωand
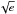 sin ωas jump
parameters instead of the more traditional e cos ωand e sin ωare detailed in Triaud et al. (2011). For all these jump parameters, we assumed a uniform prior
distribution. The photometric baseline model parameters were not actual jump parameters;
they were determined by a least-square minimization at each step of the MCMC.
sin ωas jump
parameters instead of the more traditional e cos ωand e sin ωare detailed in Triaud et al. (2011). For all these jump parameters, we assumed a uniform prior
distribution. The photometric baseline model parameters were not actual jump parameters;
they were determined by a least-square minimization at each step of the MCMC.
The effect of stellar limb-darkening on our transit light curves was accounted for using a quadratic limb-darkening law, where the quadratic coefficients u1 and u2 were allowed to float in our MCMC analysis. However, we did not use these coefficients themselves as jump parameters but their combinations, c1 = 2 × u1 + u2 and c2 = u1 − 2 × u2, to minimize the correlation of the obtained uncertainties as introduced by Holman et al. (2006). To obtain a limb-darkening solution consistent with theory, we used normal prior distributions for u1 and u2 based on theoretical values and 1σ errors interpolated in the tables by Claret & Bloemen (2011). For the non-standard I + z filter, the modes of the normal prior distributions for u1 and u2 were taken as the averages of the values interpolated in the tables for the standard filters Ic and z′, while the errors were computed as the quadratic sums of the errors for these two filters. For the three systems, the prior distributions used for u1 and u2 are presented in Table 5.
Expectations and standard deviations of the normal distributions used as prior distributions for the quadratic limb-darkening (LD) coefficients u1 and u2 in our MCMC analyses.
For each system, a preliminary analysis was performed to determine the correction factors (CF) for our photometric errors, as described in Gillon et al. (2012). For each light curve, CF is the product of two contributions, βw and βr. On one side, βw represents the under- or overestimation of the white noise of each measurement. It is computed as the ratio between the standard deviation of the residuals and the mean photometric error. On the other side, βr allows us to take into account the correlated noise present in the light curve (i.e., the inability of our model to perfectly fit the data). It is calculated from the standard deviations of the binned and unbinned residuals for different binning intervals ranging from 5 to 120 min with the largest value being kept as βr. The standard deviation of the best-fit residuals (unbinned and binned per intervals of 2 min) and the deduced values for βw, βr and CF = βw × βr for each light curve are presented in Table 4. For each RV time-series, a “jitter” noise was determined and added quadratically to the errors to equal their mean value to the standard deviation of the best-fit residuals. These RV jitters take into account the instrumental and astrophysical effects (such as stellar activity) that are not included in the initial error estimation. The derived jitter values were 6.6 ms-1 for WASP-68, 9.2 ms-1 for WASP-73 and 10.9 ms-1 for WASP-88.
Our final analyses consisted each of five Markov chains of 105 steps, whose convergence was
checked using the statistical test of Gelman &
Rubin (1992). At each step of the Markov chains, the stellar density
ρ⋆ was derived from the
Kepler’s third law and the jump parameters (Rp/R⋆)2,
b′, W, P,
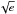 cos ωand
cos ωand
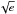 sin ω(see
e.g. Seager & Mallén-Ornelas 2003 and Winn 2010). The resulting stellar density and values
for Teff and [Fe/H] drawn from the normal distributions
deduced from our spectroscopic analysis (see Sect. 3.1) were used to determine a value for the stellar mass M⋆ through an empirical
law M⋆(ρ⋆, Teff,
[Fe/H])(Enoch et
al. 2010, Gillon et al. 2011a) that is
calibrated using the set of well-constrained detached binary systems presented by Southworth (2011). For WASP-68, this set was reduced to
the 116 stars with a mass between 0.7 and 1.7 M⊙, while the 119 stars with a mass
between 0.9 and 1.9 M⊙were used for WASP-73 and WASP-88. The
goal of these selections was to benefit from our preliminary estimation of the stellar
masses (see Sect. 3.1) to improve the determination
of the values of the systems’ parameters. To correctly propagate the error on the
empirical law, the parameters of the selected subset of calibration stars were normally
perturbed within their observational error bars and the coefficients of the law were
redetermined at each MCMC step. The other physical parameters were then deduced from the
jump parameters and stellar mass.
sin ω(see
e.g. Seager & Mallén-Ornelas 2003 and Winn 2010). The resulting stellar density and values
for Teff and [Fe/H] drawn from the normal distributions
deduced from our spectroscopic analysis (see Sect. 3.1) were used to determine a value for the stellar mass M⋆ through an empirical
law M⋆(ρ⋆, Teff,
[Fe/H])(Enoch et
al. 2010, Gillon et al. 2011a) that is
calibrated using the set of well-constrained detached binary systems presented by Southworth (2011). For WASP-68, this set was reduced to
the 116 stars with a mass between 0.7 and 1.7 M⊙, while the 119 stars with a mass
between 0.9 and 1.9 M⊙were used for WASP-73 and WASP-88. The
goal of these selections was to benefit from our preliminary estimation of the stellar
masses (see Sect. 3.1) to improve the determination
of the values of the systems’ parameters. To correctly propagate the error on the
empirical law, the parameters of the selected subset of calibration stars were normally
perturbed within their observational error bars and the coefficients of the law were
redetermined at each MCMC step. The other physical parameters were then deduced from the
jump parameters and stellar mass.
For each system, two analyses were performed: one assuming a circular orbit (e = 0) and one with a free eccentricity. For the three systems, the resulting Bayes factors (~1100 for WASP-68, ~1800 for WASP-73, and ~1800 for WASP-88) favored the circular solutions. We thus adopt the corresponding results as our nominal solutions but we present the derived parameters for both models in Table 6 (WASP-68), Table 7 (WASP-73), and Table 8 (WASP-88) for the sake of completeness. The best-fit transit models for the circular solutions are shown in Figs. 3, 5, and 7.
System parameters for WASP-68.
System parameters for WASP-73.
System parameters for WASP-88.
3.3. Stellar evolution modeling
After the completion of the MCMC analyses, we performed a stellar evolution modeling based on the CLES code (Scuflaire et al. 2008) for the three systems with the aim to assess the reliability of the deduced stellar masses and to estimate the age of the systems. We used as inputs the stellar densities deduced from the MCMC analyses, and the effective temperatures and metallicities as derived from spectroscopy (see Tables 6–8). We considered here that [Fe/H] represents the global metallicity with respect to the Sun, defined as [log (Z/X)∗ − log (Z/X)⊙], where X and Z are the fractional mass of hydrogen and elements heavier than helium respectively. We used the most recent solar mixture of Asplund et al. (2009), which gives for the current Sun (Z/X)⊙ = 0.0181. The parameter of the mixing-length theory (MLT) of convection was kept fixed to the solar calibration (αMLT = 1.8), and microscopic diffusion (gravitational settling) of elements was included.
The resulting stellar masses are 1.27 ± 0.11 M⊙(WASP-68), 1.40 ± 0.16 M⊙(WASP-73), and 1.41 ± 0.14 M⊙(WASP-88). These 1σ uncertainties were obtained by considering the respective 1σ range for the effective temperatures, metallicities, and stellar densities but also by varying the internal stellar physics. We indeed computed, since the helium atmospheric abundance cannot be directly measured from spectroscopy, evolutionary tracks with two initial helium abundances: the solar value (Y⊙ = 0.2485) and a value labelled YG that increases with Z (as expected if the local medium follows the general trend observed for the chemical evolution of galaxies; Izotov & Thuan 2010). We also investigated the effects of the possible convective core overshooting by varying αov between 0 and 0.3. Within the same hypotheses, the resulting stellar ages range 4.5−7.0 Gyr(WASP-68), 2.8−5.7 Gyr(WASP-73), and 1.8−4.3 Gyr(WASP-88). Three evolutionary tracks, respectively, for the central value for the stellar mass and metallicity of WASP-68, WASP-73, and WASP-88, are shown in Fig. 8. These evolutionary tracks span from the beginning (zero-age) of the main sequence to the beginning of the subgiant phase (core H-burning exhaustion). WASP-73 appears to be the most evolved star, close to or already in the subgiant phase. The stars WASP-68and WASP-88 are less evolved, although in an advanced stage of core H-burning. The subgiant phase is also a possibility, although very unlikely.
The masses derived for WASP-68 and WASP-88 are in excellent agreement with the MCMC results obtained through an empirical law M⋆(ρ⋆, Teff, [Fe/H])that is calibrated using a set of well-constrained detached eclipsing binary (EB) systems (see Sect. 3.2). The agreement is also good for WASP-73, which is close to core H-burning exhaustion or already in the subgiant phase, despite that the EB sample contains only a small fraction of significantly evolved objects. This shows that the EB empirical law used in the MCMC analyses is valid for the three stars considered here.
For even more evolved stars, the EB empirical law would reach its limit of applicability and could lead to inaccurate results. In such a case, a more reliable alternative would be to implement the stellar evolutionary models in the MCMC analysis, by assuming realistic prior probability distributions on the different stellar physics parameters (overshooting, diffusion, initial composition, etc.) and computing at each step M∗ from ρ∗, Teff, and [Fe/H]. This is a long-term goal we are pursuing (e.g., Triaud et al. 2011). Obtaining an accurate stellar mass from evolution modeling primarily needs accurate spectroscopic estimates for the effective temperature but also, very importantly, for the metallicity (compare the tracks of two very close stellar masses, 1.40 M⊙and 1.41 M⊙, but with quite different metallicities in Fig. 8).
 |
Fig. 8 Evolutionary tracks in a Teff − log (ρ∗/ρ⊙) HR diagram for WASP-68 (black), WASP-73 (blue), and WASP-88 (red), for their respective central masses and metallicities. These evolutionary tracks span from the zero-age main sequence to the beginning of the subgiant phase. The ages of the stars when they cross their respective 1σ box Teff − log (ρ∗/ρ⊙) are also indicated. |
4. Discussion and summary
We presented three newly discovered transiting hot Jupiters from the WASP survey, WASP-68 b, WASP-73 b, and WASP-88 b. We derived the parameters of each system from a joint analysis of the CORALIE spectroscopy and the high-precision photometry from TRAPPIST and EulerCam.
All three host stars appear to be significantly evolved (especially WASP-73, see Sect. 3.3) and thus have relatively large radii (1.7–2.2 R⊙). At the time of writing, only about 20 transiting hot Jupiters have been found to orbit such large stars4. This small number of detections might be due to the fact that large stellar radii translate into relatively shallow transits for the potential orbiting planets. These transits are therefore more difficult to detect by ground-based transit surveys. Alternatively, this might also be indicative of the tidal destruction of hot Jupiters. Due to their relatively large masses and small semi-major axes, hot Jupiters are expected to undergo tidal transfers of angular momentum with their host stars (e.g. Barker & Ogilvie 2009), which should lead to a slow spiral-in of the planets in most cases, until they are finally disrupted at their Roche limits (Gu et al. 2003). Although the timescale for orbital decay is quite uncertain and different for each system, it would thus not be surprising to find fewer close-in giant planets around larger and older stars, as there is a higher probability that these planets, if they once existed, have already been tidally disrupted. However, this correlation between the occurrence of hot Jupiters and the systems’ ageshas not been demonstrated yet.
It is also now common knowledge that tidal interactions tend to realign hot Jupiters’ orbits with their host stars’ equatorial planes (see Barker & Ogilvie 2009). Triaud (2011) demonstrated, using spin/orbit measurements for 22 hot Jupiters around stars with masses ≥1.2 M⊙, the existence of a correlation between these hot Jupiters’ orbital obliquities and their ages and estimated the typical timescale for a non-coplanar hot Jupiter’s orbit to tidally realign to be about 2.5 Gyr. Considering the estimated ages of our three systems, we can therefore expect their orbits to have realigned. However, it would be interesting to perform Rossiter-McLaughlin effect observations to confirm this tendency.
Due to the large radii of their host stars, our three planets are exposed to a relatively
high irradiation (incident flux > 109 erg s-1 cm-2). Several
works showed that hot Jupiters’ radiicorrelate well with their irradiating flux (see e.g.
Demory & Seager 2011; Enoch et al. 2012; or Weiss et al.
2013). Figure 9 shows the positions of our
three planets in an irradiation-radius diagram for the known transiting planets with 0.5
MJup < Mp < 2 MJup
and P < 12d. WASP-68 blies in a
well-populated region of the diagram. Its physical dimensions can be considered as rather
standard. Indeed, its measured radius of 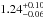 RJupis in perfect
agreement with the value of 1.24 ± 0.03 RJup predicted by the
equation derived by Weiss et al. (2013) from a sample
of 103 transiting planets with a mass between 150 M⊕and 13 MJupand that
relates planets’ sizesto their masses and irradiations. For WASP-73 b, the Weiss et al.’s
law gives a radius of
RJupis in perfect
agreement with the value of 1.24 ± 0.03 RJup predicted by the
equation derived by Weiss et al. (2013) from a sample
of 103 transiting planets with a mass between 150 M⊕and 13 MJupand that
relates planets’ sizesto their masses and irradiations. For WASP-73 b, the Weiss et al.’s
law gives a radius of  RJup, which is
slightly larger than our measured radius of
RJup, which is
slightly larger than our measured radius of 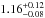 RJup. This might
suggest a possible small enrichment of the planet in heavy elements. Its density of
RJup. This might
suggest a possible small enrichment of the planet in heavy elements. Its density of
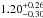 ρJupis indeed
surprisingly high, given the important irradiation the planet is exposed to (~2.3 × 109 erg s-1 cm-2). However,
the errors on its physical parameters are still too high to draw any strong inference on its
internal structure.
ρJupis indeed
surprisingly high, given the important irradiation the planet is exposed to (~2.3 × 109 erg s-1 cm-2). However,
the errors on its physical parameters are still too high to draw any strong inference on its
internal structure.
 |
Fig. 9 Irradiation–radius diagram for the known transiting hot Jupiters with 0.5 MJup < Mp < 2MJup and P < 12d (data from the NASA Exoplanet Archive). The planets WASP-68 b, WASP-73 b and WASP-88 b are shown in red. |
Unlike the first two planets, WASP-88 b appears to be a clear outlier, its measured radius
of  RJup being
significantly higher than the predicted value of 1.35±0.02 RJup. With a
density of 0.11 ± 0.03ρJup, WASP-88 b is actually the second
least dense transiting planet known to date, tied with Kepler-12 b (Fortney et al. 2011), which also has a density around 0.11
ρJup. Only WASP-17 b has a lower density
(ρp = 0.06 ρJup,
Anderson et al. 2011, Southworth et al. 2012). WASP-88 b thus joins the handful of planets with
super-inflated radii. Its large radius might be explained, at least partially, by the low
metallicity ([Fe/H] = −0.08 ± 0.12) of its star. With a mass of 0.56 MJup, WASP-88 b is
actually more Saturn-like than Jupiter-like and Enoch et al.
(2011), basing on 18 transiting exoplanets with masses below 0.6 Mp, found that
there is a strong negative correlation between the star metallicity [Fe/H] and
Rp
for these planets. Keeping in mind that the chemical composition of a planet should be
related to the one of its host star as they formed from the same cloud, the observation that
the correlation between [Fe/H] and Rp is negligible for more massive planets
agrees well with the theoretical planet models of Fortney et
al. (2007) and Baraffe et al. (2008), which
both suggest that the radius of a planet is more sensitive to its composition for low mass
planets than it is for more massive ones. The relation (3) of Enoch et al. (2011) leads to a predicted radius of 1.51 ± 0.06 RJupfor WASP-88 b, which is
better than the value of Weiss et al. (2013) but
still lower than our measured value. As WASP-88 bis the youngest of our three planets (see
Sect. 3.3), tidal circularization and dissipation
might have occurred recently enough to contribute to the observed inflated radius (see e.g.
Leconte et al. 2010). Other physical mechanisms
might also be at play, such as the deposition of kinetic energy into the planet from strong
winds driven by the large day/night temperature contrast (Showman & Guillot 2002), reduced heat transport efficiency by layered
convection inside the planet (Chabrier & Baraffe
2007), or Ohmic heating from currents induced through winds in the planetary
atmosphere (Batygin & Stevenson 2010).
RJup being
significantly higher than the predicted value of 1.35±0.02 RJup. With a
density of 0.11 ± 0.03ρJup, WASP-88 b is actually the second
least dense transiting planet known to date, tied with Kepler-12 b (Fortney et al. 2011), which also has a density around 0.11
ρJup. Only WASP-17 b has a lower density
(ρp = 0.06 ρJup,
Anderson et al. 2011, Southworth et al. 2012). WASP-88 b thus joins the handful of planets with
super-inflated radii. Its large radius might be explained, at least partially, by the low
metallicity ([Fe/H] = −0.08 ± 0.12) of its star. With a mass of 0.56 MJup, WASP-88 b is
actually more Saturn-like than Jupiter-like and Enoch et al.
(2011), basing on 18 transiting exoplanets with masses below 0.6 Mp, found that
there is a strong negative correlation between the star metallicity [Fe/H] and
Rp
for these planets. Keeping in mind that the chemical composition of a planet should be
related to the one of its host star as they formed from the same cloud, the observation that
the correlation between [Fe/H] and Rp is negligible for more massive planets
agrees well with the theoretical planet models of Fortney et
al. (2007) and Baraffe et al. (2008), which
both suggest that the radius of a planet is more sensitive to its composition for low mass
planets than it is for more massive ones. The relation (3) of Enoch et al. (2011) leads to a predicted radius of 1.51 ± 0.06 RJupfor WASP-88 b, which is
better than the value of Weiss et al. (2013) but
still lower than our measured value. As WASP-88 bis the youngest of our three planets (see
Sect. 3.3), tidal circularization and dissipation
might have occurred recently enough to contribute to the observed inflated radius (see e.g.
Leconte et al. 2010). Other physical mechanisms
might also be at play, such as the deposition of kinetic energy into the planet from strong
winds driven by the large day/night temperature contrast (Showman & Guillot 2002), reduced heat transport efficiency by layered
convection inside the planet (Chabrier & Baraffe
2007), or Ohmic heating from currents induced through winds in the planetary
atmosphere (Batygin & Stevenson 2010).
Online material
CORALIE radial-velocity measurements for WASP-68 (BS = bisector spans).
CORALIE radial-velocity measurements for WASP-73 (BS = bisector spans).
CORALIE radial-velocity measurements for WASP-88 (BS = bisector spans).
Acknowledgments
WASP-South is hosted by the South African Astronomical Observatory and we are grateful for their ongoing support and assistance. Funding for WASP comes from consortium universities and from UK’s Science and Technology Facilities Council. TRAPPIST is a project funded by the Belgian Fund for Scientific Research (Fonds National de la Recherche Scientifique, F.R.S.-FNRS) under grant FRFC 2.5.594.09.F, with the participation of the Swiss National Science Fundation (SNF). L. Delrez acknowledges the support of the F.R.I.A. fund of the FNRS. M. Gillon and E. Jehin are FNRS Research Associates. A. H. M. J. Triaud received funding from a fellowship provided by the Swiss National Science Foundation under grant number PBGEP2-14559. We thank the anonymous referee for his valuable suggestions.
References
- Anderson, D. R., Smith, A. M. S., Lanotte, A. A., et al. 2011, MNRAS, 416, 2108 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barker, A. J., & Ogilvie, G. I. 2009, MNRAS, 395, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Stevenson, D. J. 2010, ApJ, 714, L238 [NASA ADS] [CrossRef] [Google Scholar]
- Broeg, C., Fortier, A., Ehrenreich, D., et al. 2013, EPJ Web Conf., 47, 3005 [Google Scholar]
- Bruntt, H., Bedding, T. R., Quirion, P.-O., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2007, ApJ, 661, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1987, Ellipsoidal figures of equilibrium [Google Scholar]
- Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- CollierCameron, A., Pollacco, D., Street, R. A., et al. 2006, MNRAS, 373, 799 [NASA ADS] [CrossRef] [Google Scholar]
- CollierCameron, A., Wilson, D. M., West, R. G., et al. 2007, MNRAS, 380, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., & Seager, S. 2011, ApJS, 197, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, A. P., Smalley, B., Maxted, P. F. L., et al. 2013, MNRAS, 428, 3164 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, B., Collier Cameron, A., Parley, N. R., & Hebb, L. 2010, A&A, 516, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enoch, B., Cameron, A. C., Anderson, D. R., et al. 2011, MNRAS, 410, 1631 [NASA ADS] [Google Scholar]
- Enoch, B., Collier Cameron, A., & Horne, K. 2012, A&A, 540, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Demory, B.-O., Désert, J.-M., et al. 2011, ApJS, 197, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Gardner, J. P., Mather, J. C., Clampin, M., et al. 2006, Space Sci. Rev., 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Gelman, A., & Rubin, D. 1992, Stat. Sci., 7, 457 [Google Scholar]
- Gillon, M., Doyle, A. P., Lendl, M., et al. 2011a, A&A, 533, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Jehin, E., Magain, P., et al. 2011b, EPJ Web Conf., 11, 6002 [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Fortney, J. J., et al. 2012, A&A, 542, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres [Google Scholar]
- Gu, P.-G., Lin, D. N. C., & Bodenheimer, P. H. 2003, ApJ, 588, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2013 [arXiv:1310.5630] [Google Scholar]
- Holman, M. J., Winn, J. N., Latham, D. W., et al. 2006, ApJ, 652, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 2010, ApJ, 710, L67 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Jeffreys, H. 1961, The Theory of Probability (New-York: Oxford University Press) [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Leconte, J., Chabrier, G., Baraffe, I., & Levrard, B. 2010, A&A, 516, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lendl, M., Anderson, D. R., Collier-Cameron, A., et al. 2012, A&A, 544, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magain, P. 1984, A&A, 134, 189 [NASA ADS] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Anderson, D. R., Collier Cameron, A., et al. 2011, PASP, 123, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, C. D., & Correia, A. C. M. 2010, in Exoplanets, ed. S. Seager, 15 [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2002, A&A, 392, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarz, G. E. 1978, Ann. Statist., 6, 461 [Google Scholar]
- Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Ap&SS, 316, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Deming, D. 2010, ARA&A, 48, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., & Guillot, T. 2002, A&A, 385, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J. 2011, MNRAS, 417, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Hinse, T. C., Dominik, M., et al. 2012, MNRAS, 426, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Triaud, A. H. M. J. 2011, A&A, 534, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Triaud, A. H. M. J., Queloz, D., Hellier, C., et al. 2011, A&A, 531, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, L. M., Marcy, G. W., Rowe, J. F., et al. 2013, ApJ, 768, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N. 2010, in Exoplanets, ed. S. Seager, 55 [Google Scholar]
All Tables
Expectations and standard deviations of the normal distributions used as prior distributions for the quadratic limb-darkening (LD) coefficients u1 and u2 in our MCMC analyses.
All Figures
 |
Fig. 1 WASP photometry for WASP-68 (top), WASP-73 (middle), and WASP-88 (bottom) folded on the best-fitting transit ephemeris from the transit search algorithm presented in Collier Cameron et al. (2006), and binned per 0.01 d intervals. |
| In the text | |
 |
Fig. 2 Top: CORALIE RVs for WASP-68 phase-folded on the best-fit orbital period with the best-fit Keplerian model over-imposed in red. Bottom: correlation diagram CCF bisector span vs. RV. |
| In the text | |
 |
Fig. 3 Top: individual follow-up transit light curves for WASP-68 b. Bottom: combined follow-up photometry for WASP-68 b. The observations are shown as red points (bin width =2min) and are period-folded on the best-fit transit ephemeris. Each light curve has been divided by the respective photometric baseline model (see Sect. 3.2). For each filter, the superimposed, solid black line is our best-fit transit model. The light curves are shifted along the y-axis for clarity. |
| In the text | |
 |
Fig. 4 Top: CORALIE RVs for WASP-73 phase-folded on the best-fit orbital period with the best-fit Keplerian model over-imposed in red. Bottom: correlation diagram CCF bisector span vs. RV. |
| In the text | |
 |
Fig. 5 Top: individual follow-up transit light curves for WASP-73 b. Bottom: combined follow-up photometry for WASP-73 b. The observations are shown as red points (bin width =2 min) and are period-folded on the best-fit transit ephemeris. Each light curve has been divided by the respective photometric baseline model (see Sect. 3.2). For each filter, the superimposed, solid black line is our best-fit transit model. The light curves are shifted along the y-axis for clarity. |
| In the text | |
 |
Fig. 6 Top: CORALIE RVs for WASP-88 phase-folded on the best-fit orbital period with the best-fit Keplerian model over-imposed in red. Bottom: correlation diagram CCF bisector span vs. RV. |
| In the text | |
 |
Fig. 7 Top: individual follow-up transit light curves for WASP-88 b. Bottom: combined follow-up photometry for WASP-88 b. The observations are shown as red points (bin width =2min) and are period-folded on the best-fit transit ephemeris. Each light curve has been divided by the respective photometric baseline model (see Sect. 3.2). For each filter, the superimposed, solid black line is our best-fit transit model. The light curves are shifted along the y-axis for clarity. |
| In the text | |
 |
Fig. 8 Evolutionary tracks in a Teff − log (ρ∗/ρ⊙) HR diagram for WASP-68 (black), WASP-73 (blue), and WASP-88 (red), for their respective central masses and metallicities. These evolutionary tracks span from the zero-age main sequence to the beginning of the subgiant phase. The ages of the stars when they cross their respective 1σ box Teff − log (ρ∗/ρ⊙) are also indicated. |
| In the text | |
 |
Fig. 9 Irradiation–radius diagram for the known transiting hot Jupiters with 0.5 MJup < Mp < 2MJup and P < 12d (data from the NASA Exoplanet Archive). The planets WASP-68 b, WASP-73 b and WASP-88 b are shown in red. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


