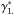| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 11 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201322507 | |
| Published online | 27 February 2014 | |
Relativistic cosmology number densities in void-Lemaître-Tolman-Bondi models
1 Observatório do Valongo, Universidade Federal do Rio de
Janeiro, Brazil
e-mail:
iribarrem@astro.ufrj.br
2
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748
Garching,
Germany
3
Astrophysics, Cosmology and Gravitation Centre, and Department of
Mathematics and Applied Mathematics, University of Cape Town,
Rondebosch 7701, Cape Town, South
Africa
4
INAF – Osservatorio Astronomico di Bologna, via Ranzani 1,
40127
Bologna,
Italy
5 Instituto de Física, Universidade Federal do Rio de Janeiro,
Brazil
6
Vatican Observatory Research Group, Steward Observatory,
University of Arizona, AZ,
85721
Tucson,
USA
Received:
20
August
2013
Accepted:
5
January
2014
Aims. The goal of this work is to compute the number density of far-IR selected galaxies in the comoving frame and along the past lightcone of observationally constrained Lemaître-Tolman-Bondi “giant void” models and to compare those results with their standard model counterparts.
Methods. We derived integral number densities and differential number densities using different cosmological distance definitions in the Lemaître-Tolman-Bondi dust models. Then, we computed selection functions and consistency functions for the luminosity functions in the combined fields of the Herschel/PACS evolutionary probe (PEP) survey in both standard and void cosmologies, from which we derived the observed values of the above-mentioned densities. We used the Kolmogorov-Smirnov statistics to study both the evolution of the consistency functions and its connection to the evolution of the comoving density of sources. Finally, we fitted the power-law behaviour of the densities along the observer’s past lightcone.
Results. The analysis of the comoving number density shows that the increased flexibility of the Lemaître-Tolman-Bondi models is not enough to fit the observed redshift evolution of the number counts, if it is specialised to a recent best-fit giant void parametrisation. The results for the power-law fits of the densities along the observer’s past lightcone show general agreement across both cosmological models studied here around a slope of −2.5 ± 0.1 for the integral number density on the luminosity-distance volumes. The differential number densities show much bigger slope discrepancies.
Conclusions. We conclude that the differential number densities on the observer’s past lightcone were still rendered dependent on the cosmological model by the flux limits of the PEP survey. In addition, we show that an intrinsic evolution of the sources must be assumed to fit the comoving number-density redshift evolution in the giant void parametrisation for the Lemaître-Tolman-Bondi models used in this work.
Key words: galaxies: distances and redshifts / cosmology: theory / galaxies: evolution / infrared: galaxies
© ESO, 2014
1. Introduction
The aim of many studies in observational cosmology is to infer to what extent the geometry of the spacetime contributes to the formation and evolution of the galaxies, i.e. the building blocks of the luminous Universe. In practical terms, most of what we can infer about galaxy formation and evolution comes from analyses of redshift surveys. Although the redshift is an observable quantity related to the energy content and geometry of the Universe – regardless of how we model it – translating these measurements into distance estimations cannot be performed without assuming a cosmological model. As a consequence, it is clear that any study that involves galaxy distances will be model dependent. This dependency cannot be overcome as long as the distance estimators used in these studies are not directly obtained, but instead derived from redshift measurements.
The standard cosmological model, often called the concordance model, is presently able to simultaneously fit most of the current observations of independent cosmological quantities. A few examples of observations that support this model include Hubble parameter measurements from the distances to Cepheids (Freedman et al. 2001), or from the massive, passively evolving early-type galaxies (Moresco et al. 2012; Liu et al. 2012), or from the extragalactic HII regions (Chávez et al. 2012); the luminosity distance-redshift relation stemming from supernovae type Ia (henceforth, simply SNe) surveys (Riess et al. 1998; Perlmutter et al. 1999), the power spectrum of the cosmic microwave background radiation (CMB, e.g. Komatsu et al. 2011), and the angular size scale obtained from baryonic acoustic oscillation (BAO) studies (e.g. Percival et al. 2010). The degree of confidence on the concordance model is such that the above-mentioned model dependency of galaxy formation and evolution nowadays sounds like an unavoidable, but otherwise less consequential fact.
Despite the sizeable constraining power of the current set of observations show, there is still room for considering alternative cosmological models. Even if most of these models are disfavoured when compared to the standard model (e.g. Sollerman et al. 2009), some of them cannot be ruled out entirely yet. Among these models, motivated mainly as alternative to dark energy, various non-homogeneous cosmologies have been proposed, with an increasing interest in the past few years (Hellaby & Alfedeel 2009; Alfedeel & Hellaby 2010; February et al. 2010; Biswas et al. 2010; Sussman 2010; Bolejko et al. 2011b; Nadathur & Sarkar 2011; Clarkson & Regis 2011; Clarkson et al. 2012; Regis & Clarkson 2012; Meures & Bruni 2012; Humphreys et al. 2012; Nishikawa et al. 2012; Bull & Clifton 2012; Valkenburg et al. 2014; Wang & Zhang 2012; Hellaby 2012; Hoyle et al. 2013; Bull et al. 2012; de Putter et al. 2012; Keenan et al. 2012; Fleury et al. 2013). Some recent reviews include Célérier (2007), Bolejko et al. (2011a), Ellis (2011), and Krasiński (2014).
The simplest non-homogeneous model assumes a Lemaître-Tolman-Bondi (LTB) metric coupled to a pressure-less (dust) energy-momentum tensor. LTB dust models yield analytical solutions to the Einstein’s field equations, e.g. Bonnor (1972), that can be reduced by an appropriate parametrisation to the standard model ones. It is, for example, quite usual to set the free equations allowed in this model in a way that it reduces to the usual Einstein-de Sitter solution at large enough redshifts, enabling the model to naturally fit many CMB constraints, albeit with very low H0. This model can be understood as a generalisation of the FLRW metric, an effective model, possibly the simplest one, in which the observed large-scale inhomogeneities play a role in the late-time dynamics and nearby geometry of the Universe.
Using the greater flexibility of these models, Mustapha et al. (1997) showed that any spherically symmetric astronomical observation, such as redshift surveys, can be fitted by the non-homogeneities allowed in these models, instead of any source evolution. This is particularly relevant for galaxy evolution since it implies that in order to establish it beyond this theoretical possibility, it is necessary to use a combination of various independent observable quantities. Garcia-Bellido & Haugbølle (2008, hereafter GBH) propose a “giant void” parametrisation for the LTB dust model that was able to reach that exactly: fit simultaneously the SNe Ia hubble diagram and some general features of the CMB. Despite the many problems this alternative model shows (Marra & Pääkkönen 2010; Moss et al. 2011; Zhang & Stebbins 2011; Zibin 2011; Planck Collaboration Int. XIII. 2013), arguably it remains the simplest and best-studied way to allow for non-homogeneities in the cosmological model. Given the theoretical possibility of fitting the redshift evolution of the number counts without any intrinsic evolution of the sources mentioned above, we aimed to investigate what our view of galaxy evolution would be under these alternative models.
To address the question of how robustly the current observations render the luminosity function (LF) of galaxies, in Iribarrem et al. (2013) we used the dataset of FIR-selected sources in Gruppioni et al. (2013) for the combined GOODS-N, GOODS-S, COSMOS and ECDF-S fields in the Herschel/PACS evolutionary probe (PEP) galaxy redshift survey, computed in both the ΛCDM standard and LTB giant void models, the latter parameterised as in Garcia-Bellido & Haugbølle (2008) with the best-fit parameters given by Zumalacárregui et al. (2012).
While the motivation of Iribarrem et al. (2013) was to probe the implications of the underlying cosmology on the redshift evolution of observable properties of the sources, such as number count and luminosity, the present work aims to further study these implications, specifically, on the characterisation of the number density of sources along the past lightcone of the assumed cosmology. The past lightcone is a direct observable: it is the only region of the Universe manifold that galaxy redshift surveys probe. In computing the densities in the lightcone, we remove the model assumption intrinsic to the usual comoving frame computations. The empirical approach of it, if not as ambitious, shares the same philosophy of the ideal observational cosmology programme as Ellis et al. (1985), where the aim was to determine the spacetime geometry of the Universe without assuming a cosmological model a priori.
The present line of work started with Ribeiro & Stoeger (2003), which connected the relativistic cosmology number counts results summarised in Ellis (1971) to the practical LF results from galaxy redshift surveys. The LF is a statistical tool to infer the formation and evolution of galaxies from a set of photometric or spectroscopic data. To compute the luminosities of the sources from their observed fluxes, a luminosity distance must be obtained from the redshift estimation, a step that requires adopting a cosmological model. To deal with incompleteness due to the flux limits, an assumption on the spatial homogeneity of the distribution is usually made. Spatial homogeneity is defined on constant time-coordinate hypersurfaces, not to be confused with observational homogeneity that is defined on the observer’s past lightcone. The spatial homogeneity assumption does not hold for non-homogeneous cosmologies in general, but Iribarrem et al. (2013) showed that it does not lead to significant differences in the LF results in the case of the LTB/GBH models adopted here.
Ribeiro (2005) considers the effect of the expansion of the spacetime in the number densities along the past lightcone leading to observational non-homogeneities in the spatially homogeneous Friedmann-Lemaître-Robertson-Walker (FLRW) model. Rangel Lemos & Ribeiro (2008) expanded on those theoretical results, showing that homogeneous distributions in the past lightcone would lead to spatial non-homogeneity, in disagreement with the usual form of the cosmological principle.
Albani et al. (2007) combined the results of the first two previous papers to compute such lightcone distributions using the LFs for the CNOC2 survey from Lin et al. (1999), confirming the presence of such light cone non-homogeneities. In Iribarrem et al. (2012) we discussed further ways to compare the relativistic effect of the expanding spacetime to the evolution of the sources in the FLRW past lightcone, using the much wider redshift range in the LFs for the FORS Deep Field survey from Gabasch et al. (2004, 2006).
The goal of the present work is to include non-FLRW spacetimes in the past lightcone studies described above. We specialised the general equations of Ribeiro & Stoeger (2003) to the LTB metric, combining the results from both Ribeiro (1992), and Garcia-Bellido & Haugbølle (2008). Finally, we used the LFs in Iribarrem et al. (2013), which were computed by assuming the LTB/GBH model from their build-up.
The question we aim to address is the following: are the number densities along the past lightcone and the characterisation of their power law behaviour, robust among the standard and void cosmological models cited above? In addition, we discuss the comoving number density in the void models, with possible implications for empirical models like that in, e.g., Gruppioni et al. (2011), Béthermin et al. (2012).
The paper is organised as follows. In Sect. 2, we specialise the results in Ribeiro & Stoeger (2003) and Ribeiro (2005) to the constrained GBH parametrisation of the LTB dust models. In Sect. 3, we compute the selection functions for the FIR datasets in Iribarrem et al. (2013). In Sect. 4 we compute the connection between the predicted comoving density of sources in both FLRW and LTB geometries to the selection functions. In Sect. 5 we compute the number densities of PEP sources down the past lightcone of both cosmologies. In Sect. 6, we present the results, show evidence of galaxy evolution in the LTB/GBH model, and compare the comoving number density evolution over both cosmologies. In Sect. 7 we discuss the dependency of the relativistic number densities on both flux limit and cosmological model. In Sect. 8 we present our conclusions.
2. Theoretical quantities in the LTB/GBH model
In the empirical approach of Albani et al. (2007), the number densities along the observer’s past lightcone were computed from LF data using different relativistic cosmology distance definitions. These distances are defined in the same cosmological model as the one assumed on the build-up of the LF. In this context no assumptions on the redshift evolution of the sources is made. The methodology is completely empirical.
The number densities used in this paper, as defined in Ribeiro (2005), are able to probe the geometrical effect of the expansion of Universe on the homogeneity of the distribution of the sources along the observer’s past lightcone. This effect depends on the distance definition used in computing these densities, which in turn depends on the line element of the cosmological model assumed.
In this section we connect the key results from Ribeiro (1992, henceforth R92) for the number count of sources in the LTB metric to the parametrisation advanced by Garcia-Bellido & Haugbølle (2008) for that cosmology. The goal here is to compute the above-mentioned number densities in the giant void parametrisation of the LTB model. Dotted quantities refer to time-coordinate derivatives and primed ones refer to radial-coordinate derivatives.
2.1. Differential number count
We started by writing the line element for the LTB model following Bonnor (1972)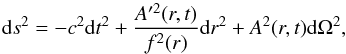 (1)where dΩ2 = dθ2 + sin2θ dφ2,
with f(r) and A(r,t)
being arbitrary functions. Assuming a pressure-less (dust) matter content with
ρM proper density, it can be shown that
the Einstein’s field equations for that line element can be combined to yield (R92)
(1)where dΩ2 = dθ2 + sin2θ dφ2,
with f(r) and A(r,t)
being arbitrary functions. Assuming a pressure-less (dust) matter content with
ρM proper density, it can be shown that
the Einstein’s field equations for that line element can be combined to yield (R92)
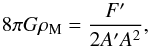 (2)where F(r) is
another arbitrary function satisfying the relation above, and G is the gravitational
constant. Starting from the general expression for the number count of sources derived by
Ellis (1971), R92 obtained
(2)where F(r) is
another arbitrary function satisfying the relation above, and G is the gravitational
constant. Starting from the general expression for the number count of sources derived by
Ellis (1971), R92 obtained 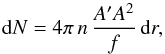 (3)where
n is the
number density per unit proper volume, and N the total number of sources down the past
lightcone. Assuming as an order of magnitude estimation of the average total mass of each
source ℳ ≈ 1011ℳ⊙, R92 wrote
(3)where
n is the
number density per unit proper volume, and N the total number of sources down the past
lightcone. Assuming as an order of magnitude estimation of the average total mass of each
source ℳ ≈ 1011ℳ⊙, R92 wrote 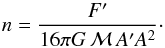 (4)Combining the last two
equations, we obtained
(4)Combining the last two
equations, we obtained 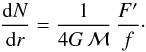 (5)The last equation
is essentially a version of the result of Ellis
(1971), specialised to the past null geodesic of the LTB model. Next, we further
specialised it to use the GBH parametrisation for their constrained model, and the
best-fit values obtained by Zumalacárregui et al.
(2012) in a simultaneous analysis of SNe Ia, CMB, and BAO data.
(5)The last equation
is essentially a version of the result of Ellis
(1971), specialised to the past null geodesic of the LTB model. Next, we further
specialised it to use the GBH parametrisation for their constrained model, and the
best-fit values obtained by Zumalacárregui et al.
(2012) in a simultaneous analysis of SNe Ia, CMB, and BAO data.
It is straightforward to relate f(r) to the spatial curvature
parameter k(r) in GBH by writing 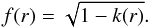 (6)The boundary condition
equations listed in GBH read as
(6)The boundary condition
equations listed in GBH read as ![\begin{eqnarray} &&H_{\ssty T}(r,t) = \frac{\dot{A}(r,t)}{A(r,t)} \label{GBHHT}, \\[1.5mm] &&F(r) = 2 \, \Omega_{\rm M}(r) \, H^2_{\ssty 0}(r) \, r^3 \label{GBHF}, \\[1.5mm] &&k(r) = -\left[1-\Omega_{\rm M}(r)\right] \, H^2_{\ssty 0}(r) \, r^2 \label{GBHk}, \end{eqnarray}](/articles/aa/full_html/2014/03/aa22507-13/aa22507-13-eq20.png) with
the gauge choice A(r,0) = r
included, where HT is the transverse
Hubble rate, H0(r) = HT(r,0),
and ΩM(r) is the dimensionless matter density
parameter. This last quantity is defined relative to the integrated critical density in
the comoving volume at radial coordinate r as
with
the gauge choice A(r,0) = r
included, where HT is the transverse
Hubble rate, H0(r) = HT(r,0),
and ΩM(r) is the dimensionless matter density
parameter. This last quantity is defined relative to the integrated critical density in
the comoving volume at radial coordinate r as 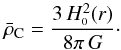 (10)The present-time
transverse Hubble parameter, H0(r), in the
constrained version of the GBH model is parametrised as
(10)The present-time
transverse Hubble parameter, H0(r), in the
constrained version of the GBH model is parametrised as ![\begin{equation} \label{zumaH0} H_{\ssty 0}(r) = H_{\rm in} \sum_{n=0}^{\infty} \frac{2 \left[1-\Omega_{\rm M}(r)\right]^n}{(2n+1)(2n+3)}\cdot \end{equation}](/articles/aa/full_html/2014/03/aa22507-13/aa22507-13-eq28.png) (11)Equations (6), (9), and (11) can be readily
combined to yield
(11)Equations (6), (9), and (11) can be readily
combined to yield ![\begin{equation} \label{kr} f(r) = \sqrt{1 + \left[1-\Omega_{\rm M}(r)\right] \left\{ \sum_{n=0}^{\infty} \frac{2 \left[1-\Omega_{\rm M}(r)\right]^n}{(2n+1)(2n+3)} \right\}^2 {H_{\rm in}}^2 r^2}. \end{equation}](/articles/aa/full_html/2014/03/aa22507-13/aa22507-13-eq29.png) (12)Combining Eqs. (8) and (11), we can write the F(r) function for the constrained
model as
(12)Combining Eqs. (8) and (11), we can write the F(r) function for the constrained
model as ![\begin{equation} \label{Fr} F(r) = H_{\rm in} \left\{ \sum_{n=0}^{\infty} \frac{2 \left[1-\Omega_{\rm M}(r)\right]^n}{(2n+1)(2n+3)} \right\} \Omega_{\rm M}(r) \, r^3, \end{equation}](/articles/aa/full_html/2014/03/aa22507-13/aa22507-13-eq30.png) (13)where the dimensionless
matter density parameter ΩM(r) in the GBH model becomes
(13)where the dimensionless
matter density parameter ΩM(r) in the GBH model becomes
![\begin{equation} \label{omr} \Omega_{\rm M}(r) = \Omega_{\rm out} + \left(\Omega_{\rm in} - \Omega_{\rm out}\right) \left\{ \frac{1-\tanh[(r-R)/2\Delta r]}{1+\tanh[R/2\Delta r]} \right\}\cdot \end{equation}](/articles/aa/full_html/2014/03/aa22507-13/aa22507-13-eq31.png) (14)Here Hin is the
transverse Hubble constant at the center of the void, Ωin is the density parameter at
the center of the void, Ωout the asymptotic density parameter at large comoving
distances, R
is the size of the under-dense region, and ΔR the width of the transition between the central
void and the exterior homogeneous region. These parameters completely determine the model.
(14)Here Hin is the
transverse Hubble constant at the center of the void, Ωin is the density parameter at
the center of the void, Ωout the asymptotic density parameter at large comoving
distances, R
is the size of the under-dense region, and ΔR the width of the transition between the central
void and the exterior homogeneous region. These parameters completely determine the model.
Because of the generality of the evolution of A(r,t) in the LTB models, the time coordinate tbb at which A(r,tbb) reduces to zero, can, in general, assume different values for different comoving distances from the centre of the under-dense region, r. This leads to different measurements for the elapsed time since the Big Bang, tbb(r), depending on the position of the observer in the void. Setting this extra degree of freedom for the big-bang time in order to make it simultaneous (same value for all observers) yields the constrained version of the GBH model, or CGBH model. The best-fit values we use in this work were obtained in Zumalacárregui et al. (2012), considering both an asymptotically flat CGBH model with Ωout = 1 and an open CGBH model (OCGBH) with Ωout = 0.87, which the authors show better fits the CMB constraints. Table 1 reproduces these values.
 |
Fig. 1 Differential number count estimates within the past lightcone of the three cosmological models used in the present work. |
Best fit values for the LTB/CGBH models from Zumalacárregui et al. (2012) used in this work.
For each comoving distance r, ΩM(r), f(r), and F(r) can be computed through Eqs. (12), and (13). The radial derivative F′(r) can be obtained numerically through central difference quotients, F(r) ≈ limΔr ≪ rΔF/Δr, which in turn allow the values of dN/dr to be computed through Eq. (5).
The redshift can be related to the radial coordinate in this model following Enqvist & Mattsson (2007)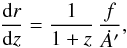 (15)and to the time
coordinate through the incoming radial null geodesic equation as in GBH
(15)and to the time
coordinate through the incoming radial null geodesic equation as in GBH 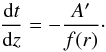 (16)Following GBH,
all the first- and second-order derivatives of A(r,t) can be written as power
series expansion, which allows Eqs. (15)
and (16) to be solved numerically. This
yielded the look-back time and radial distance tables: t(z) and
r(z). We then combined Eqs. (5) and (15) as
(16)Following GBH,
all the first- and second-order derivatives of A(r,t) can be written as power
series expansion, which allows Eqs. (15)
and (16) to be solved numerically. This
yielded the look-back time and radial distance tables: t(z) and
r(z). We then combined Eqs. (5) and (15) as ![\begin{equation} \label{dNdz} \frac{{\rm d}N}{{\rm d}z} = \frac{1}{4G \, \Mg} \, \frac{F'[r(z)]}{(1+z) \, \dot{A}'[r(z),t(z)]}, \end{equation}](/articles/aa/full_html/2014/03/aa22507-13/aa22507-13-eq57.png) (17)and computed the
differential number count dN/dz for each
value of z in
the r(z) and t(z)
tables. A comparison between the estimates for this quantity in the ΛCDM and both CGBH parametrisations in Zumalacárregui et al. (2012) can be found in Fig. 1.
(17)and computed the
differential number count dN/dz for each
value of z in
the r(z) and t(z)
tables. A comparison between the estimates for this quantity in the ΛCDM and both CGBH parametrisations in Zumalacárregui et al. (2012) can be found in Fig. 1.
2.2. Distances and number densities
Since it is impossible to measure the distance to galaxies directly, there are a few different ways of deriving this quantity from other measurements. The luminosity distance, for example, is based on the relation between the emitted and received fluxes of the source, whereas the angular diameter distance is based on the relation between the observed angular size and the actual physical size of the source. Those relations, however, depend on the expansion history of the Universe and will, in general, lead to different results simply because their dependency on the underlying cosmological model is not the same.
The angular diameter distance in LTB models can be identified as dA(z) = A [r(z),t(z)].
From that we obtain the luminosity distance dL(z) and the
galaxy-area distance dG through Etherington’s reciprocity law
(Etherington 1933; Ellis 1971, 2007) 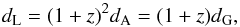 (18)whereas their redshift
derivatives, d(dA)/dz,
d(dL)/dz,
and d(dG)/dz
can be computed numerically with the same method used for computing F′(r). To compare the
theoretical results for the number densities in the past lightcone of the LTB/GBH models
with those for the FLRW geometry given in Albani et al.
(2007, Figs. 5, 6), we also compute the redshift distance
dz simply as
dz = cz/H0.
(18)whereas their redshift
derivatives, d(dA)/dz,
d(dL)/dz,
and d(dG)/dz
can be computed numerically with the same method used for computing F′(r). To compare the
theoretical results for the number densities in the past lightcone of the LTB/GBH models
with those for the FLRW geometry given in Albani et al.
(2007, Figs. 5, 6), we also compute the redshift distance
dz simply as
dz = cz/H0.
With that we can compute the relativistic differential number densities
(γi), the number of
sources per unit volume in a spherical shell at redshift z, for each distance
di in i = [A,G,L,z] and in each
cosmological model as in Ribeiro (2005):
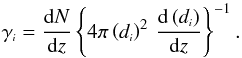 (19)Following Iribarrem et al. (2012), the integral number
densities (
(19)Following Iribarrem et al. (2012), the integral number
densities (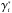 ), i.e. the
number of sources per unit volume located inside the observer’s past lightcone down to
redshift z,
can be computed for each distance definition di as
), i.e. the
number of sources per unit volume located inside the observer’s past lightcone down to
redshift z,
can be computed for each distance definition di as 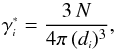 (20)with the cumulative
number count N(z) obtained simply by
(20)with the cumulative
number count N(z) obtained simply by
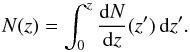 (21)Results for the
various γi and
(21)Results for the
various γi and
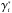 in the
different cosmologies considered in this work are plotted in Figs. 2 and 3. We note that among these
cosmological models, the differential and integral number densities show noticeable
differences in all distance definitions used, even if apparently small to the eye. These
differences may actually be observed, depending on the precision achieved by a galaxy
survey. We go on to check whether this purely geometrical effect can be detected on the LF
for the PEP survey computed in Iribarrem et al.
(2013). This requires considering the luminosity and the number evolution of the
galaxies in the survey volume.
in the
different cosmologies considered in this work are plotted in Figs. 2 and 3. We note that among these
cosmological models, the differential and integral number densities show noticeable
differences in all distance definitions used, even if apparently small to the eye. These
differences may actually be observed, depending on the precision achieved by a galaxy
survey. We go on to check whether this purely geometrical effect can be detected on the LF
for the PEP survey computed in Iribarrem et al.
(2013). This requires considering the luminosity and the number evolution of the
galaxies in the survey volume.
 |
Fig. 2 Redshift evolution of the relativistic differential densities for the three cosmological models used in the present work. Different curves correspond to the computations performed with respect to different distance estimators along the observer’s past lightcone (dA, dL, dG, and dz). |
 |
Fig. 3 Integral of the functions shown in Fig. 2. The curves show the evolution of the relativistic integral densities for the three cosmological models used in the present work as a function of the different distances. |
3. Selection functions
Selection functions are an estimate of the number density of galaxies with luminosity above a chosen threshold, Llim. Once computed, the selection functions can be used to estimate the observed number of objects per comoving volume, derived in Sect. 2.2, and from that the observed differential and integral densities in the past lightcone.
Following the empirical approach of Iribarrem et al.
(2012), we computed selection functions ψ in each redshift interval using each of the three
cosmological models (ΛCDM, CGBH,
and OCGBH) and the monochromatic 100 μm and 160 μm rest-frame LFs for the combined PEP fields in
Iribarrem et al. (2013) as 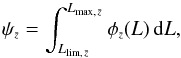 (22)where
(22)where
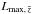 is the brightest source luminosity inside the redshift interval, and
is the brightest source luminosity inside the redshift interval, and
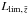 is the rest-frame luminosity associated to the flux limit of the observations.
is the rest-frame luminosity associated to the flux limit of the observations.
The dataset used in this work was built using combined fields, i.e observations carried out in different sky regions at different depths. The large number of sources per redshift interval allowed us to derive the observed quantities with better statistics, at the expense of an added difficulty related to the definition of the luminosity limits corresponding to the actual flux limits of the observations. This difficulty stems from the fact that the computation of the rest-frame luminosity involves k corrections, which in turn depend on the spectral energy distribution (SED) of the source. That is, each SED template defines a slightly different luminosity limit for the same flux limit. In the case of the PEP survey, each field – namely GOODS-N, GOODS-S, COSMOS and ECDF-S – also had a different flux limit, depending on the PACS passband in which the observation was done (Lutz et al. 2011).
To investigate how important the selection function variations caused by the different SED templates in the datasets are, we first computed the selection functions in each redshift interval assuming the lowest computed luminosity among the sources in that interval, and then compared the results to the averages and to the highest luminosities. The variations in the selection functions caused by assuming different luminosity limits were found to be many times greater than the error bars propagated from the LF uncertainties. For example, at z = 0.2, the selection function computed using the lowest monochromatic luminosity in the 100 μm dataset read (9.0 ± 1.8) × 10-3 Mpc-3, while the one computed using the average luminosity read (3.7 ± 0.7) × 10-3 Mpc-3, and the one using the highest luminosity read (2.6 ± 0.5) × 10-3 Mpc-3 – a variation more than three times larger than the combined uncertainties obtained by propagating the ones from the LF parameters. For the same dataset, at z = 1, the selection functions read as (2.3 ± 0.3) × 10-3 Mpc-3, (1.1 ± 0.1) × 10-3 Mpc-3, and (4.9 ± 0.6) × 10-4 Mpc-3, respectively, a variation almost six times larger than the propagated uncertainties.
Selection functions for the rest-frame 100 μm datasets.
Therefore, for every source in each redshift interval, we computed the rest-frame luminosity for the flux limit of the field and filter where it was observed, given its best-fit SED and redshift. Next, we computed a set of selection function values in that redshift interval, using the luminosity limits computed above for each source in the interval. Finally, we computed the average over this set of selection function values for a given redshift interval and used this average as the value for the selection function in that same interval. The uncertainties, as discussed above, are dominated by the variation in the luminosity limits and therefore can be taken simply as the standard deviation over the same set of computed selection function values for each redshift interval. The resulting monochromatic rest-frame 100 μm and 160 μm selection functions are given in Tables 2 and 3.
4. Consistency functions
In the empirical framework of Ribeiro & Stoeger
(2003), Albani et al. (2007), and Iribarrem et al. (2012), the observed quantities computed
in the past lightcone of a given cosmological model were obtained from their predicted
values through what was called a completeness function J(z). This
can be somewhat confusing from the observer’s point of view, since J(z) is not
necessarily related to incompleteness like that of missing sources in a survey, but to the
relation between a theoretical prediction for the number counts and the actual measurement
of that quantity (Iribarrem et al. 2012). In this
sense, this quantity would be better named as consistency function, a term
we use from now on. The consistency function J(z) was obtained by relating the
prediction for the comoving number density nC given by the cosmological model
![\begin{equation} \label{ncth} \nc(z) = \frac{\rho_{\rm M} (z)}{\Mg} = \frac{\Omega_{\rm M}[r(z)]}{\Mg} \, \rho_{\rm C}, \end{equation}](/articles/aa/full_html/2014/03/aa22507-13/aa22507-13-eq134.png) (23)to the selection
functions for a given galaxy survey
(23)to the selection
functions for a given galaxy survey 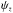 in a given redshift interval
in a given redshift interval 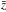 as Iribarrem et al. (2012)
as Iribarrem et al. (2012)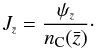 (24)The values for
(24)The values for
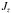 can be obtained numerically for the CGBH void models using Eqs. (10) and (14) combined with the appropriate r(z) table as described in Sect.
2 and the selection functions computed in Sect. 3.
can be obtained numerically for the CGBH void models using Eqs. (10) and (14) combined with the appropriate r(z) table as described in Sect.
2 and the selection functions computed in Sect. 3.
As discussed in Iribarrem et al. (2012), the
estimation of the comoving number density nC assumes a constant, average mass value
ℳ for normalisation purposes –
that is, getting a correct order-of-magnitude estimation of the number density. Such
estimation is not supposed to provide a detailed description of nC(z), but rather to convey
the information on the redshift evolution of the comoving number density caused solely by
the cosmological model, through ρM(z), in Eq. (23). The details of the redshift evolution of
the total masses of the sources, missing in this estimation, are imprinted on the observed
LF and inherited by its derived selection functions. By translating this purely theoretical
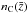 estimation to the corresponding selection functions
estimation to the corresponding selection functions 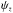 through the consistency function
through the consistency function 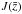 ,
we allow any theoretical quantity that assumes a nC(z) built on a
cosmological model to use the observed values given by the selection functions.
,
we allow any theoretical quantity that assumes a nC(z) built on a
cosmological model to use the observed values given by the selection functions.
Selection functions for the rest-frame 160 μm datasets.
For the purpose of obtaining the relativistic number densities empirically, this approach is sufficient. It minimises the number of theoretical assumptions about the evolution of the sources, such as including a Press & Schechter (1974) formalism, and considers as much information as possible from the observations. Since a Press-Schechter-like formalism is still not implemented on LTB models, the empirical approach described above is the simplest way to work with both standard and void cosmologies in a consistent way.
5. Observed number densities in the past lightcone
We computed the relativistic number densities using the
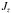 obtained in Sect. 4. By definition, the LF is the
number of sources per unit luminosity, per unit comoving volume. This allows us to identify
the selection functions in Eq. (22) as the
differential comoving density of galaxies stemming from the observations and to rewrite Eq.
(24) as
obtained in Sect. 4. By definition, the LF is the
number of sources per unit luminosity, per unit comoving volume. This allows us to identify
the selection functions in Eq. (22) as the
differential comoving density of galaxies stemming from the observations and to rewrite Eq.
(24) as 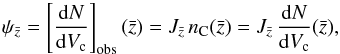 (25)which can still be
written as
(25)which can still be
written as 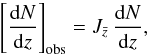 (26)since the purely
geometrical term dVc/dz
cancels out on both sides of the equation. Together with Eqs. (24) and (17), Eq. (26) allows us to obtain the differential number
counts [dN/dz] obs
from the selection function of a given dataset in the different comoving densities
nC(z) defined by the void
model parametrisations considered here.
(26)since the purely
geometrical term dVc/dz
cancels out on both sides of the equation. Together with Eqs. (24) and (17), Eq. (26) allows us to obtain the differential number
counts [dN/dz] obs
from the selection function of a given dataset in the different comoving densities
nC(z) defined by the void
model parametrisations considered here.
Because the quantity inside the parentheses in Eq. (19) is also a purely geometrical term, we can simply write 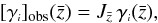 (27)which allows us to obtain
the observed differential densities [γi] obs in
the lightcones of the cosmologies considered here once
(27)which allows us to obtain
the observed differential densities [γi] obs in
the lightcones of the cosmologies considered here once
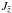 is computed.
is computed.
To obtain the observed integral densities 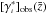 , we substitute
dN/dz in Eq.
(21) with [dN/dz] obs
from Eq. (26) and compute the observed
cumulative number counts
, we substitute
dN/dz in Eq.
(21) with [dN/dz] obs
from Eq. (26) and compute the observed
cumulative number counts 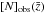 .
Then we can substitute this result back into Eq. (20), since the cosmological distance to redshift relation di(z) is
also fixed by the geometry of the given cosmology.
.
Then we can substitute this result back into Eq. (20), since the cosmological distance to redshift relation di(z) is
also fixed by the geometry of the given cosmology.
6. Results
With the quantities obtained in the last two sections, we can proceed to investigate the differences in the number densities on the comoving frame and on the past lightcone of the standard and void cosmologies.
6.1. Comoving number density evolution
As mentioned above, Mustapha et al. (1997) showed
that any spherically symmetric observation alone, e.g. redshift estimations or number
counts, can be fit purely by a general enough LTB dust model, with no evolution of the
sources required. In the context of the present discussion their argument can be
understood by combining Eqs. (23) and
(24) to write 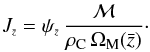 (28)Looking at the
right-hand side of the equation above, one can easily separate its two terms into an
observed quantity to the left and a fraction between theoretically obtained quantities to
the right. Moreover, one can identify the constant ℳ with the lack of a model for the secular
evolution of the average mass of the sources, and
(28)Looking at the
right-hand side of the equation above, one can easily separate its two terms into an
observed quantity to the left and a fraction between theoretically obtained quantities to
the right. Moreover, one can identify the constant ℳ with the lack of a model for the secular
evolution of the average mass of the sources, and 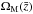 with the evolution of the matter density parameter on a given cosmology. By using the
extra degree of freedom in setting the matter density profile in the LTB model,
ΩM(z), one can obtain a number density
nC(z) that matches the
selection functions perfectly, without the need to assume an evolving average mass
ℳ(z). To
constrain this degree of freedom, it is necessary to have different sets of independent
observations. This is precisely what the GBH parametrisation of a giant void in an LTB
dust model yields: a matter density profile that is parametrised to best fit the
combination of different, independent observations.
with the evolution of the matter density parameter on a given cosmology. By using the
extra degree of freedom in setting the matter density profile in the LTB model,
ΩM(z), one can obtain a number density
nC(z) that matches the
selection functions perfectly, without the need to assume an evolving average mass
ℳ(z). To
constrain this degree of freedom, it is necessary to have different sets of independent
observations. This is precisely what the GBH parametrisation of a giant void in an LTB
dust model yields: a matter density profile that is parametrised to best fit the
combination of different, independent observations.
 |
Fig. 4 Consistency functions for the monochromatic 100 μm LFs computed in the three cosmological models used in the present work. These functions are related to the redshift evolution of the baryon-to-total mass fraction (see text for detail). |
 |
Fig. 5 As Fig. 4 for the monochromatic 160 μm LFs. From these plots, one can see that the difference between the standard model consistency function (black circles) and the void model ones (colour circles) is not very significant, since most of the points lie within the error bars. The pΛ values discussed in Sect. 6.1 quantify this conclusion and agree with it. |
We present the evolution of the consistency functions for the different PACS filters and cosmological models in Figs. 4 and 5. It is clear from these plots that this quantity evolves with redshift in both standard and void cosmologies. The behaviour of the consistency functions in all models studied here are well fit by a power law decreasing with redshift. The best-fitting slopes are given in Table 4. These results suggest that not considering the evolution of the sources leads to a systematic trend that increases the inconsistency with z. This is not as obvious as it may seem given the flexibility of the LTB models as discussed above. It is the parametrisation of ΩM(z) constrained by the combined independent observations of SNe + CMB + BAO that requires ℳ to evolve with z in the LTB models studied here. Only by allowing ℳ to evolve with z can Eq. (28) yield a constant consistency function that indicates that the theoretical term on the right of the right-hand side of Eq. (28) is proportional to the observed term on the left.
We used a Kolmogorov-Smirnoff (KS) two-sample test to check, on a statistical sense, how different the consistency functions are when assuming the different cosmological models studied here from a hypothetically constant consistency function. By design, a constant J(z) indicates that the model for the comoving number density used here, assuming ℳ(z) = ℳ, matches the observed number density. The KS test is a non-parametric, distribution-free way to compare two datasets, and it assigns to which level of confidence we can refute the hypothesis that they were obtained from the same underlying distribution. The resulting p-value of this test can be understood as the probability that both datasets come from the same distribution. For all cosmologies studied here, the no-evolution hypothesis, ℳ(z) = ℳ, is rejected at over 5σ confidence level, with p-values lower than 10-5. This means that an evolving average mass of the sources is also required by the LTB/GBH models studied here.
Next, we use the same KS test to determine how different the consistency functions in the void models are from their standard model counterparts. We present the computed p-values of these tests, pΛ, in Table 4. The pΛ value is the probability that the consistency function for a given void model and the one for the standard model are computed from the same underlying distribution or, in other words, that their differences are not statistically significant. To establish whether such a difference is significant, at a 3σ confidence level, for example, the pΛ value should be lower than approximately 0.0027. Given the listed pΛ results, we found that the computed consistency functions in void and standard cosmologies were not significantly different. This means that galaxy evolution proceeds mostly in the same way, regardless of the differences in the geometry and the composition of the Universe studied here.
Comoving, differential and integral densities statistics.
 |
Fig. 6 Best-fit power laws to the differential density γL (dots),
and the integral density |
6.2. Lightcone inhomogeneities
For this section, we used the observed differential and integral densities obtained in Sect. 5 to investigate the effects of the central underdensity prescribed by the GBH models in the redshift distortions caused by the expanding spacetime on the observer’s past lightcone.
Our previous studies of these relativistic number densities (Ribeiro 2005; Albani et al. 2007; Iribarrem et al. 2012) suggested a high-redshift power-law behaviour for both differential and integral radial distributions. In other words, that expansion distributes the sources along the lightcone in an increasingly self-similar manner. This is a purely geometrical effect, as discussed in Sect. 2, that may or may not be dominant because the hierarchical build-up of galaxies also plays a role in how the sources are distributed along the lightcone. Given that some of the alternative void models are built assuming an LTB line element instead of the standard model FLRW one, we aim in this section to better characterise those power laws and to investigate how they are affected by the secular evolution of the sources and by the direct effect of the expansion of the different geometries. We focus the discussion on the densities computed using the luminosity distance, since the results for the other distance definitions are all qualitatively the same.
As can be seen in Figs. 2 and 3, the geometrical effect increases with the redshift, deviating both
the theoretical differential and the cumulative number densities away from a constant,
homogeneous behaviour at high redshifts. At redshifts lower than z ≈ 0.1, this geometrical
effect is less pronounced, and both γL(z) and
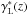 shown follow the constant
average galactic mass ℳ
assumed in their computation, as discussed in Sect. 3.
shown follow the constant
average galactic mass ℳ
assumed in their computation, as discussed in Sect. 3.
It follows that there must be a region in redshift space at which a transition occurs between the power-law behaviour induced by the expansion at high redshift and the behaviour defined by the underlying density parameter ΩM(z) combined with the evolution of the sources stemming from the LF. However, the exact size and range of this region cannot be predicted with the empirical approach for the comoving number densities used in this work. Therefore, if we are to characterise the power-law behaviour of the high-redshift end of our number densities, we must allow our fitting procedure to search for the best redshift at which the power-law behaviour begins to dominate.
To do so, we compute the best linear fit to the log γL vs. log dL tables in an iterative way. Starting with the LF values derived for the highest three redshift bins, we perform the same fit, including one extra LF value in each iteration, in decreasing order, until we have included all points. Then, we select the fit with the lowest reduced χ2 value. The selected fits for the different dataset and cosmology combinations are plotted in Fig. 6. The listed uncertainties are formally obtained taking the square root of the linear term in the covariance matrix of the fitted power law.
To quantify how significant the differences in the slopes of the power laws are, we can
start by first computing the uncertainty of the difference Δa,b, between
the αa slope of
log γL using a given dataset/cosmology
combination a
and that of a different combination b as
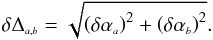 (29)The significance of this
difference in terms of its uncertainty is then obtained from Δa,b/(δΔa,b).
(29)The significance of this
difference in terms of its uncertainty is then obtained from Δa,b/(δΔa,b).
7. Discussion
Next we use the approach above to obtain comparisons between standard vs. void cosmologies, 100 μm vs. 160 μm datasets, and differential densities γ vs. integral densities γ∗.
7.1. Comparison with the LTB/CGBH models
Results for the significance of the difference between slopes of the high-redshift power-law fits to the differential densities γ and the integral densities γ∗, given a fixed cosmological model, were highly dependent on the dataset. They were fairly insignificant with the 100 μm data for all cosmologies (ΛCDM: 0.3σ, CGBH: 0.9σ, OCGBH: 1.1σ); whereas they were all at least marginally significant in the 160 μm data (ΛCDM: 5.2σ, CGBH: 3.0σ, OCGBH: 3.4σ).
Such differences in the slopes between the high-redshift power-law fits to γ and to γ∗ can be understood by checking Eqs. (19) and (20). We note that γ is proportional to dN/dz, whereas γ∗ is proportional to N. Since N is a cumulative quantity, it can only increase or remain constant with increasing redshift. That is, even if there are regions in the volume where N is not defined, which have a lower density of detected sources, N itself will remain constant. On the other hand, dN/dz is sensitive to such local density variations, which adds up to a higher degree of non-homogeneity in the higher redshift part of the past lightcone probed by the survey and as a consequence a steeper power-law slope of γ.
The differences between the slopes of the high-redshift power-law fits to the relativistic densities computed using the 100 μm, and the 160 μm PEP blind-selected datasets were fairly insignificant when assuming the void models studied here (CGBH: 0.7σ for γ, and 0.3 for γ∗; OCGBH: 1.3σ for γ, and 1.0 for γ∗), whereas, those differences showed a moderate-to-strong significance if the ΛCDM model was assumed (4.6σ for γ, and 3.0σ for γ∗).
The differences in the slopes obtained using different datasets can be understood as the effect of different redshift-evolving luminosity limits on the past lightcone distributions. The results above indicated that the distributions on the past lightcone of the void models were significantly less different, hence less affected by the detection limits of the PEP datasets, than their counterparts computed on the past lightcone of the standard model.
Finally, we computed the significance of the differences obtained by comparing the same slopes computed in two different cosmological models. The only marginally significant (≥3σ) difference we found is for the comparison between standard and void models for the integral density γ∗ slopes, using the 100 μm dataset: 3.7σ for the ΛCDM vs. CGBH comparison, and 4.3σ for the ΛCDM vs. OCGBH one. Given the striking concordance of the other γ∗ slopes around a tentative value of −2.5 ± 0.1 it is possible that the oddly low values of the slope of γ∗ in the 100 μm dataset and its uncertainty are an artefact caused by our fitting procedure.
How do we combine the results from all of those different comparisons in a coherent picture? Iribarrem et al. (2013) showed that the corrections needed to build the LF using a flux-limited survey made the results sensitive to the differences caused by changing the underlying cosmological model. Detection limits seem to play a major role in the fully-relativistic analysis used here as well. On one hand, we found significant differences caused by the kind of statistics used (γ or γ∗) with the 160 μm blind-selected catalogue. On the other hand, we found that the cosmology assumed (FLRW/ΛCDM or LTB/GBH) caused significant differences on both γ and γ∗, using the 100 μm dataset instead. Some of these discrepancies could be caused by the way we fit the power laws to the high-redshift parts of the distributions. Future observations with lower flux limits will help us check which of these discrepancies were caused by the present flux limits.
7.2. Comparison with other LTB models
It is important to notice that the results in both Sects. 6.1 and 6.2, together with the discussion presented above, are only valid for a very special case of LTB models, namely, the parametrisation for the CGBH model obtained by Zumalacárregui et al. (2012). It is not in the scope of the present work to present a complete analysis of other LTB models in the literature, which would require first recomputing the LFs presented in Iribarrem et al. (2013) from the start, but given some recent advancements in better exploiting the flexibility of these models, a qualitative discussion of their possible impact on our results is pertinent here.
Assuming different non-homogeneous cosmologies can affect the present analyses in three different ways. First, in terms of building the LF from the observations, a model with a matter density profile ΩM(r) that is different enough from the ones studied here could possibly make the average homogeneity assumption at the heart of the 1/Vmax LF estimator invalid. Using mock catalogues, Iribarrem et al. (2013) showed that the void shapes of the CGBH models used in their LF does not significantly affect the ability of the 1/Vmax estimator to recover the underlying LF.
Second, different distance-to-redshift relations could also affect the LF results, and thus its redshift evolution, through the computation of the maximum observable redshift of each source zmax, which is used in computing of the 1/Vmax value of the LF in each redshift bin. As discussed in Iribarrem et al. (2013), this comes as a result of the fainter part of the galaxies in a survey having fluxes near the limit of observation in the field and is affected mainly by differences in the luminosity distance-to-redshift relation. Also, at luminosities L ≈ L∗, the zmax of the sources is safely hitting the higher z limit of the redshift bin, leading their volume correction to be independent of their luminosity, hence of the dL(z) relation.
Finally, the expected number densities in the past-lightcone γi and
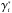 , as
computed in Sect. 2.2 are both sensitive to the
distance-to-redshift relations, as shown in Figs. 2
and 3. The differences caused on the number densities
by the different distance relations might be large enough to be detected, given the
observational uncertainties stemming from the LF. Considering the present results, such
differences in the expected number densities should be greater than the CGBH-to-FLRW ones
studied here, if we were to detect a significant effect on the observed number densities
caused by differences in their expected values alone.
, as
computed in Sect. 2.2 are both sensitive to the
distance-to-redshift relations, as shown in Figs. 2
and 3. The differences caused on the number densities
by the different distance relations might be large enough to be detected, given the
observational uncertainties stemming from the LF. Considering the present results, such
differences in the expected number densities should be greater than the CGBH-to-FLRW ones
studied here, if we were to detect a significant effect on the observed number densities
caused by differences in their expected values alone.
February et al. (2010) argue that CMB and BAO constraints may be significantly distorted by differences in the evolution of primordial perturbations caused by the curvature inside the voids. They go on to fit a number of different shapes for the inner matter profile, considering only local Universe data, namely, SNe Ia and the reconstruction of H(z) through passively evolving galaxies. They show that all their models mimic the FLRW dL(z) to sub-percent level, which should lead to the changes in the maximum redshift estimates and in the expected number densities caused by assuming such models comparable to the ones we observe here.
The authors show in their Fig. 9 that up to redshift z ≈ 1, their best-fit models follow closely the distance modulus, and thus the dL(z) relation of ΛCDM. Looking at the same plot, we can see that the luminosity distances grow increasingly smaller when compared to their standard model counterparts at higher redshifts. Looking at Eq. (20), we can expect that this could potentially lead to higher values of γ∗ and, consequentially, a lower value for its best-fit power law.
Also, their best-fit voids are much larger than the ones used here, as can be seen by comparing the upper left-hand panel of their Fig. 7 versus the upper panel of Fig. 1 in Iribarrem et al. (2013), which shows the best-fit voids of Zumalacárregui et al. (2012). Mock catalogue tests should be used to make sure these larger voids do not bias the 1/Vmax method used here. However, as argued in Iribarrem et al. (2013), if the large under-dense profiles used here varied smoothly enough not to significantly bias the LF estimator, we do not expect that the larger voids of February et al. (2010) will.
Clarkson & Regis (2011) discuss the implications of allowing for inhomogeneity in the early time radiation field and the way it affects the constraining power of CMB results for inhomogeneous models. They show, for example, that even models that are asymptotically flat at the CMB can be made to fit if the matter density profile includes a low-density shell around the central void. An under-dense shell like this could possibly lead the 1/Vmax method to over-estimate the volume correction of sources with maximum observable comoving volume inside or beyond the shell, because such corrections are based on the assumption of an average homogeneous distribution. To test in detail how accurately this LF estimator would recover the underlying distribution, we would need to build mock catalogues that assume the matter distribution of these models, but we expect that such differences, if present, would show more prominently at mid to high redshift, according to the size of the shell, and make the faint-end slope steeper by assigning higher over-estimated corrections to the fainter sources. Depending on how non-homogeneous the matter profile is, an over-estimation of the characteristic number density parameter φ∗ might also be detected.
Varying bang-time functions tbb(r) were also studied (Clifton et al. 2009) and shown to be an extra degree of freedom that helps LTB models to reconciliate CMB + H0 constraints. Bull et al. (2012), however, show that models with varying tbb(r) constrained by the combination of SNe + CMB + H0 should produce a kinetic Sunyaev-Zel’dovich effect that is orders of magnitude stronger than its expected upper limits. It is not clear how allowing for this extra degree of freedom would change the key quantities shown to affect our results: the dL(z) and r(z) relations and the shape of the central under-dense region. Only a full-fledged analysis, starting from the building up of the LF and assuming a model with a varying bang-time fit by the observations, would allow us to make any reasonable comparison with the results presented in this work.
8. Conclusions
In this paper we derived the theoretical results needed to compute the differential and integral densities along the past lightcone of LTB dust models. We applied these results to computing the theoretical predictions for such quantities in the CGBH parametrisations of Zumalacárregui et al. (2012).
We computed the selection functions stemming from the far-IR LFs of Iribarrem et al. (2013), which allowed us to establish, at an over 5σ confidence level, that geometry alone is not able to fit their behaviour, given the LTB/CGBH parametrisation of Zumalacárregui et al. (2012). This finding confirms the need to allow for evolution of the sources (either in number or in luminosity) in this particular class of void models as well. We found no strong evidence of any dependence of this evolution on the cosmological models studied here. In other words, the combined merger tree and barionic processes needed to reproduce the redshift evolution of the FIR LF in the CGBH void models are not significantly different from the hierarchical build up and astrophysical processes in the standard model.
Finally, we computed the observed differential and integral densities in the past lightcone
of both standard and void cosmologies, and fitted their high-redshift observational
non-homogeneities using power laws. We show that the systematic dependency of the
LF methodology on the cosmology that was discussed in Iribarrem et al. (2013) could still lead to significant differences in these
relativistic number densities. The integral densities showed a somewhat consistent slope
across all combinations of blind-selected datasets and cosmological models studied here. On
the other hand, the differential densities were found to be sensitive to a change in
cosmological model assumed in their computation. These results confirmed the power-law
behaviour of the galaxy distribution on the observer’s past lightcone of the LTB/GBH models
and allowed a tentative value of −2.5 ± 0.1 to be obtained for the cumulative radial statistics
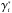 of this
distribution, regardless of the cosmological model assumed.
of this
distribution, regardless of the cosmological model assumed.
Acknowledgments
This work was jointly supported by Brazil’s CAPES and ESO studentships. S.F. is supported by the South African Square Kilometre Array (SKA) Project.
References
- Albani, V. V. L., Iribarrem, A. S., Ribeiro, M. B., & Stoeger, W. R. 2007, ApJ, 657, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Alfedeel, A. H. A., & Hellaby, C. 2010, Gen. Rel. Grav., 42, 1935 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2012, ApJ, 757, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Biswas, T., Notari, A., & Valkenburg, W. 2010, JCAP, 11, 30 [Google Scholar]
- Bolejko, K., Célérier, M.-N., & Krasiński, A. 2011a, Class. Quant. Grav., 28, 164002 [NASA ADS] [CrossRef] [Google Scholar]
- Bolejko, K., Hellaby, C., & Alfedeel, A. H. A. 2011b, JCAP, 9, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnor, W. B. 1972, MNRAS, 159, 261 [NASA ADS] [Google Scholar]
- Bull, P., & Clifton, T. 2012, Phys. Rev. D, 85, 103512 [NASA ADS] [CrossRef] [Google Scholar]
- Bull, P., Clifton, T., & Ferreira, P. G. 2012, Phys. Rev. D, 85, 024002 [NASA ADS] [CrossRef] [Google Scholar]
- Célérier, M.-N. 2007, New Adv. Phys., 1, 29 [Google Scholar]
- Chávez, R., Terlevich, E., Terlevich, R., et al. 2012, MNRAS, 425, L56 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, C., & Regis, M. 2011, JCAP, 2, 13 [Google Scholar]
- Clarkson, C., Ellis, G. F. R., Faltenbacher, A., et al. 2012, MNRAS, 426, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Clifton, T., Ferreira, P. G., & Zuntz, J. 2009, JCAP, 7, 29 [Google Scholar]
- de Putter, R., Verde, L., & Jimenez, R. 2012, AIP Conf. Proc., 1432, 136 [Google Scholar]
- Ellis, G. F. R. 1971, in General Relativity and Cosmology, ed. R. K. Sachs, 104, reprinted in Gen. Rel. Grav., 2009, 41, 581 [Google Scholar]
- Ellis, G. F. R. 2007, Gen. Rel. Grav., 39, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Ellis, G. F. R. 2011, Class. Quant. Grav., 28, 164001 [NASA ADS] [CrossRef] [Google Scholar]
- Ellis, G. F. R., Nel, S. D., Maartens, R., Stoeger, W. R., & Whitman, A. P. 1985, Phys. Rep., 124, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Enqvist, K., & Mattsson, T. 2007, JCAP, 2, 19 [Google Scholar]
- Etherington, I. M. H. 1933, Philosophical Magazine, 15, 761, reprinted in Gen. Rel. Grav., 2007, 39, 1055 [Google Scholar]
- February, S., Larena, J., Smith, M., & Clarkson, C. 2010, MNRAS, 405, 2231 [NASA ADS] [Google Scholar]
- Fleury, P., Dupuy, H., & Uzan, J.-P. 2013, Phys. Rev. Lett., 111, 091302 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Gabasch, A., Bender, R., Seitz, S., et al. 2004, A&A, 421, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gabasch, A., Hopp, U., Feulner, G., et al. 2006, A&A, 448, 101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia-Bellido, J., & Haugbølle, T. 2008, JCAP, 4, 3 [Google Scholar]
- Gruppioni, C., Pozzi, F., Zamorani, G., & Vignali, C. 2011, MNRAS, 416, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppioni, C., Pozzi, F., Rodighiero, G., et al. 2013, MNRAS, 432, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Hellaby, C. 2012, JCAP, 1, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Hellaby, C., & Alfedeel, A. H. A. 2009, Phys. Rev. D, 79, 043501 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, B., Tojeiro, R., Jimenez, R., et al. 2013, ApJ, 762, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, N. P., Maartens, R., & Matravers, D. R. 2012, Gen. Rel. Grav., 44, 3197 [NASA ADS] [CrossRef] [Google Scholar]
- Iribarrem, A. S., Lopes, A. R., Ribeiro, M. B., & Stoeger, W. R. 2012, A&A, 539, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iribarrem, A., Andreani, P., Gruppioni, C., et al. 2013, A&A, 558, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keenan, R. C., Barger, A. J., Cowie, L. L., et al. 2012, ApJ, 754, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Krasiński, A. 2014, Phys. Rev. D, 89, 0235202013 [Google Scholar]
- Lin, H., Yee, H. K. C., Carlberg, R. G., et al. 1999, ApJ, 518, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, G., Lu, Y., Chen, X., et al. 2012, ApJ, 758, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, D., Poglitsch, A., Altieri, B., et al. 2011, A&A, 532, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marra, V., & Pääkkönen, M. 2010, JCAP, 12, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Meures, N., & Bruni, M. 2012, MNRAS, 419, 1937 [Google Scholar]
- Moresco, M., Cimatti, A., Jimenez, R., et al. 2012, JCAP, 8, 6 [Google Scholar]
- Moss, A., Zibin, J. P., & Scott, D. 2011, Phys. Rev. D, 83, 103515 [NASA ADS] [CrossRef] [Google Scholar]
- Mustapha, N., Hellaby, C., & Ellis, G. F. R. 1997, MNRAS, 292, 817 [NASA ADS] [Google Scholar]
- Nadathur, S., & Sarkar, S. 2011, Phys. Rev. D, 83, 063506 [NASA ADS] [CrossRef] [Google Scholar]
- Nishikawa, R., Yoo, C.-M., & Nakao, K.-I. 2012, Phys. Rev. D, 85, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration Int. XIII. 2013, A&A, 561, A97 [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Rangel Lemos, L. J., & Ribeiro, M. B. 2008, A&A, 488, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Regis, M., & Clarkson, C. 2012, Gen. Rel. Grav., 44, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Ribeiro, M. B. 1992, ApJ, 388, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ribeiro, M. B. 2005, A&A, 429, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ribeiro, M. B., & Stoeger, W. R. 2003, ApJ, 592, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Sollerman, J., Mörtsell, E., Davis, T. M., et al. 2009, ApJ, 703, 1374 [NASA ADS] [CrossRef] [Google Scholar]
- Sussman, R. A. 2010, Class. Quant. Grav., 27, 175001 [NASA ADS] [CrossRef] [Google Scholar]
- Valkenburg, W., Marra, V., & Clarkson, C. 2014, MNRAS, 438, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., & Zhang, T.-J. 2012, ApJ, 748, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, P., & Stebbins, A. 2011, Phys. Rev. Lett., 107, 041301 [NASA ADS] [CrossRef] [Google Scholar]
- Zibin, J. P. 2011, Phys. Rev. D, 84, 123508 [NASA ADS] [CrossRef] [Google Scholar]
- Zumalacárregui, M., García-Bellido, J., & Ruiz-Lapuente, P. 2012, JCAP, 10, 9 [Google Scholar]
All Tables
Best fit values for the LTB/CGBH models from Zumalacárregui et al. (2012) used in this work.
All Figures
 |
Fig. 1 Differential number count estimates within the past lightcone of the three cosmological models used in the present work. |
| In the text | |
 |
Fig. 2 Redshift evolution of the relativistic differential densities for the three cosmological models used in the present work. Different curves correspond to the computations performed with respect to different distance estimators along the observer’s past lightcone (dA, dL, dG, and dz). |
| In the text | |
 |
Fig. 3 Integral of the functions shown in Fig. 2. The curves show the evolution of the relativistic integral densities for the three cosmological models used in the present work as a function of the different distances. |
| In the text | |
 |
Fig. 4 Consistency functions for the monochromatic 100 μm LFs computed in the three cosmological models used in the present work. These functions are related to the redshift evolution of the baryon-to-total mass fraction (see text for detail). |
| In the text | |
 |
Fig. 5 As Fig. 4 for the monochromatic 160 μm LFs. From these plots, one can see that the difference between the standard model consistency function (black circles) and the void model ones (colour circles) is not very significant, since most of the points lie within the error bars. The pΛ values discussed in Sect. 6.1 quantify this conclusion and agree with it. |
| In the text | |
 |
Fig. 6 Best-fit power laws to the differential density γL (dots),
and the integral density |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.