EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 563 (March 2014) A&A, 563 (2014) A55 Full HTML
Free Access
Issue
A&A
Volume 563, March 2014
Article Number A55
Number of page(s) 8
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201118470
Published online 06 March 2014

© ESO, 2014

1. Introduction

The interstellar medium (ISM) is the region in space between the stars. It is composed of gas-phase species (mainly hydrogen and helium atoms) and submicron dust grains (silicates, carbon-rich particles, and ices) (Hughes 2009). One of the topics of long-standing interest in astrobiology and also in prebiotic chemistry is the search for amino acids and their precursors in the ISM. Many organic compounds such as hydrocarbons, amino acids, diamino acids, aldehydes, carboxylic acids, tertiary amines, the hydroxy amino acids: serine, threonine, allothreonine, and tyrosine and even nucleobases were found in meteorites (Pizzarello & Shock 2010; Pizzarello & Holmes 2009; Pizzarello 2009). Of the molecules delivered to the early Earth, the amino acids have tremendous chemical, biochemical and biological significance as key building blocks of proteins, enzymes, and peptides. They have implications in biologically important compounds for the origin of life and therefore deserve particular attention (Largo et al. 2010; Hughes 2009; Miao et al. 2005). Amino acids have been observed in a number of carbonaceous chondrite meteorites of different classes. Thus the study of the origin and distribution of extraterrestrial amino acids has been the focus of several research studies (Kvenvolden et al. 1970; Cronin & Moore 1971; Cronin & Pizzarello 1983; Pizzarello et al. 1991; Ehrenfreund et al. 2001b; Glavin et al. 2006; Elsila et al. 2007).

We are currently concerned with serine, which is a hydroxy amino acid. This is a polar and non-essential amino acid with the molecular formula HO2CCH(NH2)CH2OH. It also has the H-bonding group -OH and -NH. It was detected in abundance in CR2 meteorites (GRA 95229 and LAP 02342), but not as much in CM2 meteorites (Pizzarello & Shock 2010; Pizzarello 2009). Bada et al. (1998) found traces of serine in ALH84001. They found a similar distribution in another Antarctic meteorite, EETA79001, and in Allan Hills glacial ice (Yockey 1998). Serine has also been detected as a product of UV irradiation of ice analogs (Blanco et al. 2007).

Elsila et al. (2007) have proposed Strecker synthesis and radical-radical mechanisms for the formation of glycine and serine using methanol (CH3OH), hydrogen cyanide (HCN), and ammonia (NH3) via UV photolysis and hydrolysis. Woon (2002a,b) demonstrated the formation of serine by direct addition of CH2OH in glycine (NH2CHCOOH). Blanco et al. (2007) have performed the spectroscopic analysis of seven conformers of serine, which is relevant to determine the existence of serine in the ISM (Perez et al. 2011). The analogs of icy interstellar grains (an ice film consisting of amorphous H2O, NH3, CH3OH, and HCN) at 15 K were irradiated by ultraviolet (UV) light in vacuum. After warming the ices to room temperature, which hydrolyzed them, the racemic amino acids glycine, alanine, and serine were obtained (Berstein et al. 2002). The mechanism for the formation of the amino acids glycine, serine, and alanine, in interstellar ice analogs was investigated using isotopic labeling techniques, which indicate the multiple pathways for the amino acid formation (Elselia et al. 2007; Fukue 2010).

Simulating the formation and reactions of amino acids and their precursors in the ISM is a difficult task, and it is necessary to propose the reactions that can occur at extremely low densities and temperatures. Reaction mechanisms that involve several intermediate and transition states can be effectively studied computationally. It is unlikely that amino acids formed by the gas-phase reactions that are normally considered for interstellar chemistry; an alternative process is that the molecules are chemically created in the bulk solvation model. In spite of experimental evidence very little is known about the reactions through which amino acids are formed. There is rapidly growing interest in the use of computational chemistry to study the mechanisms of interstellar organic reactions, which are difficult to detect and identify experimentally. Quantum mechanical calculations provide a direct tool for the understanding of systems that are too complex to be observed experimentally, and it also gives a detailed view of transition state geometries for predicting the mechanisms of organic chemical reactions.

Within this perspective we propose an entirely new exothermic reaction path for the formation of serine through some detected interstellar molecules and radicals, viz., CH (Naylor et al. 2010; Gerin et al. 2010), CO (Latter et al. 1993), NH2 (Dishoecck 1993; Kerns et al. 1972), CH2 (Polehampton 2005; Hollis et al. 1995), and the hydroxyl group OH, an oxygen-rich source in the ISM, (Robinson et al. 1967; Storey et al. 1981; Weinreb et al. 1963; Barrett 1964; Ziurys 2006). These molecules and radicals are abundant in the ISM. Radical-radical and radical-neutral reaction mechanisms are proposed in this reaction path in the gas phase. Our approach has a model character to it. Finding a viable, thermodynamically feasible, step-by step mechanism that can account for the formation of serine in the ISM was challenging. Using quantum-chemical techniques, we explored the formation of serine in five steps through the anticipated reaction path. In each step of the reaction we determined the intermediate products, transition states, and the potential energy curve with its potential barrier. This potential energy curve signifies the feasibility of serine formation through this reaction path in interstellar space.

The density functional theory (DFT) with the B3LYP functional, which employs Becke’s three exchange functionals, and Lee-Yang-Parr correlation functional, in particular have proven highly effective, at least as long as an appropriate basis set was used. It is now well established as a method that can compute potential energy surfaces (PES) for organic reactions described by a single electronic configuration. Basis set extensions with polarization and diffuse functions are useful to properly describe the lone pair and intermolecular interactions, which are very important in controlling the reactivity in the reactions of organic molecules.

2. Methodology

To gain insight into the formation mechanism of serine, electronic structure calculations were performed using GAUSSIAN09 (Frisch et al. 2003) software. Glaser (2007) reported that the DFT calculations are widely used in the chemistry community because it succeeds in reproducing the experimental data with high reliability. The geometries of the reactants, products, intermediates, and transition states were calculated using the DFT with the B3LYP functional with a 6 − 311G+(2df, 2p) basis set, and we improved the energy description even more by single-point calculations with hybrid meta exchange correlation DFT functionals M06 and M06 − 2X to calibrate the high computational cost and low-level calculations. M06 − 2X and M06 functionals are recommended to study thermo chemistry, kinetics, and non-covalent interactions (Zhao & Truhlar 2006, 2008; Morgado et al. 2010; Hohenstein et al. 2008). The chemical analysis calculates the energy requirement for the reaction path; all calculations were performed at a temperature of 273.25 K and 1 atmospheric pressure. It has also been concluded that the proposed reactions, which are feasible and exothermic at this temperature and pressure, can also have a high probability of occurrence at low temperatures (~100 K) and pressure (≤1 atm) in interstellar space (Singh et al. 2013). The results depend on the conditions of the environment such as radiation field, temperature, and pressure, but our study gives qualitative indicators for serine formation in the ISM. The most suitable reaction pathway is exothermic.

All the stable geometries were optimized and confirmed by the vibrational analysis where no imaginary frequency was found. All transition states using a quadratic synchronous transit algorithm reported here have only one imaginary frequency, and are located without imposing any symmetry constraints during the geometry optimization process. Harmonic vibrational frequencies were calculated for all the optimized structures and used to compute the zero-point energies (ZPEs) to confirm the nature of the stationary points and to produce theoretical activation parameters. In all cases, all transition states were verified to connect a specific pair of stationary points (reactants, products, or minima associated with intermediate species) by performing the necessary intrinsic-reaction coordinates (IRC) calculations. Harmonic frequencies and zero-point energies were calculated with analytical force constants at all the optimized geometries. The geometry optimization, energy calculation, vibrational analysis, and zero-point energy correction were computed with the Gaussian 09 programs. The rate coefficients of the reactions were calculated with the relationship called the “Langevin equation”, which is temperature independent (Herbst 2001; Su & Chesnavich 1982) and developed by Bates (1983), 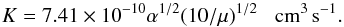K=7.41×10-10α1/2(10/μ)1/2cm3 s-1.\begin{equation} K=7.41\times10^{-10}\alpha^{1/2}(10/\mu)^{1/2}\;\;\;\rm cm^3\,s^{-1}. \end{equation}(1)The polarizable continumm model (PCM), a “bulk solvent medium”, was simulated as a continuum of the dielectric constant. The contributions of bulk solvent effects to the activation free energy of the reactions under study were calculated via the self-consistent reaction field (SCRF) method using the PCM as implemented in Gaussian 09. The solvation effect was evaluated in water solution by single point at the B3LYP, M06, and M06 − 2X level.

thumbnail Fig. 1

Energy diagram showing the geometries of reactants, intermediate products (P2, P4, P6, P8), transition states (TS) and products (P1, P3, P5, P7, P9) involved in the reaction steps of serine formation at (A) B3LYP/6-311G+(2df, 2p), single-point calculation, (B) M06 and (C) M06-2X level of theory. All the energies of the molecules including ZPE corrections are given in atomic unit (energy values given in parenthesis are in kcal/mol). (Coding of atoms is manual to distinguish between atoms. The code and its respective atom are as follows: 1-H, 2-C, 3-C, 4-O, 5-O, 6-H, 7-N, 8-H, 9-H, 10-C, 11-H, 12-H, 13-O and 14-H.)

thumbnail Fig. 1

continued.

3. Results and discussion

There are mainly two types of the radical-molecule reactions, (a) bimolecular reactions between radical and molecules, such as addition, displacement, atom abstraction; and (b) unimolecular reactions such as fragmentation and rearrangement. Out of these, the addition, displacement, and rearrangements are important for interstellar chemistry. In the proposed reaction serine is formed via radical-radical and radical-neutral mechanism reactions in following five steps:

Step 1CH + CO → HCCO Step 2CHCO + OH → CHCOOH Step 3CHCOOH + NH2 → NH2CHCOOH Step 4NH2CHCOOH + CH2 → CH2(NH2)CHCOOH Step 5 CH2(NH2)CHCOOH + OH → (OH)CH2(NH2)CHCOOH.

thumbnail Fig. 2

Structure of possible products in the steps of serine formation with the sum of electronic and zero-point energy in hartee.

Table 1

Geometrical parameter: Bond lenghts of reactants, intermediate products, transisition states, and final products in steps 1 to 5 for serine formation using B3LYP/6-311G+(2df, 2p).

The abundance of the observed CH and CO radicals in the ISM favors the initiating reaction having a relatively high rate coefficient. However, stabilization is achieved by a final electronic transition. Figure 1 presents all five steps of the reaction process with zero-point energy-corrected energies for reaction and the optimized geometries of R (reactants), TS (transition state) and P (intermediate and final product) for the reactions of serine formation at the B3LYP/6-311G+(2df, 2p) and single-point calculations with the M06/6−311G+(2df, 2p) and M06−2X/6−311G+(2df, 2p) level. The atom numbering given in Fig. 1 is used for the discussion below. Some of the bond lengths and bond angles are presented in Table 1. In each proposed reaction step, there is possibility of formation of various other products, which are shown in Fig. 2. The most stable structure was used for the final product.

3.1. Step 1 CH+CO → HCCO

This step involves the reaction between CH and CO to produce HCCO. The two reactants are well detected in interstellar space. The abundances of these molecules depend on the region and its temperature in the ISM. The averaged column density of CH is ≈1013–1014 cm-2 in diffuse clouds (Elitzur et al. 1978, 1980; Gredel et al. 1993), and the column density of CO is in the range 1012–1015 cm-2 (Frerking et al. 1982; Frederman 1980). In this process, the carbon atom (C3) (with a charge − 0.011 e.s.u.) of CO is attracted toward the C2 carbon atom (with a charge − 0.100 e.s.u.) of CH forming CHCO. Since the C2 atom has a single unpaired electron, HCCO acquirs the doublet spin or its multiplicity will be 2. This is a barrierless and exothermic reaction.

The formation of product P1 (HCCO) from reactants occurs with considerable reaction energy. This reaction energy was calculated under the three different functionals B3LYP, M06 and M06 − 2X with the basis set 6 − 311 +(2df, 2p). The obtained values are 78.89, 76.75 and 82.62 kcal/mol, respectively. These values indicate that the calculation with the M06 functional yields a high reaction energy value, that is, a high exothermic energy. These reaction energy values show the exothermicity of the reaction at various functional calculations. ΔG (Gibbs free energy) and ΔH (enthalpy) of this reaction are − 70.91 and − 80.25 kcal/mol, respectively, with the B3LYP method, that is, ΔG < 0 and ΔH < 0, which verifies that the reaction is spontaneous and exothermic.

There may be other possible products of this reaction, but the product we selected here is the most stable one and contains lowest energy amongst its isomers, which were observed using scanning process. This product closely resembles in geometry the one proposed by Sattelmeyer (2004), which shows that HCCO is the isomer that contains the lowest energy. The product formed after this step is HCCO, detected in TMC− 1 and Sgr B2 clouds (Turner & Sears 1989). HCCO is also an important intermediate in combustion chemistry and in the formation of other interstellar molecules (Huang et al. 2008).

The Mulliken charge distribution of all the atoms of the product HCCO makes the product electrically neutral. The oxygen atom (O4), carbon atoms (C3 and C2), and the hydrogen atom (H1) have charges of −0.237, 0.269, −0.206 and 0.174 e.s.u., respectively. The dihedral angle of HCCO is −179.98°.

All the optimized geometries and the potential energy curve of this reaction step are shown in step 1 of Fig. 1.

3.2. Step 2 HCCO+OH → CHCOOH

This reaction process is similar to the previous reaction. In this step the lowest-energy isomer of product of the step 1 reaction reaches OH. OH has a considerable abundance in interstellar space. The OH column densities in the spiral-arm clouds along the sightlines to W49N, W51, and G34.26 + 0.15 were found to be on the order of 1014 cm-2, which corresponds to a fractional abundance of 10-7–10-8, which is similar to that of H2O (Wiesemeyer et al. 2012). It begins with the addition of oxygen atom (O5) (with a charge −0.245 e.s.u.) of OH to C 3, by disrupting the double bond between C2 and C3, forming CHCOOH. There is no unpaired electron from which CHCOOH acquires the singlet spin, or its multiplicity will be 1. There is no potential barrier at the entrance channel between the reactants and the intermediate product P2. The relative energy of P2 under the three different functionals B3LYP, M06, and M06−2X with the basis set 6−311 +(2df,2p) is 34.87,37.74, and 40.70 kcal/mol, respectively.

The TS, with a vibrational frequency −510.20 cm-1, of this step occurs with the potential barrier of approximately 6.21,6.45, and 6.42 kcal/ mol, respectively, through the B3LYP, M06, and M06−2X calculations. All these potential barriers are low enough to be penetrated by the intermediate product to form the final product of this reaction step (P3).

The transition-state energy is higher than the energy of P2 and the reaction step product P3 (CHCOOH). Its relative energy with respect to the product is 8.58,9.20, and 9.12 kcal/mol calculated with all three functionals. As in step 1, ΔG (Gibbs free energy) and ΔH (enthalpy) of this reaction are −38.86 and −38.92 kcal/mol with the B3LYP method, that is, ΔG < 0 and ΔH < 0, which verifies that the reaction is spontaneous and exothermic. The product formed after this second step (CHCOOH) is a dehydrogenated form of the acetic acid CH3COOH, which has been detected in Sgr B2 (Mehringer et al. 1997). Bennett & Kaiser (2007) have also discussed the formation of acetic acid in interstellar ice analogs. Hence there is a high probability that exists CHCOOH in the ISM.

All the optimized geometries and the potential energy curve of this reaction step are shown in step 2 of Fig. 1.

3.3. Step 3 CHCOOH + NH2→ NH2CHCOOH

In this step the stable product of the step 2 reaction reacts to NH2. NH has a higher abundance in the interstellar space than the previously mentioned molecules. NH2 is located in the low-density envelope in front of the dense hot cores seen in emission lines of other molecules. The NH2 molecule has a column density of 5 × 1015 cm-2 and a fractional abundance relative to H2 of (1−3) × 10-8 (Dishoecck et al. 1993). The initially intermediate product P4 of this reaction step is formed with the addition of nitrogen atom (N7) (with a charge −0.356 e.s.u.) of NH2 to C2 of CHCOOH. The C2 −C3 bond loses its character and elongates to 1.53 Å. The relative energy of P4 is −110.50, −118.32, and −111.86 kcal/mol with the B3LYP, M06 and M06−2X functional. There is no positive potential barrier relative to the reactants.

The transition state is found to have a vibrational frequency − 626.50 cm-1 and a potential barrier of 15.00,13.81, and 13.77 kcal/mol relative to P4 with all three used functionals, B3LYP, M06 and M06 − 2X, respectively. After formation of TS, the PES decreases and the final product of this reaction step P5 (NH2CHCOOH) is formed, whose relative energy with respect to the transition state is 17.09,16.26, and 13.77 kcal/mol with all three above mentioned functionals. The C2 atom has a single unpaired electron, due to which NH2CHCOOH acquires the doublet spin or its multiplicity will be 2. NH2CHCOOH is the most stable form of glycine in its radical cation state (Rimola et al. 2012). Kuan et al. (2003) has claimed the detection of glycine in the ISM which was disputed by Snyder et al. (2005). Subsequently, various studies have been made on the formation of glycine and its precursors in the ISM (Largo et al. 2010; Hernandez et al. 2011). Majumdar et al. (2012) have also shown that NH2CHCOOH can be formed by fragmentation of glycine with a reaction rate 7.22 × 10-10 cm3 s-1. Belloche et al. (2008) reported positive results on the delectability of amino acetonitrile in Sgr B2 (N), which possibly is a direct precursor of glycine. These results also strengthen the possibility that glycine and its precursors exist in the ISM. Protonated glycine is predicted to be the most stable isomer of the family, although its abundance is expected to be very low (Lattelais et al. 2011). This indicates another possibility that NH2CHCOOH is present in the ISM.

As in the previous two steps of the reaction path, the ΔG (Gibbs free energy) and ΔH (enthalpy) of this reaction is − 102.49 and −114.04 kcal/mol with the B3LYP method, that is, ΔG < 0 and ΔH < 0, which verifies that the reaction is spontaneous and exothermic.

All the optimized geometries and the potential energy curve of this reaction step are shown in step 3 of Fig. 2.

3.4. Step 4 NH2CHCOOH + CH2→ CH2(NH2)CHCOOH

As in the previous steps, in this reaction step the product of step 3 reacts with another interstellar molecule, CH2. CH2 is thought to be abundant in primarily diffuse and dense clouds. The CH2 abundance based on N(H2) ~3 × 1023 cm-2 is on the order of 1015–1014 cm-2 (Hollis et al. 1995).

In the formation of the intermediate product, P6, of this step, the carbon atom C10 (with a charge − 0.216 e.s.u.) of CH2 becomes attached to the C2 of NH2CHCOOH. The relative energy of P6 is −78.48, −85.08, and − 80.95 kcal/ mol with the B3LYP, M06, and M06 − 2X functionals, respectively. There is no positive potential barrier relative to the reactants.

After decreasing to P6, the level of the potential surface increases to TS with a vibrational frequency − 218.45 cm-1 and a potential barrier of 0.56, 0.86, and 0.56 kcal/mol relative to P6 with all three used functionals. These barriers are hidden barriers because the C−C addition in this reaction is very spontaneous. Owing to the high reaction-activity of the unpaired electron at C2 of NH2CHCOOH, the lone pair of electrons of CH2 easily reacts with it and easily breaks the coordinate bond at C2 of the NH2CHCOOH. This reactivity of methylene also makes NH2CHCOOH a radical. Then both reactants can easily react with each other because they only have a hidden or negligible barrier.

After increasing to the TS, the potential surface decreases to the energy level of the final product of this reaction step P7 (CH2(NH2)CHCOOH) with a relative energy of −2.17, −2.39, and −2.13 kcal/mol with respect to the TS in the same order of the above mentioned functionals. The C10 atom has a single unpaired electron, therefore CH2(NH2)CHCOOH acquires the doublet spin or its multiplicity will be 2. CH2(NH2)CHCOOH or NH2CH2CHCOOH can be a radical form of alanine (NH2CH3CHCOOH). The amino acid alanine is not detected in interstellar space, but there are strong indications of its presence in the ISM. Alanine was detected in abundance in CR2 meteorites (GRA 95229 and LAP 02342) and the martin meteorites ALH84001 and Nakhla (Bada et al. 1998; Glavin et al. 1999; Pizzarello et al. 2010). Bernstein et al. (2002) and Ehrenfreund et al. (2001a) demonstrated the experimental synthesis of alanine in the ISM. The possibility that alanine is present in the ISM also strongly supports the existence of NH2CH2CHCOOH in the ISM.

As before, ΔG (Gibbs free energy) and ΔH (enthalpy) of this reaction are − 70.51 and − 81.50 kcal/mol with the B3LYP method, that is, ΔG < 0 and ΔH < 0, which verifies that the reaction is spontaneous and exothermic.

All the optimized geometries involved in this reaction step along with the potential energy curve are shown in step 4 of Fig. 1.

3.5. Step 5 CH2(NH2)CHCOOH + OH → (OH)CH2(NH2)CHCOOH

As mentioned above, OH is an abundant molecule and it is formed by highly abundant sources such as icy grains or water in interstellar space. This is the final step of serine formation in this reaction pathway. Initially, the intermediate product P8 of this reaction step is formed, in which OH (O13) becomes C10 in CH2(NH2)CHCOOH. It is below the energy of reactants and its relative energy is −87.04, −94.49, and −93.62 kcal/mol with the B3LYP, M06, and M06−2X functionals. There is no positive potential barrier relative to reactants.

The potential barrier corresponding to the transition state TS, with a vibrational frequency −235.88 cm-1, is 0.63,0.16, and 0.55 kcal/mol relative to P8 with all three previously mentioned functionals. These barriers are hidden barriers because it is a radical-radical interaction and the radicals are highly reactive. Therefore the reaction needs not occur through a considerable potential barrier. One can say that it is a barrier-less reaction. The OH radical is highly reactive because of high electronegativity. C10 is the most suitable site for this to react because it contains a free electron, and to gain more stability and a minimum energy, it is required that the molecule formed by their interaction is neutral in charge property. Hence OH reacts with C10 and forms the neutral molecule serine (P9).

The relative energy of P9, serine, is −88.23 kcal/mol with respect to reactants. Since there is no unpaired electron, it acquires singlet spin or contains the multiplicity 1.

As in earlier reaction steps, ΔG (Gibbs free energy) and ΔH (enthalpy) of this reaction are −77.84 and −89.91 kcal/mol with the B3LYP method, that is, ΔG < 0 and ΔH < 0, which verifies that the reaction is spontaneous and exothermic.

All the involved optimized geometries and the potential energy curve of this reaction step are shown in step 5 of Fig. 1. The infrared spectrum of the final product serine is shown in Fig. 3. The IR spectra of serine, obtained by our theoretical calculations, agree well with the spectra mentioned by Lambie et al. (2004).

Table 2

Geometrical parameter: Bond angles of reactants, intermediate products, transition states, and final products in the steps 1 to 5 for serine formation using B3LYP/6-311G+(2df, 2p).

thumbnail Fig. 3

Theoretical (DFT(B3LYP/6-311G+(2df, 2p)) infrared spectrum of serine.

The rate coefficients or radiative association coefficient of all the involved reactions in serine formation were calculated at the B3LYP/ 6−311G+(2df, 2p) level and its values are of the same order as suggested by Bates (1983) (Table 5). On the basis of the energy and geometry calculations, we conclude that the intermediate products are the conformers of the final product of each reaction step. The energy values suggest that the final products of every reaction step have a lower energy than the intermediate products and are formed after crossing the potential barrier. Hence the final products are more stable and considered as the reactant for next reaction step.

All the reported products of each reaction step are not yet identified in the ISM, but various similar/related molecules have been detected in the ISM, such as glycine and acetic acid and therefore it is very likely that they exist. HCCO has been detected in the ISM.

Bond lengths, geometry, and other parameters of the serine formed in our calculation agree well with experimental (Rauk et al. 1997) and previously calculated (Iseri 2004) values. The values of all bond lengths and angles of all geometries calculated using B3LYP/ 6 − 311G +(2df, 2p) in the gas phase and used in serine formation are listed in Table 1.

The geometry of the transition state is another important factor. The barrier energy is defined as the relative energy between the intermediate product and TS. The change of structure leads to the change of barrier energy. Our calculation predicts that in the gas phase the barrier energy of step 3 of the reaction is 15.00 kcal/mol and 6.21 kcal/ mol in step 2 using B3LYP/ 6−311G +(2df,2p). Our computed reaction barriers in step 2 of the reaction at B3LYP level are lower while in other steps it is higher than at the M06 and M06−2X level. The B3LYP single-point reaction barrier is only about 1 kcal/mol, which is higher than the M06 and M06−2X result in step 3. Moreover, an aqueous medium facilitates the reaction, because both specific and bulk solvations lower the barrier of the rate-determining step further. The computed reaction profile with low-energy barriers reveals the feasibility of serine formation under abiotic conditions. The detailed computational investigations of step-by-step formation pathways show the serine formation abiotically. These results are very encouraging and demonstrate that there is an immediate prospect of obtaining the many transitions necessary for a definitive detection of interstellar serine.

All the electronic energies obtained with the zero-point correction in the gas phase and PCM are given in Tables 2 and 3 respectively. Radiative association requires that the stabilizing radiative transitions are sufficiently fast, therefore we also performed the reactions in icy grains, which act as a third body for absorbing the additional released energy. Hence the results of the PCM model are more appropriate than those of the gas-phase model.

Table 3

Electronic (EE), zero-point correction (ZPE), and total energies of molecules and radicals in the gas phase using the B3LYP/6-311G+ (2df, 2p), M06/6-311G+ (2df, 2p), and M06(2X)/6-311G+ (2df, 2p) calculations.

Table 4

Electronic (EE), zero-point correction (ZPE), and total energies of molecules and radicals in the PCM using the B3LYP/6-311G+ (2df, 2p), M06/6-311G+ (2df, 2p), and M06(2X)/6-311G+ (2df, 2p) calculations.

We performed five reaction steps, and the product of each reaction step was used as the reactant in the next reaction step. To acquire the highest stability the product of each step should have the lowest energy, because only this lowest energy product can provide high stability in the next step product and we can achieve a lowest energy final product, serine. For obtaining the lowest energy conformation product, the potential energy surface was explored through 10-degree and 18-degree rotation along the bonding (at reacting site) at which the product was formed by the reactants. Then the geometry (isomers) that contained the lowest energy was taken as the product of that particular reaction step. This method was also used for the final product serine, which also has the lowest energy among its isomers. The graphs of the scanning process for all reaction steps are drawn and reported in the supplementary material (Fig. 1).

It is clear from the energy curves that all reactions are exothermic. All reaction steps contain ΔH < 0, which shows that the reaction is spontaneous in forward direction, although some reaction barriers are lower than 5 kcal/mol and some are higher than this, which is considerable. We showed that the transition states even have hidden barriers. Low or hidden barriers also pointout the feasibility of reactions because they can easily be crossed by an intermediate product to form the final product. The Cartesian coordinates of all the molecules are also reported in the supplementary material (Table 1).

4. Conclusion

Table 5

Rate coefficients of all involved reactions in serine formation in the gas phase at B3LYP/6-311G (d, p).

The possibility of serine formation from some simpler interstellar molecules such as CH, CO, NH2, OH, and CH2, which are detected in the ISM, was explored using quantum-chemical methods. We estimated the potential energy surfaces of each reaction step by calculating the total energies, the electronic energy of all molecules, the radicals, and the transition states formed during the reactions. The structures of reactants, intermediate products, transition-state molecules, and products were optimized. The potential energy curve as shown in Fig. 1 clearly states the finite probability that the serine formation occurs, although the potential barrier in some reactions is higher than 5 kcal/mol, but it can be penetrated and some of reactions have hidden barriers, so there exists a definite possibility for serine formation in the ISM (at very low temperatures). Because of the cold temperatures within the interstellar molecular clouds, reactions with an activation barrier were considered too slow to play an important role for most chemical reactions to occur. The low temperature hinder the molecules from drifting through space to acquire the energy needed to break their bonds, but some reactions might occur when different molecules stick to the surface of cosmic dust grains. This might give them enough time together to acquire the energy needed to react. Reactions with potential barriers of 12−15 kcal/mol can also occur in the ISM and certain key reactions can occur at temperatures below 100 K, in spite of having gas phase barriers that may be 30 kcal/mol or higher (Woon 2002a,b). On that basis our calculated energy barriers lie in the range that may be permissible in the ISM. The values of the rate coefficients and potential barriers show that if these radicals/molecules interact in low temperature and pressure, the feasibility of the reactions increases. Therefore we expect that these reactions are possible in the ISM. The study of the reaction energies, the potential energy curve and all the optimized structures of reactants, TS, intermediate and final products show that serine formation is quite possible in the gas phase as well as in icy grains in the ISM.

Acknowledgments

The authors are grateful to the anonymous referee for useful comments and suggestions, which greatly helped to improve this paper. The authors also thank E. Herbst, Ohio State University, USA for very useful suggestions. Financial support to the authors Alka Misra, Vineet Gupta and Shivani from the University Grant Commission (UGC), under major research project, DS Kothari Fellowship and UGC – BSR meritorious Fellowship, respectively, is gratefully acknowledged.

References

  1. Bada, J. L., Becker, L., Glavin, D. P., & McDonald, G. D. 1998, Science, 279, 362 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bates, D. R. 1983, ApJ, 270, 564 [Google Scholar]
  3. Belloche, A., Menten, K. M., Comito, C., et al. 2008, A&A, 482, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Blanco, S., Sanz, M. E., Lopez, J. C., & Alonso, J. L. 2007, PNAS, 104, 20183 [NASA ADS] [CrossRef] [Google Scholar]
  5. Basiuk, V. A. 2001, J. Phys. Chem. A., 105, 4252 [CrossRef] [Google Scholar]
  6. Bennett, C. J., & Kaiser, R. I. 2007, ApJ, 660, 1289 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bernstein, M. P., Dworkin, J. P., Sandford, S. A., Cooper, G. W., & Allamandola, L. 2002, Lett. Nature, 416, 401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  8. Cronin, J. R., & Moore, C. B. 1971, Science, 172, 1327 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cronin, J. R., & Pizzarello, S. 1983, Adv. Space Res., 3, 5 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  10. Dishoecck, E. F. 1993, ApJ, 416, L83 [NASA ADS] [CrossRef] [Google Scholar]
  11. Ehrenfreund, P., Bernstein, M. P., Dworkin, J. P., Sandford, S. A., & Allamandola, L. J. 2001a, ApJ, 550, L95 [NASA ADS] [CrossRef] [Google Scholar]
  12. Ehrenfreund, P., Glavin, D. P., Botta, O., Cooper, G., & Bada, J. L. 2001b, PNAS, 98, 2138 [Google Scholar]
  13. Elsila, J. E., Dworkin, J. P., Bernstein, M. P., Martin, M. P., & Sandford, S. A. 2007, ApJ, 660, 911 [NASA ADS] [CrossRef] [Google Scholar]
  14. Elitzur, M., & Watson, W. D. 1978, ApJ, L141 [Google Scholar]
  15. Elitzur, M., & Watson, W. D. 1980, ApJ, 236, 172 [NASA ADS] [CrossRef] [Google Scholar]
  16. Federman, S. R., Glassgold, A. E., Jenkins, E. B., & Shaya, E. J. 1980, ApJ, 242, 545 [NASA ADS] [CrossRef] [Google Scholar]
  17. Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
  18. Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2003, Gaussian program package [Google Scholar]
  19. Fukue, T. 2010, Recent Progress in Chirality Research Using Circularly Polarized Light, National Astronomical Observatory of Japan [arXiv:1009.6169] [Google Scholar]
  20. Gerin, M., Luca, M. De, Goicoechea, J. R., et al. 2010, A&A, 521, L16 [Google Scholar]
  21. Glavin, D. P., Bada, J. L., Brinton, K. L. F., & Mcdonald, G. D. 1999, PNAS, 96, 8835 [NASA ADS] [CrossRef] [Google Scholar]
  22. Glavin, D. P., Dworkin, J. P., Aubrey, A., et al. 2006, Meteoritics Planet. Sci., 41, 889 [NASA ADS] [CrossRef] [Google Scholar]
  23. Glaser, R., Hodgen, B., Farrelly, D., & Mckee, E. 2007, Astrobiol., 7, 455 [NASA ADS] [CrossRef] [Google Scholar]
  24. Gredel, R., van Dishoeck, E. F., & Black, J. H. 1993, A&A, 269, 477 [NASA ADS] [CrossRef] [Google Scholar]
  25. Herbst, E. 2001, Chem. Soc. Rev., 30, 168 [CrossRef] [MathSciNet] [Google Scholar]
  26. Hernandez, A. Q., Wodtke, A. M., Bennett, C. J., Kim, Y. S., & Kaiser, R. I. 2011, J. Phys. Chem. A, 115, 250 [CrossRef] [Google Scholar]
  27. Hollis, J. M., Jewell, P. R., & Lovas, F. J. 1995, ApJ, 438, 259 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hohenstein, E. G., Chill, S. T., & Sherrill, C. D. 2008, J. Chem. Theory Comput., 4, 1996 [CrossRef] [Google Scholar]
  29. Huang, C., Estillore, A. D., & Suits, A. G. 2008, J. Chem. Phys., 128, 134301 [NASA ADS] [CrossRef] [Google Scholar]
  30. Hughes, A. B. 2009, Amino Acids, Peptides and Proteins in Organic Chemistry Vol. 1 – Origins and Synthesis of Amino Acids (Wiley) [Google Scholar]
  31. Iseri, G. 2003, Diploma thesis, University of Frankfurt, http://th.physik.uni-frankfurt.de/~engel/amino.html#serine [Google Scholar]
  32. Kerns, B., & Duncan, B. F. 1972, ApJ, 172, 331 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kuan, Y. J., Charnley, S. B., Huang, H. C., Tseng, W. L., & Kisiel, Z. 2003, ApJ, 593, 848 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kvenvolden, K., Lawless, J., Pering, K., et al. 1970, Nature, 288, 923 [NASA ADS] [CrossRef] [Google Scholar]
  35. Lambie, B., Ramaekers, R., & Maes, G. 2004, J. Phys. Chem. A, 108, 10426 [CrossRef] [Google Scholar]
  36. Largo, L., Redondo, P., Rayón, V. M., Largo, A., & Barrientos, C. 2010, A&A, 516, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Latter, W. B., Walker, C. K., & Maloney, P. R. 1993, ApJ, 419, L97 [NASA ADS] [CrossRef] [Google Scholar]
  38. Lattelais, M., Pauzat, F., Pilmé, J., Ellinger, Y., & Ceccarelli, C. 2011, A&A, 532, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Majumdar, L., Das, A., Chakrabarti, S. K., & Chakrabarti, S. 2012, Res. Astron. Astrophys., 12, 1613 [NASA ADS] [CrossRef] [Google Scholar]
  40. Mehringer, D. M., Snyder, L. E., Miao, Y., & Lovas, F. J. 1997, ApJ, 480, L71 [NASA ADS] [CrossRef] [Google Scholar]
  41. Meng, Q., Zhang, C., & Huang, M.-B. 2009, Can. J. Chem., 87, 1610 [CrossRef] [Google Scholar]
  42. Miao, R., Jin, C., Yang, G., et al. 2005, J. Phys. Chem. A., 109, 2340 [CrossRef] [Google Scholar]
  43. Morgado, C. A., Jurečka, P., Svozil, D., et al. 2010, Phys. Chem., 12, 3522 [Google Scholar]
  44. Naylor, D. A., Dartois, E., Habart, E., et al. 2010, A&A, 518, L117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Perez, C., Mata S., Blanco S., Lopez, J. C., & Alonso, J. L. 2011, J. Phys. Chem. A., 115, 9653 [CrossRef] [Google Scholar]
  46. Pizzarello, S. 2009, J. Mex. Chem. Soc., 53, 253 [Google Scholar]
  47. Pizzarello, S., & Holmes, W. 2009, Geochim. Cosmochim. Acta, 73, 2150 [Google Scholar]
  48. Pizzarello, S., & Shock, E. 2010, Cold Spring Harb Perspect Biol, 2, a002105 [Google Scholar]
  49. Pizzarello, S., Krishnamurthy, R. V., Epstein, S., & Cronin, J. R. 1991, Geochim. Cosmochim. Acta, 55, 905 [NASA ADS] [CrossRef] [Google Scholar]
  50. Pizzarello, S., Wang, Yi, & Chaban, G. M. 2010, Geochim. Cosmochim. Acta, 74, 6206 [Google Scholar]
  51. Polehampton, E. T. 2005, A&A, 431, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Rauk, A., Yu, D., & Armstrong, D. A. 1997, J. Am. Chem. Soc., 119, 208 [CrossRef] [Google Scholar]
  53. Rimola, A., Sodupe, M., & Ugliengo, P. 2012, ApJ, 754, 24 [NASA ADS] [CrossRef] [Google Scholar]
  54. Robinson, B. J., & McGee, R. X. 1967, ARA&A, 5, 183 [NASA ADS] [CrossRef] [Google Scholar]
  55. Sattelmeyer, K. W., Yamaguchi, Y., & Schaefer III, H. F. 2004, Chem. Phys. Lett., 383, 266 [NASA ADS] [CrossRef] [Google Scholar]
  56. Singh, A., Shivani Misra, A., & Tandon, P. 2013, Res. Astron. Astrophys., 13, 912 [NASA ADS] [CrossRef] [Google Scholar]
  57. Snyder, L. E., Lovas, F. J., Hollis, J. M., et al. 2005, ApJ, 619, 914 [NASA ADS] [CrossRef] [Google Scholar]
  58. Storey, J. W. V., Watson, D. M., & Towns, C. H. 1981, ApJ, 244, L27 [NASA ADS] [CrossRef] [Google Scholar]
  59. Su, T., & Chesnavich, W. J. 1982, J. Chern. Phys., 10, 76 [Google Scholar]
  60. Turner, B. E., & Sears, T. J. 1989, ApJ, 340, 900 [NASA ADS] [CrossRef] [Google Scholar]
  61. Weinreb, S., Barrett, A. H., Meeks, M. L., & Henry, J. C. 1963, Nature, 200, 829 [NASA ADS] [CrossRef] [Google Scholar]
  62. Wiesemeyer, H., Güsten, R., Heyminck, S., et al. 2012, A&A, 542, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Woon, D. E. 2002a, ApJ, 571, L177 [NASA ADS] [CrossRef] [Google Scholar]
  64. Woon, D. E. 2002b, Int. J. Quant. Chem., 88, 226 [CrossRef] [Google Scholar]
  65. Yockey, H. P. 1998, Origins & Design 19, 1 [Google Scholar]
  66. Zhao, Y., & Truhlar, D. G. 2006, J. Chem. Phys., 125, 194101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  67. Zhao, Y., & Truhlar, D. G. 2008, Theor Chem Account, 120, 215 [Google Scholar]
  68. Ziurys, L. M. 2006, PNAS, 103, 12274 [Google Scholar]

All Tables

Table 1

Geometrical parameter: Bond lenghts of reactants, intermediate products, transisition states, and final products in steps 1 to 5 for serine formation using B3LYP/6-311G+(2df, 2p).

In the text
Table 2

Geometrical parameter: Bond angles of reactants, intermediate products, transition states, and final products in the steps 1 to 5 for serine formation using B3LYP/6-311G+(2df, 2p).

In the text
Table 3

Electronic (EE), zero-point correction (ZPE), and total energies of molecules and radicals in the gas phase using the B3LYP/6-311G+ (2df, 2p), M06/6-311G+ (2df, 2p), and M06(2X)/6-311G+ (2df, 2p) calculations.

In the text
Table 4

Electronic (EE), zero-point correction (ZPE), and total energies of molecules and radicals in the PCM using the B3LYP/6-311G+ (2df, 2p), M06/6-311G+ (2df, 2p), and M06(2X)/6-311G+ (2df, 2p) calculations.

In the text
Table 5

Rate coefficients of all involved reactions in serine formation in the gas phase at B3LYP/6-311G (d, p).

In the text

All Figures

thumbnail Fig. 1

Energy diagram showing the geometries of reactants, intermediate products (P2, P4, P6, P8), transition states (TS) and products (P1, P3, P5, P7, P9) involved in the reaction steps of serine formation at (A) B3LYP/6-311G+(2df, 2p), single-point calculation, (B) M06 and (C) M06-2X level of theory. All the energies of the molecules including ZPE corrections are given in atomic unit (energy values given in parenthesis are in kcal/mol). (Coding of atoms is manual to distinguish between atoms. The code and its respective atom are as follows: 1-H, 2-C, 3-C, 4-O, 5-O, 6-H, 7-N, 8-H, 9-H, 10-C, 11-H, 12-H, 13-O and 14-H.)
In the text
thumbnail Fig. 1

continued.
In the text
thumbnail Fig. 2

Structure of possible products in the steps of serine formation with the sum of electronic and zero-point energy in hartee.
In the text
thumbnail Fig. 3

Theoretical (DFT(B3LYP/6-311G+(2df, 2p)) infrared spectrum of serine.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.