EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 562 (February 2014) A&A, 562 (2014) L7 Full HTML
Free Access
Issue
A&A
Volume 562, February 2014
Article Number L7
Number of page(s) 4
Section Letters
DOI https://doi.org/10.1051/0004-6361/201323316
Published online 11 February 2014

© ESO, 2014

1. Introduction

Cygnus X-1 is a well-studied X-ray binary. The system is composed of a black-hole candidate of 14.8  M⊙ and an early-type O9.7 Iab star of ~20  M⊙ (Orosz et al. 2011). A radio jet was discovered by Stirling et al. (2001) and nonthermal high-energy emission was observed by different instruments, from hundreds of keV to GeV, and even perhaps TeV energies (McConnell et al. 2000, 2002; Albert et al. 2007; Bodaghee et al. 2013; Sabatini et al. 2010, 2013).

Recently, Laurent et al. (2011) reported the detection and measurement of polarization in the high-energy tail of the emission of Cygnus X-1 detected by the IBIS instrument of the INTEGRAL satellite. The linear polarization between 400 keV and 2 MeV is 67 ± 30%. The polarization at lower energies, in contrast, is quite low. This has been interpreted as evidence of a gamma-ray jet in the system (Hardcastle 2011). The MeV flux would be, in this interpretation, synchrotron radiation produced by ultra-relativistic primary electrons accelerated in situ close to the base of the jet (Zdziarski et al. 2012).

In this work we propose a different scenario for the origin of a polarized MeV tail: secondary leptonic emission induced by nonthermal particle injection in the hot and magnetized corona around the black hole. Proton acceleration is easier to achieve in such an environment. Then, protons interact with the thermal gas and photons injecting pions and pairs by Bethe-Heitler mechanism. The decay of pions injects muons, which in turn results in more pairs. Absorption of gamma-rays from neutral pion decay is another source of electrons and positrons. As a consequence of all these interactions and decays, a population of energetic secondary pairs appears in the corona. These particles cool mainly by synchrotron emission. The emission becomes partially polarized since part of the magnetic field, which is attached to the accretion disk and twisted around the black hole, is ordered.

In this letter we present the results of our calculations of nonthermal particle interactions in the corona of Cygnus X-1, and we provide estimates of the secondary leptonic spectra, the MeV emission, and the polarization for both the low-hard (LH) and the intermediate-soft (IS) states of the source.

2. Corona of Cygnus X-1

The existence of a corona of hot (T  ~  109 K) plasma in Cygnus X-1 was first proposed by Bisnovatyi-Kogan & Blinnikov (1977). If the corona is supported by the magnetic field and the escape of the particles occurs by diffusion instead of advection to the black hole, there is time for thermalization, and ions and electrons share the same temperature, in contrast to the advection-dominated cases (ADAFs, Narayan & Yi 1995).

The comptonization of disk photons by hot electrons in the corona produces the power-law observed in hard X-rays up to ~150 keV (Dove et al. 1997; Poutanen 1998). The existence of a corona is strongly supported by the detection of a Compton reflection feature and the 6.4 keV Fe Kα line.

The most likely shape of the corona is spherical (Dove et al. 1997). In the LH state, the size of the corona lies within ~20–50 rg (Poutanen 1998), where rg is the gravitational radius. Here we model the coronal region as a sphere centered on the black hole with a size of Rc = 30rg, and a luminosity of 1% of the Eddington luminosity, that is, Lc = 1.6 × 1037 erg s-1.

The magnetic field strength is obtained considering equipartition between the magnetic energy density and the bolometric photon density of the corona (e.g., Bednarek & Giovannelli 2007; Romero et al. 2010). This yields B ~ 5.7 × 105 G.

The hard X-ray emission of the corona is a power-law in photon energy ϵ with an exponential cut-off at high energies (nph(ϵ) ∝ ϵ−αe−ϵ/ϵc erg-1 cm-3). We adopt α = 1.6 and ϵc = 150 keV, as determined for Cygnus X-1 (Poutanen et al. 1997). The photon field of the accretion disk is modeled as a blackbody of temperature kTd = 0.1 keV.

3. Particle transport

Several works have been devoted to study the effects of nonthermal electron injection in a hot, magnetized corona (e.g., Belmont et al. 2008; Malzac & Belmont 2009; Vurm & Poutanen 2009). Models considering both relativistic electrons and protons have been developed by Romero et al. (2010) and Vieyro & Romero (2012). We adopt here a variation of the latter.

3.1. Injection

The mechanism of nonthermal particle injection in black hole coronae is likely to be fast magnetic reconnection: a topological reconfiguration of the magnetic field caused by a change in the connectivity of the field lines. A first-order Fermi mechanism takes place within the reconnection zone, caused by two converging magnetic fluxes of opposite polarity that move toward each other with a velocity vrec. The resulting injection function of relativistic particles is a power-law N(E) ∝ E−Γ with an index somewhere in the range 1 ≤ Γ ≤ 3 (Drury 2012; Bosch-Ramon 2012). The best fit of the IBIS data is obtained with Γ = 2.2, which is consistent with all simulations implemented so far (e.g., Kowal et al. 2011).

The acceleration rate 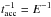dE/dt for a particle of energy E in a magnetic field B is 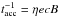/E, where η is a parameter that characterizes the efficiency of the mechanism in the magnetized plasma. We estimate η ~ 10-2 (following Vieyro & Romero 2012).

The power available in the system for accelerating particles to relativistic energies can be estimated as in del Valle et al. (2011), and it yields ~13% Lc. The total power injected into relativistic protons and electrons, Lrel, is assumed to be a fraction of the luminosity of the corona, Lrel = qrelLc, with the constraint qrel < 0.13. The way in which energy is divided between hadrons and leptons is unknown. We consider a model where the power injected in protons, Lp, is 100 times the power in leptons, Le. The injection function is both homogeneous and isotropic. The main parameters of the corona model for the LH state of Cygnus X-1 are given in Table 1.

Table 1

Main parameters of the corona of Cygnus X-1 in the LH state.

3.2. Secondaries

Primary protons are mainly cooled by photomeson production and, at low energies, by pp interactions. These processes end by injecting secondary leptons and gamma-rays. Secondary pair production is also due to photon-photon annihilation and the Bethe-Heitler process. The most important background photon field for pair creation is the thermal X-ray radiation of the corona.

thumbnail Fig. 1

Computed SED and IBIS data (left panel), and secondary-pair energy distribution (right panel) for the LH state.
Open with DEXTER

3.3. Radiative losses

Radiative losses include synchrotron radiation, IC scattering, and relativistic Bremsstrahlung for electrons and muons. Photon production by pair annihilation must also be considered. For protons, the relevant mechanisms are synchrotron radiation, photomeson production, and hadronic inelastic collisions. Non-radiative losses are dominated by diffusion.

A complete discussion of the cooling times of all these processes can be found in Romero et al. (2010) and Vieyro & Romero (2012). The injection of secondary particles, such as pions and muons, is also discussed in these works.

The maximum energy for electrons and protons can be inferred using a balance between the acceleration rate and the cooling rate. This yields 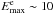GeV for electrons, and 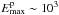TeV for protons. Particles of such energies satisfy the Hillas criterion, and can be confined within the corona.

3.4. Spectral energy distribution

In this work we aim to determine the equilibrium distribution of secondary pairs. To find it, we solved a system of coupled transport equations in the steady state and assumed spatial homogeneity and isotropy. A detailed discussion of the treatment is presented in Romero et al. (2010) and Vieyro & Romero (2012).

The left panel of Fig. 1 shows the spectral energy distribution (SED) along with the corrected INTEGRAL/IBIS data (Zdziarski et al. 2012)1. The synchrotron radiation of electron/positron pairs dominates the spectrum for Eγ < 100 MeV. Given the small size of the corona, the synchrotron radiation below E < 1 eV is self-absorbed. All radio and infrared emission of the source comes from the jet (Stirling et al. 2001; Zdziarski et al. 2012, 2013; Russell & Shahbaz 2014).

The synchrotron secondary emission provides an excellent fit of the MeV nonthermal tail of Cygnus X-1. Above 100 MeV almost all emission is absorbed by the coronal X-ray field, with dominance of stellar photons at higher energies (E > 100 GeV, see Vieyro & Romero 2012). Radiation in this energy range, as discussed by Zdziarski et al. (2013), is expected to be produced in the jet. Hadronic models of jet-wind interaction (Romero et al. 2003) might be relevant in this energy range as well.

In the right panel of Fig. 1 we present the resulting non-thermal electron/positron distribution in the corona. The spectrum can be fitted with a broken power-law with indices 2.2 at low energies and 3.8 at high energies. In contrast to the primary electrons, the most energetic pairs reach energies of ~1 TeV.

thumbnail Fig. 2

Computed SED and SPI+IBIS data (left panel), and secondary-pair energy distribution (right panel) for the IS.
Open with DEXTER

4. Polarization

A relativistic electron/positron population with a power-law energy spectrum N(E) ∝ E−Γ will produce a synchrotron flux density 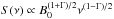for an optically thin source with a uniform magnetic field B0 (E = hν, where ν is the frequency of the radiation). In this case, the degree of linear polarization will be (e.g., Pacholczyk & Swihart 1970) 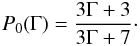(1)For an index of Γ = 3.8, as obtained in the previous section for the high-energy secondary pairs, we derive a polarization of P0 ~ 78.3%. This value is the highest possible, since the turbulent magnetic field will decrease the degree of polarization. Additional changes are introduced if the ordered field is not homogeneous (see Korchakov & Syrovatskii 1962). If the random component of the field is Br, and the ordered field has components B⊥ and B∥ normal and parallel to the accretion disk, the degree of polarization becomes 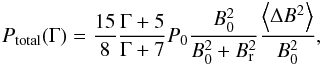(2)

with 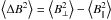and the average is carried out over the whole range of accessible angles. In the LH state the ejection of a jet requires a minimum inclination angle of the field lines with respect to the axis perpendicular to the disk of θ = 30 deg, and the dominant poloidal field is nearly parabolic (Romero & Vila 2014). Averaging from 30 to 90 deg, we obtain 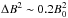. The observations by Laurent et al. (2011) are consistent with a value Ptotal ~ 50%. This would imply Br ≈ 0.73B0, with a total magnetic field B0 + Br ~ 5.7 × 105 G (Sect. 2).

5. Intermediate state

Cygnus X-1 is most of the time (up to 90%) in the LH state, but from time to time it enters the so-called intermediate state (IS), when the source transits from LH to high-soft (HS) state. In this IS, the source exhibits a relatively soft X-ray spectrum (α ~ 2.1–2.3) and a moderately strong thermal component (see Malzac et al. 2006).

We applied the model described in the previous sections to the data presented in Malzac et al. (2006) (see Fig. 2). We assumed that the luminosity of the corona is 2% of the Eddington luminosity, which results in Lc ~ 3.8 × 1037 erg s-1. This is in accordance with the count rate of Cygnus X-1 by RXTE during the period of observation (Malzac et al. 2006). The hard X-ray emission of the corona is characterized by a power-law of index α ~ 2.2 and an exponential cut-off at ϵc = 200 keV in the IS.

The data from INTEGRAL do not cover the energy range of the accretion disk emission. Therefore, we adopted kTmax = 0.3 keV, which is an intermediate value between the typical 0.1 and 0.6 keV in the LH and HS states, respectively (Malzac et al. 2006). The disk inner radius was estimated according to Vila et al. (2012); we considered a luminosity of the disk of Ld = 4 × 1037 erg  s-1 (Poutanen 1998). The disk/corona ratio was taken as 0.8, yielding Rc ~ 10  rg.

In the right panel of Fig. 2 we show the secondary-pair spectrum, which is softer at high energies than the corresponding spectrum in the LH state. In the IS there is no jet, and the accretion disk is much closer to the black hole. This suggests a small inclination angle for the field lines. Adopting a homogeneously ordered field within the Alfvén radius, we obtained a linear polarization of Ptotal = 83% 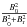from the calculated electron/positron spectrum. In this state the expected polarization is ~54%, slightly higher than in the LH state. In a jet model the polarization in the IS should be zero, since there is no jet. This is a specific prediction of our model.

6. Conclusions

We estimated the polarization of the emission predicted by a hybrid thermal/nonthermal lepto-hadronic corona model for Cygnus X-1. This provides an alternative explanation of the high polarization observed by Laurent et al. (2011). The current data correspond only to the LH state, but our predictions will be testable also with data from the IS state. If polarization is found in the IS, the coronal model will be strongly supported. This can be tested in the future using the polarimetric capabilities of the soft gamma-ray detector on board ASTRO-H.

1

As noted and corrected by Zdziarski et al. (2012), there is a calibration problem with the original spectrum presented by Laurent et al. (2011).

Acknowledgments

This work was supported by the Argentine Agencies CONICET (PIP 0078) and ANPCyT (PICT 2012-00878), as well as by grant AYA2010-21782-C03-01 (Spain). S.C. and G.E.R. acknowledge funding by the Sorbonne Paris Cité (SPC), Scientific Research Project - Argentina 2013. S.C. thanks the Centre National d’Etudes Spatiales (CNES). This work is based on observations obtained with MINE: the Multi-wavelength INTEGRAL NEtwork.

References

  1. Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 665, L51 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bednarek, W., & Giovannelli, F. 2007, A&A, 464, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Belmont, R., Malzac, J., & Marcowith, A. 2008, A&A, 491, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bisnovatyi-Kogan, G. S., & Blinnikov, S. I. 1977, A&A, 59, 111 [NASA ADS] [Google Scholar]
  5. Bodaghee, A., Tomsick, J. A., Pottschmidt, K., et al. 2013, ApJ, 775, 98 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bosch-Ramon, V. 2012, A&A, 542, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. del Valle, M. V., Romero, G. E., Luque-Escamilla, P. L., Martí, J., & RamónSánchez-Sutil, J. 2011, ApJ, 738, 115 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dove, J. B., Wilms, J., Maisack, M., & Begelman, M. C. 1997, ApJ, 487, 759 [NASA ADS] [CrossRef] [Google Scholar]
  9. Drury, L. O. 2012, MNRAS, 422, 2474 [NASA ADS] [CrossRef] [Google Scholar]
  10. Hardcastle, M. J. 2011, Science, 332, 429 [NASA ADS] [CrossRef] [Google Scholar]
  11. Korchakov, A. A., & Syrovatskii, S. I. 1962, Sov. Astron., 5, 678 [NASA ADS] [Google Scholar]
  12. Kowal, G., de Gouveia Dal Pino, E. M., & Lazarian, A. 2011, ApJ, 735, 102 [NASA ADS] [CrossRef] [Google Scholar]
  13. Laurent, P., Rodriguez, J., Wilms, J., et al. 2011, Science, 332, 438 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. Malzac, J., & Belmont, R. 2009, MNRAS, 392, 570 [NASA ADS] [CrossRef] [Google Scholar]
  15. Malzac, J., Petrucci, P. O., Jourdain, E., et al. 2006, A&A, 448, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. McConnell, M. L., Ryan, J. M., Collmar, W., et al. 2000, ApJ, 543, 928 [NASA ADS] [CrossRef] [Google Scholar]
  17. McConnell, M. L., Zdziarski, A. A., Bennett, K., et al. 2002, ApJ, 572, 984 [NASA ADS] [CrossRef] [Google Scholar]
  18. Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
  19. Orosz, J. A., McClintock, J. E., Aufdenberg, J. P., et al. 2011, ApJ, 742, 84 [NASA ADS] [CrossRef] [Google Scholar]
  20. Pacholczyk, A. G., & Swihart, T. L. 1970, ApJ, 161, 415 [NASA ADS] [CrossRef] [Google Scholar]
  21. Poutanen, J. 1998, in Theory of Black Hole Accretion Disks, eds. M. A. Abramowicz, G. Bjornsson, & J. E. Pringle, Cambridge Contemporary Astrophysics (Cambridge, UK: Cambridge University Press), 100 [Google Scholar]
  22. Poutanen, J., Krolik, J. H., & Ryde, F. 1997, MNRAS, 292, L21 [NASA ADS] [Google Scholar]
  23. Romero, G. E., & Vila, G. S. 2014, Introduction to Black Hole Astrophysics (Berlin: Springer) [Google Scholar]
  24. Romero, G. E., Torres, D. F., Kaufman Bernadó, M. M., & Mirabel, I. F. 2003, A&A, 410, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Romero, G. E., Vieyro, F. L., & Vila, G. S. 2010, A&A, 519, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Russell, D. M., & Shahbaz, T. 2014, MNRAS, in press [arXiv:1312.0942] [Google Scholar]
  27. Sabatini, S., Striani, E., Verrecchia, F., et al. 2010, ATel, 2715, 1 [NASA ADS] [Google Scholar]
  28. Sabatini, S., Tavani, M., Coppi, P., et al. 2013, ApJ, 766, 83 [NASA ADS] [CrossRef] [Google Scholar]
  29. Stirling, A. M., Spencer, R. E., de la Force, C. J., et al. 2001, MNRAS, 327, 1273 [NASA ADS] [CrossRef] [Google Scholar]
  30. Vieyro, F. L., & Romero, G. E. 2012, A&A, 542, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Vila, G. S., Romero, G. E., & Casco, N. A. 2012, A&A, 538, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Vurm, I., & Poutanen, J. 2009, ApJ, 698, 293 [NASA ADS] [CrossRef] [Google Scholar]
  33. Zdziarski, A. A., Lubiński, P., & Sikora, M. 2012, MNRAS, 423, 663 [NASA ADS] [CrossRef] [Google Scholar]
  34. Zdziarski, A. A., Pjanka, P., & Sikora, M. 2013, MNRAS, submitted [arXiv:1307.1309] [Google Scholar]

All Tables

Table 1

Main parameters of the corona of Cygnus X-1 in the LH state.

In the text

All Figures

thumbnail Fig. 1

Computed SED and IBIS data (left panel), and secondary-pair energy distribution (right panel) for the LH state.
Open with DEXTER
In the text
thumbnail Fig. 2

Computed SED and SPI+IBIS data (left panel), and secondary-pair energy distribution (right panel) for the IS.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.