| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 11 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201323120 | |
| Published online | 05 February 2014 | |
The GIRAFFE Inner Bulge Survey (GIBS)
I. Survey description and a kinematical map of the Milky Way bulge ⋆,⋆⋆
1
Instituto de Astrofísica, Facultad de Física, Pontificia
Universidad Católica de Chile, Av.
Vicuña Mackenna 4860, Santiago
22, Chile
e-mail:
mzoccali@astro.puc.cl
2
The Milky Way Millennium Nucleus, Av. Vicuña Mackenna 4860,
782-0436 Macul, Santiago, Chile
3
European Southern Observatory, A. de Cordova 3107, 19001 Casilla,
Santiago 19,
Chile
4
Laboratoire Lagrange (UMR7293), Université de Nice Sophia
Antipolis, CNRS, Observatoire de la Côte d’Azur, BP 4229, C 34339
Nice Cedex 4,
France
5
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748
Garching,
Germany
6
Excellence Cluster Universe, Boltzmannstr. 2, 85748
Garching,
Germany
7
INAF – Osservatorio Astronomico di Padova, vicolo
dell’Osservatorio 5, 35122
Padova,
Italy
8
Max-Planck-Institut für Extraterrestrische Physik,
Giessenbachstrasse,
85748
Garching,
Germany
9
Instituto de Astrofísica de Canarias, Calle Vía Láctea s/n, 38205
La Laguna, Tenerife,
Spain
10
GEPI, Observatoire de Paris, CNRS UMR 8111, Université Paris
Diderot, 92125
Meudon Cedex,
France
11
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD
21218,
USA
12
Vatican Observatory, V 00120
Vatican City State,
Italy
13
The Observatories of the Carnegie Institute of Washington,
813 Santa Barbara
Street, Pasadena,
CA
91101-1292,
USA
Received:
22
November
2013
Accepted:
2
January
2014
Context. The Galactic bulge is a massive, old component of the Milky Way. It is known to host a bar, and it has recently been demonstrated to have a pronounced boxy/peanut structure in its outer region. Several independent studies suggest the presence of more than one stellar populations in the bulge, with different origins and a relative fraction changing across the bulge area.
Aims. This is the first of a series of papers presenting the results of the Giraffe Inner Bulge Survey, carried out at the ESO-VLT with the multifibre spectrograph FLAMES. Spectra of ~5000 red clump giants in 24 bulge fields have been obtained at resolution R = 6500, in the infrared Calcium triplet wavelength region at ~8500 Å. They are used to derive radial velocities and metallicities, based on new calibration specifically devised for this project. Radial velocities for another ~1200 bulge red clump giants, obtained from similar archive data, have been added to the sample. Higher resolution spectra have been obtained for ~450 additional stars at latitude b = −3.5, with the aim of investigating chemical abundance patterns variations with longitude, across the inner bulge. In total we present here radial velocities for 6392 red clump stars.
Methods. We present here the target selection criteria, observing strategy and the catalog with radial velocity measurements for all the target stars.
Results. We derive a radial velocity, and velocity dispersion map of the Milky Way bulge, useful to be compared with similar maps of external bulges, and to infer the expected velocities and dispersion at any line of sight. The K-type giants kinematics is consistent with the cylindrical rotation pattern of M-giants from the BRAVA survey. Our sample enables to extend this result to latitude b = −2, closer to the Galactic plane than probed by previous surveys. Finally, we find strong evidence for a velocity dispersion peak at (0, −1) and (0, −2), possibily indicative of a high density peak in the central ~250 pc of the bulge.
Key words: Galaxy: bulge / Galaxy: structure / Galaxy: evolution / Galaxy: formation / Galaxy: kinematics and dynamics
Based on observations taken with ESO telescopes at the La Silla Paranal Observatory under program IDs 187.B-909 and 089.B-0830.
Full Table 2 is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/562/A66
© ESO, 2014
1. Introduction
The Giraffe Inner Bulge Survey (GIBS) is a survey of ~6500 red clump (RC) stars in the Milky Way bulge, carried out with the GIRAFFE spectrograph of the FLAMES instrument at the ESO Very Large Telescope (VLT). The aim of the GIBS survey is to derive the metallicity and radial velocity distributions of bulge stars across different fields, spread over a large area of the inner Galactic bulge, that is also part of the VISTA Variable in the Vía Láctea (VVV) survey (Minniti et al. 2010).
The inner region (≲3 kpc) of the Milky Way galaxy is known to host a bar (Blitz & Spergel 1991; Stanek et al. 1994; Dwek et al. 1995; Babusiaux & Gilmore 2005; Rattenbury et al. 2007, and references therein). Only recently, however, a split RC was discovered at l = 0 and |b| > 5, (Nataf et al. 2010; McWilliam & Zoccali 2010) and detailed 3D maps constructed using RC stars as distance indicators revealed that the bulge is in fact X-shaped (Saito et al. 2011; Wegg & Gerhard 2013). The X-shape is a pronounced boxy/peanut (B/P) structure that, in its inner region (|b| < 5), becomes a bar, hereafter the main bar. Closer yet to the center (|l| < 4, |b| < 2) the main bar changes its apparent inclination with respect to the line of sight (Nishiyama et al. 2005; Gonzalez et al. 2011a), most likely due to the presence of either a distinct, smaller bar, or a more axysimmetric structure (Gerhard & Martinez-Valpuesta 2012). The presence of a longer bar, extending to longitudes |l| > 7 (Hammersley et al. 2000; Cabrera-Lavers et al. 2007, 2008; López-Corredoira et al. 2007; Churchwell et al. 2009; Amôres et al. 2013) has been interpreted by theoreticians as most likely being an extension of the main bar itself (e.g., Martinez-Valpuesta & Gerhard 2011; Athanassoula 2012).
The axial ratio of the main bar is close to 1:0.35:0.25, but rather different values of the inclination angle with respect to the line of sight are found in the literature, spanning the range 15 to 45 degrees, depending on the method used to trace it (e.g., Binney et al. 1997; Dehnen 2000; Bissantz & Gerhard 2002; Benjamin et al. 2005; Babusiaux & Gilmore 2005; Rattenbury et al. 2007; Robin et al. 2012; Cao et al. 2013).
The ultimate goal, when studying the Galactic bulge, is to set constrains on the formation mechanism(s) of the Milky Way and, by extension, of galaxies in general. Dynamical models predict the formation of B/P structures as the outcome of the secular evolution of a disk, through the formation and successive vertical heating of a bar (e.g., Pfenniger & Friedli 1991; Athanassoula 2005; Martinez-Valpuesta et al. 2006; Debattista et al. 2006). The B/P shape in this case would be sustained by stars in the so-called banana and anti-banana orbit families, which might be identified observationally as asymmetries in the kinematics of the near and far side of the bulge (e.g., Rangwala et al. 2009; Vásquez et al. 2013).
Following early studies by Frogel & Whitford (1987), Sharples et al. (1990), Minniti (1996), and Tiede & Terndrup (1997), the first extensive kinematical study of the Galactic bulge is the Bulge Radial Velocity Assay survey (BRAVA; Rich et al. 2007b; Howard et al. 2009; Kunder et al. 2012), targetting ~10 000 M giants from the Two Micron All-Sky Survey (2MASS; Skrutskie et al. 2006), at latitudes b = −4, −6, −8 and longitudes −10 < l < 10. The main result of the BRAVA survey, based on ~4500 stars, is the determination of a cylindrical rotation pattern for bulge stars, implying that a simple B/P bulge model is sufficient to reproduce the bulge kinematics with no need for a merger-made classical bulge (Howard et al. 2009; Shen et al. 2010). Dynamical models have shown, however, that a bar could form also where a classical bulge (i.e.; formed via mergers) was already present. In this case, then, the classical bulge would spin-up to a faster rotation after the formation of the bar (Saha et al. 2012) such that it would be very difficult, a posteriori, to detect its presence via kinematics alone (Gardner et al. 2013).
Independent clues on the bulge formation mechanisms and timescale can come from the surface chemical abundance of individual stars. Following several measurements based either on photometry or on low resolution spectroscopy (e.g., Rich 1988), the bulge metallicity distribution function was first derived using high resolution spectra by McWilliam & Rich (1994) and the following works obtained consistent results (Ibata & Gilmore 1995a,b; Minniti 1996; Sadler et al. 1996; Ramírez et al. 2000; Zoccali et al. 2003; Fulbright et al. 2006). All these studies, however, were confined to a single low reddening window, close to the Baade’s Window at (l,b) = (0, −4). Zoccali et al. (2008), and Johnson et al. (2011, 2013), based exclusively on high resolution spectra, extended previous studies to a few additional windows, firmly establishing the presence of a radial metallicity gradient of ~0.6 dex per kpc, with the most metal rich stars being closer to the Galactic center. Meléndez et al. (2008); Alves-Brito et al. (2010); Johnson et al. (2011, 2013); Gonzalez et al. (2011b) found a similarity between the alpha over iron abundance ratio of bulge and thick disk stars, suggestive of a fast formation timescale for both components, perhaps sharing a common origin (see also Bensby et al. 2011). By combining [Fe/H] and [Mg/Fe] abundances and kinematics, Hill et al. (2011) and Babusiaux et al. (2010) suggested the presence of two distinct components in the galactic bulge, a metal poor one ([Fe/H] ~ −0.3) with kinematics typical of an axisymmetric spheroid, and a metal rich one, ([Fe/H] ~ +0.3) more concentrated towards the Galactic plane, with a significant vertex deviation, suggestive of a bar-like component.
A chemical and kinematical study covering a significantly larger bulge area is the Abundances and Radial velocity Galactic Origins Survey (ARGOS; Freeman et al. 2013; Ness et al. 2013a,b). The ARGOS team measured radial velocities, [Fe/H] and [α/Fe] ratios for ~28 000 stars, ~14 000 of which at a distance of <3.5 kpc from the Galactic center. They confirmed the cylindrical rotation found by the BRAVA survey, and could identify three main components within the bulge, tentatively associated with the metal rich B/P bulge (mean [Fe/H] ≈ +0.15), the thick B/P bulge ([Fe/H] ≈ −0.25) and the inner thick disk (mean [Fe/H] ≈ −0.70). A different fraction of the three populations along different lines of sight gives rise to the observed gradients. A first contiguous map of the mean metallicity of the stars over the bulge area outside |b| ~ 2 has been derived from VVV photometry by Gonzalez et al. (2013).
The GIBS and ARGOS surveys are qualitatively similar, but are complementary with respect to the area coverage. Our aim is to derive Calcium II Triplet (CaT) metallicities, radial velocities and, in the near future, proper motions for a sample of ~5000 bulge stars spread across the area covered by the VVV survey (−10 < l < +10, −10 < b < +5). We calibrate CaT equivalent widths versus [Fe/H] with a large (~400) sample of stars observed both with intermediate and high resolution spectroscopy. In the present paper we describe the target, selection, observations and we provide the radial velocity catalog for all our targets.
Observed fields, number of target stars and main characteristics of the spectra.
2. Observations
2.1. Target selection
 |
Fig. 1 Approximate location of the fields discussed in the present paper, overplotted on an optical image of the Milky Way bulge (© Serge Brunier). The large white rectangle is the area mapped by the VVV survey. Red and white circles are fields observed at low spectral resolution (R = 6500) through setup LR8, from program 187.B-0909; red and white squares are fields observed at high resolution (R = 22 500) through setup HR13, from program 187.B-0909. Crosses at b ~ −2 are the fields from program 089.B-0830, also observed through LR8. The blue star is the field, within Baade’s Window, used for the CaT calibration, and the blue triangle is the field discussed in Vásquez et al. (2013). |
 |
Fig. 2 Location of the fields discussed in the present study compared to the fields from the ARGOS survey (Freeman et al. 2013). Black open circles are the ARGOS fields. Red filled circles are fields observed at low spectral resolution (R = 6500) through setup LR8, from program 187.B-0909; open squares are fields observed at high resolution (R = 22 500) through setup HR13, from program 187.B-0909. Blue crosses are the fields from program 089.B-0830, also observed through LR8. The blue star is the field, within Baade’s Window, used for the CaT calibration, and the blue triangle is the field discussed in Vásquez et al. (2013) . The large rectangle shows the area mapped by the VVV survey. |
Target stars for the spectroscopic observations were selected from the VVV catalogs. The catalogs contain aperture magnitudes for individual stars in the J,H,Ks bands derived from the Cambridge Astronomical Survey Unit (CASU) pipeline, and have been complemented with 2MASS data (Cutri et al. 2003) for stars brighter than Ks = 12, where VVV images are saturated. Further details on the photometric catalogs can be found in Gonzalez et al. (2011c); Saito et al. (2012a).
The goal of the program was to collect spectra for representative samples of bulge field K giants spread over a grid, as regular as possible, across the bulge area covered by the VVV survey. However, starting from a regular position grid at b = −8, −6, −4, −2, +4 and l = −8, −4,0, +4, +8, the actual center of each field (see Table 1) was fine-tuned on the extinction map derived by Gonzalez et al. (2012) in order to minimize the reddening, hence maximizing the S/N at a given exposure time. Occasionally it was also moved by up to 1deg in order to overlap with previous photometric observations. The latter were used to add extra information on the target stars, such as photometry in different bands and proper motions from the OGLEII survey (Sumi et al. 2004). An additional field was observed at (l,b) = (0, −1) in order to investigate whether the radial metallicity gradient seen along the minor axis by Zoccali et al. (2008) and Johnson et al. (2011, 2013) extends to the inner regions or flattens out as suggested by Rich et al. (2007a, 2012).
Three aditional sets of spectra were added to the GIBS sample in order to obtain a finer field grid in the sky. The first one consists of LR08 spectra in 5 fields at latitude b = −2, from ESO program 089.B-0830 (PI. Gonzalez). These data were obtained with the aim of characterizing the properties of the inner Bulge, following Gonzalez et al. (2011a). The targets for this program were selected with the same criteria explained below. The location of these 5 fields is shown with crosses in Fig. 1 and Fig. 2. The second set consists of spectra for 111 RC stars, in Baade’s Window, obtained to derive the CaT calibration, used to derive metallicities for the LR8 target stars. Those stars were observed through setup LR8, but they were also observed at higher spectral resolution within our previous program (Zoccali et al. 2008). Finally, in what follows we will include in all plots also the RC stars, at (0, −6), analyzed in Vásquez et al. (2013).
Figure 1 shows the location of the 31 fields observed in the present study, at different spectral resolutions, overplotted on the stellar density map from Saito et al. (2012b). Figure 2 shows the location of the same fields shown in Fig. 1 together with the fields observed within the ARGOS Survey (Freeman et al. 2013). The two surveys nicely complement each other, in terms of distance from the Galactic center. Indeed, only four of the ARGOS fields are included within the area surveyed here.
 |
Fig. 3 Example of the GIBS target selection criteria for the LRm5m2 field. Left: the VVV CMD together with the 214 GIRAFFE targets (red) and the 14 UVES targets (cyan). Right: magnitude distribution of the GIRAFFE targets (red histogram) compared with the underlying luminosity function of the RGB stars with J − K > 1.0 (black histogram). |
For each field, after applying the reddening correction, we selected the most likely bulge members based on the red giant branch (RGB) color redder being than (J − K)0 ~ 0.4, where the exact limit was adjusted slightly from field to field. This cut excluded foreground disk dwarfs, without loosing the blue edge of the bulge red clump (RC). The RGB luminosity function was then constructed in order to identify the RC. Target stars were selected in a narrow range of J magnitude (or, whenever available, in I) close to the RC peak, as shown in Fig. 3, in order to ensure that the acquired spectra would have similar signal-to-noise (S/N). In order to avoid metallicity biases, possibly due to color selection, we sampled stars spanning the whole color range of the RC. Figure 3 also shows the nearby disk RC stars that have been observed in addition to the bulge giants, in some fields, using the simultaneous fibre connection to the UVES spectrograph (cf., Table 1). These UVES spectra will be the subject of a dedicated paper, and will not be further discussed here.
2.2. Spectra
Spectra for the selected targets have been collected with the GIRAFFE spectrograph fed by MEDUSA fibres (in some cases the observations were taken in the combined UVES+MEDUSA mode) of the FLAMES multifibre instrument (Pasquini et al. 2002) at the ESO Very Large Telescope, between May 2011 and September 2012. Observations were carried out in service mode under program 187.B-0909(A) and 187.B-0909(B), PI: Zoccali. The log of the observations is reported in Table 1. All the spectra, with the exception of those in the fields at b ~ −4, were obtained with setup LR8, at resolution R = 6500, centered on the Calcium II Triplet (CaT) feature at ~8500Å. Two different sets of fibre allocations were performed for each field, allocating up to 132 × 1.2 arcsec diameter fibres in each setup. Approximately 25 fibres in each field were allocated to empty sky positions, thus collecting spectra for a total of ~215 targets per field. Four independent allocations were done for the fields along the minor axis, thus collecting ~450 targets in these fields. Indeed, these fields are particularly interesting because they cross two arms of the X-shaped bulge, at latitude |b| > 5. For |b| < 3 the larger statistics was motivated by the need to solve the debate concerning the extension of the metallicity gradient to the inner bulge. The exposure time was optimized to reach a S/N ~ 50 per pixel. In the most reddened fields this required multiple exposures. Typical spectra, for three stars of different metallicities, are shown in Fig. 4.
Coordinates and radial velocities for all the program stars.
Stars in the fields at b ~ −4 were observed at higher resolution (R = 22 500) through setup HR13 centered at ~6300 Å in order to measure the chemical abundance of iron and the light elements, and to investigate the presence of radial gradients in the alpha element ratios across different longitudes. The typical S/N per pixel of these HR spectra is ~100.
 |
Fig. 4 Example of typical spectra observed through setup LR8 for three targets with different preliminary metallicities. Vertical ticks mark the three corresponding CaT lines. |
3. Data reduction pipeline
In this section we describe our full pipeline, including extraction and calibration of the spectra as well as the adopted procedure to obtain measurements of physical parameters from the reduced spectra. Only the radial velocitites are discussed in detail in this paper, while the analysis of the metallicity and individual elemental abundances will be discussed in forthcoming, dedicated papers (Vásquez et al. 2014; Gonzalez et al., in prep.).
The spectra were extracted and wavelength calibrated using the GIRAFFE pipeline maintained by ESO, which processes the spectra applying bias, flat-field correction, individual spectral extraction, and wavelength calibration based on daytime calibration frames. Since the pipeline does not perform sky subtraction, the correction was done using IRAF tasks. As a first step, a master sky has been obtained for each field from the 20 sky spectra, median combined and using a sigma clipping algorithm. The master sky was then subtracted from the 1D spectrum of each target using the IRAF skytweak task, shifting and/or scaling the input sky spectra to improve the subtraction of sky features from target spectra.
3.1. Radial velocities
Heliocentric radial velocities where measured by cross–correlations using IRAF fxcor task. For the low resolution spectra the adopted template was a synthetic spectrum, generated with the Turbospectrum code (Alvarez & Plez 1998), fed with the MARCS model atmosphere (Gustafsson et al. 2008), for stellar surface parameters appropriate for a metal poor bulge K giant (Teff = 4750 K, log g = 2.5 and [Fe/H] = −1.3). The template metallicity was chosen on the low side of the distribution in order to avoid including too many small lines that would add only noise in the cross-correlation peak for metal-poor stars. The same template was used for stars of all metallicities. The template covers the CaT region from 8350Å to 8950Å. The statistical error on the radial velocity from low resolution spectra is typically ~1 km s-1. The final heliocentric radial velocities for all the target stars observed both at high and low spectral resolution are listed in Table 2.
For the high resolution, HR13 spectra, the cross correlation was performed with the same IRAF routine but a template synthetic spectrum with Teff = 4500 K, log g = 2.3 and [Fe/H] = −0.3. The latter was generated adopting the MARCS model atmospheres and the MOOG code – version 2010 – for spectrum synthesis (Sneden 1973). In this case there were multiple exposures (~10) for each field in order to reach the required S/N. The cross correlation was carried out independently on each individual exposure and the results were then averaged to the final radial velocity listed in Table 2. The typical error on these velocities is ~0.6 km s-1, calculated as the standard deviation of the radial velocity distribution from individual exposures.
3.2. Chemical abundances
In forthcoming articles, we will present a catalog and analyze the [Fe/H] measurements for all the stars observed at low spectral resolution (Vásquez et al., in prep.), as well as [Fe/H] and element ratios (mainly [alpha/Fe]) for targets observed at the high resolution using HR13 setup (Gonzalez et al., in prep.). Hereafter we briefly describe our pipeline and procedure adopted to derive chemical abundance measurements.
 |
Fig. 5 Radial velocity distributions for all the GIBS fields. The two fields at (0, −6) and (0, −8) include targets both for the bright RC (red) and the faint (RC). Part of the data at b = −2, shown as black histograms, come from program 089.B-0830. The labels on the upper left corner, in each panel, list the mean velocity (M), the skewness (Sk) and the number of stars (N). On the upper right corner we list the galactic coordinates of the field. |
3.2.1. Low resolution spectra
Iron abundances from LR spectra are obtained using CaT lines as metallicity indicator. The correlation between the equivalent widths of CaT lines and global metallicity was first demonstrated by Armandroff & Zinn (1988) by means of integrated spectra of Galactic globular clusters. Later on this empirical evidence was confirmed in several studies of individual star spectra, and it has been extensively used in the study of Galactic star clusters and Milky Way satellites (e.g., Saviane et al. 2012; Battaglia et al. 2008; Starkenburg et al. 2010, and references therein). Before starting the present program we made sure that such a correlation would hold for super solar metallicities, with the [Ca/Fe] profile appropriate for bulge K giants. Specifically, we observed a set of ~200 bulge RC and red giant branch stars in Baade’s Window both through the low resolution, LR8, CaT setup and through three setups at higher resolution (Zoccali et al. 2008; Hill et al. 2011). These observations were used to derive a CaT versus [Fe/H] calibration specifically designed for the targets of the GIBS program. The calibration will be presented and discussed in Vásquez et al. (in prep.).
3.2.2. High resolution spectra
For the stars observed at R ~ 22 500, through the HR13 setup,
metallicities and element ratios are derived using the same iterative method described
in Zoccali et al. (2008) and Gonzalez et al. (2011b). Specifically, equivalent
widths of isolated Fe lines are obtained automatically by means of DAOSPEC (Stetson & Pancino 2008). A first guess
photometric temperature will be derived using the
(V − I) colors from OGLEII (Udalski et al. 2002), de-reddened based on the high resolution
extinction maps from Gonzalez et al. (2012). The
effective temperature calibration by Ramírez &
Meléndez (2005) are used. The same work yields bolometric corrections, used to
estimate photometric gravities, by means of the classical formula:
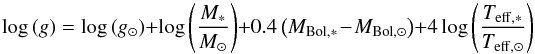 where
MBol, ⊙ = 4.72,
Teff, ⊙ = 5770 K and
log (g⊙) = 4.44 dex. Absolute visual magnitudes were
obtained assuming distances to each field from the work of Gonzalez et al. (2013). Microturbulence velocity and global
metallicity are set to 1.5 and 0.0, respectively, as a first step. These values are used
to obtain a first guest MARCS stellar model atmosphere and are subsequently refined
spectroscopically. Spectroscopic effective temperatures and microturbulence velocities
are refined by simultaneously requiring excitation equilibrium and a flat trend of iron
abundance versus equivalent width, respectively. A new iteration is then started by
re-calculating the photometric gravity with the new temperature and
iron abundance, the latter entering in the derivation of the bolometric correction.
where
MBol, ⊙ = 4.72,
Teff, ⊙ = 5770 K and
log (g⊙) = 4.44 dex. Absolute visual magnitudes were
obtained assuming distances to each field from the work of Gonzalez et al. (2013). Microturbulence velocity and global
metallicity are set to 1.5 and 0.0, respectively, as a first step. These values are used
to obtain a first guest MARCS stellar model atmosphere and are subsequently refined
spectroscopically. Spectroscopic effective temperatures and microturbulence velocities
are refined by simultaneously requiring excitation equilibrium and a flat trend of iron
abundance versus equivalent width, respectively. A new iteration is then started by
re-calculating the photometric gravity with the new temperature and
iron abundance, the latter entering in the derivation of the bolometric correction.
Alpha element abundances are derived using the final MARCS model atmosphere for each target star to produce synthetic spectra using MOOG. These synthetic spectra are compared with the observed ones and abundances for Mg, Ca, Si, and Ti are then derived by fitting their corresponding spectral lines in our spectral range.
4. Radial velocities
The radial velocity distributions for the observed fields are shown in Fig. 5. The overall distributions are in good agreement with those observed from the BRAVA survey in the overlapping regions (b < −5). Our survey allows us to investigate the radial velocity distribution of the inner bulge regions for the first time. Velocities range from −300 to +300 km s-1 with a shape that changes considerably across the bulge area. It is worth noticing that no significant peaks (nor individual outliers) are found outside the main distribution, in contrast with the findings by Nidever et al. (e.g., 2012).
In order to search for the presence of systematic trends in the shape of the distributions across the different fields, we calculated the skewness of the radial velocity distribution in each field. These values are also shown in Fig. 5. With the exception of field HRp1m4 and LRm3m8, which show a significative positive and negative skewness respectively, all fields are consistent with a symmetric distribution. This indicates that the mean radial velocity variations across the different fields are most likely due to a general shift of the distribution instead of being the result of additional features such as asymmetric tails or local peaks.
4.1. Rotation curves and cylindrical rotation
The observed rotational profiles of bulges can be directly linked to the different processes involved in the formation and evolution of bulges. In particular, bulges that originate from the buckling instability of a, previously settled, rotating bar, when viewed edge-on are expected to show little difference in their mean rotation velocities measured at different scale heights from the plane of the galaxy. This is the well known property named cylindrical rotation. For the Milky Way, Shen et al. (2010) compared models of a secularly evolved bar with the observed rotation curve obtained within the BRAVA survey. They concluded that a model with a pure disk component was sufficient to explain the observed rotation, without the need to add a merger made, classical bulge.
 |
Fig. 6 Mean galactocentric radial velocity (top) and velocity dispersion (bottom) as a function of Galactic longitude, for different latitudes, as listed in the labels. |
Mean radial velocities for each of our fields were computed and used to construct the
rotational profiles at different vertical distances from the Galactic plane. Figure 6 (top) shows the mean radial velocity, corrected for the
motion of the Sun with respect to the Galactic center using the formula (e.g., Ness et al. 2013b):
![\begin{eqnarray*} V_{\rm GC}=V_{\rm HC}&&+220\sin(l)\cos(b)\\&&+16.5[\sin(b)\sin(25) + \cos(b)\cos(25)\cos(l-53)] \end{eqnarray*}](/articles/aa/full_html/2014/02/aa23120-13/aa23120-13-eq74.png) We
will refer to VGC as galactocentric radial velocity
hereafter. The lower panel of the same figure shows the radial velocity
dispersion as a function of longitude, for different latitudes. It is clear from this
figure that the radial velocity curve, reflecting the bulge rotation, becomes steeper
towards lower latitudes. This effect, already noticed by Howard et al. (2009), is now clearly confirmed with the inclusion of the
rotation profile at b = −2. As discussed in Martinez-Valpuesta & Gerhard (2013), this is the expected
rotation pattern of a B/P bulge formed out of a bar with a non-zero position angle with
respect to the Sun-Galactic center line of sight. No further component needs to be
included (although neither necessarily excluded) to reproduce the observed rotation
curves. Indeed, a direct comparison between our rotation profiles with those of the B/P
bulge model based on Martinez-Valpuesta et al.
(2006) and presented in Martinez-Valpuesta
& Gerhard (2011) (Figs. 7 and 8) shows a remarkable agreement at all latitudes.
We
will refer to VGC as galactocentric radial velocity
hereafter. The lower panel of the same figure shows the radial velocity
dispersion as a function of longitude, for different latitudes. It is clear from this
figure that the radial velocity curve, reflecting the bulge rotation, becomes steeper
towards lower latitudes. This effect, already noticed by Howard et al. (2009), is now clearly confirmed with the inclusion of the
rotation profile at b = −2. As discussed in Martinez-Valpuesta & Gerhard (2013), this is the expected
rotation pattern of a B/P bulge formed out of a bar with a non-zero position angle with
respect to the Sun-Galactic center line of sight. No further component needs to be
included (although neither necessarily excluded) to reproduce the observed rotation
curves. Indeed, a direct comparison between our rotation profiles with those of the B/P
bulge model based on Martinez-Valpuesta et al.
(2006) and presented in Martinez-Valpuesta
& Gerhard (2011) (Figs. 7 and 8) shows a remarkable agreement at all latitudes.
In the model from Martinez-Valpuesta et al. (2006) a boxy bulge is formed out of the buckling instability of a bar with no inclusion of any merger-made component. This model successfully reproduces a number of observations of the Milky Way bulge, including the RC star counts in the innermost region (Gerhard & Martinez-Valpuesta 2012), the RC splitting at l = 0, |b| > 5, the metallicity profile across (l,b) and the observations of the apparent change in the inclination angle of the bar outside the boxy/peanut extent, at l ~ 27 (Martinez-Valpuesta & Gerhard 2011). Stars in the models were selected within a distance corresponding to ± 0.2 magnitudes, around the bar major axis. In Fig. 7 we show how it reproduces the rotation profile of the Bulge, as found with the GIBS (red) and the BRAVA (gray) data. The very good agreement between this model and the data supports the conclusion presented in Shen et al. (2010), extending it to the inner bulge at b = −2.
It should be mentioned that a few points at l < −3, b = −2 do stick out of the main observational trend, and show a galactocentric radial velocity significantly higher than predicted by the model. Keeping in mind that these points correspond to the far side of the bar, sampled very close to the Galactic plane, we believe that the discrepancy is likely due to the fact that the line of sight in that direction samples stars in the near half of the bar more than stars on the far half, due to a simple projection effect. This well known effect has been discussed by, e.g., (López-Corredoira et al. 2007, their Appendix A) to explain why the maximum density position along the line of sight does not coincide with the intersection between the bar major axis and the line of sight. The effect is present in the data more than in the models because of the different selection criteria, explained above.
 |
Fig. 7 Mean galactocentric radial velocity as a function of Galactic longitude for GIBS fields at different latitudes (red triangles) compared to the models by Martinez-Valpuesta et al. (2006, solid lines) at the same latitudes. Data from the BRAVA survey, when available, are also plotted in gray. |
 |
Fig. 8 Radial velocity dispersion as a function of Galactic longitude for GIBS fields at different latitudes (red triangles) compared to the models by Martinez-Valpuesta et al. (2006, solid lines) at the same latitudes. Data from the BRAVA survey, when available, are also plotted in gray. |
Figure 8 compares the velocity dispersion between GIBS (red) and BRAVA (gray) samples as well as a comparison with the same model mentioned above. In this plot, the data points present a larger scatter around the model, most likely because the measurement of a dispersion is more affected by the size of the target sample in each field. Nonetheless, the present data agree well both with the BRAVA ones and with the model predictions, for |b| > 3. At b = −2 the dispersion profile is steeper in the data than in the model, possibly because the mass distribution of the Galactic bulge is more centrally concentrated than assumed in the model.
4.2. A kinematical map of the Milky Way
In the following section, we describe the interpolation of radial velocity and velocity dispersion at different observed locations, in order to construct kinematical maps of the Milky Way bulge. The goal of this exercise is to derive the general rotation pattern of the Galactic bulge, to be directly compared with kinematic maps of external galaxies from IFU surveys such as SAURON, ATLAS3D and CALIFA (Emsellem et al. 2004, 2011; Krajnović et al. 2011; Husemann et al. 2013). In addition, it provides the expected ⟨ Vr ⟩ and σVr values at any location within our field of view.
 |
Fig. 9 Mean radial velocity (two leftmost panels) or velocity dispersion (two rightmost panels) values as a function of longitude, at a fixed latitude, compared to a surface cut at the same latitude. Data for a given latitude are shown with the same color of the curve at that latitude. Black dots were not included in the fits, for the reasons explained in Sect. 4.2. Points at b = +4.5 are shown here together with the curve at |b| = 4.5 in order to verify the assumption of symmetry about the Galactic plane. |
In order to derive the analytical function, F(l,b), that best describes the bulge kinematics as a function of the position in the sky, only data for the fields at negative latitude were used (i.e. excluding the fields at b = +4.5, which are used to test symmetry with respect to b). The 4 fields at l < −3, b = −2 were also excluded from the fit, because they would introduce an artificial bump that, as explained in Sect. 4.1, is most likely due only the projection of the bar density along the line of sight.
As a first step, a function was fitted to the radial velocities and dispersions at fixed
latitude, as a function of longitude. The functional form is the same at
every latitude, only the coefficients were allowed to change. A
nonlinear, least-square Marquardt-Levenberg fitting algorithm was used at this stage. The
derived coefficients were then plotted against latitude and fitted under the assumption of
symmetry in b. Combining both results we derived the set of functions
that can reproduce the observed kinematics of the inner bulge: 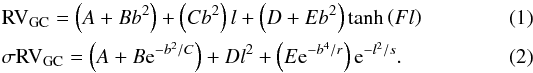 Finally,
these functions were fitted again to all the fields at negative latitude, all in one step,
yielding the coefficients listed in Table 3. Note
that, when fitting the radial velocity profile, the GIBS and BRAVA data were combined
given the excellent agreement demonstrated in Fig. 7.
Conversely, when deriving the velocity dispersion profile, only GIBS data were used
because the BRAVA profile is significantly noisier (Fig. 8).
Finally,
these functions were fitted again to all the fields at negative latitude, all in one step,
yielding the coefficients listed in Table 3. Note
that, when fitting the radial velocity profile, the GIBS and BRAVA data were combined
given the excellent agreement demonstrated in Fig. 7.
Conversely, when deriving the velocity dispersion profile, only GIBS data were used
because the BRAVA profile is significantly noisier (Fig. 8).
 |
Fig. 10 Mean radial velocity surface in the longitude-latitude plane constructed from the measured rotation profiles at negative latitudes. Gray points show the positions of the observed fields, while the black contour lines are labeled with the relevant velocity in km s-1. |
The fits at different latitudes are shown in Fig. 9 together with the data used for the fit (b < 0; left panels). In the right panels we compare the fitted surface with the data at b = 4.5 in order to verify the assumption of symmetry. This assumption turns out to be a very accurate both in radial velocity and dispersion.
The resulting analytical surfaces are shown in Figs. 10 and 11. Two features of these maps are worth noticing. The first one, in Fig. 10, is the asymmetry of the radial velocity profile versus longitude, which is only due to projection effects, as demonstrated by the agreement with theoretical models shown in Fig. 7. Indeed, the lines of sight crossing the bar in its near side (positive longitudes) and far side (negative longitudes) sample the bar density distribution in a different way. The second interesting feature is the presence of a peak in the velocity dispersion, for |l| < 2 and |b| < 3 (see Fig. 11). This is best viewed in Fig. 9 and it is due to the very large velocity dispersion in the three fields at (0, −2), (−1, −2) and (0, −1), as seen in the histograms in Fig. 5. Note that because in each of the two fields at (0, −2) and (0, −1) we sampled ~450 stars, we can safely exclude the possibility that the higher velocity dispersion could be due to small number statistics. The peak is clearly seen at b = −1 and b = −2, but it is not very evident in the data at b = −3.5, (Fig. 8), possibly due to the sparse sampling of our fields. Therefore, the elongation of the peak in the vertical direction in Fig. 11 might not be real. While the real extension of the σ-peak is not well constrained, due to the presence of only two fields in that region, we can certainly conclude that such a peak does exist, and it is most likely due to a high density peak in the bulge innermost region. It is interesting that the spatial extension of the σ-peak broadly coincides with the change in the inclination angle of the bar, interpreted as due to the presence of either an inner bar (Gonzalez et al. 2011a), or an inner axisymmetric mass distribution (Gerhard & Martinez-Valpuesta 2012).
 |
Fig. 11 Radial velocity dispersion surface in the longitude-latitude plane constructed from the measured rotation profiles at negative latitudes. Gray points show the positions of the observed fields, while the black contour lines are labeled with the relevant velocity dispersion in km s-1. |
4.3. Discussion and conclusions
We have presented the GIBS Survey, aimed at characterizing the kinematics, metallicity distribution, and element ratio of RC stars across 31 fields in the Galactic bulge. In addition to describing the survey in terms of target selection, observational strategy and data products, we provided here radial velocity measurements for a sample of 6392 individual stars. The measured velocities agree well with the results from the BRAVA survey, and confirm their finding of cylindrical rotation for the bulge, extending it to latitudes b = −2 much closer to the Galactic plane than probed before. Maps of radial velocity and velocity dispersions as a function of Galactic coordinates have been produced by interpolating among the observed fields. The radial velocity dispersion map is particularly interesting because it shows a central, high σ-peak possibly associated with a higher mass density in the inner ~2 degrees of the Bulge.
It is worth emphasizing that the σ-peak extends out to a projected distance of ~280 pc (corresponding to 2 degrees at a distance of 8 kpc) and therefore it is much bigger than (obviously) the nuclear star cluster surrounding the supermassive black hole, but also the other two massive clusters Arches (26 pc from the Galactic center), and Quintuplet (30 pc). It is also much bigger than the Central Molecular Zone, confined to |b| < 0.2 and |l| < 0.8. It does match in size with the change in the position angle of the Galactic bar (Gonzalez et al. 2011a) interpreted as evidence of either a distinct inner bar or of a central axisymmetric structure (Gerhard & Martinez-Valpuesta 2012).
Concerning the bulge formation scenarios, early merging of gas-rich galaxies and secular instabilities in stellar disks have been traditionally regarded as the two possible channels for the formation of galactic bulges (see, e.g., Kormendy & Kennicutt 2004). Bulges that would have formed by mergers (often referred to as classical bulges) would be similar to early type galaxies (ETG) in many respects, such as old ages, α-element enhancement, high Sérsic index, etc. Bulges that would have formed by (bar and bar-buckling) instabilities in a stellar disk (often referred to as pseudobulges) would be characterized by peanut-shaped isophotes, lower Sérsic index, cylindrical rotation, and possibly an extended range of stellar ages and lower α-element enhancement (e.g., Shen et al. 2010, and references therein).
Our Galactic bulge fails to fit in either of these scenarios, but appears to have some properties of both scenarios. For example, it is bar- and peanut-shaped and, as confirmed by the present investigation, it rotates cylindrically. Nonetheless, as reviewed in the Sect. 1, its stellar populations appear to be uniformly ~10 Gyr old (Ortolani et al. 1995; Zoccali et al. 2003; Clarkson et al. 2008) and are α element enhanced (e.g., Gonzalez et al. 2011b; Bensby et al. 2013, and references therein). This embarrassment has prompted the notion that our bulge may be a mixture of both kind of bulges, with attempts at identifying specific subcomponent of the bulge with one or the other kind (e.g., Hill et al. 2011; Babusiaux et al. 2010, as already mentioned in Sect.1). However, other groups interpret multimodal metallicity/kinematical distributions of bulge stars uniquely in terms of the disk instability scenario, that may have redistributed stars from different disk populations to different bulge latitudes, without the need to resort to a contribution of merging (e.g., Bensby et al. 2011, 2013; Ness et al. 2013b).
There are, however, lines of evidence suggesting that Nature may have followed also other paths for the formation of galactic bulges. First, the notion according to which ETGs are primarily the result of merging is seriously challenged by the finding that ~86% of them are fast rotators, often with cylindrical rotation, whereas only ~14% of them are slow rotators, the likely result of dry merging (Emsellem et al. 2011). Independent evidence for a marginal role of merging in shaping passively evolving (early type) galaxies comes from the characteristic mass (M∗) of their mass function being only ~0.1 dex higher in high-density regions (where merging takes place) compared to low-density regions (Peng et al. 2012).
The second evidence comes from high-redshift galaxies. Indeed, if the bulk of star in the bulge are ~10 Gyr old, then it is at a ~10 Gyr lookback time that we should look to see analogs of our bulge in formation, i.e., at z ~ 2. A great deal of evidence has accumulated in recent years on star-forming galaxies at such high redshifts. Many among them are large, clumpy, rotating disks (Genzel et al. 2006; Förster Schreiber et al. 2009) with high star formation rates (SFR, e.g., Daddi et al. 2007). Moreover, such disks are much more gas rich compared to local spirals, with gas fractions of order of ~50% or more (Tacconi et al. 2010; Daddi et al. 2010). These properties makes them very attractive in the context of bulge formation. On the one hand, their high specific SFR (≡SFR/Mstar), larger than the corrsponding inverse Hubble time (i.e., >10-9 Gyr-1) implies a very rapid mass growth and automatically leads to α-element enhanced stellar populations (Renzini 2009; Peng et al. 2010; Lilly et al. 2013). Furthermore, such gas-rich galaxies are prone to disk instabilities leading to massive clump formation, which in turn can migrate to the center and dissipatively coalesce resulting in bulge formation over timescales of a few 108 yr (e.g., Immeli et al. 2004; Carollo et al. 2007; Elmegreen et al. 2008; Bournaud et al. 2009). Such timescales are much shorter than those typically ascribed to secular instabilities in local (gas poor) disk galaxies. It should go without saying that bulges formed in this way would be relatively fast rotators and may later develop bars and X-shaped components. It is worth emphasizing that this may well be the dominant channel for the formation of both galactic bulges and most ETGs alike, with what remains to be understood being the physical processes leading to the quenching of their star formation. Also worth emphasizing, is the fundamental difference between this kind of disk instability, which is intimately related to disks being very gas rich, and the traditional secular, bar/buckling instability (à la Sellwood 1981) which instead develops in a purely stellar disk.
For this reason, we refrain from intepreting the bulge cylindrical rotation as an evidence of its RC stars tracing a pseudo-bulge component, or pointing towards its formation via secular evolution.
Acknowledgments
SV and MZ acknowledge support by Proyecto Fondecyt Regular 1110393, by the BASAL Center for Astrophysics and Associated Technologies PFB-06, the FONDAP Center for Astrophysics 15010003, Proyecto Anillo ACT-86 and by the Chilean Ministry for the Economy, Development, and Tourism’s Programa Iniciativa Científica Milenio through grant P07-021-F, awarded to The Milky Way Millennium Nucleus. V.H. and C.B. acknowledge support of the French Agence Nationale de la Recherche, under contract ANR-2010-BLAN- 0508-01OTP, and the Programme National de Cosmologie et Galaxies.
References
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Alves-Brito, A., Meléndez, J., Asplund, M., Ramírez, I., & Yong, D. 2010, A&A, 513, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amôres, E. B., López-Corredoira, M., González-Fernández, C., et al. 2013, A&A, 559, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armandroff, T. E., & Zinn, R. 1988, AJ, 96, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E. 2005, MNRAS, 358, 1477 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E. 2012, MNRAS, 426, L46 [NASA ADS] [Google Scholar]
- Babusiaux, C., & Gilmore, G. 2005, MNRAS, 358, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Babusiaux, C., Gómez, A., Hill, V., et al. 2010, A&A, 519, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, G., Irwin, M., Tolstoy, E., et al. 2008, MNRAS, 383, 183 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2005, ApJ, 630, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Adén, D., Meléndez, J., et al. 2011, A&A, 533, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Yee, J. C., Feltzing, S., et al. 2013, A&A, 549, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., Gerhard, O., & Spergel, D. 1997, MNRAS, 288, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Bissantz, N., & Gerhard, O. 2002, MNRAS, 330, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L., & Spergel, D. N. 1991, ApJ, 379, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Martig, M. 2009, ApJ, 707, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera-Lavers, A., Hammersley, P. L., González-Fernández, C., et al. 2007, A&A, 465, 825 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabrera-Lavers, A., González-Fernández, C., Garzón, F., Hammersley, P. L., & López-Corredoira, M. 2008, A&A, 491, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, L., Mao, S., Nataf, D., Rattenbury, N. J., & Gould, A. 2013, MNRAS, 434, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, C. M., Scarlata, C., Stiavelli, M., Wyse, R. F. G., & Mayer, L. 2007, ApJ, 658, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Churchwell, E., Babler, B. L., Meade, M. R., et al. 2009, PASP, 121, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, W., Sahu, K., Anderson, J., et al. 2008, ApJ, 684, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Debattista, V. P., Mayer, L., Carollo, C. M., et al. 2006, ApJ, 645, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 2000, AJ, 119, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., Arendt, R. G., Hauser, M. G., et al. 1995, ApJ, 445, 716 [CrossRef] [Google Scholar]
- Elmegreen, B. G., Bournaud, F., & Elmegreen, D. M. 2008, ApJ, 688, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Peletier, R. F., et al. 2004, MNRAS, 352, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2011, MNRAS, 414, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K., Ness, M., Wylie-de-Boer, E., et al. 2013, MNRAS, 428, 3660 [NASA ADS] [CrossRef] [Google Scholar]
- Frogel, J. A., & Whitford, A. E. 1987, ApJ, 320, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2006, ApJ, 636, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Gardner, E., Debattista, V. P., Robin, A. C., Vásquez, S., & Zoccali, M. 2013, MNRAS, submitted [arXiv:1306.4694] [Google Scholar]
- Genzel, R., Tacconi, L. J., Eisenhauer, F., et al. 2006, Nature, 442, 786 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gerhard, O., & Martinez-Valpuesta, I. 2012, ApJ, 744, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Minniti, D., et al. 2011a, A&A, 534, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2011b, A&A, 530, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., Valenti, E., & Minniti, D. 2011c, A&A, 534, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2012, A&A, 543, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2013, A&A, 552, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammersley, P. L., Garzón, F., Mahoney, T. J., López-Corredoira, M., & Torres, M. A. P. 2000, MNRAS, 317, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, V., Lecureur, A., Gomez, A., et al. 2011, A&A, 534, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, C. D., Rich, R. M., Clarkson, W., et al. 2009, ApJ, 702, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Husemann, B., Jahnke, K., Sánchez, S. F., et al. 2013, A&A, 549, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ibata, R. A., & Gilmore, G. F. 1995a, MNRAS, 275, 591 [Google Scholar]
- Ibata, R. A., & Gilmore, G. F. 1995b, MNRAS, 275, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Immeli, A., Samland, M., Gerhard, O., & Westera, P. 2004, A&A, 413, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, C. I., Rich, R. M., Fulbright, J. P., Valenti, E., & McWilliam, A. 2011, ApJ, 732, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Rich, R. M., Kobayashi, C., et al. 2013, ApJ, 765, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Kennicutt, Jr., R. C., 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Emsellem, E., Cappellari, M., et al. 2011, MNRAS, 414, 2923 [NASA ADS] [CrossRef] [Google Scholar]
- Kunder, A., Koch, A., Rich, R. M., et al. 2012, AJ, 143, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Carollo, C. M., Pipino, A., Renzini, A., & Peng, Y. 2013, ApJ, 772, 119 [NASA ADS] [CrossRef] [Google Scholar]
- López-Corredoira, M., Cabrera-Lavers, A., Mahoney, T. J., et al. 2007, AJ, 133, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Valpuesta, I., & Gerhard, O. 2011, ApJ, 734, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Valpuesta, I., & Gerhard, O. 2013, ApJ, 766, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Valpuesta, I., Shlosman, I., & Heller, C. 2006, ApJ, 637, 214 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., & Rich, R. M. 1994, ApJS, 91, 749 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., & Zoccali, M. 2010, ApJ, 724, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Alves-Brito, A., et al. 2008, A&A, 484, L21 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Minniti, D. 1996, ApJ, 459, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Minniti, D., Lucas, P. W., Emerson, J. P., et al. 2010, New A, 15, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Nataf, D. M., Udalski, A., Gould, A., Fouqué, P., & Stanek, K. Z. 2010, ApJ, 721, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2013a, MNRAS, 430, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2013b, MNRAS, 432, 2092 [NASA ADS] [CrossRef] [Google Scholar]
- Nidever, D. L., Zasowski, G., Majewski, S. R., et al. 2012, ApJ, 755, L25 [Google Scholar]
- Nishiyama, S., Nagata, T., Baba, D., et al. 2005, ApJ, 621, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Ortolani, S., Renzini, A., Gilmozzi, R., et al. 1995, Nature, 377, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Peng, Y.-j.,Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-j., Lilly, S. J., Renzini, A., & Carollo, M. 2012, ApJ, 757, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Pfenniger, D., & Friedli, D. 1991, A&A, 252, 75 [NASA ADS] [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, S. V., Stephens, A. W., Frogel, J. A., & DePoy, D. L. 2000, AJ, 120, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Rangwala, N., Williams, T. B., & Stanek, K. Z. 2009, ApJ, 691, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Rattenbury, N. J., Mao, S., Sumi, T., & Smith, M. C. 2007, MNRAS, 378, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A. 2009, MNRAS, 398, L58 [NASA ADS] [Google Scholar]
- Rich, R. M. 1988, AJ, 95, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Origlia, L., & Valenti, E. 2007a, ApJ, 665, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Reitzel, D. B., Howard, C. D., & Zhao, H. 2007b, ApJ, 658, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Origlia, L., & Valenti, E. 2012, ApJ, 746, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Marshall, D. J., Schultheis, M., & Reylé, C. 2012, A&A, 538, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadler, E. M., Rich, R. M., & Terndrup, D. M. 1996, AJ, 112, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, K., Martinez-Valpuesta, I., & Gerhard, O. 2012, MNRAS, 421, 333 [NASA ADS] [Google Scholar]
- Saito, R. K., Zoccali, M., McWilliam, A., et al. 2011, AJ, 142, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, R. K., Hempel, M., Minniti, D., et al. 2012a, A&A, 537, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saito, R. K., Minniti, D., Dias, B., et al. 2012b, A&A, 544, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saviane, I., da Costa, G. S., Held, E. V., et al. 2012, A&A, 540, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sellwood, J. A. 1981, A&A, 99, 362 [NASA ADS] [Google Scholar]
- Sharples, R., Walker, A., & Cropper, M. 1990, MNRAS, 246, 54 [NASA ADS] [Google Scholar]
- Shen, J., Rich, R. M., Kormendy, J., et al. 2010, ApJ, 720, L72 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. 1973, ApJ, 184, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, K. Z., Mateo, M., Udalski, A., et al. 1994, ApJ, 429, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Starkenburg, E., Hill, V., Tolstoy, E., et al. 2010, A&A, 513, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Sumi, T., Wu, X., Udalski, A., et al. 2004, MNRAS, 348, 1439 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Tiede, G. P., & Terndrup, D. M. 1997, AJ, 113, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A., Szymanski, M., Kubiak, M., et al. 2002, Acta Astron., 52, 217 [NASA ADS] [Google Scholar]
- Vásquez, S., Zoccali, M., Hill, V., et al. 2013, A&A, 555, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wegg, C., & Gerhard, O. 2013, MNRAS, 435, 1874 [Google Scholar]
- Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Hill, V., Lecureur, A., et al. 2008, A&A, 486, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Approximate location of the fields discussed in the present paper, overplotted on an optical image of the Milky Way bulge (© Serge Brunier). The large white rectangle is the area mapped by the VVV survey. Red and white circles are fields observed at low spectral resolution (R = 6500) through setup LR8, from program 187.B-0909; red and white squares are fields observed at high resolution (R = 22 500) through setup HR13, from program 187.B-0909. Crosses at b ~ −2 are the fields from program 089.B-0830, also observed through LR8. The blue star is the field, within Baade’s Window, used for the CaT calibration, and the blue triangle is the field discussed in Vásquez et al. (2013). |
| In the text | |
 |
Fig. 2 Location of the fields discussed in the present study compared to the fields from the ARGOS survey (Freeman et al. 2013). Black open circles are the ARGOS fields. Red filled circles are fields observed at low spectral resolution (R = 6500) through setup LR8, from program 187.B-0909; open squares are fields observed at high resolution (R = 22 500) through setup HR13, from program 187.B-0909. Blue crosses are the fields from program 089.B-0830, also observed through LR8. The blue star is the field, within Baade’s Window, used for the CaT calibration, and the blue triangle is the field discussed in Vásquez et al. (2013) . The large rectangle shows the area mapped by the VVV survey. |
| In the text | |
 |
Fig. 3 Example of the GIBS target selection criteria for the LRm5m2 field. Left: the VVV CMD together with the 214 GIRAFFE targets (red) and the 14 UVES targets (cyan). Right: magnitude distribution of the GIRAFFE targets (red histogram) compared with the underlying luminosity function of the RGB stars with J − K > 1.0 (black histogram). |
| In the text | |
 |
Fig. 4 Example of typical spectra observed through setup LR8 for three targets with different preliminary metallicities. Vertical ticks mark the three corresponding CaT lines. |
| In the text | |
 |
Fig. 5 Radial velocity distributions for all the GIBS fields. The two fields at (0, −6) and (0, −8) include targets both for the bright RC (red) and the faint (RC). Part of the data at b = −2, shown as black histograms, come from program 089.B-0830. The labels on the upper left corner, in each panel, list the mean velocity (M), the skewness (Sk) and the number of stars (N). On the upper right corner we list the galactic coordinates of the field. |
| In the text | |
 |
Fig. 6 Mean galactocentric radial velocity (top) and velocity dispersion (bottom) as a function of Galactic longitude, for different latitudes, as listed in the labels. |
| In the text | |
 |
Fig. 7 Mean galactocentric radial velocity as a function of Galactic longitude for GIBS fields at different latitudes (red triangles) compared to the models by Martinez-Valpuesta et al. (2006, solid lines) at the same latitudes. Data from the BRAVA survey, when available, are also plotted in gray. |
| In the text | |
 |
Fig. 8 Radial velocity dispersion as a function of Galactic longitude for GIBS fields at different latitudes (red triangles) compared to the models by Martinez-Valpuesta et al. (2006, solid lines) at the same latitudes. Data from the BRAVA survey, when available, are also plotted in gray. |
| In the text | |
 |
Fig. 9 Mean radial velocity (two leftmost panels) or velocity dispersion (two rightmost panels) values as a function of longitude, at a fixed latitude, compared to a surface cut at the same latitude. Data for a given latitude are shown with the same color of the curve at that latitude. Black dots were not included in the fits, for the reasons explained in Sect. 4.2. Points at b = +4.5 are shown here together with the curve at |b| = 4.5 in order to verify the assumption of symmetry about the Galactic plane. |
| In the text | |
 |
Fig. 10 Mean radial velocity surface in the longitude-latitude plane constructed from the measured rotation profiles at negative latitudes. Gray points show the positions of the observed fields, while the black contour lines are labeled with the relevant velocity in km s-1. |
| In the text | |
 |
Fig. 11 Radial velocity dispersion surface in the longitude-latitude plane constructed from the measured rotation profiles at negative latitudes. Gray points show the positions of the observed fields, while the black contour lines are labeled with the relevant velocity dispersion in km s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


