| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 6 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201322610 | |
| Published online | 04 February 2014 | |
Artificial neural network to search for metal-poor galaxies⋆
1
North China Institute of Aerospace Engineering,
Langfang, 065000
Hebei,
PR China
e-mail: fshi@bao.ac.cn
2
Center of Astrophysics, University of Science and Technology of
China, Hefei,
230026, PR
China
e-mail: xkong@ustc.edu.cn
3
Key Laboratory for Research in Galaxies and
Cosmology, USTC,
CAS, Hefei,
230026, PR
China
Received: 5 September 2013
Accepted: 5 December 2013
Aims. To find a fast and reliable method for selecting metal-poor galaxies (MPGs), especially in large surveys and huge databases, an artificial neural network (ANN) method is applied to a sample of star-forming galaxies from the Sloan Digital Sky Survey (SDSS) data release 9 (DR9) provided by the Max Planck Institute and the Johns Hopkins University (MPA/JHU).
Methods. A two-step approach is adopted: (i) The ANN network must be trained with a subset of objects that are known to be either MPGs or metal rich galaxies (MRGs), treating the strong emission line flux measurements as input feature vectors in n-dimensional space, where n is the number of strong emission line flux ratios. (ii) After the network is trained on a sample of star-forming galaxies, the remaining galaxies are classified in the automatic test analysis as either MPGs or MRGs. We consider several random divisions of the data into training and testing sets; for instance, for our sample, a total of 70 percent of the data are involved in training the algorithm, 15 percent are involved in validating the algorithm, and the remaining 15 percent are used for blind testing the resulting classifier.
Results. For target selection, we have achieved an acquisition rate for MPGs of 96 percent and 92 percent for an MPGs threshold of 12 + log (O/H) = 8.00 and 12 + log (O/H) = 8.39, respectively. Running the code takes minutes in most cases under the Matlab 2013a software environment. The ANN method can easily be extended to any MPGs target selection task when the physical property of the target can be expressed as a quantitative variable.
Key words: methods: data analysis / Galaxy: abundances / Galaxy: formation
The code in the paper is available on the web (http://fshi5388.blog.163.com).
© ESO, 2014
1. Introduction
Extremely metal-poor local galaxies are essential for understanding of star formation and enrichment in a nearly pristine interstellar medium (ISM). Metal-poor galaxies (MPGs) provide important constraints on the pre-enrichment of the ISM by previous episodes of star formation, such as those by Population III stars (Thuan et al. 2005). These galaxies are also the best objects for determining of the primordial He abundance and for constraining cosmological models (e.g. Izotov & Thuan 2004; Izotov et al. 2007). Metal-poor galaxies are possibly the closest examples we can find of elementary primordial units from which galaxies formed.
Unfortunately, MPGs are rare. The review by Kunth & Östlin (2000) cites only 31 targets with metallicity below one tenth the solar value. The first extragalactic objects with very low metal abundance were discovered by Searle & Sargent (1972), who reported on the properties of two intriguing galaxies, IZw18 and IIZw40. Their extreme metal underabundance, more than ten times less than solar, and even more extreme than that of Hii regions found in the outskirts of spiral galaxies, indicates that these objects could genuinely be young galaxies in the process of formation (Kunth & Östlin 2000). This discovery leads to extensive systematic searches for more objects with low metallicity (see Kunth & Östlin 2000 and references therein) to understand the properties of their massive stars (formation and evolution, appearance of WR stars): the evolution of the dynamics of the gas in the gravitational potential of the parent galaxy as a superbubble develops, the triggering mechanism that ignites their bursts of star formation, and the chemical enrichment of the ISM after the fresh products have been mixed well.
The number of MPGs has significantly increased since the work by Kunth & Östlin (2000), but still the number of known MPGs is small (Morales-Luis et al. 2011). The thorough bibliographic compilation described in Sect. 4 shows only 421 MPGs with metallicity below two tenths of the solar value (12 + log (O/H) < 8.0). There are several reasons that prohibit identifying more MPGs. One reason is that the MPGs are usually dwarf galaxies, which are dim and hard to observe. Another reason is that the methods that determine the metallicity of a galaxy are highly uncertain, and there is a large discrepancy between different methods (Shi et al. 2005, 2006, 2010). The metallicity is a key parameter in the search for MPGs. Oxygen is an important element that is easily and reliably determined since the most important ionization stages can be observed. The oxygen abundance from measuring electron temperature from [O iii]λλ4959,5007/[O iii]λ4363 is one of the most reliable methods, called the Te method. But [O iii]λ4363 is usually weak in low-metallicity galaxies, and there are often large errors when measuring this line. In high-metallicity galaxies, [O iii]λ4363 is hardly even observable.
Instead of the Te method, strong line methods, such as the R231, P2, N23, Ne3O24, or O3N25 methods, are widely used (Pagel et al. 1979; Kobulnicky et al. 1999; Pilyugin et al. 2001; Charlot & Longhetti 2001; Denicoló et al. 2002; Pettini & Pagel 2004; Tremonti et al. 2004; Liang et al. 2006). The R23 and P methods suffer from the double-valued problem, requiring some assumption or rough a priori knowledge of a galaxy’s metallicity in order to locate it on the appropriate branch of the relation. The N2- and O3N2 methods are monotonic, but the reasons for this are not purely physical. It is partly due to the N/O ratio increasing on average with the increase in metallicity (Stasińska 2006; Shi et al. 2006). Besides, calibrations of the O3N2 and N2 indices might be improper for interpreting the integrated spectra of galaxies because [N ii ] λ6583 and Hα may arise not only in bona fide H ii regions, but also in a diffuse ionized medium. Stasińska (2006) proposes Ar3O36 and S3O37 as new abundance indicators, which have the advantage of being unaffected by the effects of chemical evolution. The advantages are superior to previous N2 and O3N2 methods.
In short, the method using a single flux ratio is questionable. The ideal metallicity indicator should use all the strong emission lines. To use a method that capitalizes on strong emission lines to identify MPGs, we employed an automatic artificial neural network(ANN) search for metal-poor galaxies in the ninth Sloan Digital Sky Survey data release (SDSS/DR98), by combining all strong emission line flux ratio measurements including Ne3O2, [O iii]λλ4959,5007/[O iii]λ4363, [O ii]/Hβ, [O iii]/Hβ, Hα/Hβ, N2, and [S ii], provided by MPA. An ANN approach has already been successfully applied to sort out different types of astronomical spectra from supernovae (Karpenka et al. 2013) to quasars (Yèche et al. 2010).
This paper is organized as follows. In Sect. 2, we describe the data set used for training and testing in our analysis, and we present a detailed account of our methodology in Sect. 3. We test the performance of our approach in Sect. 4 by applying to the data and present our results. Finally, we conclude in Sect. 5. Throughout the paper, we adopt cosmological parameters of the ΩM = 0.27 and ΩΛ = 0.73.
2. Data sample
To use ANN, we must first construct a sample of sources with good emission line detections. All the objects in the sample must have evident and reliable flux ratio measurements, such as Ne3O2, [O iii]λλ4959,5007/[O iii]λ4363, [O ii]/Hβ, [O iii]/Hβ, Hα/Hβ, [N ii]/Hα, and [S ii]. For this purpose, we use the catalog of star-forming galaxies in SDSS DR 9 provided by MPA, which made use of the spectral diagnostic diagrams from Kauffmann et al. (2003) to classify galaxies as star-forming galaxies, active galactic nuclei (AGN), or unclassified. In total, 84 465 star-forming galaxies are adopted in our sample. All the galaxies in the sample have reliable spectral observations with reasonable values of strong line ratio and oxygen abundance. The redshifts of the galaxies in the sample are in the range of 0.02 <z < 0.3. The oxygen abundance in the sample spans a wide range from 7.1 < 12 + log (O/H) < 9.5. The distribution of the oxygen abundance in each bin is plotted in Fig. 1. It is clear that MPGs are rare than metal-rich galaxies (MRGs). There are only 8671 galaxies with 12 + log (O/H) < 8.39 (~10 percent of the star-forming galaxies sample), and among them only 421 galaxies with 12 + log (O/H) < 8.0 (~0.5 percent of the star-forming galaxies sample).
 |
Fig. 1 Distribution of 12 + log (O/H) for our data sample. |
 |
Fig. 2 Schematic representation of a 2-layer artificial neural network used here with 9 input variables (redshift, Ne3O2, [O iii]λλ4959,5007/ [O iii]λ4363, N2/Hα,[O iii]/Hβ, [S ii], [O ii]/Hβ, Hα/Hβ, [Ar iii]/[O iii]) as the input vector x, 10 hidden neurons, and 2 output neurons (MPG or MRGs as target vectors t). This schematic is taken from the MATLAB Recognizing Patterns Documentation. |
 |
Fig. 3 Confusion matrices for training, testing, and validation, and the three kinds of data combined for setting the MPG threshold to 12 + log (O/H) = 8.0 using all 9 variables. The diagonal cells show the number of cases that were correctly classified, and the off-diagonal cells show the misclassified cases. The blue cell in the bottom right shows the total percent of correctly classified cases (in green) and the total percent of misclassified cases (in red). |
3. Artificial neural network approach
The basic building block of the ANN architecture is a processing element called a neuron. The ANN architecture used in this study is illustrated in Fig. 2. For target selection, we used an nprtool package developed in the Matlab environment. The nprtool package leads us through solving a pattern-recognition classification problem using a two-layer feed-forward network with sigmoid output neurons. The neuron is the simplest kind of node, and it maps an input vector x ∈ ℜn to a scalar output f(x;w,θ) via 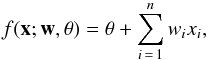 (1)where θ are “bias” and { wi } are “weights” of the ith variables in the input vector x that include n variables. We focus mainly on a two-layer feed-forward ANN, which consists of a hidden layer and an output layer as shown in Fig. 2. The default number of hidden neurons is set to ten. The number of output neurons is set to two, which is equal to the number of elements in the target vector (MPGs or MRGs).
(1)where θ are “bias” and { wi } are “weights” of the ith variables in the input vector x that include n variables. We focus mainly on a two-layer feed-forward ANN, which consists of a hidden layer and an output layer as shown in Fig. 2. The default number of hidden neurons is set to ten. The number of output neurons is set to two, which is equal to the number of elements in the target vector (MPGs or MRGs).
To classify a set of data using an ANN, we need to provide a set of training data (x t). We build the input vector x, which includes redshift, Ne3O2, [O iii]λλ4959,5007/ [O iii]λ4363, N2/Hα,[O iii]/Hβ, [S ii], [O ii]/Hβ, Hα/Hβ, and [Ar iii]/[O iii]data (9 input variables) from the data-set in Sect. 2. Target t is defined as 0 or 1 to represent MPGs or MRGs. We applied an MPG cut to 12 + log (O/H) = 8.0 (corresponding to 0.2 Z⊙), to enhance the selection. Because MPGs are much rarer than MRGs, we select 1000 MRGs galaxies for 12 + log (O/H) > 8.0 randomly to avoid systematic errors caused by too many MRGs compared to MPGs.
Then, the input vectors x and target vectors t are randomly divided into three sets as follows: 70 percent are the training set, which is used for computing the gradient and updating the network weights and biases. Fifteen percent are used to validate that the network is generalizing and to stop training before overfitting. The last 15 percent are used as a completely independent test of network generalization.
 |
Fig. 4 Receiver operating characteristic (ROC) curve for training, testing, and validation, and the three kinds of data combined. |
 |
Fig. 5 Confusion matrices for training, testing, and validation, and the three kinds of data combined for the MPG threshold to 12 + log (O/H) = 8.39 using all 9 variables. |
Once the network weights and biases are initialized, the network is ready for training. The process of training a neural network involves tuning the values of the weights and biases of the network to optimize network performance, as defined by the network performance function. The default performance function for feed-forward networks is mean squared error (ε) between the network outputs f and the target outputs t. It is defined as follows: 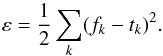 (2)Depending on the network architecture, there can be millions of network weights and biases that make network training a very complicated and computationally challenging task. The nprtool uses the simplest optimization algorithm – gradient descent. It updates the network weights and biases in the direction where the performance function decreases most rapidly, the negative of the gradient. The gradient will become very small as the training reaches a minimum of the performance function (Eq. (2)). The iteration of this algorithm can be written as
(2)Depending on the network architecture, there can be millions of network weights and biases that make network training a very complicated and computationally challenging task. The nprtool uses the simplest optimization algorithm – gradient descent. It updates the network weights and biases in the direction where the performance function decreases most rapidly, the negative of the gradient. The gradient will become very small as the training reaches a minimum of the performance function (Eq. (2)). The iteration of this algorithm can be written as 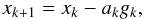 (3)where xk is a vector of current weights and biases, gk is the current gradient, and ak is the learning rate.
(3)where xk is a vector of current weights and biases, gk is the current gradient, and ak is the learning rate.
4. Spectral selection of MPGs
Once the network has been trained, it is applied to the testing dataset to obtain the predictions for each galaxy therein being either an MPG or an MRG. For illustration, we considered three ANN configurations that differ in terms of the number of variables. The first one uses all variables: redshift, Ne3O2, [O iii]λλ4959,5007/[O iii]λ4363, N2/Hα, [O iii]/Hβ, [S ii], [O ii]/Hβ, Hα/Hβ, and [Ar iii]/[O iii]. In the second configuration, We study Te method, strong line methods, such as the R23, Ar3O3, N2, Ne3O2, or O3N2, one by one to show whose strong line ratios are the most effective in identifying MPGs. In the third configuration, we plot in Fig. 5 the confusion matrices when the MPG threshold is fixed to 12 + log (O/H) = 8.39 (corresponding to 0.5 Z⊙) using all nine variables to show the changes caused by the MPG threshold. The confusion matrices of configurations are plotted in Figs. 3 and 5, respectively. For the introduction to confusion matrices, please see the Matlab Recognizing Patterns web site9.
For the first configuration (i.e., using all variables), we achieved an MPG acquisition rate of ~96 percent for MPG threshold of 12 + log (O/H) = 8.0. It is therefore apparent that the nine-variable ANN should be used for the purpose of selecting MPGs in any optical spectral catalog. We also plot the receiver operating characteristic (ROC) curves for our analysis procedure in Fig. 4. The ROC curve provides a very reliable way of sorting out the optimal algorithm in signal detection theory. The ROC curve is a plot of the true positive rate (sensitivity) versus the false positive rate (1 – specificity). A perfect test would show points in the upper left hand corner, with 100 percent accuracy. One sees in Fig. 4 that nprtool yields very reasonable ROC curves, indicating that the classifiers are quite discriminating.
For the second configuration, we identified MPGs only using the essential information for the Te-method (redshift, [O iii]λλ4959,5007/[O iii]λ4363, [O iii]/Hβ, [S ii], [O ii]/Hβ), R23-method (redshift, [O iii]/Hβ, [O ii]/Hβ), N2-method (redshift, N2/Hα), O3N2-method (redshift, N2/Hα, [O iii]/Hβ), Ne3O2-method (redshift, [Ne iii]λ3869/[O ii]λ3727) Ar3O3-method (redshift, [Ar iii]/[O iii]). We found that the acquisition rate for MPGs was reduced by a few percent when using only one method, 92.3% for the Te-method, 90.9% for the R23-method, 96.2% for the N2-method, 96.2% for the O3N2-, 85.8% for the Ne3O2-method, and 88.7% for the Ar3O3-method (see Table 1). All the oxygen abundance determination methods based on these strong line ratios are reliable to a certain degree. In any case, it is an essential parameter for having redshift identify MPGs because it is vital to make the accurate redshift correction when deriving the flux of the strong emission line.
Acquisition rate for MPGs as a function of the different variables.
It is impressive that the acquisition rate for MPGs by the N2 and Ne3O2 method is comparable to using all nine variables. It might imply that both the N2 and Ne3O2 methods are monotonic, free of internal reddening correction, and therefore superior to other oxygen abundance determination methods.
We add (Hα/Hβ) line ratio to each method to show the influence of internal reddening correction on identifying MPGs. This parameter is probed because the internal reddening correction is a fundamental step in determining 12 + log (O/H) (Shi et al. 2005, 2006). We find that the acquisition rate for MPGs increases from 85.8% to 88.1% for the Ne3O2-method, 90.9% to 92.5% for the R23-method, and 88.7% to 90.9% for the Ar3O3- method when adding (Hα/Hβ) to them (see Table 1). The acquisition rate for MPGs for the remaining three methods (Te, N2, O3N2 methods) do not change when adding (Hα/Hβ) to them, which can be explained by the uncertainty of the internal reddening correction being comparable to the uncertainty of Te-method and [N ii]λ6583/Hαλ6563, and [O iii]λ5007/Hβ/[N ii]λ6583/Hα flux ratio is not sensitive to the internal reddening correction.
To show the changes in performance caused by the MPG threshold, we plot in Fig. 5 the confusion matrices when the MPG threshold is fixed to 12 + log (O/H) = 8.39 (corresponding to 0.5 Z⊙) using all nine variables: redshift, Ne3O2, [O iii]λλ4959,5007/[O iii]λ4363, N2/Hα, [O iii]/Hβ, [S ii], [O ii]/Hβ, Hα/Hβ, and [Ar iii]/[O iii]. There are 8671 MPGs when the MPG threshold is fixed to 12 + log (O/H) = 8.39, and we select 10 000 MRGs galaxies for 12 + log (O/H) = 8.39 randomly to avoid the systematic error caused by too many MRGs compared to MPGs. It is shown that the MPGs acquisition rate decreases a few percent compared to the MPG threshold of 12 + log (O/H) = 8.0. This may imply that 12 + log (O/H) = 8.39 is a less suitable MPG threshold than 12 + log (O/H) = 8.00.
5. Conclusions
We have presented a promising new approach to selecting MPGs from spectral catalogs. It involves the application of an artificial neural network with a two-layer feed-forward architecture. The input variables are spectral measurements, i.e., redshift and the most observably strong emission line ratios.
In the target selection, we achieved an MPG acquisition rate of 96 percent and 92 percent for an MPG threshold of 12 + log (O/H) = 8.00 and 12 + log (O/H) = 8.39, respectively from ~80 000 star forming galaxies. The oxygen abundance of a galaxy in the MPG sample has a 96-percent chance of being lower than 12 + log (O/H) = 8.00 for an MPG threshold of 12 + log (O/H) = 8.00.
All the oxygen abundance determination methods based on these strong line ratios are reliable to a certain degree, such as the Te-, R23-, N2- , O3N2-, and Ne3O2- methods. The acquisition rates for MPGs by the N2-method and O3N2-methods are comparable to it using all nine variables. It shows a serious potential to search for new MPGs candidate with a single emission line ratio, such as [N ii]λ6583/Hαλ6563.
This new statistical method developed in the context of the SDSS project can be extended easily to any other analysis requiring MPG selection when the physical property of the target can be quantitative.
Finally, we note that, aside from its relative simplicity and robustness, the ANN classification method that we presented here can be extended and improved in a number of ways, such as increasing the neuron number, adopting a three-layer network, or making the multi-category classification. One has to be cautioned that both the classification accuracy and run time may change dramatically in these processes.
Acknowledgments
This work was funded by the National Natural Science Foundation of China (NSFC, Nos. 11203001, 11202003, 11225315 and 11320101002), the Specialized Research Fund for the Doctoral Program of Higher Education (SRFDP, No. 20123402110037) and Chinese Universities Scientific Fund (CUSF). Funding for the Sloan Digital Sky Survey (SDSS) has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the US Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society.
References
- Charlot, S., & Longhetti, M. 2001, MNRAS, 323, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Denicoló, G., Terlevich, R., & Terlevich, E. 2002, MNRAS, 330, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 2004, ApJ, 602, 200 [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Stasińska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Karpenka, N. V., Feroz, F., & Hobson, M. P. 2013, MNRAS, 429, 1278 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., Kennicutt, R. C., Jr., & Pizagno, J. L. 1999, ApJ, 514, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Kunth, D., & Oumlstlin, G. 2000, A&ARv, 10, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, Y. C., Yin, S. Y., Hammer, F., et al. 2006, ApJ, 652, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Morales-Luis, A. B., Sánchez Almeida, J., Aguerri, J. A. L., & Muñoz-Tuñón, C. 2011, ApJ, 743, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., et al. 1979, MNRAS, 189, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S. 2001, A&A, 369, 594 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Searle, L., & Sargent, W. L. W. 1972, ApJ, 173, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, F., Kong, X., Li, C., & Cheng, F. Z. 2005, A&A, 437, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shi, F., Kong, X., & Cheng, F. Z. 2006, A&A, 453, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shi, F., Zhao, G., & Wicker, J. 2010, J. Astrophys. Astron., 31, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Stasińska, G. 2006, A&A, 454, L127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thuan, T. X., Lecavelier des Etangs, A., & Izotov, Y. I. 2005, ApJ, 621, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Yèche, C., Petitjean, P., Rich, J., et al. 2010, A&A, 523, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Distribution of 12 + log (O/H) for our data sample. |
| In the text | |
 |
Fig. 2 Schematic representation of a 2-layer artificial neural network used here with 9 input variables (redshift, Ne3O2, [O iii]λλ4959,5007/ [O iii]λ4363, N2/Hα,[O iii]/Hβ, [S ii], [O ii]/Hβ, Hα/Hβ, [Ar iii]/[O iii]) as the input vector x, 10 hidden neurons, and 2 output neurons (MPG or MRGs as target vectors t). This schematic is taken from the MATLAB Recognizing Patterns Documentation. |
| In the text | |
 |
Fig. 3 Confusion matrices for training, testing, and validation, and the three kinds of data combined for setting the MPG threshold to 12 + log (O/H) = 8.0 using all 9 variables. The diagonal cells show the number of cases that were correctly classified, and the off-diagonal cells show the misclassified cases. The blue cell in the bottom right shows the total percent of correctly classified cases (in green) and the total percent of misclassified cases (in red). |
| In the text | |
 |
Fig. 4 Receiver operating characteristic (ROC) curve for training, testing, and validation, and the three kinds of data combined. |
| In the text | |
 |
Fig. 5 Confusion matrices for training, testing, and validation, and the three kinds of data combined for the MPG threshold to 12 + log (O/H) = 8.39 using all 9 variables. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


