Table 1
Comparison of acceleration mechanisms for systems with δy < Δy.
| Mechanism | Maximum energy gain | Condition δy < Δy | Comments | |||
|
|
||||||
| Nonadiabatic drift acceleration | 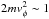 keV keV |
2vφ/ < ΔyΩ0 | ||||
| (vφ ≥ v0) single reflection | ||||||
|
|
||||||
| Nonadiabatic drift acceleration | 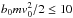 keV keV |
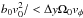
|
the same estimates are valid | |||
| (vφ ≥ v0) multiple reflections | for adiabatic acceleration | |||||
|
|
||||||
| Surfatron with Ex ≠ 0 | 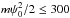 keV keV |

|
energy gain is ~m | |||
|
|
||||||
| Surfatron with 1 + b0f(φ) ~ 0 | m(Ω0Δxw)2 ≤ 1 MeV | 0.5Ω0(Δxw)2/vφ < Δy | energy gain is ~m | |||
| Surfatron with dvφ/dx ≠ 0 | 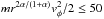 keV keV |
l0r(α − 1)/(1 + α)/ < Δy | energy gain is ~q2α/(1 + α)m(1 − α)/(1 + α) | |||
Notes. Here, we use the parameter
r = (Ω0l0/vφ)
for the system with
vφ(x) ~ (l0/x)α.
The scale Δx defines the distance between the X-line region and the
initial magnetic loop. The parameter  determines the maximum distance, which particles can pass in the resonance with the
front (here Pw is the power density of
magnetic field fluctuations measured in nT2/Hz). For
Pw taken from spacecraft
measurements in the Earth magnetotail (Zimbardo et
al. 2010), we have
Δxw ~ 104 km. Numerical
estimates of gained energy are given for
vφ ~ 200–300 km s-1 and
proton mass.
determines the maximum distance, which particles can pass in the resonance with the
front (here Pw is the power density of
magnetic field fluctuations measured in nT2/Hz). For
Pw taken from spacecraft
measurements in the Earth magnetotail (Zimbardo et
al. 2010), we have
Δxw ~ 104 km. Numerical
estimates of gained energy are given for
vφ ~ 200–300 km s-1 and
proton mass.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


