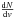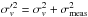| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 15 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201322445 | |
| Published online | 31 January 2014 | |
Binary-corrected velocity dispersions from single- and multi-epoch radial velocities: massive stars in R136 as a test case⋆
1 Institute for Astronomy, ETH Zurich, Wolfgang-Pauli-Strasse 27, 8093 Zurich, Switzerland
e-mail: MCottaar@phys.ethz.ch
2 Department of Physics, Faculty of Engineering and Physical Sciences, University of Surrey, Guildford, GU2 7XH, UK
e-mail: v.henault-brunet@surrey.ac.uk
3 Scottish Universities Physics Alliance (SUPA), Institute for Astronomy, University of Edinburgh, Blackford Hill, Edinburgh, EH9 3HJ, UK
Received: 5 August 2013
Accepted: 21 November 2013
Orbital motions from binary stars can broaden the observed line-of-sight velocity distribution of a stellar system and artificially inflate the measured line-of-sight velocity dispersion, which can in turn lead to erroneous conclusions about the dynamical state of the system. Recently, a maximum-likelihood procedure was proposed to recover the intrinsic velocity dispersion of a resolved star cluster from a single epoch of radial velocity data of individual stars, which was achieved by simultaneously fitting the intrinsic velocity distribution of the single stars and the centers of mass of the binaries along with the velocity shifts caused by binary orbital motions. Assuming well-characterized binary properties, this procedure can accurately reproduce intrinsic velocity dispersions below 1 km s-1 for solar-type stars. Here we investigate the systematic offsets induced when the binary properties are uncertain and we show that two epochs of radial velocity data with an appropriate baseline can help to mitigate these systematic effects. We first test the method described above using Monte Carlo simulations, taking into account the large uncertainties in the binary properties of OB stars. We then apply it to radial velocity data in the young massive cluster R136 for which the intrinsic velocity dispersion of O-type stars is known from an intensive multi-epoch approach. For typical velocity dispersions of young massive clusters (≳4 km s-1) and with a single epoch of data, we demonstrate that the method can just about distinguish between a cluster in virial equilibrium and an unbound cluster. This is due to the higher spectroscopic binary fraction and more loosely constrained distributions of orbital parameters of OB stars compared to solar-type stars. By extending the maximum-likelihood method to multi-epoch data, we show that the accuracy on the fitted velocity dispersion can be improved by only a few percent by using only two epochs of radial velocities. This procedure offers a promising method of accurately measuring the intrinsic stellar velocity dispersion in other systems for which the binary properties are poorly constrained, for example, young clusters and associations whose luminosity is dominated by OB stars.
Key words: binaries: spectroscopic / open clusters and associations: individual: R136 / stars: kinematics and dynamics / stars: early-type / Magellanic Clouds
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
An accurate measurement of the intrinsic velocity dispersion of a star cluster is required to estimate its virial state, which determines whether a cluster is currently bound or is dissolving into the field. Recent observational studies of resolved young massive clusters suggested that the majority have velocity dispersions of a few km s-1 and seem to be in virial equilibrium. These studies were based both on proper motions (e.g. Rochau et al. 2010; Clarkson et al. 2012) and multi-epoch radial velocities (e.g. Cottaar et al. 2012a; Hénault-Brunet et al. 2012a). The luminosity of these young massive clusters is dominated by massive OB stars, a large proportion of which are spectroscopic binaries (e.g. Kiminki & Kobulnicky 2012; Sana et al. 2012, 2013), therefore the radial velocity studies were designed to include multiple epochs. With this multi-epoch strategy, the significant effect of spectroscopic binaries on the observed radial velocity distribution (e.g. Gieles et al. 2010) can be reduced by identifying as many of these systems as possible and removing them from the sample. Repeated radial velocity measurements have also been used to correct for the influence of binary stars in other types of systems, for example in dwarf galaxies (e.g. Simon et al. 2011; Koposov et al. 2011).
Alternatively, one can use a maximum-likelihood procedure to recover the intrinsic velocity dispersion of a stellar system from a single epoch of radial velocity data despite the orbital motions of spectroscopic binaries by simultaneously fitting the intrinsic velocity distribution of the single stars and centers of mass of the binaries along with the radial velocities caused by orbital motions (Odenkirchen et al. 2002; Kleyna et al. 2002; Martinez et al. 2011; Cottaar et al. 2012b). This technique allows one to study the dynamical state of clusters with a low velocity dispersion without the need for multi-epoch observations to identify the spectroscopic binaries. Even when multi-epoch data are available, the same technique can still be used (with minor modifications, see Sect. 2.2) to correct for the orbital motions of undetected binaries.
Cottaar et al. (2012b) showed that this method could successfully reproduce the intrinsic velocity dispersion of 0.5 km s-1 of the old open cluster NGC 188 (Geller et al. 2008, 2009; Geller & Mathieu 2011) using a single epoch of radial velocity data and adopting the observed orbital parameter distributions (i.e. period, mass ratio, and eccentricity) for solar-type field stars (Raghavan et al. 2010; Reggiani & Meyer 2013). It is not obvious that the same method can be applied to successfully recover the intrinsic velocity dispersion of young massive clusters because (1) the OB stars dominating the light of these systems have a high spectroscopic binary fraction (e.g. Sana et al. 2012, and references therein); (2) the distributions of orbital parameters of massive binaries are relatively loosely constrained compared to solar-type stars; (3) higher masses imply more contaminations to the velocity dispersion because the orbital velocity scales with the mass of the primary as vorb ∝ M1/3; (4) the period distribution of massive binaries generally appears skewed towards shorter periods (see Sect. 2.3), which also implies more contaminations; and (5) the accuracy of radial velocity measurements is generally lower for OB stars (typically a few km s-1 or more) due to rotational broadening of their spectral lines. Dedicated tests of the method using tailored Monte Carlo experiments are therefore needed. It is also desirable to perform tests on a young massive cluster for which the intrinsic velocity dispersion was measured from an intensive dataset of multi-epoch radial velocities (i.e. after selecting out spectroscopic binaries).
In this paper, we take advantage of the unique dataset provided by the VLT-FLAMES Tarantula Survey (VFTS; Evans et al. 2011). From multi-epoch spectroscopic data of massive stars in the 30 Doradus region of the Large Magellanic Cloud, Hénault-Brunet et al. (2012a) measured the intrinsic velocity dispersion of the young massive cluster R136 (M ~ 105M⊙ − e.g. Andersen et al. 2009; age ~2 Myr − e.g. Crowther et al. 2010; de Koter et al. 1998), corrected for the orbital motions of binaries. Sana et al. (2013) studied the spectroscopic binary fraction and distributions of orbital parameters (period and mass ratio) of the O-type stars in the broader 30 Doradus region. Using the radial velocities measured in these previous studies, we applied the procedure of Cottaar et al. (2012b) and determined whether the correct velocity dispersion can be recovered from a single epoch of radial velocities. In addition, we tested the systematic and statistical uncertainties in the procedure through Monte Carlo simulations for both single- and multi-epoch observations.
In Sect. 2, we briefly outline the maximum-likelihood method presented by Cottaar et al. (2012b), introduce an extension of this procedure that is applicable to multi-epoch data, and discuss available constraints on the binary properties of OB stars. We describe Monte Carlo simulations used to test the procedure for single- and two-epoch datasets in Sect. 3. We then present the R136 dataset and the results obtained when applying the maximum-likelihood method to these data in Sect. 4. We discuss the implications of these results in Sect. 5, and finally present our conclusions in Sect. 6.
2. Method
2.1. Outline of the maximum-likelihood method
The details of the maximum-likelihood procedure used to fit an observed radial velocity distribution can be found in Cottaar et al. (2012b). We provide with the current paper the necessary python code1 for calculating the likelihood to reproduce the observed radial velocities given an intrinsic velocity distribution, measurement uncertainties, and a set of binary orbital parameter distributions. For a given set of orbital parameter distributions, we varied the cluster’s binary fraction, mean radial velocity, and intrinsic line-of-sight velocity dispersion to maximize this likelihood to reproduce the data.
The observed radial velocity of a cluster member is the sum of three components: the radial velocity of the center of mass, the radial velocity offset due to the orbital motion of the binary, and the measurement uncertainty. The likelihood function for the observed radial velocity is therefore given by the convolution of the probability density functions (pdfs) of these three components. Here we describe a method for computing this convolution.
The convolution of the intrinsic radial velocity distribution of the cluster and the measurement uncertainties, assuming they are Gaussian, yields 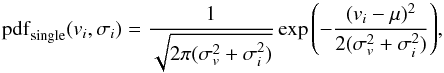 (1)where μ and σv are the mean radial velocity and intrinsic line-of-sight velocity dispersion of the cluster, and vi and σi are the observed radial velocity and corresponding uncertainty for star i. For a single star without binary orbital motion this pdf directly gives the likelihood of reproducing the observed radial velocity.
(1)where μ and σv are the mean radial velocity and intrinsic line-of-sight velocity dispersion of the cluster, and vi and σi are the observed radial velocity and corresponding uncertainty for star i. For a single star without binary orbital motion this pdf directly gives the likelihood of reproducing the observed radial velocity.
For spectroscopic binaries we convolve this pdf with the pdf of radial velocity offsets due to binary orbital motions. As no analytic form of the latter pdf is available, this convolution was performed numerically. First, we generated a large number (N) of random binaries from the adopted orbital period, mass ratio, and eccentricity distributions and calculated for each one the size of the three-dimensional velocity vector vk. As these velocities are randomly orientated with respect to the line of sight, the projected velocity offset is a random value between − vk and + vk, which yields for the pdf of velocity offsets projected along the line of sight 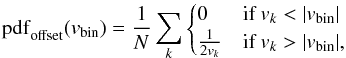 (2)where pdfoffset(vbin) gives the probability distribution of the line-of-sight velocity offset vbin due to binary orbital motions.
(2)where pdfoffset(vbin) gives the probability distribution of the line-of-sight velocity offset vbin due to binary orbital motions.
Equation (2) can be computed for a single primary stellar mass Mprim (e.g. 1 M⊙) and can then be easily extended to other primary stellar masses by using the fact that the orbital velocity increases proportionally to 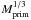 for a fixed period, mass ratio, and eccentricity distribution. If known, the primary mass of each observed star can be taken into account by multiplying (for each star) the velocity grid on which pdfoffset(vbin) was computed by (Mprim/M⊙)1/3 and dividing the pdfoffset by the same amount to conserve the normalization (see Cottaar et al. 2012b). We assumed a stellar mass of 30 M⊙ for the O-stars studied here.
for a fixed period, mass ratio, and eccentricity distribution. If known, the primary mass of each observed star can be taken into account by multiplying (for each star) the velocity grid on which pdfoffset(vbin) was computed by (Mprim/M⊙)1/3 and dividing the pdfoffset by the same amount to conserve the normalization (see Cottaar et al. 2012b). We assumed a stellar mass of 30 M⊙ for the O-stars studied here.
The pdf for the observed radial velocity distribution from binary systems can then be computed by numerically convolving the pdf for the measurement uncertainty and center-of-mass radial velocity (Eq. (1)) and the pdf for the radial velocity offset due to the binary orbital motion (Eq. (2), potentially corrected for primary mass) 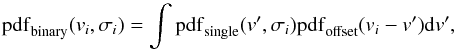 (3)where v′ is the sum of the radial velocity of the center of mass of the binary and the contribution from the measurement uncertainty, and vi − v′ is the radial velocity offset due to the binary orbital motion. In the provided code Eq. (2) is pre-computed on a dense grid, which allows for the repeated rapid computation of the integral in Eq. (3), as long as the distributions of binary orbital parameters are not varied during the fit (which would require pdfoffset to be recomputed).
(3)where v′ is the sum of the radial velocity of the center of mass of the binary and the contribution from the measurement uncertainty, and vi − v′ is the radial velocity offset due to the binary orbital motion. In the provided code Eq. (2) is pre-computed on a dense grid, which allows for the repeated rapid computation of the integral in Eq. (3), as long as the distributions of binary orbital parameters are not varied during the fit (which would require pdfoffset to be recomputed).
 |
Fig. 1 Blue line: observed radial velocity distribution for a single epoch drawn from the multi-epoch radial velocity dataset of R136 (Hénault-Brunet et al. 2012a; Sana et al. 2013, see Sect. 4.1 for details). Red dashed line: best-fit radial velocity distribution, including the effect of the orbital motions of spectroscopic binaries. Green line: intrinsic velocity distribution of the cluster, corrected for the orbital motions of binaries. This intrinsic distribution is assumed to be a Gaussian whose width and mean have been optimized to fit the data (see Sect. 2.1). |
Finally, the total likelihood ℒi of observing a given velocity is obtained by summing the contributions from single stars (Eq. (1)) and from binaries (Eq. (3)) 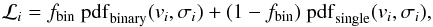 (4)where fbin is the binary fraction and 1 − fbin is the fraction of systems that are single stars.
(4)where fbin is the binary fraction and 1 − fbin is the fraction of systems that are single stars.
For a given set of binary orbital parameter distributions (Sect. 2.3), we varied the binary fraction (fbin), the intrinsic line-of-sight velocity dispersion (σv) and the mean velocity (μv) to find the maximum-likelihood to reproduce all observed radial velocities (i.e. max  ). We explored the probability distribution of the best-fit parameters and determined the uncertainties on each of these marginalized over all the other free parameters using a Metropolis-Hastings implementation of Markov chain Monte Carlo (MCMC) simulations (see Cottaar et al. 2012b).
). We explored the probability distribution of the best-fit parameters and determined the uncertainties on each of these marginalized over all the other free parameters using a Metropolis-Hastings implementation of Markov chain Monte Carlo (MCMC) simulations (see Cottaar et al. 2012b).
Figure 1 shows an example where we fitted a single epoch of the multi-epoch radial velocities observed for R136 (for more details on this dataset see Sect. 4.1). The binary orbital motions of the OB stars strongly affect the observed radial velocity distribution, as indicated by the large difference between the best-fit radial velocity distribution in red (given by Eq. (4)) and the corresponding intrinsic Gaussian velocity distribution of the cluster in green (given by Eq. (1)).
2.2. Extension to multiple epochs
For a single epoch of radial velocity data, the maximum-likelihood procedure described above gives the intrinsic velocity dispersion of a cluster corrected for the effect of binary orbital motions. This works well for stellar populations for which the binary orbital parameter distributions are well constrained (e.g. solar-type stars, Cottaar et al. 2012b). When these are more loosely constrained (e.g. for OB stars), multiple epochs can be used to identify and remove from the sample some spectroscopic binaries, thereby improving the accuracy of the final velocity dispersion determination. However, there will always remain undetected spectroscopic binaries that significantly affect the radial velocity distribution. We describe below four adjustments to the likelihood procedure that make it possible to accurately estimate the intrinsic velocity dispersion of a cluster from a multi-epoch dataset corrected for the effect of these undetected spectroscopic binaries.
First, we identified as many spectroscopic binaries as possible and removed them from the sample. To identify these binaries, we used a χ2-test to assess whether the radial velocity observations are consistent with coming from a single star without radial velocity variations. For each star, we computed 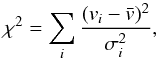 (5)where
(5)where 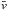 is the weighted mean velocity over all the observed epochs i, and vi and σi are the velocities at individual epochs and their uncertainties. By comparing this with the χ2-distribution (with the number of degrees of freedom equal to the number of epochs minus one), we compute the probability that a value as high as the computed χ2 can be due to measurement uncertainties alone. If this probability was low, we identified the star as a radial velocity variable and removed it from the sample. In line with previous work on R136 (Hénault-Brunet et al. 2012a), we rejected stars with a probability p < 10-4 of not being a radial velocity variable.
is the weighted mean velocity over all the observed epochs i, and vi and σi are the velocities at individual epochs and their uncertainties. By comparing this with the χ2-distribution (with the number of degrees of freedom equal to the number of epochs minus one), we compute the probability that a value as high as the computed χ2 can be due to measurement uncertainties alone. If this probability was low, we identified the star as a radial velocity variable and removed it from the sample. In line with previous work on R136 (Hénault-Brunet et al. 2012a), we rejected stars with a probability p < 10-4 of not being a radial velocity variable.
In principle, completely removing these radial velocity variables from the sample is waste of information. However, including this information would require solving the radial velocity orbit of the binary. This is computationally very expensive when only a few epochs are available. Even if it is computed, the uncertainty in the systemic velocity of the binary will tend to be very weakly constrained, therefore it will provide little useful information about the intrinsic velocity dispersion or even the mean velocity of the cluster. Of course the systemic velocity of the binary should be included in the fit of the velocity dispersion (with its appropriate uncertainty), if enough epochs have been observed to solve the binary orbit.
Secondly, we computed for the remaining and apparently single stars the effect of possible unidentified binary on the observed radial velocity distribution. For this, we generated a large population of binaries sampled from the adopted binary orbital parameter distributions and assumed that these systems have random phases and orientations. Using the same χ2-test as for the actual data, we then determined which binaries would have been detected given the timing of the observations and the measurement uncertainties. Eliminating these systems left us with a sample of binaries that would not be detected given the observational constraints. We computed the radial velocity offset distribution due to the orbital motions of these binaries, which gave us pdfoffset for binaries which are undetected in the multi-epoch dataset. This was recomputed for every star, because the detectability of binaries strongly depends on the time sampling of the observations and the measurement uncertainties.
Our proposed method differs substantially from the multi-epoch fit from Martinez et al. (2011). These authors used a very similar likelihood procedure to fit their multi-epoch radial velocity data of the dwarf spheroidal galaxy Segue 1, but they made no explicit distinction between radial velocity variables and seemingly single stars. This distinction allowed us to reach a higher precision, because the systemic velocities of the seemingly single stars have much smaller uncertainties than the systemic velocities of the radial velocity variables. By not distinguishing these populations, Martinez et al. (2011) combined the probability distribution of the systemic velocity for seemingly single stars and radial velocity variables, which led them to underestimate the constraints that the seemingly single stars can put on the intrinsic radial velocity distribution.
After computing the radial velocity offsets due to binary orbital motions for the apparently single stars, we convolved this with an assumed intrinsic velocity distribution (Eq. (3)) and added the contribution from truly single stars (Eq. (4)). However, when using Eq. (4) we kept in mind that the binary fraction among the apparently single stars (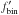 ) is lower than among the population as a whole
) is lower than among the population as a whole 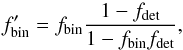 (6)where fdet is the fraction of binaries that would have been detected given the timing of the observations and the measurement uncertainties, as estimated from the random sample of binaries generated in the previous step.
(6)where fdet is the fraction of binaries that would have been detected given the timing of the observations and the measurement uncertainties, as estimated from the random sample of binaries generated in the previous step.
Finally, we added an additional constraint on the binary fraction to match the observed fraction of binaries. This is given by a binomial distribution: 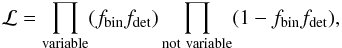 (7)where we multiplied the probability of detecting a radial velocity variability for all stars with radial velocity variability (
(7)where we multiplied the probability of detecting a radial velocity variability for all stars with radial velocity variability (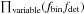 ) and the probability for detecting no radial velocity variability for all apparently single stars (
) and the probability for detecting no radial velocity variability for all apparently single stars (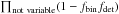 ).
).
Here we briefly summarize this approach to fitting multi-epoch radial velocity data. Before performing the fit, four preparatory steps should be taken:
-
1.
Separate the observed stars into radial velocity variables andseemingly single stars based on whether the radial velocity overthe multiple epochs is consistent with being constant (seeEq. (5)).
-
2.
Draw a random population (N ~ 105 − 106) of binaries from the assumed period, mass ratio, and eccentricity distribution and with a random phase and orientation.
-
3.
For every observed seemingly single star, select a subsample of the simulated binary population by removing all simulated binaries that would have been detected as a radial velocity variable given the time sampling and measurement uncertainty of that observed star. The fraction of radial velocity variables in the simulated population sets fdet, which can be used to compute the probability that the observed seemingly single star is still a binary (
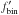 ) with Eq. (6).
) with Eq. (6). -
4.
For every observed seemingly single star, compute the distribution of orbital velocities projected onto the line of sight for the pruned simulated binary population from step 3 to derive pdfoffset(vi − v′).
We then used the distribution of radial velocity offsets due to binary orbital motions to compute the likelihood of the data being drawn from a given intrinsic velocity distribution (e.g. parametrized by the mean velocity and velocity dispersion) and binary fraction by following the steps below. These steps needed to be repeated for every evaluation of the likelihood as part of the maximization procedure and associated analysis of the parameter uncertainties (e.g. from a MCMC simulation).
-
1.
For every observed seemingly single star, use the distributionfrom step 4, the probability of the star being a binary
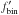 from step 3, and an assumed underlying velocity distribution to compute the likelihood of reproducing the observed radial velocity of that star using Eqs. (3) and (4).
from step 3, and an assumed underlying velocity distribution to compute the likelihood of reproducing the observed radial velocity of that star using Eqs. (3) and (4). -
2.
Compute the total likelihood to reproduce the observed velocity distribution of seemingly single stars by multiplying the likelihoods to observe the radial velocities for all the observed seemingly single stars (or adding the log-likelihood).
-
3.
Finally, multiply this likelihood from step 6 with the likelihood of detecting the observed fraction of radial velocity variables from Eq. (7) using the fdet from step 3.
When only a single epoch of radial velocity data is available, steps 3, 4 simplify to computing Eq. (2) for the binary population from step 2. As in this case no radial velocity variables can be detected (fdet = 0), the probability of a star to be a binary becomes the binary fraction (i.e. 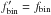 ) and the likelihood from Eq. (7) will be equal to one for any binary fraction.
) and the likelihood from Eq. (7) will be equal to one for any binary fraction.
A possible extension of this procedure would be to perform a Bayesian analysis and allow the parametrization of the period, mass ratio, and eccentricity distributions to vary within the uncertainties set by previous observations. Although this would in principle accurately deal with the effect on the fitted velocity dispersion of the uncertainties in the binary orbital parameter distributions, it would require recomputing the preparatory steps 1−4 for every step in the optimization and subsequent MCMC simulation. Unfortunately, this is currently prohibitively slow, especially when multi-epoch data are considered.
2.3. Constraints on the binary properties of OB stars
Constraints on the distributions of orbital parameters of massive binaries from the literature.
Below we focus on the orbital parameter distributions of short-period close binaries, that is those with the largest orbital velocities, the strongest impact on the fitted line of sight velocity dispersion, and that are probed efficiently by Doppler shifts of spectral lines. As we review in the appendix, there is now ample evidence that massive stars are preferentially found in binary systems, in particular in these close spectroscopic binary systems.
Unfortunately, the orbital parameter distributions of these binaries are still relatively poorly constrained, despite their fundamental importance to star formation, stellar evolution, and the early dynamical evolution of massive star clusters. Even when studies of massive binaries include a relatively large number of systems (e.g. Garmany et al. 1980; Mason et al. 2009), often only a small fraction of the identified binaries have well-constrained orbital properties (see Sana & Evans 2011). A few recent studies, which we discuss below, have achieved a better completeness in characterizing the identified binaries, in addition to correcting for observational biases in a more systematic way through Monte Carlo simulations (e.g. to translate the observed binary fraction into an intrinsic binary fraction).
Kobulnicky & Fryer (2007) attempted to constrain the distributions of orbital parameters of massive binaries by using a sample of 900 radial velocity measurements of 32 O-type and 88 B-type stars in the Cyg OB2 association and comparing the raw velocities with the expectations of Monte Carlo simulations. They were forced to make several simplifying assumptions about the orbital parameter distributions however. Building upon this work and taking advantage of an extended dataset, Kiminki & Kobulnicky (2012) used 12 years of spectroscopic observations of 114 massive stars (B3–O5 primary stars) in Cyg OB2 and modeled the observed mass ratio, orbital period, and eccentricity distributions composed of the well-constrained orbital properties of 24 known binaries in the association (22 of which have periods shorter than 30 days; see caveats about this in Appendix A).
Sana et al. (2013) analyzed the multiplicity properties of the O-type star population of 30 Doradus through multi-epoch spectroscopy obtained as part of the VLT-FLAMES Tarantula Survey. With 360 O-type stars surveyed, this is the largest homogenous sample of massive stars analyzed to date. However, given the limited number of epochs obtained (typically six), the orbital parameters could not be determined for individual binary systems. The intrinsic binary fraction and period and mass ratio distributions in this case were therefore constrained using Monte Carlo simulations to simultaneously reproduce the observed binary fraction, the distribution of the amplitudes of radial velocity variations, and the distribution of the timescales of these variations.
Sana et al. (2012) homogeneously analyzed the O-type star population of six nearby Galactic open clusters and simultaneously fitted all the relevant intrinsic multiplicity properties. The larger average number of epochs allowed for a more complete binary detection than in other studies. Over 75% of the 40 binaries identified in this sample have measured orbital properties, which also made it possible for the authors to directly model and fit the orbital parameter distributions. More details about the studies mentioned in this section and other pioneering works are presented in Appendix A.
 |
Fig. 2 Assumed period distribution (upper left) and mass ratio distribution (upper right), as well as the unprojected logarithmic velocity distribution (lower left) and the projected velocity distribution (lower right). The extrapolation of the period distribution from the observed range to an upper limit of 300 years is plotted as a dashed line. This extrapolation has been taken into account in the lower panels that show the velocity distributions. The blue lines show the distributions from Sana et al. (2012), the green lines those from Sana et al. (2013), and the red lines the distributions from Kiminki & Kobulnicky (2012), as detailed in Table 1. |
The distributions of binary orbital parameters from the three main studies discussed above are illustrated in Fig. 2 and summarized in Table 1 along with the intrinsic spectroscopic binary fractions. The domains for which the period, mass ratio, and eccentricity have been considered and to which the quoted intrinsic binary fractions apply are also listed. These studies used power laws to describe the probability density functions of orbital periods (in log 10 space), mass ratios and eccentricities with exponents π, κ, and η, respectively. In the following sections, we explore how sensitive the fitted velocity dispersion and binary fraction are to the adopted binary orbital parameter distribution by considering the differences between these orbital parameter distributions (which are consistent with each other at the two-sigma level).
We focus on the binary properties from the three papers listed in Table 1 because these studies are based on large samples and corrected for observational biases in a systematic way through Monte Carlo simulations. In contrast to some other studies, they also have the advantage that they do not a priori assume a fixed distribution for the periods or mass ratios (apart from assuming a power-law functional form). Moreover, they sample different combinations of period and mass ratio distributions, cover a relatively wide range of values of π and κ, and together are therefore representative of the current uncertainties on the binary properties of massive stars. These studies also each sample a different environment in terms of cluster mass and density. The clusters considered by Sana et al. (2012) have relatively low masses (1000 − 5000 M⊙), and it is currently unknown whether the binary fraction and orbital parameter distributions are affected in the more energetic environment around a ~105 M⊙ cluster like the 30 Doradus region, where the stars in the sample of Sana et al. (2013) are located. Thus, while we may not expect all the scenarios presented in Table 1 to be applicable to the young massive cluster R136, it is interesting to test how the maximum-likelihood method behaves under different assumptions about the binary properties.
 |
Fig. 3 Probability distribution ( |
In the studies discussed above, only binaries with a period of up to ~10 years could be detected due to the limited baselines of the observations. However, wider binaries still cause velocity offsets comparable to or larger than the velocity dispersion and hence significantly alter the observed velocity distribution. Figure 3 illustrates that large velocity offsets are likely to be caused by close binaries and small velocity offsets are more likely to be caused by wider binaries, as expected. Velocity offsets comparable to the velocity dispersion of R136 (~6 km s-1; Hénault-Brunet et al. 2012a, see also Sect. 4.1) are caused by binaries between ~1 and ~100 years, thus extending beyond the period range covered by spectroscopic surveys. To account for all the relevant binaries in our fits of the R136 data, we extrapolated the orbital period distribution to an upper limit of 300 years. We also increased the binary fraction to match the intrinsic binary fraction determined over the period range covered by the observations (last row in Table 1).
3. Monte Carlo simulations
3.1. Data generation
We used Monte Carlo simulations to
-
1.
show the self-consistency of the method (i.e. ensure that it givesthe correct result within the statistical uncertainties if allassumptions are met),
-
2.
determine how the accuracy is limited due to the uncertainties on the orbital parameter distributions of massive binaries (Sect. 2.3),
-
3.
and determine how the precision is limited due to small-number statistics.
In these simulations, we created a mock dataset of radial velocities through a two-step procedure. First, we assigned every star a systemic radial velocity from a Gaussian distribution with given mean velocity and intrinsic velocity dispersion. Then we assigned an additional velocity representing the effect of the binary orbital motions to a subset of these stars (where the probability to be a binary is set by the binary fraction). These additional velocities were computed using binary orbital parameters randomly drawn from one of the period, mass ratio, and eccentricity distributions listed in Table 1. In all cases we used the extrapolated period distribution out to 300 years and the corresponding binary fraction (last row in Table 1). In these simulations, we did not consider the effect that measurement uncertainties or a non-Gaussian velocity distribution have on the best-fit parameters. The provided python code can be used to generate these radial velocity distributions and reproduce the Monte Carlo experiments performed in this paper.
These mock radial velocity datasets were fitted using our maximum-likelihood procedure, assuming one of the three sets of binary orbital parameter distributions listed in Table 1. This was either the same set of orbital parameter distributions used to generate the data, allowing to test for self-consistency and constrain the precision of the method (goals 1 and 3 above), or a different set of orbital parameter distributions, allowing to test the accuracy of the procedure when the orbital parameter distributions in the cluster do not match those assumed (goal 2 above). We repeated these experiments for various sample sizes and intrinsic velocity distributions in the cluster.
In addition to these single-epoch Monte Carlo simulations, we ran a number of simulations where two epochs of radial velocity data were sampled for every star. The radial velocity of the second epoch was generated by increasing the phase of the binary orbit with the ratio of the observational baseline b and the binary period P and recomputing the radial velocity offset from the center of mass. The systematic center-of-mass velocity of the binary was kept constant.
Although in the single-epoch case we could safely ignore the measurement uncertainty (as long because it is sufficiently lower than the velocity dispersion such that it has a negligible effect on the observed velocity distribution2), in the multi-epoch case the measurement uncertainty is crucial as it determines whether a specific binary can be spectroscopically detected. Thus, in this case, we added an additional (Gaussian) measurement uncertainty to every observation. For simplicity we adopted the same measurement uncertainty for all stars and epochs.
3.2. Results
 |
Fig. 4 Systematic offset between the best-fit velocity dispersion (σfitted) and the input velocity dispersion (σinp) relative to the input velocity dispersion due to the uncertainties in the orbital parameter distributions of OB stars for a single epoch of radial velocity data. From top to bottom we have generated the radial velocity data using the orbital parameter distributions from Sana et al. (2012), Sana et al. (2013), and Kiminki & Kobulnicky (2012). The colors of the lines indicate the set of orbital parameter distributions assumed for the fit: blue line for Sana et al. (2012); green line for Sana et al. (2013); red line for Kiminki & Kobulnicky (2012). When the orbital parameter distributions used to generate the data are the same as those assumed in the fit, there is no systematic offset in the fitted velocity dispersion. The error bars represent the remaining uncertainty on the systematic offset after ~30 Monte Carlo simulations, each of which included a sample of 2000 radial velocities. The simulations for which we find a best-fit binary fraction of 100% in the majority of cases are marked with a black cross (see upper panel) to indicate that the fitted velocity dispersion is most likely overestimated in this case (see the main text). |
The uncertainties in the orbital parameter distributions of OB stars, encapsulated by the differences in the sets of distributions we considered, induces systematic offsets in the fitted velocity dispersion (and binary fraction) when an assumption about the underlying binary properties is made to fit the observed velocity distribution. We first considered this systematic offset in the velocity dispersion for single-epoch data and then considered how it changes for multi-epoch data. Figure 4 shows the systematic offset in the fitted velocity dispersion induced when we fit the randomly generated radial velocity datasets (Sect. 3.1) assuming each of the sets of binary orbital parameter distributions listed in Table 1.
In Fig. 4, we marked with a cross the simulations for which we found a best-fit binary fraction of 100%. Such a high best-fit binary fraction indicates that there are more high-velocity outliers in the dataset than can be explained by the assumed binary orbital parameter distributions. These high-velocity outliers could have many causes in real datasets, such as ejected stars, contaminating field stars, or poor radial velocity measurements. For the top panel of Fig. 4, the radial velocity datasets were generated using the binary properties from Sana et al. (2012), which includes a relatively large proportion of close and similar-mass binaries. This leads to many high-velocity outliers in these datasets, which cannot be matched by the other orbital parameter distributions considered here (even for a binary fraction of 100%). This situation, where the assumed orbital parameter distributions cannot explain the large number of high-velocity outliers, will cause the fitted velocity dispersion to be systematically overestimated, because this reduces the number of outliers. Accordingly irrespective of the nature of the high-velocity outliers, when a binary fraction of 100% is found the fitted velocity dispersion will tend to be inflated and be unreliable. Therefore, below we only considered the cases where we found a best-fit binary fraction below 100%.
When we used the same orbital parameter distributions to fit the data as we used to generate the data, no systematic offset between the input and retrieved velocity dispersion were found (Fig. 4). From this we conclude that the procedure is self-consistent (i.e. it yields the correct result if the assumptions made for the fit match the properties of the generated dataset). Significant systematic offsets were found when different orbital parameter distributions were used to generate the data than to fit the data. These systematic biases in the fitted velocity dispersion range from up to 60% for low input velocity dispersions (~2 km s-1) to as low as 25% for velocity dispersions of 10 km s-1 (Fig. 4) for the sets of orbital parameter distributions under study here. This suggests that without precise knowledge of the binary properties of massive stars in a given environment, we are limited to an accuracy of tens of percent when determining the line of sight velocity dispersion using a single epoch of radial velocities from OB stars. Most OB stars will form in massive clusters, whose virial velocity dispersion is generally expected to be higher than 4 km s-1. In this range the velocity dispersion can be fitted to an accuracy better than ~40%, which allows a cluster in virial equilibrium to be just barely distinguished from an unbound cluster from a single epoch of data.
If it is larger than the statistical uncertainties due to small-number statistics, this systematic offset of ~40% will limit the accuracy on the velocity dispersion. Figure 5 shows how the statistical uncertainties of the fitted velocity dispersion depends on the sample size. From this figure we find that a 2σ statistical uncertainty of ~40% is reached for a sample size of ~100 stars (for a cluster with a velocity dispersion of 5 km s-1). For a larger sample size the systematic offset due to the loosely constrained binary orbital parameter distributions will dominate the uncertainty on the velocity dispersion.
 |
Fig. 5 One-sigma statistical uncertainties due to small-number statistics in the fitted velocity dispersion as a function of the sample size N for single-epoch observations of a cluster with a velocity dispersion of 5 km s-1. The colors indicate the set of orbital parameter distributions used to generate the data and assumed for the fit: blue line for Sana et al. (2012); green line for Sana et al. (2013); red line for Kiminki & Kobulnicky (2012). The color-coding is the same as in Fig. 4. The statistical uncertainties are given relative to the input velocity dispersion of 5 km s-1. Every point in this graph represents the average statistical uncertainty (as measured by the MCMC) in 60 Monte Carlo simulations, except for sample sizes smaller than or equal to 30, where 200 Monte Carlo simulations were averaged. |
One option to decrease the systematic offset in the fitted velocity dispersion is to detect the spectroscopic binaries that alter the observed velocity distribution. This requires multiple epochs of data. The largest systematic offset was found when radial velocity data generated using the binary orbital parameter distributions from Kiminki & Kobulnicky (2012) was fitted using the distributions from Sana et al. (2012) (blue line in the lower panel of Fig. 4). For this specific case, we explored whether the systematic offset in the fitted velocity dispersion could be resolved by using two epochs of radial velocity data. The results of these Monte Carlo simulations are shown in Figs. 6 and 7 for clusters with a velocity dispersion of 2 km s-1 and 6 km s-1, for measurement uncertainties σmeas of 0.1, 0.5, and 1 km s-1 and a broad range of baselines between a few hours and hundreds of years.
 |
Fig. 6 Systematic offset in the fitted velocity dispersion for radial velocity data generated using the Kiminki & Kobulnicky (2012) binary orbital parameter distribution and fitted assuming the Sana et al. (2012) binary orbital parameter distribution, plotted against the baseline between two epochs of observations. As the baseline between the two epochs of observations increases, more spectroscopic binaries are detected, leading to a decrease in the systematic offset of the velocity dispersion. We show the results from Monte Carlo simulations for clusters with a velocity dispersion of 2 km s-1 (upper panel) and 6 km s-1 (lower panel), as well as for measurement uncertainties of 0.1 km s-1 (solid), 0.5 km s-1 (dashed), and 1 km s-1 (dotted). |
A larger fraction of the spectroscopic binaries can be detected when the baseline is longer or the measurement uncertainties are smaller. As expected, this leads to a smaller systematic offset in the fitted velocity dispersion. From Fig. 7 we find that for a broad range of intermediate baselines the systematic offset decreases linearly with log (σmeas/b), such that the systematic offset decreases by the same amount for every doubling of the baseline or halving of the measurement uncertainties. The size of the offset and the rate of decline depend on the exact binary properties assumed to compute the offset. This relation breaks down both for low σmeas/b, when only very close binaries can be identified (whose large velocity offsets already marked them as binaries in single-epoch data), and for high baselines b, when the baseline becomes comparable to the period of the widest binaries that have a significant radial velocity offset.
 |
Fig. 7 Same as Fig. 6, but with measurement uncertainty over the baseline (σmeas/b), rather than the baseline on the x-axis. Note that for a broad region of intermediate baselines, all the curves overlap. |
In Sect. 5.1, we analyze these relations in more detail. Here we note that for the typical measurement uncertainties of 4 km s-1 and the total baseline of one year of the radial velocity observations in R136, we obtain σmeas/b ≈ 4 km s-1 yr-1. Accordingly from these Monte Carlo simulations we expect a significant systematic offset in the fitted velocity dispersion of ~40% depending on the adopted binary orbital parameter distribution when analyzing a single epoch of the R136 radial velocity data. This systematic offset should be significantly reduced to ~20% when considering the full baseline of one year of the radial velocity observations (see lower panel of Fig. 7 for σmeas/b ≈ 4 km s-1 yr-1).
4. R136: a young massive cluster
4.1. Data
The dataset we used to test the maximum-likelihood method outlined in Sect. 2.1 consists of multiple epochs (at least five) of radial velocity measurements for 81 O-type systems in the inner 10 pc (in projection) of R136, all obtained with the FLAMES instrument on the VLT as part of the VLT-FLAMES Tarantula Survey (VFTS). These 81 systems include both apparently single stars and objects showing radial velocity variability. Most of the stars in the inner 5 pc have been observed with the ARGUS integral-field unit coupled to the Giraffe spectrograph, while for the vast majority of stars between 5 pc and 10 pc the Medusa fibre-feed to Giraffe has been used (for more details on the VFTS data, see Evans et al. 2011). In both cases, the radial velocities were measured by fitting Gaussians to helium absorption lines using a similar approach and the same rest wavelengths (Hénault-Brunet et al. 2012a; Sana et al. 2013). This sample of 81 objects excludes the B-type and emission-line stars observed by the VFTS in the inner 10 pc of R136, but it includes a few supergiants (or supergiant candidates) for which the absolute radial velocities might be inaccurate because of the effect of stellar winds on the line profiles. However, these were shown to have a negligible impact on the measured velocity dispersion of the apparently single stars of the sample (see Hénault-Brunet et al. 2012a). The radial velocity measurements for individual epochs are listed in Hénault-Brunet et al. (2012a) and Sana et al. (2013). The median radial velocity uncertainty of the single-epoch measurements for the objects of our sample is ~4 km s-1. Note that we did not include stars observed by the VFTS farther out than 10 pc to limit possible contamination from nearby clusters or other star formation events in the surroundings of R136.
 |
Fig. 8 Top: two-component EFF fit to the surface brightness profile of R136 as in Mackey & Gilmore (2003). The data points shown are Mackey and Gilmore’s recalibrated surface brightnesses from McLaughlin & van der Marel (2005). Stars that are farther out than ~5 pc (marked by the dotted line) from the cluster center are more likely to be part of the OB association. Within this radius stars are more likely to belong to the R136 cluster itself. Bottom: normalized histograms showing the velocity distribution of the 32 stars within 5 pc in blue (211 velocities), and the 49 stars between 5 and 10 pc in red (327 velocities). |
Mackey & Gilmore (2003) found that the light profile of R136 is best fitted with a double-component EFF profile (Elson et al. 1987), suggesting that the cluster is superimposed on an OB association, that contributes a significant fraction of its total integrated light (Maíz-Apellániz 2001). In this double-component EFF fit, the projected radius within which the two components contribute equally is at about 5 pc, as illustrated in Fig. 8 (top panel). To decide whether the velocity distributions of these two potentially distinct components should be considered separately, we also show in Fig. 8 (bottom panel) the velocity distribution of the stars more likely to be part of the inner component (i.e. the cluster) compared to the velocity distribution of the stars more likely to be part of the outer component (i.e. the OB association). We see no evidence for a difference in the velocity distribution between the two components. Similarly, Hénault-Brunet et al. (2012a) found the measured velocity dispersion profile to be relatively flat between 1 and 10 pc from the center of R1363. Because the two components appear to be indistinguishable (at least kinematically) in the inner 10 pc, we conclude that it is justified to try to fit a single velocity dispersion for all the stars of our sample.
Note that Sabbi et al. (2012) found a dual structure in the density of low-mass stars in R136, hinting at a merger event between the main core of R136 and a second cluster. Because only a very small fraction our targets are expected to be associated with this second clump, we treated all the stars within 10 pc as one population.
4.2. Results
Hénault-Brunet et al. (2012a) determined a velocity dispersion of ~6 km s-1 for the O-type stars within 10 pc in projection from the center of R1364 after selecting out identified binaries and estimating the effect of undetected binaries. To test our procedure, we fit single-epoch radial velocity datasets extracted from the full multi-epoch dataset presented in Sect. 4.1. One such fit is shown in Fig. 1.
We extracted five single-epoch radial velocity datasets without any overlap because every star in the sample was observed for at least five epochs. These datasets are not independent, because they all include observations of the same stars, albeit at different epochs.
The best-fit binary fraction, velocity dispersion and mean velocity for each of these five datasets are shown at the left side of each panel in Fig. 9. The three different colors again represent the three sets of orbital parameter distributions assumed. The 1σ error bars are somewhat larger than predicted from the Monte Carlo simulations for a sample of 81 radial velocities (see Fig. 5), because the effective sample size is smaller than 81. A significant subset of the observed radial velocities in R136 have a measurement uncertainty comparable to or larger than the velocity dispersion. These radial velocities provide (nearly) no information about the velocity dispersion of the clusters, leading to a smaller effective sample size.
We found lower binary fractions for the orbital parameter distributions where an individual binary has a higher likelihood of causing a significant radial velocity offset. This explains the low binary fraction found for the parameters from Sana et al. (2012, blue in Fig. 9, which has relatively many close and similar-mass binaries (see Table 1 and Fig. 2). In contrast, the best-fit mass-ratio distribution of Sana et al. (2013) has more low-mass binary companions, while the period distribution favored by Kiminki & Kobulnicky (2012) has a larger proportion of wide binaries and hence requires a larger binary fraction to reproduce the same number of high-velocity outliers.
 |
Fig. 9 Best-fit binary fraction, velocity dispersion, and mean velocity and the log-likelihood of the best fit for five single-epoch radial velocity datasets (labeled A-E) of the O-type stars in R136, and two datasets with two epochs with a baseline of roughly one month and one year. The colors indicate the set of orbital parameter distributions assumed in the fit: blue line from Sana et al. (2012); green line from Sana et al. (2013); and red line from Kiminki & Kobulnicky (2012). The error bars show the 1σ uncertainties on the best-fit values, estimated with MCMC simulations. The dashed lines in the upper-right and lower-left panels show the values found after removing the spectroscopic binaries identified from the full multi-epoch dataset (Hénault-Brunet et al. 2012a). |
The fitted velocity dispersion is less sensitive to the exact parameters assumed than the binary fraction, although we did still find variations of ~3 km s-1 (see central panel in Fig. 9) for the single-epoch fits, which is comparable to the ~40% systematic offset found from Monte Carlo simulations (Sect. 3). The intrinsic velocity dispersion of R136 fitted from single-epoch radial velocities is consistent with the 6 km s-1 from the multi-epoch approach (Hénault-Brunet et al. 2012a).
Finally, the best-fit mean velocity is barely sensitive to the assumed orbital parameter distributions (see Fig. 9), because as long as the projections of the binaries on the sky are random, the velocities from the binary orbital motions will be symmetrically distributed around the mean velocity. This means that the systematic uncertainties induced from an assumed binary population do not significantly affect the measurements of the mean velocity, which in turn means that parameters depending on the mean velocity (e.g. cluster rotation) can be accurately fitted.
The best-fit parameters obtained when using two epochs of data are shown at the right side of each panel of Fig. 9. As we saw from the Monte Carlo simulations of Sect. 3, the systematic offset in the fitted velocity dispersion induced when different binary orbital parameter distributions are used decreases significantly with multi-epoch data. For the single-epoch data, we found typical variations in the fitted velocity dispersion of ~3 km s-1, which decreases to only ~2 km s-1 when using two epochs that are approximately one month apart. For a baseline of one year, the systematic offset decreases even more to about 1 km s-1.
Although the fitted velocity dispersions show smaller systematic offsets between the adopted binary orbital parameter distributions when multi-epoch data are used, the fitted binary fraction is roughly the same for single- and multi-epoch data. This is consistent with a scenario where the fitted binary fraction depends on the proportion of close and similar-mass binaries. When assuming a high proportion of such systems, the fitted binary fraction will be lower, irrespective of whether these stars appear as high-velocity outliers (as in the single-epoch case) or as radial velocity variables (as in the multi-epoch case).
From inspecting the log-likelihood of the best-fit models for R136 (Fig. 9), no set of orbital parameter distributions (Sana et al. 2012, 2013; Kiminki & Kobulnicky 2012) consistently fits the data better than the others. This does not imply that there is insufficient information in the dataset to distinguish between the orbital parameter distributions. After all, our method ignores some information (e.g. the observed distribution of radial velocity offsets between epochs) in the log-likelihood, which could have been used to constrain the binary orbital parameter distributions (e.g. Sana et al. 2013), but not the intrinsic velocity dispersion.
5. Discussion
We were able to fit the intrinsic velocity dispersion from a single epoch of radial velocity data with an accuracy ranging from ~60% for a cluster velocity dispersion of ~2 km s-1 to ~25% for σv ~ 10 km s-1, given the present-day uncertainties on the orbital parameter distributions of OB spectroscopic binaries (e.g. Table 1 and Fig. 2). For typical velocity dispersions of young massive clusters (≳4 km s-1) we found that an accuracy better than 40% can be reached, which is sufficient to distinguish a cluster in virial equilibrium from an unbound cluster. This systematic offset will dominate over the statistical uncertainties from small-number statistics for a sample size larger than about 100 stars. This means that after observing 100 stars for a single epoch, the accuracy of the fitted velocity dispersion will in principle no longer increase when more stars are observed due to the uncertainties in the binary orbital parameter distributions of OB stars. Observing the same stars for multiple epochs makes it possible to reduce the systematic offset. For example, a ratio of the measurement uncertainty over the baseline of 1 km s-1yr-1 is required to reduce the systematics below 15% for an intrinsic velocity dispersion of 6 km s-1,
 |
Fig. 10 Left: period distribution with respect to the longest period needed to obtain a given velocity offset for a circular orbit (Pmax; Eq. (9)) for a flat distribution of mass ratios (blue) or only equal-mass binaries (green). Middle: distribution of the radial velocity semi-amplitude (K) relative to the velocity offset (voff) for a flat distribution of eccentricities and circular orbits. Right: distribution of the velocity gradient (dv/dt) relative to the velocity offset (voff) divided by the orbital period (P) for a flat distribution of mass ratios (blue) or only equal-mass binaries (green). These plots are independent of the period distribution of the binaries, and only weakly depend on the mass ratio and eccentricity distributions. |
To understand the systematic offsets, we directly compared the fits of the single-epoch R136 data for the orbital parameter distributions of Sana et al. (2012) and Kiminki & Kobulnicky (2012). In the case of Sana et al., the binaries typically orbit each other with tens of km s-1, an order of magnitude larger than for Kiminki & Kobulnicky (Fig. 2). Thus, an individual binary in the former case will have a much higher probability of causing a high-velocity outlier. To reproduce the high-velocity outliers in the R136 data we thus need a lower binary fraction for the binary orbital parameter distribution of Sana et al. (2012) than for Kiminki & Kobulnicky (2012), which explains the difference in the binary fraction found for the R136 data (left panel in Fig. 9).
On the other hand, the fitted velocity dispersion is affected by the abundance of wider binaries with orbital velocities comparable to the intrinsic velocity dispersion of the cluster (~6 km s-1), because these binaries are more likely to really broaden the observed peak in the velocity distribution, instead of just creating a high-velocity tail. We can see in Fig. 2 that these binaries are much more common for the orbital parameter distributions of Kiminki & Kobulnicky (2012) than for those of Sana et al. (2012), even before we take into account the fact that we find a lower overall binary fraction for Sana et al. (2012). This much higher fraction of wide binaries broadening the observed velocity distribution when assuming the binary orbital parameter distributions of Kiminki & Kobulnicky (2012) leads to a significantly lower fitted velocity dispersion (central panel in Fig. 9) than in Sana et al. (2012). Still, it is remarkable that the systematic offset in the velocity dispersion is smaller than a factor of 2 given that the peaks in the orbital velocity distributions differ by an order of magnitude (see lower left panel in Fig. 2).
Note that the differences between the sets of binary properties listed in Table 1 might be real to some extent (i.e. not only reflect uncertainties in our knowledge of these properties). There are reasons to assume that the binary properties of massive stars may depend on the environment and the age of the region in which they are located. For example, the intrinsic fraction of O-type spectroscopic binaries seems lower in 30 Doradus than in the relatively low-density Galactic clusters (see Table 1), although the two results still agree within 2σ. As discussed by Sana et al. (2013), this may suggest that the binary properties in the 30 Doradus region have already been significantly affected by dynamical and/or stellar evolution, which would induce merger events or binary disruption and decrease the observed number of binaries. This is to be expected given the presence of different populations in the region, some already quite old, and considering that a fraction of the O-star population consists of runaways. For the Galactic open cluster sample, cluster dynamics and stellar evolution are not expected to have significantly altered the orbital properties of the binaries (Sana et al. 2012). Given the young age of the clusters in this sample, the parameters reported in this case are probably a good representation of the properties of massive binaries at birth.
As discussed in Appendix A, a wide variety of possible period, mass ratio, and eccentricity distributions for OB binaries have been considered in the literature. We chose to limit our analysis to the three sets of orbital parameter distributions in Table 1, which we felt were the most representative of our present-day knowledge about these distributions. However, we offer the provided python code5 for use, which can be used to fit an observed radial velocity distribution, and to create and fit mock radial velocity distributions, using either the orbital parameter distributions described in this work or any other orbital parameter distributions. This code can thus be used to calculate the systematic offsets in the fitted velocity dispersion between any orbital parameter distributions (as in Fig. 4) or to determine the accuracy with which the velocity dispersion can be fitted as a function of sample size when planning observations (as in Fig. 5).
5.1. Effectiveness of multi-epoch radial velocities
Multi-epoch data are required to reduce the systematic offsets in the fitted velocity dispersion due to uncertainties in the adopted binary orbital parameter distributions. In particular, one needs to identify and remove from the sample the spectroscopic binaries with radial velocity offsets comparable to the intrinsic velocity dispersion. Binaries causing a larger velocity offset are easily identified in single-epoch data as high-velocity outliers and hence have little effect on the fitted velocity dispersion. Binaries causing a velocity offset smaller than the velocity dispersion have a negligible impact on the observed velocity distribution. Below, we therefore consider the properties of the critical binaries with velocity offsets similar to the intrinsic velocity dispersion, and we investigate under which conditions they can be identified as radial velocity variables in multi-epoch data.
For most of the binary orbit, the radial velocity offset is smaller but of the same order of magnitude as the radial velocity semi-amplitude K. This is illustrated in the central panel of Fig. 10, where we plot the distribution of the radial velocity semi-amplitude over the velocity offset (K/voff) at a random point in time for a random set of binaries. The distribution plotted here is independent of the period and mass ratio distribution and only depends on the eccentricity distribution. For both eccentricity distributions considered (flat and only circular), the distribution is strongly peaked at one and decreases quickly with increasing K/voff. Only for eccentric orbits can the radial velocity offset exceed the semi-amplitude.
If the time between radial velocity observations is sufficiently longer than the period of the binary, the phases of these observations become independent of each other. Radial velocities are drawn from a distribution set only by the radial velocity semi-amplitude K and eccentricity e, independent of the orbital period or mass ratio (except for their contribution to K). To allow identification as a binary under this long-baseline condition, the measurement uncertainty should be at least smaller than the radial velocity semi-amplitude of the binaries. Thus, to identify the critical binaries with velocity offsets comparable to the intrinsic velocity dispersion, measurement uncertainties lower than the velocity dispersion are required. This is not really an additional requirement, because measurement uncertainties lower than the velocity dispersion help to accurately fit the velocity dispersion even when the effect of binaries is ignored. The detection rate of binaries will increase as the measurement uncertainties decrease or the number of epochs increases (by decreasing the probability that the observations are in phase with the binary orbit), but it does not depend on the baseline of the observations as long as it remains significantly longer than the period of the binary. This explains why, in our Monte Carlo simulations of the systematic offset of the fitted velocity dispersion for two-epoch data (Fig. 6), the systematic velocity offset depends on the measurement uncertainty and not on the baseline once this baseline becomes comparable to the widest binaries in the Monte Carlo simulations (i.e. 300 years).
For a reasonable baseline, there will be many binaries causing radial velocity offsets comparable to the intrinsic velocity dispersion with periods much longer than the baseline, in which case the argument above does not hold. To illustrate this, we computed from Kepler’s third law the longest period needed to create a given velocity offset for circular orbits: 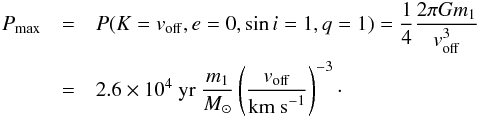 (8)Projection effects and unequal mass ratios will result in the typical period of the binary causing a given velocity offset to be lower. We found from randomly sampling a large number of binaries with a flat eccentricity distribution that even for equal-mass binaries the typical period is 0.5 dex shorter (green line in the left panel of Fig. 10). For a flat mass ratio distribution (blue line in the left panel of Fig. 10), the period distribution of stars that cause a given velocity offset is even 1.5 dex shorter than the longest period given in Eq. (9). The distributions plotted in Fig. 10 are independent of the period distribution of binaries, because they are plotted relative to Pmax. For the R136 data (σv ~ 6 km s-1; m1 ~ 30 M⊙), Pmax is about 4000 years. Most of the binaries that cause a velocity offset comparable to the intrinsic velocity dispersion of the cluster will therefore have periods longer than a baseline of even a few years, although there is a significant minority of binaries with P < 10-3Pmax < 4 years (left panel in Fig. 10) whose period may be shorter than the baseline.
(8)Projection effects and unequal mass ratios will result in the typical period of the binary causing a given velocity offset to be lower. We found from randomly sampling a large number of binaries with a flat eccentricity distribution that even for equal-mass binaries the typical period is 0.5 dex shorter (green line in the left panel of Fig. 10). For a flat mass ratio distribution (blue line in the left panel of Fig. 10), the period distribution of stars that cause a given velocity offset is even 1.5 dex shorter than the longest period given in Eq. (9). The distributions plotted in Fig. 10 are independent of the period distribution of binaries, because they are plotted relative to Pmax. For the R136 data (σv ~ 6 km s-1; m1 ~ 30 M⊙), Pmax is about 4000 years. Most of the binaries that cause a velocity offset comparable to the intrinsic velocity dispersion of the cluster will therefore have periods longer than a baseline of even a few years, although there is a significant minority of binaries with P < 10-3Pmax < 4 years (left panel in Fig. 10) whose period may be shorter than the baseline.
Long-period binaries will be detected when the measurement uncertainty is significantly smaller than the velocity change between the first and last epoch6, which we assumed below to be separated in time by a baseline b. The velocity change is given by 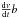 , where
, where 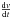 is the velocity gradient of the binary, which is roughly constant over the observed time under the condition considered here (P ≫ b). Therefore the detection of a long-period binary depends on whether the velocity gradient is sufficiently steeper than the ratio of the measurement uncertainty and baseline (σmeas/b). In the two-epoch Monte Carlo simulations (Figs. 6 and 7), we indeed found that the systematic offset in the fitted velocity dispersion mainly depends on σmeas/b for baselines shorter than a few years. For these baselines, most of the binaries causing velocity offsets comparable to the intrinsic velocity dispersion are in the regime discussed here (P ≫ b). Because these binaries need to be detected to reduce the systematic offset, the systematic offset is to first order a function of σmeas/b (see Fig. 7), until the baseline becomes comparable to the widest binaries (with periods of ~Pmax).
is the velocity gradient of the binary, which is roughly constant over the observed time under the condition considered here (P ≫ b). Therefore the detection of a long-period binary depends on whether the velocity gradient is sufficiently steeper than the ratio of the measurement uncertainty and baseline (σmeas/b). In the two-epoch Monte Carlo simulations (Figs. 6 and 7), we indeed found that the systematic offset in the fitted velocity dispersion mainly depends on σmeas/b for baselines shorter than a few years. For these baselines, most of the binaries causing velocity offsets comparable to the intrinsic velocity dispersion are in the regime discussed here (P ≫ b). Because these binaries need to be detected to reduce the systematic offset, the systematic offset is to first order a function of σmeas/b (see Fig. 7), until the baseline becomes comparable to the widest binaries (with periods of ~Pmax).
To quantify this further, we computed the velocity gradients for a large sample of binaries with flat eccentricity distributions. For binaries causing a given velocity offset voff with orbital period P, we found that the velocity gradients follow a roughly log-normal distribution with a peak at 8voff/P and a width of about 0.5 dex (right panel in Fig. 10). To detect the widest binaries causing a velocity offset comparable to the velocity distribution (i.e. with P ~ Pmax) in R136 (σv ~ 6 km s-1; Pmax ~ 4000 years) would hence require the detection of a velocity gradient of 8σv/Pmax ≈ 12 m s-1 yr-1, which is virtually impossible. However, with typical periods being 0.5−3 dex shorter (left panel in Fig. 10), a significant proportion of the critical binaries can actually be detected for the typical measurement uncertainty of 1 km s-1 and a baseline of one year. This explains the drop in the systematic offset between the velocity dispersion fitted assuming different binary orbital parameter distributions (which are represented by different colors in Fig. 10) when multi-epoch data are used.
For many lower-mass clusters, the intrinsic velocity dispersion is much lower (often at the sub-km s-1 level), leading to an increase in the longest period due to its dependence on the third power of the velocity offset (Eq. (9)). Even though the light of these generally older clusters will be dominated by lower-mass stars (lowering m1 in Eq. (9)), Pmax is still likely to occur at roughly 105 − 107 years, such that the broadening of the velocity distribution is dominated by binaries with periods of 103 − 105 years. These are virtually impossible to detect by spectroscopic means (and will only be detectable in direct-imaging surveys for the most nearby clusters). Therefore, although a multi-epoch strategy with a baseline of a few years works well for the high velocity dispersions of young massive clusters, it has little effect on the accuracy with which clusters with a much lower velocity dispersion can be measured, because this would require the detection of binaries with periods of many thousands of years. This is quite fortunate because the need for a multi-epoch strategy is much lower for lower-mass clusters, whose light is dominated by solar-type stars with much better constrained binary properties.
6. Conclusion
We explored the applicability of the maximum-likelihood method presented by Cottaar et al. (2012b) to recover the intrinsic velocity dispersion of massive stars in young clusters from a single epoch of radial velocity data. By using Monte Carlo simulations and multi-epoch stellar radial velocity data of the young massive cluster R136 as a test case, we showed that the method works reasonably well, the main limitation being uncertainties in the binary properties of OB stars which can lead to a systematic offset of tens of percent in the fitted velocity dispersion (<40% for typical young massive cluster velocity dispersions, i.e. ≳4 km s-1).
This systematic offset can be greatly reduced by directly detecting the spectroscopic binaries through radial velocity variations in multi-epoch data. Specifically, the spectroscopic binaries with velocity offsets comparable to the intrinsic velocity dispersion need to be detected to increase the accuracy of the fitted velocity dispersion. For a typical young massive cluster, these periods range from 10-2 to 104 years, meaning that many can be detected with typical baselines of observations of a few years. Indeed, we found that the accuracy of a fitted velocity dispersion of 6 km s-1 improves to better than 15% for a typical ratio of the measurement uncertainty over the baseline of 1 km s-1 yr-1. However, there will always remain undetected binaries that affect the observed velocity distribution for any reasonable baseline and measurement uncertainty, which will have to be corrected for (see Sect. 2.2). Because the orbital period scales with the orbital velocity to the third power (Kepler’s third law), multi-epoch data are far less useful in improving the accuracy of the fitted velocity dispersion of lower-mass clusters (with sub-km s-1 velocity dispersions) than of young massive clusters.
Unlike the velocity dispersion, the binary fraction fitted with the method tested in this paper is very sensitive to the assumed binary properties. In general, the method can therefore not reliably recover the binary fraction from a radial velocity dataset if the distributions of orbital parameters of the binaries are poorly constrained.
Although we have tested the method on a sample of radial velocities of O-type stars in R136 and considered binary properties that were derived mainly from spectroscopic surveys of O-type stars7, it should also be applicable to samples of B-type stars because they appear to have similar binary properties (Dunstall et al., in prep.). This means that one may only have to use one or two epochs of radial velocities to estimate the velocity dispersion of the massive star population in a large number of young Galactic open clusters that may contain a few O-type stars at most but a much larger number of B-type stars.
We may even speculate that this method may eventually be used to study the dynamics of massive stars in systems where this has been almost impossible up to now. There has been an increasing interest in near-infrared spectroscopy of massive stars in recent years (e.g. Hanson et al. 2005). This wavelength regime offers the possibility of analyzing these stars in embedded regions and near the Galactic center because of the substantially lower extinction than in the optical, and quantitative atmospheric analysis of early-type stars from near-infrared spectral lines is now providing promising results (e.g. Stap et al. 2011). Provided that precise radial velocities can be obtained from near-infrared spectra in reasonable exposure times, then the results presented in this paper offer a promising and efficient way of studying the dynamics of massive embedded clusters, or even the dynamics of the significant number of Galactic young massive clusters (e.g. Davies et al. 2012), which are strongly affected by extinction and for which we currently have very little kinematic information.
Online material
Appendix A: Review of the binary properties of OB stars
The current constraints on the binary fraction and distributions of orbital parameters of massive binaries are reviewed below.
Appendix A.1: Period distribution
Sana et al. (2012) showed that the intrinsic period distribution of their Galactic open clusters sample does not follow the widely used Öpik law (i.e., a flat distribution in the logarithm of the separation or, equivalently, of the period; Öpik 1924) but is instead overabundant in short-period systems. They found an exponent π = −0.55 ± 0.22 for the power law of the period distribution for lower and upper bounds of 0.15 and 0.35 on log 10P/d. For the same period range, Sana et al. (2013) also found from the 30 Doradus dataset a stronger preference for short periods than previously assumed, with a comparable value of π = −0.45 ± 0.30. This is in contrast with the best-fit value of π = 0.2 ± 0.4 from Kiminki & Kobulnicky (2012) for Cyg OB2 binaries, which is consistent with the Öpik law to within 1σ, although these authors argued that no single power law adequately reproduces the data at the shortest periods (P < 14 days). Although this work assumes a power-law distribution valid between 1 and 1000 days, we must also highlight that the sample does not probe this full range of periods. The power-law exponent of the period distribution was determined from 22 binaries with periods shorter than 30 days, so the results had to be extrapolated over almost two orders of magnitude.
Appendix A.2: Mass ratio distribution
It has been reported that the mass ratio distribution of massive binaries tends to peak toward unity (Bosch & Meza 2001; Pinsonneault & Stanek 2006), but this has since been contested (Lucy 2006) and more recent studies tend to favor a flat distribution of mass ratios. Kiminki & Kobulnicky (2012) indeed inferred a value of κ = 0.1 ± 0.5 for the exponent of the power-law distribution of mass ratios for the known massive binaries in Cyg OB2. Similarly, Sana et al. (2012) found no preference for equal-mass binaries (κ = −0.1 ± 0.6) in Galactic open clusters. In 30 Doradus, Sana et al. (2013) even found a mass ratio distribution that is slightly skewed toward systems with low mass ratios (κ = −1.0 ± 0.4), although this only provides a weak constraint on the distribution of mass ratios, and these results still agree within 2σ with the two previous studies reporting flat distributions. These results are all incompatible with a random pairing from a classical mass function (i.e. κ = −2.35; see Sana et al. 2013).
Appendix A.3: Eccentricity distribution
Because measuring the eccentricity of a spectroscopic binary requires many epochs of radial velocity data, we are only beginning to probe the eccentricity distribution of massive binaries. As expected from tidal dissipation that tends to circularize their orbit (Zahn 1977, 1978), a large portion of the short-period massive binary systems are found to have low eccentricities
(Sana & Evans 2011; Kiminki & Kobulnicky 2012). Kiminki & Kobulnicky (2012) found a value of η = −0.6 ± 0.3 for the exponent of the power-law distribution of eccentricities, while Sana et al. (2012) obtained η = −0.45 ± 0.17. Sana et al. (2013) could not constrain η in the 30 Doradus study and instead adopted the eccentricity distribution inferred by Sana et al. (2012) for the Galactic open clusters sample.
Appendix A.4: Binary fraction
A number of studies have investigated the observed fraction of spectroscopic binaries among massive stars. Mason et al. (2009) compiled results from the literature to show that 51% of the Galactic O-type stars investigated by multi-epoch spectroscopy are in fact spectroscopic binaries, while this fraction increases to 56% for objects in clusters or OB associations. Barbá et al. (2010) obtained a similar fraction, with 60% of the 240 Galactic O and WN stars in their survey of the southern sky displaying significant radial velocity variations (i.e. >10 km s-1). Chini et al. (2012) also observed a high binary fraction in their spectroscopic survey of Galactic O and B stars in the southern sky. Studies focusing on individual young open clusters or OB associations have reported observed binary fractions between 30 and 60% (e.g. De Becker et al. 2006; Hillwig et al. 2006; Sana et al. 2008, 2009; Mahy et al. 2009; Rauw et al. 2009; Sana et al. 2011; Mahy et al. 2013), with variations from one cluster to the other compatible with the statistical fluctuations expected given the size of the samples (Sana & Evans 2011). Thus, although it has been proposed that the spectroscopic binary fraction might be related to the cluster density (e.g. García & Mermilliod 2001), the current data are consistent with a common binary fraction in all clusters, at least for O-star-rich clusters (for details see Sana & Evans 2011).
To constrain the intrinsic fraction of spectroscopic binaries, one has to correct the observed fraction for observational biases that depend on the underlying distributions of orbital parameters. Kobulnicky & Fryer (2007) opted to fix the period distribution to the standard Öpik law because the solution of their Monte Carlo simulations for the period and mass-ratio distributions was degenerate. They inferred an intrinsic binary fraction of over 80%, but note that the range of separations considered in this study (up to 10 000 AU) extends well beyond the sensitivity domain of their spectroscopic observations. Kiminki & Kobulnicky (2012) observed a binary fraction of 21% in Cyg OB2 (24/114 objects) and inferred an intrinsic fraction of 44 ± 8% considering binaries with periods between 1 and 1000 days. Sana et al. (2012) identified 40 spectroscopic binaries for an observed binary fraction of 56% in their Galactic open clusters sample and found an intrinsic fraction of 69 ± 9% for periods in the range 0.15 < log 10P/d < 3.5. Sana et al. (2013) observed a spectroscopic binary fraction of 35 ± 3% in 30 Doradus, compatible with what Bosch et al. (2009) found from a different but overlapping sample of 54 O and early B-type stars, and inferred an intrinsic binary fraction of 51 ± 4% for periods in the range 0.15 < log 10P/d < 3.5. This binary fraction appears mostly uniform across the 30 Doradus region and independent of the spectral subtype and luminosity class.
Even though only the inner ~5−6 pc are more than a crossing time old and can be considered to be bound, and thus strictly speaking as part of the cluster according to the definition of Gieles & Portegies Zwart (2011).
The velocity dispersion was slightly lower (~5 km s-1) when we only considered the stars within 5 pc from the center. We ignored the small potential contribution (~0.5 km s-1) to the velocity dispersion from cluster rotation (Hénault-Brunet et al. 2012b).
Intermediate epochs contribute less to the capability of observing shallow velocity gradients than the first and last epoch, suggesting that it is better to focus on just two deep epochs than on many less deep epochs with the same total baseline. However, intermediate epochs can still be important in confirming whether the velocity differences measured between the first and last epoch, are real and they are crucial in solving binary orbits, which allows the binary population to be characterized.
Early B-type stars were also included in the study of Kiminki & Kobulnicky (2012).
Acknowledgments
We would like to thank Hugues Sana, Mark Gieles, Chris Evans, Nate Bastian, and Richard J. Parker for useful feedback on this paper. VHB acknowledges support from the Scottish Universities Physics Alliance (SUPA), the Natural Science and Engineering Research Council of Canada (NSERC), and the “Fonds the recherche du Québec − Nature et technologies” (FRQNT). We also wish to thank the International Space Science Institute (ISSI) in Bern, where this paper was initiated, for supporting Simon Goodwin’s international team working on “The formation of star clusters”.
References
- Andersen, M., Zinnecker, H., Moneti, A., et al. 2009, ApJ, 707, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Barbá, R. H., Gamen, R., Arias, J. I., et al. 2010, in Rev. Mex. Astron. Astrofis. Conf. Ser., 38, 30 [Google Scholar]
- Bosch, G., & Meza, A. 2001, in Rev. Mex. Astron. Astrofis. Conf. Ser., 11, 29 [Google Scholar]
- Bosch, G., Terlevich, E., & Terlevich, R. 2009, AJ, 137, 3437 [NASA ADS] [CrossRef] [Google Scholar]
- Chini, R., Hoffmeister, V. H., Nasseri, A., Stahl, O., & Zinnecker, H. 2012, MNRAS, 424, 1925 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, W. I., Ghez, A. M., Morris, M. R., et al. 2012, ApJ, 751, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Cottaar, M., Meyer, M. R., Andersen, M., & Espinoza, P. 2012a, A&A, 539, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cottaar, M., Meyer, M. R., & Parker, R. J. 2012b, A&A, 547, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crowther, P. A., Schnurr, O., Hirschi, R., et al. 2010, MNRAS, 408, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., de La Fuente, D., Najarro, F., et al. 2012, MNRAS, 419, 1860 [NASA ADS] [CrossRef] [Google Scholar]
- De Becker, M., Rauw, G., Manfroid, J., & Eenens, P. 2006, A&A, 456, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Koter, A., Heap, S. R., & Hubeny, I. 1998, ApJ, 509, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Elson, R. A. W., Fall, S. M., & Freeman, K. C. 1987, ApJ, 323, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. J., Taylor, W. D., Hénault-Brunet, V., et al. 2011, A&A, 530, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García, B., & Mermilliod, J. C. 2001, A&A, 368, 122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garmany, C. D., Conti, P. S., & Massey, P. 1980, ApJ, 242, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Geller, A. M., & Mathieu, R. D. 2011, Nature, 478, 356 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Geller, A. M., Mathieu, R. D., Harris, H. C., & McClure, R. D. 2008, AJ, 135, 2264 [NASA ADS] [CrossRef] [Google Scholar]
- Geller, A. M., Mathieu, R. D., Harris, H. C., & McClure, R. D. 2009, AJ, 137, 3743 [NASA ADS] [CrossRef] [Google Scholar]
- Gieles, M., & Portegies Zwart, S. F. 2011, MNRAS, 410, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Gieles, M., Sana, H., & Portegies Zwart, S. F. 2010, MNRAS, 402, 1750 [NASA ADS] [CrossRef] [Google Scholar]
- Hanson, M. M., Kudritzki, R.-P., Kenworthy, M. A., Puls, J., & Tokunaga, A. T. 2005, ApJS, 161, 154 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Hénault-Brunet, V., Evans, C. J., Sana, H., et al. 2012a, A&A, 546, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hénault-Brunet, V., Gieles, M., Evans, C. J., et al. 2012b, A&A, 545, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillwig, T. C., Gies, D. R., Bagnuolo, Jr., W. G., et al. 2006, ApJ, 639, 1069 [NASA ADS] [CrossRef] [Google Scholar]
- Kiminki, D. C., & Kobulnicky, H. A. 2012, ApJ, 751, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Kleyna, J., Wilkinson, M. I., Evans, N. W., Gilmore, G., & Frayn, C. 2002, MNRAS, 330, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Fryer, C. L. 2007, ApJ, 670, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Koposov, S. E., Gilmore, G., Walker, M. G., et al. 2011, ApJ, 736, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 2006, A&A, 457, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackey, A. D., & Gilmore, G. F. 2003, MNRAS, 338, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Mahy, L., Nazé, Y., Rauw, G., et al. 2009, A&A, 502, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mahy, L., Rauw, G., De Becker, M., Eenens, P., & Flores, C. A. 2013, A&A, 550, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz-Apellániz, J. 2001, ApJ, 563, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez, G. D., Minor, Q. E., Bullock, J., et al. 2011, ApJ, 738, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, B. D., Hartkopf, W. I., Gies, D. R., Henry, T. J., & Helsel, J. W. 2009, AJ, 137, 3358 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, D. E., & van der Marel, R. P. 2005, ApJS, 161, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Dehnen, W., Rix, H.-W., & Cudworth, K. M. 2002, AJ, 124, 1497 [NASA ADS] [CrossRef] [Google Scholar]
- Öpik, E. 1924, Publications of the Tartu Astrofizica Observatory, 25, 1 [Google Scholar]
- Pinsonneault, M. H., & Stanek, K. Z. 2006, ApJ, 639, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauw, G., Nazé, Y., Fernández Lajús, E., et al. 2009, MNRAS, 398, 1582 [NASA ADS] [CrossRef] [Google Scholar]
- Reggiani, M., & Meyer, M. R. 2013, A&A, 553, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rochau, B., Brandner, W., Stolte, A., et al. 2010, ApJ, 716, L90 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbi, E., Lennon, D. J., Gieles, M., et al. 2012, ApJ, 754, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., & Evans, C. J. 2011, in IAU Symp. 272, eds. C. Neiner, G. Wade, G. Meynet, & G. Peters, 474 [Google Scholar]
- Sana, H., Gosset, E., Nazé, Y., Rauw, G., & Linder, N. 2008, MNRAS, 386, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., Gosset, E., & Evans, C. J. 2009, MNRAS, 400, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., James, G., & Gosset, E. 2011, MNRAS, 416, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, J. D., Geha, M., Minor, Q. E., et al. 2011, ApJ, 733, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Stap, F. A., Sana, H., & de Koter, A. 2011, J. Phys. Conf. Ser., 328, 012025 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
- Zahn, J.-R. 1978, A&A, 67, 162 [NASA ADS] [Google Scholar]
All Tables
Constraints on the distributions of orbital parameters of massive binaries from the literature.
All Figures
 |
Fig. 1 Blue line: observed radial velocity distribution for a single epoch drawn from the multi-epoch radial velocity dataset of R136 (Hénault-Brunet et al. 2012a; Sana et al. 2013, see Sect. 4.1 for details). Red dashed line: best-fit radial velocity distribution, including the effect of the orbital motions of spectroscopic binaries. Green line: intrinsic velocity distribution of the cluster, corrected for the orbital motions of binaries. This intrinsic distribution is assumed to be a Gaussian whose width and mean have been optimized to fit the data (see Sect. 2.1). |
| In the text | |
 |
Fig. 2 Assumed period distribution (upper left) and mass ratio distribution (upper right), as well as the unprojected logarithmic velocity distribution (lower left) and the projected velocity distribution (lower right). The extrapolation of the period distribution from the observed range to an upper limit of 300 years is plotted as a dashed line. This extrapolation has been taken into account in the lower panels that show the velocity distributions. The blue lines show the distributions from Sana et al. (2012), the green lines those from Sana et al. (2013), and the red lines the distributions from Kiminki & Kobulnicky (2012), as detailed in Table 1. |
| In the text | |
 |
Fig. 3 Probability distribution ( |
| In the text | |
 |
Fig. 4 Systematic offset between the best-fit velocity dispersion (σfitted) and the input velocity dispersion (σinp) relative to the input velocity dispersion due to the uncertainties in the orbital parameter distributions of OB stars for a single epoch of radial velocity data. From top to bottom we have generated the radial velocity data using the orbital parameter distributions from Sana et al. (2012), Sana et al. (2013), and Kiminki & Kobulnicky (2012). The colors of the lines indicate the set of orbital parameter distributions assumed for the fit: blue line for Sana et al. (2012); green line for Sana et al. (2013); red line for Kiminki & Kobulnicky (2012). When the orbital parameter distributions used to generate the data are the same as those assumed in the fit, there is no systematic offset in the fitted velocity dispersion. The error bars represent the remaining uncertainty on the systematic offset after ~30 Monte Carlo simulations, each of which included a sample of 2000 radial velocities. The simulations for which we find a best-fit binary fraction of 100% in the majority of cases are marked with a black cross (see upper panel) to indicate that the fitted velocity dispersion is most likely overestimated in this case (see the main text). |
| In the text | |
 |
Fig. 5 One-sigma statistical uncertainties due to small-number statistics in the fitted velocity dispersion as a function of the sample size N for single-epoch observations of a cluster with a velocity dispersion of 5 km s-1. The colors indicate the set of orbital parameter distributions used to generate the data and assumed for the fit: blue line for Sana et al. (2012); green line for Sana et al. (2013); red line for Kiminki & Kobulnicky (2012). The color-coding is the same as in Fig. 4. The statistical uncertainties are given relative to the input velocity dispersion of 5 km s-1. Every point in this graph represents the average statistical uncertainty (as measured by the MCMC) in 60 Monte Carlo simulations, except for sample sizes smaller than or equal to 30, where 200 Monte Carlo simulations were averaged. |
| In the text | |
 |
Fig. 6 Systematic offset in the fitted velocity dispersion for radial velocity data generated using the Kiminki & Kobulnicky (2012) binary orbital parameter distribution and fitted assuming the Sana et al. (2012) binary orbital parameter distribution, plotted against the baseline between two epochs of observations. As the baseline between the two epochs of observations increases, more spectroscopic binaries are detected, leading to a decrease in the systematic offset of the velocity dispersion. We show the results from Monte Carlo simulations for clusters with a velocity dispersion of 2 km s-1 (upper panel) and 6 km s-1 (lower panel), as well as for measurement uncertainties of 0.1 km s-1 (solid), 0.5 km s-1 (dashed), and 1 km s-1 (dotted). |
| In the text | |
 |
Fig. 7 Same as Fig. 6, but with measurement uncertainty over the baseline (σmeas/b), rather than the baseline on the x-axis. Note that for a broad region of intermediate baselines, all the curves overlap. |
| In the text | |
 |
Fig. 8 Top: two-component EFF fit to the surface brightness profile of R136 as in Mackey & Gilmore (2003). The data points shown are Mackey and Gilmore’s recalibrated surface brightnesses from McLaughlin & van der Marel (2005). Stars that are farther out than ~5 pc (marked by the dotted line) from the cluster center are more likely to be part of the OB association. Within this radius stars are more likely to belong to the R136 cluster itself. Bottom: normalized histograms showing the velocity distribution of the 32 stars within 5 pc in blue (211 velocities), and the 49 stars between 5 and 10 pc in red (327 velocities). |
| In the text | |
 |
Fig. 9 Best-fit binary fraction, velocity dispersion, and mean velocity and the log-likelihood of the best fit for five single-epoch radial velocity datasets (labeled A-E) of the O-type stars in R136, and two datasets with two epochs with a baseline of roughly one month and one year. The colors indicate the set of orbital parameter distributions assumed in the fit: blue line from Sana et al. (2012); green line from Sana et al. (2013); and red line from Kiminki & Kobulnicky (2012). The error bars show the 1σ uncertainties on the best-fit values, estimated with MCMC simulations. The dashed lines in the upper-right and lower-left panels show the values found after removing the spectroscopic binaries identified from the full multi-epoch dataset (Hénault-Brunet et al. 2012a). |
| In the text | |
 |
Fig. 10 Left: period distribution with respect to the longest period needed to obtain a given velocity offset for a circular orbit (Pmax; Eq. (9)) for a flat distribution of mass ratios (blue) or only equal-mass binaries (green). Middle: distribution of the radial velocity semi-amplitude (K) relative to the velocity offset (voff) for a flat distribution of eccentricities and circular orbits. Right: distribution of the velocity gradient (dv/dt) relative to the velocity offset (voff) divided by the orbital period (P) for a flat distribution of mass ratios (blue) or only equal-mass binaries (green). These plots are independent of the period distribution of the binaries, and only weakly depend on the mass ratio and eccentricity distributions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.