| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322303 | |
| Published online | 05 February 2014 | |
Spectral formation in a radiative shock: application to anomalous X-ray pulsars and soft gamma-ray repeaters
1 University of Crete, Physics Department & Institute of Theoretical & Computational Physics, 71003 Heraklion, Crete, Greece
e-mail: kylafis@physics.uoc.gr
2 Foundation for Research and Technology-Hellas, 71110 Heraklion, Crete, Greece
3 Max-Planck-Institut für extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
4 Faculty of Engineering and Natural Sciences, Sabancı University, 34956 Orhanlı, Tuzla, İstanbul, Turkey
Received: 17 July 2013
Accepted: 21 December 2013
Context. In the fallback disk model for the persistent emission of anomalous X-ray pulsars (AXPs) and soft gamma-ray repeaters (SGRs), the hard X-ray emission arises from bulk- and thermal Comptonization of bremsstrahlung photons, which are generated in the accretion column. The relatively low X-ray luminosity of these sources implies a moderate transverse optical depth to electron scattering, with photons executing a small number of shock crossings before escaping sideways.
Aims. We explore the range of spectral shapes that can be obtained with this model and characterize the most important parameter dependencies.
Methods. We use a Monte Carlo code to study the crisscrossing of photons in a radiative shock in an accretion column and compute the resulting spectrum.
Results. As expected, high-energy power-law X-ray spectra are produced in radiative shocks with photon-number spectral index Γ ≳ 0.5. We find that the required transverse optical depth is 1 ≲ τ⊥ ≲ 7. Such spectra are observed in low-luminosity X-ray pulsars.
Conclusions. We demonstrate here with a simple model that Compton upscattering in the radiative shock in the accretion column can produce hard X-ray spectra similar to those seen in the persistent and transient emission of AXPs and SGRs. In particular, one can obtain a high-energy power-law spectrum, with photon-number spectral-index Γ ~ 1 and a cutoff at 100 − 200 keV, with a transverse Thomson optical depth of ~5, which is shown to be typical in AXPs/SGRs.
Key words: accretion, accretion disks / stars: magnetars / X-rays: stars / pulsars: general
© ESO, 2014
1. Introduction
Anomalous X-ray Pulsars (AXPs) and soft gamma-ray repeaters (SGRs) are young neutron stars that have been observed to emit X-rays both quiescently and in the form of bursts. They are commonly called magnetars, because they are thought to have super-strong magnetic fields (1014−1015 G). For recent reviews see Woods & Thompson (2006) and Mereghetti (2008, 2013). Two main models have been proposed to explain the observational data; the classical magnetar model (e.g., Thompson & Duncan 1993, 1996) and the fallback disk one (Chatterjee et al. 2000; Alpar 2001). Both models have in common that the giant and the highly super-Eddington bursts are produced by magnetic field decay. The fallback disk model puts the super-strong magnetic field in a multipole component, while the classical magnetar model puts it in the dipole component. Yet, a recent interpretation (Tiengo et al. 2013) of a variable absorption feature in the spectrum of the magnetar SGR 0418+5729 as a proton cyclotron feature invokes a multipole magnetic field. Thus, multipole components could in principle operate in both models.
For the persistent emission, the explanation is different in the two models. The classical magnetar model assumes that the persistent emission is powered by magnetic field decay and that the observed period derivative Ṗ is due to magnetic braking of an isolated neutron star with a super-strong dipole magnetic field. On the other hand, in the fallback disk model the persistent X-ray emission is powered by accretion onto the neutron star, the optical and the infrared radiation is produced by the disk, and the observed rotational properties are explained by the long-term disk – magnetosphere interaction. The evolution of AXPs and SGRs with fallback disks has been studied in a number of papers (e.g., Ertan et al. 2007, 2009) and a fallback disk has been observed in two magnetars: AXP 4U 0142+61 (Wang et al. 2006) and AXP 1E 2259+586 (Kaplan et al. 2009).
A detailed model for the formation of the quiescent spectra of AXPs/SGRs has been proposed by Trümper et al. (2010, 2013) using the fallback disk model. These spectra consist of two components (e.g., den Hartog et al. 2008a,b; Enoto et al. 2010); a quasi-thermal component at low energies, which is generally attributed to the photospheric emission from the neutron star polar cap, and a hard power-law component. In the model of Trümper et al. (2010, 2013), this power-law component is attributed to the emission from the radiative shock, located near the bottom of the accretion column. This component is emitted as a fan beam, which partly hits the surrounding polar cap, where the radiation is absorbed or scattered, leading to the quasi-thermal component. The geometry of the model ensures that both soft and hard components have approximately the same luminosity (as observed), while the observed luminosity ratio depends on the height of the radiative shock above the neutron-star surface and the angles between the line of sight on one hand and the magnetic-dipole and the spin axis on the other.
In this paper we concentrate specifically on the formation of the fan beam in the radiative shock and explore the conditions required to produce a hard power-law spectrum. Our picture is similar to that of X-ray pulsars.
It is well established that in X-ray pulsars matter from a companion star falls onto the magnetic poles of a neutron star. The accreting matter follows dipole magnetic-field lines and falls supersonically. Eventually, it has to stop on the neutron-star surface. The supersonic to subsonic transition of the accretion flow occurs in a radiative shock above the neutron-star surface (Basko & Sunyaev 1976). In such a shock, which for simplicity we consider here as a mathematical discontinuity, soft X-ray photons coming mainly from below the shock suffer a nearly head-on collision with the infalling electrons. Because of the large momentum of the infalling eletrons with respect to that of the soft photons, the photons are scattered backward, gain energy, and return to the dense, hot, subsonic flow. We will refer to this as bulk-motion Comptonization (BMC). In the subsonic flow, the photons are scattered again, more or less isotropically. If their energy is significantly less than the thermal energy of the electrons, the photons gain energy on average (thermal Comptonization, hereafter TC). After the scattering, some photons find themselves again in the supersonic flow and the above processes are repeated, albeit with progressively decreasing probability, because the photons can escape sideways, i.e., perpendicular to the accretion column. We want to remark here that in a radiative shock, like the one we envision above, it is impossible to separate BMC from TC, unlike what happens in a spherical flow, where one can have pure BMC (Blandford & Payne 1981a,b; Payne & Blandford 1981; Mastichiadis & Kylafis 1992; Titarchuk et al. 1996, 1997).
It is well known that this first-order Fermi energization of the photons results in a power-law, high-energy spectrum. Lyubarski & Sunyaev (1982, hereafter LS82) were the first to compute analytically the emergent spectrum from such a shock. They studied spectral formation due to BMC and TC in a radiative shock that is of the Rankine-Hugoniot form. This is a reasonable approximation, given the fact that, due to the large optical depth along the accretion column, the upscattered photons escape sideways.
Accretion onto magnetic neutron stars has been studied extensively by Becker & Wolff. In a series of papers (Becker & Wolff 2005, 2007; Becker et al. 2012), they have studied spectral formation in X-ray pulsars and have highlighted the role of BMC and TC for spectral formation in accretion columns. In their classic paper (Becker & Wolff 2007, hereafter BW07), they consider a smooth flow in a cylindrical column, with the flow being slowed down by radiation. The shock is treated properly, not as a mathematical discontinuity, and it is the place where BMC and TC operate with seed soft photons produced by bremsstrahlung, cyclotron, and blackbody processes inside the column. As most of the photons escape sideways, the model predicts a fan beam.
In X-ray pulsars, the accretion column has a large optical depth in all directions. This means that the radiation in the column thermalizes to a significant degree and any high-energy photons present in the column are downscattered. Thus, the emergent spectrum has a cutoff at ~20 keV (BW07). In low-luminosity pulsars, on the other hand, the sideways optical depth is expected to only be a few. Thus, a high-energy power-law spectrum with a much larger cutoff energy can in principle be produced. This is what we investigate here.
In Sect. 2 we describe the model that we have used, giving a qualitative description of the processes that occur in the radiative shock, in Sect. 3 we present our results, in Sect. 4 we discuss them, and in Sect. 5 we draw our conclusions and state the predictions of our work.
2. The model
In order to demonstrate our main ideas, we use a relatively simple model. We consider a cylindrical accretion column with two regions: the pre-shock region, where matter falls with constant velocity, and the post-shock one, which has density seven times the pre-shock one, electron temperature Te, and negligible flow velocity. To fit real data, significantly more elaborate models are needed.
Mainly bremsstrahlung photons from below the shock, but also soft X-ray photons from the neutron-star photoshpere surrounding the accretion column, enter the shock and are followed by a Monte Carlo code until they escape. Since the Thomson optical depth along the accretion column in the pre-shock region is infinite by construction in our model, the crucial parameter in our calculation is the Thomson optical depth in the transverse direction in this region.
2.1. Qualitative presentation
2.1.1. The radiative shock
If for simplicity we consider that the accreting plasma consists only of protons and electrons, the accretional energy resides in the protons. Charge neutrality guarantees that the electrons are tied to the protons. Thus, the electrons have the same free-fall velocity as the protons, but insignificant accretional energy. This energy for the infalling plasma per proton-electron pair is 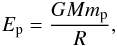 (1)where G is the gravitational constant, M is the mass of the neutron star, R is its radius, and mp is the proton mass. For a neutron star of mass M = 1.4 M⊙ and radius R = 12.5 km, Ep ≈ 150 MeV.
(1)where G is the gravitational constant, M is the mass of the neutron star, R is its radius, and mp is the proton mass. For a neutron star of mass M = 1.4 M⊙ and radius R = 12.5 km, Ep ≈ 150 MeV.
If a significant amount of this energy is to be transfered to the photons via BMC, it looks, at first sight, impossible to happen in the radiative shock. This is because the energy Eγ of a soft photon becomes after a head-on collision with a relativistic electron 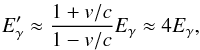 (2)for an electron speed of, say, v = 0.6c. This energy gain by the photon is orders of magnitude smaller than Ep. As we demonstrate below, though, it is possible for the photons to “steal” a significant fraction of the accretional energy, because many photons scatter off the same electron.
(2)for an electron speed of, say, v = 0.6c. This energy gain by the photon is orders of magnitude smaller than Ep. As we demonstrate below, though, it is possible for the photons to “steal” a significant fraction of the accretional energy, because many photons scatter off the same electron.
For simplicity, we think of the shock as a mathematical discontinuity, but in reality it has a finite thickness with characteristic scale equal to the photon mean free path for electron scattering 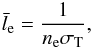 (3)where ne is the electron number density in the shock and σT is the Thomson cross section. For simplicity, in this discussion, we use the Thomson cross section, but in our Monte Carlo calculation we use the angle- and energy-dependent one, due to the magnetic field (see Sect. 2.2).
(3)where ne is the electron number density in the shock and σT is the Thomson cross section. For simplicity, in this discussion, we use the Thomson cross section, but in our Monte Carlo calculation we use the angle- and energy-dependent one, due to the magnetic field (see Sect. 2.2).
In this characteristic thickness 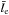 , the “optical depth” that an infalling electron sees in the “bath” of outgoing photons is
, the “optical depth” that an infalling electron sees in the “bath” of outgoing photons is 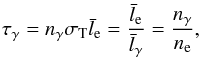 (4)where nγ is the number density of photons that mediate the shock and
(4)where nγ is the number density of photons that mediate the shock and 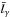 is the electron mean free path in the “bath” of photons. For the electron number density we write
is the electron mean free path in the “bath” of photons. For the electron number density we write 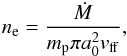 (5)where Ṁ is the mass accretion rate, a0 is the radius of the accretion column at the shock, and
(5)where Ṁ is the mass accretion rate, a0 is the radius of the accretion column at the shock, and 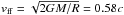 is the free-fall velocity of the plasma near the neutron star surface, where the shock is formed. Here we have taken M = 1.4 M⊙ and R = 12.5 km.
is the free-fall velocity of the plasma near the neutron star surface, where the shock is formed. Here we have taken M = 1.4 M⊙ and R = 12.5 km.
Let uγ be the energy density of the photons in the shock and Eγ their characteristic energy. Then, the accretional luminosity can be written as 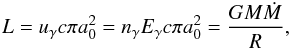 (6)from which we get
(6)from which we get 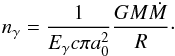 (7)Thus, the “optical depth” τγ becomes
(7)Thus, the “optical depth” τγ becomes 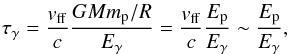 (8)which implies that the “optical depth” that an infalling electron sees in the “bath” of outgoing photons in the shock is of order the ratio of the accretional energy of a proton-electron pair to the typical energy of the outgoing photons. This means that, in the thickness of the shock, many photons scatter off the same electron and this is how the kinetic energy of the accreting plasma is reduced in the shock. As an analogy, one could think of the stopping of a diver by the water molecules in a pool. Thus, we envision the transfer of energy from the protons to the electrons and from them to the photons as follows:
(8)which implies that the “optical depth” that an infalling electron sees in the “bath” of outgoing photons in the shock is of order the ratio of the accretional energy of a proton-electron pair to the typical energy of the outgoing photons. This means that, in the thickness of the shock, many photons scatter off the same electron and this is how the kinetic energy of the accreting plasma is reduced in the shock. As an analogy, one could think of the stopping of a diver by the water molecules in a pool. Thus, we envision the transfer of energy from the protons to the electrons and from them to the photons as follows:
At the “top” of the shock, consider a head-on collision between an outgoing photon and an infalling electron. The energy gain of the photon is described by Eq. (2) and this energy is taken from the electron. Thus, the electron would slow down, and charge separation would occur, if it were not for the protons, which transfer a tiny fraction ~Eγ/Ep of their energy to replenish the lost energy of the electron. This process is repeated many times as the proton-electron pairs traverse the shock thickness. Thus, at the “bottom” of the shock, the protons have given up a significant fraction of their accretional energy to the photons that mediated the shock, with the electrons acting as intermediaries.
2.1.2. The postshock temperature
According to Eq. (2), the energy of a soft photon quadruples in a head-on collision with an infalling electron. Therefore, after several crisscrosses of the shock, the energy of a photon increases significantly, but, at the same time, the photon looses some of its energy due to electron recoil in the postshock region. This energy is deposited in the postshock region and heats the electrons (LS82).
An estimate of the electron (and proton) temperature in the postshock region can be obtained as follows:
The energy lost to the photons via BMC, is replenished by the accretional energy of the protons. This channeling of energy stops when the kinetic energy of the protons becomes comparable to the accretional energy of the electrons Ee = GMme/R ≈ 75 keV, where me is the electron mass. Thus, a rough estimate of the electron temperature Te in the postshock region is given by 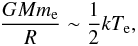 (9)where, due to the strong magnetic field, we have assumed a one-dimensional Maxwellian distribution. This gives kTe ~ 150 keV. In our calculations, and for completeness, we have considered a range of temperatures.
(9)where, due to the strong magnetic field, we have assumed a one-dimensional Maxwellian distribution. This gives kTe ~ 150 keV. In our calculations, and for completeness, we have considered a range of temperatures.
2.1.3. The size of the accretion column
In what follows, we estimate the radius of the accretion column at the radiative shock, close to the neutron-star surface.
For a neutron star with surface magnetic-dipole field B at the equator and magnetic moment μ = BR3, the Alfven radius, to within a factor of order unity, is (Lamb et al. 1973; Frank et al. 2002) 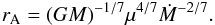 (10)The fallback disk, which is assumed to be of the Shakura & Sunyaev (1973) type, has a pressure scale height (Frank et al. 2002)
(10)The fallback disk, which is assumed to be of the Shakura & Sunyaev (1973) type, has a pressure scale height (Frank et al. 2002) 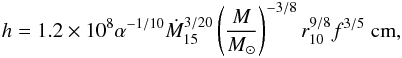 (11)where α = 0.03 is the viscosity parameter, Ṁ15 is the accretion rate in units of 1015 g s-1, r10 is the radial distance in units of 1010 cm and
(11)where α = 0.03 is the viscosity parameter, Ṁ15 is the accretion rate in units of 1015 g s-1, r10 is the radial distance in units of 1010 cm and ![\begin{eqnarray*} f=\left[1-(R/r)^{1/2}\right]^{1/4} \approx 1. \end{eqnarray*}](/articles/aa/full_html/2014/02/aa22303-13/aa22303-13-eq53.png) Assuming that the inner disk couples to the magnetic-dipole field lines in an annular region of radius rA and radial thickness Δr, the cross-sectional area (
Assuming that the inner disk couples to the magnetic-dipole field lines in an annular region of radius rA and radial thickness Δr, the cross-sectional area (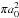 ) of the accretion column near the surface of the neutron star can be estimated from magnetic-flux conservation, namely
) of the accretion column near the surface of the neutron star can be estimated from magnetic-flux conservation, namely 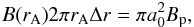 (12)where B(rA) = (1/2)Bp(R/rA)3 and Bp = 2B is the strength of the magnetic-dipole field at the pole of the star.
(12)where B(rA) = (1/2)Bp(R/rA)3 and Bp = 2B is the strength of the magnetic-dipole field at the pole of the star.
Assuming Δr ≈ ηh, where η is a scaling factor, we find 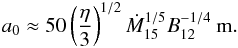 (13)Alternatively, if the inner-disk matter couples to the magnetic-dipole field lines between rA and the co-rotation radius rco = (GM/Ω2)1/3, where Ω is the angular frequency of the neutron star, then for Δr ≈ rA − rco ≈ 5 × 108 cm we find
(13)Alternatively, if the inner-disk matter couples to the magnetic-dipole field lines between rA and the co-rotation radius rco = (GM/Ω2)1/3, where Ω is the angular frequency of the neutron star, then for Δr ≈ rA − rco ≈ 5 × 108 cm we find 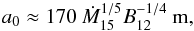 (14)which is not significantly larger than what we have found in Eq. (13).
(14)which is not significantly larger than what we have found in Eq. (13).
The Thomson optical depth τ⊥ in the direction perpendicular to the magnetic field, just above the radiative shock, is 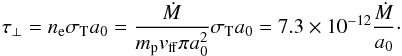 (15)For Ṁ = 2 × 1015 g s-1, which corresponds to an X-ray luminosity of 3.7 × 1035 erg s-1, and a0 ≈ 50 m, we find τ⊥ ≈ 5.8.
(15)For Ṁ = 2 × 1015 g s-1, which corresponds to an X-ray luminosity of 3.7 × 1035 erg s-1, and a0 ≈ 50 m, we find τ⊥ ≈ 5.8.
2.2. The Monte Carlo code
Our Monte Carlo code is similar to previously used codes in our work and it is based on Cashwell & Everett (1959) and Pozdnyakov et al. (1983). For simplicity, we assume cylindrical symmetry and a two-zone model: the pre-shock zone (z > 0) and the post-shock one (z < 0). The shock is of the Rakine-Hugoniot form at z = 0. The cross section of the cylinder has radius a0, which corresponds to a transverse Thomson optical depth τ⊥ in the pre-shock zone. In the pre-shock zone, matter falls freely with constant velocity vff = 0.58c, appropriate for a 1.4 M⊙ neutron star with a radius R = 12.5 km.
In the post-shock zone, the matter is compressed by a factor of seven (appropriate for an adiabatic hydrodynamic shock with γ = 4/3), hot, and with negligible flow velocity. In Sect. 2.1.2 we estimated the electron temperature behind the shock to be kTe ~ 150 keV. As this value is probably an overestimate, because we used a one-dimensional Maxwellian distribution, we use three values of kTe: 30, 50, and 100 keV.
Photons, mainly bremsstrahlung from below the shock, and to a lesser extend photospheric photons from the polar cap, enter the shock. Some of them escape unscattered, while the rest are scattered before escape. Of the last ones, some are scattered once, others a few times, and a relatively small number are scattered many times. It is this last category of photons, that have crisscrossed the shock many times, have increased their energy significantly, and have produced the high-energy power-law spectrum, as it is expected from such a first-order Fermi energization.
The input bremsstrahlung photons to the radiative shock have temperatute Te and are emitted isotropically upwards. In other words, we do not perform radiative transfer on the isotropically emitted bremsstrahlung photons in the post-shock region, but instead assume an upward flux of such photons.
The input quasi-thermal photospheric photons to the radiative shock are approximated as blackbody ones with temperature of kTBB = 0.5 keV. The polar cap that emits quasi-thermal photons has a radius r0 ~ 8 km in 4U 0142+61 (White et al. 1996; Israel et al. 1999; Juett et al. 2002). Therefore, only a relatively small fraction of the photospheric photons enter the shock (see Sect. 3.2 below).
Following BW07, we take the approximation of Arons et al. (1987) for the magnetic cross section for continuum scattering by electrons, namely ![\begin{eqnarray} \sigma(E, \theta)= \sigma(E) \left[ \sin^2\theta+k(E)\cos^2\theta \right], \end{eqnarray}](/articles/aa/full_html/2014/02/aa22303-13/aa22303-13-eq82.png) (16)where E is the photon energy, σ(E) is the Klein-Nishina cross section, θ is the angle between the directions of the photon and the magnetic field, and
(16)where E is the photon energy, σ(E) is the Klein-Nishina cross section, θ is the angle between the directions of the photon and the magnetic field, and 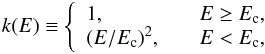 (17)where
(17)where 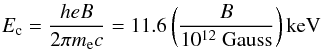 (18)is the cyclotron energy. In our calculations, we consider two indicative values of the magnetic-field strength, 1012 G and 1013 G.
(18)is the cyclotron energy. In our calculations, we consider two indicative values of the magnetic-field strength, 1012 G and 1013 G.
The mean free path to electron scattering from every point in the accretion column and in any direction, as well as the energy change and the new direction of a photon after scattering, are computed using the corresponding relativistic expressions (Pozdnyakov et al. 1983). For the thermal distribution of electron velocities we use a one-dimensional Maxwellian. When a photon escapes, both its energy and direction are recorded. Thus, we compute direction-dependent spectra as well as angle-averaged spectra.
3. Results
In what follows, we present the results of our Monte Carlo calculations in the form of E2dN/dE in arbitrary units, as a function of E in keV. The main parameter in our calculations is the transverse Thomson optical depth τ⊥ (see Eq. (15)), which is almost directly proportional to Ṁ, since a0 is of order 100 m (see Eqs. (13) and (14)). For completeness we explore also three values of the postshock temperature kTe = 30, 50 and 100 keV, and two values of the magnetic field strength B = 1012 and 1013 G. For the bremsstrahlung photons the temperature is the assumed post-shock value of Te, while for the blackbody, photospheric temperature we take kTBB = 0.5 keV.
For clarity of presentation, we treat the bremsstrahlung and the blackbody input photons separately, while in reality their upscattering in the shock occurs simultaneously (see, however, Sect. 3.3). We start with bremsstrahlung input photons.
3.1. Bremsstrahlung input
Below the shock, the main emission mechanism is bremsstrahlung (BW07). Thus, the spectrum of the emitted photons is given in the Born approximation (Greene 1959) by 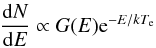 (19)where
(19)where 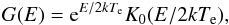 (20)is the Gaunt factor and K0 is the modified Bessel function of the second kind, zeroth order.
(20)is the Gaunt factor and K0 is the modified Bessel function of the second kind, zeroth order.
For our first calculation we use the following values of the parameters: τ⊥ = 5, kTe = 50 keV, and B = 1012 G, and refer to them as the reference values.
In Fig. 1, we show the input bremsstrahlung spectrum (crosses), with the integral of dN/dE normalized to unity, and the resulting angle-averaged output spectrum of the Monte Carlo (stars) for the reference values of the parameters.
 |
Fig. 1 Angle-averaged emergent spectrum (stars) in E2dN/dE form, with arbitrary units, as a function of energy E in keV. The spectrum of the input photons (normalized to unity) is due to bremsstrahlung emission (crosses). The parameters are at their reference values. |
Above about 10 keV, the spectrum is a power law, with photon-number spectral index Γ ≈ 1 and a peak in the E2dN/dE distribution at Ep ≈ 80 keV. This is a natural consequence of the first order Fermi energization. As it is evident from Fig. 1, most of the energy in the emergent spectrum comes out at Ep.
Below about 10 keV, the output photon-number spectrum dN/dE is essentially the input bremsstrahlung spectrum “shifted” to higher energy by a small amount. Its qualitative difference from the spectrum above 10 keV is due to the change in the cross section at the cyclotron energy Ec = 11.6 keV (see Eq. (18)). Below the cyclotron energy, the cross section is angle dependent and smaller than the Thomson value (see Eqs. (16) and (17)), while above the cyclotron energy it is isotropic and equal to the Thomson value for low-energy photons.
3.1.1. Effects of transverse optical depth
As discussed above, the larger the transverse Thomson optical depth τ⊥, the larger the number that a typical photon criscrosses the shock. This has a significant effect on the emergent spectrum.
In Fig. 2 we show the input bremsstrahlung spectrum (crosses), normalized to unity, and the emergent spectra for four values of τ⊥:1 (triangles), 3 (squares), 5 (stars), and 7 (circles). The other parameters are at their reference values.
 |
Fig. 2 Angle-averaged emergent spectrum in E2dN/dE form, with arbitrary units, as a function of energy E in keV. The spectrum of the input photons (normalized to unity) is bremsstrahlung (crosses). The various curves are the results of different values of the transverse Thomson optical depth τ⊥:1 (triagles), 3 (squares), 5 (stars), and 7 (circles). The rest of the parameters are at their reference values. |
In all cases, a high-energy power-law spectrum with a cutoff is seen. The photon-number spectral index Γ is approximately 1.5 for τ⊥ = 1, while Γ ≈ 0.7 for τ⊥ = 7.
3.1.2. Effects of magnetic-field strength
As discussed in Sect. 2.2, the larger the cyclotron energy (see Eq. (12)), the smaller the cross section of the low-energy input photons of a given energy, and the smaller the effective transverse optical depth for the same Thomson transverse optical depth τ⊥. Thus, as the magnetic-field strength increases, the average number that a photon crisscrosses the shock decreases and the resulting index Γ increases (i.e. steeper spectrum). This is clearly seen in Fig. 3, where the magnetic-field strength is B = 1013 G and four values of the Thomson transverse optical depth τ⊥: 1 (triangles), 3 (squares), 5 (stars), and 7 (circles). The rest of the parameters are at their reference values.
Comparing Fig. 3 with Fig. 2, we see that the spectra of Fig. 3 have no break at ~10 keV and the power laws extend from low energies all the way to Ep ≈ 70 keV. This is expected, because the cyclotron energy is Ec = 116 keV, which is above Ep. On the other hand, to get the same value of Γ, one needs a larger transverse Thomson optical depth in Fig. 3 than in Fig. 2. For example, to get Γ ≈ 1, one needs τ⊥ = 7 in Fig. 3, but only τ⊥ = 5 in Fig. 2. A slight deviation in the value of the peak energy Ep between Figs. 2 and 3 can be accommodated with a slight change in the temperature of the post-shock electrons (see Sect. 3.1.3).
3.1.3. Effects of post-shock temperature
As discussed in Sect. 2.1.2, the post-shock temperature is not known. We have provided a simple estimate of kTe ~ 150 keV, but this is probably an overestimate, because we have assumed a one-dimensional Maxwellian distribution. Thus, we examine two additional values: 100 keV and 30 keV.
Figure 4 is similar to Fig. 2, but for kTe = 100 keV. For the same transverse Thomson optical depth τ⊥, the emergent spectrum is flatter in Fig. 4 than in Fig. 2. For example, a τ⊥ = 3 is needed in Fig. 4 to produce a high-energy power-law index Γ ≈ 1, while a τ⊥ = 5 is needed in Fig. 2. Similarly, the peak energy Ep is larger in Fig. 4 than in Fig. 2. In particular, for kTe = 100 keV, the peak energy is Ep ≈ 150 keV.
Figure 5 is similar to Figs. 2 and 4, but for kTe = 30 keV. The conclusions are the same. A transverse Thomson optical depth τ⊥ = 6 is required to obtain Γ ≈ 1, while for kTe = 50 keV a τ⊥ = 5 is enough.
3.2. Blackbody input
As discussed extensively in Trümper et al. (2013), in the accretion model of AXPs/SGRs the ratio of the observed luminosity Ls of the soft, quasi-thermal photospheric emission to the hard, fan-beamed, power-law luminosity Lh is of order unity, but it depends on several parameters, and in particular on the height of the radiative shock. In other words, the larger the height, the larger the radius r0 of the polar cap. This is true not only for geometrical reasons but also due to gravitational bending.
Since r0 ~ 8 km for 4U 0142+61 (White et al. 1996; Israel et al. 1999; Juett et al. 2002), while the radius of the radiative shock is typically a0 ~ 100 m (see Eqs. (13) and (14)), we estimate that only a small fraction (~10-4, see Sect. 3.3) of the photospheric photons enter the shock. The majority of them come from around the footprint of the accretion column. We make the approximation that they are described by a blackbody distribution of temperature TBB and that they enter the shock at an angle θ with respect to the axis of the accretion column. For simplicity we take cosθ = 0.7. Our results are insensitive to this last approximation.
For a representative calculation with blackbody input, we use the following values of the parameters: τ⊥ = 5, kTe = 50 keV, B = 1012 G, and kTBB = 0.5 keV.
In Fig. 6, we show the input blackbody spectrum (crosses), with the integral of dN/dE normalized to unity, and the resulting angle-averaged output spectrum of the Monte carlo (stars) for the above values of the parameters. A hint of a broad peak at low energies (E ≲ 10 keV) is due to the input photons that escape unscattered or suffer a small number of scatterings, and can be thought of as a “shift” of the blackbody spectrum to higher energies, though it should be kept in mind that what is plotted is E2dN/dE and not dN/dE.
Above about 10 keV, the spectrum is a power law, with photon number spectral index Γ ≈ 1.3 and a peak in the E2dN/dE distribution at Ep ≈ 80 keV. This is again a natural consequence of first order Fermi energization. Despite the fact that only a small number of photons suffer many crisscrosses of the shock, most of the energy in the emergent spectrum comes out at Ep.
 |
Fig. 6 Angle-averaged emergent spectrum (stars) in E2dN/dE form, with arbitrary units, as a function of energy E in keV. The spectrum of the input photons (normalized to unity) is blackbody (crosses). The parameters are: τ⊥ = 5, kTe = 50 keV, B = 1012 G, and kTBB = 0.5 keV. |
Comparing Figs. 1 and 6, we see that for the same transverse optical depth τ⊥ = 5 the photon number spectral index Γ is approximately equal to 1 in Fig. 1 and approximately 1.3 in Fig. 6. This means that bremsstrahlung is more efficient in producing the high-energy power law than the blackbody. This is, of course, natural because the bremsstrahlung contains photons with energy comparable to kTe, while the typical blackbody-photon energy is 2kTBB ≪ kTe. Thus, fewer scatterings are needed for some bremsstrahlung photons to reach the peak energy Ep ≈ 80 keV than for all the blackbody ones.
3.3. Blackbody versus bremsstrahlung input
Despite the fact that the quasi-thermal, photospheric photons can in principle produce high-energy power-law spectra similar to the ones oberved in AXPs/SGRs by Comptonization in the radiative shock (e.g., Fig. 6), we will show below that their role is rather insignificant compared to that of the bremsstrahlung ones. The reasons are the following:
-
1)
Most of the photospheric photons do not enter the shock.For simplicity we assume that the polar cap is flat. This doesnot introduce any significant error, because gravitationalbending applies to both the hard X-rays from the shock to thepolar cap and to the soft X-rays from the polar cap to the shock.Let the area of the shock seen by a photospheric photon be
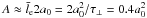 for τ⊥ = 5, where
for τ⊥ = 5, where 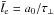 is the shock thickness (see Eq. (3)). The fractional solid angle subtended by the area A at radius r of the polar cap is dΩ/4π = A/4πr2 and for isotropic emission from the polar cap we find that the fraction of polar cap photons that reach the shock is
is the shock thickness (see Eq. (3)). The fractional solid angle subtended by the area A at radius r of the polar cap is dΩ/4π = A/4πr2 and for isotropic emission from the polar cap we find that the fraction of polar cap photons that reach the shock is 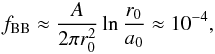 (21)for r0 = 8 km and a0 = 100 m.
(21)for r0 = 8 km and a0 = 100 m. -
2)
The number of photospheric photons that enter the radiative shock is smaller than the corresponding bremsstrahlung ones. This is because, for accretional luminosity L, the photospheric luminosity that enters the shock is about 10-4(L/2), while the corresponding bremsstrahlung luminosity, i.e., the remaining luminosity in the post-shock region is (see Sect. 2.1.2) ~ (me/mp)L. For a typical photon energy of 1 keV for the photospheric emission and less than 1 keV for bremsstrahlung, we see that bremsstrahlung dominates the soft photon input to the shock.
-
3)
As discussed in Sect. 3.2, for equal inputs to the radiative shock, the bremsstrahlung is more effectively upscattered to the high-energy power law than the photospheric input.
4. Discussion
It is known observationally (e.g., Enoto et al. 2010) that in AXPs/SGRs the hard X-ray luminosity Lh is comparable to the soft X-ray one Ls. In the accretion picture presented by Trümper et al. (2010, 2013), this is a natural consequence of the fact that only about half of the produced hard X-ray luminosity in the radiative shock is observed directly (Lh), while the other half is intercepted by the polar cap and the major fraction of it is re-emitted as soft X-rays (Ls).
With our reported calculations in Sect. 3.1, we have shown that the radiative shock can produce a fan-beam, hard X-ray, power-law spectrum similar to those seen in AXPs/SGRs. Furthermore, in Sect. 3.3 we have shown that nearly all the photospheric luminosity Ls is observed unaltered. Thus, the total X-ray spectrum, soft and hard, of an AXP/SGR with Lh = Ls can be easily produced by adding to the hard spectrum shown in Figs. 1–5 a blackbody spectrum with a peak in E2dN/dE having the same height as the peak of the hard X-ray spectrum.
As an example, we consider the hard X-ray spectrum of Fig. 1 (stars) and add to it a blackbody spectrum of temperature TBB = 0.5 keV that has the same height in E2dN/dE as the hard X-ray spectrum. The result is shown in Fig. 7.
In view of the above, it is natural to expect that low-luminosity X-ray pulsars should exhibit soft and hard X-ray spectra similar to those seen in AXPs and SGRs. Indeed, as discussed in Trümper et al. (2013), 4U 0352+309 (X-Per) and 4U 2206+54 show high-energy power-law tails extending to ~100 keV, with photon number spectral index Γ ~ 1.
 |
Fig. 7 Characteristic spectrum expected from low-luminosity accretion onto a magnetic neutron star. The high-energy spectrum is produced in the radiative shock near the bottom of the accretion column. The parameters are: τ⊥ = 5, kTe = 50 keV, and B = 1012 G. We have added to it a blackbody spectrum of temperature kTBB = 0.5 keV such that its peak has the same height as the peak at 80 keV. |
5. Conclusions and predictions
We have demonstrated with a simple quantitative model that accretion from a fallback disk onto a neutron star with normal (1012 − 1013 G) dipole magnetic field can produce hard X-ray, power-law spectra similar to the ones observed from steady-state or transient AXPs and SGRs. Furthermore, we have shown that the soft part of the X-ray spectrum, that comes from the polar cap, does not enter in a significant way in the formation of the hard part of the spectrum and can simply be added to it.
The power-law index Γ of the hard X-ray spectrum depends mainly on the accretion rate, or equivalently on the transverse optical depth of the accretion column at the radiative shock, and less on the strength of the magnetic field and the post-shock temperature. A transverse Thomson optical depth of ~5 is enough to produce a high-energy power-law index Γ ≈ 1.
The cutoff at high energies (E ~ 100 keV), is due to the limited kinetic energy of the accreting electrons, and it depends on the post-shock temperature. If the accretion rate is sufficient for the formation of a radiative shock, the cutoff energy cannot be larger than ~300 keV. Thus, if our picture is correct, we predict that no AXP or SGR will be found to have a cutoff energy of 400 keV or larger in their steady-state or transient spectra.
Acknowledgments
We thank an anonymous referee for useful comments, which have improved our paper. One of us (NDK) acknowledges partial support by the “RoboPol” project, which is implemented under the “ARISTEIA” Action of the “OPERATIONAL PROGRAM EDUCATION AND LIFELONG LEARNING” and is co-funded by the European Social Fund (ESF) and National Resources. NDK also acknowledges a grant from the European Astronomical Society in 2013. Ü.E. acknowledges research support from TÜBİTAK (The Scientific and Technical Research Council of Turkey) through grant 113F166.
References
- Alpar, M. A. 2001, ApJ, 554, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Basko, M. M., & Sunyaev, R. A. 1976, MNRAS, 175, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, P. A., & Wolff, M. T. 2005, ApJ, 630, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, P. A., & Wolff, M. T. 2007, ApJ, 654, 435 (BW07) [NASA ADS] [CrossRef] [Google Scholar]
- Becker, P. A., Klochkov, D., Schönherr, G., et al. 2012, A&A, 544, 123 [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1981a, MNRAS, 194, 1033 [NASA ADS] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1981b, MNRAS, 194, 1041 [NASA ADS] [Google Scholar]
- Cashwell, E. D., & Everett, C. J. 1959, A Practical Manual on the Monte Carlo Method for Random Walk Problems (Pergamon Press) [Google Scholar]
- Chatterjee, P., Hernquist, L., & Narayan, R. 2000, ApJ, 534, 373 [NASA ADS] [CrossRef] [Google Scholar]
- den Hartog, P. R., Kuiper, L., & Hermsen, W. 2008a, A&A, 489, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- den Hartog, P. R., Kuiper, L., Hermasen, W., et al. 2008b, A&A, 489, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enoto, T., Nakazawa, K., Makishima, K., et al. 2010, ApJ, 722, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Enoto, T., Makashima, K., Nakazawa, K., et al. 2011, PASJ, 63, 387 [NASA ADS] [Google Scholar]
- Ertan, Ü., Erkut, M. H., Ekşi, K. Y., & Alpar, M. A. 2007, ApJ, 657, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Ertan, Ü., Ekşi, K. Y., Erkut, M. H., & Alpar, M. A. 2009, ApJ, 702, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J, King, A., & Raine, D. 2002, Accretion Power in Astrophysics (Cambridge: Cambridge University Press) [Google Scholar]
- Greene, J. 1959, ApJ, 130, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Angelini, L., Burderi, L., et al. 1999, Nucl. Phys. B, 69, 141 [CrossRef] [Google Scholar]
- Juett, A. M., Marshall, H. L., Chakrabarty, D., & Schulz, N. S. 2002, ApJ, 568, 31 [Google Scholar]
- Kaplan, D. L., Chakrabarty, D., Wang, Z., & Wachter, S. 2009, ApJ, 700, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, L., Hermsen, W., den Hartog, P. R., & Urama, J. O. 2012, ApJ, 748, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, F. K., Pethick, C. I., & Pines, D. 1973, ApJ, 184, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarski, Yu. E., & Sunyaev, R. A. 1982, Sov. Astron. Lett., 8, 330 (LS82) [NASA ADS] [Google Scholar]
- Mastichiadis, A., & Kylafis, N. D. 1992, ApJ, 384, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S. 2008, A&ARv, 15, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S. 2013, Brazil. J. Phys., 43, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Payne, D. G., & Blandford, R. D. 1981, MNRAS, 196, 781 [NASA ADS] [Google Scholar]
- Pozdnyakov, L. A., Sobol, I. M., & Sunyaev, R. A. 1983, ASPRv, 2, 189 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Tiengo, A., Esposito, P., Mereghetti, S., et al. 2013, Nature, 500, 312 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Titarchuk, L., Mastichiadis, A., & Kylafis, N. D. 1996, A&AS, 120, 171 [NASA ADS] [Google Scholar]
- Titarchuk, L., Mastichiadis, A., & Kylafis, N. D. 1997, ApJ, 487, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, C., & Duncan, R. C. 1993, ApJ, 408, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, C., & Duncan, R. C. 1996, ApJ, 473, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Trümper, J. E., Zezas, A, Ertan, Ü., & Kylafis, N. D. 2010, A&A, 518, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trümper, J. E., Dennerl, K., Kylafis, N. D., Ertan, Ü., & Zezas, A. 2013, ApJ, 764, 49 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E., Angelini, L., Ebisawa, K., et al. 1996, ApJ, 463, 83 [Google Scholar]
- Wang, Z., Chakrabarty, D., & Kaplan, D. L. 2006, Nature, 440, 772 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Woods, P. M., & Thompson, C. 2006, in Compact stellar X-ray sources, eds. W. Lewin, & M. van der Klis, Cambridge Astrophysics Series, No. 39 (Cambridge: Cambridge University Press), 547 [Google Scholar]
All Figures
 |
Fig. 1 Angle-averaged emergent spectrum (stars) in E2dN/dE form, with arbitrary units, as a function of energy E in keV. The spectrum of the input photons (normalized to unity) is due to bremsstrahlung emission (crosses). The parameters are at their reference values. |
| In the text | |
 |
Fig. 2 Angle-averaged emergent spectrum in E2dN/dE form, with arbitrary units, as a function of energy E in keV. The spectrum of the input photons (normalized to unity) is bremsstrahlung (crosses). The various curves are the results of different values of the transverse Thomson optical depth τ⊥:1 (triagles), 3 (squares), 5 (stars), and 7 (circles). The rest of the parameters are at their reference values. |
| In the text | |
 |
Fig. 3 Same as in Fig. 2, but for B = 1013 G. |
| In the text | |
 |
Fig. 4 Same as in Fig. 2, but for kTe = 100 keV. |
| In the text | |
 |
Fig. 5 Same as in Fig. 2, but for kTe = 30 keV. |
| In the text | |
 |
Fig. 6 Angle-averaged emergent spectrum (stars) in E2dN/dE form, with arbitrary units, as a function of energy E in keV. The spectrum of the input photons (normalized to unity) is blackbody (crosses). The parameters are: τ⊥ = 5, kTe = 50 keV, B = 1012 G, and kTBB = 0.5 keV. |
| In the text | |
 |
Fig. 7 Characteristic spectrum expected from low-luminosity accretion onto a magnetic neutron star. The high-energy spectrum is produced in the radiative shock near the bottom of the accretion column. The parameters are: τ⊥ = 5, kTe = 50 keV, and B = 1012 G. We have added to it a blackbody spectrum of temperature kTBB = 0.5 keV such that its peak has the same height as the peak at 80 keV. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


