| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 4 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201322111 | |
| Published online | 31 January 2014 | |
Second generation planet formation in NN Serpentis?
1 Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
e-mail: marcel.voelschow@uni-hamburg.de
2 Institut für Astrophysik, Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
Received: 20 June 2013
Accepted: 18 December 2013
In this paper, we study the general impact of stellar mass-ejection events in planetary orbits in post-common envelope binaries with circumbinary planets like those around NN Serpentis. We discuss a set of simple equations that determine upper and lower limits for orbital expansion and investigate the effect of initial eccentricity. We deduce the range of possible semi-major axes and initial eccentricity values of the planets prior to the common-envelope event. In addition to spherically-symmetric mass-ejection events, we consider planetary dynamics under the influence of an expanding disk. In order to have survived, we suggest that the present planets in NN Ser must have had semi-major axes ≳10 AU and high eccentricity values which is in conflict with current observations. Consequently, we argue that these planets were not formed together with their hosting stellar system, but rather originated from the fraction of matter of the envelope that remained bound to the binary. According to the cooling age of the white dwarf primary of 106 yr, the planets around NN Ser might be the youngest known so far and open up a wide range of further study of second generation planet formation.
Key words: planets and satellites: dynamical evolution and stability / planets and satellites: formation / planet-star interactions / binaries: close / stars: AGB and post-AGB / planetary systems
© ESO, 2014
1. Introduction
The last two decades have seen a revolution in our knowledge of the properties and types of extrasolar planetary systems. Seemingly exotic objetcs like hot Jupiters, super Earths, pulsar planets, and circumbinary planets have dramatically expanded our understanding of planet formation. A particular challange is the origin of circumbinary planets in post-common envelope binary (PCEB) systems (Perets 2010): the predecessor systems are moderately close binaries with semi-major axes in the range of ~1 AU which, like Kepler 47 (Orosz et al. 2012), can contain circumbinary planets.
In PCEB systems, the common-envelope phase caused by the entry of the secondary star in the red giant envelope of the evolved primary redistributed the angular momentum budget of the stellar system and resulted in the formation of a close binary with orbital periods of just hours or days. Most of the primary’s former mass is ejected because of the transfer of angular momentum and energy to the envelope on a time scale of weeks or months (Ivanova et al. 2013).
To date, a handfull of PCEB systems have provided evidence for the presence of planets, despite their dramatic dynamical evolutionary paths (Horner et al. 2013). At the moment, the surest case is NN Ser, whose eclipse-timing variations can be explained by the presence of a planetary system consisting of two massive Jovian planets with roughly 7 and 2 MJup, orbiting their hosting binary at distances of 3 AU and 5 AU, respectively (Beuermann et al. 2010).
The dynamical stability of the first fitted planetary configurations (Beuermann et al. 2010) were investigated with detailed N-body simulations by Funk et al. (2011) and Horner et al. (2012b) who found that some were unstable, whereas others were dynamically feasible. In the first fit, the outer planet’s eccentricity was set to zero. Horner et al. (2012b) did another analysis of the observational data but also varied the outer planet’s eccentricity and obtained a new set of planetary parameters. In their study of the system’s stability, most of their fits turned out to be unstable after short periods of time which initiated some controversary about the system’s actual architecture. Recent dynamical analysis of other candidates such as HW Virginis (Horner et al. 2012a) or HU Aquarii (Wittenmyer et al. 2012) also found high orbital instability in the proposed systems. Except for pure orbital fitting and stability analysis, intrinsic effects of the binary have been investigated and might also explain the observed transit timing variations (see, e.g., Horner et al. 2012a; Wittenmyer et al. 2012).
Recently, Beuermann et al. (2013) used new observations and an equally extensive dynamical study to show that the family of stable solutions can now be constrained to be around a 2:1 resonance and moderate eccentricities (0.22 and 0.14 for the inner and outer planets, respectively)1. We summarize the results of Beuermann et al. (2013) in Table 1.
Proposed NN Serpentis system configuration by Beuermann et al. (2013).
Even if the orbital structure of the planetary system in NN Ser has been determined, the question of its origin in such an exotic binary system is still unsolved. Other than the very unlikely case of planetary capture, two distinct scenarios are possible.
-
The planets formed jointly with the binary and survived thecommon-envelope event (First Generation Formation).
-
The planets formed after the common-envelope event. Possible former planets did not survive (Second Generation Formation).
The second case is particularly fascinating as it implies a second phase of planet formation initiated by the common-envelope event. Recent studies conducted by Kashi & Soker (2011) have shown that a fraction of 1 to 10 per cent of the envelope’s mass can stay bound to the binary, falls back on it, flattens and forms a circumbinary disk out of which planets can easily form again. If a first generation origin can be ruled out in the NN Ser system, this mechanism would have to be responsible for the present planets, opening up a whole new perspective on extrasolar planets.
2. Simple estimates
We consider a planet with mass mp in an orbit with initial period Pi, velocity vi, eccentricity ei, and semi-major axis ai. In addition, we neglect all kinds of dissipative effects on the system’s energy and angular momentum budget. As a first approximation, stellar mass-ejection events can be modeled as a simple variation in the gravitational potential of the star, which affects the orbital parameters of any accompanying body in a way that it causes radial drift, changes in eccentricity, or an escape. A similar analysis was carried out by various authors. We refer the reader to Blaauw (1961), Alexander et al. (1976), or Perets (2010).
Analytic results for the final orbital parameters (f) of a planet on an initially circular orbit (i) for a given mass-loss factor μ = Mf/Mi.
2.1. Initially circular orbits
Two analytic limiting cases for stellar mass ejection and its effect on the orbiting planet(s) exist, characterized by the timescale of mass loss τ and the orbital period of the planet:
-
τ ≫ Pi (adiabatic mass loss);
-
τ ≪ Pi (instantaneous mass loss).
For both asymptotic regimes, we have summarized the analytic results in Table 2. In the case of instantaneous mass ejection, a mass-loss factor μ ≤ 1/2 causes all of the planets to reach escape velocity and get lost, while for adiabatic mass loss no such boundary exists.
What conclusions can be drawn from this for NN Ser? The former binary system itself had a separation of about 1.44 AU (Beuermann et al. 2010). Horner et al. (2012b) derived a simple stability criterion from extensive numerical simulations, enabling us to estimate a lower limit for stable planetary orbits in the former binary. The main result of the stability criterion is that configurations with close encounters lower than three Hill radii (which is ~1.1 AU for the secondary) are dynamically not feasible and require the planets to have semi-major axes of at least ~2.5 AU. Beuermann et al. (2010) argue that planets in the former NN Ser system should even have had semi-major axes of at least 3.5 AU, which is bigger than the typical extent of a 2 M⊙ red giant star and the evolving CE. These results indicate that the former planets were not engulfed in the evolving Common Envelope. In addition, the mass of the envelope was much bigger than the total mass of both stellar cores, indicating that the planets did non suffer any significant drift as a result of the orbital shrinking of the binary. Hence, the planets can be approximately treated as decoupled from the binary evolution.
According to Beuermann et al. (2010), we have μ ≈ 0.3, implying that the original planets would have been lost if mass loss took place on an instantaneous timescale. For adiabatic mass loss and assuming ei ≈ 0 for both planets, the planets’ original semi-major axes should be expanded by a factor of ~3.2, implying ai < 0.3·af. Therefore, neglecting any mutual gravitational perturbations, the present planets may have orbited the original binary at separations of a < 2 AU if other interactions between the planet and the CE can be ruled out as explained in this section. Such close orbits are not dynamically feasible in the former binary.
On the other hand, considering an expansion factor of ~3.2 for initially circular orbits and a lower limit of ~3.5 AU for stable orbits, we conclude that first generation planetary candidates should now be detected at distances of more than ~10 AU, which is obviously greater than the present planets’ proposed semi-major axes.
2.2. Initially elliptical orbits
The orbital parameters of a planet are conserved if mass loss occurs adiabatically. However, for instantaneous mass-ejection they become time-dependant. For a given orbital configuration with semi-major axis ai, eccentricity ei, and a planet located at a distance ri at a polar angle φi at the moment of mass-ejection, the planet’s new eccentricity and semi-major axis are given by 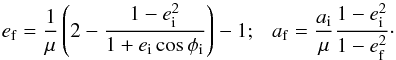 (1)Consequently, a particular mass-ejection scenario does result in planetary ejection if
(1)Consequently, a particular mass-ejection scenario does result in planetary ejection if 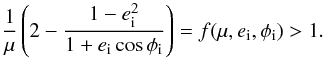 (2)Relation 2 can be directly translated into an escape probability pesc(μ,ei) defined as the fraction of unstable systems and stable configurations for a given mass-loss factor and given eccentricity by evaluating f(μ,ei,φi) for different polar angles φi (cf. Fig. 1).
(2)Relation 2 can be directly translated into an escape probability pesc(μ,ei) defined as the fraction of unstable systems and stable configurations for a given mass-loss factor and given eccentricity by evaluating f(μ,ei,φi) for different polar angles φi (cf. Fig. 1).
In contrast to planets in circular orbits, a planet in an initially elliptical orbit can stay bound to the star even for μ < 0.5 if the mass-ejection event happens near apastron, i.e., the planet moves in a sufficiently eccentrical orbit. On the other hand, the planet can escape from the system if it happens to be located near periastron even for μ > 0.5. Another consequence is that the orbit can be circularized for particular configurations: if the mass-ejection event takes place near the apastron, an initial eccentricity of ei = 1 − μ will result in a circular orbit and an orbital expansion factor of af/ai = 2 − μ.
What are the implications for NN Ser? For planets at a distance of a few AU we have orbital periods of a few years and consequently τ ≪ Pi for a typical CE event (Ivanova et al. 2013). Again, we can neglect drag effects or dissipative interactions between the envelope and the planets as well as orbital drift due to the evolution of the binary, as explained in the last section. In the case of instantaneous mass loss, from Fig. 1 it becomes clear that a mass-loss factor as dramatic as μ ≈ 0.3 requires the planets to have very high initial eccentricities of ei ≈ 0.4 individually to ensure at least small survival probabilities. However, high original eccentricities for both planets makes it even more difficult to obtain stable first-generation solutions for both planets.
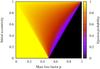 |
Fig. 1 Escape probability for a planet with varying initial eccentricity for different mass-loss factors in an instantaneous mass-ejection case. A mass-loss factor of ~0.3 allows the planet to escape the system if initial eccentricity is lower than ~0.4. |
3. Gas drag estimates
So far, we have derived analytic results of the orbital parameters for the two asymptotic regimes of slowly and rapidly changing gravitational potentials without any friction effects due to gas drag. To model the gas ejection event and estimate the effect of gas drag, we chose a self-consistent, exponential density profile ![\begin{equation} \rho(r,t) = \begin{cases} \rho_0 \exp{[\beta(r_{\rm gas}(t)) \cdot r]} & 0 \leq r \leq r_{\rm gas}(t) \\0 & r > r_{g\rm as}(t) \end{cases} \end{equation}](/articles/aa/full_html/2014/02/aa22111-13/aa22111-13-eq60.png) (3)(β > 0) and a linear velocity profile characterised by the outer rim velocity vmax and the initial outer boundary rmax,0 of the expanding envelope, mainly based on results obtained by Taam & Ricker (2010) and Ricker & Taam (2012) and the Sedov profile for blast wave propagation.
(3)(β > 0) and a linear velocity profile characterised by the outer rim velocity vmax and the initial outer boundary rmax,0 of the expanding envelope, mainly based on results obtained by Taam & Ricker (2010) and Ricker & Taam (2012) and the Sedov profile for blast wave propagation.
For a given mass, β(rgas) is determined by the total amount of gas Mgas via 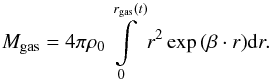 (4)Gas drag effects (see, e.g., Kokubo & Ida 2000) result in the additional force
(4)Gas drag effects (see, e.g., Kokubo & Ida 2000) result in the additional force 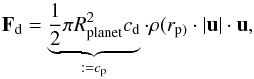 (5)where u = vgas − vplanet. A quick upper limit for | Fd | / | Fg | can be obtained by considering the planet in an initially circular orbit and also assuming vp ⊥ vgas, as well as
(5)where u = vgas − vplanet. A quick upper limit for | Fd | / | Fg | can be obtained by considering the planet in an initially circular orbit and also assuming vp ⊥ vgas, as well as 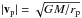 and | u | 2 = | vp | 2 + | vmax | 2:
and | u | 2 = | vp | 2 + | vmax | 2: ![\begin{equation} \frac{|\vec{F}_{\rm d}|}{|\vec{F}_{\rm g}|} = \frac{c_{\rm p} \rho(r) [\frac{GM}{r} + |\vec{v}_{\max}|^2 ]}{\frac{G M m_{\rm p}}{r^2}} = \rho_0 \frac{c_{\rm p}}{m_{\rm p}} e^{\gamma} r_{\rm p} \left[1 + \frac{|\vec{v}_{\max}|^2}{|\vec{v}_{\rm p}|^2} \right] \cdot \end{equation}](/articles/aa/full_html/2014/02/aa22111-13/aa22111-13-eq73.png) (6)For an initially close planet (rp ≈ 2 AU), we have | vgas | 2 ≪ | vp | 2 and β ≈ 10. Using mp ≈ 5 MJup for a massive Jovian planet, ρ0 = 10-15 g/cm3 for the gas sphere and typical values for the specific drag coefficient like cp ≈ 1012 cm2 (Kokubo & Ida 2000) leads to | Fd | / | Fg | ≈ 10-4. For a distant planet (rp ≈ 20 AU) we have γ → 0 and can set | u | ≈ | vmax | ≈ 10 km s-1 so that | Fd | / | Fg | ≈ 10-10. These results imply that when there is spherical symmetry geometric gas drag effects are not expected to cause any significant deviations from our solutions even in very massive ejection events.
(6)For an initially close planet (rp ≈ 2 AU), we have | vgas | 2 ≪ | vp | 2 and β ≈ 10. Using mp ≈ 5 MJup for a massive Jovian planet, ρ0 = 10-15 g/cm3 for the gas sphere and typical values for the specific drag coefficient like cp ≈ 1012 cm2 (Kokubo & Ida 2000) leads to | Fd | / | Fg | ≈ 10-4. For a distant planet (rp ≈ 20 AU) we have γ → 0 and can set | u | ≈ | vmax | ≈ 10 km s-1 so that | Fd | / | Fg | ≈ 10-10. These results imply that when there is spherical symmetry geometric gas drag effects are not expected to cause any significant deviations from our solutions even in very massive ejection events.
For the density profile discussed in this section, we also conducted a number of simulation runs with different gas velocities and μ = 0.3 where we placed a planet in an initially circular orbit between 2.0 AU and 7.0 AU. For vmax > 10 km s-1, virtually all planets have already exceeded the escape velocity. For 1 km s-1 < vmax < 10 km s-1, the planets’ semi-major axes expanded at least by a factor of ~3. As expected, the planets ended up with significantly eccentric orbits.
Based on these results, we conclude that it appears to be impossible to produce circumbinary planets resembling those in NN Ser using a spherically symmetric density profile if the planets were not part of the CE and did not interact with it. The envelope densities and hence geometric drag forces of the expanding envelope which might have resulted in the retention of the original planets are too small to cause any significant inward directed drift.
4. Disk-shaped mass-ejection
Common-envelope ejection events are, admittedly, only roughly spherical-symmetric, since the envelope is given the considerable angular momentum of the secondary star. In fact, hydrodynamical simulations of common-envelope events (see e.g., Ivanova et al. 2013; Taam & Ricker 2010; Ricker & Taam 2012) showed a significant amount of mass concentration in the orbital plane of the binary star. Thus, we conducted a few simulations of planetary dynamics under the influence of a thin expanding disk (see Huré & Hersant 2011 for further information as well as a far more rigid approach).
For zgas ≪ rgas, r(r,z,φ) ≈ r(r,φ) and the gravitational potential of the disk can be approximated as 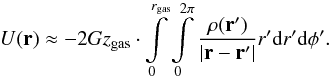 (7)This integral can be easily approximated by that of a disk split into a number of annuli segments (Δr,Δφ), where a particular segment’s mean density and position vector is evaluated in its middle. The gravitational potentials of thin exponential disks with M = 1 M⊙, ρ0 = 10-15 g cm-3, zgas = 0.05 AU, and different radii are plotted in Fig. 2. All disk potentials feature a prominent potential minimum located at the disk’s outer edge whose depth is predominantly determined by the disk’s extension.
(7)This integral can be easily approximated by that of a disk split into a number of annuli segments (Δr,Δφ), where a particular segment’s mean density and position vector is evaluated in its middle. The gravitational potentials of thin exponential disks with M = 1 M⊙, ρ0 = 10-15 g cm-3, zgas = 0.05 AU, and different radii are plotted in Fig. 2. All disk potentials feature a prominent potential minimum located at the disk’s outer edge whose depth is predominantly determined by the disk’s extension.
Because of the substantially lower volume of the disk, gas densities are expected to be significantly higher and gas drag effects might be an issue. The density profile parameter β drops more slowly and the outer rim gas densities are higher. Estimating the effect of friction is complicated, as no analytic result exists for the potential of a finite disk with non-constant density profile. For a moderately thin disk (h ≈ rmax/10) with two AU in radius and an exponential density profile with ρ0 ~ 10-15 g cm-3, numerical results give an outer rim density of 3 × 10-6 g cm-3, which is only one or two orders of magnitude higher than the outer rim density of a comparable gas sphere. Consequently, geometric gas drag effects are still negligible.
When this model is applied to NN Ser, an initially close planet (a < 5 AU) starts to drift radially inwards onto the expanding disk as the potential minimum approaches. Entering the disk, the planet is exposed to gas densities in the range of ~10-6 g cm-3. While the disk continues its expansion, the planet slows down because of potential effects (see Fig. 2) and suffers from outwards directed gravitational forces inside the disk. As a consequence, the planet increases its radial distance from the disk’s center and is carried towards the disk’s edge by gravitational forces again. In fact, most of our simulations of planetary dynamics under the influence of a massive expanding disk resulted in the ejection of the planet. In this approach, cylindrical symmetry helps the planets to get unbound.
 |
Fig. 2 Gravitational potential for a thin disk with M = 1 M⊙, ρ0 = 10-15 g/cm3, zgas = 0.05 AU, and varying disk radii in the disk plane. Potential values are normalized to U(0) for r = 1.0 AU. A point-mass potential is plotted for comparison. The disk potential is characterized by a prominent potential minimum located at the disk’s rim especially in compact disks. |
5. Conclusions and discussion
We analyzed the general impact of mass loss in both circular and eccentrical orbits. In NN Ser, simple geometric arguments
and semi-analytic stability criteria suggest that dissipative interactions between the common envelope and the planets as well as orbital variations due to the evolution of the hosting binary can be neglected. Rather, our analytic work implies that the dramatic mass loss that led to the formation of the close binary system NN Ser should have resulted in a significant orbital expansion if not loss of the planets, especially for initially eccentric orbits. As a consequence, a first generation scenario demands that the original planets had highly elliptical orbits and that the present planets should have semi-major axes of more than 10 AU. The latter is clearly in conflict with the current planets’ inferred orbital parameters. Furthermore, we examined the effect of cylindrical symmetry on the planetary dynamics and found that this scenario also helps the planets’ ejection.
Considering all of these effects, we argue that the planets around NN Ser could not have been formed together with the hosting binary star. Hence, these planets should have formed out of the back-falling material of the CE (e.g., Kashi & Soker 2011), i.e., they should be second generation planets (Perets 2010). Given a cooling age of about 106 yr (see, e.g., Beuermann et al. 2010) these planets are then the youngest planets known so far. Further efforts are essential in order to constrain orbital parameters of the planets, to get a better idea of the common envelope ejection phase, and to estimate possible planet-envelope interactions and ascertain the timescale for mean-motion resonance locking in this particular system. In any case, NN Ser should cast much light on this fascinating form of planetary evolution.
Because the naming nomenclature for exoplanets has not yet been officially determined and several different nomenclatures appear in the literature, we use the names “outer” for the planet first detected and “inner” for the second planet detected; following the nomenclature proposed by Hessman et al. (2010), these would be equivalent to NN Ser (AB)b and NN Ser (AB)c, respectively.
Acknowledgments
We would like to thank Stefan Dreizler for valuable discussions. We would also like to thank the anonymous referee for useful advice. We gratefully acknowledge funding from the Deutsche Forschungsgemeinschaft via Research Training Group (GrK) 1351 Extrasolar Planets and their HostStars.
References
- Alexander, M. E., Chau, W. Y., & Henriksen, R. N. 1976, ApJ, 204, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., Hessman, F. V., Dreizler, S., et al. 2010, A&A, 521, L60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Dreizler, S., & Hessman, F. V. 2013, A&A, 555, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blaauw, A. 1961, Bull. Astron. Inst. Netherlands, 15, 265 [NASA ADS] [Google Scholar]
- Funk, B., Eggl, S., Gyergyovits, M., Schwarz, R., & Pilat-Lohinger, E. 2011, in EPSC-DPS Joint Meeting, 1725 [Google Scholar]
- Hessman, F. V., Dhillon, V. S., Winget, D. E., et al. 2010, unpublished [arXiv:1012.0707] [Google Scholar]
- Horner, J., Hinse, T. C., Wittenmyer, R. A., Marshall, J. P., & Tinney, C. G. 2012a, MNRAS, 427, 2812 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, J., Wittenmyer, R. A., Hinse, T. C., & Tinney, C. G. 2012b, MNRAS, 425, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, J., Wittenmyer, R. A., Tinney, C. G., et al. 2013 [arXiv:1302.5247] [Google Scholar]
- Huré, J.-M., & Hersant, F. 2011, A&A, 531, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Kashi, A., & Soker, N. 2011, MNRAS, 417, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 2000, in Bioastronomy 99, eds. G. Lemarchand, & K. Meech, ASP Conf. Ser., 213, 51 [Google Scholar]
- Orosz, J. A., Welsh, W. F., Carter, J. A., et al. 2012, Science, 337, 1511 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Perets, H. B. 2010, ApJ, submitted [arXiv:1001.0581] [Google Scholar]
- Ricker, P. M., & Taam, R. E. 2012, ApJ, 746, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R. E., & Ricker, P. M. 2010, New A Rev., 54, 65 [Google Scholar]
- Wittenmyer, R. A., Horner, J., Marshall, J. P., Butters, O. W., & Tinney, C. G. 2012, MNRAS, 419, 3258 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Analytic results for the final orbital parameters (f) of a planet on an initially circular orbit (i) for a given mass-loss factor μ = Mf/Mi.
All Figures
 |
Fig. 1 Escape probability for a planet with varying initial eccentricity for different mass-loss factors in an instantaneous mass-ejection case. A mass-loss factor of ~0.3 allows the planet to escape the system if initial eccentricity is lower than ~0.4. |
| In the text | |
 |
Fig. 2 Gravitational potential for a thin disk with M = 1 M⊙, ρ0 = 10-15 g/cm3, zgas = 0.05 AU, and varying disk radii in the disk plane. Potential values are normalized to U(0) for r = 1.0 AU. A point-mass potential is plotted for comparison. The disk potential is characterized by a prominent potential minimum located at the disk’s rim especially in compact disks. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


