| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | L2 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201322936 | |
| Published online | 20 December 2013 | |
Connection between orbital modulation of Hα and gamma-rays in the Be/X-ray binary LS I+61°303
1 Institute of Astronomy and National Astronomical Observatory, Bulgarian Academy of Sciences, 72 Tsarigradsko Shose Blvd., 1784 Sofia, Bulgaria
e-mail: rkz@astro.bas.bg; kstoyanov@astro.bas.bg; tomov@astro.bas.bg, jmarti@ujaen.es
2 Departamento de Física (EPSJ), Universidad de Jaén, Campus Las Lagunillas, A3-420, 23071 Jaén, Spain
Received: 29 October 2013
Accepted: 26 November 2013
We studied the average orbital modulation of various parameters (γ-ray flux, Hα emission line, optical V band brightness) of the radio- and γ-ray emitting Be/X-ray binary LS I + 61°303. Using the Spearman rank correlation test, we found highly significant correlations between the orbital variability of the equivalent width of the blue hump of the Hα and Fermi-LAT flux with a Spearman p-value ~2 × 10-5, and the equivalent widths ratio EWB/EWR and Fermi-LAT flux with p-value ~9 × 10-5. We also found a significant anti-correlation between Fermi-LAT flux and V band magnitude with a p-value ~7 × 10-4. All these correlations refer to the average orbital variability, and we conclude that the Hα and γ-ray emission processes in LS I + 61°303 are connected. The possible physical scenario is briefly discussed.
Key words: stars: individual: LS I+61°303 / gamma rays: stars / X-rays: binaries / stars: winds, outflows / stars: emission-line, Be
© ESO, 2013
1. Introduction
LS I + 61°303 (V615 Cas) is a high-mass X-ray binary whose remarkable nature was illustrated following the discovery of its strong, non-thermal, and periodic radio outbursts (Gregory & Taylor 1978). It was first detected as a strong γ-ray source by the COS B satellite (Hermsen et al. 1977). More recently, it has also been reported as a source of high-energy (HE) and very high-energy (VHE) γ-rays by the Fermi Large Area Telescope (LAT, Abdo et al. 2009), the MAGIC Cherenkov Telescope (Albert et al. 2006), and by the VERITAS Collaboration (Maier et al. 2012). Indeed, it is currently considered one of the few confirmed representatives of the selected class of γ-ray binaries since the system’s luminosity in this energy range dominates the whole spectral energy distribution.
LS I + 61°303 consists of a massive B0Ve star and a compact object orbiting the primary every 26.5 d. According to the most recent radial velocity measurements of the absorption lines of the primary (Casares et al. 2005; Aragona et al. 2009), the orbit is elliptical (e = 0.537 ± 0.034), with periastron passage determined to occur around phase φ = 0.275. The compact object interacts with the Be circumstellar disk, thereby sampling a wide range of physical parameters and producing remarkable, periodic flaring events each orbital cycle. Such a strong orbital modulation in the LS I + 61°303 emission is observed across the whole electromagnetic spectrum, especially in the radio (Taylor et al. 1992), optical (Mendelson & Mazeh 1994), X-ray (Paredes et al. 1997; Leahy 2001), HE (Abdo et al. 2009), and VHE γ-ray (Albert et al. 2009) domains. In the optical, the orbital period signature is evident not only in visible broad band photometry, but also in the spectral properties of the Hα emission line (Zamanov et al. 1999; Grundstrom et al. 2007). The scenario of compact companion interaction with the Be disk is currently favored by Very Long Baseline Interferometry (VLBI) images that show a cometary structure on milli-arcsecond angular scales that rotates with the orbital period (Dhawan et al. 2006).
In addition to the orbital periodicity, another clock is operating in the system. A periodic modulation of about 4.4 yr in the phase and amplitude of the radio outbursts was first reported by Paredes (1987) and Gregory et al. (1989). This super-orbital modulation has also been detected in Hα (Zamanov et al. 1999), X-rays (Li et al. 2012), and γ-rays (Ackermann et al. 2013). It could be due to precession of the Be disk (Lipunov & Nazin 1994), a beat frequency between the orbital and precessional rates (Massi & Jaron 2013), or quasi-cyclical variability of the equatorial outflow of the Be star.
Previous multiwavelength observations have revealed interesting correlations between the X-ray and VHE γ-ray flares (Albert et al. 2008; Anderhub et al. 2009). This suggests that the same relativistic electrons that radiate inverse Compton VHE photons also produce synchrotron X-ray emission. In this Letter, we further explore the multiwavelength behavior of LS I + 61°303 in different spectral domains and search for correlations among them that could help to better characterize the physical mechanism behind the system’s orbital flaring episodes. In particular, we focus our attention on the two LS I + 61°303 extensive observational monitorings that are currently available, namely in γ-rays and in Hα high-resolution spectroscopy. Other observational databases in the radio and optical domains are also included in our study.
2. Observations
To create the folded light curve of LS I + 61°303, we used the following data.
For HE γ-rays,the Fermi team monitors flux values for a number of bright sources and transient sources that cross their monitoring flux threshold. Here we downloaded the Fermi LAT daily-averaged flux values for LS I + 61°303 in the energy range from 0.1 to 300 GeV. At the time of writing, this data set covered the time interval from JD 2 454 688.5 (2008 August) to JD 2 456 358.5 (2013 March).
Johnson V bandmagnitudes were taken from Lipunova (1988); Paredes et al. (1994); Zaitseva & Borisov (2003). Among the photometry available in the literature, we used only those observations that are reduced to Johnson’s system. We also calculated average orbital variability using the unfiltered optical magnitudes (149 measurements) from the Northern Sky Variability Survey (Woźniak et al. 2004). These unfiltered magnitudes are not plotted here, but they do confirm the detected V band variability.
Hα spectroscopic data were taken from Paredes et al. (1994); Steele et al. (1996); Liu & Yan (2005); Grundstrom et al. (2007); McSwain et al. (2010); and Zamanov et al. (1999, 2013). Among the various parameters of the Hα emission line we used here are the total equivalent width of the Hα emission line, hereafter EW, the equivalent width of the blue hump EW(B), the equivalent width of the red hump EW(R), the ratio between the equivalent widths of the blue and red humps EWB/EWR, and the distance between the peaks, ΔVp.
In radio photometry, flux densities were retrieved from the old Green Bank Interferometer (GBI), which is a facility of the USA National Science Foundation operated by NRAO in support of the NASA High Energy Astrophysics program. A total of 7234 observations of the flux density at 2.25 GHz and 8.3 GHz obtained from JD 2 450 410 (November 1996) untill 2 451 664 (April 2000) are available for study.
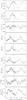 |
Fig. 1 Averaged orbital variability of LS I + 61°303. Plotted from top to bottom: the radio fluxes at 2.25 and 8.3 GHz, ΔVp, EW(B), EW(R), EWB/EWR, EW(Hα), the optical V, and the Fermi-LAT flux. The vertical (blue) line indicates the apastron passage. The data are averaged in 20 bins that are 0.05 each. |
3. Orbital variability of different parameters
The orbital phase is calculated using Porb = 26.4960 ± 0.0028 days, a value derived from Bayesian analysis of the radio observations (Gregory 2002). The zero of phase is by convention JD0 = 2 443 366.775, the date of the first radio detection of the star (Gregory & Taylor 1978).
To calculate the average orbital variability, we separated the data in 20 non-overlapping bins. The bins are all of the same size – 0.05 in each phase. In each phase bin we calculated the average value, median value, and standard deviation of the mean. The values were calculated separately for every data type. In this way we obtained 20 points per orbital period and plotted them in Fig. 1. The data are repeated over two cycles for clarity. In Fig. 1 from top to bottom we plot
- a-
the radio flux density at 2.25 GHz (in Jy),
- b-
the radio flux density at 8.3 GHz (in Jy),
- c-
the distance between the peaks of the Hα emission line, ΔVp, in km s-1,
- d-
the equivalent width of the blue hump of Hα, EW(B), in Å,
- e-
the equivalent width of the red hump of Hα, EW(R), in Å,
- f-
the dimensionless ratio between equivalent widths of the blue and red humps of Hα, EWB/EWR,
- g-
the total equivalent width of Hα emission line, EW(Hα), in Å,
- h-
the optical (Johnson) V band magnitude,
- k-
the Fermi-LAT photon flux in the 0.1–300 GeV energy range (in units 10-7 photons cm-2 s-1).
Spearman’s (rho) correlation test results.
3.1. Phase lags
In Fig. 1 it is visible that the averaged radio fluxes peak at phase ~ 0.7, while V magnitude peaks at phase ~ 0.9, EW(Hα) at phase ~ 0.5, EW(B) at phase ~ 0.4, Fermi-LAT flux at phase ~ 0.3.
To estimate the phase shift between the different bands, we used a cross correlation function (CCF) with the Fermi-LAT flux as a reference. The delay of the other parameters is as follows: radio flux at 2.25 GHz is delayed by 0.36, radio flux at 8.3 GHz is delayed by 0.30, V band brightness is delayed by 0.47, EW(Hα) is delayed by 0.14, EW(B) is delayed by 0.06, and EW(R) is delayed by 0.28. The typical error of these shifts is ± 0.03.
3.2. Correlations: Hα, V magnitude, and radio versus γ-rays
The various optical and radio parameters are plotted versus Fermi-LAT flux in Fig. 2. In each panel there are 20 data points, plotted with their errors. For each panel of this figure we performed Spearman’s (rho) rank correlation test. The results of the test (correlation coefficient and p-value) are summarized in Table 1, where the first column lists the correlated parameters, and the second the correlation coefficient and its significance (p-value). The third column notes our result, and if no correlation is detected it is empty. The fourth column refers to the figure where the data are plotted.
 |
Fig. 2 Various parameters plotted versus Fermi-LAT flux. Plotted from top to bottom: 2.25 GHz, ΔVp, EW(B), EW(R), the ratio EWB/EWR, EW(Hα), and V magnitude. Each point represents 1 bin with size 0.05 (see also Fig. 1 and Table 1). |
The highest correlations are between Fermi-LAT and EW(B), as well as Fermi-LAT and EWB/EWR. It is worth noting that EWB/EWR is one of the Hα emission parameters where the orbital period is most visible (Zamanov et al. 2013). The correlation is also highly significant (p < 0.001) for γ-rays and EW(B) and for γ-rays and the optical V band magnitude. Between γ-rays and the optical V band, there is an anti-correlation, and the optical brightness decreases when the γ flux increases. There is also a correlation between Fermi-LAT flux and total EW(Hα), which seems to be significant (p ≤ 0.01). The statistical significance of the correlations, with chance probability values p ≈ 10-4, indicates a relationship between the Hα and γ-ray emission processes.
It is worth noting that (i) there is no correlation between the EW(Hα) and V; however, a correlation does exist between EW(B) and V brightness; (ii) if we use the phase lags to match up the orbital modulation, the Spearman test gives a worse result for γ − EW(B) (0.76, p = 1.0 × 10-4), better result for γ − EWB/EWR (0.78, p = 4.1 × 10-5), considerably better result for γ − EW(Hα) (0.80 p = 2.2 × 10-5), and an even better result for γ − V (0.75 p = 1.5 × 10-4), in comparison with the values in Table 1.
4. Discussion and conclusions
The type of the secondary in LS I + 61°303 is still unknown. Several models have been proposed for the nature of the compact object in LS I + 61°303 several models have been proposed: an accreting black hole launching relativistic jets (microquasar, e.g., Massi et al. 2012), rotation-powered pulsar (Dubus 2013), ejector-propeller (Zamanov et al. 2001), and accretor-ejector model (Maraschi & Treves 1981). The properties of the short bursts recently observed are typical of those shown by high magnetic field neutron stars (magnetars), so they provide one more indication of neutron star (Papitto et al. 2012). During the ejector stage (pulsar) the gamma ray emission is thought to originate in the shock front at the boundary of the pulsar and stellar winds and/or inverse Compton process. Electrons and hadrons can also be accelerated to relativistic energies by a propeller-acting neutron star (accretion onto the magnetosphere of magnetar). These relativistic particles will produce γ-ray and neutrino emission (see Bednarek 2011, and references therein).
The Hα emission in Be stars and Be/X-ray binaries is coming from a Keplerian disk around the Be star (e.g., Hanuschik et al. 1988). This circumstellar disk also supplies the material that feeds the accretion onto the X-ray pulsars in the Be/X-ray binaries.
Phase lags. We detected and calculated the phase lags between γ-rays from one side and optical, Hα, and radio parameters from the other side (see Sect. 3.1 and Fig. 1). Chernyakova et al. (2012) used simultaneous X-ray and radio observations to show that periodic radio flares always lag behind the X-ray flare by Δφ ≃ 0.2, a behavior predicted by the ejector – propeller model. The radio outbursts are probably due to an expansion of a synchrotron emitting source (plasmon), with a prolonged injection of energetic particles (Paredes et al. 1991). In this model the phase shifts between the high-energy emission and other bands are probably connected with the ejection of relativistic wind (or jets) from the compact object, the appearance, and the expansion of the plasmon, which achieves the maximum of the radio flux a few (2–8) days after its appearance.
Correlations. We detected a highly significant anti-correlation between Fermi-LAT flux and optical V brightness. This could be due to changes in the ionization in the Be circumstellar disk in response to the high-energy emission, which changes the opacity and the emission. The γ-ray bright blazars in the sample of Bonning et al. (2012) have optical emission correlated with γ-rays. Bonning et al. (2012) suggest that this strongly supports leptonic models for the γ-ray production. We have the opposite situation, which is hard to reconcile with leptonic models based on the inverse Compton origin of the Fermi-LAT photons from LS I + 61°303.
The Fermi-LAT flux achieves the maximum at about the time of the periastron passage. The highest values of the EW(B) are reached in the phase interval 0.3–0.6, The highest values of EWB/EWR are about the orbital phase 0.40. The highest values of the total EW(Hα) are also reached in the phase interval 0.3–0.6. That the Fermi-LAT flux correlates with EW(B) and EWB/EWR, and not with EW(R) indicates that the high-energy emission does not influence all the Be disk but only the vicinity around the compact object.
For rotationally dominated profiles the peak separation can be regarded as a measure of the outer radius (e.g., Hanuschik et al. 1988). Because there is no correlation of Fermi/LAT flux and ΔVp, it means that the the size of the Hα emitting disk does not respond to the changes of the γ-ray flux. This in agrees with the above that only the surroundings of the compact object star are involved.
Conclusions. We detected highly significant correlations (chance probability value ≈ 10-4) between the orbital modulation of the blue hump of Hα emission line and Fermi-LAT flux and between the ratio EWB/EWR and Fermi-LAT flux, as well as an anti-correlation between V band brightness and Fermi-LAT flux. This implies a direct link between the Hα and γ-ray emission processes.
Acknowledgments
We are very grateful to the referee, E. Grundstrom, for valuable comments. This work was partially supported by the OP “HRD”, the ESF, and the Bulgarian Ministry of Education and Science (BG051PO001-3.3.06-0047). J.M. acknowledges support by grant AYA2010-21782-C03-03 from the Spanish Government, and Consejería de Economía, Innovación y Ciencia of Junta de Andalucía as research group FQM-322, as well as FEDER funds.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 701, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Ballet, J., et al. 2013, ApJ, 773, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2006, Science, 312, 1771 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2008, ApJ, 684, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2009, ApJ, 693, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Anderhub, H., Antonelli, L. A., Antoranz, P., et al. 2009, ApJ, 706, 27 [Google Scholar]
- Aragona, C., McSwain, M. V., Grundstrom, E. D., et al. 2009, ApJ, 698, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W. 2011, IAU Symp., 275, 305 [NASA ADS] [Google Scholar]
- Bonning, E., Urry, C. M., Bailyn, C., et al. 2012, ApJ, 756, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Casares, J., Ribas, I., Paredes, J. M., Martí, J., & Allen de Prieto, C. 2005, MNRAS, 360, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Chernyakova, M., Neronov, A., Molkov, S., et al. 2012, ApJ, 747, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Dhawan, V., Mioduszewski, A., & Rupen, M. 2006, in Proc. VI Microquasar Workshop: Microquasars and Beyond, ed. T. Belloni (Trieste: PoS), 52 [Google Scholar]
- Dubus, G. 2013, A&ARv., 21, 64 [Google Scholar]
- Gregory, P. C. 2002, ApJ, 575, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., & Taylor, A. R. 1978, Nature, 272, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., Xu, H.-J., Backhouse, C. J., & Reid, A. 1989, ApJ, 339, 1054 [Google Scholar]
- Grundstrom, E. D., Caballero-Nieves, S. M., Gies, D. R., et al. 2007, ApJ, 656, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuschik, R. W., Kozok, J. R., & Kaiser, D. 1988, A&A, 189, 147 [NASA ADS] [Google Scholar]
- Hermsen, W., Swanenburg, B. N., Bignami, G. F., et al. 1977, Nature, 269, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, D. A. 2001, A&A, 380, 516 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, J., Torres, D. F., Zhang, S., et al. 2012, ApJ, 744, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Lipunov, V. M., & Nazin, S. N. 1994, A&A, 289, 822 [NASA ADS] [Google Scholar]
- Lipunova, N. A. 1988, Sov. Astron., 32, 52 [NASA ADS] [Google Scholar]
- Liu, Q. Z., & Yan, J. Z. 2005, New ARev., 11, 130 [Google Scholar]
- Maier, G., & VERITAS Collaboration 2012, AIP Conf. Ser., 1505, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Maraschi, L., & Treves, A. 1981, MNRAS, 194, 1P [NASA ADS] [CrossRef] [Google Scholar]
- Massi, M., & Jaron, F. 2013, A&A, 554, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massi, M., Ros, E., & Zimmermann, L. 2012, A&A, 540, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McSwain, M. V., Grundstrom, E. D., Gies, D. R., & Ray, P. S. 2010, ApJ, 724, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Papitto, A., Torres, D. F., & Rea, N. 2012, ApJ, 756, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Paredes, J. M. 1987, Ph.D. thesis, University of Barcelona, Spain [Google Scholar]
- Paredes, J. M., Martí, J., Estalella, R., & Sarrate, J. 1991, A&A, 248, 124 [NASA ADS] [Google Scholar]
- Paredes, J. M., Marziani, P., Martí, J., et al. 1994, A&A, 288, 519 [NASA ADS] [Google Scholar]
- Paredes, J. M., Martí, J., Peracaula, M., & Ribo, M. 1997, A&A, 320, L25 [NASA ADS] [Google Scholar]
- Romero, G. E., Okazaki, A. T., Orellana, M., & Owocki, S. P. 2007, A&A, 474, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steele, I. A., Coe, M. J., Fabregat, J., et al. 1996, A&AS, 120, 213 [NASA ADS] [Google Scholar]
- Taylor, A. R., Kenny, H. T., Spencer, R. E., & Tzioumis, A. 1992, ApJ, 395, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, D. F., Zhang, S., Li, J., et al. 2010, ApJ, 719, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Woźniak, P. R., Vestrand, W. T., Akerlof, C. W., et al. 2004, AJ, 127, 2436 [NASA ADS] [CrossRef] [Google Scholar]
- Wynn, G. A., King, A. R., & Horne, K. 1997, MNRAS, 286, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Zaitseva, G. V., & Borisov, G. V. 2003, Astron. Lett., 29, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Zamanov, R. K., Martí, J., Paredes, J. M., et al. 1999, A&A, 351, 543 [NASA ADS] [Google Scholar]
- Zamanov, R., Martí, J., & Marziani, P. 2001, The Second National Conference on Astrophysics of Compact Objects, 50 [arXiv:astro-ph/0110114] [Google Scholar]
- Zamanov, R., Stoyanov, K., Martí, J., et al. 2013, A&A, 559, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
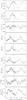 |
Fig. 1 Averaged orbital variability of LS I + 61°303. Plotted from top to bottom: the radio fluxes at 2.25 and 8.3 GHz, ΔVp, EW(B), EW(R), EWB/EWR, EW(Hα), the optical V, and the Fermi-LAT flux. The vertical (blue) line indicates the apastron passage. The data are averaged in 20 bins that are 0.05 each. |
| In the text | |
 |
Fig. 2 Various parameters plotted versus Fermi-LAT flux. Plotted from top to bottom: 2.25 GHz, ΔVp, EW(B), EW(R), the ratio EWB/EWR, EW(Hα), and V magnitude. Each point represents 1 bin with size 0.05 (see also Fig. 1 and Table 1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


