| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201322137 | |
| Published online | 17 December 2013 | |
Segmentation of coronal features to understand the solar EUV and UV irradiance variability
1
Department of Physics, APS College of Engineering,
560082
Bangalore, India
e-mail:
rkari@iiap.res.in
2
Indian Institute of Astrophysics, 560034
Bangalore,
India
3
European Space Research and Technology Center
(ESTEC), 2200 AG
Noordwijk, The
Netherlands
4
National Astronomical Observatory of Japan,
2-21-1 Osawa, Mitaka,
181-8588
Tokyo,
Japan
5
Royal Observatory of Belgium, Circular Avenue 3, 1180
Brussels,
Belgium
6
LATMOS (Laboratoire Atmosphères, Milieux, Observations
Spatiales), 11 boulevard
d’Alembert, 78280
Guyancourt,
France
7
Department of Physics, Bangalore University,
560056
Bangalore,
India
8
Harvard-Smithsonian Center for Astrophysics,
60 Garden Street, MS-15,
Cambridge, MA
02138,
USA
Received:
25
June
2013
Accepted:
31
October
2013
Context. The study of solar irradiance variability is of great importance in heliophysics, the Earth’s climate, and space weather applications. These studies require careful identifying, tracking and monitoring of active regions (ARs), coronal holes (CHs), and the quiet Sun (QS).
Aims. We studied the variability of solar irradiance for a period of two years (January 2011–December 2012) using the Large Yield Radiometer (LYRA), the Sun Watcher using APS and image Processing (SWAP) on board PROBA2, and the Atmospheric Imaging Assembly (AIA) on board the Solar Dynamics Observatory (SDO).
Methods. We used the spatial possibilistic clustering algorithm (SPoCA) to identify and segment coronal features from the EUV observations of AIA. The AIA segmentation maps were then applied on SWAP images, and parameters such as the intensity, fractional area, and contribution of ARs/CHs/QS features were computed and compared with the full-disk integrated intensity and LYRA irradiance measurements.
Results. We report the results obtained from SDO/AIA and PROBA2/SWAP images taken from January 2011 to December 2012 and compare the resulting integrated full-disk intensity with PROBA2/LYRA irradiance. We determine the contributions of the segmented features to EUV and UV irradiance variations. The variations of the parameters resulting from the segmentation, namely the area, integrated intensity, and relative contribution to the solar irradiance, are compared with LYRA irradiance. We find that the active regions have a great impact on the irradiance fluctuations. In the EUV passbands considered in this study, the QS is the greatest contributor to the solar irradiance, with up to 63% of total intensity values. Active regions, on the other hand, contribute to about 10%, and off-limb structures to about 24%. We also find that the area of the features is highly variable suggesting that their area has to be taken into account in irradiance models, in addition to their intensity variations.
Conclusions. We successfully show that the feature extraction allows us to use EUV telescopes to measure irradiance fluctuations and to quantify the contribution of each part to the EUV spectral solar irradiance observed with a calibrated radiometer. This study also shows that SPoCA is viable, and that the segmentation of images can be a useful tool. We also provide the measurement correlation between SWAP and AIA during this analysis.
Key words: Sun: UV radiation / Sun: activity / Sun: corona / Sun: atmosphere / Sun: evolution / solar-terrestrial relations
© ESO, 2013
1. Introduction
Since the radiative output of the Sun is one of the main driving forces of the terrestrial atmosphere and climate system, the study of solar energy raises is of increasing interest. Although the long-term change in total solar irradiance (the solar energy flux integrated over the entire spectrum) is considered to be one of the major natural forces of the Earth’s climate system, the study of extreme ultraviolet (EUV) and ultraviolet (UV) irradiance variability is equally important in solar physics. Indeed, EUV irradiance is the main energy input for the Earth’s upper atmosphere with important effects on the ionosphere and thermosphere. The solar EUV and UV fluxes thus play a major role in Solar-Terrestrial relationships. Understanding their variability is thus an important issue for space weather and climate applications.
For more than three decades, the total solar irradiance (TSI) has been monitored from several satellites. It has been observed that the solar energy flux changes over a solar cycle. It has been shown that the long-term irradiance variations are attributable to the changing emission of bright magnetic elements (Foukal & Lean 1988; Kariyappa & Pap 1996; Worden et al. 1998; Kariyappa 2000, 2008; Veselovsky et al. 2001; Kumara et al. 2012), whereas the short-term irradiance variations are directly associated with active regions as they evolve and move across the solar disk (Lean 1987). To understand and clarify the difference between the observed and modelled irradiance variability, to know the underlying physical mechanisms of solar irradiance variability, and to estimate the contribution of various coronal features to EUV and UV irradiance, a detailed and accurate image analysis of spatially resolved observations from space is required. To achieve this task, a successful segmentation of the solar features is necessary. The image segmentation is an important tool for the reconstruction of solar spectral irradiance (SSI) in the line of the semi-empirical reconstruction approaches (Fontenla et al. 2009; Haberreiter 2011, 2012). The segmentation of the coronal features from the solar images is a non-trivial task since all the features are dynamic in nature, and hence their morphology and magnetic configuration will be highly variable.
In this paper we use algorithms belonging to the set of Spatial Possibilistic Clustering Algorithm (SPoCA) initially developed by Barra et al. (2008, 2009) and later improved by Verbeeck et al. (2013a,b). The algorithms within the SPoCA-suite are based on fuzzy clustering and allow separating the active regions (ARs), the coronal holes (CHs), and the quiet Sun (QS) in the best way possible. The procedure is fast, stable in time and space, and allows for multi-channel inputs.
2. Observations
Our analysis is based on data from The Atmospheric Imaging Assembly (AIA; Boerner et al. 2012) instrument on board the Solar Dynamics Observatory (SDO), the Large Yield Radiometer (LYRA; Dominique et al. 2013), and The Sun Watcher with Active Pixel System detector and image Processing (SWAP) telescope (Seaton et al. 2013; Halain et al. 2013), both on board PROBA2. Level 1 data are used for both the AIA and the SWAP imagers. The data are corrected for dark currents, flat-field corrected, bad pixels are removed, and the image is rotated to put solar north on top of the array. The SWAP imager experiences a detector degradation of less than 2% per year. It manifests mostly in the increase of dark currents and is hence corrected for in the calibrated data (Halain et al. 2013). The data of the AIA imager was also cross-calibrated to the EVE calibration rocket underflight, which resulted in a good agreement of both. Additional calibration rocket flights will allow us to update the AIA instrument spectral calibration curve (Boerner et al. 2012). Level 3 data is used for the PROBA2 radiometer which is fully radiometrically calibrated; the data is then averaged over one minute (Dominique et al. 2013).
The LYRA instrument includes four broadband channels covering the spectral intervals 120–123 nm (channel 1), 190−222 nm (channel 2), 17–80 nm and a contribution below 5 nm (channel 3), and 6–20 nm and a contribution below 2 nm (channel 4). The last two channels are the ones suitable for the present analysis. Both overlap the SWAP bandpass (17.4 nm), as well as the main AIA channels (17.1 nm and 19.3 nm). The LYRA channel 3 is sensitive to chromospheric features, as its spectral response includes the 30.4 nm line. It must be noted, however, that since the beginning of the mission, channel 3 has experienced a stronger degradation than channel 4, which has resulted in a progressive rejection of the longer wavelengths of the channel, making it more similar to channel 4 from the spectral point of view (Kretzschmar et al. 2012). Dominique et al. (2013) describes additional details of the effects of the degradation on the individual channels of the LYRA instrument and discusses the algorithm used to correct for the instrument degradation. The characterization of the degradation of in-orbit EUV filters and detectors is of great interest for any data analysis, especially when applying comparative analysis. Based on the work of BenMoussa et al. (2013); Halain et al. (2013), and Boerner et al. (2012), we understand that the degradation effects on the instruments used are such that the effect on the data processing are negligible.
Since the LYRA channels 3 and 4 include both SWAP and AIA wavelengths and both channels are expected to show similar short-term variations in SSI, we have decided to use the channel 3 data set for our studies in this paper. For a period of two years, starting from January 1, 2011, we selected the nearest AIA image to map SWAP images because the AIA cadence is longer than the SWAP cadence (10 s for AIA and 2 min for SWAP). In order to study the long-term variations, we selected six equally distributed images per day, therefore SWAP images are very close to AIA images. Moreover, if the time difference between AIA and SWAP is more than 30 min then the routine will exclude both images. All the observations were processed using the standard procedures available in the solarsoft library in IDL.
3. Image segmentation with the SPoCA-suite
The SPoCA-suite is a set of multichannel fuzzy clustering algorithms that automatically segment solar EUV images into a set of features (see Barra et al. 2009; Verbeeck et al. 2013b for a complete presentation). We have chosen SPoCA because of the maturity and flexibility of the program. The SPoCA algorithm perfectly separates active region, quiet Sun, and coronal hole classes through the minimization of a fuzzy intra-class variance.
We perform a segmentation up to 0.99 R⊙, excluding the off-disk structures. A analysis limited to the on-disk part allows us to neglect detector noise.
To extract coronal holes, we use the fuzzy C-means algorithm (FCM) which was first
introduced by Bezdek (1981). With N
the number of pixels, C the number of classes to be clustered, and
xj the intensity value at pixel
j, we denote by
U = (uij)1 ≤ i ≤ C,1 ≤ j ≤ N
the fuzzy membership maps, where
uij = ui(xj) ∈ [0,1]
and by
B = { bi ∈ R|1 ≤ i ≤ C }
the cluster centres. By convention, centres are ordered by increasing intensity, i.e.
b1 < b2 < ... < bC.
The minimization of total fuzzy intra-class variance is reached when 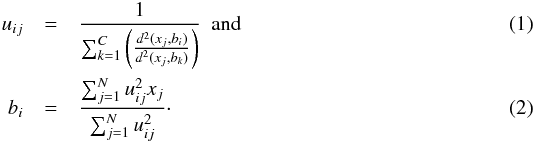 The
solution of (1)–(2) is obtained through an iterative algorithm.
The FCM gives good results even with a random initialization, and produces well separated
class centres.
The
solution of (1)–(2) is obtained through an iterative algorithm.
The FCM gives good results even with a random initialization, and produces well separated
class centres.
We use FCM with four classes on the histogram of rebinned AIA 19.3 nm images to obtain coronal holes. Indeed, coronal holes can be best seen in the AIA 19.3 nm bandpass, hence the use of a monochannel segmentation in this case. As a preprocessing, we apply a limb brightness correction, followed by a square root transformation. Indeed, Anscombe (1948) demonstrated for Poisson data, that a square root transformation will induce exact asymptotic normality and stabilizes the variance. This square root transformation is thus useful for the extraction of low-intensity regions such as coronal holes which are affected by Poisson noise. Once the fuzzy membership maps U are obtained, we use the “Maximum” rule to obtain a binary CH map. That is, we assign a pixel j to the coronal hole class (denoted “1”) whenever u1,j = maxi ∈ { 1,...,C }uij.
The FCM has its shortcomings, however. It is sensitive to noise and outliers (Krishnapuram & Keller 1993), and it is not satisfying theoretically since the membership degree of a feature to a class depends on the distance between this feature and all other class centres. Therefore Krishnapuram & Keller (1993, 1996) introduced the possibilistic C-means (PCM) algorithm in order to remedy these problems. To detect active regions, we use PCM with four classes on histogram values of 17.1 nm and 19.3 nm AIA images. Once the membership map U is obtained, we use a “Threshold” rule to obtain the AR map. The idea is to define the highly variable AR class as the right tail of another, more stable class. This rule produces more stable segmentations over time. In order to obtain AR of visually satisfying size, we decided to use the right tail of the first (dark feature) class. That is, all pixels j whose values are higher than b1 and for which u1,j is smaller than 0.0001 are attributed to the AR class.
Having determined AR maps (through multichannel PCM algorithm on 17.1 nm and 19.3 nm AIA images) and CH maps (through mono-channel FCM on 19.3 nm AIA), we determined QS maps as the set of pixels that belong neither to ARs nor to CHs.
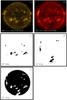 |
Fig. 1 Segmentation maps resulting from SPoCA. a) AIA 17.1 nm full-disk image, b) AIA 19.3 nm full-disk image showing coronal holes, c) segmented active regions map from AIA 17.1 nm, d) segmented coronal holes map from AIA 19.3 nm full-disk image, e) segmented quiet Sun map. |
The segmentation maps are arrays with the same dimensions as the input images; in the case of AIA it is 4k × 4k. To apply the segmentation maps on SWAP images, it is necessary to first match the image scale between the AIA and SWAP instruments. To achieve this, we rebinned the AIA maps by taking the ratio of the solar disk radii from AIA and SWAP images as a scaling parameter. For each image, both AIA and SWAP, we used the solar radius computed in each fits file, so that the computation for both AIA and SWAP take into account the solar radius changes. Furthermore, we aligned the AIA maps to achieve spatial alignment between AIA maps and SWAP images. We note that the full resolution AIA segmentation maps were used on AIA images to compute the integrated intensity values over ARs/CHs/QS. We then rebinned these segmentation maps and the AIA images to align them with the SWAP 17.4 nm images.
The pixels of the map can have either zero or non-zero values. Non-zero values correspond to the pixels located in an ARmap or CHmap. Since maps and images have the same size they share the same coordinate system. For example, all non-zero pixels in an ARmap have the same coordinates as all the pixels inside active regions in the corresponding AIA image. Extracting these coordinates is easily done using the WHERE command in IDL. Therefore, we can obtain the coordinates of all pixels inside ARs and CHs using ARmaps and CHmaps (Fig. 1). With these coordinates, we can easily extract the pixel values of the ARs and CHs. In addition to the coronal features, we have extracted the off-limb structures.
In this paper, the variations of the parameters resulting from the segmentation, i.e. the area, the integrated intensity of the coronal features, the integrated intensity of the full disk, and the relative contribution to the solar irradiance, are compared with LYRA irradiance (average for each day) of channel 3. The important results of this analysis are presented here.
4. Results
By applying SPoCA on AIA (17.1 nm, 19.3 nm) images for a period of two years, we obtain the segmented maps. From the segmented maps we compute (1) the integrated intensity on SWAP and AIA images, (2) the area occupied by each feature (ARs, CHs, and QS), and (3) the integrated intensity of these features. We then compare these parameters with the SSI as observed with LYRA channel 3 (observed Sun as a star) average for each day.
 |
Fig. 2 Integrated intensity over SWAP features (ARs, CHs, and QS), SWAP total integrated intensity, and LYRA channel 3 irradiance for a period of two years starting from January 1, 2011. |
 |
Fig. 3 Integrated intensity over AIA Features (ARs, CHs, and QS), AIA integrated intensity and LYRA channel 3 irradiance for a period of two years starting from January 1, 2011. |
4.1. Intensity variations of segmented coronal features
Figures 2 and 3 represent the time series of integrated intensity of each of the coronal features for the SWAP 17.4 nm and AIA 17.1 nm wavelength bands, respectively. It can be seen from the figures that the integrated intensity of QS is larger than the integrated intensity of CHs and ARs. We also note that there is correlation between all the parameters. In Table 1 we show the computed Spearman rank correlation coefficients of the segmented features with LYRA channel 3 observations. In Fig. 4, we have plotted the LYRA channel 3 irradiance versus integrated intensity of SWAP (in the top panel) and AIA (in the middle panel), and integrated intensity of AIA versus SWAP (in the bottom panel) for the two years. As observed through the scatter plot (Fig. 4) and the correlation results, ARs appear to be correlated very well (nearly 70% for both AIA and SWAP) to the irradiance measured by LYRA. This indicates that the relative AR variations are of the same order of magnitude as the SSI variations (although the physical units are different, the intensity is expressed in DN/s whereas the irradiance in calibrated units of W/m2). Therefore ARs appear to have a great impact on the irradiance fluctuations. The second highest correlation coefficient is the integrated intensity versus LYRA (nearly 59% for AIA and 62% for SWAP). Similarly, the QS appears to be correlated well with LYRA irradiance, but less than that of ARs. Therefore QS appear to influence the irradiance fluctuation, but less than ARs. Finally CHs have very low correlation coefficients to the LYRA irradiance, meaning CHs contribute much less to the irradiance fluctuations than the other two. In Table 2 we present the mean, minimum, maximum and standard deviation over time of the integrated intensity of ARs, CHs, and QS regions derived from SWAP and AIA full-disk images; the full-disk intensity of SWAP and AIA, and LYRA channel 3 irradiance variations for the years 2011 and 2012.
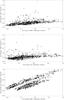 |
Fig. 4 Top panel: scatter plot between LYRA irradiance of channel 3 and integrated intensity of SWAP. Middle panel: scatter plot between LYRA irradiance of channel 3 and integrated intensity of AIA. Bottom panel: scatter plot between full-disk integrated intensity of SWAP and AIA. Here the upper band/family of data points belong to 2012 and whereas the lower family of data points correspond to 2011. |
Spearman rank correlation coefficients between LYRA Channel 3 and total integrated intensity (INT), integrated intensity of ARs/CHs/QS as seen on AIA 17.1 nm, and SWAP 17.4 nm.
 |
Fig. 5 Fractional area (normalized) covered by the coronal features (ARs, CHs, and QS) obtained from segmentation of AIA 17.1 nm and AIA 19.3 nm images. |
4.2. Area variations of segmented coronal features
Figure 5 represents the time series of the fractional area for the three coronal features (ARs, CHs, and QS) computed from the AIA maps, as described in Sect. 3 above. All areas exhibit a very strong 27 day modulation due to the solar rotation. To confirm this we have done both the wavelet and power spectrum analyses on time series of intensity of the features and integrated parameters. In Fig. 6 we show the wavelet spectrum for AIA and SWAP integrated intensity time series. Figure 7 shows the power spectrum plots of all the coronal features including the LYRA channel 3 irradiance values. It is clear from Figs. 6 and 7 that all the coronal features exhibit the expected 27 day rotational modulation similar to sunspots at the photospheric level. Most importantly, from Fig. 5 we can clearly notice that the QS covers a very large portion of the Sun’s surface, whereas ARs are small in general, but higher than the CHs. Since our study involves only two years of observations, it is not possible to make a definite statement about the way ARs/CHs/QS filling factors evolve throughout the solar cycle. We also find from Fig. 5 that the area of the features is highly variable, similar to the integrated intensity variations seen in Figs. 2 and 3, and the area of coronal features have to be taken into account in the models to explain the irradiance variations. In Table 2 we have shown the mean, minimum, maximum, and standard deviation over time of the variations in the fractional area of the ARs, CHs, and QS regions (Fig. 5) derived from the segmentation of AIA 17.1 nm and AIA 19.3 nm images for the years 2011 and 2012.
4.3. Comparison of segmented features with full-disk intensity and LYRA irradiance variations
We have observed from the time series plots (Figs. 2 and 3) and the scatter plot (Fig. 4) that the long-term variability of segmented features and full-disk intensity have shown a correlation with LYRA channel 3 if we exclude the days with a lot of flare activity in LYRA. We developed a routine that looks at each value and evaluates the average value with other surrounding values. If the change detected was too large with respect to the surrounding values, the tested value was removed from the series (replaced by a NaN value). The routine was also looked at the local average and global average as another test. In Fig. 4 from the top and middle panels we can clearly notice that for low fluctuation (small value of LYRA), SWAP and AIA integrated intensity increases linearly. If we exclude flares and look at the “low irradiance fluctuation”, the integrated intensity of EUV telescopes and the radiometer measurement show a correlation coefficient of approximately 0.6. In the bottom panel we have plotted the integrated intensity of AIA versus the SWAP full-disk image and it shows the cross-correlation coefficient of 0.7. From this figure it can be seen that both detectors are almost linearly proportional. This was expected because both instruments are EUV telescopes with almost the same wavelength and it is a good confirmation of the approach chosen, but we notice that there are two bands or families of data points. The upper band corresponds to 2012, while the lower band to 2011. The cause for the two bands or families of data points of integrated intensity values as seen in the scatter plot of Fig. 4 is unclear. A similar behaviour was observed by BenMoussa et al. (2013) when comparing SWAP integrated intensities against EVE computed intensity.
Mean, minimum, maximum, standard deviation over time of the integrated ARs/CHs/QS intensity, full-disk intensity of SWAP and AIA; and LYRA channel 3 irradiance variations.
 |
Fig. 6 Wavelet spectrum for the AIA and SWAP integrated intensity time series for the years 2011 and 2012. |
 |
Fig. 7 Power spectra for the integrated intensity of ARs, CHs, and QS and LYRA channel 3 irradiance time series derived from both AIA and SWAP images for the years 2011 and 2012. The power is plotted in units of DN/s. |
4.4. Contribution of on-disk coronal features and off-limb structures to EUV and UV irradiance variations
Figures 8 and 9 represent the contribution of the on-disk coronal features and the off-limb components of all the features, respectively, of SWAP and AIA images to the EUV and UV irradiance variations. From the figures, it is clear that the average percentage of contributions from the QS, ARs, and CHs are about 63%, 10%, and 3%, respectively. In addition to on-disk coronal features, we have extracted the total intensity of off-limb regions of all the structures up to 1.3 solar radius. We summed up all the contributions of on-disk features (ARs/CHs/QS) and then this value was subtracted from 100 to get the contribution of off-limb structures in percentage to EUV and UV irradiance variability. In Figs. 8 and 9 (the dashed curves) we show the variation of their contribution and it indicates that the average contribution from the off-limb structures is about 24%. We noticed that the QS is the greatest contributor to the solar irradiance and covers a very large portion of the Sun’s surface. Similarly ARs contribute only about 10% and appears to cover a small portion of the Sun’s surface. This means that the area appears to have more influence on the solar irradiance. However, CHs contribute much less to the EUV and UV irradiance variations than the other two. Table 3 lists the mean, minimum, maximum and standard deviation values over time in the variations of the contributions of the on-disk (ARs/CHs/QS) and off-limb (of all the features) features for the years 2011 and 2012.
 |
Fig. 8 Relative contribution of SWAP features (ARs, CHs, and QS), off-limb structure to the whole solar flux for a period of two years. a) The solid line represents ARs; b) double-dashed line QS; c) dashed line off-limb structure; and d) dotted line represents CHs. |
 |
Fig. 9 Relative contribution of AIA features (ARs, CHs, and QS), off-limb structure to the whole solar flux for a period of two years. a) The solid line represents ARs; b) double-dashed line QS; c) dashed line off-limb structure; and d) dotted line CHs. |
5. Discussion and conclusions
We have segmented coronal features using SDO/AIA (17.1 nm, 19.3 nm) and have derived the corresponding fractional area of ARs/CHs/QS. We have compared parameters such as integrated intensity of ARs/CHs/QS and total integrated intensity on SDO/AIA 17.1 nm and SWAP 17.4 nm images with LYRA irradiance observations measured in channel 3 (aluminium filter channel: 17−80 nm + a contribution below 5 nm, including strong He ii at 30.4 nm) average for each day for a period of two years starting from January 1, 2011. We have observed from the time series plots (Figs. 2 and 3) and the scatter plot (Fig. 4) that the long-term variability of segmented features and full-disk intensity have shown a correlation with LYRA channel 3 if we exclude the days with a lot of flares activity in LYRA. As observed through the correlation results, ARs appear to be correlated very well to the irradiance measured by LYRA (0.7), QS appear to be correlated well with LYRA irradiance (nearly 0.48) but less than ARs, and CHs have a very low correlation coefficient to the LYRA irradiance (nearly 0.18). This shows that ARs and QS influence the irradiance fluctuations whereas the CHs contribution is almost negligible to the irradiance fluctuations. Therefore, ARs appear to have a great impact on the irradiance fluctuations. The correlation coefficient between integrated intensity of AIA and SWAP and LYRA irradiance is 0.62. This indicates that the variation in the disk-integrated intensities detected by the EUV telescope follows the variation of the spectral irradiance as observed with LYRA channel 3.
The fractional area of the ARs, CHs, and QS exhibit a very strong 27 day modulation due to the solar rotation. Since we have analysed only two years of data, it is difficult to make any conclusions about the way ARs/CHs/QS filling factors evolve with the solar magnetic cycle. Hence, this is the subject of our future research. The QS covers a very large portion of the Sun’s surface, whereas the ARs cover a small portion, but higher than the CHs. We also find that the area of the features is highly variable and needs to be accounted for in explaining the irradiance variations.
In this work we discussed in detail the feasibility and usage of EUV observations to measure irradiance fluctuations. The observations from SWAP and AIA allow us to segment the images into different features and to study the contribution of individual features to the irradiance. This study also shows that SPoCA is an effective algorithm, and that the automatic identification and segmentation of images is very useful.
Mean, minimum, maximum, and standard deviation of the variations in the contribution of on-disk (ARs/CHs/QS) and off-limb (of all the features).
We successfully showed that it is possible to use EUV telescopes to measure irradiance fluctuations. This allows us to identify and extract the different features and to quantify the contribution of each part to the TSI. From Figs. 8 and 9 the quiet Sun appears to have a greater contribution to the solar irradiance, up to 63%, whereas the active regions appear to contribute only up to 10%. The off-limb contribution of all the features to the total is 24%. However, CHs contribution is much less (3%) to EUV and UV irradiance variations. We also show that there is a good agreement between SWAP and AIA EUV observations.
In our future work we will apply SPoCA on SDO/HMI full-disk magnetograms to segment the photospheric magnetic features corresponding to segmented coronal features. This would help us (i) to study a feature-to-feature spatial correlation; (ii) to determine the role of magnetic field in the irradiance variability; (iii) to determine the magnetic field fluctuations over the solar magnetic cycle; and (iv) to understand the line-of-sight magnetic field underlying the detected EUV features. These studies may offer a wider scope for understanding the irradiance variability as all the EUV features have magnetic origin. This work is in progress.
Acknowledgments
The authors would like to thank the PROBA2 Science Center, located at the Royal Observatory of Belgium (ROB) in Brussels for providing LYRA and SWAP data taken from January 2011 to December 2012. We also thank the Solar Dynamic Observatory (SDO) of the National Aeronautics and Space Administration (NASA) for providing AIA data taken from January 2011 to December 2012. We (R.K and G.G.) would like to express our sincere thanks to Professor B. P. Das, Director, Indian Institute of Astrophysics, for his strong support and encouragement of this research project, and for the financial support given to Giono Gabriel on his visit to Indian Institute of Astrophysics for 3 months during October 2012–January 2013. The authors thank Drs. Karel Schrijver, Paul Boerner, Daniel Seaton, and Marie Dominique for their valuable and detailed discussion on SDO/AIA/EVE, PROBA2/SWAP, and PROBA2/LYRA instrument calibration. Thanks to Dr. B.A. Varghese for his help in generating some of the figures and tables presented in this paper. We would like to express our sincere thanks to the referee for the constructive comments and suggestions given on this paper, which helped to improve the manuscript considerably.
References
- Anscombe, F. J. 1948, Biometrika, 35, 246 [Google Scholar]
- Barra, V., Delouille, V., & Hochedez, J.-F. 2008, Adv. Space Res., 42, 917 [Google Scholar]
- Barra, V., Delouille, V., Kretzschmar, M., & Hochedez, J.-F. 2009, A&A, 505, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- BenMoussa, A., Gissot, S., Schühle, U., et al. 2013, Sol. Phys. [arXiv:1304.5488] [Google Scholar]
- Bezdek, J. C. 1981, Pattern Recognition with Fuzzy Objective Function Algorithms (Norwell, MA, USA: Kluwer Academic Publishers) [Google Scholar]
- Boerner, P., Edwards, C., Lemen, J., et al. 2012, Sol. Phys., 275, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Dominique, M., Hochedez, J.-F., Schmutz, W., et al. 2013, Sol. Phys., 286, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Curdt, W., Haberreiter, M., Harder, J., & Tian, H. 2009, ApJ, 707, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Foukal, P., & Lean, J. 1988, ApJ, 328, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Haberreiter, M. 2011, Sol. Phys., 274, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Haberreiter, M. 2012, in IAU Symp. 286, eds. C. H. Mandrini, & D. F. Webb, 97 [Google Scholar]
- Halain, J.-P., Berghmans, D., Seaton, D. B., et al. 2013, Sol. Phys., 286, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Kariyappa, R. 2000, J. Astrophys. Astron., 21, 293 [Google Scholar]
- Kariyappa, R. 2008, J. Astrophys. Astron., 29, 159 [Google Scholar]
- Kariyappa, R., & Pap, J. M. 1996, Sol. Phys., 167, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Kretzschmar, M., Dammasch, I. E., Dominique, M., et al. 2012, J. Space Weather Space Clim., 2, A260000 [Google Scholar]
- Krishnapuram, R., & Keller, J. 1993, Fuzzy Systems, IEEE Trans. on, 1, 98 [Google Scholar]
- Krishnapuram, R., & Keller, J. 1996, Fuzzy Systems, IEEE Trans. on, 4, 385 [Google Scholar]
- Kumara, S. T., Kariyappa, R., Dominique, M., et al. 2012, Adv. Astron., 2012 [Google Scholar]
- Lean, J. 1987, J. Geophys. Res., 92, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, D. B., Berghmans, D., Nicula, B., et al. 2013, Sol. Phys., 286, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Verbeeck, C., Delouille, V., De Visscher, R., Mampaey, B., & Haberreiter, M. 2013a, in EGU General Assembly Conference Abstracts, 15, 9143 [Google Scholar]
- Verbeeck, C., Delouille, V., Mampaey, B., & R., D. V. 2013b, A&A, DOI: 10.1051/0004-6361/201321243 [Google Scholar]
- Veselovsky, I. S., Zhukov, A. N., Dmitriev, A. V., et al. 2001, Sol. Phys., 201, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Worden, J. R., White, O. R., & Woods, T. N. 1998, ApJ, 496, 998 [Google Scholar]
All Tables
Spearman rank correlation coefficients between LYRA Channel 3 and total integrated intensity (INT), integrated intensity of ARs/CHs/QS as seen on AIA 17.1 nm, and SWAP 17.4 nm.
Mean, minimum, maximum, standard deviation over time of the integrated ARs/CHs/QS intensity, full-disk intensity of SWAP and AIA; and LYRA channel 3 irradiance variations.
Mean, minimum, maximum, and standard deviation of the variations in the contribution of on-disk (ARs/CHs/QS) and off-limb (of all the features).
All Figures
 |
Fig. 1 Segmentation maps resulting from SPoCA. a) AIA 17.1 nm full-disk image, b) AIA 19.3 nm full-disk image showing coronal holes, c) segmented active regions map from AIA 17.1 nm, d) segmented coronal holes map from AIA 19.3 nm full-disk image, e) segmented quiet Sun map. |
| In the text | |
 |
Fig. 2 Integrated intensity over SWAP features (ARs, CHs, and QS), SWAP total integrated intensity, and LYRA channel 3 irradiance for a period of two years starting from January 1, 2011. |
| In the text | |
 |
Fig. 3 Integrated intensity over AIA Features (ARs, CHs, and QS), AIA integrated intensity and LYRA channel 3 irradiance for a period of two years starting from January 1, 2011. |
| In the text | |
 |
Fig. 4 Top panel: scatter plot between LYRA irradiance of channel 3 and integrated intensity of SWAP. Middle panel: scatter plot between LYRA irradiance of channel 3 and integrated intensity of AIA. Bottom panel: scatter plot between full-disk integrated intensity of SWAP and AIA. Here the upper band/family of data points belong to 2012 and whereas the lower family of data points correspond to 2011. |
| In the text | |
 |
Fig. 5 Fractional area (normalized) covered by the coronal features (ARs, CHs, and QS) obtained from segmentation of AIA 17.1 nm and AIA 19.3 nm images. |
| In the text | |
 |
Fig. 6 Wavelet spectrum for the AIA and SWAP integrated intensity time series for the years 2011 and 2012. |
| In the text | |
 |
Fig. 7 Power spectra for the integrated intensity of ARs, CHs, and QS and LYRA channel 3 irradiance time series derived from both AIA and SWAP images for the years 2011 and 2012. The power is plotted in units of DN/s. |
| In the text | |
 |
Fig. 8 Relative contribution of SWAP features (ARs, CHs, and QS), off-limb structure to the whole solar flux for a period of two years. a) The solid line represents ARs; b) double-dashed line QS; c) dashed line off-limb structure; and d) dotted line represents CHs. |
| In the text | |
 |
Fig. 9 Relative contribution of AIA features (ARs, CHs, and QS), off-limb structure to the whole solar flux for a period of two years. a) The solid line represents ARs; b) double-dashed line QS; c) dashed line off-limb structure; and d) dotted line CHs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


