| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 14 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201322092 | |
| Published online | 17 January 2014 | |
Self-consistent physical parameters for five intermediate-age SMC stellar clusters from CMD modelling⋆,⋆⋆,⋆⋆⋆
1
Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de
São Paulo, Rua do Matão 1226, Cidade Universitária,
05508-900
São Paulo,
SP
Brazil
e-mail:
bdias@astro.iag.usp.br
2
European Southern Observatory, Alonso de Cordova 3107, Santiago, Chile
3
LATO-DCET-UESC, Rodovia Ilhéus-Itabuna km 16, Ilhéus,
Bahia
45662-000,
Brazil
4
Universidade Federal do Rio Grande do Sul, IF,
CP 15051, 91501-970, RS, Porto Alegre,
Brazil
5
Dipartimento di Fisica e Astronomia Galileo Galilei, University of
Padova, vicolo dell’Osservatorio
3, 35122
Padova,
Italy
Received:
16
June
2013
Accepted:
15
November
2013
Context. Stellar clusters in the Small Magellanic Cloud (SMC) are useful probes for studying the chemical and dynamical evolution of this neighbouring dwarf galaxy, enabling inspection of a large period covering over 10 Gyr.
Aims. The main goals of this work are the derivation of age, metallicity, distance modulus, reddening, core radius, and central density profiles for six sample clusters, in order to place them in the context of the Small Cloud evolution. The studied clusters are AM 3, HW 1, HW 34, HW 40, Lindsay 2, and Lindsay 3; HW 1, HW 34, and Lindsay 2 are studied for the first time.
Methods. Optical colour–magnitude diagrams (V,B − V CMDs) and radial density profiles were built from images obtained with the 4.1 m Southern Astrophysical Research (SOAR) telescope, reaching V ~ 23. The determination of structural parameters were carried out by applying King profile fitting. The other parameters were derived in a self-consistent way by means of isochrone fitting, which uses likelihood statistics to identify the synthetic CMDs that best reproduce the observed ones. Membership probabilities were determined comparing the cluster and control field CMDs. Completeness and photometric uncertainties were obtained by performing artificial star tests.
Results. The results confirm that these clusters (except HW 34, identified as a field fluctuation) are intermediate-age clusters, with ages between 1.2 Gyr (Lindsay 3) and ~5.0 Gyr (HW 1). In particular HW 1, Lindsay 2 and Lindsay 3 are located in a region that we called West Halo, where studies of ages and metallicity gradients are still lacking. Moreover, Lindsay 2 was identified as a moderately metal-poor cluster with [Fe/H] = −1.4 ± 0.2 dex, lower than expected from the age-metallicity relation by Pagel & Tautvaisiene (1998). We also found distances varying from ~53 kpc to 66 kpc, compatible with the large depth of the SMC.
Key words: galaxies: star clusters: general / Magellanic Clouds / Hertzsprung-Russell and C-M diagrams
Based on observations obtained at the Southern Astrophysical Research (SOAR) telescope, which is a joint project of the Ministério da Ciência, Tecnologia, e Inovação (MCTI) da República Federativa do Brasil, the US National Optical Astronomy Observatory (NOAO), the University of North Carolina at Chapel Hill (UNC), and Michigan State University (MSU).
Appendix A is available in electronic form at http://www.aanda.org
The tables of photometry are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/561/A106
© ESO, 2014
1. Introduction
Star clusters (SCs) are useful objects for studying the complex stellar content observed in nearby galaxies, as most of them may be modelled as simple stellar populations (SSP) of a fixed age and metallicity. The Magellanic Clouds (SMC for the Small Cloud, LMC for the Large Cloud, and MCs for both) form a rich system with over >3700 stellar systems (Bica et al. 2008), with combinations of age and metallicity that are not found in the Milky Way (Santos & Piatti 2004). This information can be used to probe the dynamical and chemical evolution of these neighbouring and interacting dwarf irregular galaxies, and in particular the age-metallicity relation (AMR) of the MCs.
According to Holtzman et al. (1999), the age distribution based on clusters is probably distinct from the star formation history (SFH) as inferred from field stars in the LMC. For the SMC instead, Rafelski & Zaritsky (2005) analysed a sample of 195 clusters, showing that the populations of field stars and star clusters are similar. In particular, Piatti et al. (2005b) showed evidence of two peaks in the ages of SMC star clusters at 6.5 Gyr and 2.5 Gyr, and Piatti (2012b) indicates peaks of star formation for field stars at 2 Gyr and 7.5 Gyr. The more recent peak could be due to an encounter with the LMC. This leads to a model of bursts of star formation, in contrast with suggestions of continuous star formation (Da Costa & Hatzidimitriou 1998). The large period of quiescent star formation in the MCs between ~3 Gyr and 10 Gyr (Harris & Zaritsky 2001, 2004) is indicated by the low number of populous SCs with these ages (Rich et al. 2000, 2001), and almost all of them are in the SMC (Mighell et al. 1998; Piatti et al. 2005a,b, 2007a,b,c).
Cignoni et al. (2012) studied the SFH of two fields in the SMC, and compared their results to the SFH behaviour suggested by Harris & Zaritsky (2004). They concluded that stars older than 8.4 Gyr do not dominate the SMC stellar population, and the period between 2 Gyr and 8.4 Gyr agrees with Harris & Zaritsky (2004) in one region, but has a much higher star formation rate (SFR) in another region. Therefore, further studies of the SMC cluster and field AMR are needed.
Metallicity values for SMC star clusters, as given in the literature compilation by Parisi et al. (2009) for example, seem to be slightly underestimated when compared with the chemical evolution model predictions of Pagel & Tautvaisiene (1998), for ages in the range 3 Gyr to 10 Gyr. By adding more data points to this region of the AMR, Piatti (2011b) included a few metal-poor intermediate age star clusters (IACs). To further improve the AMR of the SMC, it is important to identify other IACs, and the metal-poor ones are particularly interesting.
In spite of its great interest, the SMC cluster system has been studied less than that of the LMC. Literature data on SMC star clusters were reviewed by Dias et al. (2010). In their Table 6, ages and metallicities for 33 among the most well-studied SMC star clusters are reported, giving particular attention to old/intermediate-age ones. In addition, based on integrated spectra, the analysis by Dias et al. showed that the clusters HW 1 and Lindsay 3 (as well as NGC 152) can be added to the list of intermediate/old clusters. Since then, newly revealed intermediate-age star clusters (IACs) were studied by Piatti (2011a,b, 2012a), and Piatti et al. (2011).
The compilation of ages and metallicities for SMC clusters by Dias et al. (2010) showed that the literature results have variations up to 7 Gyr in age and 0.9 dex in metallicity, for a given cluster. In the present work, B and V photometry combined with self-consistent statistical tools are employed to determine ages and metallicities for AM 3, HW 1, HW 40, Lindsay 2 and Lindsay 3, in order to provide more precise constraints for the AMR of the SMC. For these clusters, there are the spectroscopic analysis by Dias et al. (2010) of HW 1 and Lindsay 3, and the Washington photometry analysis of AM 3, HW 40, and Lindsay 3 (Piatti 2011a; Piatti et al. 2011). The target HW 34 is probably only a field fluctuation. For HW 1 and Lindsay 2 no previous CMD data were available in the literature. The confirmation of some of these clusters as intermediate or old age significantly improves the poor census in the age range corresponding to the age gap for the LMC clusters (~3–10 Gyr).
In Sect. 2 the observations, data reduction, and photometry are described. In Sect. 3 the modelling of colour–magnitude diagrams (CMDs) and statistical comparisons carried out to find the best fit of synthetic vs. observed CMDs are detailed. In Sect. 4 the results and a discussion of each cluster are given. In Sect. 5 comparisons with the literature, and the AMR for the SMC are presented. Finally, a summary is given in Sect. 6.
2. The data
2.1. The SOAR/SOI data
Using the SOAR Optical Imager (SOI) mounted on the 4.1 m Southern Astrophysical Research (SOAR) Telescope, B and V images were obtained for SMC SCs, under projects SO2007B-013 and SO2008B-017. We chose filters B and V since they provide the best temperature resolution for −0.2 < B − V < 1.4, which corresponds to the colours of the present CMDs; V,I would be better in high extinction fields, which is not the case of our fields, and B,V is less affected by differential reddening than is V,I (Soldera 2008). This imager has a field of view of 5.26′× 5.26′, and a pixel scale of 0.077′′/pixel, which is converted to 0.154′′/pixel because of the 2 × 2 binned observations presented here. The seeing was ~0.8 arcsec, and magnitudes up to V ~ 23 were detected. The log of observations is reported in Table 1.
Log of observations.
 |
Fig. 1 Sky maps showing the stellar distribution for all clusters, as imaged by the SOAR/SOI (1 pixel = 0.154 arcsec). The small circle (R < Rclus = 30 arcsec) corresponds to the cluster sample, whereas the large circle limits the area for the control field sample (R > Rfield = 90 arcsec). |
Reduction procedures were based on the SOAR/IRAF packages and the photometry procedures were based on the DAOPHOT/IRAF package (Stetson 1987). Classical procedures of aperture and then point spread function (PSF) photometry were performed in the B and V bands. Since PSF fitting resulted in better quality photometry, all the analyses in this paper are based on this method.
The standard stars were chosen from Sharpee et al.
(2002), having coordinates close to the SMC direction, in order to save time.
Airmass corrections were applied assuming constant values of 0.22 ± 0.03 mag/airmass and
0.14 ± 0.03 mag/airmass for the B and V bands,
respectively (as can be found at the CTIO website1).
Only standard stars observed with a seeing lower than 1.0′′, and airmasses
close to the cluster observations were considered. Moreover, stars with magnitude
variations between an aperture radius of 5 and 8 × FWHM larger than 0.010
mag were not considered in this fit. Then, the following calibration curves were fitted to
the standard stars; the results are presented in Table 2. The coefficient of determination r2 that
indicates how well the data fits a line (close to 1 is best) and the low residual values
show that both nights were photometric, which is confirmed by the CTIO monitoring2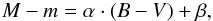 (1)where
M corresponds to either B or V, and
m corresponds to the respective instrumental magnitudes (given by
–2.5 ×log (counts/exptime)) already corrected by airmass effects.
(1)where
M corresponds to either B or V, and
m corresponds to the respective instrumental magnitudes (given by
–2.5 ×log (counts/exptime)) already corrected by airmass effects.
Figure 1 presents the sky map for each cluster, showing the stellar spatial distribution of the SOAR/SOI images, and the selected cluster and field areas. The adopted cluster (Rclus) and field radii (Rfield) for all clusters are 30 arcsec and 90 arcsec, respectively, covering solid angles (Ωclus and Ωfield) of about 0.79 arcmin2 and 20.6 arcmin2. These sky maps enable us to visually identify the overdensity inside the cluster radii (except for HW 34) and to verify which are the more/less crowded lines of sight.
2.2. Photometric errors and completeness curves
To properly determine the completeness of the photometry and the photometric errors we performed artificial star tests (ASTs). These consist of adding stars (with known magnitudes and colours) in random positions to the reduced images, and then carrying out the photometry exactly as was done with the original data. The ratio of recovered to input stars is called completeness (see Fig. 2).
 |
Fig. 2 Completeness curves for different distances from the cluster centre, based on V-band photometry. These curves correspond to a ten-order smoothed spline fitted to the data. Different lines are the completeness curves for different annuli, with the respective data points: 0 ≤ r < 10″ (red dotted/circle); 10 ≤ r < 20″ (green dashed/triangle); 20 ≤ r < 30″ (black solid/rhombus); 30 ≤ r < 40″ (blue dash dotted/inverted triangle); 40 ≤ r < 50″ (cyan long dashed/square). The magnitude limit corresponding to 50% of completeness are indicated in the plots. Completeness uncertainties are indicated in grey vertically (assumed as Poissonian), and typical magnitude uncertainties are indicated in grey horizontally. |
The procedure was carried out for both B and V images assuming an average colour of (B − V) = 0.5 for all the stars. The most important curves are those from the V band, since a V magnitude limit is applied in Fig. 4, and the curves are used to correct the radial density profiles (Fig. 5), which are better sampled by V images. In fact, B completeness curves were used only by internal checks: they differ by <0.5 mag from V curves with the same completeness values. We considered that this is a good approximation for the observed stars with colours ranging from ~0.0 < B − V < 1.0. Therefore, we used only V magnitude limits, as follows. The total range of V magnitudes covering all observed stars (from ~17 to ~24 mag) were divided into 32 intervals. For each interval, two sets of 465 stars were simulated inside a radius of 50′′from the cluster centre, with random magnitudes, separated by at least 3′′(≳3.5 × ⟨FWHM⟩) to avoid introducing additional crowding (e.g. Rubele et al. 2011). The resulting completeness curves as a function of the V magnitude are presented in Fig. 2 for diferent annuli around the cluster centre. The limiting magnitude is set where the completeness ratio is equal to 50% (see values in the figure). We adopted the Vlimit values of the annulus 20″ < r < Rclus ≡ 30″, where Rclus is defined as the outer cluster radius used for the CMD analysis.
The correspondence between Figs. 1 and 2 is evident. In particular, for the central regions (red solid curve), completeness for HW 34, HW 40, and Lindsay 3 are similar, as expected from the similar central densities of the stars. Instead, for external annuli, HW 40 and Lindsay 3 are more complete (2 mag more), while HW 34 presents roughly similar completeness to the centre. This indicates a crowded and homogeneous field in the HW 34 direction.
The observational photometric errors for V and (B − V) as given by DAOPHOT are presented in Fig. 3. The photometric uncertainties, i.e., the standard deviations of the differences between input and output magnitudes and colours derived from the ASTs, are presented together with the CMDs (Sect. 2.4).
 |
Fig. 3 V and (B − V) photometric errors given by DAOPHOT outputs. Vertical dashed lines correspond to magnitude limits in a radius of 30′′, as shown in Fig. 2. |
 |
Fig. 4 V and (B − V) colour–magnitude diagrams for all clusters. Left panels: cluster stars (R < Rclus). Right panels: control field stars (R > Rfield). The colours depend on the membership probabilities (pmember) for each star in the cluster direction (R < Rclus). The horizontal dashed lines correspond to the magnitude limits, derived from completeness curves around Rclus. |
2.3. The radial density profiles
The radial density profiles for all clusters are shown in Fig. 5. Only stars brighter than the magnitude limit presented in Fig. 4 were considered. Two profiles are presented: a) the
lower density, which is observed; and b) the higher density corresponding to those
corrected for completeness. Each star has a value for the completeness that comes from an
interpolation in radius and magnitude, based on the curves presented in Fig. 2. The error bars are the propagation of the Poissonic
errors on the star counts (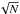 /area),
corrected by the incompleteness of the sample. Each profile is fitted with the empirical
density law of King (1962), expressed by Eq. (2) below, using a nonlinear least-squares
routine,
/area),
corrected by the incompleteness of the sample. Each profile is fitted with the empirical
density law of King (1962), expressed by Eq. (2) below, using a nonlinear least-squares
routine, ![\begin{eqnarray} n = n_0 \Bigg\{\frac{1}{[1+(r/r_{\rm c})^2]^{1/2}}-\frac{1}{[1+(r_{\rm t}/r_{\rm c})^2]^{1/2}}\Bigg\}^2 + n_{\rm field}, \label{kinglaw} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22092-13/aa22092-13-eq57.png) (2)where
n0 is the central density of the cluster,
nfield is the density of field stars,
rc is the core radius, and rt is
the tidal radius. From these parameters one can quantify the concentration parameter
c, defined as
c ≡ log (rt/rc).
For each cluster, the value of nfield was assumed to the
average density of stars outside Rfield ≡ 90′′, and
it was kept constant in the fits. The final fits are presented in Fig. 5, whereas all recovered structural parameters are shown
in Table 3.
(2)where
n0 is the central density of the cluster,
nfield is the density of field stars,
rc is the core radius, and rt is
the tidal radius. From these parameters one can quantify the concentration parameter
c, defined as
c ≡ log (rt/rc).
For each cluster, the value of nfield was assumed to the
average density of stars outside Rfield ≡ 90′′, and
it was kept constant in the fits. The final fits are presented in Fig. 5, whereas all recovered structural parameters are shown
in Table 3.
The comparison of the panels in Fig. 5 and the parameters in Table 3 reveal, as would be predicted from a visual analysis of the sky maps, that the objects present quite different stellar concentrations and field stellar densities. In all cases the core radius rc < Rcluster and the tidal radius rt < Rfield, which confirm that the adopted values of Rcluster and Rfield are reasonable. All clusters present roughly the same level of concentration, and the central density contrast with respect to the field is about 10 to 80 times the field density. We note that the original profile of Lindsay 2 and both profiles of HW 34 did not converge. The first is due to incompleteness, and the second does not have enough density contrast in the centre to be fitted by a King profile, which can be interpreted as evidence of a non-physical system.
 |
Fig. 5 Radial numerical density profiles fitted by King profiles. The empty grey circles and filled black diamonds are the observed profiles, original and corrected by completeness (Fig. 2), respectively. Solid lines are King profiles fitted to the data points. The horizontal and vertical dashed grey lines are nfield and rc, respectively, for the original profile, the dash dotted black lines for the corrected profile. HW34 does not present a high enough density contrast to be fitted by a King profile. |
2.4. The observed CMDs and cluster membership probability
Figure 4 shows the
V × B − V CMDs for the present
sample. For each object, the cluster
(R < Rclus) and
field (R > Rfield)
CMDs are presented, with stars from V ~ 17 up to V ~ 23.
It is possible to identify main sequence (MS) stars as well as red giant stars belonging
to the subgiant branch (SGB), red giant branch (RGB), and to the red clump (RC). The
comparisons with the field CMDs confirm these stellar identifications. We note that the
field CMDs are much richer in stars than the cluster CMDs, as a natural consequence of the
ratio between their covered areas (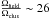 ).
).
Since the stellar samples in the direction of the clusters are contaminated by SMC field
stars, a procedure to determine the cluster membership probability
(pmember) was applied. In summary, the adopted procedure
follows the one from Kerber & Santiago
(2005) and Alves et al. (2012), where
pmember for each cluster star is determined by comparing the
density of stars inside the CMD in the cluster direction
(R < Rclus),
with a CMD representative of the local SMC field
(R > Rfield)
(see Fig. 4). The cluster and field CMDs are divided
into a grid of small boxes in V magnitude and
B − V colour, centred on each cluster star. So, for
the ith cluster star, the number of cluster
(Nclus,i) and field stars
(Nfield,i) contained in a box in magnitude
and colour (with a 3-sigma size in photometric errors) are computed, taking the inverse of
the completeness into account. Finally, the cluster membership probability for the
ith cluster star is given by 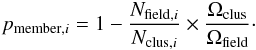 (3)The
results of these determinations are shown in Fig. 4
in a colour scale. The analysis of this figure reveals that most probable cluster members
(pmember > 75%) are red giants or
stars in the upper MS. In particular, almost all stars in the AM 3 cluster sample can be
considered physical cluster members. On the other hand, the MS stars in the HW 34 cluster
direction have a higher probability of being field stars rather than cluster stars since
they present pmember < 50%. This
strongly reinforces the argument that this stellar concentration is not a physical system,
but only a field stellar fluctuation (see also Sect. 2.3). Table 4 summarizes the star counts
in the sample CMDs.
(3)The
results of these determinations are shown in Fig. 4
in a colour scale. The analysis of this figure reveals that most probable cluster members
(pmember > 75%) are red giants or
stars in the upper MS. In particular, almost all stars in the AM 3 cluster sample can be
considered physical cluster members. On the other hand, the MS stars in the HW 34 cluster
direction have a higher probability of being field stars rather than cluster stars since
they present pmember < 50%. This
strongly reinforces the argument that this stellar concentration is not a physical system,
but only a field stellar fluctuation (see also Sect. 2.3). Table 4 summarizes the star counts
in the sample CMDs.
Stellar counts in the sample CMDs.
3. Statistical isochrone fitting
The isochrone fitting used in this work follows a numerical and statistical approach that combines CMD modelling and an objective criterion of comparing synthetic CMDs with the observed ones. It was initially developed to analyse CMDs of rich LMC clusters, observed with the Hubble Space Telescope (HST) (Kerber et al. 2002), and recently it was applied to determining physical parameters of Galactic open clusters imaged by 2MASS (Alves et al. 2012). The central idea behind this method is to statistically determine the synthetic CMDs that best reproduce the observed CMD, recovering as a consequence the physical parameters for the stellar cluster. In the present work the statistics adopted to select the best models is the likelihood, in particular following a Bayesian approach. This approach has been successfully applied to analysing CMDs of stellar clusters (Naylor & Jeffries 2006; Hernandez & Valls-Gabaud 2008; Monteiro et al. 2010) as well as CMDs of composite stellar populations (Hernandez et al. 2000, 1999; Vergely et al. 2002).
The generation of synthetic CMDs, as well as the likelihood statistics, are detailed in the next subsections.
3.1. CMD modelling
The synthetic CMDs are generated considering that they are SSPs, characterized by stars with the same age (τ) and metallicity (Z). The basic steps to generate a specific synthetic CMD are the following (see Fig. 6):
-
(i)
adoption of an evolutionary stellar model. The newPadova-Trieste models (PARSEC isochrones,Bressan et al. 2012) were adoptedin this work;
-
selection of the age and metallicity of the SSP, which is equivalent to selecting an isochrone from the library;
-
(iii)
application of the distance modulus (m − M)0 and reddening E(B − V) values to shift the isochrone from the absolute magnitudes to the observed ones;
-
(iv)
generation of 105 synthetic stars belonging to stellar systems (single and binary stars) following an initial mass function (IMF) and a fraction of unresolved binaries (fbin). A Salpeter IMF (dN/dm ∝ m-2.35) and fbin = 30% were adopted, with a minimum mass ratio (qmin = m2/m1) of 0.7 and a constant mass-ratio distribution (dN/dq = const.);
-
(v)
introduction of the observational photometric errors in magnitude and colour.
To determine the cluster parameters, a wide and regular grid of models was build for each cluster, composed typically of ~9000 combinations in log (τ/yr), Z, (m − M)0 and E(B − V) centred on the parameters found by a visual isochrone fit. To take into account the line-of-sight depth and the reddening values found for the SMC stellar clusters (Glatt et al. 2008; Crowl et al. 2001), the grids of models span distance modulii and reddening values in the range 18.50 < (m − M)0 < 19.20 and 0.00 < E(B − V) 0.20, in steps of 0.05 and 0.01, respectively. For log (τ/yr) the step is 0.05, and for Z all values provided by the isochrones are considered: 0.0001, 0.0004, 0.001, 0.002, 0.004, 0.006, 0.008, 0.010, 0.012, and 0.014.
 |
Fig. 6 Generation of synthetic V vs. B − V CMDs. Panel a) the adopted isochrone shifted by distance modulus and reddening. Panel b) the distribution of stars in accordance to the IMF and the fraction of binaries. Panel c) the introduction of photometric errors in magnitude and colour. Panel d) colours following the density of points in the CMD in a logarithmic scale. The density of points is related to pCMD,i (see Sect. 3.2). The reddening vector and the values for all physical parameters are shown in the figure. |
3.2. Likelihood statistics
 |
Fig. 7 Best isochrone fittings for all clusters. Left panels: cluster stars with colour symbols in accordance to the membership probabilities (pmember). Right panels: synthetic CMDs generated with the parameters found for the best solution. The number of points is equal to the observed CMDs within the same magnitude limits. The horizontal dashed black lines correspond to the magnitude limits used to compute the likelihood (brighter mag) and pmember (fainter mag). The solid and dashed blue lines correspond to the isochrones with the parameters found in Table 5 and take into account the uncertainties on ages and metallicities. |
Physical parameters determined in this work.
The first step in computing the likelihood for a synthetic CMD is to establish the
probabilities for each observed star cluster that it belongs to that choice of SSP
(pCMD). In general, this is done using analytical
expressions (e.g. Hernandez & Valls-Gabaud
2008; Monteiro et al. 2010), assuming that
the observed CMD positions would represent stars scattered from the isochrones following
Gaussian distributions for the photometric errors. However, in the present work these
probabilities are computed assuming that they are proportional to the density of points
generated by the synthetic CMD in each of the respective CMD positions
(N [V,(B − V)]),
which naturally incorporates the effect of unresolved binaries and photometric
uncertainties. This density map on the CMD is commonly called a Hess diagram, even though
its application is not directly related with the likelihood statistics. Therefore, the
likelihood statistics in this numerical approach is given by the product of these
probabilities over all the Nclus observed cluster stars as
stated by the expression ![\begin{eqnarray} L \propto \prod_{i\,=\,1}^{N_{\rm clus}} p_{{\rm CMD},i} \times p_{{\rm member},i} \propto \prod_{i\,=\,1}^{N_{\rm clus}} N[V_i,(B-V)_i] \times p_{{\rm member},i}, \label{likelihood} \end{eqnarray}](/articles/aa/full_html/2014/01/aa22092-13/aa22092-13-eq129.png) (4)where
the i index corresponds to the ith observed cluster
star. It can thus be stated that the best model is the one that provides the synthetic
CMD/Hess diagram that maximizes the above expression (Lmax).
The final parameters for each cluster, as well as corresponding uncertainties, are
determined by computing the average and standard deviation over the physical parameters of
the set of models that have likelihood values at the 1-sigma level from
Lmax (see Appendix A for details).
(4)where
the i index corresponds to the ith observed cluster
star. It can thus be stated that the best model is the one that provides the synthetic
CMD/Hess diagram that maximizes the above expression (Lmax).
The final parameters for each cluster, as well as corresponding uncertainties, are
determined by computing the average and standard deviation over the physical parameters of
the set of models that have likelihood values at the 1-sigma level from
Lmax (see Appendix A for details).
4. Results
The results of the isochrone fittings for the sample clusters are presented in Fig. 7 and Table 5. The panels in Fig. 7 give isochrones corresponding to the best-fit parameters, together with another two isochrones indicating 1σ uncertainties in age and metallicity: one younger and more metal-rich, and the other older and more metal-poor. The three isochrones cover most of the data points, as expected, allowing the reader to visually inspect the quality of the fits. For the [Fe/H] derivation we adopted a solar metallicity Z = 0.0152 (Caffau et al. 2011) in order to be compatible with the value assumed in the PARSEC isochrones (Bressan et al. 2012). These results are discussed cluster by cluster below.
4.1. AM 3
Although this is the cluster with the smallest number of stars in our sample, it has the
advantage of being located in the SMC field with the lowest stellar density. The results
in the present work indicate an age of 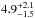 Gyr. The recovered metallicity, [Fe/H]
Gyr. The recovered metallicity, [Fe/H] 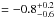 ,
is consistent with the value predicted by the SMC chemical evolution model from Pagel & Tautvaisiene (1998) for this age. Piatti (2011a) also determined physical parameters for
this cluster, based on the analysis of a CMD built with Washington photometry. Taking the
uncertainties into account, our results are in good agreement with the ones from Piatti et
al., although they derived slightly older ages (6.0 ± 1.0 Gyr) and more metal poor values
([Fe/H] = −1.25 ± 0.25). Our results are also close to the parameters derived by Da Costa (1999) of [Fe/H] = –1.27 and age of 5.5 ± 0.5
Gyr.
,
is consistent with the value predicted by the SMC chemical evolution model from Pagel & Tautvaisiene (1998) for this age. Piatti (2011a) also determined physical parameters for
this cluster, based on the analysis of a CMD built with Washington photometry. Taking the
uncertainties into account, our results are in good agreement with the ones from Piatti et
al., although they derived slightly older ages (6.0 ± 1.0 Gyr) and more metal poor values
([Fe/H] = −1.25 ± 0.25). Our results are also close to the parameters derived by Da Costa (1999) of [Fe/H] = –1.27 and age of 5.5 ± 0.5
Gyr.
The differences in age can be explained by the distance modulus. While we fitted a (m − M)0 = 19.00 for this cluster, Piatti (2011a) assumed an average value of 18.90. With a distance modulus ~0.1 lower, the isochrone should be ~0.6 Gyr older to fit the data.
This western SMC cluster was considered a galaxy member by Da Costa (1999) because it is close to the projected plan of the SMC, and its RC magnitude (distance indicator) is comparable to other SMC clusters. It is located in the West Halo region, but it is not as old and metal poor as one could expected in the case of gradients in age and [Fe/H] for this group (see Sect. 5). Although AM 3 is close to the SMC main body in the projected plan, its distance is higher than the other West Halo clusters (HW 1, Lindsay 2, and Lindsay 3). Therefore its age, metallicity, and distance do not follow exactly the general characteristics of the West Halo, which indicates a more complex history, possibly a capture by the potential well of the SMC.
4.2. HW 1 and Lindsay 2
The CMD analysis for these clusters which have never been published before, identifies these objects as intermediate-age metal-poor SMC clusters, with similar metallicities ([Fe/H] ~− 1.1 and − 1.4, respectively) and ages (4.98 and 4.0 Gyr). In particular, the age and metallicity values for HW 1 confirm the previous results from the integrated spectral analysis performed by Dias et al. (2010). We note that these two clusters are located close to each other, in the West Halo region (Fig. 8), at angular distances from the SMC centre of a = 3.4° to 3.9°, and distances from the Milky Way of 58.7 and 54.4 kpc, respectively. Their ages correspond to the epoch of a probable recent tidal interaction between the MCs, therefore they could be remnants of this period.
4.3. HW 40
The CMD analysis for this cluster indicates that it is an intermediate-age SMC cluster
with  Gyr. The presently derived metallicity ([Fe/H] =
Gyr. The presently derived metallicity ([Fe/H] = 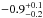 )
is in agreement with the results from Piatti
(2011a) based on photometry
([Fe/H] = –1.10 ± 0.25), and by Parisi et al. (2013, priv.
comm.; [Fe/H] = −0.78 ± 0.05 dex) using CaT spectra. The
age determined by Piatti et al. is significantly older (5.4 ± 1.0 Gyr) than our
result. More accurate CMDs are needed for this cluster to constrain its age.
)
is in agreement with the results from Piatti
(2011a) based on photometry
([Fe/H] = –1.10 ± 0.25), and by Parisi et al. (2013, priv.
comm.; [Fe/H] = −0.78 ± 0.05 dex) using CaT spectra. The
age determined by Piatti et al. is significantly older (5.4 ± 1.0 Gyr) than our
result. More accurate CMDs are needed for this cluster to constrain its age.
4.4. Lindsay 3
The age (1.2 ± 0.3 Gyr) and metallicity (–0.4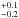 )
for this cluster is in good agreement with the results from Piatti et al. (2011): 1.25 ± 0.20 Gyr and [Fe/H] =
− 0.65 ± 0.20 dex. A remarkable result from our isochrone fitting is the small
distance modulus for this cluster (18.64 ± 0.14), suggesting that it is one of the closest
SMC clusters. We note that here too Piatti et al.
(2011) assumed a distance modulus of 18.90 and also a reddening of 0.04 instead
of our fitted value of 0.07. The combination of these two values tends to compensate the
effects on age and metallicity. Lindsay 3 is younger than the bulk of the surrounding
field stellar population in the West Halo region (HW 1 and Lindsay 2 are ~3 Gyr older, for
instance). If the MCs suffered interactions at about 4 Gyr ago, this could be a resulting
cluster in an older field, or else it is possible that there is an age gradient in the
West Halo. More data on the star clusters of this region are needed to confirm these
conclusions (see Sect. 5).
)
for this cluster is in good agreement with the results from Piatti et al. (2011): 1.25 ± 0.20 Gyr and [Fe/H] =
− 0.65 ± 0.20 dex. A remarkable result from our isochrone fitting is the small
distance modulus for this cluster (18.64 ± 0.14), suggesting that it is one of the closest
SMC clusters. We note that here too Piatti et al.
(2011) assumed a distance modulus of 18.90 and also a reddening of 0.04 instead
of our fitted value of 0.07. The combination of these two values tends to compensate the
effects on age and metallicity. Lindsay 3 is younger than the bulk of the surrounding
field stellar population in the West Halo region (HW 1 and Lindsay 2 are ~3 Gyr older, for
instance). If the MCs suffered interactions at about 4 Gyr ago, this could be a resulting
cluster in an older field, or else it is possible that there is an age gradient in the
West Halo. More data on the star clusters of this region are needed to confirm these
conclusions (see Sect. 5).
4.5. HW 34
No star cluster was identified, as made evident by the following:
-
sky maps given in Fig. 1 and radial density profilesin Fig. 5 show no significant overdensity in theregion centred on HW 34 coordinates;
-
the photometric data are of comparable quality to the other clusters (see Figs. 2 and 3), so a cluster would be recovered if present;
-
almost all stars in the direction of HW 34 coordinates were given the probability of being field stars, as shown in Fig. 4 and Table 4;
-
based on the very few RGB stars with pmember > 0.5, and no clear MS turnoff, if there was a cluster there, it would be older than ~5 Gyr, which is not expected for the central younger regions of the SMC.
 |
Fig. 8 On sky distribution of the SMC star clusters, including the catalog clusters (Bica et al. 2008), overplotted with the five sample clusters. The ellipses are used to illustrate distances from the SMC centre (Table 5). Different colours indicate subgroups, as indicated in the panel (see text for details). |
5. The age-metallicity relation and spatial distribution
Figure 8 shows the 2D positions of the five clusters in the sky plane, where clusters from the catalog of Bica et al. (2008) were overplotted. Ellipses are indicated to find the clusters’ distances from the SMC centre, following the procedure of Piatti et al. (2005a). We adopt the coordinates of the SMC centre from Crowl et al. (2001), (α,δ) = (0h52m45s, − 72°49′43′′), and a minor to major axis ratio of b/a = 1/2. Thus, the indicator of distance to the SMC centre would be the semi-major axis a, which is more appropriate for a ellipsoidal galaxy like the SMC (see Fig. 8). We consider an inclination of 45° for the major axis of all the ellipses in the projected plane of the figure. The distances a for all the clusters can be found in Table 5.
Most of the sample clusters are located outside the region sampled by Harris & Zaritsky (2004), but inspired by the different SFR that they found in different regions of the SMC, we located our targets in different groups for a > 2° (see Fig. 8). These regions were simply divided into the sky plane based on the HI structures, as described by Diaz & Bekki (2012), assuming that these structures have stellar/star cluster counterparts. They are: Bridge, Counter-Bridge, and a third region not related with the HI structures that we have called West Halo. They are indicated by different colours and symbols in Figs. 8–10.
The 3D structure of the SMC was shown to be complex (Subramanian & Subramaniam 2012), with a spread in depth of about 14 kpc, and an inclination along the main axis with the north-eastern portion towards the observer. The five clusters studied in this work follow this dispersion, in particular for West Halo clusters, where we found distances between ~54 and 63 kpc, revealing that more statistics on this region are needed in order to better describe the 3D structure of the SMC.
Figure 9 shows the AMR of the SMC, by plotting data for well-studied star clusters (Dias et al. 2010; Piatti et al. 2011; Piatti 2011a,b), overplotted by the model of Pagel & Tautvaisiene (1998). The results for the sample clusters fit well the Pagel & Tautvaisiene (1998) model, and agree with a dispersion in metallicity for the SMC cluster system in the metallicity and age ranges of − 1.5 < [Fe/H] < −1.0, and 5 < age < 10 Gyr, as indicated by Piatti (2011b), in their Fig. 3. The field stars also agree with this statement, as can be seen in Fig. 8 of Piatti (2012b). In this case, the model of Pagel & Tautvaisiene (1998) would represent an average of the chemical enrichment history of the SMC. Spectroscopic results by Parisi et al. (2009) also show a spread in [Fe/H] among intermediate-age clusters; however, their values are in the range − 1.2 < [Fe/H] < −0.7 dex. Therefore, both photometric and spectroscopic metallicities show a spread of ~0.5 dex in metallicity, with limits defined by different metallicity scales.
Another important product of this work concerns AM 3, Lindsay 2, and HW 1, the oldest clusters of the sample, with 4.9, 4.0, and 4.98 Gyr, respectively. They are close to the end of the quiescent star formation as pointed out by Harris & Zaritsky (2004), and can be among the first products of the reactivation of star formation in the MC system ~3–4 Gyr ago.
 |
Fig. 9 Age-metallicity relation for the SMC, including the new additions from the present work. The well-known clusters are listed in Table 6 of Dias et al. (2010), and other clusters from literature. The model of Pagel & Tautvaisiene (1998) is overplotted. |
The cluster distribution in the 2D projected plane of the sky is also useful for investigating gradients of age and metallicity. This is presented in Fig. 10, where the marked labels correspond to those of Fig. 9. The five clusters presented in this work are located outside the 2° ellipse. The small sample combined with the error bars do not permit us to establish a strong gradient. Nevertheless, it is possible to identify that the most internal regions of the SMC, below a = 1–2° might indicate a gradient in age and metallicity, whereas the outer regions have a spread in these parameters. Otherwise, these trends seem to be consistent with those of the SMC field population (Piatti 2012b).
Even so, if one looks at different regions of the projected SMC, they reveal different superimposed gradients (which would generate the overall dispersion with no gradients), but the dispersion is too high and more data are needed for this to be confirmed. Lindsay 2, Lindsay 3, and HW 1, which are located in the West Halo region, tend to show a possible age gradient in this region, as indicated by the blue diamonds in the figure.
 |
Fig. 10 Age and [Fe/H] as a function of the distance indicator a. The dots are the same as described in Fig. 9. |
6. Summary and conclusions
We studied intermediate-age stellar clusters in the SMC. The parameters were derived by statistical fitting of the observed CMDs with a grid of synthetic CMDs based on the PARSEC isochrones. Six targets were observed in the visible filters B and V, and we derived ages for five of them (AM 3, HW 1, HW 40, Lindsay 2, and Lindsay 3) in the age range of 1.2 Gyr to 5.0 Gyr, whereas HW 34 was identified as a field fluctuation. In particular, Lindsay 2 and HW 1 were studied for the first time in this work, and for the other clusters we derived self-consistent parameters compatible with the literature, and in principle with more precision.
The five clusters essentially follow the chemical enrichment history modelled by Pagel & Tautvaisiene (1998). Figure 9 shows a strong spread in metallicity for clusters with ages of 2–5 Gyr, also found by Piatti (2011b). Piatti (2012b) finds a metallicity spread of ~0.4 dex at ages of 2–4 Gyr, and Parisi et al. (2010) finds a dispersion of ~0.32 dex around the mean value of [Fe/H] = −1.0 from 15 fields.
This suggests that, after an initial period of rapid enrichment, that brought the metallicity up to around [Fe/H] ≈ −1.2, the SMC chemical enrichment is very inhomogeneous, since there is a spread in metallicity from ~11 to ~3 Gyr, with a trend for slow enrichment. Finally an intense burst occurred at around 2 Gyr ago, when most of the star clusters started to form.
Piatti et al. (2011) suggested the occurrence of two recent bursts at ~2 Gyr and ~6 Gyr ago (preceded by a quiescent period lasting ~3 Gyr), with roughly no metallicity variations. Our clusters improve the statistics for the two more recent bursts identifed by Piatti et al. (2011), in particular HW 1 and Lindsay 2, which are located in the West Halo region, at almost the same distance.
A gradient of age and metallicity can be found in the inner part of the SMC (a < 2°), but in the outer regions the high dispersion in ages and metallicities prevents the identification of any trends. More data on age, metallicity/abundances, distance, and kinematics of star clusters are needed in order to prove different star formation rates and chemical evolution histories in the regions due to tidal forces caused by the interactions in the SMC-LMC-Milky Way system.
Online material
Appendix A: Likelihood results and degeneracy investigation
We analysed the likelihood maps to investigate the degeneracy in age, metallicity, reddening, and distance modulus. The likelihood values were obtained from a comparison of a given synthetic CMD with the observed one (see Sect. 3 for details).
To establish the standard deviation of the likelihood statistics, we proceeded as follows. A synthetic best model CMD was created with the same numbers of stars as the observed one. We call this a false observation. We then compared this CMD with another one with the same parameters but with many more stars (e.g. 105). From this model vs. model comparison, a likelihood value is obtained, as previously done for data vs. model comparions. Then simulating 300 false observations, and comparing them with the star rich synthetic CMD, we derived the standard deviation σ. This tells how much the likelihood can vary due only to stochastic effects, i.e., due to the statistical fluctuations on the position of stars in a CMD with a number of points compatible with that of the observed CMDs.
The likelihood maps of these comparisons are displayed in Figs. A.1 to A.5, in the space of parameters of [Fe/H] vs. log (age), log (age) vs. (m − M), and E(B − V) vs. (m − M), centred in the parameters of the best-fit. The colour scale is red, green, cyan or yellow, corresponding to a difference from the best fit solution up to 1-sigma, between 1- and 2-sigma, between 2- and 3-sigma, and larger than 3-sigma of the best fit, respectively. The central panel in each figure gives the value obtained for the two fixed parameters, since in each map two parameters are varied and the two others are fixed.
These maps clearly reveal the expected anti-correlation between age and metallicity, distance modulus and age, and between distance modulus and reddening. These degeneracies are directly reflected in the physical parameter uncertainties since they correspond to the standard deviation in each parameter for the set of models with likelihood values up to 1-sigma (red points) from the best-fit solution.
 |
Fig. A.1 Likelihood from the fits for different combinations of age, metallicity, reddening, and distance modulus for AM 3. Upper panel: metallicity vs. age; middle panel: age vs. distance modulus; bottom panel: reddening vs. distance modulus. The colour scale is red, green, cyan or yellow, corresponding to a difference from the best-fit solution up to 1-sigma, between 1- and 2-sigma, between 2- and 3-sigma, and larger than 3-sigma of the best fit, respectively. |
Acknowledgments
We acknowledge partial financial support from CNPq, CAPES and FAPESP. B.D. acknowledges a CNPq studentship no. 142047/2010-4, and also an ESO studentship. B.D., B.B., L.K. thank CAPES/CNPq for their financial support with the PROCAD project number 552236/2011-0.
References
- Alves, V. M., Pavani, D. B., Kerber, L. O., & Bica, E. 2012, New Astron., 17, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Bica, E., Bonatto, C., Dutra, C. M., & Santos, J. F. C. 2008, MNRAS, 389, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Cignoni, M., Cole, A. A., Tosi, M., et al. 2012, ApJ, 754, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Crowl, H. H., Sarajedini, A., Piatti, A. E., et al. 2001, AJ, 122, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Da Costa, G. S. 1999, in New Views of the Magellanic Clouds, eds. Y.-H. Chu, N. Suntzeff, J. Hesser, & D. Bohlender, IAU Symp., 190, 446 [Google Scholar]
- Da Costa, G. S., & Hatzidimitriou, D. 1998, AJ, 115, 1934 [NASA ADS] [CrossRef] [Google Scholar]
- Dias, B., Coelho, P., Barbuy, B., Kerber, L., & Idiart, T. 2010, A&A, 520, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diaz, J. D., & Bekki, K. 2012, ApJ, 750, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Glatt, K., Grebel, E. K., Sabbi, E., et al. 2008, AJ, 136, 1703 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, J., & Zaritsky, D. 2001, ApJS, 136, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, J., & Zaritsky, D. 2004, AJ, 127, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez, X., & Valls-Gabaud, D. 2008, MNRAS, 383, 1603 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez, X., Valls-Gabaud, D., & Gilmore, G. 1999, MNRAS, 304, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez, X., Gilmore, G., & Valls-Gabaud, D. 2000, MNRAS, 317, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Holtzman, J. A., Gallagher, III, J. S., Cole, A. A., et al. 1999, AJ, 118, 2262 [NASA ADS] [CrossRef] [Google Scholar]
- Kerber, L. O., & Santiago, B. X. 2005, A&A, 435, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerber, L. O., Santiago, B. X., Castro, R., & Valls-Gabaud, D. 2002, A&A, 390, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, I. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Mighell, K. J., Sarajedini, A., & French, R. S. 1998, AJ, 116, 2395 [NASA ADS] [CrossRef] [Google Scholar]
- Monteiro, H., Dias, W. S., & Caetano, T. C. 2010, A&A, 516, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naylor, T., & Jeffries, R. D. 2006, MNRAS, 373, 1251 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J., & Tautvaisiene, G. 1998, MNRAS, 299, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Parisi, M. C., Grocholski, A. J., Geisler, D., Sarajedini, A., & Clariá, J. J. 2009, AJ, 138, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Parisi, M. C., Geisler, D., Grocholski, A. J., Clariá, J. J., & Sarajedini, A. 2010, AJ, 139, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E. 2011a, MNRAS, 416, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E. 2011b, MNRAS, 418, L69 [NASA ADS] [Google Scholar]
- Piatti, A. E. 2012a, ApJ, 756, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E. 2012b, MNRAS, 422, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E., Santos, Jr., J. F. C., Clariá, J. J., et al. 2005a, A&A, 440, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piatti, A. E., Sarajedini, A., Geisler, D., Seguel, J., & Clark, D. 2005b, MNRAS, 358, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E., Sarajedini, A., Geisler, D., Clark, D., & Seguel, J. 2007a, MNRAS, 377, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E., Sarajedini, A., Geisler, D., Gallart, C., & Wischnjewsky, M. 2007b, MNRAS, 382, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E., Sarajedini, A., Geisler, D., Gallart, C., & Wischnjewsky, M. 2007c, MNRAS, 381, L84 [NASA ADS] [Google Scholar]
- Piatti, A. E., Clariá, J. J., Bica, E., et al. 2011, MNRAS, 417, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Rafelski, M., & Zaritsky, D. 2005, AJ, 129, 2701 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Shara, M., Fall, S. M., & Zurek, D. 2000, AJ, 119, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Shara, M. M., & Zurek, D. 2001, AJ, 122, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Rubele, S., Girardi, L., Kozhurina-Platais, V., Goudfrooij, P., & Kerber, L. 2011, MNRAS, 414, 2204 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, Jr., J. F. C., & Piatti, A. E. 2004, A&A, 428, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sharpee, B., Stark, M., Pritzl, B., et al. 2002, AJ, 123, 3216 [NASA ADS] [CrossRef] [Google Scholar]
- Soldera, L. 2008, Ph.D. Thesis, University of Padova [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, S., & Subramaniam, A. 2012, ApJ, 744, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Vergely, J.-L., Köppen, J., Egret, D., & Bienaymé, O. 2002, A&A, 390, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Sky maps showing the stellar distribution for all clusters, as imaged by the SOAR/SOI (1 pixel = 0.154 arcsec). The small circle (R < Rclus = 30 arcsec) corresponds to the cluster sample, whereas the large circle limits the area for the control field sample (R > Rfield = 90 arcsec). |
| In the text | |
 |
Fig. 2 Completeness curves for different distances from the cluster centre, based on V-band photometry. These curves correspond to a ten-order smoothed spline fitted to the data. Different lines are the completeness curves for different annuli, with the respective data points: 0 ≤ r < 10″ (red dotted/circle); 10 ≤ r < 20″ (green dashed/triangle); 20 ≤ r < 30″ (black solid/rhombus); 30 ≤ r < 40″ (blue dash dotted/inverted triangle); 40 ≤ r < 50″ (cyan long dashed/square). The magnitude limit corresponding to 50% of completeness are indicated in the plots. Completeness uncertainties are indicated in grey vertically (assumed as Poissonian), and typical magnitude uncertainties are indicated in grey horizontally. |
| In the text | |
 |
Fig. 3 V and (B − V) photometric errors given by DAOPHOT outputs. Vertical dashed lines correspond to magnitude limits in a radius of 30′′, as shown in Fig. 2. |
| In the text | |
 |
Fig. 4 V and (B − V) colour–magnitude diagrams for all clusters. Left panels: cluster stars (R < Rclus). Right panels: control field stars (R > Rfield). The colours depend on the membership probabilities (pmember) for each star in the cluster direction (R < Rclus). The horizontal dashed lines correspond to the magnitude limits, derived from completeness curves around Rclus. |
| In the text | |
 |
Fig. 5 Radial numerical density profiles fitted by King profiles. The empty grey circles and filled black diamonds are the observed profiles, original and corrected by completeness (Fig. 2), respectively. Solid lines are King profiles fitted to the data points. The horizontal and vertical dashed grey lines are nfield and rc, respectively, for the original profile, the dash dotted black lines for the corrected profile. HW34 does not present a high enough density contrast to be fitted by a King profile. |
| In the text | |
 |
Fig. 6 Generation of synthetic V vs. B − V CMDs. Panel a) the adopted isochrone shifted by distance modulus and reddening. Panel b) the distribution of stars in accordance to the IMF and the fraction of binaries. Panel c) the introduction of photometric errors in magnitude and colour. Panel d) colours following the density of points in the CMD in a logarithmic scale. The density of points is related to pCMD,i (see Sect. 3.2). The reddening vector and the values for all physical parameters are shown in the figure. |
| In the text | |
 |
Fig. 7 Best isochrone fittings for all clusters. Left panels: cluster stars with colour symbols in accordance to the membership probabilities (pmember). Right panels: synthetic CMDs generated with the parameters found for the best solution. The number of points is equal to the observed CMDs within the same magnitude limits. The horizontal dashed black lines correspond to the magnitude limits used to compute the likelihood (brighter mag) and pmember (fainter mag). The solid and dashed blue lines correspond to the isochrones with the parameters found in Table 5 and take into account the uncertainties on ages and metallicities. |
| In the text | |
 |
Fig. 8 On sky distribution of the SMC star clusters, including the catalog clusters (Bica et al. 2008), overplotted with the five sample clusters. The ellipses are used to illustrate distances from the SMC centre (Table 5). Different colours indicate subgroups, as indicated in the panel (see text for details). |
| In the text | |
 |
Fig. 9 Age-metallicity relation for the SMC, including the new additions from the present work. The well-known clusters are listed in Table 6 of Dias et al. (2010), and other clusters from literature. The model of Pagel & Tautvaisiene (1998) is overplotted. |
| In the text | |
 |
Fig. 10 Age and [Fe/H] as a function of the distance indicator a. The dots are the same as described in Fig. 9. |
| In the text | |
 |
Fig. A.1 Likelihood from the fits for different combinations of age, metallicity, reddening, and distance modulus for AM 3. Upper panel: metallicity vs. age; middle panel: age vs. distance modulus; bottom panel: reddening vs. distance modulus. The colour scale is red, green, cyan or yellow, corresponding to a difference from the best-fit solution up to 1-sigma, between 1- and 2-sigma, between 2- and 3-sigma, and larger than 3-sigma of the best fit, respectively. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 for HW 1. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1 for HW 40. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.1 for Lindsay 2. |
| In the text | |
 |
Fig. A.5 Same as Fig. A.1 for Lindsay 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


