| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321780 | |
| Published online | 23 December 2013 | |
Influence of the C/O ratio on titanium and vanadium oxides in protoplanetary disks
1 Université de Franche-Comté, Institut UTINAM, CNRS/INSU, UMR 6213, Besançon Cedex, France
e-mail: mdib@obs-besancon.fr
2 Dipartimento di Astronomia, Universitá di Roma Tor Vergata, via della Ricerca Scientifica 1, 00133 Roma, Italy
3 Center for Radiophysics and Space Research, Space Sciences Building, Cornell University, Ithaca, NY 14853, USA
4 Department of Physics and Department of Astronomy, Yale University, New Haven, CT 06511, USA
Received: 26 April 2013
Accepted: 12 November 2013
Context. The observation of carbon-rich disks have motivated several studies questioning the influence of the C/O ratio on their gas phase composition in order to establish the connection between the metallicity of hot-Jupiters and that of their parent stars.
Aims. We propose a method that allows the characterization of the adopted C/O ratio in protoplanetary disks independently from the determination of the host star composition. Titanium and vanadium chemistries are investigated because they are strong optical absorbers and also because their oxides are known to be sensitive to the C/O ratio in some exoplanet atmospheres.
Methods. We use a commercial package based on the Gibbs energy minimization technique to compute the titanium and vanadium equilibrium chemistries in protoplanetary disks for C/O ratios ranging from 0.05 to 10. Our calculations are performed for pressures in the 10-6–10-2 bar domain, and for temperatures ranging from 50 K to 2000 K.
Results. We find that the vanadium nitride/vanadium oxide and titanium hydride/titanium oxide gas phase ratios strongly depend on the C/O ratio in the hot parts of disks (T ≥ 1000 K). Our calculations suggest that, in these regions, these ratios can be used as tracers of the C/O value in protoplanetary disks.
Key words: protoplanetary disks / stars: abundances / planets and satellites: formation / planets and satellites: composition / Sun: atmosphere
© ESO, 2013
1. Introduction
The recent detection of carbon-rich planets (CRPs), with C/O ratios ≥1 in their envelopes (Madhusudhan et al. 2011a), have stimulated research on their physical properties and the scenarios that may lead to their formation (Madhusudhan et al. 2011b; Öberg et al. 2011; Mousis et al. 2012). Carbon-rich disks have also been observed in recent years (Roberge et al. 2006) and have motivated several studies on the influence of the C/O ratio on their gas phase composition (Marboeuf et al. 2008; Johnson et al. 2012). These studies suggested that, as the C/O ratio increases in the gas phase of the disk, all the available O goes into organics, CO, CO2, and CH3OH, so that the gas phase becomes H2O-free and the remaining C is in the form of CH4, enabling formation conditions of a CRP. In the case of hot-Jupiters the determination of this ratio is possible because of the extremely high temperatures of their upper atmospheres. This ratio critically influences the relative concentrations of several spectroscopically dominant species. For example, H2O and CH4 abundances1 can vary by several orders of magnitude if C/O is modified by factors from 2 to 4 (Madhusudhan 2012).
The formation scenario of CRPs is still poorly understood, in particular when considering the recent observation of WASP 12b, a CRP orbiting a carbon-poor star, leading to the conclusion that the disk C/O ratio might be different from that of the host star (Madhusudhan et al. 2011a). The properties of the protoplanetary disk needed to form the CRP WASP 12b have been investigated by Madhusudhan et al. (2011b). These authors retrieved the composition of the protoplanetary disk from that of planetesimals accreted during the formation of WASP 12b and needed to match the observed volatile abundances in the planet’s atmosphere. They concluded that the C/O ratio of 1 observed in WASP 12b requires a substantial oxygen depletion in the disk (factor of ~0.4). The same approach was used by Mousis et al. (2012) to propose the formation of Jupiter through the accretion of condensed volatiles in the cold outer part of an oxygen-depleted primordial nebula. This scenario reproduces the measured Jovian elemental abundances at least as well as the hitherto canonical model of Jupiter formed in a disk of solar composition. The resulting O abundance in Jupiter’s envelope is then moderately enriched by a factor of ~2× solar (instead of ~7× solar) and is found to be consistent with values predicted by thermochemical models of the atmosphere. This model suggests that water ice might have been distributed inhomogeneously beyond the snowline in the primordial nebula. Alternatively, it has been proposed that the envelopes of CRPs could be formed from an oxygen-depleted gas from the nebula. In this case, the oxygen depletion would result from the water condensation and incorporation at earlier epochs in the building blocks of the planetary cores (Öberg et al. 2011). However, this scenario predicts that the abundances of carbon, nitrogen, and other ultravolatiles are solar in the envelopes of hot-Jupiters and are not found to be consistent with the supersolar abundances measured at Jupiter. Interestingly, another scenario proposed by Lodders (2004) suggests that Jupiter or CRPs could have formed in a zone of the disk where carbonaceous matter dominates, rather than water ice. All these models and observations outline a nontrivial relation between the C/O ratios of the host stars, their protoplanetary disks and, finally their planets. For this reason it is important to establish a reliable probe of this ratio.
Here we suggest that the sampling of the abundances of titanium – and vanadium – bearing minerals could allow us to probe the C/O ratio in protoplanetary disks. Titanium oxide (TiO, TiO2, etc.) and vanadium oxide (VO, VO2, etc.) are strong optical absorbers. They were first observed at optical wavelengths in M-type stars (Merrill et al. 1962). Since then, these molecules have been detected in various astrophysical environments; TiO and TiO2 have been observed at sub-millimeter wavelengths in the circumstellar envelope of VY Canis Majoris (Kamiński et al. 2013). Moreover, TiO and VO have been identified around protostars in optical emission bands (Hillenbrand et al. 2012) and also in the infrared emission spectrum of S-type star atmospheres (Smolders et al. 2012). Recently, TiO and VO have been proposed as the cause of the thermal inversions observed in several highly irradiated hot-Jupiters (Hubeny et al. 2003; Fortney et al. 2008) in which the determination of the C/O ratio is possible (Madhusudhan 2012). However, it has been found that an implausible eddy coefficient value is needed for the occurrence of the TiO/VO induced thermal inversion (Spiegel et al. 2009; Knutson et al. 2010). The effect of C/O on the abundances of TiO and VO in the atmospheres of hot-Jupiters has been investigated by Madhusudhan (2012) who found that C/O = 1 leads to severe depletions in TiO and VO in the atmospheres of CRPs. On the other hand, a recent HST observation of the hot Jupiter WASP 19b shows that this planet has no or low levels of TiO with a moderate C/O ratio, suggesting that this lack of observable TiO is possibly due to rainout or breakdown from stellar activity (Huitson et al. 2013). Another recent study also reports that all stars with TiO emission exhibit a low C/O ratio (Smolders et al. 2012). Given the similarities that exist between the atmospheres of giant planets and the gas phase of protoplanetary disks (some common temperature and pressure ranges, H2-dominated compositions, dynamical effects), the influence of the C/O ratio on Ti and V chemistries in disks deserves to be investigated.
In Sect. 2, we present the chemical model used to relate TiO and VO abundances to C/O for a large range of temperatures and pressures. Section 3 is devoted to the presentation of our major results and to their comparison with observations. Results obtained for some important volatile species are also included. Conclusions are given in Sect. 4.
2. Computing the chemistries of gas and solid phases in protoplanetary disks
To obtain the solid and gaseous composition of the disk, we use the HSC chemistry commercial package. It is based on the Gibbs energy minimization method, originally developed by White et al. (1958). In this method, the calculation of phase equilibrium is made by minimizing the Gibbs free energy of the system, at constant temperature T and pressure P, with respect to the number of moles of each component in each phase  . For a system with NP phases and NC components, we have
. For a system with NP phases and NC components, we have  (1)where
(1)where  and
and 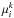 are the number of moles and the chemical potential of component i in phase k, respectively. The chemical potential is a function of the composition of phase k at temperature T and pressure P (Rossi et al. 2009). This method for equilibrium chemistry calculations assumes local thermodynamical equilibrium. Several codes, based on this approach, have been developed in the last decades. The most familiar are SOLGASMIX (Sharp & Huebner 1990), NASA’s CEA2, and the HSC Chemistry package developed by Outotec Research3. In this work we opted to use the HSC Chemistry package because its built-in database of minerals is the largest existing one. It contains, for example, ~75 Ti bearing minerals.
are the number of moles and the chemical potential of component i in phase k, respectively. The chemical potential is a function of the composition of phase k at temperature T and pressure P (Rossi et al. 2009). This method for equilibrium chemistry calculations assumes local thermodynamical equilibrium. Several codes, based on this approach, have been developed in the last decades. The most familiar are SOLGASMIX (Sharp & Huebner 1990), NASA’s CEA2, and the HSC Chemistry package developed by Outotec Research3. In this work we opted to use the HSC Chemistry package because its built-in database of minerals is the largest existing one. It contains, for example, ~75 Ti bearing minerals.
In our equilibrium calculations, usually one favors a long list of elements to get the most precise results possible, and to avoid any possible hidden nonlinear effect from an ignored molecule. For this reason, we chose to use the entire HSC Chemistry database of elements relevant to solar elemental abundances that has a total of 1224 gases and solids (excluding CnHm for n > 3). Once the initial list of elements and their respective abundances were defined (see Table 1), we selected the set of molecular species that forms from these elements (with null initial abundances). We made the reasonable assumption that the gas phase composition of the disk under study has the same elemental composition as that of the host star. Here, all our calculations are based on the solar photosphere abundances taken from Asplund et al. (2009).
Initial solar elemental abundances.
 |
Fig. 1 a) Abundances of titanium-bearing solid and gaseous compounds computed at equilibrium at a disk pressure of 10-4 bar as a function of the temperature for C/O = 0.55. Solid lines are for solid species and dashed lines for gases. b) Same as a) but for C/O = 1. c) Abundances of vanadium-bearing solid and gaseous compounds computed at equilibrium at a disk pressure of 10-4 bar as a function of the temperature for C/O = 0.55. d) Same as c) but for C/O = 1. |
3. Results
3.1. Influence of C/O on Ti and V chemistries
Figure 1 displays the abundances of solid and gaseous Ti and V bearing species, for C/O = 0.55 and 1. In order to get C/O = 1 in the gas phase of the disk, we opted to decrease the initial abundance of oxygen (Madhusudhan et al. 2011b; Mousis et al. 2012). For the sake of clarity, we just represented the abundances of species that are at most 10 times lower than the most abundant one, as more than 1000 abundances of species are simultaneously computed. All our calculations are made for a total gas pressure of 10-4 bar, which corresponds to the average pressure in the inner regions (1–2 AU) of protoplanetary disks (Hueso & Guillot 2005)4. For C/O = 0.55 and in the case of Ti chemistry, we note the dominance of the solid (s) mineral K2TiO3(s) at all temperatures except in the range 100–200 K where 4CaO3TiO(s) is the most abundant. At temperatures higher than 1600 K, we note the existence of substantial amounts of the gaseous (g) compounds TiO(g) and TiH(g). In the case of V chemistry, Na2V2O7(s) and VO(s) are the most abundant minerals at temperatures lower than ~1500 K and the gaseous compounds VO2(g), VO(g), and V(g) become dominant at higher temperatures. For C/O = 1, and in the case of Ti-bearing solids, K2TiO3(s) now dominates in the 1500–1600 K interval and also at temperatures lower than ~1200 K, except in the 100–200 K interval where 4CaO3TiO2(s) is the most abundant species; TiC(s) and TiH(g) become the most abundant solid species in the 1200–1500 K and 1650–2000 K temperature ranges, respectively. In the case of V-bearing solids, Na2V2O7(s) becomes dominant only for temperatures lower than ~800 K. Solid VO(s) now exists at temperatures centered around ~800 K and its maximum abundance is 4 times less than in the first case. At this value of C/O, we note that the abundances of gaseous VO2(g), VO(g), and TiO(g) are about one thousand times lower than in the former case, making them not visible in the panels of Fig. 1. Our calculations then suggest that Ti and V oxides present in the gas phase are orders of magnitude more abundant in the solar C/O case than in the C/O = 1 case. It should be noted that Ti and V bearing minerals have been studied in a large number of meteorites (Nittler et al. 2008; Rubin 1997; Lodders 2006; Simon et al. 2007).
Figure 2 shows the evolution of the gas phase abundances of TiO, TiH, VO, and VN computed as a function of temperature for C/O = 0.55 and 1 in the disk. The abundances of these species increase with the growth of temperature at both C/O values. One can note that the abundances of TiO and VO are significantly higher at lower C/O values and at high temperatures. On the other hand, TiH is more abundant at high C/O irrespective of temperature, and the abundance of VN only weakly depends on the C/O value.
 |
Fig. 2 Gas phase equilibrium abundances of TiO, TiH, VO, and VN computed at a disk pressure of 10-4 bar for C/O = 0.55 (dashed lines) and C/O = 1 (solid lines). |
 |
Fig. 3 VN/VO2 and TiH/TiO gas phase ratios as a function of C/O in protoplanetary disks for pressures ranging from 10-6 to 10-2 bar and for T = 1700 K. |
Figure 3b represents the VN/VO and TiH/TiO gas phase ratios computed as a function of C/O ranging between 0.1 and 10 in protoplanetary disks. As mentioned above, the C/O ratio is set to the desired value by varying the oxygen abundance. Computations have been conducted at 1700 K and at disk pressures of 10-6, 10-4, and 10-2 bar. These molecules have been selected because their abundance ratios heavily depend on the value of the adopted C/O ratio. Gaseous VN also exists in the same temperature range as VO, but its abundance is too low (by 4–5 orders of magnitude in both C/O cases) to make it visible in Fig. 1. At the considered pressures, there is a strong dependence of the VN/VO and TiH/TiO gas phase ratios with the adopted value of the C/O ratio. For example, an increase in the C/O ratio from 0.3 to 2 induces a steep increase in the TiH/TiO and VN/VO ratios by ~10 orders of magnitude at P = 10-4 bar. Between C/O = 0.1 and 0.3 and beyond C/O = 2, the two molecular ratios increase slowly.
Our calculations suggest that these ratios can be used as tracers of the C/O ratio in protoplanetary disks. It is worth mentioning that calculations similar to those presented above have been done by varying the C abundance and fixing the O abundance, i.e., the opposite approach, in order to investigate the existence of any hidden nonlinear effect. The results obtained were found to be almost identical to those presented above, with a slight increase in the abundances of C bearing species for C/O > 0.5. One should note that among the four species, VN has the lowest abundance for solar C/O, making its detection more critical than the other molecules.
3.2. Influence of the disk pressure
To quantify the effect of pressure on the Ti and V chemistries, we performed the same calculations as above but for total disk pressures in the 10-6–10-2 bar range, and for C/O = 0.55 and 1. Results for TiO, TiH, VO, and VN are presented in Fig. 4. The main conclusion is that a variation in pressure over several orders of magnitude induces some nonlinear effects on the abundances of the considered species. Although it is difficult to describe clear trends for these variations, we note that at P = 10-2 bar and for C/O = 0.55, the abundances of all four gaseous species are depleted by several orders of magnitude with respect to 10-3 bar, except for the very high temperatures (1900–2000 K). This depletion is balanced by an important increase in the abundance of solid TiO2. At the same pressure, we also note that the abundance of TiO is more important for C/O = 1 than for C/O = 0.55 at disk temperatures ≤1800 K. This last effect is also present at P ~ 10-4–10-3 bar and temperatures ≤1500 K, but is absent at 10-6 bar. At this pressure, we also note a decrease in the abundances of most species of more than two orders of magnitude at C/O = 0.55, balanced by an increase in the abundances of solid minerals (mostly FeTiO3). This decrease is restricted to the abundances of TiH and VN at C/O = 1. Figure 4 shows that the pressure variation can affect the abundances of TiO, TiH, VO, and VN, but it is not certain that a significant pressure drop can alter their detection. As mentioned below, TiO is detectable in some circumstellar environments with pressures of ~10-4 bar and the abundance of this species computed at 10-6 bar is quite close.
We also computed the TiH/TiO and VN/VO ratios as a function of pressure. The results are presented in Figs. 3a–c. The same general trend as in Fig. 3b is found for the other investigated pressures, but with some slight differences. In particular, with increasing disk pressure, the TiH/TiO and VN/VO ratios increase by 2 orders of magnitude for C/O ratios ≪1. On the other hand, the ratios will decrease by 2 orders of magnitude with increasing disk pressure for C/O ratios ≫1.
 |
Fig. 4 Abundances of gaseous TiO, TiH, VO, and VN for total disk pressures of 10-2 bar a), 10-3 bar b), 10-4 bar c), and 10-6 bar d). Solid and dashed lines represent the C/O = 1 and 0.55 cases, respectively. |
 |
Fig. 5 a) Fractional abundances of selected volatile species for C/O = 0.55 as a function of temperature. b) HCN/H2O ratio as a function of the C/O ratio. All calculations were done at P = 10-4 bar for T = 700 K. |
3.3. Comparison with observations
In this section, we are going to investigate the observability of TiO, and compare our model to observations.
Using Spitzer infrared data, Smolders et al. (2012) derived a TiO column density of ~1017.25 cm-2 in the circumstellar environment of the S star NP Aurigae at temperatures higher than 1900 K. Kamiński et al. (2013) also reported the observation of TiO and TiO2 at submillimeter wavelengths in the stellar environment of VY Canis Majoris, with column densities of ~1014 cm-2 for both species, but for T = 1000 ± 870 K. On the other hand, our calculations predict TiO abundances of ~1.0 × 10-8 and ~1.0 × 10-11 for, respectively, T ~ 1800 K and T ~ 1600 K at P ~ 10-4 bar (typical gas pressure in circumstellar environments) in the C/O = 0.5 case (see Fig. 2). For a typical scale height H ~ 5.0 × 10-3 AU, we find column densities 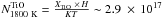 cm-2 and
cm-2 and  cm-2 for the computed TiO abundance; N1800 K is almost equal to the column density observed by Smolders et al. (2012) and N1600 K is very close to the value derived by Kamiński et al. (2013). Hence, it should be possible in principle to observe TiO in the hot inner disk. The TiO2 abundance in our calculations is about two times lower than that of TiO5 for T ~ 1600 K, a result also compatible with Kamiński et al. (2013).
cm-2 for the computed TiO abundance; N1800 K is almost equal to the column density observed by Smolders et al. (2012) and N1600 K is very close to the value derived by Kamiński et al. (2013). Hence, it should be possible in principle to observe TiO in the hot inner disk. The TiO2 abundance in our calculations is about two times lower than that of TiO5 for T ~ 1600 K, a result also compatible with Kamiński et al. (2013).
We also compared our equilibrium calculations to observations of volatile species in protoplanetary disks. To calculate the column densities, we used the one-dimensional α-disk model of Hueso & Guillot (2005) to derive the thermodynamic parameters (temperature and scale height) needed. The model follows the evolution of a cloud-disk-star system with the following initial conditions (see Hueso & Guillot (2005) for details): α = 0.01, Mcloud = 1 M⊙, Ωcloud = 3.0 × 10-14 s-1, Tcloud = 10 K, M0,star = 0.1, M⊙ and Tstar = 4000 K. We chose the model at 105 years.
Carr & Najita (2011) determined an average column density for HCN of ~6 × 1016 cm-2 at T ~ 700 K from Spitzer observations of inner regions of six different T Tauri disks. However, this value is model dependent since it is defined by Carr & Najita (2011) as the value averaged from two different (optically thin and optically thick) disk models. In the case of the optically thin disk model, these authors found N ~ 4 × 1015 cm-2, which is one order of magnitude lower than the average column density. Since HCN is observed at ~700 K, we used the disk pressure of ~10-3 bar and H = 6 × 10-2 AU as calculated using the employed disk model. The calculated HCN abundance for C/O = 0.55 is found to be ~6 × 10-11, corresponding to a column density of ~4.2 × 1014 cm-2, a value within an order of magnitude of observations for thin disks. Furthermore, we computed the abundance ratio C2H2/HCN, which is found to be ~5 × 10-5 at these disk conditions. This ratio is lower by several orders of magnitude compared to the value found by Carr & Najita (2011) (from 10-2 to 10-1). However, this important difference might be due to nonequilibrium effects (chemical kinetics, photochemistry) not taken into account in our model. For the sake of completeness, we also presented in Fig. 5a the fractional abundances with respect to H2 of some major volatiles (H2O, CO, CO2, CH4, and OH) that have been observed in disks and that are believed to be important in the planetary formation process. Another interesting observable for disk evolution and planetary formation is the HCN/H2O ratio, since Carr & Najita (2011) proposed that it is correlated to the value of the C/O ratio in T Tauri disks. In order to illustrate this correlation, we computed the HCN/H2O ratio as a function of C/O in disks. The results, displayed in Fig. 5b, show that the HCN/H2O ratio increases as a function of the C/O ratio, with a particularly sharp slope for C/O ≥ 2. Finally, it is worth mentioning that our calculations performed in the C/O = 1 case are consistent with the conclusions of Lodders (2006) who finds that TiC (observed in meteorites) is formed naturally at equilibrium under these conditions.
4. Conclusions and prospects
We have performed computations of equilibrium chemistry describing the fate of Ti- and V-bearing species in protoplanetary disks as a function of the C/O ratios, and using the Gibbs energy minimization method. This allowed us to find that the VN/VO and TiH/TiO gas phase ratios strongly depend on the degree of the C/O ratio in the hot parts of disks. Gaseous TiO and VO have been detected at optical wavelengths in the 1000–2000 K range in stellar envelopes and photospheres (Hillenbrand et al. 2012; Smolders et al. 2012) at pressure regimes very close to those encountered in the inner part of protoplanetary disks (Asplund et al. 2004).
The results presented in this study are based on equilibrium calculations. We opted to neglect the influence of photochemistry and of turbulent diffusion for the following reasons: the proposed observations will be mainly at millimeter wavelengths, probing deep in the midplane of the disk, away from the photochemically active zone of the surface. The effects of turbulent diffusion are however less straightforward. Since we did not find any kinetic data concerning the gas phase chemistries of Ti- and V-bearing species, we have not been able to quantify the quenching effects caused by the different chemical and dynamical timescales if any. Experimental studies of the kinetic properties of the Ti- and V-bearing species will be needed to investigate further these effects.
Finally, observations of gaseous TiO and VO in disks must be spatially resolved in order to eliminate any confusion from stellar emissions. Such a high resolution should be attained with the new generation submillimetter instruments such as ALMA, from which several spatially resolved observations of different types of disks have recently been reported with angular resolutions high enough to resolve the inner disks, where the molecules considered in the present work are observable (van Dishoeck & Jørgensen 2008; Krumholz et al. 2007). However, the midplane of the inner disk might be inaccessible to these instruments if dust extinction is significant at submm/mm wavelengths. Observations of TiO emission in the 10 micron spectral region from circumstellar environments around AGB stars will be more sensitive (by one order of magnitude6), and with higher spatial resolution than those of Spitzer. Detection of a better upper limit by the James Webb Space Telescope (JWST) of TiO2 and other titanium oxides not seen by Spitzer (Smolders et al. 2012) will allow testing of the chemical calculations presented here. The detection of TiO and TiO2 in the cooler region of late-type stars implies that other small transition metal–bearing molecules such as VO, might be found with sensitive interferometers in the submillimeter wave band (Kamiński et al. 2013). It is interesting to note that one might prefer the VN/VO2 ratio over the one we chose above, since the VO2 molecule exists in gaseous form at relatively lower temperatures than VO (VO2 peaks at 1600 K, VO at 1850 K; see panel c of Fig. 1), and thus farther in the disk from the host star, a feature that might allow the region to be better resolved, decreasing the chance of stellar contamination.
The reason why it is not visible in Fig. 1.
Acknowledgments
We thank an anonymous referee for his useful comments that helped us in improving our manuscript. M.A.D. acknowledges support by a grant from the city of Besançon. O. Mousis acknowledges support from CNES. J.I.L. acknowledges support from the JWST program through a grant from NASA Goddard. We thank T. Guillot and R. Hueso for having provided us with their accretion disk model. We thank A. Rajpurohit for his useful comments on stellar temperatures.
References
- Asplund, M., Grevesse, N., Sauval, A. J., Allen de Prieto, C., & Kiselman, D. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, J. S., & Najita, J. R. 2011, ApJ, 733, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Croat, T. K., Bernatowicz, T., Amari, S., Messenger, S., & Stadermann, F. J. 2003, Geochim. Cosmochim. Acta, 67, 4705 [NASA ADS] [CrossRef] [Google Scholar]
- Cyr, K. E., Sears, W. D., & Lunine, J. I. 1998, Icarus, 135, 537 [NASA ADS] [CrossRef] [Google Scholar]
- De Marco, O., Crowther, P. A., Barlow, M. J., Clayton, G. C., & de Koter, A. 2001, MNRAS, 328, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., & Hueso, R. 2006, MNRAS, 367, L47 [CrossRef] [Google Scholar]
- Harrington, J., & Weisshaar, J. C. 1992, J. Chem. Phys., 97, 2809 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., Knapp, G. R., Padgett, D. L., Rebull, L. M., & McGehee, P. M. 2012, AJ, 143, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Hrivnak, B. J., Lu, W., Maupin, R. E., & Spitzbart, B. D. 2010, ApJ, 709, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., Burrows, A., & Sudarsky, D. 2003, ApJ, 594, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Hueso, R., & Guillot, T. 2005, A&A, 442, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huitson, C. M., Sing, D. K., Pont, F., et al. 2013, MNRAS, 434, 3252 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, T. V., Mousis, O., Lunine, J. I., & Madhusudhan, N. 2012, ApJ, 757, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Kamiński, T., Gottlieb, C. A., Menten, K. M., et al. 2013, A&A, 551, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knutson, H. A., Howard, A. W., & Isaacson, H. 2010, ApJ, 720, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Klein, R. I., & McKee, C. F. 2007, ApJ, 665, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2004, ApJ, 611, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2006, ApJ, 647, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N. 2012, ApJ, 758, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., Harrington, J., Stevenson, K. B., et al. 2011a, Nature, 469, 64 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Madhusudhan, N., Mousis, O., Johnson, T. V., & Lunine, J. I. 2011b, ApJ, 743, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Marboeuf, U., Mousis, O., Ehrenreich, D., et al. 2008, ApJ, 681, 1624 [NASA ADS] [CrossRef] [Google Scholar]
- Merrill, P. W., Deutsch, A. J., & Keenan, P. C. 1962, ApJ, 136, 21 [Google Scholar]
- Mousis, O., Lunine, J. I., Madhusudhan, N., & Johnson, T. V. 2012, ApJ, 751, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Nittler, L. R., Alexander, C. M. O., Gallino, R., et al. 2008, ApJ, 682, 1450 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Murray-Clay, R., & Bergin, E. A. 2011, ApJ, 743, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Ramirez, R. 2011, IAU Symp., 280, 188 [NASA ADS] [Google Scholar]
- Roberge, A., Feldman, P. D., Weinberger, A. J., Deleuil, M., & Bouret, J.-C. 2006, Nature, 441, 724 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rossi, L., Cardozo-Filho, R., & Guirardello 2009, Fluid Phase Equilib., 278, 117 [CrossRef] [Google Scholar]
- Rubin, A. E. 1997, Meteor. Planet. Sci., 32, 231 [Google Scholar]
- Sappey, A. D., Eiden, G., Harrington, J. E., & Weisshaar, J. C. 1989, J. Chem. Phys., 90, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., & Wiebe, D. 2011, ApJS, 196, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Sharp, C. M., & Huebner, W. F. 1990, ApJS, 72, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, S. B., Sutton, S. R., & Grossman, L. 2007, Geochim. Cosmochim. Acta, 71, 3098 [NASA ADS] [CrossRef] [Google Scholar]
- Smolders, K., Verhoelst, T., Neyskens, P., et al. 2012, A&A, 543, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spiegel, D. S., Silverio, K., & Burrows, A. 2009, ApJ, 699, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., & Jørgensen, J. K. 2008, Ap&SS, 313, 15 [NASA ADS] [CrossRef] [Google Scholar]
- White, W. B., Johnson, S. M., & Dantzig, G. B. 1958, J. Chem. Phys., 28, 751 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 a) Abundances of titanium-bearing solid and gaseous compounds computed at equilibrium at a disk pressure of 10-4 bar as a function of the temperature for C/O = 0.55. Solid lines are for solid species and dashed lines for gases. b) Same as a) but for C/O = 1. c) Abundances of vanadium-bearing solid and gaseous compounds computed at equilibrium at a disk pressure of 10-4 bar as a function of the temperature for C/O = 0.55. d) Same as c) but for C/O = 1. |
| In the text | |
 |
Fig. 2 Gas phase equilibrium abundances of TiO, TiH, VO, and VN computed at a disk pressure of 10-4 bar for C/O = 0.55 (dashed lines) and C/O = 1 (solid lines). |
| In the text | |
 |
Fig. 3 VN/VO2 and TiH/TiO gas phase ratios as a function of C/O in protoplanetary disks for pressures ranging from 10-6 to 10-2 bar and for T = 1700 K. |
| In the text | |
 |
Fig. 4 Abundances of gaseous TiO, TiH, VO, and VN for total disk pressures of 10-2 bar a), 10-3 bar b), 10-4 bar c), and 10-6 bar d). Solid and dashed lines represent the C/O = 1 and 0.55 cases, respectively. |
| In the text | |
 |
Fig. 5 a) Fractional abundances of selected volatile species for C/O = 0.55 as a function of temperature. b) HCN/H2O ratio as a function of the C/O ratio. All calculations were done at P = 10-4 bar for T = 700 K. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


