| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A11 | |
| Number of page(s) | 10 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201321177 | |
| Published online | 17 December 2013 | |
On the disruption of pulsar and X-ray binaries in globular clusters
1
Department of Astrophysics/IMAPPRadboud University Nijmegen,
PO Box 9010,
6500 GL
Nijmegen,
The Netherlands
e-mail:
F.Verbunt@astro.ru.nl
2
SRON Netherlands Institute for Space Research,
Utrecht, The
Netherlands
3
Max-Planck-Institut für Radioastronomie,
auf dem Hügel 69, 53121
Bonn,
Germany
e-mail:
pfreire@mpifr-bonn.mpg.de
Received: 28 January 2013
Accepted: 17 October 2013
The stellar encounter rate Γ has been shown to be strongly correlated with the number of X-ray binaries in globular clusters (GCs) and also to the number of radio pulsars. However, the pulsar populations in different GCs show remarkably different characteristics: in some GCs the population is dominated by binary systems, in others by single pulsars and exotic systems that result from exchange encounters. In this paper, we describe a second dynamical parameter for GCs, the encounter rate for a single binary, γ. We find that this parameter provides a good characterization of the differences between the pulsar populations of different GCs. The higher γ is for any particular GC, the more isolated pulsars and products of exchange interactions are observed. Furthermore, we also find that slow and “young” pulsars are found almost exclusively in clusters with a high γ; this suggests that these kinds of objects are formed by the disruption of X-ray binaries, thus halting the recycling of a previously dead neutron star. We discuss the implications of this for the nature of young pulsars and for the formation of neutron stars in GCs.
Key words: globular clusters: general / stars: neutron / pulsars: general
© ESO, 2013
1. Introduction
Millisecond pulsars (MSPs), also known as recycled pulsars, are the progeny of X-ray binaries in which a neutron star (NS) accretes matter from a companion (as reviewed by e.g. Phinney & Kulkarni 1994; Stairs 2004). Since X-ray binaries are overabundant in GCs with respect to the Galactic disc (as reviewed by e.g. Heinke 2011), it was predicted that MSPs would be present in GCs (Fabian et al. 1983). This prediction has been abundantly verified by the observations.
Close encounters between stars and/or binaries are much more frequent in GCs than in the Galactic disc (Hills 1975), and this is thought to be the cause of the overabundance of X-ray binaries in GCs (Clark 1975). In early publications, three types of encounter were suggested to bring a NS into a binary: direct collision with a giant, tidal capture, and exchange encounters (Sutantyo 1975; Fabian et al. 1975; Hills 1976). We will refer to these as primary encounters. The numbers of NSs were estimated from an assumed initial mass function, e.g. Salpeter’s, the parameters of which were determined from the number counts of the main-sequence stars, adapting the method devised (for white dwarfs) by Tinsley (1968); or by proxy from the central surface brightness with an assumed mass-to-light ratio. The rate of each type of encounter roughly scales with the encounter number Γ (Verbunt & Hut 1987): 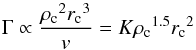 (1)where ρc and rc are the density and radius of the cluster core, v is the velocity dispersion, and K a constant. From the virial theorem
(1)where ρc and rc are the density and radius of the cluster core, v is the velocity dispersion, and K a constant. From the virial theorem  . The encounter number Γ has been fairly successful in describing the numbers of X-ray binaries, both bright and quiescent (Pooley et al. 2006; Heinke et al. 2006), and the numbers of MSPs (Johnston et al. 1992). When the number of radio pulsars is estimated from a luminosity function, however, results for a correlation with the encounter number are mixed (Hui et al. 2010; cf. Bagchi et al. 2011). Bahramian et al. (2013) make an effort to compute more accurate values for Γ from photometric cluster profiles, which enables them to treat core-collapsed clusters in the same manner as other clusters, and conclude that the correlations between numbers of X-ray and radio sources with Γ are, in fact, strong. Interestingly, they find that core-collapsed clusters may contain fewer X-ray sources than predicted by their Γ values.
. The encounter number Γ has been fairly successful in describing the numbers of X-ray binaries, both bright and quiescent (Pooley et al. 2006; Heinke et al. 2006), and the numbers of MSPs (Johnston et al. 1992). When the number of radio pulsars is estimated from a luminosity function, however, results for a correlation with the encounter number are mixed (Hui et al. 2010; cf. Bagchi et al. 2011). Bahramian et al. (2013) make an effort to compute more accurate values for Γ from photometric cluster profiles, which enables them to treat core-collapsed clusters in the same manner as other clusters, and conclude that the correlations between numbers of X-ray and radio sources with Γ are, in fact, strong. Interestingly, they find that core-collapsed clusters may contain fewer X-ray sources than predicted by their Γ values.
The successful use of Γ should not obscure the fact that there are many aspects of the formation of X-ray binaries and their possible evolution into MSPs which Γ does not describe. Examples are the differences between clusters in the slope of the initial mass function, in the properties of the binary population, in the fraction of stars lost from the cluster, and in the retention fraction of NSs. In addition, the importance of encounters subsequent to the primary encounters is not taken into account by Γ. We will refer to such subsequent encounters as secondary encounters. To investigate the importance of these aspects, detailed numerical calculations have been made by e.g., Sigurdsson & Phinney (1995) and Ivanova et al. (2008).
Sigurdsson & Phinney (1995) assumed that 10% of the NSs are born with velocity low enough to remain in the cluster. They consider stationary, albeit evolved, GCs. Their calculations show that collisions with low-mass stars are important only in low-density clusters; for clusters with increasing central density the encounters are dominated more and more by the more massive stars, including the NSs, that fully dominate the encounters in a model with a central density similar to that of M 15. Secondary encounters in high-density clusters ionize low-mass binary pulsars to produce a population of single pulsars. Other single NSs and NSs with a companion of very low mass are produced by direct collisions in high-density clusters between main-sequence stars and NSs (as originally suggested by Krolik et al. 1984). Such direct collisions occur also in three-body encounters between a NS and a binary and in four-body encounters – i.e. the encounter between two binaries (e.g. Bacon et al. 1996; Fregeau et al. 2004). In the model for the high-density cluster discussed by Sigurdsson & Phinney (1995), for example, a NS involved in a three-body encounter merges with both other stars involved. If this NS accretes enough material from the remnants of the merger stars, it may become a single MSP.
Ivanova et al. (2008) allow the clusters to evolve. Importantly, Ivanova et al. assume that NSs due to core collapse are born with high velocities (based on Hobbs et al. 2005), so that only a tiny fraction of them is retained. The NS population in GCs in their calculations are dominated by those formed in electron-capture supernovae, which are assumed to be born with velocities ten times lower (see Podsiadlowski et al. 2004). Electron capture may occur in single stars, but may also be induced by accretion in a merger of two white dwarfs (WDs), or in a binary. In the latter case the low velocity enhances the probability that the newly formed NS remain in the binary. A result of these new channels for the formation of a NS is an increased importance and bewildering variety of secondary encounters, as graphically illustrated in Fig. 1 of Ivanova et al. (2008). Ivanova et al. (2008) find that most low-mass X-ray binaries are formed by such accretion-induced collapse in low-density clusters, whereas in high-density clusters binary exchange, collisions with giants and tidal capture together also contribute significantly (some 50%) to the formation of low-mass X-ray binaries. NSs formed by accretion-induced collapse probably are not spun-up to MSPs in the same binary, but by companions obtained after secondary encounters. In high-density clusters single MSPs arise from NSs that merge with a main-sequence donor, or by ionization in an exchange encounter. The fraction of single MSPs increases with the density of the cluster, reaching 70% in the densest models considered.
The description in the previous two paragraphs cannot do full justice to the complexity of the numerical calculations. Even so, major uncertainties remain, as may be illustrated by two examples. The life time of a low-mass X-ray binaries is determined among others by the loss of mass and angular momentum from the binary, both of which are essentialy unknown. The susceptibility of a binary to secondary encounters scales directly with its life time. An uncertainty by a factor ten in the life time of the binary translates into a major uncertainty in the importance for its evolution of secondary encounters. The velocity distribution of newly born NSs must have a low-velocity component, but the size and form of this component is not much constrained by the observations due to significant measurement uncertainties (Hartman 1997; Brisken et al. 2002). To what extent this low-velocity component is dominated by NSs formed via electron-capture is equally unknown. The importance of this question is illustrated if we juxtapose the conclusion from Sigurdsson & Phinney (1995): “We do not find it necessary to invoke AIC to account for any globular cluster MSP formation” to the one by Ivanova et al. (2008): “To reproduce the empirically derived formation rate of LMXBs we must assume that NSs can be formed via electron-capture supernovae”.
 |
Fig. 1 Central density ρc as a function of core radius rc for clusters with ρc > 2000 L⊙/pc3 (Harris 1996, update of 2010), with lines of constant Γ (blue) and constant γ (red). Letter labels refer to clusters in Table 1, coloured red if Ns > Nb, blue if Nb > Ns, and yellow if Nb ≃ Ns. Clusters with products of secondary interactions include i) and g), and – indicated in black, with numerical labels – 1: NGC 1851, 2: NGC 6342, 3: NGC 6397 and 4: NGC 6544. |
In this our paper we take a closer look at the observed properties of MSPs in GCs, to see whether they provide clues to the importance and nature of secondary encounters. We do so on the basis of the single-binary encounter rate γ. In Sect. 2 we explain this number and show that it correlates well with the ratio of the number of single pulsars to the number of pulsars in a binary (Sect. 2.1) and that binary systems that resulted from exchange encounters occur mostly in GCs with high γ (Sect. 2.4). In Sect. 3 we analyse the spin period distribution for several GCs, and discuss the occurrence of slow (Sect. 3.1) and young, high-B field (Sect. 3.2) pulsars in different clusters. Unlike the previous section, which just discusses binary disruption in general, this section discusses objects that are more likely to be produced by the disruption of X-ray binaries and the resulting truncation of the spin-up and field “burial” processes. A discussion of our results is given in Sect. 4, in particular regarding the implications for the origin of NSs in GCs, their formation rates and their relation to the young pulsars observed in GCs.
2. The single-binary encounter rate
Those pulsars in GCs that are recycled by accretion from a binary companion, are in binaries with the donor remnants, in particular low-mass WDs. As explained above, their formation rate scales roughly with the encounter rate Γ of the cluster. However, once a binary exists, it may undergo subsequent encounters. Analogously to Eq. (1) one may estimate the encounter rate for one object, e.g. a binary, as (Verbunt 2003): 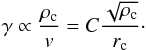 (2)If one considers the cross section for a specific type of encounter, the expected life time of the binary until the encounter may be written
(2)If one considers the cross section for a specific type of encounter, the expected life time of the binary until the encounter may be written 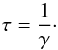 (3)In clusters with a high value of γ, binaries are prone to encounters that increase their average orbital eccentricities and increase their chances of being disrupted, leading either to the formation of single pulsars or the replacement of the companion of a recycled NS with another star (an “exchange encounter”). We investigate the results of such encounters in the following sub-sections.
(3)In clusters with a high value of γ, binaries are prone to encounters that increase their average orbital eccentricities and increase their chances of being disrupted, leading either to the formation of single pulsars or the replacement of the companion of a recycled NS with another star (an “exchange encounter”). We investigate the results of such encounters in the following sub-sections.
Structural parameters and numbers of single and binary pulsars of globular clusters with three or more pulsars.
2.1. Fractions of isolated pulsars in globular clusters
In Fig. 1 we show the central density as a function of core radius for clusters with ρc > 2000 L⊙/pc3. In the figure we indicate lines of constant collision number Γ and lines of constant single-binary disruption rate γ, normalizing both on the values for the GC M 4 to eliminate the constants K and C from Eqs. (1) and (2). The central density is expressed in solar luminosity per cubic parsec, and in plotting Γ and γ we implicity assume that the mass density scales linearly with the luminosity density. In clusters with high γ, we expect a relatively short life time of a binary before it is disrupted or undergoing an exchange (depending also on its size, i.e. semi-major axis), and thus expect a relatively high fraction of the pulsars to be released from the binary in which it was spun up, and thus a high fraction of single pulsars (Sigurdsson & Phinney 1995). Single pulsars are also formed by merging with a main-sequence donor, according to Ivanova et al. (2008), who also predict a larger fraction of single pulsars in high-density clusters.
To see whether these predictions are supported by observations, we list in Table 1 some parameters for all GCs in which three or more pulsars have been detected. In addition to the central density, core radius and (normalized) single-binary disruption rate we list the numbers of single pulsars Ns, and of pulsars in a binary Nb. We have ordered the clusters on γ, and it is seen that the clusters in which Ns > Nb are at the top of the table, and those in which Nb > Ns at the bottom.
For most individual clusters the numbers are too small for significant conclusions. To illustrate this we test the null hypothesis that the probability for a pulsar to be single is the same for all clusters and equal to the observed fraction of single pulsars for all clusters listed in Table 1 combined: p = 58/(58 + 67) = 0.464. For each cluster we compute the probability Qs that the observed number or more of single pulsars are found; and the probability Qb that the observed number or more of pulsars in a binary are found, given the above value of p and the total number of pulsars observed in that cluster, with use of binomial statistics. Only two significant (>2σ) deviations from the null hypothesis are found: Qs = 0.022 for NGC 7078, and Qb = 0.024 for NGC 6266.
Collectively, however, the differences between the clusters with highest and lowest values of γ are very significant. For the four clusters with the highest γ together, Qs is 0.0015; for the four (three) clusters with the lowest γ together Qb is 0.0029 (0.015). This is further illustrated in Fig. 1 where the clusters with Ns > Nb are indicated in red, those with Nb > Ns in blue, and those with Ns ≃ Nb in yellow.
Given that many of the caveats made in Sect. 1 for the use of Γ apply equally to the use of γ, the overall correlation of the fraction of single pulsars with γ is remarkable. NGC 7078 is an exception. We wish to make two remarks concerning this. First, NGC 7078 is the only cluster, to our knowledge, for which a pulsar search was made by performing a very long fast Fourier transform after stacking data from several days. This method is only sensitive for single pulsars, and found several very faint pulsars (Anderson 1993). Thus the number of single pulsars is biased in NGC 7078. (In contrast, a search on stacked data sets of up to 6 h of 47 Tuc did not discover new pulsars; Knight 2007.) The second remark is that NGC 7078 illustrates another complication in the use of Γ and γ: the uncertain values of the cluster parameters. Many values for the core radius have been published. Those based on HST imaging yield small estimates of rc: 2 2 (Lauer et al. 1991), <1′′ (Guhathakurta et al. 1996), 1
2 (Lauer et al. 1991), <1′′ (Guhathakurta et al. 1996), 1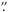 78 (Dull et al. 1997), <1
78 (Dull et al. 1997), <1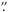 3 (Sosin & King 1997), 4
3 (Sosin & King 1997), 4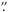 07 (Noyola & Gebhardt 2006); such values would yield a much higher values γ and smaller value of Γ for this GC. The compilation we use, Harris (1996, updated 2010), gives 014, the average of the values in Trager et al. (1995) and in Lehmann & Scholz (1997), both of which are based on ground-based imaging.
07 (Noyola & Gebhardt 2006); such values would yield a much higher values γ and smaller value of Γ for this GC. The compilation we use, Harris (1996, updated 2010), gives 014, the average of the values in Trager et al. (1995) and in Lehmann & Scholz (1997), both of which are based on ground-based imaging.
Clusters that show no clear flattening in the central light distribution, as measured with ground-based telescopes, have traditionally been classified as “core-collapsed”. Since clusters just before core collapse may observationally be very similar to clusters just after core collapse (e.g. Trenti et al. 2010), the classification “core-collapsed” is perhaps best interpreted as reflecting a very small core, and thus probably a high γ. In this view, it is remarkable that all clusters in Table 1 that have more single than binary pulsars are classified as core-collapsed.
Figure 4 shows the pulse period as a function of γ for all GCs, including those in which only one or two pulsars are found. This plot shows 60 single pulsars and 84 binary pulsars. In clusters with low γ (γ < 3γM4) we find 5 single pulsars and 20 pulsars in a binary; taking the probability for a pulsar to be single as 60/(60+84), we find Qb = 0.02. In clusters with high γ (γ > 16γM4) we find 15 single pulsars and 9 pulsars in a binary; for these clusters Qs = 0.03. Our conclusion that high-γ clusters are more likely to hold single pulsars thus holds when we consider all known pulsars in clusters.
 |
Fig. 2 Angular offsets of the pulsars with published timing solutions from the centres of their clusters, in core radii. The larger the encounter rate per binary γ, the larger are the odds of finding pulsars far from the centres of their clusters. Some of the clusters are labelled as in Table 1, colours are used to discriminate isolated and binary pulsars, and symbols to indicate the companion mass. Binaries created by exchange products are shown light blue. The dashed line indicates a distance of 4 core radii. |
2.2. Dynamical state of the pulsar populations in globular clusters
Whenever a pulsar is involved in an exchange encounter, it suffers a kick, no matter whether it finds itself in a binary or in isolation. This can unbind the pulsar (or binary pulsar) from the cluster, or give it a highly elliptical orbit about its centre (Phinney 1992, and references therein). If it still remains bound by the cluster, then with time it will interact with other cluster stars (generally lighter) and gradually lose kinetic energy to them (a phenomenon known as “dynamical friction”), therefore returning to the core of the cluster, where most pulsars are found in a state often described as of relaxed equilibrium – which means that the average kinetic energy of all stellar species there are very similar, and therefore their radial distributions have no tendency to change.
Indeed, the latter state is what is found for all GCs with a low γ, where all pulsars are within 4 core radii of the centre (see Fig. 2). The pulsar distribution in 47 Tuc, which is thought to be relaxed, is also limited to within this radius. As γ increases, we start seeing pulsars at much larger distances from the centres of their clusters. These have been involved in strong dynamical interactions in the relatively recent past and had yet no time to sink back to the core of the cluster through dynamical friction. The exclusive presence of distant pulsars in high-γ clusters is consistent with the idea that these large positional offsets really are the result of binary disruption and exchange interactions.
2.3. Eccentricities
Initially circular binaries may be made eccentric by a mild encounter with a third star, and the eccentricity of non-circular binaries generally increases when mild encounters occur (e.g. Rasio & Heggie 1995). Indeed, the dissolution of a binary discussed in Sect. 2.1 may be considered as the inducing of an eccentricity larger than unity. The probability of an encounter scales linearly with the semi-major axis of the binary, or in terms of Eq. (2): γ ∝ a. The induced eccentricity has a stronger dependence on the semi-major axis, or more precisely on the ratio of the semi-major axis and the closest approach rp of the third body; in particular for rp ≫ a it scales with (a/rp)5/2 for a circular orbit and with (a/rp)3/2 for an already eccentric orbit (Heggie & Rasio 1996).
Collisions between a NS and a giant may directly produce an eccentric binary of a NS and WD, with orbital periods less than a day (Ivanova et al. 2005).
In Fig. 3 we plot the orbital eccentricities of cluster pulsars as a function of their binary periods. Pulsars in binaries with orbital periods less than a day may have evolved from binaries with main-sequence companions, or from binaries with WD donors that were acquired by the NS as it collided with a giant. For most of these only upper limits to the eccentricity are known. This agrees with the fact that short-period binaries have small probabilities of engaging in a secondary encounter.
The orbital periods (≳1 d) and companions masses (0.1–0.44 M⊙) of many of the systems shown in Fig. 3 indicate an origin from a binary with a (sub)giant donor. From the fluctuation-dissipation theorem such binaries – when unperturbed – have expectation values for the eccentricity given by (Phinney 1992): 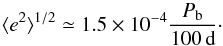 (4)For binary radio pulsars in the Galactic disc, shown in Fig. 3 as gray dots, this relation holds quite well. In globular clusters, the eccentricities of all binary radio pulsars with companion masses 0.1–0.44 M⊙ are larger, which indicates that all of them have had eccentricity-enhancing secondary encounters with third stars.
(4)For binary radio pulsars in the Galactic disc, shown in Fig. 3 as gray dots, this relation holds quite well. In globular clusters, the eccentricities of all binary radio pulsars with companion masses 0.1–0.44 M⊙ are larger, which indicates that all of them have had eccentricity-enhancing secondary encounters with third stars.
For binary pulsars in GCs with intermediate and high γ (shown black and red in the figure) the orbits with periods longer than about a day are concentrated in Fig. 3 towards higher eccentricities. These binaries may have experienced several eccentricity-enhancing secondary encounters, which indicates that encounters leading to eccentricities larger than 1, i.e. unbinding the pulsar, are not uncommon.
Several of the pulsars in orbits with high eccentricities have companions with masses 0.45 ≤ Mc/M⊙ ≲ 1.0. These companions are possibly carbon-oxygen WDs, evolved from donors on the asymptotic giant branch. This evolution leaves a wide binary, initially with very small eccentricity, but highly susceptible to eccentricity-enhancing secondary encounters.
 |
Fig. 3 Eccentricity as a function of orbital period for binary radio pulsars in globular clusters. Colours are used to indicate γ of the cluster in which the pulsar resides, symbols to indicate the companion mass. For the outcome of recycling by a (sub)giant donor one expects Pb ≳ 1 d and 0.1 < Mc/M⊙ < 0.44; such systems in the Galactic disc are shown in gray, and the expectation values for the eccentricity according to Eq. (4) and ten times this value, are shown as dotted lines. Eccentricies 0.0, for which no upper limits have been specified, are shown at the bottom (with smaller symbols to avoid overlap). Data from http://www.naic.edu/~pfreire/GCpsr.html |
2.4. Exchange encounters
Carbon-oxygen WDs or NSs can also become companions to pulsars via an alternative route: having formed from a single star, they subsequently replaced a lower-mass WD companion to the pulsar in an exchange encounter. Companions in GCs with masses Mc ≳ M⊙ certainly entered the binary with the NS in an exchange encounter, irrespective of whether they are high-mass WDs or NSs. They are indicated in Fig. 3 with a star. One of the striking features of this Figure is that all such massive companions have very eccentric orbits, as one would expect from exchange encounters.
We now discuss these products of exchange encounters. PSR J1807−2500B in NGC 6544 (Lynch et al. 2012) has a massive (Mc = 1.2064(20) M⊙) companion, which is either a massive WD or a light NS, in a highly eccentric (e = 0.75) orbit with a period close to ten days. Whatever the companion is, its progenitor was too massive and too short lived to recycle the pulsar to its present spin period of 4.15 ms. This implies that the pulsar was recycled in a binary formed in a primary encounter, and that its current companion exchanged into the binary in a secondary encounter, in which the first companion of the NS was expelled. As discussed above, the probability of a secondary encounter does not depend on Γ, only on γ. NGC 6544 in fact has the highest single-binary encounter rate, γ = 276γM4, of all clusters containing a pulsar.
Another example of a secondary exchange interaction is PSR B2127+11C, in NGC 7078 = M15 (Anderson et al. 1990), a 30.5-ms pulsar in a tight (8.0 h), eccentric (e = 0.68) orbit with a NS. Timing this pulsar, Prince et al. (1991) derived a characteristic age of about 0.1 Gyr (this is little affected by the acceleration of the binary in the potential of M15). Although the system superficially resembles the first binary pulsar, B1913+16 (see Weisberg et al. 2010 and references therein), the progenitor of its massive companion could not have recycled the pulsar 0.1 Gyr ago – at that time there were no such massive stars in the cluster. The system must have therefore formed through one or more exchange interactions (Prince et al. 1991). The pulsar is found quite far from the cluster centre, again consistent with an exchange interaction and associated recoil (Sect. 2.2). As discussed above, M15 has an intermediate value of γ (see Table 1).
The third clear example of an exchange encounter is PSR J0514−4002A, in NGC 1851 (Freire et al. 2004); this is the most eccentric binary pulsar in all GCs and it also has a massive companion (Freire et al. 2007), which again might be a massive WD or a very light NS (or even the core of a giant star, which might explain the anomalous presence of diffuse gas in the system). NGC 1851 has an intermediate single-binary encounter rate, γ = 12.4γM4.
An exchange encounter may also result in a pulsar acquiring a normal main-sequence star companion. An example of this is another remarkable binary, PSR B1718−19 in NGC 6342 (Lyne et al. 1993). The pulsar has a relatively young characteristic age, with a spin period of 1 s, and is orbited every 6.2 h by a non-degenerate star (van Kerkwijk et al. 2000). This secondary is likely to have replaced the pulsar’s previous companion in a secondary exchange encounter; the system’s position, far from the cluster centre, offers further support of this hypothesis (Sect. 2.2). The short binary period has enabled the non-degenerate star to reduce the eccentricity, which is observed to be small: e < 0.0051. NGC 6342 has a single-binary encounter rate γ = 28γM4 = 28.
A final example of this is PSR J1740−5340 (D’Amico et al. 2001a,b) in NGC 6397, the cluster with the second highest γ among all in the Galaxy. The pulsar has a spin period of 3.65 ms; its companion is a bloated, optically bright star (Ferraro et al. 2001). The system is at least 20 core radii from the cluster centre, which again suggests a large recoil produced by an exchange encounter.
The resulting pattern is very clear: only clusters with intermediate or high encounter rates per binary (γ) host pulsar binaries formed in secondary exchange encounters.
3. Pulse period distributions and incidence of young pulsars with strong magnetic fields
 |
Fig. 4 Pulse periods as function of single-binary disruption rate γ. Some of the clusters are labelled as in Table 1, colours are used to discriminate isolated and binary pulsars, and symbols to indicate the companion mass. Binaries created by exchange products are shown in light blue. The horizontal dotted lines indicate pulse periods of 0.15 and 0.015 s. |
A striking result from the previous Section is that all pulsar binaries with Pb ≳ 1 d have had an encounter that significantly enhanced their eccentricity. This encounter can have happened during the phase of mass transfer, as the NS was being spun up, or after cessation of the mass transfer. Three time scales are involved: the duration of the mass transfer phase, the time passed since the cessation of the mass transfer during which the NS is a recycled radio pulsar, and the waiting time for an encounter given by Eq. (3). In clusters with a very low γ, a binary is expected to complete its mass-transfer phase and remain unperturbed; from Fig. 3 we see that no pulsars have been found in wide, unperturbed binaries, presumably because clusters with very low central density have very low Γ as well, and thus are unlikely to harbour any recycled pulsar. Clusters with a somewhat higher γ will allow completion of the mass-transfer phase for most systems, and induce the eccentricity only afterwards. In clusters with an even higher γ the mass transfer is liable to disruption, either permanently or temporarily, by a close encounter, in particular in systems with wide orbits.
Can we discriminate between systems that had their encounter during or after the mass-transfer phases? During the mass-transfer phase the NS is being spun up and its magnetic field is being reduced. Systems in which mass transfer has been disrupted by an encounter may therefore be expected to have, on average, longer pulse periods and stronger magnetic fields. The characteristic age of the pulsars in such systems reflects the time passed since the interaction, which may be much smaller than the age of the cluster.
3.1. Pulse periods
In Fig. 4 we display the spin periods of the pulsars in GCs as a function of the single-binary disruption rate γ. It is apparent that the pulsar populations in different GCs have different spin period distributions. This is not caused by observational biases. First, there is generally no bias against the detection of slow pulsars, which could be detected for all GCs but are only detected in some. There are biases against the detection of fast pulsars, but they have been largely overcome in recent years. As an example, until recently the pulsars in Terzan 5 had the highest dispersion measures (DMs) among all known MSPs (~240 cm-3 pc), which precluded the detection of fast MSPs. However, improvements in instrumentation now allow the detection of pulsars with very fast spin periods (Ransom et al. 2005), including the fastest known, PSR J1748−2446ad (Hessels et al. 2006), even for such high DMs.
This means that we can now have a very good idea of the spin period distribution in GCs, particularly when several GCs are surveyed with consistent observational setups. Hessels et al. (2007) observed many of the GCs within the Arecibo declination range with a very high time resolution. Although they discovered fast-spinning pulsars in M3, M5, M13, M71 and NGC 6749 they did not find any new fast-spinning pulsars in M15, which has significantly smaller dispersive smearing than M71 and NGC 6749. Such bright, fast-spinning pulsars would have eluded previous 430 MHz surveys surveys but should be easily detectable in this survey. This means that the relatively small fraction of fast-spinning pulsars in M15 is a real effect, not a selection effect.
In Fig. 4 we see that short pulse periods are observed at all values of γ. However, the pulsars with pulse periods in the intermediate range of 0.015–0.15 s are observed mostly at intermediate values of γ, and those with pulse periods longer than 0.15 s at intermediate to high values of γ. Of the 19 pulsars with pulse periods above 0.015 s, 9 are single. Two pulsars in this period range are in clusters with low γ. The distribution of intermediate pulse periods forms a bridge between the shortest pulse periods and the longest pulse periods, which suggests that the latter are the tail of a continuous distribution rather than a separate group.
Figure 4 suggests the following scheme for the spin-up of pulsars in GCs. In clusters with low γ X-ray binaries of all periods mostly live long enough for their NSs to be spun up to MSPs. In clusters with intermediate γ the binaries with short periods live long enough for full spin-up to occur, but some binaries with long orbital periods can be disrupted or changed in such a way that mass transfer stops, leaving pulsars with intermediate pulse periods, either isolated (in the first case) or in a binary (in the second case). Finally, in clusters with high γ only short-period binaries live long enough for spin-up to short periods to be completed, and long-period binaries tend to be disrupted before much spin-up has occurred, hence the presence of pulsars with large spin periods there. The prevalence of single pulsars in high-γ clusters indicates that even binaries with extended periods of mass transfer are eventually disrupted, either during the X-ray binary phase or later as binary MSPs, as discussed in Sect. 2.
This scenario explains very well the result of Hessels et al. (2007) that there are many fast pulsars in M3, M5 and M13, and slower pulsars in M15: the former clusters have low γ. However, γ cannot be the whole story. The GC M 53 has γ = 0.21γM4, but the pulsar in it has a pulse period of 0.033 s. The orbital period of this pulsar is the longest one observed in a GC, 255.8 d, with a companion mass of 0.35 M⊙. When mass transfer started in the progenitor binary, the giant was already close to the tip of the giant branch, and rapidly expanding. Its envelope may have been transferred quickly and at super-Eddington rate, leading to inefficient spin-up. Similar cases in the Galactic disc are J0407+1607 and J2016+1948, which have orbital periods of a few hundred days and spin periods of tens of ms (Lorimer et al. 2005; Navarro et al. 2003).
Also, when Freire et al. (2008) observed NGC 6440/6441 with exactly the same system used to find the fast-spinning pulsars in Terzan 5 they found distinctively slower populations in NGC 6440/6441, even though these clusters have a slightly lower dispersive smearing and no detectable scattering, i.e., pulsars as fast and bright as PSR J1748−2446ad should be clearly detectable. In a Kolmogorov-Smirnoff test, they found <2% probability for the pulsars populations of NGC 6440 and 6441 being drawn from the same sample as the pulsars in Terzan 5. The γ’s for these three clusters are very similar, which implies that the assumptions made in simplifying the estimate of γ (similar initial mass function, similar escape velocity, etc., see Sect. 1) may be violated.
 |
Fig. 5 Pulse period derivatives as function of pulse period for GC pulsars with a strong magnetic field and/or short characteristic age. Numbers according to Table 2. Grey points indicate single pulsars in the Galactic disc, the grey solid line the death-line, the black solid lines are the spin-up line according to Eq. (5) and a line shifted by a factor 7 in Ṗ. Dashed lines of constant magnetic field (black) and constant age (blue) are marked with their respective values. |
3.2. Magnetic fields and characteristic ages
The magnetic field strength and characteristic age of a pulsar are estimated from the product and the ratio, respectively, of its spin period P and its derivative, Ṗ. The problem in GCs is that pulsars accelerate in their gravitational fields. The line-of-sight component of this acceleration, a, introduces a contribution to the observed Ṗobs which is of the order of aP/c. For most MSPs, this is of the same order of magnitude or larger than their instrinsic spin-down Ṗ, which implies that for most pulsars in GCs we cannot estimate the magnetic fields. However, for some pulsars in GCs Ṗ is so large (and positive) that it cannot be attributed to the cluster acceleration a. We list those that have strong magnetic fields and/or short characteristic ages in Table 2, and show them in Fig. 5.
Pulsars with small characteristic ages in globular clusters.
The four objects with the longest pulse periods in Table 2 are PSR B1718−19 (Lyne et al. 1993), PSR B1820−30B (Biggs et al. 1994), J1823−3021C (Lynch et al. 2012) and B1745−20 (Lyne et al. 1996). In the P vs. Ṗ diagram these pulsars are located in the same area as the single pulsars in the Galactic disc, with strong magnetic fields and young characteristic ages, compared to most pulsars in GCs. This has led to the suggestion that these NSs were formed recently. We note, however, that the magnetic fields of three of these four pulsars are at the low end of the distribution for young pulsars in the Galactic disc, where the typical magnetic field is on the order of 1012 G, and that all four are in GCs with intermediate or high values of γ. This suggests that they have undergone some loss of field strength due to accretion in a short-lived X-ray binary, and that their relatively high remaining magnetic-field strengths and long periods are due to disruption of the X-ray binary by a close encounter and consequent interruption of the spin-up process. Alternatively, these NSs were spun up by a limited amount of material that they collected in a direct collision with a main-sequence star or giant.
In both scenarios, the characteristic age reflects the time passed since the encounter – which indeed may be much less than the cluster age. We already noted in Sect. 2.4 that PSR B1718−19 may also be a product of an exchange encounter. The strong magnetic fields and long periods suggest that only a small amount of mass was accreted by the NS before accretion stopped.
The three other pulsars in Table 2, B2127+11C, B1820−30A (Biggs et al. 1994; Freire et al. 2011) and B1821−24A (Lyne et al. 1987; Foster et al. 1988; Johnson et al. 2013), have lower magnetic fields but very small characteristic ages. This has led to the suggestion that these NSs were also formed recently. Again, we suggest that these PSRs are not young NSs, but recently recycled old NSs. As discussed in Sect. 2.4, the B2127+11C system must be the result of an exchange encounter, possibly the same that disrupted the X-ray binary that spun up the pulsar.
The hypothesis that the young pulsars are recently recycled old NSs implies that they must be below the spin-up line in the P vs. Ṗ diagram. This line indicates the shortest period that can be reached by spin-up due to accretion at the Eddington limit onto a NS (see Pringle & Rees 1972)  (5)where we substitute (B12)2 ≃ 1015PṖ. We plot this spin-up line in Fig. 5. The exact values of the constants in Eq. (5) depend on details that are not well understood and are therefore uncertain. Indeed, the constants may be different for different evolutionary histories (Tauris et al. 2012). Therefore, we also plot an alternative spin-up line for which Ṗ is a factor 7 higher at the same P.
(5)where we substitute (B12)2 ≃ 1015PṖ. We plot this spin-up line in Fig. 5. The exact values of the constants in Eq. (5) depend on details that are not well understood and are therefore uncertain. Indeed, the constants may be different for different evolutionary histories (Tauris et al. 2012). Therefore, we also plot an alternative spin-up line for which Ṗ is a factor 7 higher at the same P.
If we opt for the line according to Eq. (5), we find that we must accept not only some pulsars with B > 1011 G but also two – B1820−30A and B1821−24A – with rather lower magnetic fields as young, rather than recycled NSs. This means that we must not only accept that NSs are still being formed in GCs, but also that they are formed at least in part with rather weak magnetic fields and very high spin period2.
On the other hand, if we opt for the higher spin-up line, all apparently young pulsars in GCs may be old NSs recently spun up in now disrupted X-ray binaries. This is more consistent with the fact that they only appear in GCs with intermediate or high γ.
4. Discussion
In the previous Sections we have assumed that the single-binary disruption rate γ is the factor which determines the fraction of single pulsars, and – together with the binary period – the degree in which the spin-up process can be completed. Sigurdsson & Phinney (1995) and Ivanova et al. (2008) discuss the results of their calculations mainly in terms of the central density of the cluster. From Table 1 and Fig. 1 it is evident that for the clusters under discussion there is an almost perfect correlation between γ and ρc, and an equally perfect anti-correlation between γ and rc. Thus we cannot, on the basis of the current evidence, decide from observations which of the three is the determining factor. Our choice for γ is on the basis of theory. It may be noted that ρc varies over two orders of magnitude for the clusters in Table 1, and rc over one order of magnitude in anticorrelation with ρc. Since 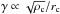 , the variations in central density and core radius contribute in approximately equal measure to the variation in γ. As may be seen in Fig. 1 we can exclude that the collision number Γ determines the fraction of single pulsars, which clusters harbour the products of exchange encounters, or even which clusters have slow pulsars and pulsars with high magnetic fields.
, the variations in central density and core radius contribute in approximately equal measure to the variation in γ. As may be seen in Fig. 1 we can exclude that the collision number Γ determines the fraction of single pulsars, which clusters harbour the products of exchange encounters, or even which clusters have slow pulsars and pulsars with high magnetic fields.
We have already noted that all clusters in Table 1 with more single than binary pulsars are core-collapsed. In this context it is interesting to note a difference between Γ and γ when these numbers are integrated over the cluster history. Semi-analytic models for the cluster evolution (Lynden-Bell & Eggleton 1980; Goodman 1984) show that the central density scales with core radius as ρc ∝ rc−α, with α ≃ 2.22, and that the time that the core spends at radius rc scales as trc ∝ v3/ρc. The number of encounters at each radius thus scales as 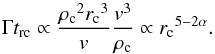 (6)For α ≃ 2.22 the number of close encounters over the history of a cluster is thus dominated by the times at large core radius. We may write the number of encounters for a single object at given radius as
(6)For α ≃ 2.22 the number of close encounters over the history of a cluster is thus dominated by the times at large core radius. We may write the number of encounters for a single object at given radius as 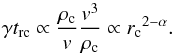 (7)Thus the encounter rate for a single object peaks during core collapse, provided that the object participates in the collapse. We suggest that this may be an extra reason for the prevalence of single pulsars in core-collapsed clusters. It should be noted that the scaling relations we use here are for drastically simplified cluster models – in particular all stars in these models have the same mass. Therefore it is a pity that Ivanova et al. (2008) note that their computations cannot be applied to core-collapsed clusters.
(7)Thus the encounter rate for a single object peaks during core collapse, provided that the object participates in the collapse. We suggest that this may be an extra reason for the prevalence of single pulsars in core-collapsed clusters. It should be noted that the scaling relations we use here are for drastically simplified cluster models – in particular all stars in these models have the same mass. Therefore it is a pity that Ivanova et al. (2008) note that their computations cannot be applied to core-collapsed clusters.
We note in passing that the enhanced number of secondary encounters, as expressed in γ, in core-collapsed clusters may explain the result by Bahramian et al. (2013), mentioned in our Introduction, that core-collapsed clusters contain fewer X-ray binaries than non-collapsed clusters with similar Γ.
The pulsars in Table 2 have characteristic ages much younger than the cluster age, and to explain this it has been suggested that NSs are still being formed in GCs. To explain the observed magnetic fields of the young pulsars in this way, one must accept that NSs formed via electron capture (possibly induced by accretion) are born with fields ranging from 109 to 1012 G, in marked contrast to the NSs formed from core collapse, which lead to a magnetic field distribution centred on 1012 G and ranging 1011 to 1013 G. The exclusive presence of young pulsars in GCs with intermediate or high γ indicates, as we highlighted above, that the “young” pulsars are the result of mild accretion episodes, where for instance the pulsar is a member of an X-ray binary for only a short period until that binary gets disrupted, or alternatively accretion following a direct collision. This hypothesis automatically explains why the young MSPs are single, or in the case of PSR B1718−19 and B2127+11C why they have currently companions acquired through exchange encounters. It also explains the large range in magnetic fields, which reflects the duration and rate of the mass transfer before disruption occurred. In particular the contrast in γ between NGC 6624 and 47 Tuc may explain the remarkable fact that 3 of 6 pulsars in NGC 6624 are apparently young, but none of the 23 in 47 Tuc, despite the fact that the latter cluster has a higher Γ.
Assuming that the pulsars in GCs are young, Boyles et al. (2011) estimate that a birth rate of 1 every 104 yr is required to explain the observed number of young pulsars in the GC system. Since under our hypothesis a single NS can go through several short-duration recycling and radio pulsar episodes, the required NS formation and retention rate is potentially much smaller and the characteristic age reflects the time since the most recent encounter.
Note that secondary encounters are expected to occur in the dense central core of the GC. This implies that the primary encounter bringing the NS into the binary produce only a small systemic velocity of the binary; or alternatively that enough time has passed for dynamic friction to reduce higher systemic velocities which would put the binary outside the central region. Figure 2 shows that such is indeed the case.
A final question is why we see so many isolated pulsars compared to results of exchange encounters in high-γ clusters. After all, in an exchange encounter involving a NS, the most likely outcome is the formation of a binary system containing the two most massive components, i.e. most often the NS with a main-sequence companion. The calculations of Sigurdsson & Phinney (1995) point to two reasons in clusters with central densities as high as in M 15: first, frequent encounters with NSs ionize low-mass pulsar binaries, and second, direct collisions, both in two- and three-body encounters, lead to single pulsars. The calculations by Ivanova et al. (2008) indicate two other channels as the most important ones: direct collisions of a NS with a main-sequence star leading to a merger, and exchange encounters releasing a pulsar from its binary. From the current observations we cannot discriminate between these possibilities.
5. Conclusions and further work
In this paper we use the encounter rate per binary in a GC, γ, to complement the total stellar encounter rate in the cluster, Γ. The latter has been shown to be a reasonable indicator of the number of X-ray binaries and pulsars in GCs; the former provides a first indication of the characteristics of the pulsar populations in GCs. The larger γ is the more disturbed are the MSP binaries: we see more secondary exchange encounters, more isolated pulsars, and more pulsars in the outer parts of the clusters, far from where one would expect them to be given mass segregation. These large offsets result from the recoils caused by binary interactions so recent that the pulsar has not yet had time to sink back to the core by dynamical friction. The correlation is not perfect: some clusters with similar Γ and γ have markedly different pulsar populations. This reflects in part a lack of detailed and uniform characterization of all the clusters, but might also be caused by different dynamical histories, e.g. the occurrence of a core collapse.
We find that in general the placement of particular types of GC objects in a log ρc − rc (or Γ−γ) diagram of the parent cluster can provide a useful diagnostic of the evolution of that particular type of object. An example of this is the young, high-B field pulsars: these objects appear exclusively in GCs with intermediate or high γ. This, together with the finding that they are all near the same spin-up line suggests that they are produced when X-ray binaries are disrupted or single-NSs accrete a limited amount of debris after a direct collision with a giant or main-sequence star. Further evidence for this is the large fraction of these systems that appear as members of exchange products. This greatly diminishes the large required rate of NS formation in GCs calculated in Boyles et al. (2011) under the assumption that these young pulsars are newly created NSs: in our scenario, one single NS can go through several recycling and radio pulsar episodes. Each recycling episode diminishes the magnetic field of the NS, which for each pulsar incarnation appears successively closer to the normal MSPs in the P-Ṗ diagram.
This interpretation can be put to the test in two ways. First, any pulsar found in a GC well above the (upper) spin-up line in Fig. 5, must be a genuinely young pulsar, rather than an old pulsar recently involved in a secondary encounter. Second, when more pulsars become known in low-γ clusters, our interpretation predicts that apparently young and long-period pulsars, as well as highly eccentric pulsar binaries and systems clearly the product of exchange encounters, should be very rare among these.
Finally, this work suggests that exotic systems like MSP-MSP or MSP-black hole binaries should appear almost exclusively in medium to high-γ clusters. Therefore, future radio pulsar surveys for these objects may be more successful in those GCs.
These unusual objects would have to be forming in rather large numbers as well. As discussed in Freire et al. (2011), NGC 6624A and M28A are about 100 times less numerous than the normal MSPs in GCs, but they will be visible as MSPs for a time that is ~100 times shorter as well. This implies that both groups must be forming at similar rates.
Acknowledgments
We thank the Lorentz Center in Leiden for organizing the “Compact Binaries in Globular Clusters” meeting, where the idea for this paper started germinating. PF also thanks Ed van den Heuvel for suggesting his attendance to said meeting. We also thank Thomas Tauris for an interesting discussion regarding the implication of our results for the origin of neutron stars in globular clusters, and the referee Fred Rasio for helpful comments.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, A&A, 524, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, S. B., Gorham, P. W., Kulkarni, S. R., Prince, T. A., & Wolszczan, A. 1990, Nature, 346, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, S. B. 1993, Ph.D. Thesis, California Institute of Technology, USA [Google Scholar]
- Bacon, D., Sigurdsson, S., & Davies, M. B. 1996, MNRAS, 281, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Bagchi, M., Lorimer, D. R., & Chennamangalam, J. 2011, MNRAS, 418, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Bahramian, A., Heinke, C. O., Sivakoff, G. R., & Gladstone, J. C. 2013, ApJ, 766, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Biggs, J. D., Bailes, M., Lyne, A. G., Goss, W. M., & Fruchter, A. S. 1994, MNRAS, 267, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Boyles, J., Lorimer, D. R., Turk, P. J., et al. 2011, ApJ, 742, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Brisken, W., Benson, J., Goss, W. M., & Thorsett, S. 2002, ApJ, 571, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Burgay, M., D’Amico, N., Possenti, A., et al. 2003, Nature, 426, 531 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Clark, G. W. 1975, ApJ, 199, L143 [NASA ADS] [CrossRef] [Google Scholar]
- D’Amico, N., Lyne, A. G., Manchester, R. N., Possenti, A., & Camilo, F. 2001a, ApJ, 548, L171 [NASA ADS] [CrossRef] [Google Scholar]
- D’Amico, N., Possenti, A., Manchester, R. N., et al. 2001b, ApJ, 561, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, M. B., & Hansen, B. M. S. 1998, MNRAS, 301, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Dull, J. D., Cohn, H. N., Lugger, P. M., et al. 1997, ApJ, 481, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A., Pringle, J., & Rees, M. 1975, MNRAS, 172, 15p [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A., Pringle, J., Verbunt, F., & Wade, R. A. 1983, Nature, 301, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Possenti, A., D’Amico, N., & Sabbi, E. 2001, ApJ, 561, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, R. S., Backer, D. C., Taylor, J. H., & Goss, W. M. 1988, ApJ, 326, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Fregeau, J. M., Cheung, P., Portegies Zwart, S. F., & Rasio, F. A. 2004, MNRAS, 352, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C., Gupta, Y., Ransom, S. M., & Ishwara-Chandra, C. H. 2004, ApJ, 606, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C. C., Ransom, S. M., & Gupta, Y. 2007, ApJ, 662, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C. C., Ransom, S. M., Bégin, S., et al. 2008, ApJ, 675, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C. C., Abdo, A. A., Ajello, M., et al. 2011, Science, 334, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., & Goss, W. M. 2000, ApJ, 536, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J. 1984, ApJ, 280, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Guhathakurta, P., Yanny, B., Schneider, D. P., & Bahcall, J. N. 1996, AJ, 111, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. W. 1997, A&A, 322, 127 [NASA ADS] [Google Scholar]
- Heggie, D. C., & Rasio, F. A. 1996, MNRAS, 282, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Heinke, C. O., Wijnands, R., Cohn, H. N., et al. 2006, ApJ, 651, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W. T., Ransom, S. M., Stairs, I. H., et al. 2006, Science, 311, 1901 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hessels, J. W. T., Ransom, S. M., Stairs, I. H., Kaspi, V. M., & Freire, P. C. C. 2007, ApJ, 670, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. 1975, AJ, 80, 809 [Google Scholar]
- Hills, J. 1976, MNRAS, 175, 1p [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, C. Y., Cheng, K. S., & Taam, R. E. 2010, ApJ, 714, 1149 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Rasio, F. A., Lombardi, J. C., Dooley, K. L., & Proulx, Z. F. 2005, ApJ, 621, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Heinke, C. O., Rasio, F. A., Belczynski, K., & Fregeau, J. M. 2008, MNRAS, 386, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, T. J., Guillemot, L., Kerr, M., et al. 2013, ApJ, 778, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, H. M., Kulkarni, S. R., & Phinney, E. S. 1992, in X-ray binaries and the formation of binary and millisecond radio pulsars, eds. E. P. J. van den Heuvel, & S. A. Rappaport (Kluwer: Dordrecht), 349 [Google Scholar]
- Joss, P. C., Rappaport, S. A., & Lewis, W. 1987, ApJ, 319, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Knight, H. S. 2007, Ph. D. Thesis, Swinburne University of Technology, Australia [Google Scholar]
- Lauer, T. R., Holtzman, J. A., Faber, S. M., et al. 1991, ApJ, 369, L45 [Google Scholar]
- Lehmann, I., & Scholz, R.-D. 1997, A&A, 320, 776 [NASA ADS] [Google Scholar]
- Lorimer, D. R., Xilouris, K. M., Fruchter, A. S., et al. 2005, MNRAS, 359, 1524 [NASA ADS] [CrossRef] [Google Scholar]
- Lynch, R. S., Freire, P. C. C., Ransom, S. M., & Jacoby, B. A. 2012, ApJ, 745, 109 [Google Scholar]
- Lynden-Bell, D., & Eggleton, P. P. 1980, MNRAS, 191, 483 [NASA ADS] [Google Scholar]
- Lyne, A. G., & Lorimer, D. R. 1994, Nature, 369, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Brinklow, A., Middleditch, J., Kulkarni, S. R., & Backer, D. C. 1987, Nature, 328, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Biggs, J. D., Harrison, P. A., & Bailes, M. 1993, Nature, 361, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Manchester, R. N., & D’Amico, N. 1996, ApJ, 460, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J., Anderson, S. B., & Freire, P. C. 2003, ApJ, 594, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Noyola, E., & Gebhardt, K. 2006, AJ, 132, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Phinney, E. S. 1992, Phil. Trans. R. Soc. London Ser. A, 341, 39 [Google Scholar]
- Phinney, E. S., & Kulkarni, S. R. 1994, ARA&A, 32, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Langer, N., Poelarends, A. J. T., et al. 2004, ApJ, 612, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Pooley, D., Lewin, W. H. G., Anderson, S. F., et al. 2003, ApJ, 591, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Prince, T. A., Anderson, S. B., Kulkarni, S. R., & Wolszczan, A. 1991, ApJ, 374, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E., & Rees, M. J. 1972, A&A, 21, 1 [NASA ADS] [Google Scholar]
- Ransom, S. M., Greenhill, L. J., Herrnstein, J. R., et al. 2001, ApJ, 546, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Ransom, S. M., Hessels, J. W. T., Stairs, I. H., et al. 2005, Science, 307, 892 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rasio, F. A., & Heggie, D. C. 1995, ApJ, 445, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Sigurdsson, S., & Phinney, E. S. 1995, ApJS, 99, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Sosin, C., & King, I. R. 1997, AJ, 113, 1328 [NASA ADS] [CrossRef] [Google Scholar]
- Stairs, I. H. 2004, Science, 304, 547 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sutantyo, W. 1975, A&A, 44, 227 [NASA ADS] [Google Scholar]
- Tauris, T. M., Langer, N., & Kramer, M. 2012, MNRAS, 425, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. 1968, ApJ, 151, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., King, I. R., & Djorgovski, S. 1995, AJ, 109, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Trenti, M., Vesperini, E., & Pasquato, M. 2010, ApJ, 708, 1598 [NASA ADS] [CrossRef] [Google Scholar]
- van Kerkwijk, M. H., Kaspi, V. M., Klemola, A. R., et al. 2000, ApJ, 529, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Verbunt, F. 1987, ApJ, 312, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Verbunt, F. 1988, in The physics of compact objects: theory vs. observation, eds. N. E. White, & L. Filipov (Pergamon Press), 529 [Google Scholar]
- Verbunt, F. 2003, in New horizons in globular cluster astronomy, eds. G. Piotto et al., ASP Conf. Ser., 296, 245 [Google Scholar]
- Verbunt, F., & Hut, P. 1987, in The Origin and Evolution of Neutron Stars, eds. D. J. Helfand, & J. H. Huang, IAU Symp., 125, 187 [Google Scholar]
- Weisberg, J. M., Nice, D. J., & Taylor, J. H. 2010, ApJ, 722, 1030 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Structural parameters and numbers of single and binary pulsars of globular clusters with three or more pulsars.
All Figures
 |
Fig. 1 Central density ρc as a function of core radius rc for clusters with ρc > 2000 L⊙/pc3 (Harris 1996, update of 2010), with lines of constant Γ (blue) and constant γ (red). Letter labels refer to clusters in Table 1, coloured red if Ns > Nb, blue if Nb > Ns, and yellow if Nb ≃ Ns. Clusters with products of secondary interactions include i) and g), and – indicated in black, with numerical labels – 1: NGC 1851, 2: NGC 6342, 3: NGC 6397 and 4: NGC 6544. |
| In the text | |
 |
Fig. 2 Angular offsets of the pulsars with published timing solutions from the centres of their clusters, in core radii. The larger the encounter rate per binary γ, the larger are the odds of finding pulsars far from the centres of their clusters. Some of the clusters are labelled as in Table 1, colours are used to discriminate isolated and binary pulsars, and symbols to indicate the companion mass. Binaries created by exchange products are shown light blue. The dashed line indicates a distance of 4 core radii. |
| In the text | |
 |
Fig. 3 Eccentricity as a function of orbital period for binary radio pulsars in globular clusters. Colours are used to indicate γ of the cluster in which the pulsar resides, symbols to indicate the companion mass. For the outcome of recycling by a (sub)giant donor one expects Pb ≳ 1 d and 0.1 < Mc/M⊙ < 0.44; such systems in the Galactic disc are shown in gray, and the expectation values for the eccentricity according to Eq. (4) and ten times this value, are shown as dotted lines. Eccentricies 0.0, for which no upper limits have been specified, are shown at the bottom (with smaller symbols to avoid overlap). Data from http://www.naic.edu/~pfreire/GCpsr.html |
| In the text | |
 |
Fig. 4 Pulse periods as function of single-binary disruption rate γ. Some of the clusters are labelled as in Table 1, colours are used to discriminate isolated and binary pulsars, and symbols to indicate the companion mass. Binaries created by exchange products are shown in light blue. The horizontal dotted lines indicate pulse periods of 0.15 and 0.015 s. |
| In the text | |
 |
Fig. 5 Pulse period derivatives as function of pulse period for GC pulsars with a strong magnetic field and/or short characteristic age. Numbers according to Table 2. Grey points indicate single pulsars in the Galactic disc, the grey solid line the death-line, the black solid lines are the spin-up line according to Eq. (5) and a line shifted by a factor 7 in Ṗ. Dashed lines of constant magnetic field (black) and constant age (blue) are marked with their respective values. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


