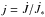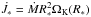| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 13 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322542 | |
| Published online | 05 December 2013 | |
The boundary layer in compact binaries
1 Institut für Astronomie und Astrophysik, Abt. Computational Physics, Auf der Morgenstelle 10, 72076 Tübingen, Germany
e-mail: marius.hertfelder@gmail.com
2 Institut für Astronomie und Astrophysik, Abt. Astronomie, Sand 1, 72076 Tübingen, Germany
3 Kazan (Volga region) Federal University, Kremlevskaya 18, 420008 Kazan, Russia
Received: 26 August 2013
Accepted: 14 October 2013
Context. Disk accretion onto stars leads to the formation of a boundary layer (BL) near the stellar surface where the disk makes contact with the star. Although a large fraction of the total luminosity of the system originates from this tiny layer connecting the accretion disk and the accreting object, its structure has not been fully understood yet.
Aims. It is the aim of this work to obtain more insight into the BL around the white dwarf in compact binary systems. There are still many uncertainties concerning the extent and temperature of the BL and the rotation rate of the white dwarf.
Methods. We perform numerical hydrodynamical simulations, where the problem is treated in a one-dimensional, radial approximation (slim disk). The turbulence is described by the α parameter viscosity. We include both cooling from the disk surfaces and radial radiation transport. The radiation energy is treated in a one-temperature approximation.
Results. For a given Ṁ our results show a strong dependence on the stellar mass and rotation rate. The midplane and the effective temperature rise considerably with increasing stellar mass or decreasing stellar rotation rate. Our simulations also show that the radiation energy and pressure are indeed important in the BL. However, some models show a low optical depth in the BL, making it necessary to find a better representation for optically thin regions.
Conclusions. The combination of a high mass and a small radius, characteristic of white dwarfs, can lead to an enormous energy release in the BL, provided the WD rotates slowly. Since the radial extent of BLs is typically very small (about 0.02 to 0.05 R∗), this leads to surface temperatures of a few hundred thousand Kelvin. All of our models showed subsonic infall velocities with Mach numbers of <0.4 at most.
Key words: accretion, accretion disks / binaries: close / white dwarfs / methods: numerical / hydrodynamics
© ESO, 2013
1. Introduction
Accretion of matter on compact objects via a disk is a ubiquitous phenomenon in astrophysics and can be observed in a variety of systems such as protostars, close binary systems, and active galactic nuclei. Since accretion disks appear very frequently in astrophysical situations, they have been studied extensively and several analytical models of stationary disks assuming axial symmetry and neglecting the vertical direction (the equations have been vertically integrated) have been constructed (e.g. Shakura & Sunyaev 1973; Lynden-Bell & Pringle 1974; Pringle 1981; Verbunt 1982). The vertical structure was investigated afterwards with the help of these models (e.g. Meyer & Meyer-Hofmeister 1982).
While about one half of the accretion energy is released over almost the whole radial extent of the accretion disk, the other half is still stored in terms of kinetic energy of the gas near the surface of the central object. Only when the flow reaches the surface of the star is it slowed down from the Keplerian rotation rate to the rotation of the star, which will usually be much slower. This tiny region with a radial extent of less than one percent of the stellar radius where the accretion disk connects to the central object is called the boundary layer (BL). Since a great deal of energy is released in a spatially restricted area, the BL can get very hot and might account for the observed soft and hard X-ray and UV emission in several cataclysmic variable systems (e.g. Cordova et al. 1981a,b; Cordova & Mason 1984). It is therefore of great importance when it comes to understanding star-disk systems. The first models of the BL were stationary calculations or estimates of timescales that were made under various assumptions by different authors (Lynden-Bell & Pringle 1974; Pringle 1977; Tylenda 1977, 1981; Pringle & Savonije 1979; Regev 1983). However, because of the simplification made there have been debates concerning the consistency of these models with the observations (e.g. Ferland et al. 1982). The first evolutionary calculations were performed soon afterwards (Robertson & Frank 1986; Kley & Hensler 1987; Kley 1989a,b, 1991; Godon et al. 1995), and for the first time allowed non-stationary phenomena like instabilities to be investigated. Among the first analytical studies of the BL were the efforts of Bertout & Regev (1992) and Regev & Bertout (1995), who dealt with the one-dimensional, stationary equations by using the method of matched asymptotic expansions (MAE).
Most of the one-dimensional BL models focus on the radial evolution of the variables, where an infinitesimal thin disk is connected directly to the star. The vertical velocity is set to zero and the fast moving accretion flow is slowed down within the midplane of the disk and accreted by the star. The deceleration of the gas in the BL is accomplished by a mechanism that is not yet fully understood (cf. Pessah & Chan 2012; Belyaev et al. 2012). Here, we assume a viscous medium and use the classical α-parametrisation from Shakura & Sunyaev (1973). The radiation emitted by the BL strongly depends on the mass accretion rate of the accreting object. For rather low mass accretion rates (Ṁ ≤ 10-10 M⊙/yr, Warner 1987), the BL is optically thin, reaching very high temperatures (~ 108 K) and emitting soft and hard X-rays in the case of cataclysmic variables (e.g. Mukai & Patterson 2004; Pandel et al. 2003, 2005, King & Shaviv 1984; Shaviv 1987; Narayan & Popham 1993; Popham 1999). An optically thick BL, on the contrary, shows a lower temperature of about 105 K (Pringle 1977; Syunyaev & Shakura 1986; Popham & Narayan 1995) and emits radiation that is mostly thermalized and resembles a black body spectrum (see e.g. Cordova et al. 1980; Mauche 2004).
It should be noted that in addition to the above-mentioned radial models, there are also one-dimensional models that investigate the vertical flow of the gas in the near proximity of the star. Here, it is assumed that the gas spreads around the star because of the ram pressure in the BL. In contrast to the radial models, the gas is not slowed down in the midplane of the disk, but rather on the whole surface of the star. This alternative model is called the spreading layer (Inogamov & Sunyaev 1999, 2010). While this model was originally designed for the BL of a neutron star, Piro & Bildsten (2004a,b) adapted it for cataclysmic variables systems. The spreading layer concept was extended by Suleimanov & Poutanen (2006), who included general relativity and different chemical compositions of the accreted matter.
In contrast to these 1D models, a number of multidimensional studies of the BL have been performed, mostly under the assumption of axial symmetry. Full radiation hydrodynamical simulations of that kind were performed by Kley (1989a,b, 1991), but only very few dynamical timescales could be followed in low spatial resolution. In recent years, local BL models with higher resolution have been presented by Fisker & Balsara (2005) and Fisker et al. (2006) for the purely adiabatic cases. Calculations including magnetic fields have been done in 2D by Küker et al. (2003) and in 3D by Armitage (2002), though with only low resolution and short dynamical timescales. Additional 2D simulations were performed by Kley & Lin (1996, 1999) for protostars, by Babkovskaia et al. (2008) for neutron stars in LMXB, or by Balsara et al. (2009), who simulated the BL around a white dwarf and used a simplified energy dissipation function without radiation transport. Three-dimensional magnetohydrodynamical simulations including magnetospheric accretion were performed by Romanova et al. (2012), but without the inclusion of radiation transport. Non-axial-symmetric phenomena were investigated only very recently by Belyaev et al. (2012), though only with an isothermal equation of state.
In this paper we focus on the BL structure around white dwarfs in compact binaries such as cataclysmic variable systems. Despite the existing multidimensional studies, we opted for new one-dimensional models because of the moderate computational effort. These are made more realistic by including radiation transport in the radial direction and local cooling in the vertical direction. To allow variability studies, we solve the time-dependent equations. This extends the approach of Popham & Narayan (1995), who solved the stationary equations (see Sect. 4.4 for more details). Furthermore, we have implemented force and dissipation terms of the radiation field and a quasi-two-dimensional radiation transport to treat the radiation field consistently in our calculations, where the radiation pressure (energy) is comparable to the thermal pressure (energy). This work is the first step and will be used to expand the simulations to more dimensions. The results presented in this paper will be used to calculate synthetic, theoretical spectra and thereby considerably narrow the regimes for various parameters of binary systems, like the stellar rotation rate of the white dwarf. More detailed theoretical spectra and observational consequences will be presented in a subsequent paper.
The paper itself is organized as follows: in Sect. 2, an overview of the used equations and assumptions is given, and basic physics of the models is described. Section 3 is devoted to the numerical methods that were utilized in order to solve the equations. In Sect. 4, the models are presented and discussed. We conclude with Sect. 5.
2. Equations
In this section, we present the one-dimensional, vertically integrated Navier-Stokes equations used in the numerical code. Although one-dimensional BL calculations are certainly not sufficient to describe the structure of the BL, they are adequate to model the emitted energy, since the gas is slowed down in the midplane before it engulfs the star (e.g. Kley 1989b).
2.1. Vertical averaging
The 1D equations of motion are obtained through vertical integration of the Navier-Stokes equations over the z coordinate. Assuming a Gaussian profile for the three-dimensional density ρ in the vertical direction, the surface density is given by 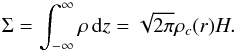 (1)Here, ρc denotes the mass density in the midplane and H is the pressure scale height, which is a measure of the vertical extent of the disk. If we also assume hydrostatic balance and an isothermal equation of state in the vertical direction, the pressure scale height reads
(1)Here, ρc denotes the mass density in the midplane and H is the pressure scale height, which is a measure of the vertical extent of the disk. If we also assume hydrostatic balance and an isothermal equation of state in the vertical direction, the pressure scale height reads 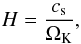 (2)where cs denotes the (isothermal) sound speed, and
(2)where cs denotes the (isothermal) sound speed, and 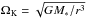 the Keplerian angular velocity (G is the gravitational constant and M∗ is the mass of the star).
the Keplerian angular velocity (G is the gravitational constant and M∗ is the mass of the star).
In our 1D approximation, the vertical component of the velocity vector u is assumed to be negligible. Formally, this can no longer be true in the regions where the gas leaves the midplane and spreads to the poles of the star.
2.2. Continuity equation (conservation of mass)
The vertically integrated continuity equation in polar coordinates is then given by 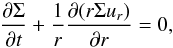 (3)where ur denotes the velocity component in the radial direction.
(3)where ur denotes the velocity component in the radial direction.
2.3. Equations of motion (conservation of momentum)
The vertically integrated equations of motion read 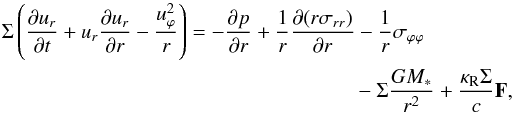 (4)in the radial direction and
(4)in the radial direction and 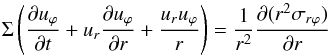 (5)in the azimuthal direction. Here p denotes the vertically integrated thermal pressure and κR and F are the Rosseland mean opacity and the radiative flux, respectively, which we will describe in detail in the next section. The term
(5)in the azimuthal direction. Here p denotes the vertically integrated thermal pressure and κR and F are the Rosseland mean opacity and the radiative flux, respectively, which we will describe in detail in the next section. The term 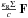 acts as a radiative force on the material; σ denotes the vertically integrated viscous stress tensor with the components σrr,σϕϕ and σrϕ (Papaloizou & Stanley 1986), where we assume a vanishing bulk viscosity.
acts as a radiative force on the material; σ denotes the vertically integrated viscous stress tensor with the components σrr,σϕϕ and σrϕ (Papaloizou & Stanley 1986), where we assume a vanishing bulk viscosity.
2.4. Energy equation (conservation of energy)
Since the temperatures in the BL region around white dwarfs are expected to be very hot even if they are optically thick (the temperature is of the order of 105 Kelvin, Pringle & Savonije 1979; Tylenda 1981), radiation pressure and radiation energy play an important role in our models and cannot be ignored. Instead of simultaneously solving one equation for the gas energy and one for the radiation energy separately (called the two-temperature approximation1), we chose a different approach in order to speed up the calculations. In this so-called one-temperature radiation transport (see e.g. Flaig et al. 2010), we add the two equations for the gas and the radiation energy and obtain ![\begin{equation} \rho\frac{\text{d}}{\text{d} t}\left(\varepsilon + \frac{E}{\rho}\right) = -P \nabla\vec{u} + \left[\sigma_{ij}-\mathcal{P}_{ij}\right]\nabla_i u_j - \nabla\vec{F} , \end{equation}](/articles/aa/full_html/2013/12/aa22542-13/aa22542-13-eq31.png) (6)where
(6)where 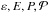 and F denote the specific thermal energy of the gas, the radiative energy density, the 3D thermal pressure of the gas, the radiation pressure tensor, and the radiative flux, respectively.
and F denote the specific thermal energy of the gas, the radiative energy density, the 3D thermal pressure of the gas, the radiation pressure tensor, and the radiative flux, respectively.
The assumption of a local thermodynamic equilibrium is justified for optically thick regions, as is the one-temperature approach (see e.g. Kuiper et al. 2010). Since we concentrate here on high mass accretion rates during outbursts, the BL will stay optically thick even for slow stellar rotation rates. In the approximation of local thermal equilibrium (LTE), the radiation energy simplifies to read E = aT4, where a is the radiation constant and T is the gas temperature.
In addition to the one-temperature approximation, we use the flux-limited diffusion approximation (FLD; Levermore & Pomraning 1981; Levermore 1984), which allows us not to consider an equation for the radiative momentum. The radiation flux is then set to 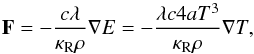 (7)where λ is a dimensionless number called the flux-limiter. Here, we adopt the formulation by Levermore & Pomraning (1981),
(7)where λ is a dimensionless number called the flux-limiter. Here, we adopt the formulation by Levermore & Pomraning (1981),  For the given flux-limiter, the corresponding approximation for the radiation pressure tensor reads (Levermore 1984)
For the given flux-limiter, the corresponding approximation for the radiation pressure tensor reads (Levermore 1984) ![\begin{equation} \mathcal{P}= \frac{E}{2}\left[(1-f_\text{Edd})\mathcal{I} + (3f_\text{Edd}-1)\,\vec{n}\vec{n}\right].\label{eq:pressure_tensor} \end{equation}](/articles/aa/full_html/2013/12/aa22542-13/aa22542-13-eq39.png) (10)Here, ℐ is the identity tensor of rank 2, n = (∇E)/ | ∇E | is the unit vector parallel to the gradient of E, and the Eddington factor is given by
(10)Here, ℐ is the identity tensor of rank 2, n = (∇E)/ | ∇E | is the unit vector parallel to the gradient of E, and the Eddington factor is given by 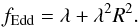 (11)This approximation reflects the correct behaviour of the radiation pressure tensor in the optically thick regime where it is isotropic and E/3, and in the optically thin regions where its absolute value parallel to ∇E is E. If one considers a purely isotropic radiative pressure tensor, a approximation in the flux-limited diffusion theory is given by
(11)This approximation reflects the correct behaviour of the radiation pressure tensor in the optically thick regime where it is isotropic and E/3, and in the optically thin regions where its absolute value parallel to ∇E is E. If one considers a purely isotropic radiative pressure tensor, a approximation in the flux-limited diffusion theory is given by 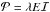 (Commerçon et al. 2011). Our simulations showed that the difference between Eq. (10) and the purely isotropic approximation is in general very small.
(Commerçon et al. 2011). Our simulations showed that the difference between Eq. (10) and the purely isotropic approximation is in general very small.
Furthermore, if we assume that the radiation pressure tensor is diagonal (Eddington approximation) and use the relation between the specific thermal energy and temperature ε = cvT, the energy equation in the one-temperature approximation becomes after a vertical integration ![\begin{eqnarray} \label{eq:one_temp_temp} && \left[\Sigma c_v + 4aT^3\cdot\widetilde{H} \right] \left(\frac{\partial T}{\partial t} + u_r\frac{\partial T}{\partial r}\right) + 4aT^4\cdot\frac{1}{r}\frac{\partial(ru_r)}{\partial r} =\nonumber \\ &&\quad -p\frac{1}{r}\frac{\partial(r u_r)}{\partial r} - \mathcal{P}_{ij}\nabla_i u_j\nonumber \\ &&\quad + 2 \nu \Sigma \left[\left(\frac{\partial u_r}{\partial r}\right)^2 + \left(\frac{u_r}{r}\right)^2\right] + \nu \Sigma \left(r\frac{\partial\Omega}{\partial r}\right)^2 -\frac{2}{3} \nu \Sigma\left(\frac{1}{r}\frac{\partial(r u_r)}{\partial r}\right)^2\nonumber \\ &&\quad - 2\sigma_\text{SB} T_\text{eff}^4 + \widetilde{H}\frac{1}{r}\frac{\partial}{\partial r}\left[\frac{16\sigma_\text{SB}\lambda}{\kappa_\text{R}\Sigma}r\widetilde{H}T^3\frac{\partial T}{\partial r}\right], \end{eqnarray}](/articles/aa/full_html/2013/12/aa22542-13/aa22542-13-eq48.png) (12)where σSB is the Stefan-Boltzmann constant, Teff the effective temperature, κR the Rosseland opacity, and
(12)where σSB is the Stefan-Boltzmann constant, Teff the effective temperature, κR the Rosseland opacity, and 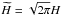 . The second line describes the pressure work exerted by the thermal and radiative pressure. The third line contains viscous dissipation, where ν denotes the kinematic viscosity. The last line describes emission of radiation from the disk surface and diffusion of the radiative flux in the disk midplane. By this means we employ a quasi-2D radiation transport.
. The second line describes the pressure work exerted by the thermal and radiative pressure. The third line contains viscous dissipation, where ν denotes the kinematic viscosity. The last line describes emission of radiation from the disk surface and diffusion of the radiative flux in the disk midplane. By this means we employ a quasi-2D radiation transport.
To close the set of equations, we need some constitutive relationships. For the equation of state, we use the ideal gas law. The vertically integrated pressure then reads 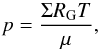 (13)where RG = kB/mH with kB being the Boltzmann constant, mH the mass of hydrogen, and μ is the mean molecular weight. In order to take the radiation pressure effects into account, we have defined an effective sound speed (Krumholz et al. 2007)
(13)where RG = kB/mH with kB being the Boltzmann constant, mH the mass of hydrogen, and μ is the mean molecular weight. In order to take the radiation pressure effects into account, we have defined an effective sound speed (Krumholz et al. 2007) 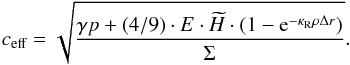 (14)The factor (1 − e− κRρΔr) (Δr is the width of a cell) is used to interpolate between the optically thick region, where the radiation pressure increases the effective sound speed since it contributes to the restoring force and optically thin regions, where radiation pressure plays no role.
(14)The factor (1 − e− κRρΔr) (Δr is the width of a cell) is used to interpolate between the optically thick region, where the radiation pressure increases the effective sound speed since it contributes to the restoring force and optically thin regions, where radiation pressure plays no role.
For the opacity we use Kramer’s law, 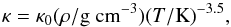 (15)where κ0 = 5 × 1024 cm2 g-1. If the temperature is high enough for the gas to be fully ionized, we can assume a lower threshold for the opacity given by free electron scattering processes (Thomson scattering). The corresponding opacity has the constant value κThomson = 0.335 cm2 g-1 (assuming a hydrogen mass fraction of X = 0.675 for the gas composition) and is added to Kramer’s opacity. Because we estimate the local cooling of the disk via a blackbody radiation of temperature Teff, we need a relation that links the effective temperature to the temperature in the midplane of the disk. Therefore, we employ the relation by Hubeny (1990) which is a generalisation of the grey atmosphere (e.g. Rybicki & Lightman 1986) and approximates the optical depth in the vertical direction of the disk. The relations read (Suleymanov 1992)
(15)where κ0 = 5 × 1024 cm2 g-1. If the temperature is high enough for the gas to be fully ionized, we can assume a lower threshold for the opacity given by free electron scattering processes (Thomson scattering). The corresponding opacity has the constant value κThomson = 0.335 cm2 g-1 (assuming a hydrogen mass fraction of X = 0.675 for the gas composition) and is added to Kramer’s opacity. Because we estimate the local cooling of the disk via a blackbody radiation of temperature Teff, we need a relation that links the effective temperature to the temperature in the midplane of the disk. Therefore, we employ the relation by Hubeny (1990) which is a generalisation of the grey atmosphere (e.g. Rybicki & Lightman 1986) and approximates the optical depth in the vertical direction of the disk. The relations read (Suleymanov 1992)  where τR and τP (
where τR and τP (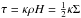 ) are the Rosseland and the Planck mean optical depth (see also Kley & Crida 2008).
) are the Rosseland and the Planck mean optical depth (see also Kley & Crida 2008).
2.5. Viscosity
The mechanism that accounts for the angular momentum transport in the BL region is still a matter of concern (Papaloizou & Szuszkiewicz 1994; Narayan et al. 1994; Kato & Inagaki 1994; Godon 1995). The most likely driving force for the anomalous viscosity in accretion disks with magnetic Prandtl numbers of the order of unity is the magneto-rotational instability (e.g. Balbus & Lesaffre 2008) that gives rise to the onset of turbulence (Balbus & Hawley 1991, 1998; Balbus 2003) which acts like a genuine viscosity on macroscopic scales. However, this cannot be the case for the BL, since the magneto-rotational instability is effectively damped out for a increasing rotation profile Ω(r) (Godon 1995; Abramowicz et al. 1996). For lack of a better representation, we assume that the angular momentum transport in the BL is managed by turbulence of some kind (cf. Pringle 1981). In that case we can use the classic α-prescription by Shakura & Sunyaev (1973), which is a parametrisation for the stresses caused by turbulence in an accretion disk and therefore is still valid for MRI unstable disks, provided that a viable value for the numerical parameter α is given. This α ansatz, which is a frequently used expression for the disk viscosity is written as 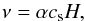 (18)where
(18)where 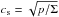 is the isothermal sound speed. Unless stated otherwise, Eq. (18) was used to calculate the viscosity in our models. In the BL, the radial pressure scale height becomes smaller than the vertical one. This is considered in the viscosity prescription by Papaloizou & Stanley (1986), which reads
is the isothermal sound speed. Unless stated otherwise, Eq. (18) was used to calculate the viscosity in our models. In the BL, the radial pressure scale height becomes smaller than the vertical one. This is considered in the viscosity prescription by Papaloizou & Stanley (1986), which reads ![\begin{equation} \nu = \alpha c_\text{s}\left[\frac{1}{H^2} + \frac{(\text{d} p/\text{d} r)^2}{p^2}\right]^{-1/2}\cdot\label{eq:pn95_viscosity} \end{equation}](/articles/aa/full_html/2013/12/aa22542-13/aa22542-13-eq72.png) (19)We used Eq. (19) when we compared our calculations with that of Popham & Narayan (1995) in Sect. 4.4.
(19)We used Eq. (19) when we compared our calculations with that of Popham & Narayan (1995) in Sect. 4.4.
3. Numerical methods
3.1. General remarks
The partial differential equations, Eqs. (3)–(5) and (12), are discretized on a fixed Eulerian grid using the finite differences method and propagated in time using a semi-implicit-explicit scheme. For this purpose a new framework, guided by the ZEUS code by Stone & Norman (1992), has been programmed completely from scratch and tested extensively before it was used to perform the calculations. To ensure a formal second-order accuracy in time and space, we employed a staggered grid in space (see e.g. Tscharnuter & Winkler 1979) and a multistep procedure for the time integration (operator-splitting, e.g. Hawley et al. 1984). The computational domain typically ranges from one to two stellar radii, ![\hbox{$\mathcal{D}=\left[R_\ast,2\,R_\ast\right]$}](/articles/aa/full_html/2013/12/aa22542-13/aa22542-13-eq73.png) , and is divided into 512 logarithmically spaced grid cells.
, and is divided into 512 logarithmically spaced grid cells.
3.2. Implicit methods
For some source terms, a special treatment for the time integration is necessary, because using a time-explicit scheme would constrain the time step considerably and slow down the simulations. Hence those parts of the equations, namely the radial diffusion (radiation transport) and the viscous torques and forces, have to be solved with an implicit scheme that does not limit the time step if we are looking for a stationary solution. In contrast to an explicit time integration, the equations are now solved assuming the value of the physical quantity at the new time step n + 1. This leads to a system of linear equations, which can be written as a matrix-vector multiplication in a space of dimension N, where N is the number of active grid cells. However, this system can become very large if we are using a large number of cells. Fortunately, in our one-dimensional case the use of this implicit method only leads to a tridiagonal matrix, and the equations can be solved easily.
3.3. The time step
One undesirable feature of explicit numerical methods in hydrodynamics is the limitation of the largest possible time step (Courant et al. 1928). It must be limited with respect to the characteristics of the system according to the relation known as the CFL condition, ![\begin{equation} \Delta t = f_\text{C}\cdot\text{min}_j\left[\frac{\Delta r_j}{\left|u_j\right| + c_{\text{s},j} }\right],\label{eq:cfl} \end{equation}](/articles/aa/full_html/2013/12/aa22542-13/aa22542-13-eq76.png) (20)where Δrj is the extent of the cell j, uj its velocity, and cs,j the sound speed. The minimum of all active cells is taken. Typically, we use a Courant factor fC = 0.8 in Eq. (20).
(20)where Δrj is the extent of the cell j, uj its velocity, and cs,j the sound speed. The minimum of all active cells is taken. Typically, we use a Courant factor fC = 0.8 in Eq. (20).
3.4. Boundary and initial conditions
The modelling of the BL surrounding a star is a classical boundary value problem, meaning that the solution we try to obtain must satisfy not only the partial differential equations but also the boundary conditions because of the finite space domain. In mathematical terms those conditions are given as either Dirichlet or Neumann boundary conditions where either a value or the normal derivative of a variable is specified.
Physically speaking, at the outer boundary of our computational domain, we have to allow for an incoming mass flux that corresponds to the accretion of matter. Additionally, we require the angular velocity to be Keplerian 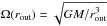 and consider a pressure correction. At the inner boundary, where the stellar surface is located, we set the angular velocity of the gas to the stellar rotation rate Ω(rin) = Ω∗, i.e. we impose a no-slip boundary condition in ϕ-direction. Instead, the radial velocity is not set to zero, but rather to a small but finite fraction of the Keplerian velocity,
and consider a pressure correction. At the inner boundary, where the stellar surface is located, we set the angular velocity of the gas to the stellar rotation rate Ω(rin) = Ω∗, i.e. we impose a no-slip boundary condition in ϕ-direction. Instead, the radial velocity is not set to zero, but rather to a small but finite fraction of the Keplerian velocity, 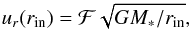 (21)in order to enable a mass flux out of the domain. For ℱ we choose a value much smaller than one, typically 10-5. This open inner boundary is necessary to avoid the accumulation of mass and allow for accretion onto the star. The value of ℱ determines how much of the stellar interior is taken into account in the simulation. The extreme case of ℱ = 0 would imply that the whole star is considered which does not make sense in this type of simulation. Our choice of ℱ ensures that a sufficient part of the stellar envelope is contained in the domain but not too much, otherwise the temperatures become too high and slow down the simulations. For testing purposes we have varied ℱ and do not find any differences in the results despite a small shift in radius.
(21)in order to enable a mass flux out of the domain. For ℱ we choose a value much smaller than one, typically 10-5. This open inner boundary is necessary to avoid the accumulation of mass and allow for accretion onto the star. The value of ℱ determines how much of the stellar interior is taken into account in the simulation. The extreme case of ℱ = 0 would imply that the whole star is considered which does not make sense in this type of simulation. Our choice of ℱ ensures that a sufficient part of the stellar envelope is contained in the domain but not too much, otherwise the temperatures become too high and slow down the simulations. For testing purposes we have varied ℱ and do not find any differences in the results despite a small shift in radius.
The stellar radiation is taken care of by including the flux 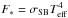 in the radiative diffusion routine as an inner boundary condition. Because the temperature at rin is inside the star, it is not known a priori and cannot be specified. Hence, a simple zero gradient condition for the temperature is assumed in all other routines that require a temperature. Previous studies suggest that the thermal boundary condition at the star is of great importance for the BL (Regev & Bertout 1995; Godon et al. 1995). We would like to point out that the influence of the incoming flux is virtually nil, as test calculations have shown. Apart from the Dirichlet conditions that have been shown above, for most other physical variables we imposed zero gradient boundary conditions, which means that the normal derivative at the boundary equals zero (Neumann type).
in the radiative diffusion routine as an inner boundary condition. Because the temperature at rin is inside the star, it is not known a priori and cannot be specified. Hence, a simple zero gradient condition for the temperature is assumed in all other routines that require a temperature. Previous studies suggest that the thermal boundary condition at the star is of great importance for the BL (Regev & Bertout 1995; Godon et al. 1995). We would like to point out that the influence of the incoming flux is virtually nil, as test calculations have shown. Apart from the Dirichlet conditions that have been shown above, for most other physical variables we imposed zero gradient boundary conditions, which means that the normal derivative at the boundary equals zero (Neumann type).
Initially, we have to prescribe values for all variables. Here, it is vital to ensure that the initial conditions are compatible with the boundary conditions and are physically reasonable. We have found that a reliable set of initial conditions is given by the Shakura & Sunyaev (1973) disk solution (see e.g. Frank et al. 2002, for a compact representation), even though they are not completely consistent with all boundary conditions. To avoid any problems in this context, we have interpolated both regions smoothly. For a given stellar mass M∗, radius R∗, temperature T∗, and rotation rate ω∗, the solution will be given by the mass inflow rate Ṁ and the viscosity parameter α.
3.5. Model parameters
In this paper, we focus on the BL around the white dwarf in cataclysmic variable systems, and investigate its structure. We computed several models, where we vary the mass of the white dwarf and its rotation rate. We ran the simulations with the following three masses, M = 0.8 M⊙, 1.0 M⊙, and 1.2 M⊙, which are typical white dwarf masses in cataclysmic variables. Another important parameter that also determines the entire amount of energy released in the accretion disk and BL is the radius of the star. Here we used the mass-radius relation from Nauenberg (1972). We imposed an effective temperature of T∗ = 50 000 K that is, for example, consistent with the estimates of Sion et al. (2010) for SS Cyg, where a mass accretion rate of Ṁ = 1.51 × 10-8 M⊙/yr was assumed. Since we are interested in the thermodynamics of the BL, the rotation rate of the white dwarf is an important parameter. It determines how much energy is dissipated in the BL region and therefore has a major influence on the temperature. We simulated a variety of models where the white dwarf is non-rotating (Ω∗ = 0), fast rotating (Ω∗ = 0.8ΩK), and in between. We took α = 0.01 for the viscosity parameter throughout, which is probably too small a choice for the disk. In the BL, however, the viscosity is supposed to be far smaller than in the disk. Test calculations with α = 0.1 showed no major structural differences compared to the models presented here, except for the inflow velocity that reaches the sonic point for models with high mass and low rotation rates. If we use Eq. (19) instead of the classical α ansatz for the viscosity, the sonic point is hit only for greater values of α. To avoid unphysical, supersonic infall velocities, it is possible to include a causality preserving factor (e.g. Narayan 1992).
4. Results
4.1. The 1.0 M⊙ model
First, we will describe the basic properties of the BL for our standard model of a one solar mass white dwarf. In doing this, we are going to emphasise the dependence of the structure and thermodynamics on the rotation rate of the central star, a parameter whose exact value is still unclear in many systems. We usually show five different stellar rotation rates (a fraction of { 0.0,0.2,0.4,0.6,0.8 } of the Keplerian rotation rate at the stellar surface) and use the abbreviation ω: = Ω∗/ΩK(R∗).
4.1.1. Dynamic structure of the disk
Figure 1 shows the angular rotation rate of the gas in units of the Keplerian rotation rate, 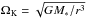 . We can clearly see that outside the BL, for r/R∗ ≳ 1.2, the gas rotates with the Keplerian angular velocity. When moving farther inwards, the gas rotates slightly super-Keplerian in order to compensate the large inward-pointing pressure gradient that is present in this region. Not until the gas is at a distance of less than a percent of the stellar radius does its angular velocity decrease to connect smoothly to the stellar rotation rate. The more the angular velocity differs from the Keplerian value, the more the gas loses radial stabilisation via the centrifugal force. This is, however, compensated by a large, now outward-pointing pressure gradient since the star has a much higher temperature and density and so the pressure is much higher than in the BL. Although the connection between the angular velocity of the gas and the star does not involve discontinuities, the angular velocity strongly changes in a very small region. The width of the BL is defined as the distance from the star (here R∗) to the point where the radial derivative of Ω(r) vanishes. We note that this point does not in general coincide with the point where ∂/∂r(Ω/ΩK) = 0. Table 1 gives an overview of the width of the BL for different stellar rotation rates. We also note that R∗ is not defined unambiguously owing to the continuous transition to the star, and the observed width may depend on the value of ℱ, see Eq. (21). With an increasing stellar rotation rate, the width of the BL decreases up to ω = 0.2 at first. After that, however, it gets wider again. In general, the width of the BL is governed by the viscosity, which in turn depends on the temperature and the surface density for the case of an α-prescription. An increasing temperature and surface density leads to a broadening of the BL region. A look at Fig. 4, which shows the temperature in the midplane of the disk, indicates, that the temperature in the disk decreases with increasing stellar rotation rate. This behaviour is in line with our expectations, since a faster moving star means less friction and therefore less heating. As a consequence of this overall temperature variation with ω, the faster the rotation of the star, the smaller the width of the BL; however, the surface density rises with increasing ω, as can be seen in the inset in Fig. 3, because of an increasingly inefficient mass transport through the disk (more mass can accumulate in the disk). This is the reason for the turnaround of the trend at ω = 0.2, when the BL starts to become broader again. Another interesting feature is the comparatively large width of the BL for ω = 0.8 that stands out both in Table 1 and Fig. 1, and does not match the shape of the other models. This effect is caused by a slightly different temperature evolution, as can be seen in the inset in Fig. 4. Here, as a result of reduced friction and hence less energy release, the green line (representing ω = 0.8) is missing a peak (compared to the other curves) and is wider than most other temperatures over a small region.
. We can clearly see that outside the BL, for r/R∗ ≳ 1.2, the gas rotates with the Keplerian angular velocity. When moving farther inwards, the gas rotates slightly super-Keplerian in order to compensate the large inward-pointing pressure gradient that is present in this region. Not until the gas is at a distance of less than a percent of the stellar radius does its angular velocity decrease to connect smoothly to the stellar rotation rate. The more the angular velocity differs from the Keplerian value, the more the gas loses radial stabilisation via the centrifugal force. This is, however, compensated by a large, now outward-pointing pressure gradient since the star has a much higher temperature and density and so the pressure is much higher than in the BL. Although the connection between the angular velocity of the gas and the star does not involve discontinuities, the angular velocity strongly changes in a very small region. The width of the BL is defined as the distance from the star (here R∗) to the point where the radial derivative of Ω(r) vanishes. We note that this point does not in general coincide with the point where ∂/∂r(Ω/ΩK) = 0. Table 1 gives an overview of the width of the BL for different stellar rotation rates. We also note that R∗ is not defined unambiguously owing to the continuous transition to the star, and the observed width may depend on the value of ℱ, see Eq. (21). With an increasing stellar rotation rate, the width of the BL decreases up to ω = 0.2 at first. After that, however, it gets wider again. In general, the width of the BL is governed by the viscosity, which in turn depends on the temperature and the surface density for the case of an α-prescription. An increasing temperature and surface density leads to a broadening of the BL region. A look at Fig. 4, which shows the temperature in the midplane of the disk, indicates, that the temperature in the disk decreases with increasing stellar rotation rate. This behaviour is in line with our expectations, since a faster moving star means less friction and therefore less heating. As a consequence of this overall temperature variation with ω, the faster the rotation of the star, the smaller the width of the BL; however, the surface density rises with increasing ω, as can be seen in the inset in Fig. 3, because of an increasingly inefficient mass transport through the disk (more mass can accumulate in the disk). This is the reason for the turnaround of the trend at ω = 0.2, when the BL starts to become broader again. Another interesting feature is the comparatively large width of the BL for ω = 0.8 that stands out both in Table 1 and Fig. 1, and does not match the shape of the other models. This effect is caused by a slightly different temperature evolution, as can be seen in the inset in Fig. 4. Here, as a result of reduced friction and hence less energy release, the green line (representing ω = 0.8) is missing a peak (compared to the other curves) and is wider than most other temperatures over a small region.
 |
Fig. 1 Angular velocity Ω = uϕ/r in terms of the Keplerian angular velocity for a central star with mass M∗ = 1.0 M⊙ and five different stellar rotation rates Ω∗, denoted by ω = Ω∗/ΩK(R∗). The plot depicts two regions separated by a light grey bar that differ in the radial scaling and enable us to show both the rapid variation in the BL and the constant overall trend. |
Width of the BL for M∗ = 1.0 M⊙ and different stellar rotation rates ω = Ω∗/ΩK(R∗).
 |
Fig. 2 Radial Mach number of the gas for a stellar mass of 1.0 M⊙. The Mach number is defined as a quotient of radial velocity and the sound speed Ma = | ur | /cs. The different colours correspond to the different stellar rotation rates ω = Ω∗/ΩK(R∗). The smaller box inside the graph is a zoom in of the inner edge; the light grey frame denotes the zoom area. |
 |
Fig. 3 Surface density Σ ~ ρH (log-scale) of the disk and a stellar mass of 1.0 M⊙ for five different stellar rotation rates ω = Ω∗/ΩK(R∗). The inset is a zoom in of the inner edge; the light grey frame denotes the zoom area. |
The Mach number of the gas, which is defined as the quotient of the radial velocity and the speed of sound Ma = | ur | /cs is shown in Fig. 2. Since the radial velocity is negative throughout the computational domain, in principle the Mach number outlines the velocity of the radially inward-falling material. While the gas is moving inwards with a rather low velocity over most parts of the disk, there is a distinct maximum of the radial velocity in the BL. What drives the material to move inwards more rapidly in the BL is the loss of angular momentum caused by friction in the disk. Hence the radial velocity is increasing strongly in the BL region, as can be observed in the inset in Fig. 2. After peaking in the BL, the radial velocity decreases again as the gas approaches the surface of the star. Here, the gas slows down as it settles onto the atmosphere of the star, where the individual layers are stabilized by the pressure (hydrostatic balance). The inflow velocity of the gas depends on how much angular momentum can be removed from the material, which in turn is dependent on the strength of the shearing. Accordingly, the faster the stellar rotation rate, the weaker is the shearing in the disk and hence the radial velocity should decrease with increasing stellar rotation rate in the BL. We can observe this trend in Fig. 2 where we can also see that the radial velocity is clearly subsonic throughout the computational domain and especially in the BL. Thus there are no problems concerning causality (e.g. Pringle 1977) in our simulations because of the small value of α.
4.1.2. Thermal structure of the disk
In the previous section, we looked closely at the dynamical structure of the disk and the BL, which is determined by the radial and azimuthal velocities. From an observational point of view, however, we are much more interested in the thermodynamics of the disk, since the quantity that we can actually observe, the emitted radiation, depends on the temperature; therefore, we will now explore the surface density and the temperature structure of our models.
The surface density Σ for the 1.0 M⊙ model is shown in Fig. 3. We can observe a heavy depletion of material in the BL. The surface density drops by approximately two orders of magnitude compared to the weakly varying value in the disk. If we go farther in, the surface density rises rapidly since we encounter the surface of the star which has a density that is orders of magnitudes higher than in the disk. The reason for the strong decrease of the surface density in the BL is the aforementioned increase in inflow velocity. Since for the equilibrium state the mass accretion rate Ṁ is constant throughout the disk (see also Fig. 9 below), a local increase in inflow velocity leads to a reduced density at this point. The BL resembles a bottleneck with a higher velocity and a lower density. In the disk the distinction between models with different values of ω is very small; it is more pronounced in the BL. The models with a slower rotating star have a smaller surface density in the BL that is accounted for by the greater inflow velocity.
 |
Fig. 4 Temperature Tc in the midplane of the disk, i.e. z = 0, for M∗ = 1.0 M⊙. The five models displayed differ in the stellar rotation rate ω = Ω∗/ΩK(R∗). The inset is a zoom in of the inner edge; the light grey frame denotes the zoom area. The small peak in the inset is a clear indication of a hot BL. |
Even more interesting than the density structure is the temperature of the disk. In our one-dimensional models, we distinguish between the temperature in the midplane of the disk Tc and the effective or surface temperature, which is close to the disk temperature at τ ≈ 1. Figure 4 shows the midplane temperature for M∗ = 1.0 M⊙ and five different stellar rotation rates. The local heat production is proportional to the square of the shear. Hence in the disk the temperature decreases with increasing radius r. In the BL, Ω reaches its maximum and the shear in the gas vanishes; therefore, there is a location in the disk where the viscous dissipation vanishes and the local heating is approximately zero (apart from pressure work). For that reason, the temperature must drop in the region where ∂Ω/∂r = 0, so in or near the BL. The minimum of Tc does, however, not coincide with the maximum of Ω, since heat is transported radially through the disk via advection and radiation. Furthermore, the cooling of the disk through emission of radiation depends on the local optical depth and hence is different at each location. On the other hand, after the zero-gradient point of Ω, the shearing is very strong where the angular velocity connects to the stellar rotation rate. As a consequence, the temperature again rises, whereby the considerably declined surface density compensates the strong shearing to some extent. The little peak in Tc, which is located very close to the star in the BL, is a result of the heat production in the BL (see the inset in Fig. 4) and is a clear indication of a hot BL. The influence of the stellar rotation rate on the temperature is twofold. In the disk, the temperature is slightly hotter for faster stellar rotation rates because of the larger surface density. This trend is reversed in the area of the BL, where a smaller rotation rate causes more shear and supersedes the influence of the surface density. A special case is obviously given for very fast rotating stars, as can be seen in Fig. 4 for ω = 0.8, where the BL is broader and is missing a peak in the midplane temperature. The overall temperature regime of 400 000 to 840 000 Kelvin is very hot.
 |
Fig. 5 Effective temperature Teff of the disk, calculated according to Eq. (16). The plot shows five different models, all of which have the same stellar mass of 1.0 M⊙, but different stellar rotation rates ω = Ω∗/ΩK(R∗). The plot depicts two regions separated by a light grey bar that differ in the radial scaling and enable us to show both the narrow but very distinct peak of the effective temperature in the BL and the nearly constant behaviour in the disk all in one graph. |
While the temperature shown in Fig. 4 corresponds to the temperature in the midplane of the disk, we are particularly interested in the emergent spectrum from the disk, which – in the LTE approximation – is determined by the temperature on the surface, see Eq. (16). The effective temperature Teff is shown in Fig. 5 for the M∗ = 1.0 M⊙ case. For outer parts of the simulation domain, Teff changes only slightly and the difference in temperature between various choices of ω is hardly noticeable. The reason for the almost constant behaviour of the effective temperature in the disk is the strong increase in the BL that somewhat masks the variation in the disk. While the midplane temperature changes at most by a factor of 2 over the whole simulation area, the effective temperature changes considerably more, by a factor of 4–5. This is caused by a strong drop in the optical depth in the BL by several orders of magnitude due to the drop of the surface density. While, generally, the accretion disk is optically thick, under certain circumstances, the BL can become optically thin, since the dilution of matter is severe in this region. While the shear and the energy production are confined to a small region called the dynamical BL, the release of the produced energy occurs over a slightly wider area, called the thermal BL (Regev & Bertout 1995; Popham & Narayan 1995). Therefore, the peak in Fig. 5 is less intense than the one in Fig. 4, but instead it is wider because of the radial diffusion. According to what has already been said above, the magnitude of the peak of Teff in the BL depends on the stellar rotation rate to the effect that a slower rotating star causes more shear in the BL, hence a higher energy dissipation and eventually a higher effective temperature.
 |
Fig. 6 Scale height H (see Eq. (2)) of the disk for M∗ = 1.0 M⊙ and five different stellar rotation rates ω = Ω∗/ΩK(R∗). The disk is obviously very thin and not flared. In the BL, it is puffed up to some extent, which is, however, not unexpected. The inset is a zoom in of the inner edge; the light grey frame denotes the zoom area. |
Finally, we investigate the vertical extent of the disk. According to Sect. 2.1, a measure for the height is the variable H, which is the point where the density drops by a factor of 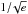 compared to the midplane density. The scale height H(r) is depicted in Fig. 6 for the 1.0 M⊙ model. The disk in the system is, according to our simulations, rather thin with an aspect ratio h = H/r of roughly h = 0.029 (arithmetic mean) and has a slope of dH/dr ≈ 0.05. In the region of the BL, the disk height increases noticeably because of the strong growth of temperature in the BL that causes a high pressure which puffs up the disk in the innermost region. Figure 6 confirms the picture of the BL being a bottleneck that we introduced earlier. When approaching the BL from the outside, the disk first starts to get thinner and thinner until it suddenly grows in height. In the disk the vertical extent is nearly identical for different ω, but in the BL it clearly depends on the stellar rotation rate. The faster the star spins, the less puffed out the BL is. We have already pointed out, that the temperature depends on the stellar rotation rate. Since the pressure depends on the temperature, the scale height in the BL changes with different stellar rotation rates.
compared to the midplane density. The scale height H(r) is depicted in Fig. 6 for the 1.0 M⊙ model. The disk in the system is, according to our simulations, rather thin with an aspect ratio h = H/r of roughly h = 0.029 (arithmetic mean) and has a slope of dH/dr ≈ 0.05. In the region of the BL, the disk height increases noticeably because of the strong growth of temperature in the BL that causes a high pressure which puffs up the disk in the innermost region. Figure 6 confirms the picture of the BL being a bottleneck that we introduced earlier. When approaching the BL from the outside, the disk first starts to get thinner and thinner until it suddenly grows in height. In the disk the vertical extent is nearly identical for different ω, but in the BL it clearly depends on the stellar rotation rate. The faster the star spins, the less puffed out the BL is. We have already pointed out, that the temperature depends on the stellar rotation rate. Since the pressure depends on the temperature, the scale height in the BL changes with different stellar rotation rates.
4.2. Dependence on the stellar mass
After having discussed the basic properties of the BL using the example of a solar mass white dwarf, we now focus on the dependence of the BL on the stellar mass. First, we will again examine the dynamical structure of the BL (see Table 2 and Fig. 12). The shape of the angular velocity profile is identical for each of the three stellar masses. There is, however, a difference in the width of the BL. The higher the stellar mass, the less broad is the BL. Table 2 shows the width of the BL for the three different stellar masses and two different stellar rotation rates, along with the maximum value of Ω for ω = 0.0. Here it becomes more obvious that the width of the BL strongly depends on the mass of the central star. The absolute value of the angular velocity also depends on the stellar mass and varies significantly. The reason for the decreasing width of the BL is the mass radius relation of white dwarfs. The more massive the star is, the smaller the stellar radius R∗ is. This causes a non-linear variation of gravity and so affects the width of the BL. The Mach number stays more or less the same and the inflow occurs subsonically throughout all models.
Width of the BL for three different stellar masses and the stellar rotation rates of ω = 0.0 and ω = 0.8.
The dynamical structure is affected by the mass of the central star, and also the thermodynamics of the BL. To gain more insight into this dependence, we first consider the surface density Σ for the different models. The general trend of the 0.8 and 1.2 M⊙ models is closely related to that shown in Fig. 3. We note, however, that the more massive the central star is, the higher the surface density in the BL and in the disk is, for the same reason as for the decrease of the BL width, namely a lower effective viscosity. If the viscosity becomes smaller, the transport of matter through the disk is not as effective as it is for a higher viscosity because the shear viscosity drives the accretion of matter. Thus, more matter can accumulate in the disk and the surface density rises. Again, the minima of Σ are located at different radii, corresponding to different widths of the BL. Apart from these features, the evolution of the surface density looks identical for different stellar masses. The midplane temperature, on the other hand, shows considerable differences in magnitude between the three models. As Table 3 shows, the 1.2 M⊙ model is hotter than the 0.8 M⊙ by a factor of 1.7 throughout the BL and the disk. This is due to the higher surface density in the high stellar mass model. Since the viscous dissipation is proportional to the surface density, an increasing Σ ensures an increase in the midplane temperature. This effect prevails, although the viscosity is, as we have seen, smaller than in the low mass models.
A direct comparison is shown in Fig. 7, where we have plotted Tc for the three different stellar masses and ω = 0.4 in one single diagram. This makes it clear how the midplane temperature increases overall with increasing stellar mass.
Table 3 also describes the effective temperature Teff for the three different masses, whose general trend is given by Fig. 5. As we have expected, the more massive the central star is, the higher the effective temperature of the BL (and also the disk) is and the harder the radiation emerging from the BL is, because of the ratio of stellar mass and radius, which exclusively determines the total amount of accretion energy that is released in the disk and the BL. The total luminosity that can be extracted from the process of accretion on a body with mass M and radius R is given by 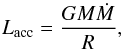 (22)where Ṁ is the mass accretion rate and G the gravitational constant. The luminosity of the BL is at most one half of Lacc. Therefore, the greater the relation M∗/R∗, the higher the effective temperature. The inverse mass-radius-relation of white dwarfs enhances Lacc even more. We can also see that the width of the thermal BL follows the trend of the dynamical BL. With increasing stellar mass, the width of the peak of Teff decreases. Again, we have plotted all three stellar masses in one diagram (Fig. 8) that emphasizes the points mentioned above. To give an overview of the radiation energy that corresponds to these temperatures, we focus on two models that are located at the opposite edges of the parameter space. The ω = 0.0,1.2 M⊙ model peaks at nearly 700 000 Kelvin. This corresponds to a black body radiation spectrum where the maximum of the distribution is located at a photon energy of 300 eV. The other model, where the parameters are given by ω = 0.8,0.8 M⊙, peaks at an effective temperature of about 170 000 Kelvin. This corresponds to a photon energy of 73 eV at the maximum of the black body spectrum. The effective temperature, or in other words, the spectrum emerging from the BL, is obviously a good way to try to determine the actual mass of the white dwarf in cataclysmic variable systems.
(22)where Ṁ is the mass accretion rate and G the gravitational constant. The luminosity of the BL is at most one half of Lacc. Therefore, the greater the relation M∗/R∗, the higher the effective temperature. The inverse mass-radius-relation of white dwarfs enhances Lacc even more. We can also see that the width of the thermal BL follows the trend of the dynamical BL. With increasing stellar mass, the width of the peak of Teff decreases. Again, we have plotted all three stellar masses in one diagram (Fig. 8) that emphasizes the points mentioned above. To give an overview of the radiation energy that corresponds to these temperatures, we focus on two models that are located at the opposite edges of the parameter space. The ω = 0.0,1.2 M⊙ model peaks at nearly 700 000 Kelvin. This corresponds to a black body radiation spectrum where the maximum of the distribution is located at a photon energy of 300 eV. The other model, where the parameters are given by ω = 0.8,0.8 M⊙, peaks at an effective temperature of about 170 000 Kelvin. This corresponds to a photon energy of 73 eV at the maximum of the black body spectrum. The effective temperature, or in other words, the spectrum emerging from the BL, is obviously a good way to try to determine the actual mass of the white dwarf in cataclysmic variable systems.
Illustration of the midplane and effective temperature for the models with 0.8 and 1.2 M⊙.
 |
Fig. 7 Comparison of the temperature in the disk midplane Tc of the three different models with stellar masses of 1.0,0.8, and 1.2 M⊙. The stellar rotation rate Ω has been chosen to amount to 0.4ΩK, as an illustrative case. It is clearly observable that with increasing stellar mass the temperature in the disk also rises. |
 |
Fig. 8 Analogous to Fig. 7, we compare the effective temperatures of the three different stellar masses (1.0,0.8, and 1.2 M⊙) in this plot. Again, Ω = 0.4ΩK has been chosen as an example of the stellar rotation rate. We note that the effective temperature rises with increasing stellar mass. |
Finally, we want to have a look at the vertical structure of the disk. The scale height H of the different models again follows the trend of Fig. 6. The aspect ratio of the 0.8 M⊙ model is H/r ≈ 0.032, while the model with 1.2 M⊙ is slightly thinner with H/r ≈ 0.026. The solar mass model lies in between with H/r ≈ 0.029, as has been said earlier. We can therefore deduce that with increasing stellar mass, the vertical extent of the accretion disk diminishes. This also holds true for the BL, even though the midplane temperature is much higher in the high mass model and accordingly the pressure will try to puff out the BL with much more force. However, the gravitational field of the central star exerts a force against the pressure and is strong enough to outrange it. The disks are still not flared for all three stellar masses.
4.3. Mass accretion rate and angular momentum flux
 |
Fig. 9 Mass accretion rate Ṁ = −2πrΣur for M∗ = 1.0 M⊙ and five different stellar rotation rates ω = Ω∗/ΩK(R∗). The imposed value equals Ṁ = 1.51 × 10-8 M⊙ yr-1. Since Ṁ is constant in a stationary state, this plot is also an indication that a good equilibrium has been reached. |
For a stationary state the continuity Eq. (3) reduces to Ṁ = −2πrΣur, where Ṁ is the constant mass accretion rate that represents the amount of mass flowing through an annulus at a given radius per time. Since we imposed a mass accretion rate of Ṁ = 1.51 × 10-8 M⊙/yr at the outer boundary, we require Ṁ to attain this value throughout the disk if a steady state is reached. The mass accretion rate after a simulation time of about 10 000 orbits at r = R∗ is shown as an example in Fig. 9 for the 1.0 M⊙ model. At first glance, the attained equilibrium state looks very good and stable. The maximum deviation from the imposed value is only about 4% for the heaviest white dwarf. The most constant Ṁ is reached for the models that correspond to ω = 0.8. Apart from the inner and outer boundary, where Ṁ matches the imposed value to an accuracy of far less than one percent, the agreement between the simulation and the imposed value is perfect. This holds true for any of the three stellar masses. However, with decreasing stellar rotation rate and increasing stellar mass the mass accretion rate starts to deviate slightly from the constant value of 1.51 × 10-8 M⊙/yr. The deviations near the outer boundary, however, are induced by the boundary conditions.
Another quantity that should attain a constant value in the steady state, is the angular momentum flux 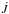 . It plays the role of an eigenvalue in the stationary equations, whose value has to be determined while solving the set of equations (Popham & Narayan 1995; Kley & Papaloizou 1997). In our model, the total angular momentum flux is composed of the angular momentum carried in with the accreting material, and the angular momentum transported by shear viscosity. Therefore, it is given as
. It plays the role of an eigenvalue in the stationary equations, whose value has to be determined while solving the set of equations (Popham & Narayan 1995; Kley & Papaloizou 1997). In our model, the total angular momentum flux is composed of the angular momentum carried in with the accreting material, and the angular momentum transported by shear viscosity. Therefore, it is given as 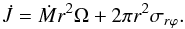 (23)Usually, the angular momentum (AM) flux is displayed as the normalized, dimensionless j, which is
(23)Usually, the angular momentum (AM) flux is displayed as the normalized, dimensionless j, which is 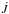 from Eq. (23) divided by the advective AM flux at the surface of the star,
from Eq. (23) divided by the advective AM flux at the surface of the star, 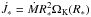 . This value is shown in Fig. 10 for the 1 M⊙ star. Again, good equilibrium states have been reached, since the deviations of j are very small. We also note the same trend as for the mass accretion rate: with increasing stellar mass and decreasing stellar rotation rate the deviations gain in strength. Since j is an eigenvalue in the stationary equations, it should be constant throughout the domain. For convenience, Ṁ is defined to be positive when mass is flowing to the center of the accretion disk and
. This value is shown in Fig. 10 for the 1 M⊙ star. Again, good equilibrium states have been reached, since the deviations of j are very small. We also note the same trend as for the mass accretion rate: with increasing stellar mass and decreasing stellar rotation rate the deviations gain in strength. Since j is an eigenvalue in the stationary equations, it should be constant throughout the domain. For convenience, Ṁ is defined to be positive when mass is flowing to the center of the accretion disk and 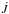 is positive for inward-moving angular momentum (see Eq. (23)). Therefore, the net flux of angular momentum is directed inward and the absolute value is slightly above the advected angular momentum at the stellar surface and equals the accreted angular momentum of the star. The mean values of the normalized total angular momentum fluxes for ω = 0.0 and ω = 0.8 are given in Table 4, along with the numerical value of the corresponding
is positive for inward-moving angular momentum (see Eq. (23)). Therefore, the net flux of angular momentum is directed inward and the absolute value is slightly above the advected angular momentum at the stellar surface and equals the accreted angular momentum of the star. The mean values of the normalized total angular momentum fluxes for ω = 0.0 and ω = 0.8 are given in Table 4, along with the numerical value of the corresponding 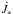 in cgs-units. These values of j correspond very nicely with those found by other numerical calculations, for example by Popham & Narayan (1995) who obtained a value of j = 1.01 for a 0.6 M⊙ mass white dwarf with a radius of 8.7 × 108 cm and a mass accretion rate Ṁ = 10-8 M⊙ yr-1. Other deviations from the parameters used here are the usage of a different viscosity prescription and α = 0.1. We have run a test calculation with their set of parameters and were able to reproduce j nearly perfectly.
in cgs-units. These values of j correspond very nicely with those found by other numerical calculations, for example by Popham & Narayan (1995) who obtained a value of j = 1.01 for a 0.6 M⊙ mass white dwarf with a radius of 8.7 × 108 cm and a mass accretion rate Ṁ = 10-8 M⊙ yr-1. Other deviations from the parameters used here are the usage of a different viscosity prescription and α = 0.1. We have run a test calculation with their set of parameters and were able to reproduce j nearly perfectly.
 |
Fig. 10 Normalized angular momentum flux |
The advected AM flux is pointing inward throughout the disk since the radial velocity ur only attains negative values, that is, matter is only moving to the center of the disk. The transport of AM due to shear viscosity, on the other hand, changes its direction at the zero-gradient location, which is the radius where ∂Ω/∂r = 0 (and also the beginning of the BL, coming from the outside). Thus, in the disk, angular momentum is transported outward by the shear viscosity, while in the BL, it is transported inward. The sum of 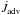 and
and 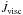 remains constant. This means that in the disk, where
remains constant. This means that in the disk, where 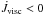 , the advected angular momentum flux must be greater than the total flux,
, the advected angular momentum flux must be greater than the total flux, 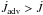 . In the BL, however, the viscous AM flux becomes positive and therefore
. In the BL, however, the viscous AM flux becomes positive and therefore 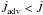 . At the inner boundary,
. At the inner boundary, 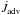 drops to nearly zero because ur drops to nearly zero. Hence,
drops to nearly zero because ur drops to nearly zero. Hence, 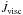 must be approximately equal to
must be approximately equal to 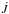 although there is only very weak shearing. Here, νΣ becomes very large, since the radial velocity is very small and the temperature is very high, which produces a high viscosity. If we compare the models with different stellar masses, we find that
although there is only very weak shearing. Here, νΣ becomes very large, since the radial velocity is very small and the temperature is very high, which produces a high viscosity. If we compare the models with different stellar masses, we find that 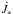 gets smaller with increasing stellar mass (see Table 4). Two points affect the absolute value of
gets smaller with increasing stellar mass (see Table 4). Two points affect the absolute value of 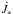 for different stellar masses. On the one hand, there is the mass-radius-relation of white dwarfs, meaning that with increasing mass, the stellar radius gets smaller. On the other hand, with increasing stellar mass, the Keplerian angular velocity also increases. Both effects together cause
for different stellar masses. On the one hand, there is the mass-radius-relation of white dwarfs, meaning that with increasing mass, the stellar radius gets smaller. On the other hand, with increasing stellar mass, the Keplerian angular velocity also increases. Both effects together cause 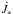 to decrease only weakly with increasing stellar mass. The values of j also decrease with increasing stellar mass. While
to decrease only weakly with increasing stellar mass. The values of j also decrease with increasing stellar mass. While 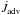 gets slightly bigger with increasing stellar mass (Ṁ is equal for all models and equals the imposed value while the angular velocity increases),
gets slightly bigger with increasing stellar mass (Ṁ is equal for all models and equals the imposed value while the angular velocity increases), 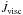 also has to be larger to yield a smaller value of j. The reason for the increasing AM transport by viscosity is that the disk has a higher surface density and midplane temperature and thus a greater viscosity. We also observe a clear trend concerning the various values of j for different stellar rotation rates ω and constant stellar mass. With increasing stellar rotation rate Ω∗, j clearly decreases, as it also does with increasing stellar mass and constant rotation rate. Both trends were also found by Popham & Narayan (1995). From Eq. (23) we deduce that in the disk,
also has to be larger to yield a smaller value of j. The reason for the increasing AM transport by viscosity is that the disk has a higher surface density and midplane temperature and thus a greater viscosity. We also observe a clear trend concerning the various values of j for different stellar rotation rates ω and constant stellar mass. With increasing stellar rotation rate Ω∗, j clearly decreases, as it also does with increasing stellar mass and constant rotation rate. Both trends were also found by Popham & Narayan (1995). From Eq. (23) we deduce that in the disk, 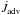 must be nearly the same for every ω. In the BL, by contrast, it increases with higher stellar rotation rate since Ω does not drop as much. It is harder to make a reliable point concerning
must be nearly the same for every ω. In the BL, by contrast, it increases with higher stellar rotation rate since Ω does not drop as much. It is harder to make a reliable point concerning 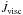 . In the disk, however, both the midplane temperature and the density are slightly greater for increasing ω (see Figs. 3 and 4), yielding a higher viscosity and hence a greater
. In the disk, however, both the midplane temperature and the density are slightly greater for increasing ω (see Figs. 3 and 4), yielding a higher viscosity and hence a greater 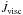 . This explains the smaller values of j in the disk. In the BL, however, the situation is not as clear, since the surface density increases with ω while the midplane temperature decreases.
. This explains the smaller values of j in the disk. In the BL, however, the situation is not as clear, since the surface density increases with ω while the midplane temperature decreases.
Normalized angular momentum flux j for three different stellar masses and two different stellar rotation rates.
4.4. Comparison with other BL models and equatorial radius increase
In this section we put our simulations in context with other work, that has been done in the field of BLs. As has been mentioned before, our results are closely related to those presented in Popham & Narayan (1995, hereafter PN95), at least qualitatively. However, the approach we took is quite different from this work. While Popham & Narayan have used the time-independent equations and performed stationary calculations, we have also propagated the physical quantities in time. Therefore, we are able to study time-dependent phenomena as well and we are not limited by the prerequisite that a stationary state exists for the given choice of parameters. Also, as we have seen in the last section, the BL is in permanent motion, even though most physical quantities do not change perceptibly. We have seen this by analysing the constant parameters Ṁ and j. Other differences involve the treatment of the radiation in the equations. While the authors of the quoted publication have taken care of the radiation field by adding an expression to the gas pressure, hence defining a total pressure, we have explicitly added the radiation force term in the momentum equation and a special pressure work term in the energy equation, both in the flux limited diffusion approximation. Although both approaches are identical in the optically thick limit, this is not necessarily the case for the optically thin and transition regions.
In order to compare our results quantitatively with the computations of Popham & Narayan (1995), we ran a set of simulations with the same parameters, the basis of which is their standard model. It is composed of a 0.6 M⊙ white dwarf with a radius of 8.7 × 108 cm and a mass accretion rate of Ṁ = 10-8 M⊙/yr. The white dwarf does not rotate and they used a special viscosity prescription (see Eq. (19)) and a α-parameter of 0.1. For the standard model, we found a dynamical BL width of Δr = 1.017 R∗, which is exactly the same as in PN95, and an AM flux of j = 1.004, as opposed to jPN95 = 1.00994. The dynamical quantities, viz. Ω and ur, match the calculations of PN95 very closely (~ 1%). Only the peak value of the infall velocity deviates by about 10%. The peak position, on the other hand, is accurate to about 0.4%. The good agreement is also reflected in the thermodynamical quantities, namely the disk and the surface temperatures Tc and Teff. The second has a peak value in the BL of 227 000 K and about 54 000 K in the disk. Both temperatures agree to approximately one percent with the results of PN95. While the peak position of the midplane temperature Tc accurately matches that of PN95, our Tc as a whole is about 30% hotter. It is, however, Teff that determines the emergent spectra of the BL and the disk, and since we find a very good match here, we conclude that our simulations are in very good agreement with the results of PN95.
Starting from the standard model described above, we performed the same Ω∗ parameter study as in Popham & Narayan (1995). We have done this in particular to state an important point that has not been taken into account in the simulations shown above. Since the white dwarf flattens out considerably with increasing Ω∗, in principal we have to consider an equatorial radius increase. The radius of a rotating white dwarf in turn has to be calculated from stellar structure simulations. However, one finds (see e.g. Hachisu 1986) that for moderately rotating white dwarfs (ω ≲ 0.8), R∗ increases at most by a factor of ~ 1.4. The change in stellar radius affects the effective temperature of the BL and the disk through Eq. (22), yielding slightly smaller values. This is in agreement with the standard solution for accretion disks, where the radius enters the effective temperature to the power − 3/4. Because of the non-linear variation of gravity, the width of the BL also changes somewhat. Owing to the minor effect of the small radius increase and since the majority of white dwarfs are supposed to be slow rotators (Livio & Pringle 1998; Sion & Godon 2012), we have neglected this effect in the simulations above. Nevertheless, we want to illustrate the equatorial radius increase on the basis of the fastest rotating white dwarf in the aforementioned Ω∗ study, which has a rotation rate in terms of the fraction of the breakup rotation rate of ω = 0.86.
The width of the dynamical BL changes from Δr ≈ 1.018 R∗ for the model with equatorial radius increase (M1, R∗ ≈ 1.25 × 109 cm) to Δr ≈ 1.017 R∗ for the model without an increase in radius (M2), i.e. R∗ = 8.7 × 108 cm. This is a variation of about one per mill. The difference concerning the normalized AM flux j between both models is even smaller, where jM1 = 1.0038 and jM2 = 1.0033. The agreement of the angular velocities is very good, as can be seen from the width of the BL. The radial velocities of both models do match each other very closely, as well. However, the absolute peak value of M2 is about 15% greater than that of M1. If instead we compare the Mach numbers, the deviation shrinks to about 1%, but the differing radii manifest themselves more obviously in the disk and effective temperature of the models. Thus, the disk temperature Tc of model M2 is about 30% higher throughout the whole domain which comes to approximately 40 000 K. This is due to the greater gravitational pull for smaller radii. We also find the same 30% deviation in the surface temperature Teff, although here it accounts for only 13 000 K because of the lower temperature regime of the surface temperature. Apart from this vertical shift, both graphs are identical, meaning that the peak is at the same location and the thermal BL has the same radial extent. Model M1 peaks at ~ 65 000 K in the BL.
Godon et al. (1995) used a time-dependent spectral numerical code and performed one-dimensional calculations of the BL that are closely related to ours. The aim of their simulations was to investigate the influence of the thermal inner boundary condition, which can lead to both cool and hot BLs, depending on whether the temperature is held fixed at the inner boundary or the flux of the star is fed into the computational domain. We have performed a simulation for the case of flux BC with the same parameter choice as in Godon et al. (1995), their model 3, and were able to reproduce the results very closely.
4.5. Simulations with larger domain
For the Navier-Stokes equations it is still uncertain whether the same solution is reached for a small, bounded domain as for an unbounded domain. Of course, we cannot simulate our problem on an unbounded domain. We can, however, prove that the solution we presented above does not depend on the choice of the domain. In order to do this, we ran a test simulation, where we enlarged the computational domain by a factor of 10, so that it reaches from r = 1 R∗ up to r = 10 R∗. Except for the number of grid cells, all parameters were chosen according to the 0.8 M⊙,0.4ΩK model. We find a nearly perfect agreement between the models with the small and the large domain. Differences are, apart from the boundaries, nearly imperceptible, except for the disk temperature, where the larger domain overestimates the peak temperature in the BL by approximately 5%. This is, however, due to the lower resolution of the model in this region.
Finally, to show the agreement of our models with the standard solution for accretion disks by Shakura & Sunyaev (1973), we compare our results with the analytically derived formulae for thin accretion disks. Since these equations are supposed to be a good approximation in the disk, we used the model with the large domain for the comparison, so that we could also compare both solutions in the disk over a farther region. The equations of a Shakura-Sunyaev-type solution can, for example, be found in Frank et al. (2002). In these equations, we have modified the typical factor [1 − (R∗/R)1/2] by a factor of the form [1 − j(R∗/R)1/2], where j is the normalized angular momentum flux. The solution cuts off not at R∗, but a little farther outside (~ 1.02 R∗). We find that the S-S-type solution provides a very good approximation of the physical variables in the disk. In the BL the standard solution is insufficient. We also find that the surface temperature of our simulation peaks at r = 1.4092 R∗ in the disk (there is also a far more distinct peak in the BL). The S-S standard solution for the surface temperature reads ![\begin{equation} T(r) = \left\{\frac{3GM_\ast\dot{M}}{8\pi r^3\sigma_\text{SB}}\left[1-j\left(\frac{R_\ast}{r}\right)^{1/2}\right]\right\}^{1/4}.\label{eq:teff_standard} \end{equation}](/articles/aa/full_html/2013/12/aa22542-13/aa22542-13-eq294.png) (24)If we plug j = 1.0175 into Eq. (24), which is the normalized angular momentum flux for this simulation, we find that the above function T(r) has a maximum at r ≈ 1.4093. Thus, our simulation is in perfect agreement with the theoretically derived formula. The temperature in Eq. (24) peaks at a value of Tmax ≈ 0.475T∗, where T∗ is defined by
(24)If we plug j = 1.0175 into Eq. (24), which is the normalized angular momentum flux for this simulation, we find that the above function T(r) has a maximum at r ≈ 1.4093. Thus, our simulation is in perfect agreement with the theoretically derived formula. The temperature in Eq. (24) peaks at a value of Tmax ≈ 0.475T∗, where T∗ is defined by 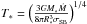 . According to (24), for our model this means that the temperature peaks at Tmax = 74 406 K. The simulation shows a temperature of T = 74 335 K of the peak of the surface temperature in the disk. Again, this is in perfect agreement with the theoretical value. Having matched the other quantities of our simulations against the S-S standard solution as well, we come to the conclusion that outside the BL, our simulations are perfectly described by the standard solution.
. According to (24), for our model this means that the temperature peaks at Tmax = 74 406 K. The simulation shows a temperature of T = 74 335 K of the peak of the surface temperature in the disk. Again, this is in perfect agreement with the theoretical value. Having matched the other quantities of our simulations against the S-S standard solution as well, we come to the conclusion that outside the BL, our simulations are perfectly described by the standard solution.
5. Summary and conclusion
We have presented new models of the structure of the BL around white dwarfs in compact binary star systems. One-dimensional, time dependent radial models have been constructed which include radiative diffusion in the radial direction, vertical cooling from the disk surfaces, and radiative pressure effects.
For a fixed mass accretion rate of Ṁ = 1.51 × 10-8 M⊙/yr, which corresponds to systems in outburst, we have analysed the BL for different masses and rotation rates of the white dwarf.
The strong shear in the BL region leads to an enormous energy release and to surface temperatures of a few hundred thousand Kelvin. For a non-rotating white dwarf (with 1 M⊙) the maximum temperature is about 500 000 K, while for a star rotating with ω = 0.8 of the break-up velocity the maximum is about 200 000 K. Hence, knowledge of the white dwarf mass, for example through a dynamical mass estimate of the binary star, and of the mass accretion rate, allows an estimate of the stellar rotation rate through the observed peak temperatures. Radial diffusion of energy leads to a more extended thermal BL with a width of typically 0.02 to 0.05 R∗. The models for slow rotation showed a tendency for instability due to the very high temperatures, small vertical thicknesses, and resulting low optical depths.
For the viscosity we use the α-parametrisation with α = 0.01. For this value, the radial velocity remains subsonic throughout with maximum radial Mach numbers of 0.35 for ω = 0 and 0.18 for ω = 0.8. A higher value of α = 0.1 left the disk structure unchanged and Mach numbers close to unity within the BL.
Varying the stellar mass leads to hotter BL for larger masses (and smaller radii) and cooler BL for smaller masses. Hence, when trying to infer stellar parameter through an analysis of the BL radiation one is faced with an ambiguity that models with different combinations of R∗ and ω∗ may yield similar peak temperatures. There is the indication, however, that the width of the thermal BL is different in these cases, such that the model spectra will lead to different results. In this paper we did not calculate synthetic, theoretical spectra for our numerical models, but leave that for a future paper.
The validity of our simulations has been demonstrated convincingly by comparing the results with related calculations and with the standard solution for thin accretion disks by Shakura & Sunyaev (1973). We found very good agreement with our results, both in the disk where the standard solutions holds true, and in the BL, where we were able to reproduce basic features shown in other works and match their results to an accuracy of about one percent for the dynamical and observed quantities. We also showed that our results are independent of the computational domain and the resolution. Simulations that have the same parameters, except for the simulation area, do match each other perfectly.
An equatorial radius increase due to a flattening of a fast rotating white dwarf in our simulations showed the following results. Even for the unlikely case of a rotation rate of 86% of the breakup rotation rate, the variation of the physical quantities that differ most is in the range of 30%, according to whether we take the flattening into account or not. The width of the thermal BL, which is also important for the emergent spectra, does not change perceptibly, however. For a 0.6 M⊙ white dwarf, the shift in the effective temperature is of the order of 10 000 K.
Analysing the data of our simulations, we also found that the consideration of radiation energy is indeed necessary in our models. We see this from the radiation pressure Prad = aT4/3, which becomes comparable to the thermal pressure P in the BL and even exceeds it by a factor of the order of unity for a small radial extent. If Prad is not taken into account in the simulations, the effective temperature peaks at far higher temperatures and the width of the thermal BL is distinctly smaller because of the lack of the widening effect of Prad.
Owing to the slim disk approximation, our models do not allow us to answer the question of how the material settles onto the central white dwarf. This question can only be answered by two dimensional r-z simulations, similar to those by Balsara et al. (2009) but with radiative transport (Kley 1991). The strong shear in the BL can lead to unstable behaviour when considering the ϕ-direction, as described by Belyaev et al. (2012) for isothermal disks. This behaviour could not be found in our simulations as they are purely radial. The next step would be to extend these to two-dimensional r-ϕ disks.
Additional figures can be found at: http://www.tat.physik.uni-tuebingen.de/~hertfelder/BL2013.
Acknowledgments
M. Hertfelder received financial support from the German National Academic Foundation (Studienstiftung des deutschen Volkes). The work of V. Suleimanov is supported by the German Research Foundation (DFG) grant SFB/Transregio 7 “Gravitational Wave Astronomy”. We also thank the referee for his constructive comments which helped to improve this paper.
References
- Abramowicz, M., Brandenburg, A., & Lasota, J.-P. 1996, MNRAS, 281, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J. 2002, MNRAS, 330, 895 [NASA ADS] [CrossRef] [Google Scholar]
- Babkovskaia, N., Brandenburg, A., & Poutanen, J. 2008, MNRAS, 386, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A. 2003, ARA&A, 41, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
- Balbus, S. A., & Lesaffre, P. 2008, New A Rev., 51, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Balsara, D. S., Fisker, J. L., Godon, P., & Sion, E. M. 2009, ApJ, 702, 1536 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, M. A., Rafikov, R. R., & Stone, J. M. 2012, ApJ, 760, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Bertout, C., & Regev, O. 1992, ApJ, 399, L163 [Google Scholar]
- Commerçon, B., Teyssier, R., Audit, E., Hennebelle, P., & Chabrier, G. 2011, A&A, 529, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cordova, F. A., & Mason, K. O. 1984, MNRAS, 206, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Cordova, F. A., Nugent, J. J., Klein, S. R., & Garmire, G. P. 1980, MNRAS, 190, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Cordova, F. A., Jensen, K. A., & Nugent, J. J. 1981a, MNRAS, 196, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cordova, F. A., Mason, K. O., & Nelson, J. E. 1981b, ApJ, 245, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Courant, R., Friedrichs, K., & Lewy, H. 1928, Math. Ann., 100, 32 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ferland, G. J., Pepper, G. H., Langer, S. H., et al. 1982, ApJ, 262, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Fisker, J. L., & Balsara, D. S. 2005, ApJ, 635, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Fisker, J. L., Balsara, D. S., & Burger, T. 2006, New A Rev., 50, 509 [Google Scholar]
- Flaig, M., Kley, W., & Kissmann, R. 2010, MNRAS, 409, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. 2002, Accretion Power in Astrophysics (Cambridge University Press) [Google Scholar]
- Godon, P. 1995, MNRAS, 277, 157 [NASA ADS] [Google Scholar]
- Godon, P., Regev, O., & Shaviv, G. 1995, MNRAS, 275, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I. 1986, ApJS, 61, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Smarr, L. L., & Wilson, J. R. 1984, ApJS, 55, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I. 1990, ApJ, 351, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Inogamov, N. A., & Sunyaev, R. A. 1999, Ast. Lett., 25, 269 [Google Scholar]
- Inogamov, N. A., & Sunyaev, R. A. 2010, Astron. Lett., 36, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, S., & Inagaki, S. 1994, PASJ, 46, 289 [NASA ADS] [Google Scholar]
- King, A. R., & Shaviv, G. 1984, Nature, 308, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W. 1989a, A&A, 208, 98 [NASA ADS] [Google Scholar]
- Kley, W. 1989b, A&A, 222, 141 [NASA ADS] [Google Scholar]
- Kley, W. 1991, A&A, 247, 95 [NASA ADS] [Google Scholar]
- Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., & Hensler, G. 1987, A&A, 172, 124 [NASA ADS] [Google Scholar]
- Kley, W., & Lin, D. N. C. 1996, ApJ, 461, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Lin, D. N. C. 1999, ApJ, 518, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Papaloizou, J. C. B. 1997, MNRAS, 285, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Klein, R. I., McKee, C. F., & Bolstad, J. 2007, ApJ, 667, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, R., Klahr, H., Dullemond, C., Kley, W., & Henning, T. 2010, A&A, 511, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Küker, M., Henning, T., & Rüdiger, G. 2003, ApJ, 589, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Levermore, C. D. 1984, J. Quant. Spectr. Rad. Transf., 31, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Pringle, J. E. 1998, ApJ, 505, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Mauche, C. W. 2004, in Rev. Mex. Astron. Astrofis. Conf. Ser. 20, eds. G. Tovmassian, & E. Sion, 174 [Google Scholar]
- Meyer, F., & Meyer-Hofmeister, E. 1982, A&A, 106, 34 [NASA ADS] [Google Scholar]
- Mukai, K., & Patterson, J. 2004, in Rev. Mex. Astron. Astrofis. Conf. Ser. 20, eds. G. Tovmassian, & E. Sion, 244 [Google Scholar]
- Narayan, R. 1992, ApJ, 394, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Popham, R. 1993, Nature, 362, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., Loeb, A., & Kumar, P. 1994, ApJ, 431, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Nauenberg, M. 1972, ApJ, 175, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Pandel, D., Córdova, F. A., & Howell, S. B. 2003, MNRAS, 346, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Pandel, D., Córdova, F. A., Mason, K. O., & Priedhorsky, W. C. 2005, ApJ, 626, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J., & Szuszkiewicz, E. 1994, MNRAS, 268, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Stanley, G. Q. G. 1986, MNRAS, 220, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Pessah, M. E., & Chan, C.-k. 2012, ApJ, 751, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Bildsten, L. 2004a, ApJ, 616, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Bildsten, L. 2004b, ApJ, 610, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Popham, R. 1999, MNRAS, 308, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Popham, R., & Narayan, R. 1995, ApJ, 442, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1977, MNRAS, 178, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E., & Savonije, G. J. 1979, MNRAS, 187, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Regev, O. 1983, A&A, 126, 146 [NASA ADS] [Google Scholar]
- Regev, O., & Bertout, C. 1995, MNRAS, 272, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, J. A., & Frank, J. 1986, MNRAS, 221, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2012, MNRAS, 421, 63 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics (Wiley) [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shaviv, G. 1987, Ap&SS, 130, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Sion, E. M., & Godon, P. 2012, Mem. Soc. Astron. Italiana, 83, 539 [NASA ADS] [Google Scholar]
- Sion, E. M., Godon, P., Myzcka, J., & Blair, W. P. 2010, ApJ, 716, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [Google Scholar]
- Suleimanov, V., & Poutanen, J. 2006, MNRAS, 369, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Suleymanov, V. F. 1992, Sov. Astron. Lett., 18, 104 [NASA ADS] [Google Scholar]
- Syunyaev, R. A., & Shakura, N. I. 1986, Sov. Astron. Lett., 12, 117 [NASA ADS] [Google Scholar]
- Tscharnuter, W. M., & Winkler, K.-H. A. 1979, Comput. Phys. Commun., 18, 171 [Google Scholar]
- Tylenda, R. 1977, Acta Astron., 27, 235 [NASA ADS] [Google Scholar]
- Tylenda, R. 1981, Acta Astron., 31, 267 [NASA ADS] [Google Scholar]
- Verbunt, F. 1982, Space Sci. Rev., 32, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 1987, MNRAS, 227, 23 [NASA ADS] [Google Scholar]
All Tables
Width of the BL for M∗ = 1.0 M⊙ and different stellar rotation rates ω = Ω∗/ΩK(R∗).
Width of the BL for three different stellar masses and the stellar rotation rates of ω = 0.0 and ω = 0.8.
Illustration of the midplane and effective temperature for the models with 0.8 and 1.2 M⊙.
Normalized angular momentum flux j for three different stellar masses and two different stellar rotation rates.
All Figures
 |
Fig. 1 Angular velocity Ω = uϕ/r in terms of the Keplerian angular velocity for a central star with mass M∗ = 1.0 M⊙ and five different stellar rotation rates Ω∗, denoted by ω = Ω∗/ΩK(R∗). The plot depicts two regions separated by a light grey bar that differ in the radial scaling and enable us to show both the rapid variation in the BL and the constant overall trend. |
| In the text | |
 |
Fig. 2 Radial Mach number of the gas for a stellar mass of 1.0 M⊙. The Mach number is defined as a quotient of radial velocity and the sound speed Ma = | ur | /cs. The different colours correspond to the different stellar rotation rates ω = Ω∗/ΩK(R∗). The smaller box inside the graph is a zoom in of the inner edge; the light grey frame denotes the zoom area. |
| In the text | |
 |
Fig. 3 Surface density Σ ~ ρH (log-scale) of the disk and a stellar mass of 1.0 M⊙ for five different stellar rotation rates ω = Ω∗/ΩK(R∗). The inset is a zoom in of the inner edge; the light grey frame denotes the zoom area. |
| In the text | |
 |
Fig. 4 Temperature Tc in the midplane of the disk, i.e. z = 0, for M∗ = 1.0 M⊙. The five models displayed differ in the stellar rotation rate ω = Ω∗/ΩK(R∗). The inset is a zoom in of the inner edge; the light grey frame denotes the zoom area. The small peak in the inset is a clear indication of a hot BL. |
| In the text | |
 |
Fig. 5 Effective temperature Teff of the disk, calculated according to Eq. (16). The plot shows five different models, all of which have the same stellar mass of 1.0 M⊙, but different stellar rotation rates ω = Ω∗/ΩK(R∗). The plot depicts two regions separated by a light grey bar that differ in the radial scaling and enable us to show both the narrow but very distinct peak of the effective temperature in the BL and the nearly constant behaviour in the disk all in one graph. |
| In the text | |
 |
Fig. 6 Scale height H (see Eq. (2)) of the disk for M∗ = 1.0 M⊙ and five different stellar rotation rates ω = Ω∗/ΩK(R∗). The disk is obviously very thin and not flared. In the BL, it is puffed up to some extent, which is, however, not unexpected. The inset is a zoom in of the inner edge; the light grey frame denotes the zoom area. |
| In the text | |
 |
Fig. 7 Comparison of the temperature in the disk midplane Tc of the three different models with stellar masses of 1.0,0.8, and 1.2 M⊙. The stellar rotation rate Ω has been chosen to amount to 0.4ΩK, as an illustrative case. It is clearly observable that with increasing stellar mass the temperature in the disk also rises. |
| In the text | |
 |
Fig. 8 Analogous to Fig. 7, we compare the effective temperatures of the three different stellar masses (1.0,0.8, and 1.2 M⊙) in this plot. Again, Ω = 0.4ΩK has been chosen as an example of the stellar rotation rate. We note that the effective temperature rises with increasing stellar mass. |
| In the text | |
 |
Fig. 9 Mass accretion rate Ṁ = −2πrΣur for M∗ = 1.0 M⊙ and five different stellar rotation rates ω = Ω∗/ΩK(R∗). The imposed value equals Ṁ = 1.51 × 10-8 M⊙ yr-1. Since Ṁ is constant in a stationary state, this plot is also an indication that a good equilibrium has been reached. |
| In the text | |
 |
Fig. 10 Normalized angular momentum flux |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.