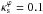EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 560 (December 2013) A&A, 560 (2013) A86 Full HTML
Free Access
Issue
A&A
Volume 560, December 2013
Article Number A86
Number of page(s) 11
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201321618
Published online 10 December 2013

© ESO, 2013

1. Introduction

Gravitational arcs are powerful tools to probe the mass distribution in galaxies (Koopmans et al. 2009; Barnabè et al. 2011; Suyu et al. 2012) and clusters of galaxies (Kovner 1989; Miralda-Escude 1993; Hattori et al. 1997; Comerford et al. 2006). In addition, their abundance can help to constrain cosmological models (Bartelmann et al. 1998; Golse et al. 2002; Bartelmann et al. 2003; Meneghetti et al. 2005; Jullo et al. 2010).

Two techniques have been used to extract information from gravitational arcs. The first is arc-statistics: counting arcs as a function of their properties, such as the length-to-width ratio or angular separation, for a lens sample (Wu & Hammer 1993; Grossman & Saha 1994; Bartelmann & Weiss 1994; Bartelmann et al. 1995; Bartelmann 1995). The second is inverse modeling: using arcs in individual clusters or galaxies aiming to determine the mass distribution of the lens and source properties (Kneib et al. 1993; Keeton 2001b; Golse et al. 2002; Wayth & Webster 2006; Jullo et al. 2007, 2010).

These approaches have motivated arc searches in wide field surveys (Gladders et al. 2003; Estrada et al. 2007; Cabanac et al. 2007; Belokurov et al. 2009; Kubo et al. 2010; Kneib et al. 2010; Gilbank et al. 2011; Wen et al. 2011; More et al. 2012; Bayliss 2012; Wiesner et al. 2012, Erben et al., in prep.), as well as in images targeting clusters (Luppino et al. 1999; Ebeling et al. 2001; Zaritsky & Gonzalez 2003; Smith et al. 2005; Sand et al. 2005; Hennawi et al. 2008; Kausch et al. 2010; Horesh et al. 2011; Furlanetto et al. 2013; Postman et al. 2012) and galaxies (Ratnatunga et al. 1999; Fassnacht et al. 2004; Bolton et al. 2006; Willis et al. 2006; Moustakas et al. 2007; Kubo & Dell’Antonio 2008; Faure et al. 2008; Jackson 2008). Moreover, the upcoming wide-field surveys, such as the Dark Energy Survey1 (Annis et al. 2005, Frieman et al., in prep.; Lahav et al., in prep.), which started taking data in 2012, are expected to detect strong lensing systems in the thousands, about an order of magnitude more than the current homogeneous samples.

A widely used model for representing the radial distribution of dark matter from galaxy to cluster of galaxies mass scales is the Navarro-Frenk-White profile (Navarro et al. 1996, 1997, hereafter NFW), whose mass density is given by 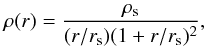ρ(r)=ρs(r/rs)(1+r/rs)2,\begin{eqnarray} \rho(r)=\frac{\rho_{\rm s}}{(r/r_{\rm s})(1+r/r_{\rm s})^2}, \label{nfw_den_profile} \end{eqnarray}(1)where rs and ρs are the scale radius and characteristic density, respectively. It is useful to define the characteristic convergence 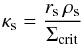κs=rs ρsΣcrit\begin{eqnarray} \kappa_{\rm s} = \frac{r_{\rm s} \,\rho_{\rm s}}{\Sigma_{\rm crit}} \label{kappa_s_nnfw} \end{eqnarray}(2)as a mass parameter, where, Σcrit is the critical surface mass density (Schneider et al. 1992; Petters et al. 2001; Mollerach & Roulet 2002).

Some observational properties of many arcs systems (such as arc multiplicity, relative positions, morphology) imply that the mass distribution of the lens is not axially symmetric. Furthermore, results from N-body simulations predict that dark matter halos are typically triaxial in shape and can be modeled by ellipsoids (Jing & Suto 2002; Macciò et al. 2007). A first approximation to model realistic lenses is to consider elliptical lens models, where the ellipticity is introduced either on the mass distribution (the so-called elliptical models, Schramm 1990; Barkana 1998; Keeton 2001b; Oguri et al. 2003) or on the lensing potential (the so-called pseudo-elliptical models, Blandford & Kochanek 1987; Kassiola & Kovner 1993; Kneib 2002; Golse & Kneib 2002). While elliptical models are generally more realistic, they are usually much more time-consuming for lensing calculations than are pseudo-elliptical ones. As a consequence, both have been used in the literature, depending on the application.

In this work we consider both elliptical and pseudo-elliptical lens models in which the radial mass distribution is given by the projected NFW profile. When used to represent lenses on galactic mass scales (see, e.g., Asano 2000; Davis et al. 2003; Vegetti & Koopmans 2009; Suyu et al. 2012; Ludlow et al. 2013), the characteristic convergence of the NFW model (Eq. (2)) takes very low values. For instance, lensing systems with M200 < 1013 M⊙ h-1, zL ≤ 1 and sources with zS = 2zL, have values2 of κs < 0.05. In this regime high numerical precision is required to accurately compute the functions involved in gravitational lensing, such as the deflection angle and its derivatives. Therefore, the numerical codes become either slower or, worse, they provide unreliable results as we go to low values of κs.

This issue has apparently not been addressed in the literature so far. A solution is to obtain analytical expressions, which are valid in this regime, providing at the same time a fast and reliable way to compute the relevant lensing functions. In this work, we present approximations for the deflection angle, convergence, and shear of the circular, pseudo-elliptical, and elliptical NFW models in the strong lensing regime. We use them to derive analytical solutions for iso-convergence contours, critical curves, and constant distortion curves. We compare these solutions with the exact calculations to determine a domain of validity for these approximations. Moreover, for applications to arc statistics, we apply these solutions to the calculation of the deformation cross section.

The outline of this work is as follows. In Sect. 2 we present a few basic definitions of lensing quantities and introduce the notation used in this paper. In Sect. 3 we show the approximations for the lensing functions of the circular NFW model and their extension to the pseudo-elliptical NFW (PNFW) and elliptical NFW (ENFW) models. We also derive analytical expressions for iso-convergence contours and critical curves for these models. In Sect. 4 we obtain analytical solutions for constant distortion curves and for the deformation cross section. In Sect. 5 we determine a domain of validity of these solutions in terms of the characteristic convergences and ellipticity parameters. In Sect. 6 we obtain a mapping among the PNFW and ENFW model parameters. In Sect. 7 we present the summary and concluding remarks. In Appendix A we present the expressions for the potential derivatives of elliptical models. In Appendix B we provide fitting functions giving upper limits of κs for the validity of the analytical solutions as a function of ellipticity.

2. Definitions and notation

We present below some basic definitions of gravitational lensing in order to set up the notation throughout this work. More details on the subject can be found, say, in Schneider et al. (1992); Petters et al. (2001); and Mollerach & Roulet (2002).

The lensing properties are encoded in the lens equation, which relates the observed image position ξ to a given source position η (both with respect to the optical axis). By defining the length scales ξ0 on the lens plane and η0 = ξ0DOS/DOL on the source plane, where DOS and DOL are the angular-diameter distances to the lens and source planes, respectively, the lens equation is given in its dimensionless form by 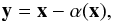y=x−α(x),\begin{eqnarray} \vec{y}=\vec{x}-\vec{\alpha}(\vec{x}), \label{lens_eq_adim} \end{eqnarray}(3)where y = η/η0, x = ξ/ξ0 and 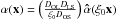α(x)=(DOLDLSξ0DOS)α̂(ξ0x)\hbox{$\vec{\alpha}(\vec{x})=\left(\frac{D_{\rm OL} D_{\rm LS}}{\xi_0 D_{\rm OS}} \right)\vec{\hat{\alpha}}(\xi_0\vec{x})$}, where 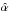\hbox{$\hat{\alpha}$} is the deflection angle due to the lensing mass distribution.

Properties of the local mapping are described by the Jacobian matrix of Eq. (3) 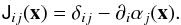Jij(x)=δij−∂iαj(x).\begin{eqnarray} \tens{J}_{ij}(\vec{x})=\delta_{ij}-\partial_i\alpha_j(\vec{x}). \end{eqnarray}(4)The two eigenvalues of this matrix are written as 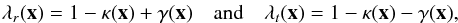λr(x)=1−κ(x)+γ(x) and λt(x)=1−κ(x)−γ(x),\begin{eqnarray} \lambda_r(\vec{x})=1-\kappa(\vec{x}) + \gamma(\vec{x}) \quad \mathrm{and} \quad \lambda_t(\vec{x})=1-\kappa(\vec{x}) - \gamma(\vec{x}), \label{eigen_r-t} \end{eqnarray}(5)where 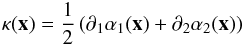κ(x)=12(∂1α1(x)+∂2α2(x))\begin{eqnarray} \kappa(\vec{x}) = \frac{1}{2}\left( \partial_1\alpha_1(\vec{x})+\partial_2\alpha_2(\vec{x}) \right) \label{conv} \end{eqnarray}(6)is the convergence and 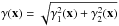γ(x)=γ12(x)+γ22(x)\hbox{$\gamma(\vec{x})=\sqrt{\gamma^2_1(\vec{x})+\gamma^2_2(\vec{x})}$}, is the shear, which has components 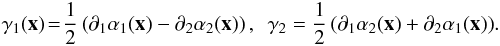γ1(x)=12(∂1α1(x)−∂2α2(x)),γ2=12(∂1α2(x)+∂2α1(x)).\begin{eqnarray} \gamma_1(\vec{x}) \!=\! \frac{1}{2}\left(\partial_1\alpha_1(\vec{x})-\partial_2\alpha_2(\vec{x})\right), \ \ \gamma_2 = \frac{1}{2}\left(\partial_1\alpha_2(\vec{x})+\partial_2\alpha_1(\vec{x})\right)\!. \label{shear1_2} \end{eqnarray}(7)Magnification in the radial direction is given by 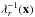λr-1(x)\hbox{$\lambda^{-1}_r(\vec{x})$} and in the tangential by 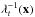λt-1(x)\hbox{$\lambda^{-1}_t(\vec{x})$}. Points satisfying the conditions λr(x) = 0 and λt(x) = 0 are the radial and tangential critical curves, respectively. Mapping these curves onto the source plane, we obtain the corresponding caustics.

3. Solutions for iso-convergence contours and critical curves

In this section we present the approximations for the lensing functions of the the circular NFW (Sect. 3.1), the PNFW (Sect. 3.2), and the ENFW (Sect. 3.3) models.

3.1. Circular NFW model

Following Bartelmann (1996), from the density profile (1) and taking ξ0 = rs, the dimensionless deflection angle is given by 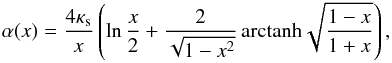α(x)=4κsx(lnx2+21−x2arctanh1−x1+x),\begin{eqnarray} \alpha(x)=\frac{4\kappa_{\rm s}}{x}\left(\ln{\frac{x}{2}}+\frac{2}{\sqrt{1-x^2}}\arctan{\rm\!h}{\sqrt{\frac{1-x}{1+x}}} \right), \label{angle_nfw_tot} \end{eqnarray}(8)from which the convergence and shear are derived. In the limit of κs ≲ 0.1, the typical scales corresponding to the strong lensing regime (e.g., the size of critical curve and caustics) are much smaller than unity. In this case high numerical precision is required to accurately compute lensing quantities, such as the shear and convergence. However, simple analytic expressions can be found in this regime by avoiding such numerical difficulties. Keeping the first terms in a series expansion of (8) for x ≪ 1 leads to 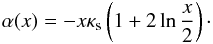α(x)=−xκs(1+2lnx2)·\begin{eqnarray} \alpha(x)=-x\kappa_{\rm s}\left(1+2\ln{\frac{x}{2}}\right)\cdot \label{alpha_nfw} \end{eqnarray}(9)In this case, the convergence and shear are given by 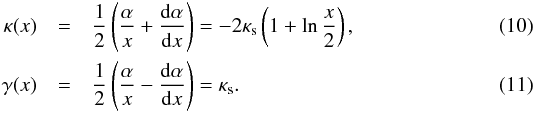κ(x)=γ(x)=\begin{eqnarray} \kappa(x) &=& \frac{1}{2}\left(\frac{\alpha}{x}+\frac{{\rm d}\alpha}{{\rm d}x}\right)= -2\kappa_{\rm s}\left(1+\ln{\frac{x}{2}}\right), \label{kappa_nfw}\\ \gamma(x)&=& \frac{1}{2}\left(\frac{\alpha}{x}-\frac{{\rm d}\alpha}{{\rm d}x}\right)= \kappa_{\rm s}. \label{shear_nfw} \end{eqnarray}Allowing a relative deviation of less than 1% (0.1%) with respect to the exact expression, we found that Eq. (9) is a good approximation to the deflection angle for x ≤ 0.12 (x ≤ 0.04), while the same holds for Eqs. (10) and (11) for the convergence and shear for x ≤ 0.08 and x ≤ 0.05 (x ≤ 0.025 and x ≤ 0.015), respectively.

From Eq. (10) and fixing a value for the iso-convergence contour as κconst., the equation κ(x) = κconst. has the solution 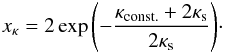xκ=2exp(−κconst.+2κs2κs)·\begin{eqnarray} x_\kappa = 2 \exp{\left(- \frac{\kappa_{\rm const.}+2\kappa_{\rm s}}{ 2\kappa_{\rm s}} \right)}\cdot \label{xk_nfw} \end{eqnarray}(12)From Eqs. (5), (10), and (11) it follows that 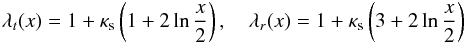λt(x)=1+κs(1+2lnx2), λr(x)=1+κs(3+2lnx2)\begin{eqnarray} \lambda_t(x)=1+\kappa_{\rm s}\left(1+2\ln{\frac{x}{2}} \right), \quad \lambda_r(x)=1+\kappa_{\rm s}\left(3+2\ln{\frac{x}{2}} \right) \label{lt-lr_nfw} \end{eqnarray}(13)such that the determinant of the Jacobian matrix is 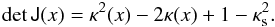det J(x)=κ2(x)−2κ(x)+1−κs2.\begin{eqnarray} {\rm det}\,\tens{J}(x)=\kappa^2(x)-2\kappa(x)+1-\kappa^2_{\rm s}. \label{det_nfw} \end{eqnarray}(14)The solutions for the tangential and radial critical curves follow from the equations above. The radial coordinates of these curves are3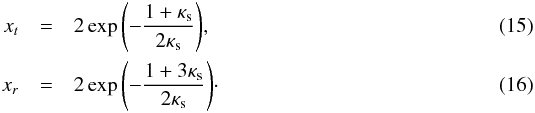xt=xr=\begin{eqnarray} x_t &=& 2 \exp{\left( -\frac{1+\kappa_{\rm s}}{2\kappa_{\rm s}} \right)}, \label{xt_nfw} \\ x_r &=& 2 \exp{\left( -\frac{1+3\kappa_{\rm s}}{2\kappa_{\rm s}} \right)}\cdot \label{xr_nfw} \end{eqnarray}The expressions for the caustics are obtained straightforwardly by inserting the expressions above in the lens equation with the deflection angle given in Eq. (9). The validity of these solutions is discussed in Sect. 5.

3.2. Pseudo-elliptical NFW model

The construction of pseudo-elliptical models is made by replacing the radial coordinate of the lensing potential by 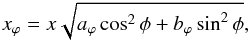xϕ=xaϕcos2φ+bϕsin2φ,\begin{eqnarray} x_\varphi=x\sqrt{a_{\varphi}\cos^2{\phi}+b_{\varphi} \sin^2{\phi}}\label{rad_coord_pnfw}, \end{eqnarray}(17)where aϕ and bϕ are two parameters that define the lensing potential ellipticity. Adopting the approach of the angle deflection method introduced by Golse & Kneib (2002; see also Dúmet-Montoya et al. 2012, hereafter DCM), from Eqs. 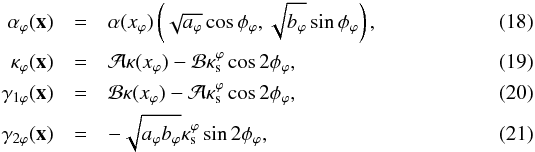(9)–(11), the deflection angle, convergence, and components of the shear of the PNFW model are αϕ(x)=κϕ(x)=γ1ϕ(x)=γ2ϕ(x)=\begin{eqnarray} \vec{\alpha}_\varphi(\vec{x})&=&\alpha(x_\varphi)\left(\sqrt{a_{\varphi} }\cos{\phi_\varphi},\sqrt{b_{\varphi}}\sin{\phi_\varphi} \label{alpha_pnfw}\right), \label{aphi}\\ \kappa_\varphi(\vec{x}) &=&\mathcal{A}\kappa(x_\varphi)-\mathcal{B}\kappa_{\rm s}^\varphi\cos{2\phi_\varphi}, \label{kappa_pnfw}\\ \gamma_{1\varphi}(\vec{x})&=& \mathcal{B}\kappa(x_\varphi)-\mathcal{A}\kappa_{\rm s}^\varphi\cos{2\phi_\varphi}, \label{g1_pnfw}\\ \gamma_{2\varphi}(\vec{x})&=& -\sqrt{a_{\varphi} b_{\varphi} }\kappa_{\rm s}^\varphi\sin{2\phi_\varphi}, \label{g2_pnfw} \end{eqnarray}where 𝒜=12(aϕ+bϕ),ℬ=12(aϕ−bϕ)andφϕ=arctan(bϕ/aϕtanφ),\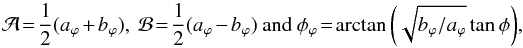begin{equation} \mathcal{A}\!=\!\frac{1}{2}(a_{\varphi} +b_{\varphi} ),\ \mathcal{B}\!=\!\frac{1}{2}(a_{\varphi} -b_{\varphi} ) \ \textrm{and}\ \phi_\varphi\!=\!\arctan{\left(\sqrt{b_{\varphi} /a_{\varphi} }\tan{\phi}\right)}, \label{phivarphi} \end{equation}(22)and we denote the NFW characteristic convergence, Eq. 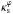(2), by κsϕ\hbox{$\kappa_{\rm s}^\varphi$}.

From Eq. (19) and fixing a value for the iso-convergence contour as κconst., the equation κϕ(x) = κconst. has the solution 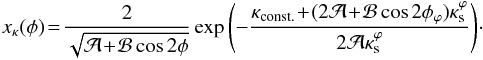xκ(φ)=2𝒜+ℬcos2φexp(−κconst.+(2𝒜+ℬcos2φϕ)κsϕ2𝒜κsϕ)·\begin{eqnarray} x_{\kappa}(\phi)\!=\!\frac{2}{\sqrt{\mathcal{A}\!+\!\mathcal{B}\cos{2\phi}}}\exp{\left(-\frac{\kappa_{\rm const.}\!+\!(2\mathcal{A}\!+\!\mathcal{B}\cos{2\phi_\varphi})\kappa^\varphi_{\rm s}}{2\mathcal{A}\kappa^\varphi_{\rm s}} \right)}\cdot\label{xk_pnfw} \end{eqnarray}(23)Therefore, the iso-convergence contours are not elliptical, as is well known for pseudo-elliptical models.

The solutions for critical curves are a bit more involved. From Eqs. (19)–(21), the determinant of the Jacobian matrix is 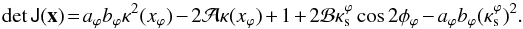det J(x)=aϕbϕκ2(xϕ)−2𝒜κ(xϕ)+1+2ℬκsϕcos2φϕ−aϕbϕ(κsϕ)2.\begin{equation} {\rm det}\,\tens{J}(\vec{x})\!=\!a_{\varphi} b_{\varphi} \kappa^2(x_\varphi)-2\mathcal{A}\kappa(x_\varphi)+1 +2\mathcal{B}\kappa_{\rm s}^\varphi\cos{2\phi_\varphi}-a_{\varphi} b_{\varphi} (\kappa_{\rm s}^\varphi)^2. \label{jacob_pnfw} \end{equation}(24)Then, solving the equation det J(x) = 0 for κ(xϕ), defining 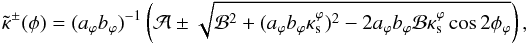κ±˜(φ)=(aϕbϕ)-1(𝒜±ℬ2+(aϕbϕκsϕ)2−2aϕbϕℬκsϕcos2φϕ),\begin{eqnarray*} \tilde{\kappa}^{\pm}(\phi)= (a_{\varphi} b_{\varphi} )^{-1}\left(\mathcal{A}\pm \sqrt{\mathcal{B}^2+(a_{\varphi} b_{\varphi} \kappa_{\rm s}^\varphi)^2-2a_{\varphi} b_{\varphi} \mathcal{B}\kappa_{\rm s}^\varphi\cos{2\phi_\varphi}} \right), \end{eqnarray*}and inverting 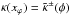κ(xϕ)=κ±˜(φ)\hbox{$\kappa(x_\varphi)= \tilde{\kappa}^{\pm}(\phi)$}, using Eq. (17), we obtain 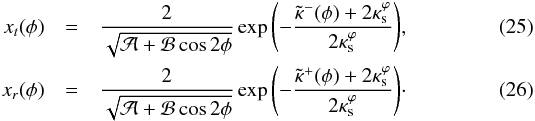xt(φ)=xr(φ)=\begin{eqnarray} x_{t}(\phi)&=&\frac{2}{\sqrt{\mathcal{A}+\mathcal{B}\cos{2\phi}}}\exp{\left(-\frac{\tilde{\kappa}^{-}(\phi)+2\kappa^\varphi_{\rm s}}{2\kappa^\varphi_{\rm s}} \right)},\label{xt_pnfw} \\ x_{r}(\phi) &=& \frac{2}{\sqrt{\mathcal{A}+\mathcal{B}\cos{2\phi}}}\exp{\left(-\frac{\tilde{\kappa}^{+}(\phi)+2\kappa^\varphi_{\rm s}}{2\kappa^\varphi_{\rm s}} \right)}\cdot\label{xr_pnfw} \end{eqnarray}These curves are mapped onto the source plane by using the lens equation with the deflection angle given in Eq. (18). The validity of these solutions is discussed in Sect. 5.

3.3. Elliptical NFW model

We construct the ENFW model by replacing the radial coordinate of the surface mass density, Eq. (10), by 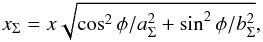xΣ=xcos2φ/aΣ2+sin2φ/bΣ2,\begin{eqnarray} x_\Sigma=x\sqrt{\cos^2{\phi}/a^2_\Sigma + \sin^2{\phi}/b^2_\Sigma},\label{coord_enfw} \end{eqnarray}(27)where aΣ and bΣ define the ellipticity of the mass distribution.

The lensing functions of this model can be written as (see Appendix A) α1Σ(x)=α2Σ(x)=κΣ(x)≡γ1Σ(x)=γ2Σ(x)=\begin{eqnarray} \alpha_{1\Sigma}(\vec{x}) & = & a_{\Sigma}b_{\Sigma} x\left[ \mathcal{J}_0\kappa(x)-2\kappa^\Sigma_{\rm s}\mathcal{L}_0(\phi)\right] \cos{\phi}, \label{alpha1_enfw} \\ \alpha_{2\Sigma}(\vec{x}) & = & a_{\Sigma}b_{\Sigma} x \left[\mathcal{J}_1\kappa(x)-2\kappa^\Sigma_{\rm s}\mathcal{L}_1(\phi)\right] \sin{\phi}, \label{alpha2_enfw} \\ \kappa_\Sigma(\vec{x})& \equiv &\kappa(x_\Sigma)=1-\frac{1}{2}\left[\mathcal{P} +\mathcal{Q}-a_{\Sigma}b_{\Sigma}(\mathcal{J}_0+\mathcal{J}_1)\kappa(x) \right], \label{kappa_enfw}\\ \gamma_{1\Sigma}(\vec{x})&=&\frac{1}{2}\left[a_{\Sigma}b_{\Sigma} (\mathcal{J}_0-\mathcal{J}_1)\kappa(x)+\mathcal{Q}-\mathcal{P}\right], \label{g1_enfw}\\ \gamma_{2\Sigma}(\vec{x})&=&-a_{\Sigma}b_{\Sigma}\kappa_{\rm s}^\Sigma\sin{2\phi}\mathcal{K}_1(\phi), \label{g2_enfw} \end{eqnarray}where we denote the characteristic convergence, Eq. 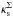(2), by κsΣ\hbox{$\kappa_{\rm s}^\Sigma$} and define 𝒫=𝒬=\begin{eqnarray} \mathcal{P}&=&1+2a_{\Sigma}b_{\Sigma}\kappa_{\rm s}^\Sigma\left[\mathcal{K}_0(\phi)\cos^2{\phi}+\mathcal{L}_0(\phi) \right], \label{p_enfw}\\ \mathcal{Q}&=&1+2a_{\Sigma}b_{\Sigma}\kappa_{\rm s}^\Sigma \left[\mathcal{K}_2(\phi)\sin^2{\phi}+\mathcal{L}_1(\phi) \right]. \label{q_enfw} \end{eqnarray}We computed the accuracy of Eqs. (28) and (29) with respect to the exact expressions (Eq. (A.1)) for the angles φ in which the deviations are maximal. For a percentile deviation less than 1% (0.1%), such expressions are good approximations of the exact components of the deflection angle for x ≤ 0.11 (x ≤ 0.03) and x ≤ 0.10 (x ≤ 0.025), respectively, within the ellipticity parameter range 0.1–0.6.

For an iso-convergence contour value κconst., the solution for κΣ(x) = κconst. is 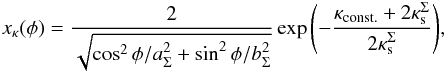xκ(φ)=2cos2φ/aΣ2+sin2φ/bΣ2exp(−κconst.+2κsΣ2κsΣ),\begin{eqnarray} x_{\kappa}(\phi)=\frac{2}{\sqrt{\cos^2{\phi}/a^2_{\Sigma}+\sin^2{\phi}/b^2_{\Sigma}}}\exp{\left(-\frac{\kappa_{\rm const.}+2\kappa_{\rm s}^\Sigma}{2\kappa_{\rm s}^\Sigma} \right)}, \label{xk_enfw} \end{eqnarray}(35)which are ellipses, as expected.

From the definitions in (5) and Eqs. (30)–(32), the determinant of the Jacobian matrix is 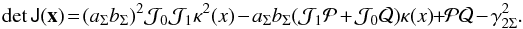det J(x)=(aΣbΣ)2𝒥0𝒥1κ2(x)−aΣbΣ(𝒥1𝒫+𝒥0𝒬)κ(x)+𝒫𝒬−γ2Σ2.\begin{equation} {\rm det}\,\tens{J}(\vec{x})\!=\!(a_{\Sigma} b_{\Sigma})^2\mathcal{J}_0\mathcal{J}_1\kappa^2(x) -a_{\Sigma} b_{\Sigma}(\mathcal{J}_1\mathcal{P}+\mathcal{J}_0\mathcal{Q})\kappa(x)\!+\!\mathcal{P}\mathcal{Q}-\gamma^2_{2\Sigma}. \label{jacob_enfw} \end{equation}(36)Following a similar procedure to obtain the critical curves for the PNFW model, the solutions of the equation det J(x) = 0 are 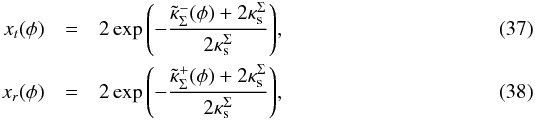xt(φ)=xr(φ)=\begin{eqnarray} x_t(\phi) &=& 2\exp{\left(-\frac{\tilde{\kappa}^{-}_\Sigma(\phi) +2\kappa_{\rm s}^\Sigma}{2\kappa_{\rm s}^\Sigma} \right)}, \label{xt_enfw}\\ x_r(\phi) &=& 2\exp{\left(-\frac{\tilde{\kappa}^{+}_\Sigma(\phi) +2\kappa_{\rm s}^\Sigma}{2\kappa_{\rm s}^\Sigma} \right)},\label{xr_enfw} \end{eqnarray}where we define 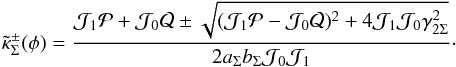κΣ±˜(φ)=𝒥1𝒫+𝒥0𝒬±(𝒥1𝒫−𝒥0𝒬)2+4𝒥1𝒥0γ2Σ22aΣbΣ𝒥0𝒥1·\begin{eqnarray*} \tilde{\kappa}^{\pm}_\Sigma(\phi)= \frac{\mathcal{J}_1\mathcal{P}+\mathcal{J}_0 \mathcal{Q}\pm \sqrt{(\mathcal{J}_1\mathcal{P}-\mathcal{J}_0\mathcal{Q})^2+4\mathcal{J}_1\mathcal{J}_0\gamma^2_{2\Sigma}}}{2 a_{\Sigma} b_{\Sigma}\mathcal{J}_0\mathcal{J}_1}\cdot \end{eqnarray*}The corresponding caustics are obtained by using the lens equation with the deflection angle given in Eqs. (28) and (29). The validity of these solutions is discussed in Sect. 5.

4. Solutions for the deformation cross section

Gravitational arcs are usually defined as images with length-to-width ratio, L/W, greater than a threshold Rth. For fast calculations in arc statistics, it is useful to approximate L/W to the ratio of the eigenvalues of the Jacobian matrix (Wu & Hammer 1993; Bartelmann & Weiss 1994; Hamana & Futamase 1997) 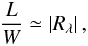LW≃|Rλ|,\begin{eqnarray} \frac{L}{W} \simeq \left| R_\lambda \right |, \label{lw} \end{eqnarray}(39)where Rλ = λr/λt. This approximation holds for infinitesimal circular sources and breaks down for arcs generated by the merger of multiple images (Rozo et al. 2008) or by large or noncircular sources.

In this section, using the approximation above, we derive analytical solutions for constant distortion curves for the NFW models (Sect. 4.1). We thereafter employ these solutions to compute the arc cross section (Sect. 4.2).

4.1. Constant distortion curves

A typical arc-forming region in the lens plane is determined by the so-called constant distortion curves, corresponding to the | Rλ | = Rth contours. An often used value for Rth is 10. As the value of Rth is decreased, the inner curve (corresponding to Rλ = −Rth) gets closer to the center, while the outer enclosing curve (Rλ = + Rth) reaches higher radii, where the analytic approximations derived in Sect. 3 are less accurate. Therefore by using a lower value of Rth to determine the limit of validity of these approximations, we are assuring they are even more accurate in the arc formation region. For this reason, we adopt Rth = 5 when we make the numerical comparisons to the exact solution throughout this paper.

From the approximations given in Sect. 3, it is possible to obtain analytical solutions for the radial coordinates of constant distortion curves. For the circular NFW model, from Eq. (13), the equation Rλ(x) = Rth has the solution 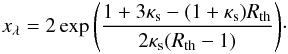xλ=2exp(1+3κs−(1+κs)Rth2κs(Rth−1))·\begin{eqnarray} x_\lambda=2\exp{\left(\frac{1+3\kappa_{\rm s}-(1+\kappa_{\rm s})R_{\rm th}}{2\kappa_{\rm s}(R_{\rm th}-1)} \right)}\cdot \label{cdc_nfw} \end{eqnarray}(40)For the PNFW model, calculating the radial coordinates of the constant distortion curves is a bit more complicated. From Eqs. 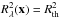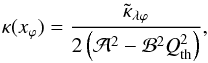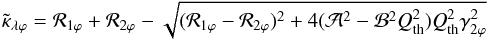(19)–(21), solving the equation Rλ2(x)=Rth2\hbox{$R^2_\lambda(\vec{x})= R^2_{\rm th}$} for κ(xϕ), we obtain κ(xϕ)=˜κλϕ2(𝒜2−ℬ2Qth2),\begin{eqnarray} \kappa(x_\varphi)=\frac{\tilde{\kappa}_{\lambda \varphi}}{2\left(\mathcal{A}^2-\mathcal{B}^2 Q^2_{\rm th}\right)},\label{prev_rl_pnfw} \end{eqnarray}(41)where ˜κλϕ=ℛ1ϕ+ℛ2ϕ−(ℛ1ϕ−ℛ2ϕ)2+4(𝒜2−ℬ2Qth2)Qth2γ2ϕ2\begin{eqnarray*} \tilde{\kappa}_{\lambda \varphi} = \mathcal{R}_{1\varphi} +\mathcal{R}_{2\varphi} -\sqrt{(\mathcal{R}_{1\varphi}-\mathcal{R}_{2\varphi})^2+4(\mathcal{A}^2-\mathcal{B}^2 Q^2_{\rm th})Q^2_{\rm th} \gamma^2_{2\varphi}} \end{eqnarray*}with Qth=Rth+1Rth−1,ℛ1ϕ=(𝒜−ℬQth)(1+(𝒜Qth+ℬ)κsϕcos2φϕ),ℛ2ϕ=(𝒜+ℬQth)(1−(𝒜Qth−ℬ)κsϕcos2φϕ),\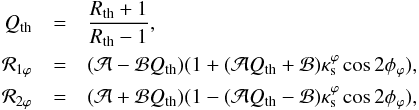begin{eqnarray*} Q_{\rm th} &= &\frac{R_{\rm th}+1}{R_{\rm th}-1}, \\ \mathcal{R}_{1\varphi} &=& (\mathcal{A}-\mathcal{B}Q_{\rm th})(1+(\mathcal{A}Q_{\rm th}+\mathcal{B})\kappa^\varphi_{\rm s}\cos{2\phi_\varphi}),\\ \mathcal{R}_{2\varphi} &=& (\mathcal{A}+\mathcal{B}Q_{\rm th})(1-(\mathcal{A}Q_{\rm th}-\mathcal{B})\kappa^\varphi_{\rm s}\cos{2\phi_\varphi}), \end{eqnarray*}where φϕ is given in Eq. (22). Inverting Eq. (41) and using Eq. (17), we obtain for any angular position 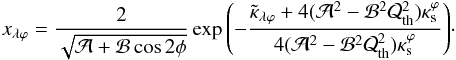xλϕ=2𝒜+ℬcos2φexp(−˜κλϕ+4(𝒜2−ℬ2𝒬th2)κsϕ4(𝒜2−ℬ2𝒬th2)κsϕ)·\begin{eqnarray} x_{\lambda \varphi} =\frac{2}{\sqrt{\mathcal{A}+\mathcal{B}\cos{2\phi}}}\exp{\left(-\frac{\tilde{\kappa}_{\lambda\varphi}+4(\mathcal{A}^2-\mathcal{B}^2\mathcal{Q}^2_{\rm th})\kappa^\varphi_{\rm s}}{4(\mathcal{A}^2-\mathcal{B}^2\mathcal{Q}^2_{\rm th})\kappa^\varphi_{\rm s}}\right)}\cdot \label{cdc_pnfw} \end{eqnarray}(42)Following the same procedure as above, for the ENFW model, from Eqs. (30)–(32), we obtain for each angular position 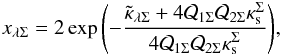xλΣ=2exp(−˜κλΣ+4𝒬1Σ𝒬2ΣκsΣ4𝒬1Σ𝒬2ΣκsΣ),\begin{eqnarray} x_{\lambda \Sigma}=2\exp{\left(-\frac{\tilde{\kappa}_{\lambda \Sigma} + 4\mathcal{Q}_{1\Sigma}\mathcal{Q}_{2\Sigma}\kappa^\Sigma_{\rm s}}{4\mathcal{Q}_{1\Sigma}\mathcal{Q}_{2\Sigma}\kappa^\Sigma_{\rm s}}\right)}, \label{cdc_enfw} \end{eqnarray}(43)where we have defined ˜κλΣ=ℛ1Σ𝒬2Σ+ℛ2Σ𝒬1Σ−(ℛ1Σ𝒬2Σ−ℛ2Σ𝒬1Σ)2+16𝒬1Σ𝒬2ΣQth2γ2Σ2\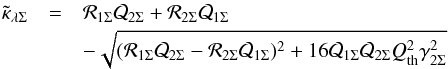begin{eqnarray*} \tilde{\kappa}_{\lambda \Sigma}&=& \mathcal{R}_{1\Sigma}\mathcal{Q}_{2\Sigma}+\mathcal{R}_{2\Sigma}\mathcal{Q}_{1\Sigma} \\ & & - \sqrt{(\mathcal{R}_{1\Sigma}\mathcal{Q}_{2\Sigma} -\mathcal{R}_{2\Sigma}\mathcal{Q}_{1\Sigma})^2+16 \mathcal{Q}_{1\Sigma}\mathcal{Q}_{2\Sigma}Q^2_{\rm th}\gamma^2_{2\Sigma}} \end{eqnarray*}with ℛ1Σ=𝒫+𝒬+Qth(𝒫−𝒬),ℛ2Σ=𝒫+𝒬−Qth(𝒫−𝒬),Q1Σ=aΣbΣ[𝒥0+𝒥1+Qth(𝒥0−𝒥1)],Q2Σ=aΣbΣ[𝒥0+𝒥1−Qth(𝒥0−𝒥1)],\begin{eqnarray*} \mathcal{R}_{1\Sigma} &=& \mathcal{P}+\mathcal{Q}+Q_{\rm th}(\mathcal{P}-\mathcal{Q}), \\ \mathcal{R}_{2\Sigma} &=& \mathcal{P}+\mathcal{Q}-Q_{\rm th}(\mathcal{P}-\mathcal{Q}), \\ Q_{1\Sigma} &=& a_\Sigma b_\Sigma[\mathcal{J}_0+\mathcal{J}_1+Q_{\rm th}(\mathcal{J}_0-\mathcal{J}_1)],\\ Q_{2\Sigma}& =& a_\Sigma b_\Sigma[\mathcal{J}_0+\mathcal{J}_1-Q_{\rm th}(\mathcal{J}_0-\mathcal{J}_1)], \end{eqnarray*}where \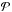hbox{$\mathcal{P}$}, \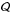hbox{$\mathcal{Q}$}, and \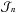hbox{$\mathcal{J}_n$} are given in Eqs. (33), (34), and (A.8), respectively.

In Eqs. (40), (42), and (43) the solution for the equation Rλ(x) = −Rth is obtained by replacing Rth by − Rth. Also, at the limits Rth → ∞ and Rth → 0, these expressions yield the radial coordinates of the tangential (Eqs. (15), (25), and (37)) and radial (Eqs. (16), (26), and (38)) critical curves of the corresponding models.

4.2. Arc cross section

The arc cross section, σRth, is defined as the weighted area in the source plane, such that sources within it will be mapped into arcs with L/W ≥ Rth. This cross section is usually computed using a large sample of arcs obtained from ray-tracing an even larger number of finite sources and is computationally demanding. An alternative for fast calculations is to use the approximation (39). In this case, the arc cross section is calculated in the lens plane as (Fedeli et al. 2006, DCM) 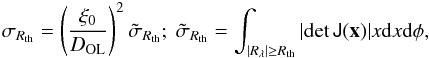σRth=(ξ0DOL)2˜σRth;˜σRth=∫|Rλ|≥Rth|det J(x)|xdxdφ,\begin{eqnarray} \sigma_{R_{\rm th}}= \left(\frac{\xi_0}{D_{\rm OL}}\right)^2\tilde{\sigma}_{R_{\rm th}}; \ \tilde{\sigma}_{R_{\rm th}}=\int_{|R_\lambda|\geq R_{\rm th}}|{\rm det}\,\tens{J}(\vec{x})| x{\rm d}x{\rm d}\phi, \label{sigma} \end{eqnarray}(44)where the quantity 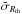˜σRth\hbox{$\tilde{\sigma}_{R_{\rm th}}$} is known as (dimensionless) deformation cross section.

For low values of the characteristic convergences, the determinant of the Jacobian (see Eqs. (14), (24), and (36)) takes the form 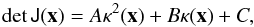det J(x)=Aκ2(x)+Bκ(x)+C,\begin{eqnarray*} {\rm det}\,\tens{J}(\vec{x}) = A \kappa^2(\vec{x}) + B \kappa(\vec{x}) + C, \end{eqnarray*}where A, B, and C are independent of the radial coordinates. It is possible to reduce the calculation of (44) to a one-dimensional integral. Inserting the expression above into Eq. 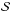(44) and integrating over the radial coordinate, within the lower and upper limits given by the constant distortion curves (i.e., from − Rth to Rth), we obtain ˜σRth=12∫02π[𝒮(x+)+𝒮(x−)−2𝒮(xt)]dφ,\begin{eqnarray} \tilde{\sigma}_{R_{\rm th}}=\frac{1}{2}\int_{0}^{2\pi}\left[\mathcal{S}(x_{+})+\mathcal{S}(x_{-})-2\mathcal{S}(x_t)\right]{\rm d}\phi \label{sigma_medio}, \end{eqnarray}(45)where \hbox{$\mathcal{S}$}, is a function (given below) resulting from the integration of det J(x) over the radial coordinate, x± = x±(φ) are the solutions for the radial coordinate of the constant distortion curves for − Rth and Rth, and xt = xt(φ) is the solution for the radial coordinate of the tangential critical curve.

For the circular NFW model we have 𝒮=x2[1−κs−κ(x)]2,\begin{eqnarray} \mathcal{S}=x^2\left[1-\kappa_{\rm s}-\kappa(x)\right]^2, \end{eqnarray}(46)such that Eq. (45) gives ˜σRth=4πκs2(Rth2−1)2[(Rth+1)2x+2+(Rth−1)2x−2]\begin{eqnarray} \tilde{\sigma}_{R_{\rm th}}=\frac{4\pi\kappa^2_{\rm s}}{(R^2_{\rm th}-1)^2}\left[(R_{\rm th}+1)^2x^2_{+}+(R_{\rm th}-1)^2x^2_{-} \right] \label{dcs_nfw_analytic} \end{eqnarray}(47)where x± are given in Eq. (40) for Rth and − Rth, respectively. This expression shows the exponential dependence of the cross section on κs (Caminha et al. 2013). 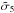For instance, varying κs from 0.01 to 0.1, ˜σ5\hbox{$\tilde{\sigma}_{5}$} changes approximately by 41 orders of magnitude. Further, 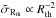˜σRth∝Rth-2\hbox{$\tilde{\sigma}_{\rm R_{\rm th}}\propto R^{-2}_{\rm th}$} for Rth ≫ 1 as expected from the behavior of sources near the caustics (Mollerach & Roulet 2002; Caminha et al. 2013).

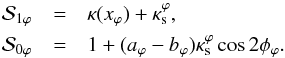For the PNFW model we have 𝒮(φ)=x2[aϕbϕ𝒮1ϕ2−(aϕ+bϕ)𝒮1ϕ+𝒮0ϕ],\begin{eqnarray} \mathcal{S}(\phi)=x^2\left[a_{\varphi} b_{\varphi} \mathcal{S}^{2}_{1\varphi}-(a_{\varphi} +b_{\varphi} )\mathcal{S}_{1\varphi}+\mathcal{S}_{0\varphi}\right], \label{S_pnfw} \end{eqnarray}(48)where 𝒮1ϕ=κ(xϕ)+κsϕ,𝒮0ϕ=1+(aϕ−bϕ)κsϕcos2φϕ.\begin{eqnarray*} \mathcal{S}_{1\varphi}&=&\kappa(x_\varphi) +\kappa_{\rm s}^\varphi, \\ \mathcal{S}_{0\varphi}&=&1 +(a_{\varphi} -b_{\varphi} )\kappa_{\rm s}^\varphi\cos{2\phi_\varphi}. \end{eqnarray*}In this case, this function must be evaluated at xt and x± given in Eqs. (25) and (42), respectively.

For the ENFW model we have 𝒮(φ)=x2[(aΣbΣ)2(𝒥0𝒥1)×𝒮1Σ2−aΣbΣ(𝒥1𝒫+𝒥0𝒬)𝒮1Σ+𝒮0Σ],\begin{equation} \mathcal{S}(\phi)\!=\!x^2\left[(a_\Sigma b_\Sigma)^2(\mathcal{J}_0\mathcal{J}_1) \!\times\! 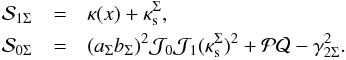\mathcal{S}^2_{1\Sigma}-a_\Sigma b_\Sigma(\mathcal{J}_1\mathcal{P}+\mathcal{J}_0\mathcal{Q})\mathcal{S}_{1\Sigma}\!+\!\mathcal{S}_{0\Sigma}\right], \label{S_enfw} \end{equation}(49)with 𝒮1Σ=κ(x)+κsΣ,𝒮0Σ=(aΣbΣ)2𝒥0𝒥1(κsΣ)2+𝒫𝒬−γ2Σ2.\begin{eqnarray*} \mathcal{S}_{1\Sigma} &=&\kappa(x)+\kappa_{\rm s}^\Sigma,\\ \mathcal{S}_{0\Sigma}&=&(a_\Sigma b_\Sigma)^2\mathcal{J}_0\mathcal{J}_1(\kappa_{\rm s}^\Sigma)^2+\mathcal{PQ}-\gamma^2_{2\Sigma}. \end{eqnarray*}This function must be evaluated at xt, Eq. (37), and x± Eq. (43).

5. Domain of validity of the solutions

In this section we quantify the deviation of the analytic solutions (Sects. 3 and 4) with respect to their corresponding exact calculations, seeking to determine their domains of validity in terms of the model parameters (Sect. 5.1). Then, aiming to test the domain of validity of these solutions for computing other lensing quantities, we compare the deformation cross sections in Sect. 5.2.

thumbnail Fig. 1

Mean weighted squared radial fractional difference \hbox{$\mathcal{D}^2$} for the constant distortion curve with Rth = 5 for the circular NFW lens model as a function of the characteristic convergence κs.

5.1. Limits for constant distortion curves and critical curves

thumbnail Fig. 2

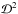Mean weighted squared radial fractional difference \hbox{$\mathcal{D}^2$}, for constant distortion curves with Rth = 5, as a function of the characteristic convergences, for some values of ellipticity parameters. Left panel: PNFW model. Right panel: ENFW model.

To compare the analytic solutions for critical curves and constant distortion curves to their exact calculations, we use as a figure-of-merit the mean weighted squared fractional difference between the two curves (Dúmet-Montoya et al. 2013) 𝒟2=∑i=1Nwi[xex(φi)−xapp(φi)]2∑i=1Nwixex2(φi),\begin{eqnarray} \mathcal{D}^2 = \frac{\sum_{i=1}^N w_i\left[x_{\rm ex}(\phi_i) - x_{\rm app}(\phi_i) \right]^2}{\sum_{i=1}^N w_i x^2_{\rm ex}(\phi_i)}, \label{D2_funct} \end{eqnarray}(50)where N is the number of points of the curves, φi is their polar angle, wi = φi − φi − 1 is a weight (to account for a possible non-uniform distribution of points), xex(φi) and xapp(φi) are the radial coordinates of the curves curves obtained from the exact and approximated calculations, respectively. We notice that, the \hbox{$\mathcal{D}^2$} in Eq. (50) is independent both on the lens length scale and on the discretization.

Choosing a maximum value for 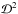\hbox{$\mathcal{D}^2$}, we can define upper values for the characteristic convergences (for a given ellipticity) such that the contour curves obtained with both the exact and approximated calculations will be close enough to each other. This maximum value is chosen by visually comparing the approximated and exact solutions for critical curves and constant distortion curves for several values of 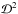\hbox{$\mathcal{D}^2$} and combinations of the NFW model parameters.

We compute 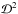\hbox{$\mathcal{D}^2$} on the Rλ = + Rth curves since their points are the farthest from the lens center. Thus, imposing a limit on the NFW parameters to match the Rλ = Rth curve, we automatically match the curves enclosed by it. We have checked that for a broad range of the NFW model parameters and ellipticities (for both elliptical and pseudo-elliptical models), a good visual matching of the exact and approximated curves if obtained for a maximum value of 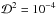\hbox{$\mathcal{D}^2 = 10^{-4}$} (for Rth = 5). This value also ensures a good matching of the critical curves, and we found that the corresponding curves in the source plane are well-matched, too. We thus fix this as the upper value of 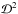\hbox{$\mathcal{D}^2$} throughout this work.

In Fig. 1 we show 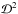\hbox{$\mathcal{D}^2$} for the Rth = 5 curve as a function of κs for the circular NFW model. Setting the above upper value for 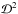\hbox{$\mathcal{D}^2$} leads to a maximum value of κs = 0.18, for which all curves | Rλ | = Rth ( ≥ 5), and the radial critical curves are well matched.

thumbnail Fig. 3

Constant distortion curves Rλ = + Rth (dot-dashed lines), Rλ = −Rth (dot-dot-dashed lines) for Rth = 5, tangential curves (dashed lines), and radial curves (dash-dash-dotted lines) obtained with the exact (thick gray lines) and approximated (black lines) calculations in the lens plane (left panels) and source plane (right panels). Upper panels: NFW model for κs = 0.15. Middle panels: PNFW model for κsϕ=0.1\hbox{$\kappa^\varphi_{\rm s}=0.1$} and ε = 0.5. Bottom panels: ENFW model for κsΣ=0.1\hbox{$\kappa^\Sigma_{\rm s}=0.1$} and εΣ = 0.4. In the right panels the axes are in units of η0 = rsDOS/DOL.

For the PNFW model, we chose the convention (Blandford & Kochanek 1987; Golse & Kneib 2002) 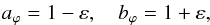aϕ=1−ε, bϕ=1+ε,\begin{eqnarray} a_{\varphi}=1-\varepsilon, \quad b_{\varphi}=1+\varepsilon, \label{choice_gk02} \end{eqnarray}(51)where the ellipticity parameter ε is defined in the range 0 ≤ ε < 1. As shown in DCM, for low values of 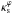κsϕ\hbox{$\kappa^\varphi_{\rm s}$} we must have ε ≲ 0.5 to avoid dumbbell-shape mass distributions. In the forthcoming analyses, we therefore adopt an upper value of ε = 0.5. In the left panel of Fig. 2 we show 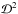\hbox{$\mathcal{D}^2$} as a function of 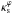κsϕ\hbox{$\kappa^\varphi_{\rm s}$} for some values of ε. For the higher value of ε considered, 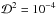\hbox{$\mathcal{D}^2 = 10^{-4}$} is reached for 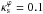κsϕ=0.1\hbox{$\kappa_{\rm s}^\varphi=0.1$}, providing an upper limit for the characteristic convergence for the validity of the approximations. However, higher values of 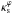κsϕ\hbox{$\kappa^\varphi_{\rm s}$} are allowed as ε decreases. For instance, when ε → 0, we find that 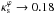κsϕ→0.18\hbox{$\kappa^\varphi_{\rm s} \rightarrow 0.18$} (in agreement with the result for the circular NFW model).

For the ENFW model, we chose the parametrization 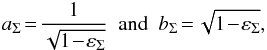aΣ=11−εΣandbΣ=1−εΣ,\begin{eqnarray} a_\Sigma\!=\! \frac{1}{\sqrt{1\!-\!\varepsilon_{\Sigma}}} \ \ \mathrm{and} \ \ b_\Sigma\! =\! \sqrt{1\!-\!\varepsilon_{\Sigma}}, \end{eqnarray}(52)where the ellipticity εΣ is defined in the range 0 ≤ εΣ < 1. In the right hand panel of Fig. 2 we show 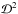\hbox{$\mathcal{D}^2$} as a function of 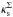κsΣ\hbox{$\kappa^\Sigma_{\rm s}$} for some values of εΣ. The behavior of 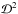\hbox{$\mathcal{D}^2$}, as well as the maximum values of εΣ for each 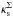κsΣ\hbox{$\kappa_{\rm s}^\Sigma$}, is qualitatively similar to that of the PNFW model. In this case, we find that a maximum value of 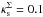κsΣ=0.1\hbox{$\kappa^\Sigma_{\rm s}=0.1$} is allowed for εΣ = 0.7. Again the maximum value 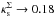κsΣ→0.18\hbox{$\kappa^\Sigma_{\rm s} \rightarrow 0.18$} as εΣ → 0.

In Appendix B we present fitting functions for the maximum values of ε (εΣ) as a function of 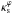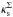κsϕ\hbox{$\kappa^\varphi_{\rm s}$} (κsΣ\hbox{$\kappa^\Sigma_{\rm s}$}) for which the approximation is accurate following the criteria of this section. In Fig. 3 we show the constant distortion curves (including tangential and radial critical curves) in both the lens and source planes, for some values of the NFW, PNFW, and ENFW parameters, both using the approximations introduced in this work, as well as through the numerical computation with no approximations. The parameters were chosen such that 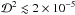\hbox{$\mathcal{D}^2 \lesssim 2\times 10^{-5}$}, i.e. less than our cut 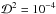\hbox{$\mathcal{D}^2=10^{-4}$}. We see that the exact and approximated curves are almost indistinguishable, visually illustrating the validity of using 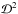\hbox{$\mathcal{D}^2$} to determine the domain of validity of the approximations.

5.2. Comparison between deformation cross sections

We compare the exact calculations and the solutions derived in Sect. 4.2, in order to verify that the limits derived in Sect. 5.1 also give a domain of validity for the deformation cross section. To quantify this comparison, we compute the relative difference 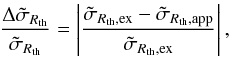Δ˜σRth˜σRth=|˜σRth,ex−˜σRth,app˜σRth,ex|,\begin{eqnarray} \frac{\Delta \tilde{\sigma}_{R_{\rm th}}}{\tilde{\sigma}_{R_{\rm th}}}=\left|\frac{\tilde{\sigma}_{R_{\rm th},\rm ex}-\tilde{\sigma}_{R_{\rm th},\rm app}}{\tilde{\sigma}_{R_{\rm th},\rm ex}} \right|,\label{dif_rela_sigma} \end{eqnarray}(53)where the subscripts ex and app refer to the exact and approximated calculations, respectively.

thumbnail Fig. 4

Deformation cross section for the circular NFW lens model as a function of κs. Solid line corresponds to expression (47). Filled circles correspond to the exact (numerical) calculation.

In Fig. 4 we show 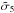˜σ5\hbox{$\tilde{\sigma}_{5}$} (upper panel) and 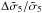Δ˜σ5/˜σ5\hbox{$\Delta \tilde{\sigma}_{5}/\tilde{\sigma}_{5}$} (bottom panel) as a function of κs for both the exact and approximated calculations. Considering the limit of the previous section, i.e., κs ≤ 0.18, Eq. (47) deviates from the exact calculation by at most 2.5%.

In the left panels of Fig. 5 we show 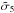˜σ5\hbox{$\tilde{\sigma}_{5}$} (upper panel) and 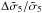Δ˜σ5/˜σ5\hbox{$\Delta \tilde{\sigma}_{5}/\tilde{\sigma}_{5}$} (bottom panel) as a function of 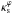κsϕ\hbox{$\kappa^\varphi_{\rm s}$} for the PNFW model for both the exact and the approximated calculations. Considering the limit of applicability obtained in the previous section (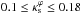0.1≤κsϕ≤0.18\hbox{$0.1 \leq \kappa^\varphi_{\rm s} \leq 0.18$} and ε ≤ 0.5), Eq. (45), with Eq. (48), deviates at most 2.6% from the exact calculation. A very similar result is found for the ENFW model. In this case, for 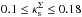0.1≤κsΣ≤0.18\hbox{$0.1\leq \kappa_{\rm s}^\Sigma \leq 0.18$} and εΣ ≤ 0.7, we find that 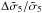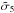Δ˜σ5/˜σ5\hbox{$\Delta \tilde{\sigma}_{5}/\tilde{\sigma}_{5}$} (˜σ5\hbox{$\tilde{\sigma}_{5}$} calculated by Eq. (45) with Eq. (49)) is at most 2.5%.

thumbnail Fig. 5

Deformation cross sections for the PNFW model (left panel) and ENFW model (right panel). Symbols correspond to the exact calculations.

6. Mapping among PNFW and ENFW parameters

As mentioned in the introduction, elliptical models are more physically motivated than pseudo-elliptical ones. However, determination of lensing quantities, such as the shear, for the former requires evaluating integrals (Schramm 1990; Keeton 2001a, see also Appendix A), which generally have to be computed numerically. On the other hand, pseudo-elliptical models do not require such integrals to be evaluated (see, e.g., Eqs. (18)–(21)) allowing for fast calculations for the same quantities. However, it is well known that pseudo-elliptical models have two main limitations: their surface mass density can assume negative values in some regions (Blandford & Kochanek 1987) and may present a “dumbbell” shape for high ellipticities (Kovner 1989; Schneider et al. 1992; Kassiola & Kovner 1993). At least in the case of the NFW model, the first problem does not affect the region of arc formation (DCM). Regarding the shape of the iso-convergence contours, for each value of 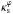κsϕ\hbox{$\kappa_{\rm s}^\varphi$}, there is a range in ε for which the contours are approximately elliptical (DCM). In principle, within this range of parameters, the pseudo-elliptical models could be employed instead of elliptical ones in studies that require numerous evaluations of lensing quantities. 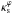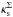For this sake, a correspondence among model parameters has to be established, which associates a pair of the PNFW parameters (ε, κsϕ\hbox{$\kappa_{\rm s}^{\varphi}$}) to a pair of the ENFW ones (εΣ, κsΣ\hbox{$\kappa_{\rm s}^{\Sigma}$}).

To obtain εΣ from the PNFW model we use the same procedure as in Golse & Kneib (2002, see also DCM). From Eq. (23) we define the semi-major axis a by xκ(φ = 0) and the semi-minor axis b by xκ(φ = π/2) such that εΣ=1−ba=1−aϕbϕexp[(aϕ−bϕ)(aϕ+bϕ)],=\begin{eqnarray} \varepsilon_\Sigma = 1-\frac{b}{a} & = & 1-\sqrt{\frac{a_{\varphi} }{b_{\varphi} }}\exp{\left[\frac{(a_{\varphi} -b_{\varphi} )}{(a_{\varphi} +b_{\varphi} )} \right]}, \nonumber \\ & =& 1-\sqrt{\frac{1-\varepsilon}{1+\varepsilon}}\exp{\left[-\frac{\varepsilon}{2} \right]}\cdot \label{ellip_gk} \end{eqnarray}(54)This expression has no dependence on Rth or on κsϕ\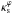hbox{$\kappa^\varphi_{\rm s}$}.

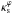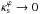The qualitative behavior of εΣ(ε) from this equation is very similar to what was found numerically for generic values of κsϕ\hbox{$\kappa^\varphi_{\rm s}$} in DCM (see, e.g., their Fig. 6). For ε ≪ 1, the expression above gives εΣ ≃ 2ε, in agreement with DCM (see, e.g., Eq. (B.2), which gives εΣ = 1.97ε, for κsϕ→0\hbox{$\kappa^\varphi_{\rm s} \rightarrow 0$}).

Interestingly, Eq. (54) is a good approximation of the exact relation for values of 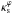κsϕ\hbox{$\kappa^\varphi_{\rm s}$} well above the limit of validity of the approximation derived in Sect. 5. Indeed, the relative deviation with respect to the exact calculation of 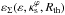εΣ(ε,κsϕ,Rth)\hbox{$\varepsilon_\Sigma(\varepsilon,\kappa^\varphi_{\rm s}, R_{\rm th})$} (see the elliptical fit method in Sect. 4 of DCM) is at most 5% for 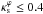κsϕ≤0.4\hbox{$\kappa^\varphi_{\rm s} \leq 0.4$}, with ε ≤ 0.5 and Rth ≥ 5.

To associate a value of 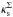κsΣ\hbox{$\kappa^\Sigma_{\rm s}$} to a pair (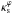κsϕ\hbox{$\kappa^\varphi_{\rm s}$}, ε), we require that the tangential critical curves of the PNFW and ENFW models match at φ = 0. This condition, from Eqs. 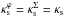(25) and (37), gives κsΣ=bϕκsϕaΣbΣ[𝒥1+bϕκsϕ(𝒥1logaϕ−𝒥1−2ℒ1(0))]·\begin{eqnarray} \kappa_{\rm s}^\Sigma=\frac{b_{\varphi} \kappa_{\rm s}^\varphi}{a_\Sigma b_\Sigma\left[\mathcal{J}_1 +b_{\varphi} \kappa^\varphi_{\rm s}(\mathcal{J}_1\log{a_{\varphi} }-\mathcal{J}_1-2\mathcal{L}_1(0))\right]}\cdot \label{ka_rela_gk} \end{eqnarray}(55)For ε = εΣ = 0 the expression above reduces to κsϕ=κsΣ=κs\hbox{$\kappa_{\rm s}^\varphi=\kappa_{\rm s}^\Sigma=\kappa_{\rm s}$}, as it should be.

We determine the upper value of 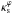κsϕ\hbox{$\kappa^\varphi_{\rm s}$} such that the expression above deviates by at most 5% with respect to the exact calculation. This yields 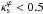κsϕ<0.5\hbox{$\kappa^\varphi_{\rm s} < 0.5$} for ε ≤ 0.5 and Rth ≥ 5. Again, the domain of validity of the approximate mapping is greater than for the lensing equations.

7. Summary and concluding remarks

When considering low values of the characteristic convergence of the NFW model (i.e., on the galactic and galaxy group mass scales), some strong lensing quantities require high numerical precision to yield accurate results, which can demand a lot of time. Motivated by this issue, we obtained analytic solutions for several strong lensing quantities for elliptical and pseudo-elliptical NFW models and quantified their corresponding limits of validity.

The starting point is approximation (8) for the deflection angle of the circular NFW model. This approximation was applied to the standard prescriptions for obtaining the convergence and shear for circular, elliptical, and pseudo-elliptical models, leading to analytic solutions for these quantities (Sect. 3). Those were in turn used to derive analytic expressions for iso-convergence contours and critical curves (see Sect. 3) and for the constant distortion curves as a function of Rth (Sect. 4.1).

As a practical application of these results, we computed the deformation cross section (σRth). In the case of the circular NFW model, we obtained an analytical formula for σRth (Eq. (47)), which reproduces the behavior with respect to κs and the scaling with Rth obtained numerically in previous works (see, e.g., Caminha et al. 2013). We have shown that the computation of this cross section is reduced to a one-dimensional integral for both the PNFW and ENFW models (Eq. (45) with either Eq. (48) or Eq. (49), respectively). These expressions speed up the numerical computations by two orders of magnitude for the PNFW model and one order of magnitude for the ENFW one, independently of the values of the ellipticity parameter.

We used the figure-of-merit 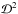\hbox{$\mathcal{D}^2$}, Eq. (50), to quantify the deviation of the solutions of the constant distortion curves with respect to their exact calculations. Setting a maximum value of 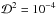\hbox{$\mathcal{D}^2 = 10^{-4}$}, we find that Eqs. (42), (43), match its corresponding exact calculation up to 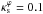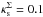κsϕ=0.1\hbox{$\kappa^\varphi_{\rm s} =0.1$} (κsΣ=0.1\hbox{$\kappa^\Sigma_{\rm s} =0.1$}) for ε ≤ 0.5 (εΣ ≤ 0.7) and Rth > 5. In particular, we find that the characteristic convergence can go up to 0.18 as the ellipticity parameters tend to zero, as expected from the limit derived for the circular NFW model. In Appendix B we provide fitting functions for the maximum ellipticity allowed as a function of the characteristic convergences (in the range 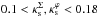0.1<κsΣ,κsϕ<0.18\hbox{$0.1 <\kappa^\Sigma_{\rm s},\kappa^{\varphi}_{\rm s} < 0.18$}) to ensure the validity of the approximations. We emphasize that these limits also ensure a good match for critical curves and the Rλ = −Rth curves to their corresponding exact calculations, since these curves are enclosed by the Rλ = Rth curve. We verified that the corresponding curves in the source plane also match the exact solution for the parameters within the limits derived above.

We compared the deformation cross sections (obtained from both the exact and approximated calculations) in order to check that the domain of validity derived for the constant distortion curves also holds for this quantity (Sect. 5.2), which we found to be the case. For instance, for the circular NFW model, for κs ≤ 0.18 and Rth = 5, Eq. (47) deviates at most 2.5% from the exact calculation, while for the PNFW and ENFW, 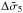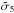Δ˜σ5\hbox{$\Delta\tilde{\sigma}_5$}/˜σ5\hbox{$\tilde{\sigma}_5$} (Eq. (53)) is at most 2.5%, for 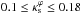0.1≤κsϕ≤0.18\hbox{$0.1 \leq \kappa^\varphi_{\rm s} \leq 0.18$} and ε < 0.5, and 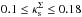0.1≤κsΣ≤0.18\hbox{$ 0.1 \leq \kappa^\Sigma_{\rm s} \leq 0.18$} and εΣ < 0.7, respectively.

Overall, the approximate solutions presented here are accurate for all strong lensing quantities that were addressed in this work, within the considered parameter ranges, for κs ≤ 0.1. In some cases they are valid for higher κs, such as for low ellitpcities. Furthermore, some derived quantities are valid up to much higher characteristic convergences. For example, the ellipticity of the iso-convergence contours of the PNFW model is reproduced well by the simple analytic form of Eq. (54) up to 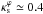κsϕ≃0.4\hbox{$\kappa^\varphi_{\rm s} \simeq 0.4$}. We found that in this range the relation εΣ(ε) is independent of 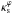κsϕ\hbox{$\kappa^\varphi_{\rm s}$} and of the chosen value of the contour. To complete the association of the PNFW to ENFW model parameters we derived a relation among characteristic convergences, Eq. (55), which also matches the values obtained in DCM for 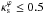κsϕ≤0.5\hbox{$\kappa^\varphi_{\rm s} \le 0.5$} and Rth ≥ 5.

The analytic solutions presented here allow for a robust and fast computation of several strong lensing quantities to be carried out in the low characteristic convergence regime. They may thus be useful for the lensing community and could be readily included in strong lensing codes, considering the domain of applicability derived in this work.

In principle, the approximate solutions derived in this paper could be extended to other quantities, such as the lensing magnification and the magnification cross section. They might also be applied to finding solutions of the lens equation, for multiple images and arcs. One way of finding approximate solutions for arcs, for low ellitpicities, is through the perturbative approach (Alard 2007, 2008; Peirani et al. 2008), for which the Einstein ring solution (given analytically in Eq. (15)) is the starting point. Therefore, analytic solutions for arcs might be derived in this framework. The investigation of these and other possible extensions is left for future work.

2

To obtain this value of κs we use the expressions in Caminha et al. (2013) with the same choices for the NFW and cosmological parameters as described in Sect. 2.2 of Dúmet-Montoya et al. (2012).

3

These solutions are shown in Meneghetti et al. (2003). However, there is a typo in this reference as they appear in their Eq. (11) as the eigenvalues of the Jacobian matrix.

Acknowledgments

We thank the anonymous referee for useful suggestions that helped improve this manuscript. We thank the anonymous referee of DCM for pushing us to consider the low κs regime. H. S. Dúmet-Montoya is funded by the Brazilian agency CNPq. G. B. Caminha is funded by CNPq and CAPES. M. Makler is partially supported by CNPq (grant 309804/2012-4) and FAPERJ (grant E-26/110.516/2012).

References

  1. Alard, C. 2007, MNRAS, 382, L58 [NASA ADS] [Google Scholar]
  2. Alard, C. 2008, MNRAS, 388, 375 [NASA ADS] [CrossRef] [Google Scholar]
  3. Annis, J., Bridle, S., Castander, F. J., et al. 2005 [arXiv:astro-ph/0510195] [Google Scholar]
  4. Asano, K. 2000, PASJ, 52, 99 [NASA ADS] [Google Scholar]
  5. Barkana, R. 1998, ApJ, 502, 531 [NASA ADS] [CrossRef] [Google Scholar]
  6. Barnabè, M., Czoske, O., Koopmans, L. V. E., Treu, T., & Bolton, A. S. 2011, MNRAS, 415, 2215 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bartelmann, M. 1995, A&A, 299, 11 [NASA ADS] [Google Scholar]
  8. Bartelmann, M. 1996, A&A, 313, 697 [NASA ADS] [Google Scholar]
  9. Bartelmann, M., & Weiss, A. 1994, A&A, 287, 1 [NASA ADS] [Google Scholar]
  10. Bartelmann, M., Steinmetz, M., & Weiss, A. 1995, A&A, 297, 1 [NASA ADS] [Google Scholar]
  11. Bartelmann, M., Huss, A., Colberg, J. M., Jenkins, A., & Pearce, F. R. 1998, A&A, 330, 1 [NASA ADS] [Google Scholar]
  12. Bartelmann, M., Meneghetti, M., Perrotta, F., Baccigalupi, C., & Moscardini, L. 2003, A&A, 409, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bayliss, M. B. 2012, ApJ, 744, 156 [NASA ADS] [CrossRef] [Google Scholar]
  14. Belokurov, V., Evans, N. W., Hewett, P. C., et al. 2009, MNRAS, 392, 104 [NASA ADS] [CrossRef] [Google Scholar]
  15. Blandford, R. D., & Kochanek, C. S. 1987, ApJ, 321, 658 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bolton, A. S., Burles, S., Koopmans, L. V. E., Treu, T., & Moustakas, L. A. 2006, ApJ, 638, 703 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cabanac, R. A., Alard, C., Dantel-Fort, M., et al. 2007, A&A, 461, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Caminha, G. B., Estrada, J., & Makler, M. 2013, ApJ, submitted [arXiv:1308.6569] [Google Scholar]
  19. Comerford, J. M., Meneghetti, M., Bartelmann, M., & Schirmer, M. 2006, ApJ, 642, 39 [NASA ADS] [CrossRef] [Google Scholar]
  20. Davis, A. N., Huterer, D., & Krauss, L. M. 2003, MNRAS, 344, 1029 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dúmet-Montoya, H. S., Caminha, G. B., & Makler, M. 2012, A&A, 544, A83 (DCM) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Dúmet-Montoya, H. S., Caminha, G. B., Moraes, B., et al. 2013, MNRAS, 433, 2975 [NASA ADS] [CrossRef] [Google Scholar]
  23. Ebeling, H., Edge, A. C., & Henry, J. P. 2001, ApJ, 553, 668 [Google Scholar]
  24. Estrada, J., Annis, J., Diehl, H. T., et al. 2007, ApJ, 660, 1176 [NASA ADS] [CrossRef] [Google Scholar]
  25. Fassnacht, C. D., Moustakas, L. A., Casertano, S., et al. 2004, ApJ, 600, L155 [NASA ADS] [CrossRef] [Google Scholar]
  26. Faure, C., Kneib, J.-P., Covone, G., et al. 2008, ApJS, 176, 19, Erratum 2008, 178, 382 [NASA ADS] [CrossRef] [Google Scholar]
  27. Fedeli, C., Meneghetti, M., Bartelmann, M., Dolag, K., & Moscardini, L. 2006, A&A, 447, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Furlanetto, C., Santiago, B. X., Makler, M., et al. 2013, MNRAS, 432, 73 [NASA ADS] [CrossRef] [Google Scholar]
  29. Gilbank, D. G., Gladders, M. D., Yee, H. K. C., & Hsieh, B. C. 2011, AJ, 141, 94 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gladders, M. D., Hoekstra, H., Yee, H. K. C., Hall, P. B., & Barrientos, L. F. 2003, ApJ, 593, 48 [NASA ADS] [CrossRef] [Google Scholar]
  31. Golse, G., & Kneib, J.-P. 2002, A&A, 390, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Golse, G., Kneib, J.-P., & Soucail, G. 2002, A&A, 387, 788 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Grossman, S. A., & Saha, P. 1994, ApJ, 431, 74 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hamana, T., & Futamase, T. 1997, MNRAS, 286, L7 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hattori, M., Watanabe, K., & Yamashita, K. 1997, A&A, 319, 764 [NASA ADS] [Google Scholar]
  36. Hennawi, J. F., Gladders, M. D., Oguri, M., et al. 2008, AJ, 135, 664 [NASA ADS] [CrossRef] [Google Scholar]
  37. Horesh, A., Maoz, D., Hilbert, S., & Bartelmann, M. 2011, MNRAS, 418, 54 [NASA ADS] [CrossRef] [Google Scholar]
  38. Jackson, N. 2008, MNRAS, 389, 1311 [NASA ADS] [CrossRef] [Google Scholar]
  39. Jing, Y. P., & Suto, Y. 2002, ApJ, 574, 538 [NASA ADS] [CrossRef] [Google Scholar]
  40. Jullo, E., Kneib, J.-P., Limousin, M., et al. 2007, New J. Phys., 9, 447 [Google Scholar]
  41. Jullo, E., Natarajan, P., Kneib, J.-P., et al. 2010, Science, 329, 924 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  42. Kassiola, A., & Kovner, I. 1993, ApJ, 417, 450 [NASA ADS] [CrossRef] [Google Scholar]
  43. Kausch, W., Schindler, S., Erben, T., Wambsganss, J., & Schwope, A. 2010, A&A, 513, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Keeton, C. R. 2001a [arXiv:astro-ph/0102341] [Google Scholar]
  45. Keeton, C. R. 2001b [arXiv:astro-ph/0102340] [Google Scholar]
  46. Kneib, J.-P. 2002, in Proc. The shapes of galaxies and their dark halos, ed. P. Natarajan, 50 [Google Scholar]
  47. Kneib, J. P., Mellier, Y., Fort, B., & Mathez, G. 1993, A&A, 273, 367 [NASA ADS] [Google Scholar]
  48. Kneib, J.-P., Van Waerbeke, L., Makler, M., & Leauthaud, A. 2010, CFHT programs 10BF023, 10BC02, 10BB009 [Google Scholar]
  49. Koopmans, L. V. E., Bolton, A., Treu, T., et al. 2009, ApJ, 703, L51 [NASA ADS] [CrossRef] [Google Scholar]
  50. Kovner, I. 1989, ApJ, 337, 621 [NASA ADS] [CrossRef] [Google Scholar]
  51. Kubo, J. M., & Dell’Antonio, I. P. 2008, MNRAS, 385, 918 [NASA ADS] [CrossRef] [Google Scholar]
  52. Kubo, J. M., Allam, S. S., Drabek, E., et al. 2010, ApJ, 724, L137 [NASA ADS] [CrossRef] [Google Scholar]
  53. Ludlow, A. D., Navarro, J. F., Boylan-Kolchin, M., et al. 2013, MNRAS, 432, 1103 [NASA ADS] [CrossRef] [Google Scholar]
  54. Luppino, G. A., Gioia, I. M., Hammer, F., Le Fèvre, O., & Annis, J. A. 1999, A&AS, 136, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Macciò, A. V., Dutton, A. A., van den Bosch, F. C., et al. 2007, MNRAS, 378, 55 [NASA ADS] [CrossRef] [Google Scholar]
  56. Meneghetti, M., Bartelmann, M., & Moscardini, L. 2003, MNRAS, 340, 105 [NASA ADS] [CrossRef] [Google Scholar]
  57. Meneghetti, M., Baccigalupi, C., Bartelmann, M., et al. 2005, in Gravitational lensing impact on cosmology, eds. Y. Mellier & G. Meylan, IAU Symp., 225, 185 [Google Scholar]
  58. Miralda-Escude, J. 1993, ApJ, 403, 497 [NASA ADS] [CrossRef] [Google Scholar]
  59. Mollerach, S., & Roulet, E. 2002, Gravitational lensing and microlensing (World Scientific Publishing Co. Pte. Ltd.) [Google Scholar]
  60. More, A., Cabanac, R., More, S., et al. 2012, ApJ, 749, 38 [Google Scholar]
  61. Moustakas, L. A., Marshall, P., Newman, J. A., et al. 2007, ApJ, 660, L31 [NASA ADS] [CrossRef] [Google Scholar]
  62. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
  63. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
  64. Oguri, M., Lee, J., & Suto, Y. 2003, ApJ, 599, 7, Erratum 2004, 608, 1175 [NASA ADS] [CrossRef] [Google Scholar]
  65. Peirani, S., Alard, C., Pichon, C., Gavazzi, R., & Aubert, D. 2008, MNRAS, 390, 945 [NASA ADS] [CrossRef] [Google Scholar]
  66. Petters, A. O., Levine, H., & Wambsganss, J. 2001, Singularity theory and gravitational lensing (Berlin: Birkhäuser) [Google Scholar]
  67. Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [NASA ADS] [CrossRef] [Google Scholar]
  68. Ratnatunga, K. U., Griffiths, R. E., & Ostrander, E. J. 1999, AJ, 117, 2010 [NASA ADS] [CrossRef] [Google Scholar]
  69. Rozo, E., Nagai, D., Keeton, C., & Kravtsov, A. 2008, ApJ, 687, 22 [NASA ADS] [CrossRef] [Google Scholar]
  70. Sand, D. J., Treu, T., Ellis, R. S., & Smith, G. P. 2005, ApJ, 627, 32 [NASA ADS] [CrossRef] [Google Scholar]
  71. Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational lenses (Berlin: Springer-Verlag) [Google Scholar]
  72. Schramm, T. 1990, A&A, 231, 19 [NASA ADS] [Google Scholar]
  73. Smith, G. P., Kneib, J.-P., Smail, I., et al. 2005, MNRAS, 359, 417 [NASA ADS] [CrossRef] [Google Scholar]
  74. Suyu, S. H., Hensel, S. W., McKean, J. P., et al. 2012, ApJ, 750, 10 [NASA ADS] [CrossRef] [Google Scholar]
  75. Vegetti, S., & Koopmans, L. V. E. 2009, MNRAS, 392, 945 [NASA ADS] [CrossRef] [Google Scholar]
  76. Wayth, R. B., & Webster, R. L. 2006, MNRAS, 372, 1187 [NASA ADS] [CrossRef] [Google Scholar]
  77. Wen, Z.-L., Han, J.-L., & Jiang, Y.-Y. 2011, RA&A, 11, 1185 [Google Scholar]
  78. Wiesner, M. P., Lin, H., Allam, S. S., et al. 2012, ApJ, 761, 1 [NASA ADS] [CrossRef] [Google Scholar]
  79. Willis, J. P., Hewett, P. C., Warren, S. J., Dye, S., & Maddox, N. 2006, MNRAS, 369, 1521 [NASA ADS] [CrossRef] [Google Scholar]
  80. Wu, X.-P., & Hammer, F. 1993, MNRAS, 262, 187 [NASA ADS] [CrossRef] [Google Scholar]
  81. Zaritsky, D., & Gonzalez, A. H. 2003, ApJ, 584, 691 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Lensing functions for elliptical lens models

The lensing functions of models with elliptical mass distribution can be obtained following the expressions derived in Schramm (1990) and Keeton (2001a), which were generalized for any choice of the ellipticity parameterization in Caminha et al. (2013) and are given by 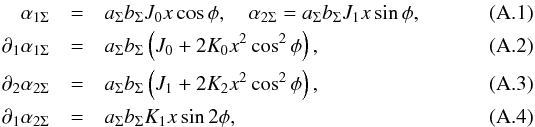α1Σ=∂1α1Σ=∂2α2Σ=∂1α2Σ=\appendix \setcounter{section}{1} \begin{eqnarray} \alpha_{1\Sigma} & = & a_{\Sigma}b_{\Sigma} J_0 x \cos{\phi}, \quad \alpha_{2\Sigma} = a_{\Sigma}b_{\Sigma} J_1 x \sin{\phi} \label{d1-2_ellip}, \\ \partial_1\alpha_{1\Sigma} & = & a_{\Sigma}b_{\Sigma} \left(J_0 + 2 K_0 x^2 \cos^2{\phi}\right), \label{d11_ellip} \\ \partial_2\alpha_{2\Sigma} & = & a_{\Sigma}b_{\Sigma} \left(J_1 + 2 K_2 x^2 \cos^2{\phi}\right),\label{d22_ellip} \\ \partial_1\alpha_{2\Sigma} & = & a_{\Sigma}b_{\Sigma} K_1 x \sin{2\phi}, \label{d12_ellip} \end{eqnarray}where aΣ and bΣ are defined in Eq. (27), Jn:=∫01κ(m(u))[1−(1−bΣ2)u]1/2+n[1−(1−aΣ2)u]3/2−n\appendix \setcounter{section}{1} \begin{eqnarray} J_n := \int_0^1 \frac{\kappa(m(u))}{[1 - (1 - b^2_\Sigma)u]^{1/2 + n}[1 - (1 - a^2_\Sigma)u]^{3/2 - n}} \end{eqnarray}(A.5)and Kn:=∫01uκ′(m(u))[1−(1−bΣ2)u]1/2+n[1−(1−aΣ2)u]5/2−n,\appendix \setcounter{section}{1} \begin{eqnarray} K_n := \int_0^1 \frac{u\kappa^\prime(m(u))}{[1 - (1 - b^2_\Sigma)u]^{1/2 + n}[1 - (1 - a^2_\Sigma)u]^{5/2 - n}}, \end{eqnarray}(A.6)where κ is the convergence of the circular model, κ′=12mdκ(m)dm\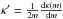hbox{$\kappa^\prime=\frac{1}{2m}\frac{{\rm d}\kappa(m)}{{\rm d}m}$} and we have defined the variable m2 = x2g(u,φ) such that 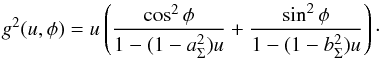g2(u,φ)=u(cos2φ1−(1−aΣ2)u+sin2φ1−(1−bΣ2)u)·\appendix \setcounter{section}{1} \begin{eqnarray*} g^2(u,\phi) = u \left( \frac{\cos^2\phi}{1 - (1-a_{\Sigma}^2)u} + \frac{\sin^2\phi}{1 - (1-b_{\Sigma}^2)u} \right)\cdot \end{eqnarray*}For the ENFW model, with the approximation (10), we can rewrite the potential derivatives as 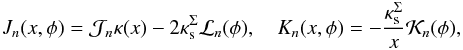Jn(x,φ)=𝒥nκ(x)−2κsΣℒn(φ), Kn(x,φ)=−κsΣx𝒦n(φ),\appendix \setcounter{section}{1} \begin{eqnarray} J_n(x,\phi)=\mathcal{J}_n\kappa(x)-2\kappa^\Sigma_{\rm s}\mathcal{L}_n(\phi), \quad K_n(x,\phi)= -\frac{\kappa^\Sigma_{\rm s}}{x}\mathcal{K}_n(\phi), \label{JK} \end{eqnarray}(A.7)where 𝒥n=𝒦n(φ)=ℒn(φ)=\appendix \setcounter{section}{1} \begin{eqnarray} \mathcal{J}_n &=& \int_0^1 \frac{{\rm d}u}{[1 - (1 - b^2_\Sigma)u]^{1/2 + n}[1 - (1 - a^2_\Sigma)u]^{3/2 - n}}, \label{an_enfw}\\ \mathcal{K}_n(\phi) &=&\int_0^1 \frac{ug(\phi,u)^{-2}{\rm d}u}{[1 - (1 - b^2_\Sigma)u]^{1/2 + n}[1 - (1 - a^2_\Sigma)u]^{5/2 - n}}\cdot \label{dn_enfw} \\ \mathcal{L}_n(\phi) &=&\int_0^1 \frac{\log{g(\phi, u) {\rm d}u}}{[1 - (1 - b^2_\Sigma)u]^{1/2 + n}[1 - (1 - a^2_\Sigma)u]^{3/2 - n}}, \label{bn_enfw} \label{Ln} \end{eqnarray}Substituting the expressions above in Eq. (A.1) we obtain Eqs. (28) and (29). Similarly, by substituting Eqs. (A.7)–(A.10) in (A.2)–(A.4) and using the definitions (6) and (7) we obtain Eqs. (30)–(32).

Appendix B: Fitting functions

Table B.1

Results from the regression analysis using the Padé approximant for ˜ε(κs)\hbox{$\tilde{\varepsilon}(\kappa_{\rm s})$}.

Applying the procedure outlined in Sect. 5.1, we obtained the maximum values of ε (εΣ) as a function of 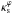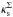κsϕ\hbox{$\kappa^\varphi_{\rm s}$} (κsΣ\hbox{$\kappa^\Sigma_{\rm s}$}) such that the analytic solutions derived in the paper are accurate. We find that these functions are well fitted by a Padé approximant of the form 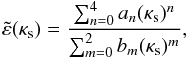˜ε(κs)=∑n=04an(κs)n∑m=02bm(κs)m,\appendix \setcounter{section}{2} \begin{eqnarray} \tilde{\varepsilon}(\kappa_{\rm s})=\frac{\sum_{n=0}^{4}a_n(\kappa_{\rm s})^n}{\sum_{m=0}^{2}b_m(\kappa_{\rm s})^m}, \label{emax_fit_funct} \end{eqnarray}(B.1)where 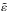˜ε\hbox{$\tilde{\varepsilon}$} and κs correspond either to 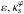ε,κsϕ\hbox{$\varepsilon,\kappa^\varphi_{\rm s}$} (for the PNFW) or 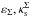εΣ,κsΣ\hbox{$\varepsilon_\Sigma,\kappa^\Sigma_{\rm s}$} (for the ENFW), and the values of coefficients are given in Table B.1.

All Tables

Table B.1

Results from the regression analysis using the Padé approximant for ˜ε(κs)\hbox{$\tilde{\varepsilon}(\kappa_{\rm s})$}.

In the text

All Figures

thumbnail Fig. 1

Mean weighted squared radial fractional difference \hbox{$\mathcal{D}^2$} for the constant distortion curve with Rth = 5 for the circular NFW lens model as a function of the characteristic convergence κs.
In the text
thumbnail Fig. 2

Mean weighted squared radial fractional difference \hbox{$\mathcal{D}^2$}, for constant distortion curves with Rth = 5, as a function of the characteristic convergences, for some values of ellipticity parameters. Left panel: PNFW model. Right panel: ENFW model.
In the text
thumbnail Fig. 3

Constant distortion curves Rλ = + Rth (dot-dashed lines), Rλ = −Rth (dot-dot-dashed lines) for Rth = 5, tangential curves (dashed lines), and radial curves (dash-dash-dotted lines) obtained with the exact (thick gray lines) and approximated (black lines) calculations in the lens plane (left panels) and source plane (right panels). Upper panels: NFW model for κs = 0.15. Middle panels: PNFW model for κsϕ=0.1\hbox{$\kappa^\varphi_{\rm s}=0.1$} and ε = 0.5. Bottom panels: ENFW model for κsΣ=0.1\hbox{$\kappa^\Sigma_{\rm s}=0.1$} and εΣ = 0.4. In the right panels the axes are in units of η0 = rsDOS/DOL.
In the text
thumbnail Fig. 4

Deformation cross section for the circular NFW lens model as a function of κs. Solid line corresponds to expression (47). Filled circles correspond to the exact (numerical) calculation.
In the text
thumbnail Fig. 5

Deformation cross sections for the PNFW model (left panel) and ENFW model (right panel). Symbols correspond to the exact calculations.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.