| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201322692 | |
| Published online | 01 November 2013 | |
Coupled jet-disk model for Sagittarius A*: explaining the flat-spectrum radio core with GRMHD simulations of jets
1
Department of Astrophysics/IMAPPRadboud University Nijmegen,
PO Box 9010,
6500 GL
Nijmegen,
The Netherlands
e-mail: m.moscibrodzka@astro.ru.nl; h.falcke@astro.ru.nl
2
ASTRON, Dwingeloo, The Netherlands
Received: 17 September 2013
Accepted: 16 October 2013
Context. The supermassive black hole in the center of the Milky Way, Sgr A*, displays a nearly flat radio spectrum that is typical for jets in active galactic nuclei. Indeed, time-dependent magnetized models of radiatively inefficient accretion flows (RIAFs), which are commonly used to explain the millimeter, near-infrared, and X-ray emission of Sgr A*, often also produce jet-like outflows. However, the emission from these models has so far failed to reproduce the flat radio spectrum.
Aims. We investigate whether current accretion simulations can produce the compact flat spectrum emission by simply using a different prescription for the heating of the radiating particles in the jet.
Methods. We studied the radiative properties of accretion flows onto a black hole produced in time-dependent general-relativistic magnetohydrodynamic (GRMHD) simulations. A crucial free parameter in these models has always been the electron temperature, and here we allowed for variations in the proton-to-electron temperature ratios in the jet and disk.
Results. We found that the flat spectrum is readily reproduced by a standard GRMHD model if one has an almost isothermal jet coupled to a two-temperature accretion flow. The low-frequency radio emission comes from the outflowing sheath of matter surrounding the strongly magnetized nearly empty jet. The model is consistent with the radio sizes and spectrum of Sgr A*.
Conclusions. Hence, GRMHD models of accreting black holes can in principle naturally reproduce jets that match observed characteristics. For Sgr A* the model fit to the spectrum predicts higher mass-accretion rates when a jet is included than without a jet. Hence, the impact of the recently discovered G2 cloud that is expected to be accreted onto Sgr A* might be less severe than currently thought.
Key words: accretion, accretion disks / black hole physics / magnetohydrodynamics (MHD) / radiative transfer / Galaxy: center
© ESO, 2013
1. Introduction
Blandford & Königl (1979) suggested that the flat-spectrum radio cores seen in many active galactic nuclei are the optically thick parts of conical plasma jets. Very Long Baseline Interferometry (VLBI) has indeed revealed a jet-like geometry in many flat-spectrum compact radio cores. Interestingly, the center of our Galaxy also hosts a flat-spectrum core, called Sgr A*, and it has been suggested that it may be associated with a relativistic downsized jet from a starving supermassive black hole (BH; Falcke et al. 1993; Falcke & Markoff 2000; Markoff et al. 2007). Unfortunately, scattering by interstellar electrons smears out the source structure. Nonetheless, the presence of a relativistic outflow in Sgr A* is strengthened by the size-frequency relation (Bower et al. 2004) and by a 20-min time-lag between flares in the 43 and 22 GHz light curves (Yusef-Zadeh et al. 2006), which can be well explained by a jet model (Falcke et al. 2009).
At millimeter wavelengths, the spectrum of Sgr A* peaks in the so-called submillimeter bump (Falcke et al. 1998), which can be modeled by synchrotron emission arising from a radiatively inefficient accretion flow onto a BH (RIAFs; first applied to Sgr A* by Narayan et al. 1995). Over the past years, the RIAF model has progressed from a simple semi-analytical model to more complex time-dependent general-relativistic magnetohydrodynamic (GRMHD) models. In these models relativistic jets are often produced (e.g., Beckwith et al. 2008). The synchrotron emission from a GRMHD-RIAF can now be calculated with a high degree of precision using general relativistic radiative-transfer codes (e.g., Broderick et al. 2009; Dolence et al. 2009; Dexter & Agol 2009; Shcherbakov et al. 2012). Advances in numerical modeling, together with less scattered, mm-wave VLBI measurements of Sgr A*, provide an opportunity to put tight constraints on jet-plus-disk models for BHs (Broderick & Loeb 2009; Dexter et al. 2012).
 |
Fig. 1 Overall structure of the flow (upper half of the simulation domain). Panels from left to right show maps of the density, magnetic field strength, gas temperature, and bulk speed of the gas. The first two are given in dimensionless numerical code units. Solid and dashed contours illustrate our jet and disk definitions, which are introduced in Sect. 2. The solid line separates the jet from the disk, and the dashed line separates the jet spine from jet sheath. |
So far, GRMHD-RIAF models have not naturally reproduced the radio spectrum of Sgr A* – with or without a jet. This may be partly because of the uncertainty in how to treat plasma temperatures. The dynamics of the plasma around the BH is sensitive to the temperature of protons Tp, whereas the radio synchrotron spectra depend on the temperature of electrons Te. In a collisionless plasma system, such as Sgr A*, the strength of e–p coupling is unknown. Modeling the effect of the e–p energy exchange is very simplified or not considered in typical MHD simulations. In a standard approach one often assumes that Tp/Te = const. in the entire simulation domain (e.g., Mościbrodzka et al. 2009, 2012 consider Tp/Te = 1,3, and 10). The constant Tp/Te everywhere suppresses emission from a GRMHD outflow because the outflow from near the event horizon naturally must have much lower densities than the inflow.
In this work, we relax the assumption of constant Tp/Te. Indeed, early RIAF disk models assumed a high Tp/Te to account for the submillimeter bump, while early jet models assumed a rather high Te to reproduce the radio emission of Sgr A*. Only later Tp/Te was decreased in RIAF models to allow for lower accretion rates imposed by Faraday rotation measurements (Bower et al. 2005; Marrone et al. 2007).
Yuan et al. (2002) pointed out that the electron temperature in the disk should be lower than that of the jet by a factor of ten to make both disk and jet contribute to the emerging spectrum. Here, we adopt a similar approach. The use of a higher Te in the GRMHD jets is motivated by the presence of several physical processes that are enhanced in the outflows and may cause stronger heating, such as stronger plasma magnetization, stronger shearing motion in the jet sheath, and shocks. All these processes are observed in the GRMHD simulations of jets (Brinkerink et al., in prep.).
The paper is organized as follows. In Sect. 2, we briefly describe the GRMHD model of the BH accretion flow, the radiative transfer technique, and the electron temperature parameterization used to compute spectra and images of the jet-plus-disk system. We present and discuss the new results in Sects. 3 and 4, respectively.
2. Model description
To investigate the radiative properties of the jet-disk-BH triad, we split the numerical modeling into three steps: (1) we computed the evolution of the GRMHD flow onto a BH; (2) we rescaled the dynamical model to Sgr A*; and (3) we computed synchrotron spectra and images of the system.
The accretion-flow evolution was calculated by using the axisymmetric GRMHD code HARM-2D (Gammie et al. 2003). The simulation’s initial conditions and its computational grid are similar to those adopted in Mościbrodzka et al. (2009, and references therein). The initial condition is a weakly magnetized torus in orbit around a Kerr black hole with a∗ = 0.94, where a∗ is the BH angular momentum. The inner and outer radius of the initial torus are 6Rg and 42Rg (Rg = GMBH/c2 and MBH ≡ BH mass), respectively. The difference between the previous (Mościbrodzka et al. 2009) and the current model is the size of the computational domain. Here we extended the outer boundary to r = 1000Rg. This large computational domain is necessary to model the radio spectrum from 1−104 GHz. The simulation was evolved until tfinal = 4000Rg/c, which corresponds to 16 orbital rotations at pressure maximum of the initial disk.
 |
Fig. 2 Time- and θ-angle-averaged (see Eq. (1)) profiles of ne, B, and Θe = kTe/mec2 (assuming Tp/Te = 1) in the jet and in the disk. The dotted lines correspond to the quantities measured in the turbulent accretion flow, and the solid lines are the averaged profiles of quantities measured in the jet region. The solid green lines are the profiles measured in the jet without the empty jet spine (i.e. excluding zones where B2/ρ0 > 0.1). The plasma density and magnetic-field strength are shown in the numerical code units. |
As the simulation advances in time, the magnetorotational instability (MRI) turns the smooth torus into a turbulent accretion flow. The turbulence transports angular momentum of the gas outward and inner portions of the disk fall toward the BH horizon. During the simulation, the accretion flow produces a variety of outflows. A low-density strongly magnetized relativistic outflow develops above the BH poles (Blandford & Znajek 1977; McKinney & Gammie 2004), the inner accretion disk launches a mildly relativistic outflow, and subrelativistic winds are produced by the outer regions of the disk. The latter outflow is formed because the outer-disk plasma gains an excess angular momentum from the accreting matter.
Figure 1 shows the overall structure of the GRMHD jet-disk-BH model. We defined the jet produced by the accretion flow as an unbound gas outflowing with a minimum bulk velocity βmin = 0.21. Everything beyond the jet region we refer to as an accretion disk/flow/wind. In Fig. 1, the jet region is separated from the accretion flow by a solid contour. Our formal definition of the jet indicates that it has two components. The first component is a strongly magnetized nearly empty funnel where B2/ρ0 > 0.1, hereafter called jet spine (the region within the dashed contour in Fig. 1). The second component is the mildly relativistic outflow along the funnel wall (the region between the dashed and solid contours in Fig. 1), hereafter called jet sheath. The choice of βmin = 0.2 was arbitrary, but proved to be a relatively robust threshold to separate jet and disk winds, which exhibit a sharp boundary (in the jet sheath ⟨β⟩ = 0.4). With βmin = 0.2 the simulation grid resolves the jet sheath with a few points. The mass-outflow rate in the jet sheath can be as high as 20% of the average mass-inflow rate onto the BH. Hence, radiation from the jet region is dominated by the jet sheath.
The dynamical models of the accreting BH are scale-free, but the radiative transfer models are not. We rescaled the numerical model to the Sgr A* system. We fixed the BH mass (MBH = 4.5 × 106 M⊙, Ghez et al. 2008) and distance (D = 8.4 kpc, Gillessen et al. 2009). The remaining model parameters are the source inclination i, the density scaling constant ne,0, and the electron temperature Te. The magnetic-field strength is given by multiplying the dimensionless B field by 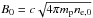 . We chose ne,0 so that the radio flux (at ν = 1−100 GHz) matched the observed data points. Te was parameterized as follows. In the disk we have (Tp/Te)d = const., where Tp is given by the dynamical model and (Tp/Te)d is a free parameter. In the jet we have Te,j = 30mec2/k, independently of the proton temperature. The last assumption was motivated by results presented in the next section and models of isothermal jets. However, as explained in the next section, the value of Te,j is similar to the average Tp found in the GRMHD model in the jet region, that is, (Tp/Te)j ~ 1.
. We chose ne,0 so that the radio flux (at ν = 1−100 GHz) matched the observed data points. Te was parameterized as follows. In the disk we have (Tp/Te)d = const., where Tp is given by the dynamical model and (Tp/Te)d is a free parameter. In the jet we have Te,j = 30mec2/k, independently of the proton temperature. The last assumption was motivated by results presented in the next section and models of isothermal jets. However, as explained in the next section, the value of Te,j is similar to the average Tp found in the GRMHD model in the jet region, that is, (Tp/Te)j ~ 1.
Spectral energy distributions (SEDs) and images of the plasma around the BH are produced by a 3D general relativistic ray-tracing radiative-transfer code. In the radiative-transfer computations, we assumed that the plasma has a Maxwellian energy distribution. We used an independent numerical radiative-transfer scheme as described for instance in Noble et al. (2007).
3. Results
We analyzed the radial structure of inflows and outflows produced in the simulation. Figure 2 shows profiles of three quantities measured in the accretion flow (dotted lines), in the jet spine (solid black lines), and in the jet sheath (solid green lines). The time- and shell- volume-averaged radial profiles of ne, B and the dimensionless electron temperature, Θe = kTe/mec2, were calculated using the following definition: 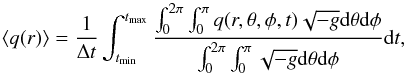 (1)where q is a scalar quantity,
(1)where q is a scalar quantity, 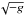 is the determinant of the metric, tmin = 3500M, and Δt = tmax − tmin = 500M.
is the determinant of the metric, tmin = 3500M, and Δt = tmax − tmin = 500M.
The radial profiles of the three quantities show approximately power-law shapes. The density in the accretion flow decreases with radius as ne ~ r-3. The steep power-law dependence is an artifact caused by the adopted initial conditions (small size of the torus). The density in the jet decreases with radius as ne ~ r-2. Close to the BH, the density of the disk is about 100 times higher than the density in the outflow. The magnetic fields, both in the inflow and in the outflow, decrease with distance as B ~ r−3/2. The protons in the accretion flow are near their virial temperature, Tp ~ r-1. The temperature of the gas in the jet is approximately constant between 5Rg (where the jet starts) and r ~ 100Rg, and decreases for r > 100Rg. For r ≤ 100Rg, the gas temperature is ⟨Θe⟩ = 30. The break in the temperature power-law at r ≈ 100Rg may be caused by decollimation of the jet (because of the small disk size) and/or by a poor numerical resolution of the model at large radii.
Interestingly, density ne and B-fields in the outflow decrease with radius in a similar manner as the ne and B fields in the semi-analytical relativistic jet models by Falcke & Markoff (2000). Their model, which produces a flat radio SED, assumes that the temperature of electrons (or, to be more precise, the electron energy distribution function) is almost constant along the jet. Hence, we simply adopted an isothermal jet with Θe = 30, in our radiative-transfer models, which corresponds to (Tp/Te)j ~ 1 up to r ≲ 100Rg. Outside the jet Te is given by (Tp/Te)d = const. > 1.
The radiative-transfer model parameters are given in Table 1. Figure 3 shows time-averaged SEDs of the jet-plus-disk system. In Fig. 3, three lines in each panel correspond to models with various (Tp/Te)d = 10,15, and 20.
Indeed, the jet spectrum is nearly flat, whereas the disk produces a hump at submillimeter wavelengths. The two components together are able to reproduce the spectrum remarkably well. At this point, we do not intend to conduct a full statistical exploration of the parameter space and, therefore, there is no strong reason to favor any specific parameter combination yet. However, it is already clear that the jet is crucial for filling in the low-frequency radio spectrum.
List of radiative-transfer models.
As predicted in Yuan et al. (2002), the disk Te has to be low and (Tp/Te)d ~ 10−20 to smoothly connect jet and disk emission. The spectral shape at lower frequencies depends weakly on the observing inclination angle. For i = 30°, the slope of the SED is somewhat shallower (αν ~ 0) than the slope seen under higher inclinations (αν ~ 0.3). This dependence is in line with previous analytical estimates (Falcke & Biermann 1999).
 |
Fig. 3 SEDs computed for parameters given in Table 1. SEDs are time averaged. Each line corresponds to a model with a different temperature ratio in the accretion disk, (Tp/Te)d = 10,15 and 20, and various inclinations. The red dashed line is the “best-bet” model from Mościbrodzka et al. (2009), which assumes i ≈ 90° and Tp/Te = 3 in the entire computational domain. The data points are the same as those used in Mościbrodzka et al. (2009). The bottom-right panel shows the sizes of the GRMHD jet model including scatter-broadening. Open symbols are Sgr A* measured sizes from Bower et al. (2006) and Doeleman et al. (2008) (1.3 mm). |
Are size and structure of Sgr A* also consistent with the model? Scattering is, of course, a major problem and the relative orientation between scattering disk and jet axis adds another free parameter. We approached this here by scatter-broadening our model images for one arbitrary orientation and comparing them to the available data (Falcke et al. 2009). Given the very limited structural information we have – a size in east-west direction – this is the best we can do for now.
We proceeded as follows: our radiative-transfer model computes images of the flow at λ = 3,7 and 13 millimeters. The synthetic images are then convolved with the symmetric scattering Gaussian profile with a FWHM = 1.309λ2 (Bower et al. 2006). Next, the size of the scatter-broadened image is measured by computing the eigenvalues of the matrix formed by taking the second angular moments of the image (the principal axis lengths). This method yields an accurate size of the emitting region if the brightness distribution is Gaussian-like and is therefore most accurate for strongly scattered images.
In the bottom-right panel of Fig. 3, we compare the measured major-axis sizes of Sgr A* at λ = 0.3−2 cm with those predicted by the model. We did not extend the model size to λ = 1.3 mm, because here the simulated image is highly non-Gaussian and a single major-axis size is meaningless. Furthermore the VLBI data were measured on a single, very narrow triangle of baselines only. We also cannot extend our model sizes to λ > 2 cm because the size of the scattered image becomes larger than our computational domain. However, in the region around λ ~ 0.7 cm, where the sizes are most reliably determined, the major-axis sizes are of the correct order. Moreover, the images look Gaussian-like despite the underlying jet-structure.
4. Summary
We have reanalyzed the structure of inflows (disk) and outflows (jets) produced in some GRMHD models of accreting BH (Gammie et al. 2003). We pointed out that the time-averaged radial profiles of plasma density and B-fields in the jet-like outflows are similar, though not exactly identical, to those used in semi-analytic jet models that readily explain the radio SED of Sgr A* (Falcke & Markoff 2000; Yuan et al. 2002) based on a scaled-down Blandford & Königl (1979) model combined with a radiatively inefficient accretion flow or RIAF. Consequently, we were able for the first time to relatively easily reproduce the radio spectrum and size of Sgr A* at mm-waves with a standard GRMHD model by simply allowing for different electron heating in jet and disk.
In particular, we found that the flat radio spectrum of jets is indeed reproduced by the simulations when we kept the electron temperature constant along the jet, as assumed in the Blandford & Königl (1979) model. In the inner parts the jet is well-described by a single-temperature plasma with a proton-to-electron temperature ratio on the order of unity. To reproduce the overall spectrum, however, the electron temperature in the disk needs to be lower than in the jet by at least an order of magnitude to avoid strong absorption and huge emission at submillimeter waves. In turn, this requires the presence of a two-temperature plasma in the accretion flow, with a high proton-to-electron temperature ratio (~ 10−20). This is expected because two-temperature plasmas were actually postulated in the earliest models for RIAFs (Narayan et al. 1995). Interestingly, Tp/Te = 10−20 is consistent with results of local (shearing box) simulations of collisionless plasma in which kinetic effects are included (Sharma et al. 2007).
In the jet models, Ṁ is about 20 times higher than Ṁ ≈ 2 × 10-9 M⊙ yr-1 in the “Tp/Te = 3 everywhere” best-bet model from Mościbrodzka et al. (2009). Our Ṁ = 4.5 × 10-8 M⊙ yr-1 (see Table 1) is consistent with Ṁ = 6 × 10-8 M⊙ yr-1 found in models where the BH is fed by stellar winds (Shcherbakov & Baganoff 2010, but see Quataert 2004), and with estimates by Sharma et al. (2007) based on local collisionless plasma models. A higher Ṁ may also change expectations for the recently discovered cloud-like object G2 that moves toward Sgr A* (Gillessen et al. 2012), which is expected to be accreted onto the BH soon. For a higher pre-impact accretion rate the increase in Ṁ due to the cloud would be much less dramatic than predicted (e.g., in Mościbrodzka et al. 2012; or Sa¸dowski et al. 2013).
Summarizing, the electron distribution function in GRMHD models is a free function that can vary with space and time. We showed that a natural modification of this distribution function produces SEDs that fit the observations well. The re-heating (or re-acceleration) of electrons in the jet might be due to effects that were described in the GRMHD models, such as shear, strong magnetization, or shocks in the jet sheath, but this requires a more detailed investigation. We conclude that the exact nature of the electron heating in jets and disks deserves more attention in the future.
Acknowledgments
We thank C. Gammie and J. Dexter for comments.
References
- Beckwith, K., Hawley, J. F., & Krolik, J. H. 2008, ApJ, 678, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Falcke, H., Herrnstein, R. M., et al. 2004, Science, 304, 704 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bower, G. C., Falcke, H., Wright, M. C., & Backer, D. C. 2005, ApJ, 618, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Goss, W. M., Falcke, H., Backer, D. C., & Lithwick, Y. 2006, ApJ, 648, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., & Loeb, A. 2009, ApJ, 697, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., Fish, V. L., Doeleman, S. S., & Loeb, A. 2009, ApJ, 697, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., & Agol, E. 2009, ApJ, 696, 1616 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., McKinney, J. C., & Agol, E. 2012, MNRAS, 421, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Doeleman, S. S., Weintroub, J., Rogers, A. E. E., et al. 2008, Nature, 455, 78 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dolence, J. C., Gammie, C. F., Mościbrodzka, M., & Leung, P. K. 2009, ApJS, 184, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Falcke, H., & Biermann, P. L. 1999, A&A, 342, 49 [NASA ADS] [Google Scholar]
- Falcke, H., & Markoff, S. 2000, A&A, 362, 113 [NASA ADS] [Google Scholar]
- Falcke, H., Mannheim, K., & Biermann, P. L. 1993, A&A, 278, L1 [NASA ADS] [Google Scholar]
- Falcke, H., Goss, W. M., Matsuo, H., et al. 1998, ApJ, 499, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Falcke, H., Markoff, S., & Bower, G. C. 2009, A&A, 496, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gammie, C. F., McKinney, J. C., & Tóth, G. 2003, ApJ, 589, 444 [Google Scholar]
- Ghez, A. M., Salim, S., Weinberg, N. N., et al. 2008, ApJ, 689, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Gillessen, S., Genzel, R., Fritz, T. K., et al. 2012, Nature, 481, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Markoff, S., Bower, G. C., & Falcke, H. 2007, MNRAS, 379, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2007, ApJ, 654, L57 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., & Gammie, C. F. 2004, ApJ, 611, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Mościbrodzka, M., Gammie, C. F., Dolence, J. C., Shiokawa, H., & Leung, P. K. 2009, ApJ, 706, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Mościbrodzka, M., Shiokawa, H., Gammie, C. F., & Dolence, J. C. 2012, ApJ, 752, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., Yi, I., & Mahadevan, R. 1995, Nature, 374, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, S. C., Leung, P. K., Gammie, C. F., & Book, L. G. 2007, Classic. Quant. Grav., 24, 259 [Google Scholar]
- Quataert, E. 2004, ApJ, 613, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Sądowski, A., Narayan, R., Sironi, L., & Özel, F. 2013, MNRAS, 433, 2165 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, P., Quataert, E., Hammett, G. W., & Stone, J. M. 2007, ApJ, 667, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Shcherbakov, R. V., & Baganoff, F. K. 2010, ApJ, 716, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Shcherbakov, R. V., Penna, R. F., & McKinney, J. C. 2012, ApJ, 755, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., Markoff, S., & Falcke, H. 2002, A&A, 383, 854 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yusef-Zadeh, F., Roberts, D., Wardle, M., Heinke, C. O., & Bower, G. C. 2006, ApJ, 650, 189 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Overall structure of the flow (upper half of the simulation domain). Panels from left to right show maps of the density, magnetic field strength, gas temperature, and bulk speed of the gas. The first two are given in dimensionless numerical code units. Solid and dashed contours illustrate our jet and disk definitions, which are introduced in Sect. 2. The solid line separates the jet from the disk, and the dashed line separates the jet spine from jet sheath. |
| In the text | |
 |
Fig. 2 Time- and θ-angle-averaged (see Eq. (1)) profiles of ne, B, and Θe = kTe/mec2 (assuming Tp/Te = 1) in the jet and in the disk. The dotted lines correspond to the quantities measured in the turbulent accretion flow, and the solid lines are the averaged profiles of quantities measured in the jet region. The solid green lines are the profiles measured in the jet without the empty jet spine (i.e. excluding zones where B2/ρ0 > 0.1). The plasma density and magnetic-field strength are shown in the numerical code units. |
| In the text | |
 |
Fig. 3 SEDs computed for parameters given in Table 1. SEDs are time averaged. Each line corresponds to a model with a different temperature ratio in the accretion disk, (Tp/Te)d = 10,15 and 20, and various inclinations. The red dashed line is the “best-bet” model from Mościbrodzka et al. (2009), which assumes i ≈ 90° and Tp/Te = 3 in the entire computational domain. The data points are the same as those used in Mościbrodzka et al. (2009). The bottom-right panel shows the sizes of the GRMHD jet model including scatter-broadening. Open symbols are Sgr A* measured sizes from Bower et al. (2006) and Doeleman et al. (2008) (1.3 mm). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


