| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 11 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201322563 | |
| Published online | 19 November 2013 | |
Kinematics of massive star ejecta in the Milky Way as traced by 26Al
1
François Arago Centre, APC, Université Paris Diderot, CNRS/IN2P3,
CEA/Irfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet,
75205
Paris Cedex 13,
France
e-mail:
kkretsch@apc.univ-paris7.fr
2
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstrasse
1, 85741
Garching,
Germany
3
Excellence-Cluster “Origin & Structure of the
Universe”, Boltzmannstrasse
2, 85748
Garching,
Germany
4
Universitätssternwarte der Ludwig-Maximilians-Universität,
Scheinerstrasse 1,
81679
München,
Germany
5
National Astronomical Observatories, Chinese Academy of Sciences,
100012
Beijing, PR
China
Received: 29 August 2013
Accepted: 19 September 2013
Context. Massive stars form in groups and their winds and supernova explosions create superbubbles up to kpc in size. The fate of their ejecta is of vital importance for the dynamics of the interstellar medium, for chemical evolution models, and the chemical enrichment of galactic halos and the intergalactic medium. However, ejecta kinematics and the characteristic scales in space and time have not been explored in great detail beyond ~10 Ka.
Aims. Through measurement of radioactive 26Al with its decay time constant at ~106 years, we aim to trace the kinematics of cumulative massive-star and supernova ejecta independent of the uncertain gas parameters over million-year time scales. Our goal is to identify the mixing time scale and the spatio-kinematics of such ejecta from the pc to kpc scale in our Milky Way.
Methods. We use the SPI spectrometer on the INTEGRAL observatory and its observations along the Galactic ridge to trace the detailed line shape systematics of the 1808.63 keV gamma-ray line from 26Al decay. We determine line centroids and compare these to Doppler shift expectations from large-scale systematic rotation around the Galaxy centre, as observed in other Galactic objects.
Results. We measure the radial velocities of gas traced by 26Al, averaged over the line of sight, as a function of Galactic longitude. We find substantially higher velocities than expected from Galactic rotation, the average bulk velocity being ~200 km s-1 larger than predicted from Galactic rotation. The observed radial velocity spread implies a Doppler broadening of the gamma-ray line that is consistent with our measurements of the overall line width. We can reproduce the observed characteristics with 26Al sources located along the inner spiral arms, when we add a global blow-out preference into the forward direction away from arms into the inter-arm region, as is expected when massive stars are offset towards the spiral-arm leading edge. With the known connection of superbubbles to the gaseous halo, this implies angular-momentum transfer in the disk-halo system and consequently also radial gas flows. The structure of the interstellar gas above the disk affects how ionizing radiation may escape and ionize intergalactic gas.
Key words: Galaxy: structure / gamma rays: ISM / ISM: kinematics and dynamics / stars: massive / techniques: spectroscopic / nuclear reactions, nucleosynthesis, abundances
© ESO, 2013
1. Introduction
Massive stars are important agents of the evolution of gas and stellar content in a galaxy, because they evolve rapidly within millions of years (Ma) and are powerful sources of energy through their ionizing radiation, their winds, and the final supernova explosions (Zinnecker & Yorke 2007). Mostly formed in groups (Lada & Lada 2003), they create superbubbles up to kpc in size (Jaskot et al. 2011; Weaver et al. 1977), and drive large scale outflows (von Glasow et al. 2013). Ejecta transfer their kinetic energy in a complex way to the structured interstellar gas. The global picture of how the gas, metal, and energy output of these massive stars in the form of stellar winds and supernova ejecta interacts with their surroundings is still unclear. Our knowledge of the transport of gas and energy is derived from measurements of observables of different types, each with biases and imperfections: dense molecular gas seen in CO (Dame et al. 2001), atomic gas through H i (Kalberla & Haud 2006), X-ray emission partly in interacting shells and from hot cavity interiors (Snowden et al. 1997), free-free emission from decomposition of radio emission (Bennett et al. 1996), and gamma-rays from the decay of unstable isotopes tracing nucleosynthesis ejecta (Voss et al. 2009). The initial release of matter and energy is reflected in supernova remnants, which can be studied in a variety of wavelength regimes over periods of up to several 10 000 years; thereafter, interstellar radiative effects from massive stars fade away. Only long-lived radio-isotopes then provide a new and different type of radiation, observable through a radioactive afterglow in characteristic gamma-rays over millions of years from 26Al (τ ~ 106 a) and 60Fe (τ ~ 3.8 × 106 a). Here we report on observations of 26Al through its characteristic gamma-ray line at an energy of 1808.63 keV that has been measured with the SPI telescope (Vedrenne et al. 2003) on the INTEGRAL satellite (Winkler et al. 2003).
Earlier analysis of these observations had provided hints of systematic Doppler shifts of the 26Al gamma-ray line with Galactic longitude consistent with large-scale Galactic rotation (Diehl et al. 2006). This showed that 26Al is sampled throughout the Galaxy with gamma-ray line observations like these, as gamma-rays penetrate even molecular clouds which may be assumed to surround some of the youngest source regions. Comparing 26Al emission with the spatial distribution of candidate sources, it has been confirmed that groups of massive stars are the most-plausible origins (Prantzos & Diehl 1996). Among several tracers of 26Al sources, diffuse emission from ionized gas through free-free emission has been found most promising (Knödlseder et al. 1999), although diffuse dust emission or cosmic-ray interactions with interstellar gas as seen in continuum gamma-ray emission also provide a good correlation to 26Al emission. These studies of correlations between the angular distribution of different observables are limited by the spatial resolution achieved in the 1808.63 keV line, which does not exceed 3 degrees in any existing measurement. For sources that are very close, such as the Orion OB1 subgroups, COMPTEL observations had suggested that 26Al emission may be offset from its sources and instead might arise from extended emission in a cavity blown by earlier activity of the massive-star association (Diehl et al. 2003). These superbubbles may have an important role in the transport of energy and ejecta from their sources back into interstellar-medium phases which may form stars again. A hint of this also may be derived from indications that the 26Al emission scale height perpendicular to the Galactic plane of ~130 pc appears to fall on the high side of scale heights which characterize the 26Al sources (e.g. molecular gas measured in CO has ~50 pc scale height) (Wang et al. 2009).
With accumulating exposure, we now extend our study of 26Al throughout the Galaxy to better trace and compare the kinematics of 26Al in the inner 4 kpc to 5 kpc of our Galaxy (Figs. 7 and 8). We present the methods we used to obtain these measurements and discuss the sources of uncertainty involved (Sect. 2). We then discuss our longitude-velocity measurements in relation to previous measurements of longitude-velocity dependence obtained using other observables, such as CO (Sect. 3). We find that our kinematic results support the notion that superbubbles are the structures that are most important in the transport of energy and ejecta on the longer (Ma) time scales, which are characteristic for recycling of matter and energy. To suggest additional interpretations, we then present a first-order spatio-kinematic model capable of explaining the differences between these measurements and our 26Al data (Sect. 4).
2. Data and their analysis
2.1. Mission and data
The INTEGRAL space observatory (Winkler et al. 2003) carries the gamma-ray spectrometer instrument SPI as one of its two main instruments (Vedrenne et al. 2003; Roques et al. 2003). The SPI spectrometer features a camera consisting of 19 high-resolution Ge detectors; the camera measures celestial gamma-rays through coded-mask shadowgrams, above a large instrumental background. The SPI data consist of energy-binned spectra for each of the 19 Ge detectors of the SPI telescope camera (Vedrenne et al. 2003), typically taken in 30 min exposures of a sky region. For our analysis, we used exposures across the plane of the Galaxy accumulated over more than nine years of the INTEGRAL mission (Winkler et al. 2003, 2011).
 |
Fig. 1 Exposure map of the sky with the SPI telescope on INTEGRAL for the data used in this analysis (Feb. 2003 to Feb. 2012). |
2.2. Generating spectra of celestial emission
Generally, in our spectroscopy analysis we fit the intensity scaling factor of a model of the 26Al sky intensity distribution plus a scaled model of the instrumental background to the set of spectra accumulated during multi-year observations from our 19 Ge detectors and instrument pointings. Our nine-year observation set includes 65302 instrument pointings that add up to the exposure shown in Fig. 1. Data dk are modelled as a linear combination of the sky model components Mij, to which the instrument response matrix Rjk is applied, and the background components Bjk:  (1)i.e. the comparison is performed in data space, which consists of the counts per energy bin measured in each of the SPI detectors for each single exposure of the complete observation.
(1)i.e. the comparison is performed in data space, which consists of the counts per energy bin measured in each of the SPI detectors for each single exposure of the complete observation.
Using the Mij characteristics, we make use of prior knowledge in the form of a sky intensity distribution such as the measured 26Al intensity, or a plausible model such as an exponential disk. We use the 1.8 MeV sky map from the COMPTEL gamma-ray telescope (Schönfelder et al. 1993) on the NASA CGRO mission (1991–2000) (Plüschke et al. 2001) as derived through maximum-entropy deconvolution (Strong 1995). Our analysis also includes a model for the behaviour of the instrumental background, which is derived from separate analysis of the continuum intensity in energy bands adjacent to the 1808.63 keV line and instrumental background tracers in data of the entire INTEGRAL mission. The result of this background study using independent data is a prediction of counts per detector, energy bin, and spacecraft pointing, which is adjusted to the data together with the predicted contribution from the sky (i.e. the sky intensity model folded into data space using the instrument imaging response function). We then repeat this for 0.5 keV wide energy intervals to obtain the sky intensity spectra for the adopted sky distribution model. In Fig. 2 the spectrum is shown for the entire inner Galaxy, while in Fig. 7 different spectra are shown for spatially separated regions of the sky. The background and sky models and fitting method used in this step are identical to previous work (Wang et al. 2009) and are summarised briefly below.
 |
Fig. 2 Spectrum around the gamma-ray line from 26Al obtained for the entire inner Galactic plane (ROI = 128° × 12° at l = 0°) |
To improve the sensitivity to Doppler shifts of lines with respect to previous SPI results (Diehl et al. 2006), we implemented a new approach for scanning the Galactic plane, employing sky models which are split into two independent components. The sky model we use (the 26Al observed with COMPTEL, Plüschke et al. 2001), is divided into two complementary parts: the inside of the spherical rectangle l ∈ [l0 − Δl/2, l0 + Δl/2], b ∈ [b0 − Δb/2, b0 + Δb/2] defines our region of interest (ROI), and its complement with respect to the full-sky map constitutes the second component of the model (Fig. 3). A full-sky model is required, because SPI observation data include events from within the entire telescope field of view of ~30° extent, although the intrinsic spatial resolution of SPI has been determined as 2.7°. The sky model thus represents the spatial detail of the fitted intensity within a longitude/latitude bin (ROI); the intensity is fitted to SPI data for the entire ROI; spatial details within ROI bins have little impact on the spectral-line results because of to the low total 26Al signal per ROI. This was confirmed, using different plausible 26Al sky maps with different amounts of structural detail on the scale below ~few degrees.
 |
Fig. 3 Two sky model components: The region of interest (ROI) 12° × 10° centred around l = 24° (bottom) and its complement (top) taken as subsets of the COMPTEL 1.8 MeV sky map. The rectangular outline shows the region covered by our scan along the Galactic plane. |
The intensities of these two components, together with a model of the instrumental background, are then fitted to the SPI data. Our background model reproduces the time variability of the background at short time scales (<3 days) with the rate of events saturating the germanium detectors, which has been found to be a sensitive measure of the instantaneous charged particle environment of the instrument. The long-term background variation (>3 days) is extracted from the continuum intensity in energy intervals adjacent to the 1808.63 keV line.
Thus we obtain spectra in the energy range 1800 keV to 1820 keV around the 26Al line for the two complementary sky model components. We repeat this process, varying l0 to scan the ROI along the Galactic plane, and obtain measurements of the 26Al line signal as a function of Galactic longitude. Figure 4 shows sample results for a particular ROI in the fourth quadrant of the Galaxy towards longitude l ~ −27° to –28°. The centre longitude is not the same in all spectra shown because we use raster spacings of one quarter or one half of the ROI longitude extent that do not have a common multiple at this longitude.
 |
Fig. 4 Spectra of the region around l ~ –27° to –28° for ROI latitude extents of 16°, 12°, 8°, 6°. |
The latitude range Δb = ±5° in our analysis was chosen to cover the full expected scale height for both ejecta, as well as gas streaming away from the plane of the Galaxy towards the halo, even for nearby segments of the Galaxy. This is equivalent to ±270 pc at 3 kpc distance. The CO disk scale height is ~50 pc (Dame et al. 2001); a previous 26Al scale height estimate (Wang et al. 2009) finds a range from ~60 pc to ~250 pc. Foreground emission, which would predominantly show up at intermediate or higher latitudes, may lead to possible biases. The ROI, which corresponds to a pyramid in 3D space, covers different distances from the Galactic plane depending on the distance to the emitting region. Nearby sources, taking up a large solid angle on the sky across the plane, would thus be sampled only partially depending on the ROI latitude extent. The influence of the choice of ROI longitude and latitude extent on the model fit results is discussed in greater detail in Appendix A.
The spread of radial velocities over the longitude range covered implies an overall broadening of the line emission when considering the integrated emission coming from a large ROI on the sky. When we vary the extent of the ROI and with it the range of radial velocities being integrated, and compare this to the measured line width, we can check the broadening effect of different samples of the sky and its varying kinematic properties. This is shown in Fig. 5, where the error bars show the variation of the measured line width’s confidence intervals with longitude extent. For small regions on the sky, only upper limits on the 26Al line width can be obtained. The upper limits become smaller with increasing region size as more signal is covered by the ROI before increasing again for Δl ≲ 30° as the covered radial velocity range increases. For the large region along the entire inner Galaxy (128° × 12°, Fig. 2), we derive (1.4 ± 0.4) keV (FWHM) additional broadening, or (230 ± 70) km s-1. This is consistent with the spread of radial velocities we measure spatially resolved along the inner Galaxy (Sect. 3.1). The root mean square of our radial velocity measurements (Fig. 8) weighted with the corresponding intensity measurements (Fig. A.2) is ≈200 km s-1. We thus conclude that observed line broadenings are consistent with systematic variation of line position along the plane of the Galaxy, attributed to large-scale rotation of gas within the Galaxy.
2.3. Characterizing celestial emission lines
 |
Fig. 5 Limits on the width of the 26Al line emission from ROIs around the Galactic centre with an extent in latitude of ±6° and longitude extents ranging from 6° to 128°. The error bars of decreasing thickness show the Bayesian highest posterior density credible regions corresponding to 68.3%, 95.4%, and 99.7%, corresponding to 1σ, 2σ, and 3σ. |
In a second step, we fit these spectra of sky intensity values obtained per energy bin and per component by a model description based on the instrument’s spectral response. This yields the 26Al line parameters of total intensity, Doppler shift with respect to laboratory energy, and intrinsic width of the celestial 26Al emission for the respective component of the sky. The spectral model we use in our line fitting consists of a linear continuum and a line at the position a3, where the line is the convolution of the instrument spectral response R and a Gaussian G with the width a4 (E0 is the midpoint of the energy interval): 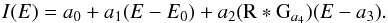 (2)Such detailed modelling of the instrument response is required, as the impact of cosmic radiation onto SPI detectors gradually deteriorates the charge collection properties of detectors, and leads to a degraded spectral response.
(2)Such detailed modelling of the instrument response is required, as the impact of cosmic radiation onto SPI detectors gradually deteriorates the charge collection properties of detectors, and leads to a degraded spectral response.
The degradation of Ge detectors from cosmic-ray irradiation and its restoration in annealings results in a time variable width and asymmetry of the spectral response. This variation of the spectral response dominates over all other spectral changes, and is found to be consistent across the SPI energy range. Figure 6 shows how the degradation, measured by the width of a one-sided exponential tail on the low-energy side of the line response, varies for lines in four different energy regimes. The degradation increases in an approximately linear fashion with time and is reduced periodically by the annealing operations which heat the detectors for a period of ~2 weeks to ~100 °C, restoring the original high spectral resolution. The annealing cycle of one roughly every six months (as needed) leads to a sawtooth-like variation of the spectral response during our data taking. Clearly, the absolute magnitude of degradation increases with energy, yet changes occur consistently for all instrumental lines, and are in the range of tenths of keV. Spectroscopic analysis at high precision needs to account for these effects.
 |
Fig. 6 Degradation of the spectral response over mission time. With degradation, a one-sided tail at the low-energy side develops. The plot shows its extent versus time (one revolution =3 days). |
 |
Fig. 7 Trace of systematic Doppler shifts of the 26Al line along the inner Galaxy. |
We estimate the spectral-model parameters (continuum intensity and slope, line intensity, Doppler shift, and width) using the Metropolis-Hastings MCMC algorithm (Neal 1993), which samples the parameter space statistically to generate detailed probability distributions for the model parameters. This approach allows us to determine accurate limits on the width of the emission line even though the differences between the measured line profiles and the instrumental line response are small. Figure 7 compares the observed Doppler shifts of the 26Al line to the spectral appearance of a nearby instrumental line for exactly the same data, i.e. all selected SPI pointings around the respective longitude ROI. It is evident that the energy calibration is stable, and the relative changes of the response are small (see Sect. 3.1 below and Fig. 6). The Markov chain Monte Carlo (MCMC) analysis also determines the Bayes factor (Gelman et al. 2003), i.e. the ratio of the marginal likelihoods of the model including a line and the alternative model that consists of continuum only. If the Bayes factor is larger than one, the model with a line is more probable than the one without, although the line detection may still be insignificant in terms of statistical acceptance criteria. Because of the large numbers involved, it is more convenient to state the Bayes factor on the logarithmic decibel (dB) scale. The longitude-velocity graph (Fig. 8) shows the result of this process for Δl = 12°, Δb = 10°. For our 12° × 10° ROI, the Bayes factor reaches a maximum of 135 dB, which corresponds to a detection significance of 7.6σ. For the sky distribution model from the 26Al emission derived with COMPTEL, and evaluated over the region |l| < 60°, |b| < 30°, the Bayes factor and detection significance values are 2100 dB and 31σ, respectively. Therefore, for sky region sizes as we use here in our ROIs with ~120 square degrees or less, the line widths are not tightly constrained, and we give upper limits only; these are: <1.9 keV (i.e. <315 km s-1; 95.4%, 2σ), or <2.75 keV (<455 km s-1; 99.7%, 3σ). Only integrating the signal over a larger solid angle allows a more precise line width measurement (Fig. 2 and Sect. 3.1).
 |
Fig. 8 Longitude-velocity diagram comparing γ-ray-measured velocities (crosses, including error bars) with other objects in our Galaxy. 26Al line-centroid energies were fitted to determine velocities in longitude bins of 12° and latitude ranges ±5°. For comparison, different models are shown (blue solid, red dotted, and green dashed lines), as well as the velocity information from molecular gas seen in CO (see Sect. 4 for details). |
The basic instrument spectral response is obtained from the instrumental background line at 1764.494 keV, which is due to the 214Bi β-decay inside SPI’s anticoincidence shield. This response is shown in Fig. 7 (right-hand set of spectra). Its shape is nearly Gaussian; it exhibits, however, an excess towards the low-energy side that is due to partial charge collection and which varies with the degradation state of the detectors between annealings (Roques et al. 2003) described above.
For a given ROI position, we determine the spectral response from all exposures where SPI was pointed at a location within a field-of-view radius (16°) around the ROI. We add the spectral responses of the active SPI detectors; we also adjust the absolute energy scale to compensate for the radial velocity due to the Earth’s orbital motion, and additionally adjust the energy scale relative to the line centroid to extrapolate the widening of the instrument energy response with increasing photon energy. We sum these per-exposure spectra, subtract the linear continuum, and normalize the result to obtain the SPI energy response for this ROI.
We also tested a different spectral response determination, which uses a parametrized analytic function (the convolution of a Gaussian with an exponential defined on x ≤ 0) to describe the line shape, and extracts the line shape parameters from a set of eleven strong instrumental background lines with high time resolution (3 days) over the multi-year observation. The impact of the choice of the energy response model on the measured longitude-velocity dependence is negligible, as shown in Fig. A.4. The RMS difference for the longitude range −36° ≤ l ≤ 36° is 0.15 keV (25 km s-1), i.e. small by comparison. Appendix A discusses the systematic uncertainties due to the instrumental response modelling in greater detail.
3. Results
3.1. Longitude-velocity diagrams
With the parametrization of the sky along the plane of the Galaxy in bins of different Galactic longitude (at fixed latitude bin width), we obtain spectra near the 26Al line along the plane of the Galaxy (Fig. 7), as compared to a nearby instrumental background line. The line from decay of 26Al (laboratory energy 1808.63 keV) is seen for different regions along the plane of the Galaxy (left), at Galactic longitude l − 24° to 24°, for a latitude range Δb = ±5° centred at b = 0°. The shift of the line centroid with Galactic longitude is apparent, in particular when compared to an instrumental line nearby (right; line at 1764.494 keV, from activation of Bi in SPI’s anticoincidence detector made of bismuth germanate (BGO) scintillator; background-line data are selected from the same observations which contribute to the longitude bin shown on the left). The instrumental line at 1764.494 keV demonstrates a stable energy calibration for all observations, and in particular absence of a bias with Galactic longitude. The line shape of the instrumental line was used to represent the instrumental spectral response, and used to fit the data in the left-side graphs, thus determining the line position accurately even for weak signals. The systematic shift of the 26Al line with Galactic longitude can clearly be seen in this subset of spectra, which are selected from non-overlapping, independent sky regions.
We convert the measured offsets in the centroids of the 26Al line from the expected 26Al decay at the laboratory value into the corresponding bulk Doppler velocity. This allows us to construct a longitude-velocity diagram from 26Al measurements. Figure 8 shows the result derived from the spectra shown in Fig. 7. This longitude-velocity result is assembled from the above analysis, which we repeated for the ROI defined by rectangular bins in longitude (widths 6°,8°, 12°, and 16°) and latitude (heights 4°, 6°, 8°, and 10°, Fig. A.1). Increasing the ROI size trades spatial resolution against energy resolution. Our choice of a 12° × 10° ROI offers balanced statistical and systematic energy uncertainties (see Appendix A). By moving the ROI in Galactic longitude, we can trace velocities along the plane of the Galaxy. In the figure, we show data points (crosses with error bars showing one standard deviation) spaced 12° apart, i.e. offset by integer multiples of the ROI width and therefore measuring non-overlapping ROIs. We also show (in blue shading) measurements obtained by a closer spaced 3° longitude sampling which implies that neighbouring ROIs overlap by 3/4. This oversampling leads to a stronger correlation between neighbouring measurements, but it shows more information than the data points. The blue shaded areas show a colour saturation proportional to the Bayes factor of the spectral model compared to continuum-only, i.e. they show the significance of the signal for each ROI position. The systematic blueshift in the fourth and redshift in the first Galactic quadrant are expected from large-scale Galactic rotation.
4. Discussion
Extraction of the spatio-kinematic characteristics of interstellar gas in the inner Galaxy remains a challenge owing to distance ambiguities, observational biases, and the model-dependence of velocity and distance derivations, in addition to the intrinsic differences in resolution of different observables. Our derived line centroids along the Galactic ridge at l ∈ [−50°,50°] (Sect. 3.1) represent the average radial velocities, subject to distance-dependent weighting, of 26Al in volume slices covering the whole inner Galactic plane. As shown in Fig. 8, we clearly find observed line-of-sight velocities (relative to the local standard of rest) between approximately 200 km s-1 (redshifted) and –200 km s-1 (blueshifted). The excess velocities beyond those globally expected from Galactic rotation are 100 km s-1 and higher at the velocity maxima, which are near longitudes ±30°.
We believe the most likely explanation for our findings to be the preferential expansion of superbubbles towards the leading edges of spiral arms. This implies a net asymmetry of the million-year-scale bubble expansions that results in a blow out of massive star ejecta into the low-density region ahead of and outward from the spiral arms. For the kinematic description of 26Al we must adopt a model for the large-scale spatial distribution and kinematic behaviour of 26Al as it decays. In the following sections we discuss different large-scale kinematic models, which should explain the signature with longitude of 26Al data points, and finally support our suggested interpretation.
4.1. Spatio-kinematic modelling of the 26Al longitude-velocity signature
4.1.1. Galaxy models with different large-scale rotation components
In Fig. 8, we show in the continuous blue line what the signature from 26Al would be, if we assume that the density distribution of the 26Al in the disk and spiral arms of the Galaxy is proportional to large-scale distribution of the free electron density (Cordes & Lazio 2002), and that the gas is in circular orbits with the velocity given by a Galactic rotation measurement compilation (Sofue et al. 2009). This line shows what our gamma-ray telescope would have measured in longitude-velocity space, while averaging over the same 12° longitude range used in our data analysis. This is, expectedly, similar to the ridge seen in CO, which is shown in Fig. 8 as a colour scale overlay for comparison (from Dame et al. 2001). Clearly, in high-spatial-resolution CO data, additional Galactic features can be resolved, such as the peculiar motions in the nuclear disk close to the centre of the Galaxy. The kinematics of molecular gas displays dominant features along the Galactic ridge beyond this peculiar motion in the central ~few 100 pc at rather high velocities. Our 26Al results, however, do not follow these expectations along the Galactic ridge, hence clearly the hot, ejecta-carrying gas does not move as molecular gas does on these larger scales. Apparently, 26Al carrying interstellar gas moves at systematically higher velocities on a large scale than does the CO-traced molecular gas along the ridge of the Galaxy. For longitudes |l| ≳ 20°, its average velocity even exceeds the terminal velocity of CO, the highest radial velocity seen at a given longitude (Englmaier & Gerhard 1999).
What about the influence of the inner bar in our Galaxy? The dotted red line shows what would be expected if 1/3 of the 26Al were distributed along the Galaxy’s long bar, and 2/3 were distributed throughout the disk and spiral arms as above. Here, the observed slope of the longitude-velocity signature of 26Al is reproduced in the inner part, but apparently 26Al kinematics is still characteristically different outside the regions of the Galaxy’s bar itself, and so the inner spiral arm regions are involved.
The dashed green line in Fig. 8 combines spiral-arm sources outside a radius r0 at large-scale galactic rotation with a new leading-edge blow-out of ~200 km s-1, which we suggest is an essential part of explaining the 26Al kinematics. Apparently, a bar-like distribution of sources could reproduce our data only for the inner longitude range, while a model based on two spiral arms extending from the tips of the bar, with large-scale rotation and a leading-edge blow-out at 200 km s-1, provides a closer match to the data and explains the general longitude-velocity trace as observed in 26Al gamma-rays. We describe this model and provide more details on its variants in the following sections.
4.1.2. Two-arm spiral models
A simple first-order model to better explain the kinematic properties of the observed 26Al emission is based on the following assumptions. The spatial distribution of 26Al in the Galaxy is along a two-arm spiral structure as derived from density wave theory (see below for a four-arm model),  (3)where φ and i denote the azimuth and pitch angle, respectively, and the galactocentric radius r0 defines the inner end of the spiral arms, which are also assumed to constitute the outer ends of the Galactic bar. The bar itself does not contribute to the emission in this model, it only defines the points where the spiral arms begin. We assume R0 = 8 kpc for the distance of the Sun from the Galactic centre. From observations of stars and gas, the spiral-arm pitch angle has been constrained (Francis & Anderson 2012) to 5.56°. The 26Al emission is assumed to originate from a 0.5 kpc thick layer around the above-defined spiral arms as emission zones (the model results below are not sensitive to reasonable variations of this number), and declines from inner to outer arm regions as a power law in azimuth angle, i.e. ~φa. For the intrinsic velocity of 26Al nuclei at their decay, we adopt an additional azimuthal motion (the blow-out velocity vbo), in addition to the rotational velocity, which is adopted as 250 km s-1 everywhere (Reid et al. 2009; and discussion in Dobbs & Burkert 2012). We also parametrize the bar angle α, i.e. the angle between the line from the Galactic centre to the Sun and the line from the Galactic centre to the near end of the bar, as seen from the Galactic centre; it is taken to be 38°, towards the upper end of the range reported by different studies (Francis & Anderson 2012; Green et al. 2011; Long et al. 2013; Wang et al. 2012; Martinez-Valpuesta & Gerhard 2011). Smaller bar angles tend to decrease the fit quality and increase the blow-out velocity by about 10%. Our assumption on the bar angle is consistent with recent measurements from star counts; Wegg & Gerhard (2013) find an angle of (27 ± 2)°. There is the possibility that the outer bar is twisted (the so-called long bar, see Benjamin et al. 2005; Cabrera-Lavers et al. 2008), e.g. the bar could have leading ends (Martinez-Valpuesta & Gerhard 2011). The spiral arm ends could be leading the bar even more. In fact, our bar angle is defined by the spiral arm ends and not by the major axis of the bar. Our model is vertically unresolved just as our data are (latitude bin width 10°); for comparison, the nearest spiral arm at ~3 kpc distance extends over ~1/2 of our latitude bin width for an assumed 26Al scale height of 130 pc (Wang et al. 2009).
(3)where φ and i denote the azimuth and pitch angle, respectively, and the galactocentric radius r0 defines the inner end of the spiral arms, which are also assumed to constitute the outer ends of the Galactic bar. The bar itself does not contribute to the emission in this model, it only defines the points where the spiral arms begin. We assume R0 = 8 kpc for the distance of the Sun from the Galactic centre. From observations of stars and gas, the spiral-arm pitch angle has been constrained (Francis & Anderson 2012) to 5.56°. The 26Al emission is assumed to originate from a 0.5 kpc thick layer around the above-defined spiral arms as emission zones (the model results below are not sensitive to reasonable variations of this number), and declines from inner to outer arm regions as a power law in azimuth angle, i.e. ~φa. For the intrinsic velocity of 26Al nuclei at their decay, we adopt an additional azimuthal motion (the blow-out velocity vbo), in addition to the rotational velocity, which is adopted as 250 km s-1 everywhere (Reid et al. 2009; and discussion in Dobbs & Burkert 2012). We also parametrize the bar angle α, i.e. the angle between the line from the Galactic centre to the Sun and the line from the Galactic centre to the near end of the bar, as seen from the Galactic centre; it is taken to be 38°, towards the upper end of the range reported by different studies (Francis & Anderson 2012; Green et al. 2011; Long et al. 2013; Wang et al. 2012; Martinez-Valpuesta & Gerhard 2011). Smaller bar angles tend to decrease the fit quality and increase the blow-out velocity by about 10%. Our assumption on the bar angle is consistent with recent measurements from star counts; Wegg & Gerhard (2013) find an angle of (27 ± 2)°. There is the possibility that the outer bar is twisted (the so-called long bar, see Benjamin et al. 2005; Cabrera-Lavers et al. 2008), e.g. the bar could have leading ends (Martinez-Valpuesta & Gerhard 2011). The spiral arm ends could be leading the bar even more. In fact, our bar angle is defined by the spiral arm ends and not by the major axis of the bar. Our model is vertically unresolved just as our data are (latitude bin width 10°); for comparison, the nearest spiral arm at ~3 kpc distance extends over ~1/2 of our latitude bin width for an assumed 26Al scale height of 130 pc (Wang et al. 2009).
When we perform a χ2 minimization of this model for our 26Al longitude-velocity data with free parameters r0, i, vbo, and α, we obtain the results shown in Table 1. This includes fitting or fits adopting i as constant i = 5.56°, and two different bar angles α.
Best-fit parameters for our two-armed spiral emission model with different assumptions about the input parameters.
We show the relative contributions along each line of sight of the assumed source distribution for the preferred two-arm model (Fig. 9) in Fig. 10. The foreground part of the source emission along each line of sight dominates the observed signal. Towards the far bar end, the velocity of the 26Al carrying gas is similar to the velocity of the gas in the foreground arm. Moreover, the foreground arm dominates in brightness. Hence, the far end of the bar cannot be disentangled.
In summary, the blow-out velocity depends only very weakly on changes to any of the parameters of the model. For the results of our paper we have adopted the fit for a fixed α = 38° and i = 5.56°, and blow-out velocity vbo = (225 ± 50) km s-1, because χ2 is only marginally worse, and for consistency with a recent study (Francis & Anderson 2012). This model is shown in Fig. 9.
 |
Fig. 9 Properties of our preferred model. The top-left plot shows the adopted 26Al source distribution in the plane of the Milky Way as seen from above. Also indicated is the position of the Sun (8 kpc from the Galactic centre), the location of the bar (dashed), and several longitudinal directions of interest. The colour indicates the 26Al density (yellow: highest, black: lowest). The other plots show quantities derived from this source distribution as a function of Galactic longitude as solid black lines (top right: received flux in arbitrary units, bottom left: velocity centroid shift, bottom right: velocity width). Overplotted are the observed data points with error bars showing one standard deviation, and upper limits of three standard deviations in the case of the velocity width. The flux excess at l = −24° may be due to foreground emission from the Sco-Cen association (Diehl et al. 2010) leaking from higher latitudes into our ROI bin. The observational limits on the velocity width are not constraining and are compatible with expectations (see Sect. 2.2). |
4.1.3. Four-arm spiral models
We also investigated four-arm spiral models for the Galaxy, with characteristics similar to the two-arm model. The best-fit four-arm model (Fig. 11) leads to a reduced χ2 of 0.93, thus formally fits much better than the two-arm model. However, the improved fit quality is mainly due to a better, but still not fully satisfactory match of the flux at l = −24°, which we believe to be related to foreground emission. We therefore prefer the best-fit two-arm model over the four-arm model, because it has fewer parameters. The inferred blow-out velocity depends weakly on this choice (compare Table 1).
 |
Fig. 10 Left: map of the local velocity relative to the Sun in our preferred model. The white contours indicate the 26Al mass distribution. Right: relative flux contribution per surface area in the standard model, separate for each longitude bin. Several longitude bins are indicated by black lines. |
4.2. Comparison to other studies
4.2.1. Spiral arm structure
Confidence levels for two respective pairs of our model parameters are shown in Fig. 12. Clearly, a pitch angle of 5.56° is consistent with our data, within uncertainties. Our favoured Galactic-bar radius falls into the range of published values (Francis & Anderson 2012; Martinez-Valpuesta & Gerhard 2011).
 |
Fig. 12 Reduced χ2 and confidence contours as a function of galactocentric bar radius. The pitch angle for the Galactic spiral structure (left, the value from Francis & Anderson 2012), is also indicated, including one standard deviation error bars) and as a function of the 26Al drop-off exponent and the blow-out velocity (right). The 68%, 90%, and 95% confidence levels are shown by the solid, dashed, and dotted lines. For the left plot, the overall best-fit values of a = 0.35 and vbo = 220 km s-1 have been kept fixed. For the right plot, the pitch angle from Francis & Anderson (2012) (i = 5.56°) and the best-fit bar radius for fixed i = 5.56°, r0 = 4.6 kpc, has been used (see also Martinez-Valpuesta & Gerhard 2011). The blow-out velocity depends only weakly on these parameters (compare Table 1). |
4.2.2. Gas components in our Galaxy and other galaxies
The blow-out velocity that we derive is inconsistent with velocity variations expected at spiral shocks in the context of simple density wave theory without explicit consideration of the interaction of massive star feedback with the underlying density structure. Our obtained velocities significantly exceed the ones found in molecular (Dame et al. 2001) and atomic gas (Kalberla & Dedes 2008). Gas-kinematics models (Fux 1999; Bissantz et al. 2003; Baba et al. 2010; Khoperskov et al. 2013) are in good agreement with these observations, but do not produce velocities that come close to the ones we find. Shetty et al. (2007) extract the azimuthal velocity variations from CO data for the galaxy M51, which features very prominent spiral arms. Even for the stronger spiral arm in M51, the azimuthal velocity shear does not exceed ≈120 km s-1. The massive stars are, however, observed downstream of the maximum of the CO intensity, where only a small fraction of the velocity shear would appear as 26Al velocities in M51. Further, most of the velocity shear in M51 is due to the slowing down of the gas at the spiral shock, such that the azimuthal velocity drops significantly below the circular velocity. Our observations require, however, velocities of at least 130 km s-1 (three standard deviations) above the circular velocity. The picture derived by detailed molecular gas observations for M51 (Egusa et al. 2011) would explain our data well: molecular clouds enter the spiral shock from behind and merge there to larger clouds. This triggers the formation of massive stars downstream of the density maximum. Thus the massive star ejecta are impeded by the upstream density maximum and obtain a net velocity in the direction of rotation.
Our results imply that blow out occurs from the star-forming regions of the spiral arms within the plane and plausibly also towards the halo. We expect star formation to occur as gas falls into the spiral-arm potential (Wada et al. 2011; Athanassoula 1992). Observed young star clusters tend to be associated with spiral arms, particularly towards their inner ends and at the near (López-Corredoira et al. 1999) and far (Davies et al. 2012) ends of the Galaxy’s bar. Simulations (Athanassoula 2012) and face-on images (Elmegreen 2012) of barred spiral galaxies confirm this general picture. Inside the corotation radius objects move faster than the large-scale patterns of the bar and of the spiral arms. Consequently, gas clouds which enter the pattern and form stars will create stellar groups that appear offset towards the leading edge of the pattern. For the Galactic bar, a corotation radius of ~4 kpc has been found (Gerhard 2011), though estimates increase to 5 kpc or even 6 kpc if both a boxy bulge and bar are considered (Martinez-Valpuesta & Gerhard 2011). A corotation of ~8.4 kpc has been found for the spiral arms of our Galaxy (Lépine et al. 2011). For a pattern velocity difference of ~50 km s-1, an offset of ~200 pc between superbubble-blowing massive stars and spiral-arm density maximum would be expected at the end of a typical massive-star lifetime of a few million years. The 26Al sources typically located in a density gradient on one side of the large-scale density enhancement in arms would trace non-isotropic superbubble growth around massive star groups, that otherwise cannot easily be seen in remains from parental molecular clouds (Louie et al. 2013). Although systematic velocity variation across spiral arms is expected from density wave theory and has been found in M51 (Shetty et al. 2007), such velocity differences across a spiral arm are only ~100 km s-1 or lower, and cannot explain our measurement (see Sect. 4.1). Simulations show that the initially isotropic ejecta from massive stars face and enhance the high-pressure region on one side, and a champagne-like outflow into the opposite direction occurs within a rather short time (Fierlinger et al. 2012; Baumgartner & Breitschwerdt 2009). Our observations require that 26Al-enriched superbubbles preferentially expand in the direction of galactic rotation relatively unimpeded, whereas they are blocked by denser gas in the opposite direction. This probably occurs along spiral arms and near the tip of the bar where the two prominent inner spiral arms curve towards the bar. Interestingly, velocities around 200 km s-1 are close to the sound speed in the hot gas (106 K). Von Glasow et al. (2013) model the absorption systems seen at similar velocities against Lyman break galaxies as cooled-down shells from expanding superbubbles. In both cases, the velocity would be set by the sound speed of the hot phase the superbubbles are expanding into.
4.2.3. Hot gas in and above the Galactic plane
Similar velocities perpendicular to the Galactic plane are also consistent with the scale height of 26Al measured (Wang et al. 2009) as  pc. The characteristic scale height of parental molecular clouds is about 50 pc (Dame et al. 2001), while, for example, a velocity of 200 km s-1 implies that a height of about 200 pc above the parental clouds is reached within the decay time of 106 years. These velocities cannot support a wind from the Galaxy into the intergalactic medium. Since 26Al traces superbubbles with ongoing input by massive stars, these should exhibit the highest velocities, whereas older bubbles that are not highlighted by 26Al will be less dynamic. Hot gas at higher latitudes above the Galactic disk is also seen in O vi absorption (Sembach et al. 2003). Such high ionization states appear in hot and relatively dense gas, as the superbubble wall interacts with ambient gas, and these data reflect more closely the average hot gas in general, including the later stages of superbubble evolution: the observed O vi height is 2 kpc to 3 kpc (Sembach et al. 2003).
pc. The characteristic scale height of parental molecular clouds is about 50 pc (Dame et al. 2001), while, for example, a velocity of 200 km s-1 implies that a height of about 200 pc above the parental clouds is reached within the decay time of 106 years. These velocities cannot support a wind from the Galaxy into the intergalactic medium. Since 26Al traces superbubbles with ongoing input by massive stars, these should exhibit the highest velocities, whereas older bubbles that are not highlighted by 26Al will be less dynamic. Hot gas at higher latitudes above the Galactic disk is also seen in O vi absorption (Sembach et al. 2003). Such high ionization states appear in hot and relatively dense gas, as the superbubble wall interacts with ambient gas, and these data reflect more closely the average hot gas in general, including the later stages of superbubble evolution: the observed O vi height is 2 kpc to 3 kpc (Sembach et al. 2003).
Within the Galactic disk, the velocities inferred from absorption also do not directly follow the molecular gas velocities, but are closer (Sembach et al. 2003) to them than to the higher velocities we infer for 26Al. Therefore, asymmetries that we observe during the active superbubble phase are apparently dissipated, and the flow is more isotropic at later times.
5. Conclusions
Our measurements of the Doppler shifts of the 1808.63 keV line as a function of Galactic longitude show that the radial velocity of the interstellar gas containing 26Al in the inner Galaxy differs significantly from that of other components of the ISM such as those seen in CO or H i. We observe the same qualitative behaviour: there is almost no average radial motion in the direction towards the Galactic centre, the magnitude of the radial velocity increases with the angular separation from the centre up to |l| ~ 30°, and the sign of the radial velocity is positive (redshift) in the first and negative (blueshift) in the fourth Galactic quadrant. However, the absolute velocities of the 26Al-carrying gas are much larger. Since the line emission happens over a large radial velocity range, the total emission from the inner Galaxy is Doppler-broadened. Our measurements of the line width of the 26Al emission are compatible with this implication. The variation of our measured radial velocity values with the extent of the ROI we average over is comparable to the statistical uncertainties, and the systematic uncertainties related to the time dependent variation of the instrument’s spectral response are small in comparison. Since the majority of 26Al is produced in massive stars, we conclude that our observations are probably due to large-scale asymmetric outflows from the regions where massive stars have recently formed.
The inner spiral arms, which are the plausible source regions producing most of the 26Al, show blow out of their massive-star ejecta preferentially in the direction of the leading edges. This increases 26Al velocities to ~200 km s-1 in addition to large-scale galactic rotation. Superbubbles are expected to form around massive star groups on the Ma time scale (Krause et al. 2013). In a wind-blown cavity or supernova remnant, initially freely-travelling ejecta would be decelerated within a time much shorter than a radioactive-decay lifetime. The 26Al-rich ejecta accumulate behind the swept up ambient medium, expanding at a similar velocity. When estimating the line-of-sight averaged velocities of 26Al as it decays, we should distinguish between the velocity of the bubble expansion itself and the velocities of ejecta flows within a bubble. Bubbles from single stars are expected to reach sizes of the order of 10 pc with associated expansion velocities of the order of 10 km s-1. Our inferred expansion velocity of ~200 km s-1 shows that the bubbles highlighted by 26Al have to be powered by many, hence clustered, massive stars. While we defer detailed consistency checks via cluster-population synthesis to future work, our measurement together with the fact that 26Al ejection is strongly correlated to the energy injection (Voss et al. 2009) suggests that massive star feedback in the inner few kpc of the Galaxy and its spiral arms is dominated by sizeable star clusters producing superbubbles, constituting a fundamental unit of large-scale stellar feedback. This does not imply expansion of the superbubble as an entity with these velocities, but rather provides a measurement from its interior reflecting its size and position with respect to the 26Al sources.
Our measurements reveal new aspects of large-scale gas kinematics in the Galaxy, derived from data originating in the hot and tenuous phase of the ISM that is otherwise hard to measure. Flow asymmetries require distinct structure within the spiral arms of the Galaxy; dense gas, which marks the spiral-arm potential, must be offset upstream from massive stars, and these must be located towards the leading edges of the spiral arm, with ejecta blowing out into the inter-arm low density environment (and halo). The origins of spiral arms are being debated (Wada et al. 2011), and massive star offsets from their gas density maxima remain controversial (Louie et al. 2013; Ferreras et al. 2012). The excess velocity of 26Al-traced gas over stars and cold/dense gas (Fig. 8) thus constitutes a clear, though indirect, demonstration of the offsets between star-forming gas and young stars, which seemed plausible in density-wave theory and have also been found in molecular gas observations (Vogel et al. 1988) and images of galaxies (Elmegreen 2012) (see also Sect. 4.1).
This one sided blow out will impart a local braking torque on the cold gas as it rotates in the plane of the Galaxy. Once injected into the halo, hot gas will likely exchange its angular momentum with the 106 K corona (Gupta et al. 2012) over ~108 a before cooling and returning to the Galactic disk elsewhere (Marinacci et al. 2011). The total mass of 26Al in the Milky Way is measured (Diehl et al. 2006) to be ~ 2 M⊙. This traces about 106M⊙ of total massive-star ejecta, hence a hot gas flow of ~1 M⊙ a-1, ejected into the direction of Galactic rotation, with an excess velocity comparable to the Galactic rotation velocity itself. These 26Al data measure primarily a torque of a specific, and otherwise hard to observe, gas component, which also couples to the total of Galactic gas flows. The global recoil may slow down denser gas in its rotation in the Galaxy. Its global torque of 1 M⊙ a-1 × 4 kpc × 200 km s-1 ≈ 106M⊙ kpc2 Ma-2 can be compared to the total angular momentum of the Milky Way’s gas of roughly 1010M⊙ × 5 kpc × 250 km s-1 ≈ 1010M⊙ kpc2 Ma-1. To estimate potential impacts, this blow out could remove the entire angular momentum from the dense gas within 10 Ga. This estimate assumes that the angular momentum would not return to the disk. More realistically, some angular momentum exchange with the gaseous halo will take place, and some fraction of the angular momentum will return to the disk when the ejecta fall back. Estimated radial inflow rates toward the inner Galaxy for other processes are (Crocker 2012) 0.1 M⊙ a-1 due to gravitational or 0.2 M⊙ a-1 due to magnetic torque, and 0.2 M⊙ a-1 by mass loss from the bulge stars. Radial gas diffusion is implied by one-sided superbubble blow out even if there was no global loss of angular momentum from the Galactic disk, because it would require substantial fine-tuning of the angular momentum-exchange between the off-streaming 26Al-traced gas and the halo gas to get the 26Al-traced gas back to its original position. One-sided superbubble blow out may thus contribute both to linking general star formation on kpc scales to large-scale gas flows and to subsequent star formation in the inner regions of our Galaxy. Our measured characteristic ejecta velocity suggests that superbubbles are the dominant structure of the ISM around massive stars.
The UV luminosity associated with massive stars is important in ionizing gas at higher Galactic latitudes and towards the halo (Razoumov & Sommer-Larsen 2006). Its propagation and escape from the denser parts of the disk depend critically on the structure of the interstellar medium around its sources and the erosion of spiral-arm gas around massive stars. The morphology of surrounding interstellar gas determines the extent to which UV from massive stars may reach more distant gas, and contributes to the ionization state of the intergalactic medium. Blow out from massive star regions in superbubbles is thus a fundamental aspect of large-scale stellar feedback in a star-forming galaxy such as our own. This effect must be accounted for in models (Veilleux et al. 2005) of galactic winds and galaxy evolution, which currently consider either single, non-interacting bubbles, or the galaxy as a whole with simplified structural assumptions at scales below ~kpc scales.
Acknowledgments
This research was supported by the German DFG cluster of excellence “Origin and Structure of the Universe”. The INTEGRAL/SPI project has been completed under the responsibility and leadership of CNES; we are grateful to ASI, CEA, CNES, DLR, ESA, INTA, NASA, and OSTC for support of this ESA space science mission.
References
- Athanassoula, E. 1992, MNRAS, 259, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E. 2012, EPJ Web Conf. 19, 6004 [Google Scholar]
- Baba, J., Saitoh, T. R., & Wada, K. 2010, PASJ, 62, 1413 [NASA ADS] [Google Scholar]
- Baumgartner, V., & Breitschwerdt, D. 2009, Astron. Nachr., 330, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2005, ApJ, 630, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Banday, A. J., Gorski, K. M., et al. 1996, ApJ, 464, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bissantz, N., Englmaier, P., & Gerhard, O. 2003, MNRAS, 340, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera-Lavers, A., González-Fernández, C., Garzón, F., Hammersley, P. L., & López-Corredoira, M. 2008, A&A, 491, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002, unpublished [arXiv:astro-ph/0207156] [Google Scholar]
- Crocker, R. M. 2012, MNRAS, 423, 3512 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., de La Fuente, D., Najarro, F., et al. 2012, MNRAS, 419, 1860 [NASA ADS] [CrossRef] [Google Scholar]
- Diehl, R., Kretschmer, K., Plüschke, S., et al. 2003, Astron. Nachr. Suppl., 324, 18 [NASA ADS] [Google Scholar]
- Diehl, R., Halloin, H., Kretschmer, K., et al. 2006, Nature, 439, 45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Diehl, R., Lang, M. G., Martin, P., et al. 2010, A&A, 522, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobbs, C. L., & Burkert, A. 2012, MNRAS, 421, 2940 [NASA ADS] [CrossRef] [Google Scholar]
- Egusa, F., Koda, J., & Scoville, N. 2011, ApJ, 726, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 2012, in IAU Symp. 284, eds. R. J. Tuffs, & C. C. Popescu, 317 [Google Scholar]
- Englmaier, P., & Gerhard, O. 1999, MNRAS, 304, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., Cropper, M., Kawata, D., Page, M., & Hoversten, E. A. 2012, MNRAS, 424, 1636 [NASA ADS] [CrossRef] [Google Scholar]
- Fierlinger, K. M., Burkert, A., Diehl, R., et al. 2012, in Advances in Computational Astrophysics: Methods, Tools, and Outcome, eds. R. Capuzzo-Dolcetta, M. Limongi, & A. Tornambè, ASP Conf. Ser., 453, 25 [Google Scholar]
- Francis, C., & Anderson, E. 2012, MNRAS, 422, 1283 [NASA ADS] [CrossRef] [Google Scholar]
- Fux, R. 1999, A&A, 345, 787 [NASA ADS] [Google Scholar]
- Gelman, A., Carlin, J. B., Stern, H. S., & Rubin, D. B. 2003, Bayesian data analysis (CRC press) [Google Scholar]
- Gerhard, O. 2011, Mem. Soc. Astron. It. Suppl., 18, 185 [Google Scholar]
- Green, J. A., Caswell, J. L., McClure-Griffiths, N. M., et al. 2011, ApJ, 733, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A., Mathur, S., Krongold, Y., Nicastro, F., & Galeazzi, M. 2012, ApJ, 756, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Jaskot, A. E., Strickland, D. K., Oey, M. S., Chu, Y.-H., & García-Segura, G. 2011, ApJ, 729, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., & Dedes, L. 2008, A&A, 487, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., & Haud, U. 2006, A&A, 455, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S. A., Vasiliev, E. O., Sobolev, A. M., & Khoperskov, A. V. 2013, MNRAS, 428, 2311 [NASA ADS] [CrossRef] [Google Scholar]
- Knödlseder, J., Bennett, K., Bloemen, H., et al. 1999, A&A, 344, 68 [NASA ADS] [Google Scholar]
- Krause, M., Fierlinger, K., Diehl, R., et al. 2013, A&A, 550, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lépine, J. R. D., Roman-Lopes, A., Abraham, Z., Junqueira, T. C., & Mishurov, Y. N. 2011, MNRAS, 414, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Long, R. J., Mao, S., Shen, J., & Wang, Y. 2013, MNRAS, 428, 3478 [NASA ADS] [CrossRef] [Google Scholar]
- López-Corredoira, M., Garzón, F., Beckman, J. E., et al. 1999, AJ, 118, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Louie, M., Koda, J., & Egusa, F. 2013, ApJ, 763, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Marinacci, F., Fraternali, F., Nipoti, C., et al. 2011, MNRAS, 415, 1534 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Valpuesta, I., & Gerhard, O. 2011, ApJ, 734, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Neal, R. M. 1993, Technical Report CRG-TR-93-1, Dept. of Computer Science, University of Toronto [Google Scholar]
- Plüschke, S., Diehl, R., Schönfelder, V., et al. 2001, in Exploring the Gamma-Ray Universe, eds. A. Gimenez, V. Reglero, & C. Winkler, ESA SP, 459, 55 [Google Scholar]
- Prantzos, N., & Diehl, R. 1996, Phys. Rep., 267, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Razoumov, A. O., & Sommer-Larsen, J. 2006, ApJ, 651, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., et al. 2009, ApJ, 700, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Roques, J. P., Schanne, S., von Kienlin, A., et al. 2003, A&A, 411, L91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönfelder, V., Aarts, H., Bennett, K., et al. 1993, ApJS, 86, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Sembach, K. R., Wakker, B. P., Savage, B. D., et al. 2003, ApJS, 146, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Vogel, S. N., Ostriker, E. C., & Teuben, P. J. 2007, ApJ, 665, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., Egger, R., Freyberg, M. J., et al. 1997, ApJ, 485, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Sofue, Y., Honma, M., & Omodaka, T. 2009, PASJ, 61, 227 [NASA ADS] [Google Scholar]
- Strong, A. W. 1995, Exp. Astron., 6, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Vedrenne, G., Roques, J.-P., Schönfelder, V., et al. 2003, A&A, 411, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [Google Scholar]
- Vogel, S. N., Kulkarni, S. R., & Scoville, N. Z. 1988, Nature, 334, 402 [NASA ADS] [CrossRef] [Google Scholar]
- von Glasow, W., Krause, M. G. H., Sommer-Larsen, J., & Burkert, A. 2013, MNRAS, 434, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Voss, R., Diehl, R., Hartmann, D. H., et al. 2009, A&A, 504, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wada, K., Baba, J., Fujii, M., & Saitoh, T. R. 2011, in Computational Star Formation, eds. J. Alves, B. G. Elmegreen, J. M. Girart, & V. Trimble, IAU Symp., 270, 363 [Google Scholar]
- Wang, W., Lang, M. G., Diehl, R., et al. 2009, A&A, 496, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y., Zhao, H., Mao, S., & Rich, R. M. 2012, MNRAS, 427, 1429 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Wegg, C., & Gerhard, O. 2013, MNRAS, 435, 1874 [Google Scholar]
- Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winkler, C., Diehl, R., Ubertini, P., & Wilms, J. 2011, Space Sci. Rev., 161, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Systematic uncertainties
We investigated the impact of choosing sky region bins of different sizes, e.g. smaller at the expense of a smaller signal, but aiming to obtain a better spatial resolution for our velocity information (spectra in Fig. 4 illustrate this specifically towards longitude l ~ –27° to –28°, the brightest part of the fourth Galactic quadrant). Figure A.1 shows the dependence of the 26Al velocity results on the ROI extent in longitude (varying between 6° and 16°), and in latitude (between 6° and 10°). We can obtain higher spatial resolution, but only in regions of high intensity. In our longitude-velocity figures, we include the Bayes factor information for B > 1 also for the data points where detections are insignificant, and the data point values therefore are not shown in the figure. In order to maximize the 26Al signal for best determination of its line centroid position, we chose a latitude range of ±5° for our definite analysis.
The variation of intensity (per solid angle, averaged over the ROI) with latitude extent offers some indication that the intensity falloff with latitude is slower in the inner (|l| < 10°) Galactic plane. Figure A.2 shows these intensity variations for latitude extents of 6°, 8°, and 10° as well as the difference between 10° and 6° ROIs as “high latitude” (units are relative). We can see that the intensity distribution varies consistently for different latitude integration regions of 6° to 10°, except for a possible additional component between longitudes +5° and –12°. This component may arise from the Scorpius-Centaurus region (Diehl et al. 2010). This different behaviour in the inner Galaxy also is seen in the shape of the 26Al line: It appears that we see a superposition in the region l ~ [−15°,10°] (see Fig. A.2) of a nearby (and more extended in latitude) component that is approximately at rest with respect to the observer, and the Doppler-shifted component from the Galactic plane. Therefore, the line shape is not represented as well by a single Gaussian, and the uncertainties in centroid determination are larger in this inner region of the Galactic plane (see Fig. A.1). Additionally, in l ~ [−15°,15°] the line is less bright than at |l| ~ [15°,30°], further increasing the line centroid’s uncertainty.
 |
Fig. A.1 26Al longitude-velocity results for different bin sizes in Galactic longitude (above) and latitude (below). |
 |
Fig. A.2 26Al intensities along the inner Galaxy, for different bin sizes in Galactic latitude, and 16° bins in longitude, offset in 4° steps. The emission that can be attributed to higher latitudes, hence potential foreground sources, is indicated in the lowest (blue) data points derived from the difference in intensities for the 6° and 10° bins. |
Detailed tracking of the spectral response variation with degradations and annealings has been found necessary for determining the width of the 26Al line (as shown in Fig. 2), but the effect of the spectral response variation on the line position measurements for smaller emission regions is small (compare Fig. 2 and Fig. 7). For example, with an instrumental line width of 3 keV and a celestial line width of 1.4 keV (Fig. 2), the measured width is  , which is a 10% excess above the instrumental width.
, which is a 10% excess above the instrumental width.
 |
Fig. A.3 Offset in line centroids from the effect of time-variable degradation, if a line with fixed centroid were represented by a Gaussian fit. Periods where the respective longitude range was observed are used, so that the impact on our longitude-velocity result can be directly seen. |
We then investigated this variation for a correlation with the times of our observations along the plane of the Galaxy, possibly leading to a longitude-dependent bias. For this, we determine the maximum position shift in units of velocity, measured by fitting an instrumental line to the data that were taken while pointing at the respective longitude intervals. As shown in Fig. A.3, the bias which may result from this time-variable spectral response is small (<10 km s-1) compared to our reported line-shift values.
 |
Fig. A.4 Longitude-velocity results using different methods of determining the spectral response (see Sect. 2.3). For comparison we show: blue data points and blue shading in the background: measured instrumental background line; red hatched regions in the foreground: line shape model fitted to a set of instrumental background lines. |
The observed velocity values for different latitude ranges are all consistent within the uncertainties.
We conclude that the systematic uncertainties in our longitude-velocity measurement are smaller than statistical uncertainties and do not alter the results reported, specifically the asymmetry of blow-out as discussed. Furthermore, our background method and spectral-response treatment does not have an impact on the results. Systematics are dominated by the selection of the ROI used, and may affect the detailed velocity value derived for a particular region along the Galactic plane by ~50 km s-1.
All Tables
Best-fit parameters for our two-armed spiral emission model with different assumptions about the input parameters.
All Figures
 |
Fig. 1 Exposure map of the sky with the SPI telescope on INTEGRAL for the data used in this analysis (Feb. 2003 to Feb. 2012). |
| In the text | |
 |
Fig. 2 Spectrum around the gamma-ray line from 26Al obtained for the entire inner Galactic plane (ROI = 128° × 12° at l = 0°) |
| In the text | |
 |
Fig. 3 Two sky model components: The region of interest (ROI) 12° × 10° centred around l = 24° (bottom) and its complement (top) taken as subsets of the COMPTEL 1.8 MeV sky map. The rectangular outline shows the region covered by our scan along the Galactic plane. |
| In the text | |
 |
Fig. 4 Spectra of the region around l ~ –27° to –28° for ROI latitude extents of 16°, 12°, 8°, 6°. |
| In the text | |
 |
Fig. 5 Limits on the width of the 26Al line emission from ROIs around the Galactic centre with an extent in latitude of ±6° and longitude extents ranging from 6° to 128°. The error bars of decreasing thickness show the Bayesian highest posterior density credible regions corresponding to 68.3%, 95.4%, and 99.7%, corresponding to 1σ, 2σ, and 3σ. |
| In the text | |
 |
Fig. 6 Degradation of the spectral response over mission time. With degradation, a one-sided tail at the low-energy side develops. The plot shows its extent versus time (one revolution =3 days). |
| In the text | |
 |
Fig. 7 Trace of systematic Doppler shifts of the 26Al line along the inner Galaxy. |
| In the text | |
 |
Fig. 8 Longitude-velocity diagram comparing γ-ray-measured velocities (crosses, including error bars) with other objects in our Galaxy. 26Al line-centroid energies were fitted to determine velocities in longitude bins of 12° and latitude ranges ±5°. For comparison, different models are shown (blue solid, red dotted, and green dashed lines), as well as the velocity information from molecular gas seen in CO (see Sect. 4 for details). |
| In the text | |
 |
Fig. 9 Properties of our preferred model. The top-left plot shows the adopted 26Al source distribution in the plane of the Milky Way as seen from above. Also indicated is the position of the Sun (8 kpc from the Galactic centre), the location of the bar (dashed), and several longitudinal directions of interest. The colour indicates the 26Al density (yellow: highest, black: lowest). The other plots show quantities derived from this source distribution as a function of Galactic longitude as solid black lines (top right: received flux in arbitrary units, bottom left: velocity centroid shift, bottom right: velocity width). Overplotted are the observed data points with error bars showing one standard deviation, and upper limits of three standard deviations in the case of the velocity width. The flux excess at l = −24° may be due to foreground emission from the Sco-Cen association (Diehl et al. 2010) leaking from higher latitudes into our ROI bin. The observational limits on the velocity width are not constraining and are compatible with expectations (see Sect. 2.2). |
| In the text | |
 |
Fig. 10 Left: map of the local velocity relative to the Sun in our preferred model. The white contours indicate the 26Al mass distribution. Right: relative flux contribution per surface area in the standard model, separate for each longitude bin. Several longitude bins are indicated by black lines. |
| In the text | |
 |
Fig. 11 Similar to Fig. 9, but for the best-fit four-arm spiral. |
| In the text | |
 |
Fig. 12 Reduced χ2 and confidence contours as a function of galactocentric bar radius. The pitch angle for the Galactic spiral structure (left, the value from Francis & Anderson 2012), is also indicated, including one standard deviation error bars) and as a function of the 26Al drop-off exponent and the blow-out velocity (right). The 68%, 90%, and 95% confidence levels are shown by the solid, dashed, and dotted lines. For the left plot, the overall best-fit values of a = 0.35 and vbo = 220 km s-1 have been kept fixed. For the right plot, the pitch angle from Francis & Anderson (2012) (i = 5.56°) and the best-fit bar radius for fixed i = 5.56°, r0 = 4.6 kpc, has been used (see also Martinez-Valpuesta & Gerhard 2011). The blow-out velocity depends only weakly on these parameters (compare Table 1). |
| In the text | |
 |
Fig. A.1 26Al longitude-velocity results for different bin sizes in Galactic longitude (above) and latitude (below). |
| In the text | |
 |
Fig. A.2 26Al intensities along the inner Galaxy, for different bin sizes in Galactic latitude, and 16° bins in longitude, offset in 4° steps. The emission that can be attributed to higher latitudes, hence potential foreground sources, is indicated in the lowest (blue) data points derived from the difference in intensities for the 6° and 10° bins. |
| In the text | |
 |
Fig. A.3 Offset in line centroids from the effect of time-variable degradation, if a line with fixed centroid were represented by a Gaussian fit. Periods where the respective longitude range was observed are used, so that the impact on our longitude-velocity result can be directly seen. |
| In the text | |
 |
Fig. A.4 Longitude-velocity results using different methods of determining the spectral response (see Sect. 2.3). For comparison we show: blue data points and blue shading in the background: measured instrumental background line; red hatched regions in the foreground: line shape model fitted to a set of instrumental background lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


