| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322484 | |
| Published online | 26 November 2013 | |
Rotating hybrid compact stars
1 Department of Physics, Yerevan State University, Alex Manoogian 1, 0025 Yerevan, Armenia
2 Institute for Theoretical Physics, J. W. Goethe University, 60438 Frankfurt am Main, Germany
3 Frankfurt Institute for Advanced Studies, J. W. Goethe University, 60438 Frankfurt am Main, Germany
4 Max-Planck-Institut für Gravitationsphysik, Albert-Einstein-Institut, 14476 Potsdam, Germany
e-mail: sedrakian@th.physik.uni-frankfurt.de
Received: 14 August 2013
Accepted: 2 October 2013
Starting from equations of state of nucleonic and color-superconducting quark matter and assuming a first-order phase transition between these, we construct an equation of state of stellar matter, which contains three phases: a nucleonic phase, as well as two-flavor and three-flavor color-superconducting phases of quarks. Static sequences of the corresponding hybrid stars include massive members with masses of ~2 M⊙ and radii in the range of 13 ≤ R ≤ 16 km. We investigate the integral parameters of rapidly rotating stars and obtain evolutionary sequences that correspond to constant rest-mass stars spinning down by electromagnetic and gravitational radiation. Physically new transitional sequences are revealed that are distinguished by a phase transition from nucleonic to color-superconducting matter for some configurations that are located between the static and Keplerian limits. The snapshots of internal structure of the star, displaying the growth or shrinkage of superconducting volume as the star’s spin changes, are displayed for constant rest mass stars. We further obtain evolutionary sequences of rotating supramassive compact stars and construct pre-collapse models that can be used as initial data to simulate a collapse of color-superconducting hybrid stars to a black hole.
Key words: dense matter / equation of state / stars: neutron / stars: rotation
© ESO, 2013
1. Introduction
It has been suggested long ago that compact stars could be dense enough for a transition from baryonic matter to deconfined quarks (Ivanenko & Kurdgelaidze 1965; Itoh 1970; Iachello et al. 1974; Collins & Perry 1975). If so, the properties of matter should be described in terms of colored quarks as the fundamental degrees of freedom. Therefore, compact-star phenomenology offers a unique tool to address the challenge of understanding the phase structure of dense quantum chromodynamics (QCD). The integral parameters of compact stars, such as the mass, radius, and moment of inertia, depend sensitively on their theoretically deduced equation of state (EoS) at high densities. Currently, the measurements of pulsar masses in binaries provide the most clean and stringent observational constraints on the underlying EoS. Important examples are the mass measurements of two solar mass pulsars, PSR J1614-2230 and PSR J0348+0432, using independent methods (Demorest et al. 2010; Antoniadis et al. 2013).
Because of their compactness neutron stars can rotate extremely fast. Among them, millisecond pulsars offer a unique laboratory for simultaneous measurements of high spins, masses, and moments of inertia in binary systems. The last two integral parameters depend on the EoS of dense matter and thus shed light on its properties. In particular, the Keplerian limit at which the star starts shedding mass from the equator depends on the EoS. Thus, a way to constrain the EoS of dense matter is provided by observations of high-spin pulsars. The Keplerian frequency sets an absolute upper limit on the rotation frequency, whereas other (less certain) mechanisms, such as gravitational radiation reaction instabilities, could impose lower limits on the maximal rotation frequency of a star. Because the centrifugal potential counteracts the compressing stress exerted on matter by gravity, rotating configurations are more massive than their non-rotating counterparts. New-born hybrid stars can be formed with large internal circulation, but viscosity and magnetic stress act to dampen such motions at least in non-superfluid compact stars. Therefore, we can assume that cold single-component stellar configurations are uniformly rotating to a good approximation.
These considerations motivate our study of the compact stars with quark cores in a range of rotation periods from the Keplerian limit down to the static limit. There are evolutionary considerations, which make such a study physically relevant: compact stars that are born rapidly rotating evolve adiabatically by losing energy to gravitational waves and electromagnetic (to lowest order, dipole) radiation. This evolution is well represented by star sequences with constant rest mass and varying spin. The most massive members of rapidly rotating configurations may not have a stable static limit; that is, the evolution may terminate with a formation of a black hole. These configurations are known as supramassive configurations (Cook et al. 1994). The spin-up of a pulsar to millisecond frequencies via accretion from a companion involves changes in the rest mass and the spin of the star; that is, simple one-parameter evolutionary scenarios cannot be constructed without additional physical input (e.g., mass accretion rate, etc.). Nevertheless, we are able to draw the boundary of the region in this case, where stable configurations with given spin and mass can exist. The evolution of supramassive configurations were studied in detail in Cook et al. (1994) for a large set of EoS for baryonic matter by using an exact numerical integration method for Einstein’s equations.
The spin evolution of hybrid stars, or stars with quark-matter cores surrounded by a nuclear envelope, may differ from the evolution of purely nucleonic stars. Because the spin-down compresses the matter within the star, it can induce a phase transition to the quark-matter phase once the critical density of the phase transition has been reached (Glendenning et al. 1997; Chubarian et al. 2000; Glendenning & Weber 2001; Spyrou & Stergioulas 2002; Grigorian et al. 2003; Zdunik et al. 2006; Dimmelmeier et al. 2009; Abdikamalov et al. 2009; Haensel et al. 2009; Weber et al. 2013).
Intense studies of stationary (nonrotating) hybrid compact stars began after the measurement of two solar mass pulsars PSR J1614-2230 (Demorest et al. 2010) to reconcile the phase transition from baryonic matter to quark matter with these observations (Bejger et al. 2011; Lastowiecki et al. 2012; Chen et al. 2011; Lai & Xu 2011; Bonanno & Sedrakian 2012; Lenzi & Lugones 2012; Chu & Chen 2012; Sedrakian 2013; Masuda et al. 2013b; Sasaki et al. 2013; Lenzi & Lugones 2013; Klahn et al. 2013; Masuda et al. 2013a; Dexheimer et al. 2013; Chamel et al. 2013). Massive stable compact stars with color-superconducting cores were obtained only in a few studies prior to these observations (Alford et al. 2005; Ippolito et al. 2008; Knippel & Sedrakian 2009; Agrawal & Dhiman 2009; Kurkela et al. 2010). Rotating configurations of color-superconducting stars were previously constructed by Ippolito et al. (2008); however, evolutionary aspects of the problem were not discussed so far.
In this work, we explore the full parameter space that characterizes rotating hybrid configurations on the basis of a carefully chosen EoS, which permits a phase transition from nucleonic matter to color-superconducting quark matter at some pre-selected density. The nucleonic EoS is based on a relativistic density functional of nuclear matter with density-dependent (DD) couplings, according to parametrization of Lalazissis et al. (2005). This parameterization was recently used in Colucci & Sedrakian (2013) to address the hyperonization puzzle in compact stars, and our approach follows the one adopted in that work. The quark-matter EoS is based on the phenomenological four-fermion interaction Nambu–Jona-Lasinio Lagrangian, that is supplemented with repulsive vector interactions and that is the same as that used by Bonanno & Sedrakian (2012). The energy of quark matter is minimized by allowing the color-superconducting phases of two- and three-flavor quark matter. Our construction of the EoS has two key parameters: one is the onset density of the phase transition from nucleonic to quark matter and the second is the strength of the repulsive vector interactions.
Solutions of Einstein’s equations for rotating, axially symmetric configurations have been obtained by a number of authors using either perturbative methods (Hartle 1967; Hartle & Thorne 1968; Sedrakyan & Chubaryan 1968a,b; Arutyunyan et al. 1971) or direct numerical integration (Komatsu et al. 1989b,a; Bonazzola et al. 1993, 1998; Cook et al. 1994; Stergioulas & Friedman 1995; Nozawa et al. 1998). For a review and further references, see Stergioulas (2003). The computations reported below are based on a direct numerical integration of the Einstein’s equations and were carried out using the public domain RNS code1.
This paper is structured as follows. In Sect. 2 we discuss the input EoS of hybrid stars. Section 3 contains our results for the sequences of non-rotating and rapidly rotating hybrid stars. Rotational properties of evolutionary sequences are discussed in Sect. 4. In Sect. 5, we discuss the rotationally induced phase transition to the color-superconducting state of quarks and its implications for the physics of hybrid stars. Our conclusions are collected in Sect. 6.
2. Equation of state
At the fundamental level, zero-temperature, β-equilibrated matter is described in terms of two equations of state for nucleonic matter (at low densities) and quark matter (at high densities). The EoSs of these phases that are used in our study were introduced earlier (Bonanno & Sedrakian 2012), whereas the nucleonic EoS has been improved further by Colucci & Sedrakian (2013), where a density functional with DD couplings has been implemented. Here, we combine these EoS to describe hybrid-star matter by assuming a first-order phase transition from nucleonic to quark matter. Our approach allows quark matter to support two types of color-superconducting phases: the low-density phase is the two-flavor color-superconducting (2SC) phases, and the high-density phase is the three-flavor color-flavor-locked (CFL) phase. Readers interested in detailed discussions of color superconductivity should consult the reviews (Bailin & Love 1984; Rajagopal & Wilczek 2000; Alford 2001; Rischke 2004; Shovkovy 2005; Alford et al. 2008; Anglani et al. 2013).
Because the physics underlying these EoSs has been described elsewhere, we provide only a brief overview of these EoSs to keep our discussion self-contained.
2.1. Nuclear matter
Nucleonic matter is described by the relativistic Lagrangian, ![\begin{eqnarray} \label{eq:lagrangian} \nonumber {\cal L}_H & = & \sum_N\bar\psi_N\bigg[\gamma^\mu \left({\rm i}\partial_\mu-g_{\omega N}\omega_\mu - \frac{1}{2} g_{\rho N}\tauvec\cdot\rhovec_\mu\right)\\ \nonumber & &- (m_N - g_{\sigma N}\sigma)\bigg]\psi_N + \frac{1}{2} \partial^\mu\sigma\partial_\mu\sigma-\frac{1}{2} m_\sigma^2\sigma^2\\ \nonumber & &- \frac{1}{4}\omega^{\mu\nu}\omega_{\mu\nu} + \frac{1}{2} m_\omega^2\omega^\mu\omega_\mu - \frac{1}{4}\rhovec^{\mu\nu}\rhovec_{\mu\nu} + \frac{1}{2} m_\rho^2\rhovec^\mu\cdot\rhovec_\mu\\ & &+ \sum_{\lambda}\bar\psi_\lambda({\rm i}\gamma^\mu\partial_\mu - m_\lambda)\psi_\lambda - \frac{1}{4}F^{\mu\nu}F_{\mu\nu}, \end{eqnarray}](/articles/aa/full_html/2013/11/aa22484-13/aa22484-13-eq5.png) (1)where the N-sum is over the nucleons, ψN are the nucleonic Dirac fields with masses mN, the λ-sum runs over the leptons e − ,μ − ,νe, and νμ with masses mλ and the last term is the electromagnetic energy density. The interaction among the nucleons is mediated by the σ,ωμ, and ρμ meson fields with ωμν and ρμν being the corresponding field strength tensors and with masses mσ, mω, and mρ. The nucleon (N) and meson coupling constants (giN) are density-dependent:
(1)where the N-sum is over the nucleons, ψN are the nucleonic Dirac fields with masses mN, the λ-sum runs over the leptons e − ,μ − ,νe, and νμ with masses mλ and the last term is the electromagnetic energy density. The interaction among the nucleons is mediated by the σ,ωμ, and ρμ meson fields with ωμν and ρμν being the corresponding field strength tensors and with masses mσ, mω, and mρ. The nucleon (N) and meson coupling constants (giN) are density-dependent: ![\begin{eqnarray} g_{iN}(\rho_N) &=& g_{iN}(\rho_{0})h_i(x), \qquad i=\sigma,\omega, \\ g_{\rho N}(\rho_N) &=& g_{\rho N}(\rho_{0})\exp[-a_\rho(x-1)], \end{eqnarray}](/articles/aa/full_html/2013/11/aa22484-13/aa22484-13-eq21.png) where ρN is the nucleon density, x = ρN/ρ0, ρ0 is the nuclear saturation density, and
where ρN is the nucleon density, x = ρN/ρ0, ρ0 is the nuclear saturation density, and 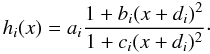 (4)We use the DD-ME2 parameterization of Lalazissis et al. (2005). The parameter values listed in Table 1 are adjusted to reproduce the properties of symmetric and asymmetric nuclear matter, binding energies, charge radii, and neutron radii of spherical nuclei.
(4)We use the DD-ME2 parameterization of Lalazissis et al. (2005). The parameter values listed in Table 1 are adjusted to reproduce the properties of symmetric and asymmetric nuclear matter, binding energies, charge radii, and neutron radii of spherical nuclei.
Meson masses and couplings to the nucleons in the DD-ME2 effective interaction.
The Lagrangian density (1) yields the zero-temperature pressure of nucleonic matter as a function of density ![\begin{eqnarray} \label{eq:thermodynamic} P_H& = & - \frac{m_\sigma^2}{2} \sigma^2 + \frac{m_\omega^2}{2} \omega_0^2 + \frac{m_\rho^2 }{2} \rho_{03}^2 + \frac{1}{3}\sum_N \frac{2J_N+1}{2\pi^2} \nonumber\\ &&\times \int_0^{\infty}\!\!\! \frac{k^4 \ {\rm d}k}{(k^2+m^{* 2}_N)^{1/2}} \left[\theta(-E_k^B+\mu_N^*)+\theta(-E_k^B-\mu_N^*)\right]\nonumber\\ & &+ \frac{1}{3\pi^2} \sum_{\lambda} \int_0^{\infty}\!\!\! \frac{k^4 \ {\rm d}k}{(k^2+m^2_\lambda)^{1/2}}\nonumber\\ &&\times \left[\theta(-E_k^{\lambda}+\mu_\lambda)+\theta(-E_k^{\lambda}-\mu_\lambda)\right] + \rho_N\Sigma_{r}, \end{eqnarray}](/articles/aa/full_html/2013/11/aa22484-13/aa22484-13-eq35.png) (5)where σ, ω0, and ρ03 are the nonvanishing mesonic mean fields, JN is the nucleon spin,
(5)where σ, ω0, and ρ03 are the nonvanishing mesonic mean fields, JN is the nucleon spin, 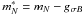 is the effective nucleon mass,
is the effective nucleon mass,  is the effective baryon chemical potential, I3 is the third component of baryon isospin,
is the effective baryon chemical potential, I3 is the third component of baryon isospin,  and
and 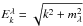 are the single-particle energies of baryons and leptons (electrons e and muons μ), respectively; and θ(x) is the step function. The lepton masses mλ (λ ∈ e,μ) are taken to be equal to their free-space values.
are the single-particle energies of baryons and leptons (electrons e and muons μ), respectively; and θ(x) is the step function. The lepton masses mλ (λ ∈ e,μ) are taken to be equal to their free-space values.
2.2. Quark matter
Quark matter is described by an extended Nambu–Jona-Lasinio Lagrangian: ![\begin{eqnarray} \label{eq:NJL_Lagrangian} \mathcal{L}_{Q}&=&\bar\psi({\rm i}\gamma^{\mu}\partial_{\mu}-\hat m)\psi +G_S \sum_{a=0}^8 \left[(\bar\psi\lambda_a\psi)^2+(\bar\psi {\rm i}\gamma_5 \lambda_a\psi)^2\right]\nonumber\\ &&+ G_D \sum_{\gamma,c}\left[\bar\psi_{\alpha}^a {\rm i} \gamma_5 \epsilon^{\alpha\beta\gamma}\epsilon_{abc}(\psi_C)^b_{\beta}\right]\left[(\bar\psi_C)^r_{\rho} {\rm i} \gamma_5\epsilon^{\rho\sigma\gamma}\epsilon_{rsc}\psi^8_{\sigma}\right]\nonumber\\ &&-K \left \{ {\rm det}_{f}\left[\bar\psi(1+\gamma_5)\psi\right]+{\rm det}_{f}\left[\bar\psi(1-\gamma_5)\psi\right]\right\}\nonumber\\ &&+G_V(\bar\psi {\rm i} \gamma^{\mu}\psi)^2, \end{eqnarray}](/articles/aa/full_html/2013/11/aa22484-13/aa22484-13-eq49.png) (6)where the quark spinor fields
(6)where the quark spinor fields 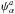 carry color (a = r,g,b) and flavor (α = u,d,s) indices, the matrix of the quark current masses is given by
carry color (a = r,g,b) and flavor (α = u,d,s) indices, the matrix of the quark current masses is given by 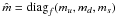 , λa with a = 1,...,8 are the Gell-Mann matrices in color space, and λ0 = (2/3)1f. The charge-conjugate spinors are defined as
, λa with a = 1,...,8 are the Gell-Mann matrices in color space, and λ0 = (2/3)1f. The charge-conjugate spinors are defined as  and
and  , where C = iγ2γ0 is the charge conjugation matrix. The standard Nambu–Jona-Lasinio Lagrangian is extended here to include vector interactions ( ∝ GV) among quarks and the ’t Hooft interaction term ( ∝ K).
, where C = iγ2γ0 is the charge conjugation matrix. The standard Nambu–Jona-Lasinio Lagrangian is extended here to include vector interactions ( ∝ GV) among quarks and the ’t Hooft interaction term ( ∝ K).
The pressure of quark matter at zero temperature follows from the saddle-point evaluation of the partition function of quark matter as described by the Lagrangian (6),  (7)where ϵi are the quasiparticle spectra of quarks, kFi their Fermi-momenta, Λ is the cut-off,
(7)where ϵi are the quasiparticle spectra of quarks, kFi their Fermi-momenta, Λ is the cut-off, 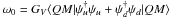 and
and 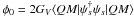 are the mean-field expectation values of the vector mesons ω and φ in quark matter, P0 is the vacuum pressure, and B ∗ is an effective bag constant. The first θ-function guarantees that the Fermi sphere of quarks lies within the momentum space spanned by the model, which is limited by the cut-off Λ. In the 2SC phase, leptons contribute to the pressure of quark matter and, as in the case of baryonic matter, we assume that the leptons form an ideal gas. The quark chemical potentials are modified by the vector fields as follows:
are the mean-field expectation values of the vector mesons ω and φ in quark matter, P0 is the vacuum pressure, and B ∗ is an effective bag constant. The first θ-function guarantees that the Fermi sphere of quarks lies within the momentum space spanned by the model, which is limited by the cut-off Λ. In the 2SC phase, leptons contribute to the pressure of quark matter and, as in the case of baryonic matter, we assume that the leptons form an ideal gas. The quark chemical potentials are modified by the vector fields as follows:  . The numerical values of the parameters of the Lagrangian are mu,d = 5.5 MeV, ms = 140.7 MeV, Λ = 602.3 MeV, GSΛ2 = 1.835, KΛ5 = 12.36, and GD/GS = 1. The strength of the vector coupling GV and the transition density from nucleonic matter to quark matter are free parameters of our model.
. The numerical values of the parameters of the Lagrangian are mu,d = 5.5 MeV, ms = 140.7 MeV, Λ = 602.3 MeV, GSΛ2 = 1.835, KΛ5 = 12.36, and GD/GS = 1. The strength of the vector coupling GV and the transition density from nucleonic matter to quark matter are free parameters of our model.
2.3. Matching the equations of state
Because the surface tension between nuclear and quark matter is not well determined, the matching between the nuclear and quark EoS can be carried out in two possible ways. If the tension between these phases is low, then a mixed phase of quark and nuclear matter forms. The second possibility is that the transition boundary is sharp, which is the case when there is sufficiently high tension between the phases. In this case, the transition occurs at a certain baryo-chemical potential at which the pressures of the two phases become equal. This is equivalent to the condition that curves of pressure, P, vs. baryo-chemical potential, μ for these phases cross; that is, the phase equilibrium is determined by a Maxwell construction. This implies (according to the standard Maxwell construction) that at the deconfinement phase transition, there is a jump in density at constant pressure. Because the transition is first order, latent heat is released during the transition. However, the transition density itself cannot be fixed, because the Nambu–Jona-Lasinio model does not allow us to fix the low-density normalization of the pressure (this is a consequence of the fact that this class of models does not capture the confinement feature of QCD). Therefore, we introduced an additional “bag” parameter B∗ above, which allows us to vary the density at which the quark phase sets in, thus fixing the density of deconfinement ρtr.
The resulting EoS of pure nucleonic and nucleonic plus quark matter is shown in Fig. 1. For brevity we shall refer to these EoS as EoS A and EoS B, respectively. The EoS B displays two (first-order) transitions, one from nuclear matter to 2SC phase and the second from the 2SC phase to the CFL phase. The segment of the EoS B between points 1 and 2 in Fig. 1 corresponds to the 2SC phase; the segment to the right from point 3 corresponds to the CFL phase. In the following, we fix the values of the two parameters ρtr = 2.5ρ0, where ρ0 is the nuclear saturation density and the ratio GV/GS = 0.8.
 |
Fig. 1 EoS of nucleonic matter (dashed, red line) and of hybrid matter (solid, black line). The interval between the points 1 and 2 corresponds to the 2SC phase, whereas the interval to the right from point 3 corresponds to the CFL phase. |
3. Mass, radius, and moment of inertia
 |
Fig. 2 Dependence of masses of hybrid compact stars in solar units on their central density for EoS A (upper panel) and EoS B (lower panel). Solid (black online) lines show the non-rotating sequence. The dash-dotted (red online) lines show the maximally fast rotating sequence. The horizontal dashed (blue online) lines show constant rest-mass sequences, some of which are labeled by the value of their rest mass (in solar units). The mass step between two sequential evolutionary sequences is 0.2 M⊙. |
A well-known feature of the static (spherically-symmetric) or uniformly rotating (axially symmetric) equilibrium configurations in General Relativity is the existence of a maximum mass for sequences parameterized by their central density ρc. This feature is independent of any particular EoS and is illustrated for the sequences based on the EoS A and B in Fig. 2. If the central density of a configuration is larger than the value corresponding to the maximum mass, it becomes unstable toward collapse to a black hole. This condition is a sufficient condition for a secular instability in uniformly rotating stars (Friedman et al. 1988). A necessary criterion for instability is the neutrality (zero) of the frequency of the fundamental (pulsation) modes. The turning points, where dM/dρc = 0, and the neutrality lines of fundamental frequency modes are close to each other for models of rotating configurations, but they do not coincide (Takami et al. 2011). Thus, some uniformly rotating configurations that are stable according to the turning point criterion can be still unstable either dynamically or secularly. However, one can still use the turning point criterion for practical purpose of locating the instability of uniformly rotating stars.
Our purely nuclear EoS belongs to the class of hard equations of states based on relativistic density functionals; therefore, we find a large maximum mass for the purely nucleonic sequences, which is on the order of 2.7 M⊙ (Fig. 2, upper panel). Hybrid configurations branch off from the nuclear configurations when the central density of a configuration reaches the density of the deconfinement phase transition (Fig. 2, lower panel). The jump in the density at constant pressure is translated into a plateau in the M(ρc) dependence, where dM/dρc = 0. At the maximal value of ρc, where this plateau ends, the hybrid stars emerge.
Equilibrium configurations with central densities located within the plateau cannot exist, because the gravitational force cannot be balanced if there are no pressure gradients. Indeed, dP/dr = (dP/dρ)(dρ/dr) = 0, dρ/dr ≠ 0, and dP/dρ = 0 at any point on the plateau (see Fig. 1). Thus, there are two stable families of purely hadronic stars and hybrid stars on the left and right sides of the plateau, respectively, but there are no equilibria in-between. Any perturbation of the central density of a configuration, which results in a new central density located on the plateau makes the central region of the star unstable. This does not necessarily imply that the star would become entirely unstable.
Dynamical processes, such as accretion, collapse, or secular spin-down, may result in a transient configuration with a central density located on the plateau. In this case, a rearrangement of matter should take place such that the pressure gradients are restored, and the central density of the configuration is outside of the plateau. Thus, for example, catastrophic rearrangement of matter in accreting systems may take place because of gradual compression. This occurs once the transition density from hadronic to the color-superconducting quark matter is reached. These rearrangements are accompanied with an energy release equal to the difference in the energies of configurations located at the end points of the plateau. Since the plateau also appears in the case of rotating configurations, the arguments above are valid for rotating stars as well. Furthermore, similar arguments apply to the transition from the purely 2SC core to the 2SC plus CFL core hybrid stars, which are separated by another plateau (see Fig. 1).
The non-rotating sequences terminate at the maximum mass, where stability is lost. Rotating nucleonic and hybrid compact stars cover an area in Fig. 2, which is bounded from above by the mass-shedding configurations (dash-dotted lines) and from below by the static configurations. These static configurations are simply the solutions of the spherically symmetric Tolman-Oppenheimer-Volkoff equations. In our plots, these are connected to their maximally fast-rotating counterparts via their evolutionary sequences, which corresponds to the rotational evolution at constant rest-mass (almost horizontal dashed curves). The rest masses of evolutionary sequences were computed with a mass step 0.2 M⊙. As classified by Cook et al. (1994), the constant rest-mass sequences naturally fall into two classes: the normal sequences, which always have a stable static (non-rotating) limiting configuration, and the supramassive sequences, which do not have such limit. These sequences terminate on the line that joins the maximal masses in the static and Keplerian limits, which thus provides a boundary of the area of stable configurations in the upper right-hand corner of Fig. 2. The area where stable stars are possible is bounded from below by the minimum possible mass of configurations; the latter bound is not of interest to us, because the central densities of the minimal-mass configurations are well below the phase-transition density.
 |
Fig. 3 Mass-radius relationship for hybrid compact stars as described by EoS A (upper panel) and EoS B (lower panel). The labeling is the same as in Fig. 2. |
Because the phase-transition density is independent of rotation frequency and the rotating sequences lie above the static sequences, there always exist evolutionary sequences, whose Keplerian limit corresponds to purely nucleonic configurations, whereas the static limit corresponds to a hybrid one (see Fig. 2). Consequently, the evolutionary sequences must involve a rotational frequency range, which is characterized by a phase transition to a color-superconducting quark state in the interior of the star. We shall call such evolutionary sequences as transitional sequences. It is clear from this figure that all supramassive sequences are either transitional or contain quark matter already at the Keplerian limit. However, not all transitional sequences are supramassive; one such example is the 2.2 M⊙ rest-mass star shown in Fig. 2. Therefore, it is not excluded that slowly rotating hybrid stars that are close to the static limit have undergone a phase transition to the superconducting state in the course of the spin-down from the initial spin acquired at the birth.
Figure 3 shows the gravitational masses of the sequences as a function of equatorial circumferential radius for static, maximally rotating, and evolutionary sequences. Along the evolutionary sequences, the radius of a star shrinks to its limiting value corresponding to the static configuration. For the transitional sequences, this is accompanied by the onset of quark superconductivity and growth of the radius of the quark core.
 |
Fig. 4 Dependence of moment of inertia of the hybrid configurations on the mass of configuration (in solar mass units) for EoS A (upper panel) and EoS B (lower panel). The labeling is the same as in Fig. 2. |
Figure 4 shows the dependence of moments of inertia of the sequences on the masses of the stars. The decrease in the moments of inertia from the value at the Keplerian to the value in the static limit as one moves along the evolutionary sequences is the consequence of the decreasing radius of a star at constant rest mass. This feature is not affected by the emergence of superconducting quark matter in the transitional sequences for uniformly rotating stars.
4. Rotational evolution
The variation of spin frequency along the normal evolutionary and transitional sequences as a function of angular momentum of the star is shown in Fig. 5. For all masses, the stars belonging to the normal evolutionary sequences spin down as they lose angular momentum. The transitional sequence with the rest mass 2 M⊙ shows the same feature, assuming that the quark superconductor rotates uniformly with the hadronic matter. We verified that supramassive sequences spin up as they lose angular momentum, which agree with the results of Cook et al. (1994) as obtained for a number of nucleonic EoSs. This effect is independent of the onset (or presence from the outset) of quark matter in the cores of compact stars, as long as they are assumed to rotate uniformly with the nucleonic envelope.
 |
Fig. 5 Dependence of spin frequency of configurations on the angular momentum. The constant rest mass evolutionary sequences are shown by dashed lines and the Keplerian sequence by the solid line. The low-J results (cJ/GM⊙ ≤ 0.4) were obtained by interpolation. The supramassive sequences (not shown) spin-up as they approach the onset of instability. The upper panel corresponds to EoS A and the lower panel to EoS B. |
Figure 6 displays the dependence of the rotation frequency of a configuration on its mass. For low-mass objects belonging to the normal evolutionary sequences, the gravitational mass is unaffected by the rotation. For the large rest-mass sequences, M ≥ 2.4 M⊙ the gravitational mass increases with the spin frequency. Furthermore, the limiting frequency of a (e.g. M = 2 M⊙) purely nucleonic star is larger than that for a hybrid star of the same mass, which is explained by the result that the nucleonic stars are more compact.
 |
Fig. 6 Dependence of spin frequency of configurations on gravitational mass. The conventions are the same as in Fig. 5. The dots show the four pulsars listed in Table 2, which are among fast rotating pulsars with available mass measurements. The horizontal dashed line is the spin frequency of the fastest rotating pulsar J1748 − 2446. The upper panel corresponds to EoS A and the lower panel to EoS B. |
 |
Fig. 7 Dependence of the spin frequency of configurations on the ratio of the kinetic to potential energy T/W. The conventions are the same as in Fig. 5. |
Masses and spin periods of several pulsars taken from the references quoted in the fourth column.
For some pulsars, the mass and the spin frequency are measured. A representative collection of these objects, which includes the subgroup of massive and rapidly rotating stars is shown in Table 2 and in Fig. 6. Within this collection, the most massive pulsar J1614 − 2230 would be, according to our model, a hybrid star. It is also found to be on a transitional sequence, since its asymptotically fast-rotating limit corresponds to a purely nucleonic star. Thus, this pulsar must have experienced a phase transition to color-superconducting quark phase during its evolution (see the discussion in the next section).
Figure 7 shows the dependence of the angular velocity on the ratio of the kinetic energy T to the gravitational binding energy W. The latter quantity is especially useful for the discussion of the location of the instabilities of the stars toward non-axisymmetrical perturbations. For perturbations classified in terms of an expansion in spherical functions, the instabilities arise to the lowest order for modes that belong to l = 2 and m = ± 2 perturbations. In the case of classical uniformly rotating incompressible ellipsoids, the onset of secular (i.e., viscosity driven) and gravitational wave-emission instabilities occurs at the same point along a sequence when T/W = 0.14 for l = 2 modes with m = 2 and m = − 2, respectively. For compressible Newtonian and general relativistic models, the point of the onset of the gravitational instability occurs at lower values of T/W ≃ 0.08, which we take as a reference for the discussion. (Viscosity-driven instabilities would evolve stars to a non-uniformly rotating quasi-equilibrium state, which need not be stationary. The onset of secular instabilities in general relativistic stars requires values of T/W that are larger than the value 0.08 quoted above for gravitational wave-emission instabilities). According to Fig. 7, the nucleonic and hybrid models with masses M ≥ 1.4 M⊙ would undergo an instability starting at some frequency, whereas lower-mass stars would not. From Figs. 8 and 9 we conclude that a M ~ 2 M⊙ mass star, which is predicted to be on the transitional sequence, should have been in the unstable region at high rotation rates, which corresponds to a purely nucleonic interior.
The evolution of an isolated star would require a slow-down due to the emission of gravitational waves, which are accompanied by a phase transition that leads to superconducting quark matter in the core of the star due to the compression.
5. Phase transition to a color-superconducting state via spin up or spin down
Rotationally induced phase transitions to quark matter have been discussed in the literature and have been claimed to have strong observational consequences in the timing of isolated pulsars, as well as accreting X-ray binaries. If the phase transition is weakly first order (or second order) the EoS of matter may not experience strong changes as the phase transition sets in. In contrast, the density jump associated with a strong first-order phase transition may cause sudden changes in the integral parameters of stars. Previous work concentrated on the phase transition to normal quark matter (Glendenning et al. 1997; Chubarian et al. 2000; Glendenning & Weber 2001; Spyrou & Stergioulas 2002; Grigorian et al. 2003; Zdunik et al. 2006; Dimmelmeier et al. 2009; Abdikamalov et al. 2009; Haensel et al. 2009; Weber et al. 2013). Contrary to this, we argue here that the transition for sufficiently cold stars occurs to one of the color-superconducting phases of quark matter. If the phase of interest is a superfluid, as is the case with the CFL phase, the onset of superfluidity doubles the dynamical degrees of freedom of the fluid and induces a differential rotation between the normal component, which is coupled to the star on short dynamical timescales and the superfluid component, which couples to the rest of the star via mutual friction (Mannarelli et al. 2008). In the case of the 2SC phase, color magnetism of this phase requires generation of color magnetic flux tubes in quark matter (Alford & Sedrakian 2010). This may alter the magnetic properties of the stars and their spin-down under electromagnetic radiation. These aspects of the rotationally induced phase transition deserve separate studies. Here, we restrict ourselves to a discussion of the internal structure of the stars as they are spun up or down.
Figure 8 shows the dependence of the equatorial density profile of a 2.2 M⊙ rest-mass star on the internal radius for four spin frequencies in the range 0 ≤ Ω ≤ 5.6 × 103 s-1. For the largest spin frequency, it is seen that the star is purely nucleonic. A reduction of the spin frequency by about 10% induces a phase transition to the 2SC phase in the central region of the star. As expected the stellar radius shrinks with the spin down. We also note the density jump at the interface between the 2SC and nucleonic phase as implied by the first-order phase transition. At asymptotically slow rotation rates, the star represents a dense 2SC quark phase that extends up to 4 km and is surrounded by a nuclear shell enclosed in the region 4 ≤ r ≤ 13 km. The snapshots of the internal structure of the star displayed in Fig. 8 would give a true reflection of the internal structure of the stars, as it spins up or down, if the dynamical timescales are much larger than the timescales required for the nucleation of the color-superconducting phase.
Figure 9 displays the same dependence as Fig. 8 but for a supramassive star with a rest mass 2.4 M⊙. In this case, the Keplerian configuration contains a 2SC quark core. As the spin frequency is lowered, the region occupied by the 2SC phase expands. A reduction of the spin frequency by 20% induces a new phase transition to the CFL phase. The phase transition from the 2SC to the CFL is first order and is accompanied by a jump in the density at the interface of these two phases. We recall that because this configuration is supramassive it does not posses a static limit. At about Ω = 4.6 × 103 s-1, the star reaches the stability limit. While the CFL phase expanded further, we see that the 2SC phase started to shrink. Consequently, there must be a maximum of the superconducting quark core radius as a function of the spin frequency along the evolutionary sequence. The fate of the supramassive stars is not known: most likely, they undergo a collapse. Our models can be used as initial data for simulations of the collapse of hybrid stars with color-superconducting cores to a black hole.
 |
Fig. 8 Equatorial density profiles of a rotating compact star of rest mass Mr/M⊙ = 2.2 at various rotation frequencies given in units of 104 s-1. The shaded areas correspond to a quark matter core in the 2SC phase and the empty areas to nucleonic matter. |
 |
Fig. 9 Same as in Fig. 8 but for a configuration with a rest mass Mr/M⊙ = 2.4. The hatched region corresponds to the 2SC phase and the dotted region to the CFL phase. |
6. Conclusions
We examined the properties of rotating hybrid stars constructed from a low-density nucleonic EoS and a high-density color-superconducting quark matter EoS by assuming a first-order phase transition between these phases at some interface. At high densities, the 2SC phase is replaced by the CFL phase of superfluid quark matter. We constructed the normal and supramassive families of purely nuclear and hybrid configurations. Both families produce massive M ~ 2 M⊙ compact stars; the maximum mass of the hybrid stars is close to this observational limit, while the purely nucleonic family can sustain masses of order 2.6 M⊙ in the static limit.
The properties of the evolutionary sequences were examined for both EoSs, where each star loses angular momentum to radiation and slows down while maintaining its rest mass. The integral parameters of these sequences and their dependence on the angular rotation frequency agree with the studies of nucleonic stars. A new feature of these sequences is the rotationally induced phase transition to a color-superconducting phase of quark matter, which occurs for sufficiently massive stars. We note that latent heat, associated with the first order phase transition, is released as the transition proceeds from the baryonic matter to 2SC phase and from the 2SC phase to the CFL phase.
We defined a new subclass of transitional sequences. These are constant rest-mass sequences that feature a superconducting phase transition point when the rotation frequency is reduced from the Keplerian frequency to zero. These sequences are characterized by an onset and growth of the volume of the superconducting phases as the star slows down to the static limit. In the case of supramassive sequences (for which the static limit is absent) the radius of the superconducting quark phase shows a non-monotonic dependence of the radius (and the volume) of the quark core on the spin frequency. Our models of supramassive color-superconducting stars provide the initial data that can be used to simulate the collapse of an unstable star to a black hole.
Because the star contains a superconducting quark core, the collapse dynamics and potential gravitational wave signal (which are sensitive to the rotation rate of the star and to its internal composition) may be affected. The differential rotation of the superfluid phases and the existence of density jumps at the phase transition boundaries can leave a detectable mark on the signal. Moreover, the fast radio bursts recently observed on cosmological distances (Thornton et al. 2013) have been interpreted as a supramassive compact star that collapses to a black hole (Falcke & Rezzolla 2013). In this scenario, the electromagnetic emission is produced by the snapping of the magnetosphere as the stellar surface collapses. If this suggestion is correct, fast radio bursts will provide sufficiently common sources to explore the presence of a superconducting quark core because the dynamics of the stellar surface will depend on the internal structure of the collapsing matter.
Acknowledgments
NSA thanks the Frankfurt University for hospitality, where part of this work was done. A.S. acknowledges the hospitality of the Albert-Einstein-Institut, Potsdam. This research was supported by a collaborative research grant of the Volkswagen Foundation (Hannover, Germany).
References
- Abdikamalov, E. B., Dimmelmeier, H., Rezzolla, L., & Miller, J. C. 2009, MNRAS, 392, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Agrawal, B. K., & Dhiman, S. K. 2009, Phys. Rev. D, 79, 103006 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M. 2001, Ann. Rev. Nucl. Part. Sci., 51, 131 [Google Scholar]
- Alford, M., Braby, M., Paris, M., & Reddy, S. 2005, ApJ, 629, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M. G., Schmitt, A., Rajagopal, K., & Schafer, T. 2008, Rev. Mod. Phys., 80, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M. G., & Sedrakian, A. 2010, J. Phys. G Nucl. Phys., 37, 075202 [Google Scholar]
- Anglani, R., Casalbuoni, R., Ciminale, M., et al. 2013 [arXiv:1302.4264] [Google Scholar]
- Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 448 [Google Scholar]
- Arutyunyan, G. G., Sedrakyan, D. M., & Chubaryan, É. V. 1971, AZh, 48, 496 [NASA ADS] [Google Scholar]
- Bailin, D., & Love, A. 1984, Phys. Rep., 107, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Bejger, M., Zdunik, J. L., Haensel, P., & Fortin, M. 2011, A&A, 536, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonanno, L., & Sedrakian, A. 2012, A&A, 539, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonazzola, S., Gourgoulhon, E., Salgado, M., & Marck, J. A. 1993, A&A, 278, 421 [NASA ADS] [Google Scholar]
- Bonazzola, S., Gourgoulhon, E., & Marck, J.-A. 1998, Phys. Rev. D, 58, 104020 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Haensel, P., Zdunik, J. L., & Fantina, A. F. 2013, Int. J. Mod. Phys. E, 22, 1330018 [NASA ADS] [CrossRef] [Google Scholar]
- Champion, D. J., Ransom, S. M., Lazarus, P., et al. 2008, Science, 320, 1309 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chen, H., Baldo, M., Burgio, G. F., & Schulze, H.-J. 2011, Phys. Rev. D, 84, 105023 [NASA ADS] [CrossRef] [Google Scholar]
- Chu, P.-C., & Chen, L.-W. 2012 [arXiv:1212.1388] [Google Scholar]
- Chubarian, E., Grigorian, H., Poghosyan, G., & Blaschke, D. 2000, A&A, 357, 968 [NASA ADS] [Google Scholar]
- Collins, J. C., & Perry, M. J. 1975, Phys. Rev. Lett., 34, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Colucci, G., & Sedrakian, A. 2013, Phys. Rev. C, 87, 055806 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, G. B., Shapiro, S. L., & Teukolsky, S. A. 1994, ApJ, 422, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dexheimer, V., Steinheimer, J., Negreiros, R., & Schramm, S. 2013, Phys. Rev. C, 87, 015804 [NASA ADS] [CrossRef] [Google Scholar]
- Dimmelmeier, H., Bejger, M., Haensel, P., & Zdunik, J. L. 2009, MNRAS, 396, 2269 [NASA ADS] [CrossRef] [Google Scholar]
- Falcke, H., & Rezzolla, L. 2013, A&A, submitted [arXiv:1307.1409] [Google Scholar]
- Friedman, J. L., Ipser, J. R., & Sorkin, R. D. 1988, ApJ, 325, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. K., & Weber, F. 2001, ApJ, 559, L119 [Google Scholar]
- Glendenning, N. K., Pei, S., & Weber, F. 1997, Phys. Rev. Lett., 79, 1603 [NASA ADS] [CrossRef] [Google Scholar]
- Grigorian, H., Blaschke, D., & Poghosyan, G. 2003, Nucl. Phys. A, 715, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., Zdunik, J. L., Bejger, M., & Lattimer, J. M. 2009, A&A, 502, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartle, J. B. 1967, ApJ, 150, 1005 [Google Scholar]
- Hartle, J. B., & Thorne, K. S. 1968, ApJ, 153, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W. T., Ransom, S. M., Stairs, I. H., et al. 2006, Science, 311, 1901 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Iachello, F. D., Langer, W., & Lande, A. 1974, Nucl. Phys. A, 219, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Ippolito, N. D., Ruggieri, M., Rischke, D. H., Sedrakian, A., & Weber, F. 2008, Phys. Rev. D, 77, 023004 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N. 1970, Prog. Theoret. Phys., 44, 291 [Google Scholar]
- Ivanenko, D. D., & Kurdgelaidze, D. F. 1965, Astrophysics, 1, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, B. A., Bailes, M., van Kerkwijk, M. H., et al. 2003, ApJ, 599, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, B. A., Hotan, A., Bailes, M., Ord, S., & Kulkarni, S. R. 2005, ApJ, 629, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Kaluzny, J., Rucinski, S. M., & Thompson, I. B. 2003, AJ, 125, 1546 [NASA ADS] [CrossRef] [Google Scholar]
- Klahn, T., Blaschke, D. B., & Łastowiecki, R. 2013, Phys. Rev. D, 88, 085001 [NASA ADS] [CrossRef] [Google Scholar]
- Knippel, B., & Sedrakian, A. 2009, Phys. Rev. D, 79, 083007 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, H., Eriguchi, Y., & Hachisu, I. 1989a, MNRAS, 237, 355 [NASA ADS] [Google Scholar]
- Komatsu, H., Eriguchi, Y., & Hachisu, I. 1989b, MNRAS, 239, 153 [NASA ADS] [Google Scholar]
- Kurkela, A., Romatschke, P., & Vuorinen, A. 2010, Phys. Rev. D, 81, 105021 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, X.-Y., & Xu, R.-X. 2011, Res. Astron. Astrophys., 11, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lalazissis, G. A., Nikšić, T., Vretenar, D., & Ring, P. 2005, Phys. Rev. C, 71, 024312 [NASA ADS] [CrossRef] [Google Scholar]
- Lastowiecki, R., Blaschke, D., Grigorian, H., & Typel, S. 2012, Acta Phys. Pol. B Proc. Suppl., 5, 535 [Google Scholar]
- Lenzi, C. H., & Lugones, G. 2012, ApJ, 759, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lenzi, C. H., & Lugones, G. 2013 [arXiv:1307.1928] [Google Scholar]
- Mannarelli, M., Manuel, C., & Sa’d, B. A. 2008, Phys. Rev. Lett., 101, 241101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Masuda, K., Hatsuda, T., & Takatsuka, T. 2013a, Prog. Theoret. Exp. Phys., 2013, 070003 [Google Scholar]
- Masuda, K., Hatsuda, T., & Takatsuka, T. 2013b, ApJ, 764, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Nozawa, T., Stergioulas, N., Gourgoulhon, E., & Eriguchi, Y. 1998, A&AS, 132, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rajagopal, K., & Wilczek, F. 2000 [arXiv:hep-ph/0011333] [Google Scholar]
- Rischke, D. H. 2004, Prog. Part. Nucl. Phys., 52, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Sasaki, T., Yasutake, N., Kohno, M., Kouno, H., & Yahiro, M. 2013 [arXiv:1307.0681] [Google Scholar]
- Sedrakian, A. 2013, PoS (Confinment X) 251 [Google Scholar]
- Sedrakyan, D. M., & Chubaryan, E. V. 1968a, Astrofizika, 4, 551 [NASA ADS] [Google Scholar]
- Sedrakyan, D. M., & Chubaryan, E. V. 1968b, Astrophysics, 4, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Shovkovy, I. A. 2005, Foundations of Physics, 35, 1309 [Google Scholar]
- Spyrou, N. K., & Stergioulas, N. 2002, A&A, 395, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stergioulas, N. 2003, Liv. Rev. Relativity, 6, 3 [Google Scholar]
- Stergioulas, N., & Friedman, J. L. 1995, ApJ, 444, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Takami, K., Rezzolla, L., & Yoshida, S. 2011, MNRAS, 416, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Thornton, D., Stappers, B., Bailes, M., et al. 2013, Science, 341, 53 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Weber, F., Orsaria, M., & Negreiros, R. 2013 [arXiv:1307.1103] [Google Scholar]
- Zdunik, J. L., Bejger, M., Haensel, P., & Gourgoulhon, E. 2006, A&A, 450, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Masses and spin periods of several pulsars taken from the references quoted in the fourth column.
All Figures
 |
Fig. 1 EoS of nucleonic matter (dashed, red line) and of hybrid matter (solid, black line). The interval between the points 1 and 2 corresponds to the 2SC phase, whereas the interval to the right from point 3 corresponds to the CFL phase. |
| In the text | |
 |
Fig. 2 Dependence of masses of hybrid compact stars in solar units on their central density for EoS A (upper panel) and EoS B (lower panel). Solid (black online) lines show the non-rotating sequence. The dash-dotted (red online) lines show the maximally fast rotating sequence. The horizontal dashed (blue online) lines show constant rest-mass sequences, some of which are labeled by the value of their rest mass (in solar units). The mass step between two sequential evolutionary sequences is 0.2 M⊙. |
| In the text | |
 |
Fig. 3 Mass-radius relationship for hybrid compact stars as described by EoS A (upper panel) and EoS B (lower panel). The labeling is the same as in Fig. 2. |
| In the text | |
 |
Fig. 4 Dependence of moment of inertia of the hybrid configurations on the mass of configuration (in solar mass units) for EoS A (upper panel) and EoS B (lower panel). The labeling is the same as in Fig. 2. |
| In the text | |
 |
Fig. 5 Dependence of spin frequency of configurations on the angular momentum. The constant rest mass evolutionary sequences are shown by dashed lines and the Keplerian sequence by the solid line. The low-J results (cJ/GM⊙ ≤ 0.4) were obtained by interpolation. The supramassive sequences (not shown) spin-up as they approach the onset of instability. The upper panel corresponds to EoS A and the lower panel to EoS B. |
| In the text | |
 |
Fig. 6 Dependence of spin frequency of configurations on gravitational mass. The conventions are the same as in Fig. 5. The dots show the four pulsars listed in Table 2, which are among fast rotating pulsars with available mass measurements. The horizontal dashed line is the spin frequency of the fastest rotating pulsar J1748 − 2446. The upper panel corresponds to EoS A and the lower panel to EoS B. |
| In the text | |
 |
Fig. 7 Dependence of the spin frequency of configurations on the ratio of the kinetic to potential energy T/W. The conventions are the same as in Fig. 5. |
| In the text | |
 |
Fig. 8 Equatorial density profiles of a rotating compact star of rest mass Mr/M⊙ = 2.2 at various rotation frequencies given in units of 104 s-1. The shaded areas correspond to a quark matter core in the 2SC phase and the empty areas to nucleonic matter. |
| In the text | |
 |
Fig. 9 Same as in Fig. 8 but for a configuration with a rest mass Mr/M⊙ = 2.4. The hatched region corresponds to the 2SC phase and the dotted region to the CFL phase. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


