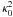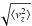| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322175 | |
| Published online | 31 October 2013 | |
Structure, stability, and evolution of 3D Rossby vortices in protoplanetary disks
1 Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille), UMR 7326, 38 rue F. Joliot-Curie, 13388 Marseille Cedex 13, France
e-mail: samuel.richard@oamp.fr; pierre.barge@oamp.fr
2 Aix-Marseille Université, CNRS, Centrale Marseille, IRPHE (Institut de Recherche sur les Phénomènes Hors Equilibre), UMR 7342, 49 rue F. Joliot Curie, 13013 Marseille, France
e-mail: ledizes@irphe.univ-mrs.fr
Received: 28 June 2013
Accepted: 13 September 2013
Context. Large-scale persistent vortices could play a key role in the evolution of protoplanetary disks, particularly in the dead zone where no turbulence associated with a magnetic field is expected. These vortices are known to form easily in 2D disks via the Rossby wave or the baroclinic instability. In three dimensions, however, their formation and stability is a complex problem and still a matter of debate.
Aims. We study the formation of vortices by the Rossby wave instability in a stratified inviscid disk and describe their 3D structure, stability, and long-term evolution.
Methods. Numerical simulations were performed using a fully compressible hydrodynamical code based on a second-order finite volume method. We assumed a perfect-gas law and a non-homentropic adiabatic flow.
Results. The Rossby wave instability is found to proceed in 3D in a similar way as in 2D. Vortices produced by the instability look like columns of vorticity in the whole disk thickness; the weak vertical motions are related to the weak inclination of the vortex axis that appears during the development of the RWI. Vortices with aspect ratios higher than 6 are unaffected by the elliptical instability. They relax into a quasi-steady columnar structure that survives hundreds of rotations while slowly migrating inward toward the star at a rate that reduces with the vortex aspect ratio. Vortices with a lower aspect ratio are by contrast affected by the elliptic instability. Short aspect ratio vortices (χ < 4) are completely destroyed in a few orbital periods. Vortices with an intermediate aspect ratio (4 < χ < 6) are partially destroyed by the elliptical instability in a region away from the midplane where the disk stratification is sufficiently strong.
Conclusions. Elongated Rossby vortices can survive many orbital periods in protoplanetary disks in the form of vorticity columns. They could play a significant role in the evolution of the gas and the gathering of solid particles to form planetesimals or planetary cores, a possibility that receives a renewed interest with the recent discovery of a particle trap in the disk of Oph IRS 48.
Key words: instabilities / hydrodynamics / planets and satellites: formation / protoplanetary disks
© ESO, 2013
1. Introduction
Barge & Sommeria (1995) pointed out the potential role of vortices in protoplanetary disks: they can capture large amounts of solid particles and can thus participate in the process of planet formation by speeding up the formation of planetesimals and the rapid growth of planetary cores. The formation, stability, and evolution of these vortices in protoplanetary disks have since raised a number of challenging questions.
Most numerical studies of protoplanetary disks have been performed in 2D using quantities averaged over the disk thickness. For Keplerian disks, numerical simulations have shown that vortices can be created if the disk possesses some heterogeneities (Bracco et al. 1999). These are created at the border of the dead zone of protoplanetary disks (Varnière & Tagger 2006), for instance, or at the edge of a gap opened by a sufficiently massive planet (de Val-Borro et al. 2007). They can make the disk unstable with respect to the Rossby wave instability (RWI). This instability was first studied by Lovelace et al. (1999) and Li et al. (2000, 2001) in the context of the protoplanetary disks and was proposed as a way to produce large-scale vortices. The RWI is a global, linear, and non-axisymmetric instability that occurs when an extremum of potential vorticity exists in the disk. 2D vortices can also be produced by a non-linear baroclinic instability, as explored by Klahr & Bodenheimer (2003); Johnson & Gammie (2005); Petersen et al. (2007a,b) and Lesur & Papaloizou (2010). These vortices are known to migrate inward toward the star (Li et al. 2000; Paardekooper et al. 2010; Surville & Barge 2012, 2013).
The dynamics of the disk in three dimensions is a much more complex problem that has been addressed by a few authors only. The creation of vortices in 3D by itself is a problem. In homentropic disks, Méheut et al. (2010, 2012a) showed that the RWI could lead to the formation of complex 3D vortical structures with strong vertical motions. The RWI was studied in more detail both theoretically and numerically for locally isothermal (Lin 2012) and non-barotropic disks (Lin 2013). Lin provided explanations for the different observations by Méheut et al. (2010, 2012a). He also showed that the most unstable mode of the RWI can remain quasi-2D in a non-homentropic disk. Our simulations for a non-homentropic disk show that stable quasi-2D vortices can indeed be created by the RWI.
The vortices may exhibit a complex dynamics. Barranco & Marcus (2005) were the first to show that the dynamics of 2D vortices can be completely different in 3D, using anelastic numerical simulations in vertically stratified disks. Due to the strong shear they support, 2D vortices in a disk could a priori be unstable with respect to the 3D elliptical instability (Kerswell 2002). This instability generically affects strained vortices (Pierrehumbert 1986; Bayly 1986) and is modified by the stratification and the background rotation of the disk (Miyazaki 1993; Guimbard et al. 2010). Lesur & Papaloizou (2009, thereafter LP09) have considered the specific case of the vortices in a Keplerian disk. Using simple vortex models in a shearing box, they analyzed the stability of the vortices according to their aspect ratio in a weak and moderately stratified case. Interestingly, they showed that a moderate stratification tends to destabilize vortices that were stable without stratification.
3D studies are also important to better understand the concentration of the solid particles in the vortices. Indeed, the preliminary two-phase simulations we performed showed that the dust-to-gas ratio depends strongly on height in the disk due to the vertical component of the Sun’s gravity. A comprehensive study of the evolution of protoplanetary disks will be investigated with 3D two-phase simulations in a future work, in continuation of a preliminary 2D approach (Inaba & Barge 2006).
In this paper, we are interested in the formation of 3D vortices by the RWI and in their long-term evolution. The basic equations, the disk model, and the numerical method are presented in Sect. 2. Section 3 is devoted to the description of the linear growth and non-linear evolution of the RWI. The characteristics of the final vortex, that are obtained after a succession of merging processes, are also provided in this section. The stability properties of the vortex with respect to the elliptical instability are examined in Sect. 4, together with its property of migrating toward the star. A brief conclusion is provided in Sect. 5.
2. Fluid equations and numerical method
2.1. Standard disk assumptions
The gas of the nebula was assumed to be a mixture of molecular hydrogen (75%) and helium (25%) with a mean molecular weight μ = 2.34 g/mol. The low-pressure conditions inside the disk justify using perfect-gas law as the appropriate equation of state. At steady-state the gas is stratified with a hydrostatic equilibrium in the vertical direction and a pressure-modified centrifugal equilibrium in the radial direction.
As commonly done in the modeling of circumstellar disk observations, the surface density and temperature of the gas were assumed to decrease as simple power-laws of the distance to the star as r − p and r − q. The disk self-gravity was neglected and we focused on optically thick regions of the nebula where the coupling of the gas with the magnetic field is negligible due to weak ionization. The problem was addressed by numerically solving the full set of the 3D compressible hydrodynamical equations in cylindrical coordinates.
2.2. Governing equations
The standard equations for an inviscid gas flowing around a central gravitational potential reads 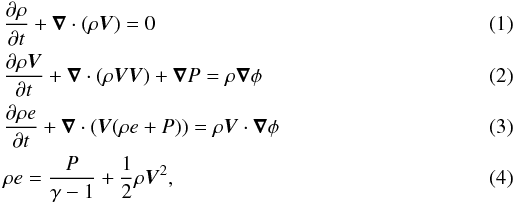 where ρ and P are the density and pressure of the gas, and u, v and w are the radial, azimuthal, and vertical components of the gas velocity ; ρe denotes the total specific energy of the gas with adiabatic index γ = 1.4 and φ = GM ⋆ /(r2 + z2)1/2 is the gravitational potential. Because no heat transfer was assumed in the disk, the energy equation is equivalent to the isentropic relation
where ρ and P are the density and pressure of the gas, and u, v and w are the radial, azimuthal, and vertical components of the gas velocity ; ρe denotes the total specific energy of the gas with adiabatic index γ = 1.4 and φ = GM ⋆ /(r2 + z2)1/2 is the gravitational potential. Because no heat transfer was assumed in the disk, the energy equation is equivalent to the isentropic relation 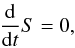 (5)where S = ln(P/ργ) is the entropy and d/dt = ∂/∂t + V·∇ is the Lagrangian derivative.
(5)where S = ln(P/ργ) is the entropy and d/dt = ∂/∂t + V·∇ is the Lagrangian derivative.
The equations were used in non-dimensional form thanks to the following normalization: 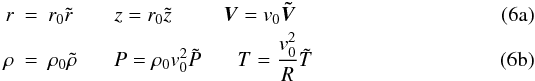 where the 0 index refers to their values at r0 from the star in the midplane:
where the 0 index refers to their values at r0 from the star in the midplane: 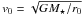 , ρ0 = ρ(r0,z = 0). In the following, the tilde over the dimensionless variables is dropped. With these new variables, Eqs. (1)–(4)are unchanged except for the gravitational potential, which reads φ = 1/(r2 + z2)1/2. The important parameter is then the Mach number
, ρ0 = ρ(r0,z = 0). In the following, the tilde over the dimensionless variables is dropped. With these new variables, Eqs. (1)–(4)are unchanged except for the gravitational potential, which reads φ = 1/(r2 + z2)1/2. The important parameter is then the Mach number 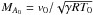 , where T0 is the temperature computed at r0 from the star.
, where T0 is the temperature computed at r0 from the star.
2.3. Stable equilibrium of the disk
In the absence of perturbation, the gas is in a steady-state equilibrium, flowing nearly at the Keplerian velocity around the star. The vertical and centrifugal equilibrium equations for the axisymmetric steady-state are 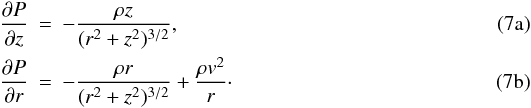 If we assume that the temperature does not depend on the height z, we can write TD as
If we assume that the temperature does not depend on the height z, we can write TD as 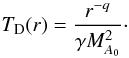 (8)From Eq. (7a) and
(8)From Eq. (7a) and 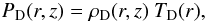 (9)we then easily find the density
(9)we then easily find the density 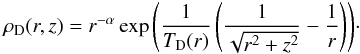 (10)Integrated over the disk thickness, Eq. (10)produces the surface density
(10)Integrated over the disk thickness, Eq. (10)produces the surface density 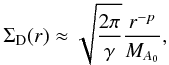 (11)provided that α = p + (3 − q)/2. The pressure height is given by
(11)provided that α = p + (3 − q)/2. The pressure height is given by 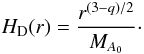 (12)The azimuthal velocity deduced from the radial centrifugal equilibrium is
(12)The azimuthal velocity deduced from the radial centrifugal equilibrium is 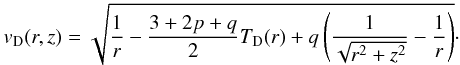 (13)This equilibrium solution only depends on three parameters: the indices p and q, and the Mach number MA0. Note in particular that the disk structure does not depend on its mass. Except for the comparison with Lin’s results, we took q = 0.5, p = 1.5, and MA0 = 25 throughout. This value of the Mach number is obtained for r0 = 1 AU, T0 = 280 K, and M ⋆ = 1 M⊙.
(13)This equilibrium solution only depends on three parameters: the indices p and q, and the Mach number MA0. Note in particular that the disk structure does not depend on its mass. Except for the comparison with Lin’s results, we took q = 0.5, p = 1.5, and MA0 = 25 throughout. This value of the Mach number is obtained for r0 = 1 AU, T0 = 280 K, and M ⋆ = 1 M⊙.
2.4. Unstable equilibrium state
The above solution is linearly stable. To render the solution unstable with respect to the Rossby wave instability, we chose to add an annular bump in the density and pressure fields while keeping the temperature profile unchanged,  with
with 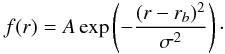 (15)The velocity field is then obtained from Eq. (7b). In a protoplanetary disk, this density bump may be caused, for example, by an axisymmetrical accumulation of gas at the edge of the dead zone. The Rossby wave instability is characterized in 2D by the function ℒ defined by
(15)The velocity field is then obtained from Eq. (7b). In a protoplanetary disk, this density bump may be caused, for example, by an axisymmetrical accumulation of gas at the edge of the dead zone. The Rossby wave instability is characterized in 2D by the function ℒ defined by 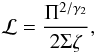 (16)where γ2 is the adiabatic index, and Π and ζ are the vertically integrated pressure and total axial vorticity. Following Lin (2013), we assumed the relation γ2 = (3γ − 1)/(γ + 1) ≈ 1.33 obtained by Goldreich et al. (1986).
(16)where γ2 is the adiabatic index, and Π and ζ are the vertically integrated pressure and total axial vorticity. Following Lin (2013), we assumed the relation γ2 = (3γ − 1)/(γ + 1) ≈ 1.33 obtained by Goldreich et al. (1986).
 |
Fig. 1 Radial dependance of the function ℒ (top) and the function |
As shown by Lovelace et al. (1999), the function ℒ must exhibit a local maximum for instability. The centrifugal instability is characterized by the function 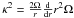 , which becomes negative in the presence of centrifugal instability. The function κ2 weakly depends on z. In the following, we consider the value in the midplane (z = 0), where the absolute value of κ2 is maximum, and denote this value by
, which becomes negative in the presence of centrifugal instability. The function κ2 weakly depends on z. In the following, we consider the value in the midplane (z = 0), where the absolute value of κ2 is maximum, and denote this value by 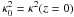 . For A = 0.2, rb = 7.5 and σ = 0.3, we obtain the typical plots shown in Fig. 1 for the functions ℒ and
. For A = 0.2, rb = 7.5 and σ = 0.3, we obtain the typical plots shown in Fig. 1 for the functions ℒ and 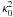 . The function ℒ does exhibit a local maximum, while
. The function ℒ does exhibit a local maximum, while 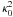 remains positive. For higher values of A,
remains positive. For higher values of A, 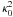 can become negative, which implies centrifugal instability. For σ = 0.3, rb = 7.5, the threshold for centrifugal instability is Ac = 0.334. Except in Sect. 4, A was chosen to be sufficiently small to remain in the centrifugally stable regime.
can become negative, which implies centrifugal instability. For σ = 0.3, rb = 7.5, the threshold for centrifugal instability is Ac = 0.334. Except in Sect. 4, A was chosen to be sufficiently small to remain in the centrifugally stable regime.
The disk is stably stratified. The stratification is characterized by the Brunt-Väisälä frequency, 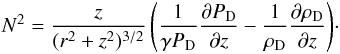 (17)In our case, both the stable and unstable equilibrium states have a Brunt-Väisälä frequency given by
(17)In our case, both the stable and unstable equilibrium states have a Brunt-Väisälä frequency given by 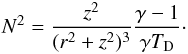 (18)This function vanishes in the equatorial plane, and increases with height until it reaches a maximum at
(18)This function vanishes in the equatorial plane, and increases with height until it reaches a maximum at 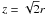 .
.
2.5. Numerical method and validation
The system of non-linear equations was solved using the finite-volume method. We used a second-order finite-volume scheme, the MUSCL Hancock scheme, and an exact Riemann solver. The present 3D version of the code was issued from a 2D version described in a previous paper (Inaba et al. 2005), which was recently improved with a well-balanced numerical scheme that enables one to preserve the stationary solution over very many rotation periods. This scheme was developed in 2D by C. Surville (unpublished report) and is implemented in the 3D version of the code used here.
The computational domain for our simulations was defined as 5 < r < 10, 0 < θ < 2π and 0 < z < 1 (equivalent to 2.4 scale heights for a ring centered at r = 7.5). The mesh was a regular one with 200 cells in the radial direction, 300 in the azimuthal direction and 100 in the vertical direction which, per scale height, corresponds to 20 cells in the radial direction, 3 cells in the azimuthal direction and 50 in the vertical direction (priority was given to the z direction for studying the vertical effects). The boundary conditions were imposed using two ghost cells at each boundary. In the azimuthal direction periodic conditions were used to be consistent with a global disk geometry. In the radial direction steady-state values were imposed on the ghost cells to connect the computational domain with the rest of the disk; these conditions are relatively permeable to perturbations of the steady-state and avoid spurious wave reflexions. In the vertical direction, boundary conditions were symmetric at level z = 0 and extrapolated at z = 1, imposing zero vertical derivatives for the relative velocity and for the density and pressure ratios: 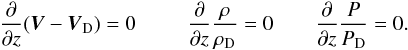 (19)Other boundary condition were also tested, but turned out to be less efficient because of stronger residual perturbations.
(19)Other boundary condition were also tested, but turned out to be less efficient because of stronger residual perturbations.
To test the stability of the code we first performed a number of long-term simulations starting from the stable stationary solution presented above. We found that after a hundred rotations, deviations from the initial solution are very weak and have no systematic trends: the radial and vertical velocities are lower than 10-12, the relative error on the density is smaller than 10-9. Therefore we are confident that our code can preserve the unperturbed steady-state solution even on the long runs made here.
We also tried to reproduce one of the linear stability results obtained by Lin (2013).
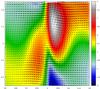 |
Fig. 2 Density contour and velocity field in the midplane (r, θ) for the most unstable mode m = 4 and for the parameters of Lin (2013)q = 0, p = 1.5, MA0 = 23.15, A = 0.25, and σ = 0.53. |
The parameters used by Lin (2013), Sect. 6.3 give in our notation q = 0, p = 1.5, α = 3, MA0 = 23.15, and a Gaussian bump with A = 0.25 and σ = 0.53. Analyzing the time evolution of very weak perturbations, we were able to compute the linear growth rate of each azimuthal mode. We found that the most amplified mode is for m = 4 with a growth rate ωi ≈ 0.190, which is close to the value ωi ≈ 0.1937 obtained by Lin. In Fig. 2, we display the density field (colors) and the velocity field in the midplane (arrows) of the m = 4 mode during the linear phase. When we compare this figure with the Fig. 18 (top) of Lin (2013), we see that the perturbation fields are very similar. This confirms the good agreement between the two results and also validates our numerical code.
3. Formation and structure of Rossby vortices
In this section, we compute the non-linear evolution of the disk that results from introducing a small-amplitude white noise on the first five modes for the parameters given in Sect. 2.4. We monitored density, pressure, and velocity fields of the disk by considering relative quantities with respect to the stable equilibrium state.
 |
Fig. 3 Evolution of the density (ρ − ρD) in a Rossby-unstable inviscid disk. Top: evolution in the r − θ plane (z = 0); bottom: evolution in a 3D perspective (visualisations performed with glnemo2). From left to right, density values are plotted at initial time and after 20, 40, and 530 rotations. |
The 3D evolution of the density (ρ − ρD) is presented in Fig. 3. First, the instability grows linearly way and the annular overdensity fragments in a chain of vortices coupled to spiral waves that propagate on each side of the initial ring. After the instability saturates, vortices tend to catch one another and successively merge into increasingly larger structures. After a few hundred rotations, a single vortex remains in the computational domain. This vortex persists for a long time (more than 600 rotations), slowly drifting toward the star. A slight decay is observed that corresponds to the unavoidable numerical diffusion. We now detail the different steps of this evolution.
3.1. Growth and merging
The first step in the development of the Rossby wave instability is a linear growth phase. The growth rate of the different instability modes is plotted in Fig. 4. From this figure, we expect all the modes with 2 ≤ m ≤ 12 to possibly grow during the linear phase. Mode m = 6 is expected to be the most unstable mode. In the simulation, where white noise was added to the first five modes, the growth of the modes m = 2,3,4, and 5 follows the linear prediction (see Fig. 5). Mode m = 1, which is linearly stable, starts to grow when the amplitude of the other modes has reached a sufficiently large amplitude. During the linear growth phase, the axial vorticity exhibits the form of a tilted structure, as observed in Fig. 6 (top). This agrees with the structure of the most unstable linear mode described by Lin (2013).
We point out that the vertical shear of the background flow cannot be the cause of the observed tilt. Indeed, tilted vorticity columns are also found in simulations with q = 0, that is, without any vertical shear, and in the linear calculations performed by Lin (2013). No significant differences have been observed between simulations with vertical shear (q ≠ 0) and simulations without vertical shear (q = 0).
Finally, after 22 rotations when the instability has saturated, the tilt has almost completely disappeared (Fig. 6 bottom). This non-linear phenomenon is not observed in the linear framework of Lin (2013). Then the vortices evolve in the form of straight columns.
 |
Fig. 4 Growth rate of the most unstable mode versus the azimuthal wavenumber m. |
 |
Fig. 5 Time evolution of the amplitude of modes 1 to 5 during the first 20 rotations. |
 |
Fig. 6 Vertical component of the vorticity in the (θ,z) plane after 11 rotations (top) and 22 rotations (bottom). |
The vortices are strongly deformed by the background shear. In the (θ,r) plane, the axial vorticity contours take the form of elongated ellipses with an aspect of order 7. As soon as the vortices are formed, they start to interact with each other. A first merging of two pairs of vortices is observed at 45 rotations, then a second merging process occurs at 65 rotations, before the last merging of the two remaining vortices after 500 rotations.
The Rossby number and the aspect ratio of the largest observed vortex were monitored during this evolution and are reported in Fig. 7. The Rossby number is defined by 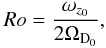 (20)where ωz0 = ωz(0) is the relative axial vorticity of the vortex in the midplane (i.e., the total vorticity in the midplane after removing of the background vorticity), and ΩD0 the background angular velocity in the midplane at the vortex center.
(20)where ωz0 = ωz(0) is the relative axial vorticity of the vortex in the midplane (i.e., the total vorticity in the midplane after removing of the background vorticity), and ΩD0 the background angular velocity in the midplane at the vortex center.
 |
Fig. 7 Time evolution of the main characteristics of the largest observed vortex. Top: Rossby number of the vortex as defined in (20); bottom: aspect ratio measured from the axial vorticity contours (solid line) and obtained from formula (21) (dashed line). |
Despite the difficulty fo defining an aspect ratio during the merging processes, we observe that the aspect ratio tends to increase. After the last merging process, the final vortex has an aspect ratio of close to 10. This evolution of the aspect ratio agrees with the evolution of the norm of the axial vorticity maximum, which tends to decrease. For a vortex with uniform vorticity (Kida 1981; Chavanis 2000), aspect ratio and vorticity are linked by the relation 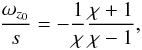 (21)where s = −rb∂rΩ(rb) is the local shear rate in the midplane at the position of the vortex. We observe that this formula provides a good estimate of the aspect ratio of our non-uniform vortices if we take the maximum vorticity for ωz0 in Eq. (21). Note that the resulting vortices always have an aspect ratio higher than or equal to 7. This property can explain their 3D stability, as shown below.
(21)where s = −rb∂rΩ(rb) is the local shear rate in the midplane at the position of the vortex. We observe that this formula provides a good estimate of the aspect ratio of our non-uniform vortices if we take the maximum vorticity for ωz0 in Eq. (21). Note that the resulting vortices always have an aspect ratio higher than or equal to 7. This property can explain their 3D stability, as shown below.
Barranco & Marcus (2005) found that synthetic vortices are unstable under anti-symmetric perturbations. To examine this point a global simulation was performed without imposing the symmetry in the midplane. We obtained similar results. In particular, we did not observe the growth of any anti-symmetric perturbation.
3.2. Structure of the vortices
After the last merging process a single vortex remains in the simulated region of the disk. This vortex is isolated, with no observed residual of the initial density bump, and can be characterized by a Rossby number Ro ≃ − 0.12 . It is advected by the background flow and is found to form a quasi-steady solution of Eqs. (1)–(4) in the rotating frame. The characteristics of this final vortex are given in Fig. 8 after 530 rotations. The first five plots in the left column provide the relative fields (where the stable equilibrium state has been removed) of density, pressure, axial vorticity, and the radial and azimuthal velocity of the vortex in the equatorial plane. They are typical of an anti-cyclonic motion around a pressure and density bump. These plots are very similar to that obtained with 2D simulations starting from identical initial conditions. The axial dependence is shown in the right column of Fig. 8. We observe that axial vorticity, and the radial and azimuthal velocity have a columnar structure in the whole thickness of the disk. The vorticity defects observed at the disk edge (z = 1) are weak imperfections due to the use of not purely transparent boundary conditions. Inside the vortex, the pressure and density fields are found to have a Gaussian profile like the background-disk state.
 |
Fig. 8 Structure of a 3D Rossby vortex. From top to bottom the various rows show the fields (where the stable equilibrium state has been removed) of density, pressure, axial vorticity, radial velocity, azimuthal velocity, and vertical velocity. The left column shows these values in the r − θ plane at z = 0 except for the vertical velocity (last row), which is at z = 0.5. The right column shows the vertical profiles of the same values in the r − z plane at θ = 2.67; radial velocity (fourth row) and vertical velocity (last row) are plotted in the θ − z plane at r = 8. |
In the equatorial plane, the axial velocity is null by symmetry. It is non-zero outside this plane but, takes values one order of magnitude lower than the other velocity components. In particular, the highest Mach number of the vertical motions is lower than 0.02. This field is characterized in two perpendicular planes in the last row of Fig. 8. We observe higher values close to the vortex center, but the field is not as well localized. The highest axial velocity is so weak that we can even observe the trace of gravity waves in the axial flow contours. These waves result from the stratification of the disk. Note, however, that the axial velocity field has a structure that resembles the radial velocity field. Therefore, the axial flow structure is most likely caused by a slight tilt of the vortex axis.
In conclusion, this 3D evolution of the Rossby wave instability is very similar to the 2D evolution. The 3D effects are weak perturbations that mostly result from the initial 3D structure of the background disk. A slight vortex tilting, which is characteristic of the linear RWI in a non-homentropic disk (Lin 2013), seems to survive in the non-linear regime.
Méheut et al. (2010, 2012a) have also performed 3D simulations of the Rossby wave instability, but they have obtained a different evolution. They observed a strong axial recirculation inside the vortices. Although Méheut et al. (2010, 2012a) considered a different framework (homentropic flow, whereas we consider adiabatic flow), we assume that the different evolution mainly comes from the different nature of the instability. In their case, the density bump is so large that it induces a change of sign of κ2. Then, the disk also becomes unstable with respect to the centrifugal instability. This instability induces strong axial recirculation. The formation of the Rossby vortices has probably been modified by this instability, and the axial flow observed in their simulation is the trace of the centrifugal instability. Méheut et al. (2012b) have also considered a case where κ2 remains positive, so that the centrifugal instability is absent. In that case, they observed that the RWI remains mainly 2D and that the axial flow in the vortices is low. However, they obtained a different axial flow structure, which is probably related to their isothermal hypothesis.
4. Stability and long-term evolution
In the above section we have found that the RWI produces columnar vortices that can persist over many rotation periods. This implicitly means that the vortices are stable.
This evolution is different from the evolution described by Barranco & Marcus (2005). In the local shearing box approximation, they observed that columnar vortices are rapidly destroyed and tend to reorganize in a layer of off-midplane vortices. It is not clear what causes this instability. We assume that it might be caused by elliptical instability that affects strained vortices in the stratified and unstratified medium (Lesur & Papaloizou 2009). In the following section, we show that this instability can indeed destroy vortices within our framework.
4.1. Elliptical instability
The elliptical instability has been studied in the context of vortices in accretion disks by Lesur & Papaloizou (2009). They obtained with a local stability approach a condition for the instability of Kida-like vortices that depends on the horizontal aspect ratio of the vortices χ and on the stratification strength N/s of the flow.
In this section, we analyze the conditions under which the instability develops and discuss why the elliptical instability was not observed in the simulation presented in the previous section.
The high resolution required for the simulations was achieved by reducing the computational domain to a periodic box in the azimuthal direction; this is a simple way to avoid prohibitive increases of the CPU time. The box size was (6 < r < 9, 0 < θ < 2π/10, 0 < z < 1), and we used a resolution of 200 × 100 × 100 in the r, θ, and z directions (that is 33 × 10 × 50 in number of cells per scale height).
We considered two different cases: (i) disks without vertical stratification; and (ii) disks with the same stratification as in Sect. 3. For each case, different values of the aspect ratio were tested. The aspect ratio was varied by changing the amplitude A of the annular density bump used to trigger the RWI. From the expression of the velocity field given in Sect. 2.4, we can obtain an estimate of the maximum vorticity in the annular bump, and thus of the resulting vortex formed by the RWI, 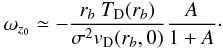 (22)The aspect ratio χ obtained from this formula and Eq. (21) is plotted in Fig. 9. As observed in Fig. 7, this theoretical prediction provides a good approximation of the measured aspect ratio in the centrifugally stable regime.
(22)The aspect ratio χ obtained from this formula and Eq. (21) is plotted in Fig. 9. As observed in Fig. 7, this theoretical prediction provides a good approximation of the measured aspect ratio in the centrifugally stable regime.
Strong bump amplitudes A are expected to produce vortices with a low aspect ratio, but they also imply negative values of 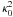 . For this reason, low aspect ratio vortices are difficult to create. As soon as A > Ac, where Ac ≈ 0.334 for the parameters of the simulation, the centrifugal instability is active during the primary evolution of the bump. The Rossby wave instability is modified in such a way that no columnar vortices are formed if the dynamics is not restricted to 2D. Three values of A were considered in our study: 1.5, 0.3, and 0.2, corresponding to the aspect ratios 2.5, 5, and 7. For A = 1.5 we obtained
. For this reason, low aspect ratio vortices are difficult to create. As soon as A > Ac, where Ac ≈ 0.334 for the parameters of the simulation, the centrifugal instability is active during the primary evolution of the bump. The Rossby wave instability is modified in such a way that no columnar vortices are formed if the dynamics is not restricted to 2D. Three values of A were considered in our study: 1.5, 0.3, and 0.2, corresponding to the aspect ratios 2.5, 5, and 7. For A = 1.5 we obtained 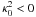 near the center of the bump. The stratification effect of the low aspect ratio vortex that correspond to this value of A is analyzed by a specific procedure.
near the center of the bump. The stratification effect of the low aspect ratio vortex that correspond to this value of A is analyzed by a specific procedure.
4.1.1. Unstratified disks
A disk without vertical stratification is obtained by replacing the gravitational potential 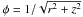 in Eqs. (1)–(4) by φ = 1/r. With this potential, the characteristics of the steady disk become independent of z. In two dimensions, the Rossby wave instability is also active and gives rise to the formation of quasi-steady 2D Rossby vortices.
in Eqs. (1)–(4) by φ = 1/r. With this potential, the characteristics of the steady disk become independent of z. In two dimensions, the Rossby wave instability is also active and gives rise to the formation of quasi-steady 2D Rossby vortices.
In the simulated azimuthal sector, a single 2D vortex is formed. Its 3D evolution is analyzed by considering this vortex in a 3D environment, with periodic boundary conditions in the vertical direction. Because the vortices are formed in 2D, the centrifugal instability is filtered out. The centrifugal instability, which is characterized by the formation of axisymmetric rolls, is indeed inhibited when no axial displacement is allowed (see for instance Drazin & Reid 1981). Even for A = 1.5, for which 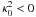 , a nice 2D vortex is obtained with an aspect ratio of 2.5, as predicted from the theory. As shown by LP09, the vortex aspect ratio is an important parameter for the stability. Figure 10 shows that different evolutions are observed for low and high aspect ratios. For low χ, we observed the rapid growth of a 3D instability and the destruction of the vortex in a few orbital periods. A typical evolution for χ = 2.5 is illustrated in Fig. 11. This evolution is very similar to the 3D evolution shown in LP09. For χ > 4, no instability growth was observed: the vortex retains its columnar structure throughout the simulation. For example, for χ = 7, we found that the vortex persists for at least 200 rotations without being affected by any instability. These stable evolutions are consistent with LP09 for 4 < χ < 6, but not for higher χ. LP09 predicted a destabilization of the vortex for χ > 6 with a low growth rate around 10-2 the shear rate s. We have not seen such an instability. But one has to keep in mind that the theoretical predictions by LP09 are local and inviscid. Both the non-uniform character of the vortex and the numerical diffusion are expected to affect the instability growth rate. We verified that our results remained unchanged when the resolution was increased by a factor 2 in each direction.
, a nice 2D vortex is obtained with an aspect ratio of 2.5, as predicted from the theory. As shown by LP09, the vortex aspect ratio is an important parameter for the stability. Figure 10 shows that different evolutions are observed for low and high aspect ratios. For low χ, we observed the rapid growth of a 3D instability and the destruction of the vortex in a few orbital periods. A typical evolution for χ = 2.5 is illustrated in Fig. 11. This evolution is very similar to the 3D evolution shown in LP09. For χ > 4, no instability growth was observed: the vortex retains its columnar structure throughout the simulation. For example, for χ = 7, we found that the vortex persists for at least 200 rotations without being affected by any instability. These stable evolutions are consistent with LP09 for 4 < χ < 6, but not for higher χ. LP09 predicted a destabilization of the vortex for χ > 6 with a low growth rate around 10-2 the shear rate s. We have not seen such an instability. But one has to keep in mind that the theoretical predictions by LP09 are local and inviscid. Both the non-uniform character of the vortex and the numerical diffusion are expected to affect the instability growth rate. We verified that our results remained unchanged when the resolution was increased by a factor 2 in each direction.
 |
Fig. 9 Theoretical prediction of the aspect ratio of the formed vortex as a function of the initial amplitude of the bump (σ = 0.3, rb = 7.5, p = 1.5, q = 0.5, MA0 = 25). For these parameters, the basic flow is centrifugally unstable for A > 0.334. |
 |
Fig. 10 Time evolution of |
 |
Fig. 11 Evolution of a vortex of aspect ratio χ = 2.5 in an unstratified disk; from left to right: at initial time and after 2, 2.5, and 4 rotations. Top: vorticity in the θ–z plane at the center of the vortex. Bottom: vorticity in the r–θ plane at level z = 0.5. |
 |
Fig. 12 Stratification in the disk. The color map represents the iso-contours of N/s in an angular sector going through the center of a vortex. The lines are the values obtained from Eq. (23) without vortices. |
4.1.2. Stratified disks
Lesur & Papaloizou (2009) have shown that vertical stratification affects the development of the elliptical instability. They have considered a uniformly stratified environment with a constant Brunt-Väisälä frequency N for two values of the parameter N/s (N/s = 0.1 and N/s = 1). They have shown that in the regime of a low aspect ratio χ < 4, the local growth rate of the elliptical instability is not modified by the stratification. For χ > 6, the instability is still present, but with a smaller growth rate. For intermediate aspect ratios 4 < χ < 6, they interestingly found a destabilization for N/s = 1.
Here, the background disk is non-uniformly stratified with a parameter N/s given by 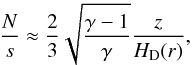 (23)where the pressure scale height HD(r) has been defined in Eq. (12). The parameter N/s therefore depends on the position. Figure 12 shows the contours of N/s in the presence of the vortices (along a cut crossing the vortex). The lines are the contours obtained from Eq. (23). This figure demonstrates that the vortices do not significantly modify the stratification and that N/s is thus well predicted by Eq. (23). This formula shows that N/s vanishes in the midplane, but increases linearly with the vertical position in the disk. It is important to note that N/s varies from 0 to 0.8 between the midplane and the disk edge at the location of the vortex. We can therefore expect the top of the vortex to be affected by the stratification.
(23)where the pressure scale height HD(r) has been defined in Eq. (12). The parameter N/s therefore depends on the position. Figure 12 shows the contours of N/s in the presence of the vortices (along a cut crossing the vortex). The lines are the contours obtained from Eq. (23). This figure demonstrates that the vortices do not significantly modify the stratification and that N/s is thus well predicted by Eq. (23). This formula shows that N/s vanishes in the midplane, but increases linearly with the vertical position in the disk. It is important to note that N/s varies from 0 to 0.8 between the midplane and the disk edge at the location of the vortex. We can therefore expect the top of the vortex to be affected by the stratification.
As above, we considered the evolution of bumps of three different amplitudes A = 1.5, A = 0.3, and A = 0.2. For the weak-amplitude cases (A = 0.3 and A = 0.2), we observed the rapid formation of a columnar vortex by the RWI in a few rotations.
The amplitude A = 0.3 gives rise to a vortex of aspect ratio χ = 5, as expected. In this case, eventually, the higher part of the vortex (z > 0.7) is destabilized and progressively disappears (see Fig. 13). This occurs on a longer timescale than the rapid evolution observed in the unstratified case for χ = 2.5. After 60 rotations, a stable but shorter vortex is obtained.
 |
Fig. 13 Vorticity in the θ − z plane at the center of the vortex after 6 rotations, 15 rotations, 30 rotations, and 65 rotations. |
This evolution is consistent with the theoretical prediction of LP09 for the elliptical instability. In the weakly stratified region close to the midplane, the elliptical instability is not active for χ = 5. By contrast, at the top, where N/s exceeds 0.5, the instability is probably present and responsible for the destruction of the higher part of the vortex. Interestingly, we observe that the vortex apparently retains its shape in the region where the elliptical instability is not active.
For the vortex of aspect ratio χ = 7 obtained with A = 0.2, we observed no destabilization. This is consistent with the results obtained in the unstratified case. High aspect ratio vortices are indeed expected to be more stable in the presence of stratification. As they were found stable in the unstratified case, the observed stable behavior in the stratified disk is not surprising. This stable behavior also explains why the elliptical instability was not observed in the simulation of the full disk. During the disk evolution, we notice indeed that the aspect ratio of the vortices remains higher than or equal to 7. The vortices are therefore always stable with respect to the elliptical instability and retain their essentially 2D structure throughout the simulation.
For A = 1.5, the bump evolves in such a way that the vortices are destroyed during their formation. The vortex of aspect ratio 2.5 that was obtained in the unstratified 2D environment is not created in a stratified 3D disk. We assume that the reason is the presence of the centrifugal instability, which affects the vortex formation. Note also that the elliptic instability mechanism in low aspect ratio vortices is related to the centrifugal instability mechanism (LP09, Lyra 2013). Consequently, it is very difficult to determine whether the elliptic instability becomes active in this case.
To study the effect of the stratification on the dynamics of low aspect ratio vortices, we therefore used a different approach and considered isothermal disks with a uniform stratification along the height. For such a disk, a 2D simulation of a bump of amplitude A = 1.5 is always possible and leads to the formation of vortices of aspect ratio 2.5, as before. These vortices can then be analyzed in a 3D environment with or without stratification. We considered two cases, N/s = 0 and N/s = 0.5. Figure 14 shows the growth rate of 3D perturbations during the first instants as a function of the vertical wavelength kz in both cases. The growth rate here is normalized by the background angular velocity ΩD(rb) at the position of the vortex. We see that the growth rate curves are almost the same in both cases, which demonstrates that the stratification effect on the stability characteristics of these vortices is very weak. This observation agrees with the results of LP09 who predicted no stratification effect when χ < 4. The maximum growth rate also agrees with the value of 0.89 derived by LP09 for a Kida vortex of aspect ratio 2.5. We also examined the non-linear evolution of the perturbation and observed that the vortex is rapidly destroyed in a way very similar to the case documented above in Fig. 11.
 |
Fig. 14 Growth rate normalized by the local background angular velocity of 3D perturbations in a vortex with an aspect ratio of 2.5 in an isothermal stratified disk for N/s = 0 and N/s = 0.5. |
We have mentioned the different evolution of the columnar vortices described in Barranco & Marcus (2005). In their simulation, the columnar vortex has a low aspect ratio χ = 4. In light of the above results, it is not surprising to observe the destabilization of the vortex because the elliptical instability is indeed active probably up to the midplane for such a low aspect ratio.
4.2. Migration of 3D vortices
2D simulations show that vortices tend to migrate in Keplerian flows Li et al. (2000). This migration process is due to the compression of the flow around the vortex and to the asymmetries in the position of the sonic lines and the associated density waves (Paardekooper et al. 2010). It also depends on the size of the vortex, on its aspect ratio and on the radial stratification of the disk (e.g., Surville & Barge 2012, 2013). Basically, it is observed that the higher the aspect ratio, the weaker the migration. In this section, we present the first numerical study of the migration of 3D vortices. Our study focuses on vortices with high aspect ratios, first because we know from the previous section that vortices with χ > 6 are stable against the elliptical instability, but also because these vortices should migrate slowly due to their strong similarities with 2D vortices.
Studying the migration of 3D vortices requires time-consuming long-term simulations. accordingly, as for the elliptical instability simulations, we simulated an azimuthal sector of the disk only. A single vortex was formed from the RWI in a few rotations in the computational domain. The dimension of the box was set up by the size and the aspect ratio of the vortex to be simulated. In practice we used a box size of (5 < r < 10, 0 < θ < π/2, 0 < z < 1) with a numerical resolution of 200 × 100 × 100 (or 33 × 4 × 50 in number of cells per scale height). As for the elliptical instability, we changed the aspect ratio of the vortex by changing the amplitude of the initial density bump. We fixed σ = 0.3 and took the values A = 0.2, A = 0.15, and A = 0.1 to obtain vortices with an aspect ratio χ = 7, χ = 8.5, and χ = 14.
The first steps of the evolutions are similar to what we described above. The RWI developed and after around 35 rotations, we obtained a single vortex in the computational domain that started to migrate toward the star. Paardekooper et al. (2010) have noted that migration can stop close to a bump of the surface density, which has been interpreted by Méheut et al. (2012a) as the reason why they did not observe migration. In our simulations, the initial density bump completely disappeared, when the vortices were formed. It therefore cannot disturb the vortex migration.
The vortex survived more than 150 rotations and its structures were quasi-steady with only a weak time-evolution associated with the numerical diffusion. Figure 15 shows the radial position of each vortex as a function of time and for different aspect ratios. The migration rate over one rotation period was 1.5 × 10-3 AU for χ = 7, 9.3 × 10-4 AU for χ = 8.5, and 1.3 × 10-4 AU for χ = 14. In non-dimensional values, the migration speed is vm = 3.1 × 10-5r0Ω0, vm = 2 × 10-5r0Ω0, and vm = 3 × 10-6r0Ω0.
These values for the migration rate are of the same order of magnitude as in the 2D case (Paardekooper et al. 2010; Surville & Barge 2012, 2013). This result is consistent with the structure of the vortices, which remained columnar and quasi-2D. In particular, migration seems to be independent of the disk thickness and no systematic deformation of the vertical vortex structure was observed in the radial direction. Of course we do not exclude that vortices with a different structure than ours may migrate in a different way.
 |
Fig. 15 Radial position of the vortex as a function of time |
5. Conclusion
Using fully compressible non-linear simulations in non-homentropic disks, we have found that the RWI can grow in 3D in nearly the same way as in 2D. Columnar vortices can be formed in a few rotations and merge until a single vortex remains in the disk. This vortex survives many rotation periods and slightly drifts toward the star. Both the structure and the dynamics of the vortices were found to be mainly 2D. A small tilt of the vortex axis has nevertheless been observed.
We showed that the linear phase of the RWI agrees with the results by Lin (2013) both for the growth rate and the structure of the unstable mode. This result contrasts with the simulations by Méheut et al. (2010, 2012a), which showed the formation of vortices with a strongly z-dependent structure. This difference is probably mainly associated with the simultaneous presence of the centrifugal instability in their simulations. In the centrifugally unstable case we simulated (for A = 1.5), the vortices were found to be destroyed during their formation.
The stability of the quasi-2D vortices with respect to the elliptical instability was explained by the high aspect ratio χ of the vortices. Using specific simulations, we showed that vortices with χ > 6 are stable with respect to the elliptic instability in both a stratified disk and an unstratified disk. For intermediate values of χ (4 < χ < 6), we observed that the vortices survive close to the midplane, but are destroyed farther away, at altitudes where the stratification is significant. We showed that this evolution is consistent with the theoretical results by Lesur & Papaloizou (2009) on the stratification effect on the elliptical instability. For a low aspect ratio χ < 4, the vortices were shown to be strongly unstable. They are rapidly destroyed in unstratified disks and isothermal stratified disks. These results can perhaps explain the rapid destruction of the columnar vortex of aspect ratio 4 simulated by Barranco & Marcus (2005). Here, we argued that the destruction of 2D vortices cannot be systematic and that the vortices probably remain columnar for a long time when their aspect ratio is sufficiently high, that is, when they are sufficiently weak.
The migration process of these quasi-2D vortices was studied as well. We showed that the drift velocity decreases with the aspect ratio, as previously observed in 2D.
In actual protoplanetary disks, the initial overdensities necessary to trigger the RWI may be caused by an axisymmetrical accumulation of gas at the edge of the dead zone. As the density would increase gradually under the turbulent transport outside of the dead zone, we would expect the RWI to occur close to its critical stability condition, that is, for a low density bump amplitude. The vortices formed by the instability would therefore be weak and have a high aspect ratio. They would then be stable with respect to the elliptic instability and have a low migration speed. This means that these vortices would survive a sufficiently long time far away from the star to be able to capture
and confine large amounts of solid particles. These weak vortices would therefore be good sites for the formation of planetesimals or planetary cores.
The recent discovery of an asymmetry in the dust distribution in the disk of Oph IRS 48 by ALMA reported by van der Marel et al. (2013) and Armitage (2013) has been interpretred as an assembly of particles captured by a large-scale Rossby vortex. According to the authors, this vortex has formed by an RWI occurring at the edge of the gap opened by a massive planet orbiting in the inner part of the disk. These observations indeed seem to confirm the efficiency of the capture in vortex mechanism pointed out by Barge & Sommeria (1995) and open up the possibility to derive other observational constraints.
Acknowledgments
We thank the anonymous referee for his useful comments. Computations were performed on a Bull multicore machine funded by the Aix-Marseille University and the Laboratoire d’Astrophysique de Marseille; the most demanding computations were performed on CURIE at TGCC (contract gen6832 2012/2013). This project was also supported by the French “Programme National de Planétologie” (PNP2012). This work has received support from the French National Research Agency under the A*MIDEX grant ANR-11-IDEX-0001-02, and is part of the LABEX MEC project ANR-11-LABX-0092. 3D visualisations were performed with glnemo2 developped at CeSAM – http://projets.lam.fr/projects/glnemo2.
References
- Armitage, P. J. 2013, Science, 340, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
- Barranco, J. A., & Marcus, P. S. 2005, ApJ, 623, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Bayly, B. J. 1986, Phys. Rev. Lett., 57, 2160 [NASA ADS] [CrossRef] [Google Scholar]
- Bracco, A., Chavanis, P. H., Provenzale, A., & Spiegel, E. A. 1999, Phys. Fluids, 11, 2280 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P. H. 2000, A&A, 356, 1089 [NASA ADS] [Google Scholar]
- de Val-Borro, D., Edgar, R., Artymowicz, P., et al. 2006, MNRAS, 370, 529 [NASA ADS] [CrossRef] [Google Scholar]
- de Val-Borro, M., Artymowicz, P., D’Angelo, G., & Peplinski, A. 2007, A&A, 471, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drazin, P. G., & Reid, W. H. 1981, Hydrodynamic stability (Cambridge University Press) [Google Scholar]
- Goldreich, P., Goodman, J., & Narayan, R. 1986, MNRAS, 221, 339 [NASA ADS] [Google Scholar]
- Guimbard, D., Le Dizès, S., Le Bars, M., Le Gal, P., & Leblanc, S. 2010, J. Fluid Mech., 660, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Inaba, S., & Barge, P. 2006, ApJ, 649, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inaba, S., Barge, P., Daniel, E., & Guillard, H. 2005, A&A, 431, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, B. M., & Gammie, C. F. 2005, ApJ, 626, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Kerswell, R. R. 2002, Annu. Rev. Fluid Mech., 34, 83 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kida, S. 1981, J. Phys. Soc. Jpn, 50, 3517 [Google Scholar]
- Klahr, H. 2004, ApJ, 606, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H. H., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Papaloizou, J. C. B. 2009, A&A, 498, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., & Papaloizou, J. C. B. 2010, A&A, 513, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H., Colgate, S. A., Wendroff, B., & Liska, R. 2001, ApJ, 551, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., Finn, J. M., Lovelace, R. V. E., & Colgate, S. A. 2000, ApJ, 533, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, M.-K. 2012, ApJ, 754, 21 [Google Scholar]
- Lin, M.-K. 2013, ApJ, 765, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Lithwick, Y. 2007, ApJ, 670, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Lovelace, R. V. E., Li, H., Colgate, S. A., & Nelson, A. F. 1999, ApJ, 513, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W. 2013, EPJ Web Conf., 46, 4003 [CrossRef] [EDP Sciences] [Google Scholar]
- Méheut, H., Casse, F., Varnière, P., & Tagger, M. 2010, A&A, 516, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Méheut, H., Keppens, R., Casse, F., & Benz, W. 2012a, A&A, 542, A9 [Google Scholar]
- Méheut, H., Yu, C., & Lai, D. 2012b, MNRAS, 422, 2399 [NASA ADS] [CrossRef] [Google Scholar]
- Miyazaki, T. 1993, Phys. Fluids A, 5, 2702 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Lesur, G., & Papaloizou, J. C. B. 2010, ApJ, 725, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Petersen, M. R., Julien, K., & Stewart, G. R. 2007a, ApJ, 658, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Petersen, M. R., Stewart, G. R., & Julien, K. 2007b, ApJ, 658, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Pierrehumbert, R. T. 1986, Phys. Rev. Lett., 57, 2157 [NASA ADS] [CrossRef] [Google Scholar]
- Surville, C., & Barge, P. 2012, 20th French Congress of Mechanics, Besançon, France [arXiv:1201.3257] [Google Scholar]
- Surville, C., & Barge, P. 2013, EPJ Web Conf., 46, 5002 [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Varnière, P., & Tagger, M. 2006, A&A, 446, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Radial dependance of the function ℒ (top) and the function |
| In the text | |
 |
Fig. 2 Density contour and velocity field in the midplane (r, θ) for the most unstable mode m = 4 and for the parameters of Lin (2013)q = 0, p = 1.5, MA0 = 23.15, A = 0.25, and σ = 0.53. |
| In the text | |
 |
Fig. 3 Evolution of the density (ρ − ρD) in a Rossby-unstable inviscid disk. Top: evolution in the r − θ plane (z = 0); bottom: evolution in a 3D perspective (visualisations performed with glnemo2). From left to right, density values are plotted at initial time and after 20, 40, and 530 rotations. |
| In the text | |
 |
Fig. 4 Growth rate of the most unstable mode versus the azimuthal wavenumber m. |
| In the text | |
 |
Fig. 5 Time evolution of the amplitude of modes 1 to 5 during the first 20 rotations. |
| In the text | |
 |
Fig. 6 Vertical component of the vorticity in the (θ,z) plane after 11 rotations (top) and 22 rotations (bottom). |
| In the text | |
 |
Fig. 7 Time evolution of the main characteristics of the largest observed vortex. Top: Rossby number of the vortex as defined in (20); bottom: aspect ratio measured from the axial vorticity contours (solid line) and obtained from formula (21) (dashed line). |
| In the text | |
 |
Fig. 8 Structure of a 3D Rossby vortex. From top to bottom the various rows show the fields (where the stable equilibrium state has been removed) of density, pressure, axial vorticity, radial velocity, azimuthal velocity, and vertical velocity. The left column shows these values in the r − θ plane at z = 0 except for the vertical velocity (last row), which is at z = 0.5. The right column shows the vertical profiles of the same values in the r − z plane at θ = 2.67; radial velocity (fourth row) and vertical velocity (last row) are plotted in the θ − z plane at r = 8. |
| In the text | |
 |
Fig. 9 Theoretical prediction of the aspect ratio of the formed vortex as a function of the initial amplitude of the bump (σ = 0.3, rb = 7.5, p = 1.5, q = 0.5, MA0 = 25). For these parameters, the basic flow is centrifugally unstable for A > 0.334. |
| In the text | |
 |
Fig. 10 Time evolution of |
| In the text | |
 |
Fig. 11 Evolution of a vortex of aspect ratio χ = 2.5 in an unstratified disk; from left to right: at initial time and after 2, 2.5, and 4 rotations. Top: vorticity in the θ–z plane at the center of the vortex. Bottom: vorticity in the r–θ plane at level z = 0.5. |
| In the text | |
 |
Fig. 12 Stratification in the disk. The color map represents the iso-contours of N/s in an angular sector going through the center of a vortex. The lines are the values obtained from Eq. (23) without vortices. |
| In the text | |
 |
Fig. 13 Vorticity in the θ − z plane at the center of the vortex after 6 rotations, 15 rotations, 30 rotations, and 65 rotations. |
| In the text | |
 |
Fig. 14 Growth rate normalized by the local background angular velocity of 3D perturbations in a vortex with an aspect ratio of 2.5 in an isothermal stratified disk for N/s = 0 and N/s = 0.5. |
| In the text | |
 |
Fig. 15 Radial position of the vortex as a function of time |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.