| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 10 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201321962 | |
| Published online | 20 November 2013 | |
Stellar ages through the corners of the boxy bulge⋆,⋆⋆
1
European Southern Observatory,
Karl Schwarzschild-Straße 2,
85748
Garching bei München,
Germany
e-mail:
evalenti@eso.org
2
Instituto de Astrofísica, Facultad de Física, Pontificia
Universidad Católica de Chile, Av.
Vicuña Mackenna 4860, 782-0436 Macul, Santiago, Chile
3
INAF-Osservatorio Astronomico di Padova, Vicolo dell’ Osservatorio
5, 35122
Padova,
Italy
4
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD
21218,
USA
5
European Southern Observatory, 19001 Casilla, Santiago, Chile
6
Jeremiah Horrocks Institute, University of Central
Lancashire, Preston
PR1 2HE,
UK
7
Institute for Theoretical Physics, University of
Zurich, Winterthurestrasse
190, 8057
Zurich,
Switzerland
Received: 25 May 2013
Accepted: 13 September 2013
Aims. In some scenarios for the formation of the Milky Way bulge, the stellar population at the edges of the boxy bulge may be younger than those on the minor axis or close to the Galactic center. So far the only bulge region where deep color–magnitude diagrams have been obtained is indeed along the minor axis. To overcome this limitation, we aim to age-date the bulge stellar populations far away from the bulge minor axis.
Methods. Color–magnitude diagrams and luminosity functions have been obtained from deep near-IR VLT/HAWK-I images taken at the two Southern corners of the boxy bulge, i.e., near the opposite edges of the Galactic bar. The foreground disk contamination has been statistically removed using a pure disk field observed with the same instrument and located approximately at similar Galactic latitudes of the two bulge fields and ~30° in longitude away from the Galactic center. For each bulge field, mean reddening and distance are determined using the position of red clump stars, and the metallicity distribution is derived photometrically using the color distribution of stars in the upper red giant branch.
Results. The resulting metallicity distribution function of both fields peaks around [Fe/H] ~ −0.1 dex, with the bulk of the stellar population having a metallicity within the range: −1 dex ≲ [Fe/H] ≲ +0.4 dex, quite similar to that of other inner bulge fields. As for the previously explored inner fields, the color–magnitude diagrams of the two bar fields are consistent with their stellar population being older than ~10 Gyr, with no obvious evidence of younger population.
Conclusions. The stellar population of the corners of the boxy bulge appears to be coeval with those within the innermost ~4° from the Galactic center.
Key words: Galaxy: bulge / Galaxy: formation / methods: observational / techniques: polarimetric
The derived photometric catalogs are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/559/A98
© ESO, 2013
1. Introduction
The formation of the central regions of disk galaxies that we call galactic bulges remains a debated topic in galaxy evolution. At very early times (z ≳ 4) the rapid and chaotic congregation of merging gas-rich lumps may have established a first, slowly rotating nucleus around which disk galaxies could start to grow. Later, at z ~ 2, when an extended gas-rich disk has formed, fed by a quasi-steady cold streams, instabilities are likely to have caused fragmentation into massive star-forming clumps that dynamical friction may have driven to coalesce at the bottom of the potential well, thus adding a rotating component (e.g., Noguchi 1999; Immeli et al. 2004; Carollo et al. 2007; Elmegreen et al. 2008). At even later times (z ≲ 1), a dynamical instability of the now dominant stellar disk may have caused the inner part of the disk to collapse into a rotating bar (e.g., Shen et al. 2010), from then on sharing the same potential well with previously formed structures.
Alternatively, the recent cosmological hydrodynamical Eris simulations show that bar instabilities can start early, at z > 3, quickly establishing a compact rotating component with the structural properties of a pseudobulge in low redshift galaxies, which weakens due to mergers and strengthens at low z, after the merging activity has faded away (Guedes et al. 2013). In this scenario it is only the last part of the evolution that resembles the conventional secular bulge formation scenario, since the initial growth phase is highly dynamical. These simulations show that, owing to its early assembly, the pseudobulge is dominated by stars with ages of 10 Gyr or more.
The relative role and timing of these processes (and possibly others) in establishing the galactic bulges we observe in the local Universe still need to be assessed, and they may well differ from one galaxy to another. Our own Galactic bulge offers a unique opportunity to investigate in detail to what extent these processes have operated in one specific case. Indeed, extensive photometric, astrometric, and spectroscopic data have started to accumulate, allowing us to measure age, chemical compositions, and kinematic properties for a large number of bulge stars, thereby tempting us to identify bulge components that may be ascribed to one of these processes or another.
Photometric and spectroscopic observations have established that the metallicities of bulge stars span a broad range from [Fe/H] ≃ −1 to well above solar (e.g., Zoccali et al. 2003, 2008; Fulbright et al. 2006; Johnson et al. 2011, 2013), with a gradient of ~0.6 dex/kpc for |b| > 4° along the bulge minor axis (Zoccali et al. 2008). The α elements appear to be enhanced relative to solar proportions with [α/Fe] ≃ +0.4 at low metallicities, then decreasing to reach near-solar reference value at high metallicities (Rich et al. 2007; Fulbright et al. 2007; Zoccali et al. 2006; Lecureur et al. 2007; Johnson et al. 2011; Gonzalez et al. 2011a), following a trend quite similar to the thick-disk stars (Meléndez et al. 2008; Alves-Brito et al. 2010; Gonzalez et al. 2011a).
Star counts and radial velocity studies have shown that the bulge is significantly elongated (it is, in fact, a bar) with axial ratios ~1:0.41:0.38 and an inclination between 29° and 32° with respect to the line of sight to the Galactic center (Cao et al. 2013, and references therein).
As shown in Fig. 1, the bulge isophotes exhibit a boxy structure that appears to be a natural product of the bar formation process. Indeed, simulations show that a substantial vertical thickening tends to occur near the ends of the bar (e.g., Combes et al. 1990; Pfenniger & Friedli 1991; Raha et al. 1991; Debattista et al. 2004). Moreover, counts of red giant branch clump stars in several directions towards the outer bulge have revealed the presence of an X-shaped structure (McWilliam & Zoccali 2010; Nataf et al. 2010; Saito et al. 2011), similar to the one in the boxy bulges of other galaxies (Bureau et al. 2006).
 |
Fig. 1 2MASS image of the Galactic bulge (Skrutskie et al. 2006). The peanut shape of the Bulge is clearly visible. From left to right (decreasing longitude), the location of the fields observed with HAWK-I is approximately marked with filled squares, red for the two bulge fields and green for the disk control field. |
One can argue that successively operating such bulge-forming processes via early merging and later instabilities in gas-rich and gas-poor disks should have left an imprint on the age distribution of bulge stars and on correlations among their ages, compositions, and kinematical properties. Nevertheless, deep color–magnitude diagrams (CMDs) of bulge fields have so far revealed a uniformly old stellar population, older than ~10 Gyr, with no appreciable trace of younger stars (Ortolani et al. 1995; Kuijken & Rich 2002; Zoccali et al. 2003; Sahu et al. 2006; Clarkson et al. 2008, 2011), thus arguing for an early formation of the bulge, as opposed to a slow, secular growth extended over a large portion of the Hubble time. Some exceptions are younger stars as suggested by microlensing follow-up spectroscopy (Bensby et al. 2013).
However, one limitation of these studies is that they all have explored small fields (called windows) that lie on or near the bulge minor axis1, a region that may be avoided by the orbits of stars added to the bulge by the bar instability. In this respect, because the boxy shape is directly linked to the bar formation, the four corners of the boxy bulge instead appear to be ideal places to search for younger stellar populations. To explore this possibility, we obtained deep near-IR images of two fields near the edges of the boxy bulge, located as shown in Fig. 1. Here we present the resulting CMDs from which we constrain the stellar ages.
Galactic coordinates, image quality, and log of the observed fields.
An accurate dating of the bulge component allows one to gauge at which lookback time (i.e., at which redshift) one should look for possible analogs of the Milky Way, when their bulge formation processes were about to start, well on their way, or already concluded. Indeed, with an age of ~10 Gyr or older, it is at z ≳ 2 that such analogs can be searched, or at lower redshifts if components that are several Gyr younger are to be found. Much progress has been made in recent years by mapping galaxy populations at these redshifts, with large, rotating disks quite common, along with other more compact, velocity-dispersion-dominated galaxies (e.g, Genzel et al. 2006; Förster Schreiber et al. 2009; Mancini et al. 2011). In such disks star formation activity often peaks at the center, as judged from the surface brightness distribution of the Hα emission, hence suggesting rapid, in situ bulge formation. Moreover, these disk galaxies are characterized by high-velocity dispersions (≳50 km s-1), and are far more gas rich than local spirals of the same mass, with gas fractions of ~50% or more (Daddi et al. 2010; Tacconi et al. 2010). Thus, it is among galaxies of this kind that we may find progenitors of the Milky Way galaxy and its bulge, suggesting that bulge formation took place at a time when the Galaxy was a gas-rich, actively star-forming object in which stellar dynamics was only one of the actors in play. Dating the stellar populations of the bulge in various directions would set important constraints on its formation and on the cosmic epochs (redshifts) where one looks for analog progenitors. This is indeed the focus of the present paper.
The paper is organized as follows. The observations and data reduction are presented in Sect. 2, while in Sect. 3 we show the derived CMDs and discuss their general properties. Section 4 is devoted to discussing the main photometric and physical differences of the two bulge regions. The photometric metallicity distribution of the bulge fields is presented in Sect. 5, while in Sect. 6 we derive the bulge age. Finally, Sect. 7 is devoted to discussing and summarizing our results.
2. Observation and data reduction
Two bulge fields, BUL-SC29 and BUL-SC9, located at the opposite edges of the Galactic bar (see Table 1 and Fig. 1) were observed with HAWK-I on the Yepun (VLT-UT4) telescope at ESO Paranal Observatory through the J and Ks filters. HAWK-I is a near-IR imager with a pixel scale of 0.106″/pix and a total field of view of 7.5′ × 7.5′.
Both fields have been previously observed by the OGLE-II survey, so in this work we adopted their name: BUL-SC9 and BUL-SC29 (Udalski et al. 2000; Sumi 2004). BUL-SC9 is located on the nearest bar edge, whereas BUL-SC29 is at the far end with respect to the Sun’s position. The two fields have slightly different latitudes because of the need to avoid very bright sources (i.e., Ks ≲ 8) that cause detector persistence problems (see HAWK-I user manual for further details). Exposures of a disk control field located at (l,b) = (29.9°, −3.9°) were also obtained in order to estimate and statistically subtract the contamination by disk stars towards the two bulge fields.
Each bulge and disk frame is the combination of 20 exposures each 1.3 s long. The observation was repeated with a random dithering pattern until reaching the total exposure time listed in Table 1. A random dithering technique was applied with a jitter box width of 30″ both for background subtraction and for covering the small cross-shaped gap of ~15″ width between the four detectors. The observations were taken in service mode during Periods 81 and 83 (i.e., in 2008 and 2009) with an average seeing on image of 0.5′′ ± 0.1 (see Table 1 for more details). From Table 1, one can see that the planned J-band observations for BUL-SC29 field were not completed, resulting in shallower images compared to the data obtained for the other fields.
The processing of the raw data was performed with standard IRAF routines. For both filters, we obtained a sky image by median combination of the dithered images and subtracted it from each frame. To normalize the pixel-to-pixel response, all frames were then divided by a normalized twilight flat. Finally, all the flat- and sky-corrected frames were averaged into a single image for each of the two filters. In what follows we will refer to frame as the combination of each of these sets.
We carried out standard photometry, including PSF modeling, on each frame using DAOPHOTII and ALLSTAR (Stetson 1987). For each observed field, a photometric catalog listing the instrumental J and Ks magnitudes was obtained by cross-correlating the single-band catalogs. We used more than 200 stars in common between the derived catalogs and 2MASS data to perform the absolute calibration and astrometrization onto the 2MASS photometric and astrometric system (Skrutskie et al. 2006).
Completeness and error estimates were derived via artificial-star experiments. About 4000 stars were randomly added to the original bulge and disk frames with magnitudes and colors consistent with the red giant branch (RGB) and main sequence (MS) instrumental fiducial lines. To avoid artificially increasing the crowding in each independent experiment, the artificial stars were added along the corners of an hexagonal grid (see Zoccali et al. 2000, for more technical details). Figure 2 shows the results of the completeness experiments as the difference between the input and output J and Ks magnitudes of the artificial stars for all the observed fields. The asymmetry in the distributions shown in Fig. 2 is due to occasional blending of two or more stars that the photometric package is not able to resolve. This effect is present over the whole magnitude range, but becomes quite prominent around J ~ 17, which is at the level of the MS turnoff (TO) of the dominant population, an effect that must be quantitatively taken into account when trying to identify a possible intermediate-age population, or set limits to it. The simulations demonstrated that the photometry is more than 50% complete above J ~ 20 and Ks ~ 19.
3. The color–magnitude diagrams
The derived (Ks,J − Ks) CMD of the observed bulge fields, BUL-SC29 and BUL-SC9, is shown in panel c) of Figs. 3 and 4, respectively. In both cases, the large number of detected stars saturates the plots for Ks ≳ 16 making it difficult to distinguish the different evolutionary sequences, such as the subgiant branch (SGB) and the MS-TO. To improve the CMDs we then excluded stars with errors of too large J and Ks. In doing this, we applied an error cut (see panels a) and b)) following the lower envelope of the Poisson error distribution, hence excluding all stars with errors larger than expected at their respective magnitude levels. The result of this procedure is a cleaner CMD (panel c)) in which the color distribution of stars fainter than Ks = 16 is much narrower. Our photometry turns out to be deep enough to properly sample a good fraction of the RGB, from about one magnitude above the horizontal branch (HB) down to a couple of magnitudes below the MS-TO. The saturation magnitude limit occurs around Ks ~11, so to recover the brightest part of the RGB we have combined our photometry with 2MASS data (panel c)).
 |
Fig. 2 Difference between the input and output magnitude of the artificial star experiments on the HAWK-I frames for the observed bulge and disk fields. Notice the typical asymmetry of these differences, with blending with fainter sources making some stars brighter than they are. |
 |
Fig. 3 Right panel c): the derived (Ks,J − Ks) CMD of all stars measured in the BUL-SC29 field, including both bulge and disk contributions. Black dots refer to stars with errors smaller than the selection applied in panels a) and b) (see text for more details), with green points referring to stars whose errors exceed such limits. Black crosses show stars from 2MASS, which are saturated in the HAWK-I images. |
Both fields have very similar CMDs; the major difference is, however, the spread in the various evolutionary sequences. In the case of BUL-SC9, all sequences appear to be quite broad because of the higher differential reddening and larger distance dispersion along the line of sight (see Sect. 4 for more details). As expected, the characteristic double red clump signature of the X-shape structure is not present in any of the derived CMDs. In fact, as demonstrated by McWilliam & Zoccali (2010) the X-shape bulge structure is visible at latitudes |b| ≥ 5.5° and ranges over ~13° in longitude and 20° in latitude. The lower MS of the BUL-SC29 field is actually broader, owing to the poorer S/N in the J band. The bulge HB clump is clearly visible at Ks ~ 13 and (J − Ks) ~ 1, as is the RGB, which can be easily traced down to Ks ~ 16.5 as a distinct and separate sequence. Conversely, the SGB is barely detectable because it is heavily contaminated by the foreground disk stars. The vertical blue sequences departing from the bulge MS-TO and from the HB clump and extending upwards correspond, respectively, to the foreground disk MS and its disk red clump descendants (see Sect. 3.1 for more details).
In Figs. 5a and 6a we compare the bulge field CMDs with a 1 Gyr isochrone (Pietrinferni et al. 2006) for a solar metallicity population and helium abundance Y = 0.273 by using a distance modulus and reddening correction of (m − M)0 = 14.57, 14.12 and E(B − V) = 0.38, 0.65 for BUL-SC29 and BUL-SC9, respectively (see Sect. 4 for details on reddening and distance). As can be clearly noticed, a young (~1 Gyr) population belonging to the bulge would have a much bluer color than the disk MS appearing in these CMDs. Increasing the age, the isochrone turnoff color and luminosity get progressively redder and fainter. Therefore to investigate the possible presence of intermediate-age population in the bulge, it is necessary to remove the foreground disk stars from the CMDs. Actually, the MS of disk stars hits the bulge CMD right on top of its MS-TO, this hampering a reliable age measurement.
3.1. Disk decontamination
 |
Fig. 5 Panel a): the observed CMD of the bulge BUL-SC29 field . The red solid line is the 1 Gyr isochrone for a solar metallicity population (Pietrinferni et al. 2006). Panel b): the observed CMD of the disk control field ~30° away from the Galactic center. The region within the box has been used to normalize the number of disk stars seen through the bulge line of sight. Panel c): the CMD of the bulge BUL-SC29 field as statistically decontaminated from the disk population. Panel d): the CMD of the stars that were statistically subtracted from the CMD in panel a) in order to obtain the decontaminated CMD shown in panel c). |
To proceed with age dating of our two bulge fields, we must then try to remove as many disk stars as possible from their CMDs. The best decontamination procedure would consist of selecting proper motion members, such as in Kuijken & Rich (2002) and Clarkson et al. (2011), even though the result depends on disk kinematics assumptions. As we do not have suitable first-epoch data, we adopted a statistical disk decontamination as in Zoccali et al. (2003), which has the advantage over the proper motions method of being free of kinematics biases. Moreover, being less time-consuming in terms of observations, the statistical approach is generally more suitable to decontaminating large areas.
The contamination of bulge CMDs from foreground disk stars strongly depends on the latitude of the line of sight, and therefore was used a control disk field located approximately at the same Galactic latitude of the bulge fields but about 30° away from the Galactic center (see Table 1). The derived (Ks, J − Ks) CMD of the control disk field is shown in Figs. 5b and 6b. This procedure assumes that the disk CMD is the same in the two bulge fields and in the field at l ≃ 30°, which of course may not strictly be the case. To reduce the bias that field-to-field differences would induce as much as possible we checked for difference in extinction between the fields. In the case of the BUL-SC29 field, to match the location of the blue, nearly vertical disk sequence, the disk control field was shifted by 0.21 mag in color and in magnitude by the corresponding AK = 0.35ΔE(B − V) (Cardelli et al. 1989). We found no appreciable difference in extinction between BUL-SC9 and the disk-control fields, so no shift in color and magnitude was applied. For each bulge field, we then calculated the bulge-to-disk normalization factor which gives us the number of stars to be removed from the bulge CMD for each given disk star. To do so, after the mentioned reddening adjustment, we used a region of the CMDs where no bulge stars are present, i.e., within the box in the upper left hand corners in Figs. 5a,b and 6a,b. In the disk control field, the number of stars within the box is 1.3 and 1.2 times less than in the corresponding box of BUL-SC29 and BUL-SC9 field, respectively. Therefore, for each star in the disk CMD of Figs. 5b and 6b we have selected the closest star in the bulge CMDs of Figs. 5a and 6a, and subtracted by adopting these normalization factors and the star completeness found in Sect. 2.
Following the prescription of Zoccali et al. (2003), the distance on the CMD from a disk star to each bulge star is computed as ![\hbox{$d=\sqrt{[5\times\Delta(J-\ks)]^2+\Delta J^2}$}](/articles/aa/full_html/2013/11/aa21962-13/aa21962-13-eq59.png) , where the factor 5 has the function of giving a weight to color differences close to that of magnitude differences, since the color range is much narrower than that spanned by magnitudes. For the BUL-SC29 field, the decontamination procedure worked quite well as demonstrated in Fig. 5 panels c) and d), which respectively show the CMD of the disk-free bulge field and the CMD of the stars statistically removed. In the BUL-SC29-cleaned CMD one can now clearly follow most of the bulge evolutionary sequences: from the HB clump and lower RGB down to the SGB and the MS-TO. What looks like an excess of stars at the faint end of the cleaned bulge MS, at Ks ≥17 and (J − Ks) ≥1.2, is instead an artifact due to the different J-band magnitude limit reached in the bulge and disk CMDs, since the broader color distribution of the shallower data (of the bulge field) is not matched by the deeper disk data. As far as the BUL-SC9 field is concerned (see panel c) of Fig. 6), the disk decontamination is more accurate at faint magnitudes because the photometry is equally deep in the bulge and in the disk control field. However, the presence of larger differential reddening in this field combined with larger distance spread along the line of sight and a lower density make the CMD sequences at and above MS-TO broader than in the case of the BUL-SC29 field, hence the MS-TO is less sharply defined. In fact, when we use one of the analytic models from (Dwek et al. 1995, Eq. (3e)) with the parameters recently derived by Cao et al. (2013, i.e., x0 = 0.68 Kpc, y0 = 0.28 Kpc, z0 = 0.26, we calculate that the bulge star density in BUL-SC9 is a factor ~2.2 lower than in BUL-SC29.
, where the factor 5 has the function of giving a weight to color differences close to that of magnitude differences, since the color range is much narrower than that spanned by magnitudes. For the BUL-SC29 field, the decontamination procedure worked quite well as demonstrated in Fig. 5 panels c) and d), which respectively show the CMD of the disk-free bulge field and the CMD of the stars statistically removed. In the BUL-SC29-cleaned CMD one can now clearly follow most of the bulge evolutionary sequences: from the HB clump and lower RGB down to the SGB and the MS-TO. What looks like an excess of stars at the faint end of the cleaned bulge MS, at Ks ≥17 and (J − Ks) ≥1.2, is instead an artifact due to the different J-band magnitude limit reached in the bulge and disk CMDs, since the broader color distribution of the shallower data (of the bulge field) is not matched by the deeper disk data. As far as the BUL-SC9 field is concerned (see panel c) of Fig. 6), the disk decontamination is more accurate at faint magnitudes because the photometry is equally deep in the bulge and in the disk control field. However, the presence of larger differential reddening in this field combined with larger distance spread along the line of sight and a lower density make the CMD sequences at and above MS-TO broader than in the case of the BUL-SC29 field, hence the MS-TO is less sharply defined. In fact, when we use one of the analytic models from (Dwek et al. 1995, Eq. (3e)) with the parameters recently derived by Cao et al. (2013, i.e., x0 = 0.68 Kpc, y0 = 0.28 Kpc, z0 = 0.26, we calculate that the bulge star density in BUL-SC9 is a factor ~2.2 lower than in BUL-SC29.
 |
Fig. 7 LFs of the observed bulge fields as obtained from the disk-decontaminated CMDs. The black arrows mark the location of the HB-RC whereas the gray areas refer to the approximate location of the MS-TO. |
Derived parameters for the observed bulge fields
4. The luminosity function of the two fields
We used the statistically decontaminated catalogs derived in Sect. 3.1 to construct the J- and Ks-band luminosity functions (LF) of the two bulge fields. In case of BUL-SC29, we also applied a color cut in the low MS to avoid the artifact due to the different J-band magnitude limit reached in the bulge and disk CMDs (see Sect. 3.1). The result is shown in Fig. 7, where the location in magnitude of the observed HB red clump (RC) is marked with a black arrow (see also Table 2). To quantify the reddening along the two bulge lines of sight, we adopted a differential method based on the comparison between the HB-RC color, (J − Ks)RC, of the observed fields and that of Baade’s window. In fact, the color shift needed to overlap the HB-RC of two bulge fields with comparable age and metallicity is only a function of the reddening. According to Gonzalez et al. (2011b), in the Baade’s Window the HB-RC is located at KsRC = 13.15 and JRC = 14.11. With the Cardelli et al. (1989) extinction coefficients and assuming E(B − V) = 0.55 for Baade’s window (Gonzalez et al. 2011b), an average reddening E(J − Ks) = 0.20 ± 0.03 (i.e. E(B − V) = 0.38) was derived for the BUL-SC29 field and E(J − Ks) = 0.34 ± 0.05 (i.e., E(B − V) = 0.65) for the BUL-SC9 field. These estimates agree nicely with the corresponding values from Gonzalez et al. (2012), that are reported in Table 2.
We derived the mean distance of the two bulge fields by using these reddening estimates and adopting 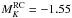 , which is the intrinsic Ks magnitude of the HB-RC for a 10 Gyr old population with solar metallicity (Pietrinferni et al. 2004). This value of
, which is the intrinsic Ks magnitude of the HB-RC for a 10 Gyr old population with solar metallicity (Pietrinferni et al. 2004). This value of 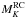 was adopted by Gonzalez et al. (2011b) to map the reddening over the whole bulge, and it is within 0.02 mag of the empirical calibration of van Helshoecht & Groenewegen (2007). The derived mean intrinsic distance moduli of the BUL-SC29 and BUL-SC9 fields are listed in Table 2. They indicate that the BUL-SC29 field is located at the far edge of the bar and the BUL-SC9 field is located at the near edge. This is consistent with the larger distance spread in the BUL-SC9 field indicated by its broader CMD sequences. Indeed, we notice from Fig. 7 that the RC feature is much sharper in the BUL-SC29 field than it is in the BUL-SC9 field, as expected.
was adopted by Gonzalez et al. (2011b) to map the reddening over the whole bulge, and it is within 0.02 mag of the empirical calibration of van Helshoecht & Groenewegen (2007). The derived mean intrinsic distance moduli of the BUL-SC29 and BUL-SC9 fields are listed in Table 2. They indicate that the BUL-SC29 field is located at the far edge of the bar and the BUL-SC9 field is located at the near edge. This is consistent with the larger distance spread in the BUL-SC9 field indicated by its broader CMD sequences. Indeed, we notice from Fig. 7 that the RC feature is much sharper in the BUL-SC29 field than it is in the BUL-SC9 field, as expected.
5. The photometric metallicity distributions
In this section we derive the metallicity distribution function (MDF) of the two bulge fields by adopting a procedure similar to the one described by Zoccali et al. (2003) and used in Gonzalez et al. (2013). For this purpose we only need to use the bright part of the RGB, which however is saturated in the HAWK-I data and poorly populated as illustrated in Figs. 3 and 4. Therefore, we resort to 2MASS data, using the CMD of 30′ × 30′ regions centered on the two bulge fields, together with an empirical grid of Galactic cluster RGB ridge lines selected from the sample of Valenti et al. (2004a). Such comparisons must be performed in the absolute CMDs [MK, (J − Ks)0]; as a result, for the two fields we use the reddening and distance values derived in Sect. 4 and listed in Table 2. We then derive the photometric metallicity estimate for each star from its color by interpolating within the templates grid.
 |
Fig. 8 Upper panels: the CMDs from 2MASS of the upper RGB for the two 30′ × 30′ fields including our Hawk-I bulge fields in the absolute [MK, (J − Ks)0] plane. The empirical globular cluster RGB templates are over plotted with metallicities from [Fe/H] = −2.1 to +0.35 (see text in Sect. 5 for details on cluster names and metallicities). Black symbols indicate the stars used to derive the photometric MDF. Bottom panels: derived photometric MDF of the observed bulge fields with a bin size of 0.15 dex. |
 |
Fig. 9 Comparison between the CMDs of the bulge fields observed in this work (left and right panels). The magnitude difference between the HB-RC and MS-TO of the BUL-SC29 field (dashed horizontal lines) is compared with the same quantity for the BUL-SC9 field. The CMD of the BUL-SC9 field has been shifted in magnitude and color to match the location of BUL-SC29 HB-RC. In both these panels the solid red line is the empirical ridge line of the CMD of the BUL-SC29 field. The central panel shows the J − (J − H) CMD of the bulge globular cluster NGC 6528, showing that the luminosity difference between the HB–RC and the MS–TO is virtually identical to that of the two bulge fields. |
We selected the following globular clusters as empirical RGB templates: M 92 ([Fe/H] = −2.1), M 55 ([Fe/H] = −1.61), NGC 6752 ([Fe/H] = −1.42), NGC 362 ([Fe/H] = −1.15), M 69 ([Fe/H] = −0.68), NGC 6440 ([Fe/H] = −0.50), NGC 6528 ([Fe/H] = −0.17), and the old open cluster NGC 6791 ([Fe/H] = +0.35). The selection was made in order to cover the widest metallicity range in suitable fine steps.
As shown in the upper panels of Fig. 8, the derived MDF of the two bulge fields is obtained considering only RGB stars i) fainter than the RGB-Tip as derived by Valenti et al. (2004b); ii) brighter than MK = −4.5, to retain the region of the RGB with the highest sensitivity to metallicity variations, to avoid contamination by red clump stars and to exclude the AGB clump stars, which are predicted to lie around MK ~ −2.7 (Pietrinferni et al. 2004); and iii) excluding stars bluer than (J − Ks)0 = 0.7 to minimize any possible residual contamination by disk stars.
The derived MDF for the two fields is shown in the lower panels of Fig. 8, together with the number of selected stars. The major source of uncertainty in the inferred MDFs is the reddening E(J − Ks) and its spread within each field (which will tend to broaden the distribution). To quantify the errors we also compute the MDF by assuming reddening estimates that differ from those listed in Col. 3 of Table 2 by ±0.03 and ±0.05 for BUL-SC29 and BUL-SC9, respectively. The result is a shift of the peak distribution by ≲0.15 dex. For further details on the error estimates, the reader can refer to Gonzalez et al. (2013) who derive the photometric metallicity map of the bulge by using the same empirical grid and 2MASS photometric catalog. It should be mentioned that given the uncertainties associated to reddening, depth effects, and possible mixing of populations, the adopted method provides a reliable description of the overall metallicity range spanned by the bulk of the population (i.e. mean and dispersion of the distribution). Here we are interested in deriving the metallicity range to be adopted in Sect. 6 by the theoretical isochrones to derive the stellar ages.
Within the errors, the derived MDFs are very similar in the two fields. They are quite broad, with the bulk of the stars lying within the metallicity range −0.8 ≲ [Fe/H] ≲ +0.6 and with a peak around [Fe/H] ~ −0.1. As expected, the peak of the derived MDFs agree nicely with the results by Gonzalez et al. (2013) who find [Fe/H] = −0.20 dex and –0.15 dex, for BUL-SC29 and BUL-SC9 respectively.
Given the limitations of the method, these MDFs are broadly consistent with the spectroscopic MDFs of the bulge (Zoccali et al. 2008) and, in the case of the BUL-SC29 field, with the multiband photometric MDF of Brown et al. (2010). In both cases, the secondary peak at low metallicity is most likely due to a contamination from foreground disk stars in the HB-RC. We conclude that the two bulge fields have indistinguishable MDFs.
6. Stellar ages
Using the statistically decontaminated CMDs presented in Sect. 3.1 we now estimate the age of the bulge stellar populations at the two opposite edges of the bar. For the sake of comparison, in Fig. 9 the CMD of BUL-SC9 has been shifted in magnitude and color to match the location of the HB-RC in the BUL-SC29 field, after having identified the magnitude of the HB–RCs from Fig. 7. The difference between the magnitude of the HB-RC and the MS-TO is essentially the same in the two fields as emphasized by the horizontal dashed lines, implying that the stellar population in these two bulge regions are coeval. Moreover, to further show the similarity between the two fields in Fig. 9 we have over plotted the CMD ridge line for the BUL-SC29 field in both panels. As one can easily appreciate, the fiducial ridge line of BUL-SC29 also nicely fits all the observed CMD sequences of the BUL-SC9 field, from the MS–TO up to the RGB, thus ruling out any appreciable differences between the two fields in terms of mean metallicity and age.
The central panel in Fig. 9 shows the J,(J − H) CMD of the bulge globular cluster NGC 6528 from HST/NICMOS data (Ortolani et al. 2001) tranformed into the 2MASS photometric system by applying the Brandner et al. (2001) color transformations. The J-band magnitude has been shifted to have the HB-RC of the cluster at the same level as that of the two bulge fields. As measured from high-resolution optical and near-IR spectroscopy, the metallicity of NGC 6528 ranges −0.1 ≤ [Fe/H] ≤ +0.07 (Carretta et al. 2001; Zoccali et al. 2004; Origlia et al. 2005); i.e., it is very close to the mean metallicity of the two bulge fields. The figure shows that the J-band luminosity difference between the HB-RC and the MS–TO 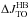 of the cluster is virtually the same as that of the two bulge fields, which ensures that the cluster and the bulk stellar population in the bar fields are virtually coeval. This extends the same age dating procedure pioneered by Ortolani et al. (1995) for the Baade’s window field in the bulge to the edges of the bar. Still, the turnoff region of the BUL-SC29 field – and even more so of the BUL-SC9 field – appears to be more extended in luminosity compared to that of the cluster. There are indeed important differences between cluster and fields; namely, the cluster stars are chemically homogeneous, are all at the same distance, and suffer relatively little differential reddening because sampled in the small
of the cluster is virtually the same as that of the two bulge fields, which ensures that the cluster and the bulk stellar population in the bar fields are virtually coeval. This extends the same age dating procedure pioneered by Ortolani et al. (1995) for the Baade’s window field in the bulge to the edges of the bar. Still, the turnoff region of the BUL-SC29 field – and even more so of the BUL-SC9 field – appears to be more extended in luminosity compared to that of the cluster. There are indeed important differences between cluster and fields; namely, the cluster stars are chemically homogeneous, are all at the same distance, and suffer relatively little differential reddening because sampled in the small  NICMOS field of view. Conversely, stars in the two bulge fields span a wide range in metallicity and distance and are more affected by differential reddening over the much larger field of view of HAWK-I. Of course, we cannot completely exclude the presence of a minority of metal-rich, younger stars of a few Gyr (see below).
NICMOS field of view. Conversely, stars in the two bulge fields span a wide range in metallicity and distance and are more affected by differential reddening over the much larger field of view of HAWK-I. Of course, we cannot completely exclude the presence of a minority of metal-rich, younger stars of a few Gyr (see below).
 |
Fig. 10 CMD of the BUL-SC29 field with overplotted theoretical isochrones (Valcarce et al. 2012). Isochrone ages, metallicities, and helium abundances are indicated near the top-left corner of each panel. Sub-solar isochrones are α-enhanced, and solar-scaled otherwise. The metallicity range covered by the bulk of the stars in the BUL-SC29 field is 0.002 ≲ Z ≲ 0.060, as derived in Sect. 5. Open circles mark stars that are most likely blue stragglers (see text for more details). |
To more accurately quantify this conclusion we consider the case of the BUL-SC29 field in more detail, which is less affected by differential reddening and distance dispersion effects. The left hand panel of Fig. 10 shows that the bulk of the bulge population has an age ≳10 Gyr. In fact, when comparing the BUL-SC29 CMD with 10 Gyr theoretical isochrones of various metallicities, the observed spread in color is fully consistent with the metallicity dispersion measured in Sect. 5. Indeed, most stars have metallicity in the range between [Fe/H] ~ −1 and [Fe/H] ~ +0.6, with a peak around [Fe/H] ~ −0.10 dex. Most stars in the BUL-SC29 field are in fact confined within the two extreme isochrones.
Moreover, as we pointed out in Sect. 2, our artificial star experiments have shown that the accuracy of our photometry suffers from blending effects. In particular in the MS-TO luminosity range (i.e. Ks ~ 17.15 ± 0.2), the blending could affect the star measurements up to ~15%, leading to a systematic overestimate of the luminosity (see also Fig. 2). This effect increases rapidly with decreasing luminosity along the MS, which accounts for the increasing mismatch between the isochrones and the data seen in Fig. 10. The observed luminosity dispersion affecting the MS-TO region can therefore be well accounted for when considering the blending effect, together with ~0.26 mag 1σ dispersion due to the distance distribution along the line of sight (see Sect. 5 in Gonzalez et al. 2013), with very little room left for an intermediate-age population.
It is worth emphasizing that blending can make stars brighter but never bluer than the true turnoff. Therefore, the blue cutoff of the MS can put a stronger constraint on age than the measured MS–TO luminosity, providing that an appropriate set of isochrones is used. This is further illustrated by the comparison between the observed CMD and 3 and 5 Gyr isochrones for super-solar metallicity, shown in the right hand panel of Fig. 10, which demonstrates that there is indeed little room left for young/intermediate-age populations.
The spur of stars that are bluer than J − Ks ~ 0.6 and brighter than Ks ~ 17 (right and panel of Fig. 10) are most likely the blue straggler progeny of binary star evolution, as demonstrated for an inner bulge field by Clarkson et al. (2011). To verify this we calculated the blue straggler frequency (SBSS = NBSS/NHB) as the number of blue stragglers (NBSS) normalized to the total number of HB stars (NHB) used as reference population. The value of NHB has been estimated by using the LFs shown in Fig. 7: by subtracting from the RC-HB peak the contribution of the RGB stars, previously derived by fitting the LF in the range J ≥ (JRC + 1) and J ≤ (JRC−1). We found SBSS = 0.4, which is consistent with the result of (Clarkson et al. 2011, i.e. 0.31 ≤ SBSS ≤ 1.23). Finally, it is worth mentioning that our estimate of SBSS should be regarded as a lower limit because the derived NHB only refers to the number of red HB stars, because the small contribution from blue HB stars is very difficult to estimate from our photometry.
As mentioned earlier, the BUL-SC29 field was also observed with HST/WFC3 by Brown et al. (2010), who noted that its J − (J − H) CMD is virtually identical to that of three other inner bulge fields, just a few degrees from the Galactic center. Though a detailed age-dating of such fields was beyond the scope of the Brown et al. (2010) paper, they note that all such fields are dominated by an old (~10 Gyr) population.
7. Discussion and conclusion
The near-IR CMDs we have constructed for the two southern corners of the boxy bulge indicate a uniformly old stellar population (~10 Gyr, or older), similar to that of the more central fields close to the minor axis of the bulge, when the same CMD method is employed (Ortolani et al. 1995; Zoccali et al. 2003; Brown et al. 2010; Clarkson et al. 2011). The CMDs of these bulge fields are indeed very similar to that of the bulge globular cluster NGC 6528, which has a metallicity that is very close to the mean metallicity of the bulge fields. In particular, the luminosity difference between the HB-RC and the MS-TO is virtually identical as shown in Fig. 9, with 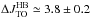 , which ensures that there are cluster and fields with essentially the same age within ~20%. Thus, here rather than trying to date a detailed isochrone fitting dating of the bulge fields, we report prior age estimates of the bulge cluster NGC 6528.
, which ensures that there are cluster and fields with essentially the same age within ~20%. Thus, here rather than trying to date a detailed isochrone fitting dating of the bulge fields, we report prior age estimates of the bulge cluster NGC 6528.
This is in very good agreement with results from the recent Eris cosmological simulations (Guedes et al. 2013), which coincidentally produce a galaxy that by z = 0 resembles very closely the internal structure and mass distribution of an Sb-Sbc spiral galaxy, such as our own Milky Way (Guedes et al. 2011). This prompts comparison with more profound aspects of pseudobulge formation between simulations and detailed observations, such as metallicity evolution and metallicity-age relation, which can in turn aid the interpretation of current and future datasets. Detailed multi wavelength mock photometry and spectroscopy of the simulated galaxies will be important tools for any progress in this direction.
By restricting it to age estimates based on HST data, NGC 6528 was given an age 13 ± 3 Gyr by Ortolani et al. (2001) based on NICMOS data, 11 ± 2 Gyr by Feltzing & Johnson (2002) based on two epoch WFPC2 data (hence using only proper-motion cluster members), 12.6 Gyr by Momany et al. (2003) based on proper motion members and a combination of WFPC2 and near-IR data, and finally 12.5 Gyr by Brown et al. (2005) based on ACS data. We concluded that the bulk stellar population of the galactic bar edges (identified with the two corners of the boxy bulge indicated in Fig. 1) is over ~10 Gyr old, and this age is indistinguishable from the one reported for more inner bulge fields, a few degrees from the Galactic center or lying along the bulge minor axis. On this basis, we did not find any evidence that the age distribution in these fields far off the minor axis is any different from that on the minor axis. Thus, if the bar instability had the effect of injecting disk stars into the bulge, it might have done so a long time ago.
Partly at variance with our present results and all previous ones based on the CMDs of specific bulge fields (Ortolani et al. 1995; Zoccali et al. 2003; Clarkson et al. 2008, 2011; Brown et al. 2010) is the age-dating of bulge stars based on the microlensing dwarf project of Bensby et al. (2013, and references therein). Rather than being from magnitudes and colors, their ages are derived from the effective temperature and gravity from the high-resolution spectra obtained during the microlensing events, then using isochrones in the (Teff,log g) plane. They find that 31 of their 58 microlensed dwarfs (~53%) are younger than 9 Gyr, with 13 of them (~23%) younger than 5 Gyr. Whereas those dwarfs that are more metal-poor than [Fe/H] ≃ −0.4 appear to be uniformly old (older than ~10 Gyr), the more metal-rich dwarfs appear to span a very wide range of ages from virtually the age of the Universe down to less than ~2 Gyr.
There appears to be a discrepancy between the ages inferred from the CMD of bulge fields and those derived for the microlensed dwarfs and subgiants. Admittedly, age errors for individual microlensing events are quite large, and when such uncertainties are taken into account only 3 out of 58 stars (~5%) within 1σ are younger than 5 Gyr (Bensby et al. 2013). This is not too far from the upper limit of ~3% estimated by Clarkson et al. (2011). Of course, each of the two methods has its own advantages and disadvantages. The traditional CMD method deals with very large numbers of stars, and therefore can in principle also reveal traces of young populations. However, the metallicities of individual stars are not known, and one does not know if, for example, some of the stars above the MS-TO of the Z = 0.060 isochrone in Fig. 10 are old and have lower metallicity, or whether they are metal-rich stars younger than 10 Gyr. On the other hand, besides forcefully dealing with very small number statistics, the microlensing approach depends more heavily on model atmospheres that may introduce systematic effects, especially at high metallicity. However, it has the advantage that the metallicity of each individual star is known.
The Galactic bulge HST/WFC3 Treasury Project (Brown et al. 2009, 2010) is designed to overcome the limitations of the CMD method by measuring metallicities photometrically, using a purposely tailored multiband dataset. It will also do so for a very large number of stars around the MS-TO in four different bulge fields, and using proper motion to select pure bulge stars. For these reasons we believe that a more sophisticated, thorough isochrone dating procedure will be best attempted using the Treasury Project data, rather than the present dataset, where individual metallicities are not known and the disk decontamination of the bulge population must be statistical.
Still, our most solid result is that no appreciable age differences appear to exist between the central regions of the bulge (the innermost ~4° from the Galactic center) and the two explored fields at two corners of the boxy bulge, at the edges of the galactic bar.
Acknowledgments
This material is based upon work supported in part by the National Science Foundation under Grant No. 1066293 and the hospitality of the Aspen Center for Physics. M.Z. acknowledge support by Proyecto Fondecyt Regular 1110393, the BASAL Center for Astrophysics and Associated Technologies PFB-06, the FONDAP Center for Astrophysics 15010003, Proyecto Anillo ACT-86 and by the Chilean Ministry for the Economy, Development, and Tourism’s Programa Iniciativa Científica Milenio through grant P07-021-F, awarded to The Milky Way Millennium Nucleus. A.R. acknowledges the kind hospitality and support of the Astronomy Department of the Pontificia Universitad Catolica where this paper was finished. V.P.D. is supported in part by STFC Consolidated grant # ST/J001341/1. This work has made use of BaSTI and PGPUC isochrones web tools. This publication makes use of data products from the Two Micron All Sky Survey (2MASS), which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, founded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Alves-Brito, A., Meléndez, J., Asplund, M., Ramírez, I., & Yong, D. 2010, A&A, 513, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Yee, J. C., Feltzing, S., et al. 2013, A&A, 549, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandner, W., Grebel, E. K., Barbá, R. H., Walborn, N. R., & Moneti, A. 2001, AJ, 122, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Ferguson, H. C., Smith, E., et al. 2005, AJ, 130, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Sahu, K., Zoccali, M., et al. 2009, AJ, 137, 3172 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Sahu, K., Anderson, J., et al. 2010, ApJ, 725, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Bureau, M., Aronica, G., Athanassoula, E., et al. 2006, MNRAS, 370, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, L., Mao, S., Nataf, D., Rattenbury, N. J., & Gould, A. 2013, MNRAS, 434, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, C. M., Scarlata, C., Stiavelli, M., Wyse, R. F. G., & Mayer, L. 2007, ApJ, 658, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Cohen, J. G., Gratton, R. G., & Behr, B. B. 2001, AJ, 122, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, W., Sahu, K., Anderson, J., et al. 2008, ApJ, 684, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, W. I., Sahu, K. C., Anderson, J., et al. 2011, ApJ, 735, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., Debbasch, F., Friedli, D., & Pfenniger, D. 1990, A&A, 233, 82 [NASA ADS] [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Debattista, V. P., Carollo, C. M., Mayer, L., & Moore, B. 2004, ApJ, 604, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., Arendt, R. G., Hauser, M. G., et al. 1995, ApJ, 445, 716 [CrossRef] [Google Scholar]
- Elmegreen, B. G., Bournaud, F., & Elmegreen, D. M. 2008, ApJ, 688, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Feltzing, S., & Johnson, R. A. 2002, A&A, 385, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2006, ApJ, 636, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2007, ApJ, 661, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Tacconi, L. J., Eisenhauer, F., et al. 2006, Nature, 442, 786 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2011a, A&A, 530, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., Valenti, E., & Minniti, D. 2011b, A&A, 534, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2012, A&A, 543, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2013, A&A, 552, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guedes, J., Callegari, S., Madau, P., & Mayer, L. 2011, ApJ, 742, 76 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Guedes, J., Mayer, L., Carollo, M., & Madau, P. 2013, ApJ, 772, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Immeli, A., Samland, M., Gerhard, O., & Westera, P. 2004, A&A, 413, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, C. I., Rich, R. M., Fulbright, J. P., Valenti, E., & McWilliam, A. 2011, ApJ, 732, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Rich, R. M., Kobayashi, C., et al. 2013, ApJ, 765, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K., & Rich, R. M. 2002, AJ, 124, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Lecureur, A., Hill, V., Zoccali, M., et al. 2007, A&A, 465, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mancini, C., Förster Schreiber, N. M., Renzini, A., et al. 2011, ApJ, 743, 86 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., & Zoccali, M. 2010, ApJ, 724, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Alves-Brito, A., et al. 2008, A&A, 484, L21 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Momany, Y., Ortolani, S., Held, E. V., et al. 2003, A&A, 402, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nataf, D. M., Udalski, A., Gould, A., Fouqué, P., & Stanek, K. Z. 2010, ApJ, 721, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Noguchi, M. 1999, ApJ, 514, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Valenti, E., & Rich, R. M. 2005, MNRAS, 356, 1276 [NASA ADS] [CrossRef] [Google Scholar]
- Ortolani, S., Renzini, A., Gilmozzi, R., et al. 1995, Nature, 377, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Ortolani, S., Barbuy, B., Bica, E., et al. 2001, A&A, 376, 878 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfenniger, D., & Friedli, D. 1991, A&A, 252, 75 [NASA ADS] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Raha, N., Sellwood, J. A., James, R. A., & Kahn, F. D. 1991, Nature, 352, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Origlia, L., & Valenti, E. 2007, ApJ, 665, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Sahu, K. C., Casertano, S., Bond, H. E., et al. 2006, Nature, 443, 534 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Saito, R. K., Zoccali, M., McWilliam, A., et al. 2011, AJ, 142, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, J., Rich, R. M., Kormendy, J., et al. 2010, ApJ, 720, L72 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Sumi, T. 2004, MNRAS, 349, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Udalski, A., Zebrun, K., Szymanski, M., et al. 2000, Acta Astron., 50, 1 [NASA ADS] [Google Scholar]
- Valcarce, A. A. R., Catelan, M., & Sweigart, A. V. 2012, A&A, 547, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, E., Ferraro, F. R., & Origilia, L. 2004a, MNRAS, 351, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, E., Ferraro, F. R., & Origilia, L. 2004b, MNRAS, 354, 815 [NASA ADS] [CrossRef] [Google Scholar]
- van Helshoecht, V., & Groenewegen, M. A. T. 2007, A&A, 463, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Cassisi, S., Frogel, J. A., et al. 2000, ApJ, 530, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Barbuy, B., Hill, V., et al. 2004, A&A, 423, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Lecureur, A., Barbuy, B., et al. 2006, A&A, 457, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Hill, V., Lecureur, A., et al. 2008, A&A, 486, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 2MASS image of the Galactic bulge (Skrutskie et al. 2006). The peanut shape of the Bulge is clearly visible. From left to right (decreasing longitude), the location of the fields observed with HAWK-I is approximately marked with filled squares, red for the two bulge fields and green for the disk control field. |
| In the text | |
 |
Fig. 2 Difference between the input and output magnitude of the artificial star experiments on the HAWK-I frames for the observed bulge and disk fields. Notice the typical asymmetry of these differences, with blending with fainter sources making some stars brighter than they are. |
| In the text | |
 |
Fig. 3 Right panel c): the derived (Ks,J − Ks) CMD of all stars measured in the BUL-SC29 field, including both bulge and disk contributions. Black dots refer to stars with errors smaller than the selection applied in panels a) and b) (see text for more details), with green points referring to stars whose errors exceed such limits. Black crosses show stars from 2MASS, which are saturated in the HAWK-I images. |
| In the text | |
 |
Fig. 4 As Fig. 3 but for the observed bulge BUL-SC9 field. |
| In the text | |
 |
Fig. 5 Panel a): the observed CMD of the bulge BUL-SC29 field . The red solid line is the 1 Gyr isochrone for a solar metallicity population (Pietrinferni et al. 2006). Panel b): the observed CMD of the disk control field ~30° away from the Galactic center. The region within the box has been used to normalize the number of disk stars seen through the bulge line of sight. Panel c): the CMD of the bulge BUL-SC29 field as statistically decontaminated from the disk population. Panel d): the CMD of the stars that were statistically subtracted from the CMD in panel a) in order to obtain the decontaminated CMD shown in panel c). |
| In the text | |
 |
Fig. 6 Same as Fig. 5 but for the bulge BUL-SC9 field. |
| In the text | |
 |
Fig. 7 LFs of the observed bulge fields as obtained from the disk-decontaminated CMDs. The black arrows mark the location of the HB-RC whereas the gray areas refer to the approximate location of the MS-TO. |
| In the text | |
 |
Fig. 8 Upper panels: the CMDs from 2MASS of the upper RGB for the two 30′ × 30′ fields including our Hawk-I bulge fields in the absolute [MK, (J − Ks)0] plane. The empirical globular cluster RGB templates are over plotted with metallicities from [Fe/H] = −2.1 to +0.35 (see text in Sect. 5 for details on cluster names and metallicities). Black symbols indicate the stars used to derive the photometric MDF. Bottom panels: derived photometric MDF of the observed bulge fields with a bin size of 0.15 dex. |
| In the text | |
 |
Fig. 9 Comparison between the CMDs of the bulge fields observed in this work (left and right panels). The magnitude difference between the HB-RC and MS-TO of the BUL-SC29 field (dashed horizontal lines) is compared with the same quantity for the BUL-SC9 field. The CMD of the BUL-SC9 field has been shifted in magnitude and color to match the location of BUL-SC29 HB-RC. In both these panels the solid red line is the empirical ridge line of the CMD of the BUL-SC29 field. The central panel shows the J − (J − H) CMD of the bulge globular cluster NGC 6528, showing that the luminosity difference between the HB–RC and the MS–TO is virtually identical to that of the two bulge fields. |
| In the text | |
 |
Fig. 10 CMD of the BUL-SC29 field with overplotted theoretical isochrones (Valcarce et al. 2012). Isochrone ages, metallicities, and helium abundances are indicated near the top-left corner of each panel. Sub-solar isochrones are α-enhanced, and solar-scaled otherwise. The metallicity range covered by the bulk of the stars in the BUL-SC29 field is 0.002 ≲ Z ≲ 0.060, as derived in Sect. 5. Open circles mark stars that are most likely blue stragglers (see text for more details). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


