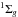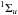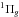| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A70 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201321712 | |
| Published online | 15 November 2013 | |
Blue satellites on He lines due to He-He collisions⋆
1
Observatoire de Paris, GEPI, UMR 8111, CNRS, Université Paris VII, 61
avenue de l’Observatoire,
75014
Paris,
France
e-mail:
nicole.allard@obspm.fr
2
Institut d’Astrophysique de Paris, UMR 7095, CNRS, Université
Paris VI, 98bis Boulevard
Arago, Paris,
France
3
Laboratoire de Physique et Chimie Quantique, Université de
Toulouse (UPS) and CNRS, 118 route
de Narbonne, 31400
Toulouse,
France
4
Department of Physics and Astronomy, University of
Louisville, Louisville, Kentucky
40292,
USA
Received:
16
April
2013
Accepted:
3
September
2013
The shape and broadening of He lines affects radiative transport in dense, He-rich, stellar atmospheres. At wavelengths inaccessible for direct observation, we rely on theoretical calculations of self-broadening to support stellar structure and spectral modeling. In this work, we examine lines of He due to 1s–2p and 2p–3s transitions. The line profiles are analyzed in terms of a unified theory of spectral line broadening using ab initio potential energies that have been recently determined. For temperatures up to 20 000 K, the linear dependence of width and shift on gas density and the non-linear dependence on temperature of the Lorentzian core of the resonance line are described. Beyond the conventional symmetrical Lorentzian core, we show that they are asymmetrical and have significant additional contributions on the short wavelength side. This blue asymmetry is a consequence of maxima in the corresponding He2 potential energy difference curves at short and intermediate internuclear distance. Over a limited range of density and temperature, laboratory measurements in the visible and near infrared can be used to validate the potentials that underlie the spectral line profile theory, which is useful for modeling spectra over the extreme ranges of temperature and density encountered in stellar and planetary atmospheres.
Key words: line: profiles / stars: atmospheres / brown dwarfs / white dwarfs
Data of Fig. 6 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/559/A70
© ESO, 2013
1. Introduction
Despite being the second most abundant element in the universe, He produces few strong features in the spectra of stars. The resonance line is a singlet transition at 584 Å in the extreme ultraviolet, which is out of reach for direct detection by most space-based assets and ground-based observatories. Yet, self-broadening of the line affects radiative energy transport, the structure of star, its cooling, and evolution in the atmospheres of cool He-rich stars. In the solar atmosphere, the strongest observable spectral features produced by helium are in the extreme ultraviolet below 584 Å. The D3 triplet line at 5876 Å and the near-infrared triplet line at 10 830 Å are widely used indicators of chromospheric activity. Deep in the atmosphere of stars, radiative transport depends on the opacity and thereby on the line broadening that results from collisions primarily with H and He. For example, a primary consideration in He-rich degenerate stars would be the opacity from the He atomic lines broadened by He atomic collisions (Jeffery 2008; Pandey & Lambert 2011), while broadening by He remains a significant determinant for the spectral line shapes in other stars.
The effect of collision broadening by atomic and molecular H and by He on the spectral lines of other elements is central to understanding the opacity of stellar atmospheres, yet there have been only a few definitive comparisons with experimental work. For atomic H, this is because of the difficulty of creating an environment in a laboratory experiment simulating a stellar atmosphere. While there are limited experiments for He for broadening of alkali and alkaline earths, there are only a few for many other elements of astrophysical interest. Instead, there is a reliance on simplified models of line-broadening physics that remain in the code in current use (Hauschildt et al. 1999; Schweitzer et al. 1996). These models, typically described as van der Waals broadening with impact approximation Lorentzian line shapes, have long been known to be not valid, but they remain the only fast approximation available (Allard & Kielkopf 1982). To make them more tractable, the coefficients are typically adjusted empirically, or on the basis of semi-empirical pseudo-potential models for the relevant atomic interactions. Unfortunately, the interaction potentials and radiative transition moments for many atomic species that are needed to compute broadening have not been known until recently with sufficient accuracy. On the other hand, the maturing capability of ab initio methods and the availability of both open source and commercial packages that can be applied to these problems now offer the possibility of accurately computing the interaction of H and He with atoms and small molecules that are likely to be found in the Sun, other stars, and exoplanet atmospheres. In this paper, we focus our attention on the He spectrum itself by considering the effects of He collisions with radiating He atoms. Although these effects are largely indirect except in type DB white dwarfs, they are the foundation of a more expansive effort to establish a rigorous and physically justifiable framework that includes neutral atom collision broadening in all types of stellar atmospheres. Furthermore, they suggest observational and laboratory tests that can validate the applicability of the potentials to spectral line profile calculations.
The potentials of He2 that come into play in this discussion are more complex than those of H2, because there are more electrons to include in an a priori calculation and there have been few other theoretical studies to explore resonance spectral line broadening accurately in either experiment or theory. The singlet resonance line in the extreme ultraviolet is not accessible for high resolution spectroscopy, but visible and near-infrared singlet lines were studied with high precision at low density and low temperature by Kuhn & Vaughan (1963) and Vaughan (1966) who found the Lorentzian line cores and measured line widths and shifts. Mullamphy et al. (1991) computed self-broadening of the He singlet lines 2s1S – np1P for n = 3, 4, 5 and 6, and 2p1P – nd1D for n = 3, 4 and 5 using a semiclassical impact broadening theory with model potentials to compare to the experiments of Vaughan (1966). Similarly, the self-broadening of the triplet transitions was also calculated by Leo et al. (1992) using the framework of a semiclassical impact broadening with model potentials. Close-coupled calculations for self-broadening of He triplet lines based on the Baranger theory, which uses adiabatic model molecular potentials, revealed sensitivity of the line parameters. This suggests that width and shift could be used to verify potentials within the limits of validity of the line-shape theory (Leo et al. 1995). Unfortunately, there is sparse experimental data that can be compared to these line core calculations, although recent astrophysical analyses of degenerate white dwarf stars using self-broadening calculations by Leo et al. (1995) and estimates based on van der Waals broadening with more reliable calculations were not available (Kleinman et al. 2013).
Although comprehensive line shape experiments on the He spectrum at high density would be far more definitive than line core measurements, there are none available at this time. However, recent observations of a corona discharge in liquid He revealed a feature-rich spectrum, and an analysis based on line broadening theory and precise He2 potentials provided a powerful aid in interpreting these data (Allard 2012).
Line profile calculations in our work have been done in unified line-shape semiclassical theory (Anderson 1952). Moreover, the impact approximation determines the asymptotic behavior of the unified line shape correlation function. In this way the results described here are applicable to a more general line profile and opacity evaluation for the same perturbers at any given layer in the photosphere. We examine the dependence on temperature of the line wing and of the line parameters.
 |
Fig. 1 Potential energies for the singlet 3s, 2p and 2s states of the He2
molecule. As noted, |
2. He2 molecular potential energy
Very recently, significant progress in the description of He2 singlet and triplet potential energies has been achieved (Allard et al. 2009; Dell’Angelo et al. 2012; Bonifaci et al. 2012).
In this work, the ab initio computation of the adiabatic potential energy curves of
He2 have been carried out using the MOLPRO 2009 package1. A huge multi reference configuration interaction (MRCI) computation
has been performed by starting from a very large multi configuration self consistent field
(MCSCF). The MCSCF calculation involved 26 active orbitals and a very large basis set
(called basis E) composed of 118 orbitals for each He atom (21s, 12p, 8d, 3f). For the
lowest quintet state this approach was shown (Deguilhem
2009) to be very effective compared to full CI results, leading to differences much
less than a tenth of a wavenumber. We have also checked that using orbitals optimized from
state-averaged or the quintet state lead to almost identical results, which is a strong
indication that this is very close to the full CI result. Therefore, the main limitation in
the accuracy of these adiabatic potential curves resides in a limitation due to the finite
basis set used. However, this error is expected to be small considering the quality of the
basis set. The basis set was initially optimized to give spectroscopic accuracy
(≈1 cm-1) interaction potentials between metastable atoms through the
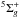 state
(Gadéa et al. 2002). It was then considerably
enlarged to improve the accuracy below 0.1 cm-1. It was reduced to a reasonable,
although still huge, size and further increased to consider the n = 2, 3
Rydberg states involved in the photoassociation of cold metastable atoms (Deguilhem et al. 2009). The refined basis set is thus
accurate for states involving He atoms in the ground state and in the excited
n = 2, 3 Rydberg states. As shown by many previous calculations, almost
all the lower excited states present large barriers at intermediate distances
(R between 3 and 4 a.u.) and deep wells at equilibrium distances close to
R = 2 a.u. These barriers are often called “nonessential maxima”. The
wells are clearly imprinted by the deep well of the ionic ground state
(Re = 2.042 a.u.,
De = 19 956 cm-1, Chicheportiche et al. 2013). However, we require the
complete calculation because a simple picture with an ionic core and a Rydberg electron
alone cannot describe these potentials with the accuracy needed for finding spectral line
shapes.
state
(Gadéa et al. 2002). It was then considerably
enlarged to improve the accuracy below 0.1 cm-1. It was reduced to a reasonable,
although still huge, size and further increased to consider the n = 2, 3
Rydberg states involved in the photoassociation of cold metastable atoms (Deguilhem et al. 2009). The refined basis set is thus
accurate for states involving He atoms in the ground state and in the excited
n = 2, 3 Rydberg states. As shown by many previous calculations, almost
all the lower excited states present large barriers at intermediate distances
(R between 3 and 4 a.u.) and deep wells at equilibrium distances close to
R = 2 a.u. These barriers are often called “nonessential maxima”. The
wells are clearly imprinted by the deep well of the ionic ground state
(Re = 2.042 a.u.,
De = 19 956 cm-1, Chicheportiche et al. 2013). However, we require the
complete calculation because a simple picture with an ionic core and a Rydberg electron
alone cannot describe these potentials with the accuracy needed for finding spectral line
shapes.
 |
Fig. 2 Potential energy curve for the 1s |
Potential energy curves V(R) for the He2 molecule in the 2s1S, 2p1P and 3s1S states are shown in Fig. 1, where R denotes the internuclear distance between the radiator and the perturber. Recently the ground state, 1s1S, has been determined using other high level ab initio methods, namely, a complete active space self-consistent field-multireference configuration interaction (CASSCF-MRCI) by Dell’Angelo et al. (2012). Our potential is in excellent agreement with their determination as shown in Fig. 2.
3. Theoretical profiles
Starting from the Anderson (1952) theory of pressure
broadening, which is suitably generalized to include degeneracy, a unified theory of
spectral line broadening (Allard et al. 1999) has been
developed to calculate neutral atom spectra, given the interaction and the radiative
transition moments of relevant states of the radiating atom with other atoms in its
environment. The spectrum, I(Δω), is the Fourier transform
(FT) of the dipole autocorrelation function, Φ(s). It is given by
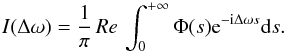 (1)A pairwise additive
assumption allows us to calculate I(Δω), when
N perturbers interact as the FT of the Nth
power of the autocorrelation function φ(s) of a unique
atom-perturber pair. For a perturber density np, we obtain
(1)A pairwise additive
assumption allows us to calculate I(Δω), when
N perturbers interact as the FT of the Nth
power of the autocorrelation function φ(s) of a unique
atom-perturber pair. For a perturber density np, we obtain
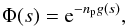 (2)where decay of the
autocorrelation function with time leads to atomic line broadening.
(2)where decay of the
autocorrelation function with time leads to atomic line broadening.
For a transition α = (i,f) from an initial state
i to a final state f, we have ![\begin{eqnarray} g_{\alpha}(s) &=& \frac{1} {\sum_{e,e'} \, \! ^{(\alpha)} \, |d_{ee'}|^2 } \sum_{e,e'} \, \! ^{(\alpha)} \; \; \nonumber \\ && \times~ \int^{+\infty}_{0}\!\!2\pi\rho {\rm d}\rho \int^{+\infty}_{-\infty}\!\! {\rm d}x \; \tilde{d}_{ee'}[ \, R(0) \, ] \, \nonumber \\ &&\times~[ \, {\rm e}^{\frac{i}{\hbar}\int^s_0 \, {\rm d}t \; V_{e'e }[ \, R(t) \, ] } \, \, \tilde{d^{*}}_{ee'}[ \, R(s) \, ] \, - \, \tilde{d}_{ee'} [ \, R(0) \, ] \, ] . \label{eq:gcl} \end{eqnarray}](/articles/aa/full_html/2013/11/aa21712-13/aa21712-13-eq33.png) (3)We
define
(3)We
define 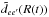 as a modulated dipole (Allard et al. 1999)
as a modulated dipole (Allard et al. 1999) ![\begin{equation} D(R) \equiv \tilde{d}_{ee'}[R(t)] = d_{ee'}[R(t)]{\rm e}^{-\frac{\beta}{2}V_{e}[R(t)] } , \label{eq:mod} \end{equation}](/articles/aa/full_html/2013/11/aa21712-13/aa21712-13-eq35.png) (4)where
β is the inverse temperature (1/kT).
Here Ve is the ground state potential when we
consider absorption profiles, or an excited state for the calculation of a profile in
emission.
(4)where
β is the inverse temperature (1/kT).
Here Ve is the ground state potential when we
consider absorption profiles, or an excited state for the calculation of a profile in
emission.
In the present context, the perturbation of the frequency of the atomic transition during
the collision results in a phase shift, η(s), that is
calculated along a classical path R(t) assumed to be
rectilinear. The phase shift is ![\begin{equation} \eta(s) = \frac{{i}}{\hbar}\int^s_0 \, {\rm d}t \; \; V_{e'e }[ \, R(t) \, ] , \label{eq:phase} \end{equation}](/articles/aa/full_html/2013/11/aa21712-13/aa21712-13-eq41.png) (5)where
Ve′e [R(t)],
the difference of potential energies, is given by
(5)where
Ve′e [R(t)],
the difference of potential energies, is given by
![\begin{equation} \Delta V(R) \equiv V_{e' e}[R(t)] = V_{e' }[R(t)] - V_{ e}[R(t)] . \end{equation}](/articles/aa/full_html/2013/11/aa21712-13/aa21712-13-eq43.png) (6)This represents the
difference between the electronic energies of the quasimolecular transition. The potential
energy for a state e is
(6)This represents the
difference between the electronic energies of the quasimolecular transition. The potential
energy for a state e is
![\begin{equation} V_{e}[R(t)] = E_e[ R(t) ]-E_e^{\infty} . \end{equation}](/articles/aa/full_html/2013/11/aa21712-13/aa21712-13-eq45.png) (7)At time
t from the point of closest approach, the path is
(7)At time
t from the point of closest approach, the path is
![\begin{equation} R(t) = \left[\rho ^2 + (x+\bar{v} t)^2 \right]^{1/2} \end{equation}](/articles/aa/full_html/2013/11/aa21712-13/aa21712-13-eq47.png) (8)with
ρ as the impact parameter of the perturber trajectory and
x as the position of the perturber along its trajectory at time
t = 0. In Eq. (3), the
e and e′ label the energy surfaces on which
the interacting atoms approach the initial and final atomic states of the transition as
R → ∞. The sum
(8)with
ρ as the impact parameter of the perturber trajectory and
x as the position of the perturber along its trajectory at time
t = 0. In Eq. (3), the
e and e′ label the energy surfaces on which
the interacting atoms approach the initial and final atomic states of the transition as
R → ∞. The sum 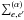 is over all pairs (e,e′), such that
ωe′,e(R) → ωα
as R → ∞. In this work, we are limited by a lack of knowledge of the
dependence of the radiative transition dipole moment on atom-atom separation. For the
purpose of this evaluation, we suppose it is constant and equal to its asymptotic value.
is over all pairs (e,e′), such that
ωe′,e(R) → ωα
as R → ∞. In this work, we are limited by a lack of knowledge of the
dependence of the radiative transition dipole moment on atom-atom separation. For the
purpose of this evaluation, we suppose it is constant and equal to its asymptotic value.
4. Astrophysical applications
The construction of model atmospheres and synthetic spectra for cool He-rich white dwarfs (DB, DC) is necessary to derive reliable atmospheric parameters and the surface chemical composition for these objects. Pressure broadening by molecular H and He is also the major broadening mechanism in the atmospheres of brown dwarfs. In extreme He stars, the H Balmer lines are very weak or totally absent, with their place being taken by neutral He. The absence of H spectral lines means that the metallic-line spectrum is much stronger than in a normal star. This is a major concern for the calculation of model atmospheres, when the effect of all other opacity sources on the structure of the atmosphere is significantly enhanced in the absence of H. An incomplete or inaccurately calculated opacity results in systematic errors in the predicted flux distribution and hence, in the effective temperature. While Heber & Schoenberner (1981) first introduced the blanketing effect of strong ultraviolet metal lines, methods to include all the broadened lines remain elusive.
The atmospheres of DB and many DC white dwarfs are almost pure helium, and the correct treatment of the He resonance lines strongly influences the predicted spectrum and effective temperature. In about 20% or more of these stars, type DBZ show metal lines. Because metals would rapidly settle, only H and He should appear in the spectra, unless there is dredging from the interior or accretion of material from a disk or remnant of a former exoplanetary system. The analysis of DBZ spectra is therefore a potentially valuable method to determine the existence in the stellar progenitor of exoplanetary systems and their chemical abundances (Farihi 2011; Koester et al. 2011; Dufour et al. 2012).
In this work, we consider broadening of He by He to develop an accurate treatment of the resonance lines that enable correct calculations of radiative transport in DB white dwarfs. The potentials used also allow calculation of profiles that can be tested in the laboratory as a first stage in developing a robust and validated methodology for computing neutral collision broadened opacities that will be incorporated into general stellar atmosphere codes.
5. Study of the resonance line at 584 Å
Full collisional line profiles were evaluated for the conditions prevailing in brown dwarf atmospheres from 1000 to 6000 K. The line cores were also studied to higher temperature, as described below. The line wings show a structure resulting from the details of the atomic interactions, while the impact broadened Lorentzian core has a linear dependence of width and shift on density with a non-linear power-law dependence on temperature.
 |
Fig. 3 1s → 2p line profile for T = 1000 K and nHe = 1020 cm-3. |
5.1. Prediction of satellite lines in the 1s–2p line wing
The unified profile shown in Fig. 3 is the Fourier
transform of the autocorrelation function as given by Eq. (3) in which the contributions from the two components of the transition
enter with their statistical weights. The unified theory predicts that there will be line
satellites centered periodically at frequencies corresponding to integer multiples of the
extrema of ΔV. The interpretation of the asymmetrical shape of the 1s →
2p line requires us to study ΔV, as shown in Fig. 4. The difference potential maxima are respectively 4300 and 3000
cm-1 for 1s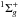 →
2p
→
2p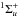 and
1s
and
1s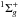 →
2p
→
2p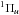 , which lead
to a far blue satellite at 4000 cm-1 (571.4 Å) and a small bump at 2600
cm-1 (576 Å) (Figs. 3 and 5). Figure 5 shows
the individual components for comparison, weighted as if they were the only contribution
to the profile. The satellite at 4000 cm-1 is the prominent feature in the blue
wing that is very well-separated from the main line. There is a linear variation with
helium density for the strength of the blue wing as shown in Fig. 5, as long as nHe ≤ 1020
cm-3.
, which lead
to a far blue satellite at 4000 cm-1 (571.4 Å) and a small bump at 2600
cm-1 (576 Å) (Figs. 3 and 5). Figure 5 shows
the individual components for comparison, weighted as if they were the only contribution
to the profile. The satellite at 4000 cm-1 is the prominent feature in the blue
wing that is very well-separated from the main line. There is a linear variation with
helium density for the strength of the blue wing as shown in Fig. 5, as long as nHe ≤ 1020
cm-3.
 |
Fig. 4 ΔV for the two transitions contributing to 1s → 2p line:
1s |
 |
Fig. 5 Variation with nHe, the He atom density, of the blue
wing at T = 1000 K:
nHe = 1020 cm-3 (full line) and
nHe = 1019 cm-3 (dashed dotted
lines). Individual components are superimposed:
1s |
 |
Fig. 6 Variation with the temperature of the 1s → 2p line for nHe = 1019 cm-3. |
In the range of temperatures prevailing in atmospheres of brown dwarfs, the blue wing shown in Fig. 6 is not very sensitive to the temperature. However, the wing strength relative to the total line strength increases linearly in density.
 |
Fig. 7 Variation with the temperature of the two line parameters, the half-width at half-maximum and the shift, of the 1s → 2p resonance line at approximately 584 Å. |
5.2. Study of the line core parameters
Since the resulting line profile in a model atmosphere calculation is the integration of the flux in all layers from the deepest to the uppermost, it is important that the centers be adequately represented; that is, they can be non-Lorentzian at high densities of the innermost layers, while Lorentzian in the upper atmosphere. However, they are characterized with different widths than predicted by the hydrogenic van der Waals approximation, which is usually used for the cores, as it was emphasized by Allard et al. (2007) and Peach (2011).
An atomic line broadened by collisions in a low density gas has a Lorentzian profile near
the line center, which can be related to the FT of a radiative wave where short duration
collisions produce sudden phase changes. The core shape does not depend on the assumption
that the interaction is given by a van der Waals approximation, but the width and shift of
the core are very dependent on the nature of the interactions between the atoms. In the
theory of impact broadened line shapes, the phase shifts are given by Eq. (5) with the integral taken between
s = 0 and ∞. At sufficiently low densities of helium, which are found
in the upper atmospheres of stars or planets, the symmetric Lorentzian center of the
spectral line can be defined by the two line parameters given in Fig. 7, the half-width at half maximum
w/2 and the shift d of the Lorentzian
main line. The half-width and shift of the core are often represented by
γ and σ in atomic physics literature. For the
densities and temperatures of interest, these parameters were found to be given by
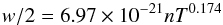 (9)and
(9)and
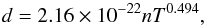 (10)where n
is the atom density in units of cm-3 and T the temperature in
K.
(10)where n
is the atom density in units of cm-3 and T the temperature in
K.
6. Study of the line profile due to the 2p–3s transitions
In an extreme He environment with very high densities, and very low temperatures, spectroscopic investigations of a corona discharge in liquid helium (LHe) at 4.2 K have revealed a complex behavior (Li et al. 2009). Clearly, studying the variation of shape of the 2p–3s line with increasing helium density allows us to understand the blue shift observed in these experiments. The analysis and interpretation of these experimental spectra require the use of a suitable theoretical framework with the most accurate He2 molecular potentials. Allard et al. (2009) presented the first calculations of He-He collisional profiles due to the triplet 2p–3s transitions in a unified line-shape semiclassical theory that uses ab initio molecular potentials. The excellent agreement seen in Fig. 8 between experimental and theoretical determinations of the near wing of the line profiles established the accuracy of the interaction potentials. This exceptional concordance with the underpinning theoretical physics allowed us to interpret the experimental profiles that were obtained at temperatures up to that of LHe at 4.2 K (Allard et al. 2011; Allard 2012). We review the similarities and differences in the theoretical spectra due to the singlet and triplet 3s–2p transitions.
 |
Fig. 8 Experimental profile at a pressure of 1.6 MPa and temperature of 300 K, (nHe(T,P) = 3.8 × 1020 cm-3) as compared to the unified profile. (Extracted from Allard et al. 2009). |
6.1. Quasi-molecular line satellites for the 3s–2p transitions
A detailed description of the triplet 3s–2p line at 706 nm has been given by Allard et al. (2009) and Allard et al. (2011). The singlet line at 728 nm in emission has also been investigated by Li (2008) for a large range of He densities and temperatures of the order of 300 K. While we observe the same general shape for the singlet line, the important feature of these lines is the development of a blue wing. Their study reveals the complexity of this spectral region where different molecular systems overlap, and the importance of non-Lorentzian line shapes. The molecular states Σg,u combining with the Πg,u and Σg,u shown in Fig. 1 states are associated with the transition 3s–2p transition.
6.2. Analysis of the profiles
Table 1 lists the electronic states connecting the 3s and 2p states. The potential energy curves for these states are shown in Fig. 1. Line satellite positions ΔωHe2 are functions of the maxima of the potential difference ΔV shown in Fig. 10. These values are smaller for the singlet line than for the triplet, which leads to a less extended singlet blue wing shown in Fig. 9. The line profile depends on four individual transitions with each contribution given by the FT of an autocorrelation function for one component in Fig. 11. The distinction allows the identification of the transition, which gives rise to each line satellite. The distinct shoulder at about 80 cm-1 in Fig. 11 is due to the 3sΣu − 2pΠg transition, but the line satellites at low density blend into the total profile.
The triplet line provides an example of a transition that is intermediate between the evident satellites seen in the 1s–2p line and the totally unresolved satellites associated with a singlet line in Fig. 9. Because the satellite feature is broad, there is little effect on the shift and the profile has the appearance of a reasonably sharp line with a pronounced smooth blue asymmetry.
Physical parameters in the study of the 3s–2p line.
 |
Fig. 9 Unified profiles for singlet (dashed lines) and triplet (full line) 3s → 2p line at T = 300 K and nHe = 1019 cm-3. |
 |
Fig. 10 ΔV for the four transitions contributing to the 2p–3s line. |
 |
Fig. 11 Individual components of the blue far wing compared to the total at T = 300 K and for nHe = 1019 cm-3. |
 |
Fig. 12 Unified profiles for the singlet 3s1S → 2p1P line at T = 300 K and nHe varying from 3 × 1020 to 1021 cm-3. |
 |
Fig. 13 Variation with nHe of the full width w of the singlet (dashed lines) and triplet (full line) 3s → 2p lines for 300 K. |
6.3. Line parameters
A theoretical analysis of the variation of the line parameters with He density has been extensively done for the triplet line by Allard et al. (2011), and the same analysis can be done for a brief comparison to the evolution of the singlet line profile at 300 K.
The dependence of the parameter curves for the 3p–3s lines on perturber density is very well explained by the existence of satellites close to the line. Although the singlet parameter curves are smooth and apparently featureless, it is possible to predict their shapes just by examining ΔV. The greater slope for the singlet line is associated with the line satellites that are closer to the parent line. In Figs. 13, 14 we have plotted the width and shift as a function of nHe. These curves are easily understood by examining Fig. 12. The general shape of the singlet line is changing very fast between 1020 and 1021 cm-3. When the density reaches 3 × 1020 cm-3, the blue shoulder at 80 cm-1 starts to be detectable. Its development leads to the sudden change in the slope of the width curve, as seen in Fig. 13. The reason for this transition to very non-linear behavior is that one is first measuring the width proper at lower density. Then, as the density increases and the satellite grows to more than one half the height of the line, one is measuring the combined width of line and satellites in Fig. 15. Figure 16 reveals that the development of the blue wing leads to the overwhelming of the line by the satellites, when the density is about 1021 cm-3. For the triplet line in Fig. 15, there is a very clear blue satellite. At 7 × 1020 cm-3, the top of this satellite is about half way up the line, and this effect is again responsible for an abrupt transition from the linear variation when the line core was not affected by the blue satellites to a strongly non-linear effect when it is. When the density reaches reaches 1.2 × 1021 cm-3, the satellite completely blends with the line seen in Fig. 17.
The evolution of the line profiles reveals the same influences by the blue satellites. However, corresponding features occur at lower density due to the closer relative proximity of the satellites to the line at about 80 cm-1 for the singlet and 100 cm-1 for the triplet.
 |
Fig. 14 Variation with nHe of the shift of the singlet (dashed lines) and triplet (full line) 3s → 2p lines for 300 K. |
 |
Fig. 15 Unified profiles for singlet (dashed lines) and triplet (full line) 3s → 2p lines at T = 300 K and nHe = 7 × 1020 cm-3. |
 |
Fig. 16 Unified profiles for singlet (dashed lines) and triplet (full line) 3s → 2p lines at T = 300 K and nHe = 1021 cm-3. |
 |
Fig. 17 Unified profiles for singlet (dashed lines) and triplet (full line) 3s → 2p lines at T = 300 K and nHe = 1.2 × 1021 cm-3. |
As shown in Fig. 14 at low density, both the singlet and triplet are about equally shifted. However at densities larger than nHe = 6 × 1020 cm-3, the slope of the singlet shift with density increases, whereas it remains almost unchanged for the triplet. The spacing of the satellite compared to the width of the line influences this behavior, since the blue satellite is less important for the triplet. An increased He density results in a new change of the slope shown in Fig. 14. At nHe = 1021, the singlet profile shift towards the position of the satellite band. It is a smooth transition for the singlet, whereas the triplet has a sharper transition, and one sees the characteristic shift discontinuity at nHe = 1.2 × 1021 cm-3.
We see that the profiles, shifts, and widths of the singlet and triplet lines are thus very sensitive to helium density and temperature (Allard et al. 2011). Consequently, they provide information on the conditions present in the observed helium medium. They clearly illustrate how non-linear the non-Lorentzian shapes can become outside the limited range of validity of the impact approximation usually used in stellar and planetary atmosphere modeling.
7. Conclusion
The main purpose of this work is to analyze He line profiles by examining the development of quasi-molecular effects in He-He collisions. Profiles of the 1s–2p and 2p–3s transitions computed with unified line-shape theory exhibit a blue asymmetric behavior illustrated in Figs. 3 and 12.
We have found that the 1s → 2p line is totally asymmetric outside the line core without any contribution in the red wing. This effect is of increasing importance with He density, and as a result, the full treatment of the He resonance line at 584 Å reveals strong effects on its opacity outside the impact approximation. Consequently, we conclude that these effects are not always negligible when models of stellar spectra are compared with observations to determine abundances, structural properties, or ages.
We have also reported the first analysis of the line parameters of the He(3s1S)–He(2p1P) line outside of the impact approximation. This serves as a test for the use of ab initio atomic potentials in spectral line-shape calculations, because the predictions of the theory agree with laboratory experiments. We have shown that the presence of line satellites in the near line wing leads to a complex behavior of the dependence of the line shape, and the conventional line width and shift parameters on He density. Previously, Allard (2011) discussed the major importance of temperature and perturber density in the broadening and shift of the He 706 nm triplet 2p–3s transition. That work allowed Allard (2012) to determine the physical conditions of temperature and pressure in an electric discharge in liquid He from experimental spectra. More generally, the important sensitivity of He-line shapes to temperature and density suggests that they could be used as a spectroscopic diagnostic tool.
Acknowledgments
We are grateful to Dr. G. Guillon and Dr. A. Viel for kindly providing the up-to-date He2 molecular potential. One of us (NFA) would like to thank Dr. D. Koester for useful discussion. This work was supported in part by PNPS which allows the collaboration with the Laboratoire de Chimie et Physique Quantique in Toulouse.
References
- Allard, N. F. 2011, in ASP Conf. Ser. 450, eds. J. P. Beaulieu, S. Dieters, & G. Tinetti, 87 [Google Scholar]
- Allard, N. F. 2012, J. Phys. Conf. Ser., 397, 012065 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, N. F., & Kielkopf, J. F. 1982, Rev. Mod. Phys., 54, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, N. F., Royer, A., Kielkopf, J. F., & Feautrier, N. 1999, Phys. Rev. A, 60, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, N. F., Kielkopf, J. F., & Allard, F. 2007, EPJ D, 44, 507 [Google Scholar]
- Allard, N. F., Deguilhem, B., Gadéa, F. X., Bonifaci, N., & Denat, A. 2009, Europhys. Lett., 88, 53002 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allard, N. F., Bonifaci, N., & Denat, A. 2011, EPJ D, 61, 365 [Google Scholar]
- Anderson, P. W. 1952, Phys. Rev., 86, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifaci, N., Aitken, F., Atrazhev, V. M., Fiedler, S. L., & Eloranta, J. 2012, Phys. Rev. A, 85, 042706 [NASA ADS] [CrossRef] [Google Scholar]
- Chicheportiche, A., Lepetit, B., Nenhenni, M., Gadea, F., & YousfiK, M. 2013, J. Chem. Phys., 46, 4720 [Google Scholar]
- Deguilhem, B. 2009, Ph.D. Thesis, Université Paul Sabatier, France [Google Scholar]
- Deguilhem, B., Leininger, T., Gadea, F. X., & Dickinson, A. S. 2009, J. Phys. B: At. Mol. Opt. Phys., 42, 015102 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Angelo, D., Guillon, G., & Viel, A. 2012, J. Chem. Phys., 136, 114308 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dufour, P., Kilic, M., Fontaine, G., et al. 2012, ApJ, 749, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Farihi, J. 2011, in AIP Conf. Ser. 1331, eds. S. Schuh, H. Drechsel, & U. Heber, 193 [Google Scholar]
- Gadéa, F. X., Leininger, T., & Dickinson, A. 2002, J. Chem. Phys., 117, 7122 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., Allard, F., Ferguson, J., Baron, E., & Alexander, D. R. 1999, ApJ, 525, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U., & Schoenberner, D. 1981, A&A, 102, 73 [NASA ADS] [Google Scholar]
- Jeffery, C. S. 2008, in Hydrogen-Deficient Stars, eds. A. Werner, & T. Rauch, ASP Conf. Ser., 391, 53 [Google Scholar]
- Kleinman, S. J., Kepler, S. O., Koester, D., et al. 2013, ApJSS, 204, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, D., Girven, J., Gänsicke, B. T., & Dufour, P. 2011, A&A, 530, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuhn, H. G., & Vaughan, J. M. 1963, Proc. Roy. Soc. A, 277, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Leo, P. J., Mullamphy, D. F. T., Peach, G., & Whittingham, I. B. 1992, J. Phys. B: At. Mol. Opt. Phys., 25, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Leo, P. J., Peach, G., & Whittingham, I. B. 1995, J. Phys. B: At. Mol. Opt. Phys., 28, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z. 2008, Ph.D. Thesis, University of J. Fourier Grenoble, France [Google Scholar]
- Li, Z., Bonifaci, N., Aitken, F., et al. 2009, EPJ AP, 47, 22821 [CrossRef] [EDP Sciences] [Google Scholar]
- Mullamphy, D. F. T., Peach, G., & Whittingham, I. B. 1991, J. Phys. B: At. Mol. Opt. Phys., 24, 3709 [NASA ADS] [CrossRef] [Google Scholar]
- Pandey, G., & Lambert, D. L. 2011, ApJ, 727, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Peach, G. 2011, Balt. Astron., 20, 516 [NASA ADS] [Google Scholar]
- Schweitzer, A., Hauschildt, P. H., Allard, F., & Basri, G. 1996, MNRAS, 283, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, J. M. 1966, Proc. Roy. Soc. A, 295, 164 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Potential energies for the singlet 3s, 2p and 2s states of the He2
molecule. As noted, |
| In the text | |
 |
Fig. 2 Potential energy curve for the 1s |
| In the text | |
 |
Fig. 3 1s → 2p line profile for T = 1000 K and nHe = 1020 cm-3. |
| In the text | |
 |
Fig. 4 ΔV for the two transitions contributing to 1s → 2p line:
1s |
| In the text | |
 |
Fig. 5 Variation with nHe, the He atom density, of the blue
wing at T = 1000 K:
nHe = 1020 cm-3 (full line) and
nHe = 1019 cm-3 (dashed dotted
lines). Individual components are superimposed:
1s |
| In the text | |
 |
Fig. 6 Variation with the temperature of the 1s → 2p line for nHe = 1019 cm-3. |
| In the text | |
 |
Fig. 7 Variation with the temperature of the two line parameters, the half-width at half-maximum and the shift, of the 1s → 2p resonance line at approximately 584 Å. |
| In the text | |
 |
Fig. 8 Experimental profile at a pressure of 1.6 MPa and temperature of 300 K, (nHe(T,P) = 3.8 × 1020 cm-3) as compared to the unified profile. (Extracted from Allard et al. 2009). |
| In the text | |
 |
Fig. 9 Unified profiles for singlet (dashed lines) and triplet (full line) 3s → 2p line at T = 300 K and nHe = 1019 cm-3. |
| In the text | |
 |
Fig. 10 ΔV for the four transitions contributing to the 2p–3s line. |
| In the text | |
 |
Fig. 11 Individual components of the blue far wing compared to the total at T = 300 K and for nHe = 1019 cm-3. |
| In the text | |
 |
Fig. 12 Unified profiles for the singlet 3s1S → 2p1P line at T = 300 K and nHe varying from 3 × 1020 to 1021 cm-3. |
| In the text | |
 |
Fig. 13 Variation with nHe of the full width w of the singlet (dashed lines) and triplet (full line) 3s → 2p lines for 300 K. |
| In the text | |
 |
Fig. 14 Variation with nHe of the shift of the singlet (dashed lines) and triplet (full line) 3s → 2p lines for 300 K. |
| In the text | |
 |
Fig. 15 Unified profiles for singlet (dashed lines) and triplet (full line) 3s → 2p lines at T = 300 K and nHe = 7 × 1020 cm-3. |
| In the text | |
 |
Fig. 16 Unified profiles for singlet (dashed lines) and triplet (full line) 3s → 2p lines at T = 300 K and nHe = 1021 cm-3. |
| In the text | |
 |
Fig. 17 Unified profiles for singlet (dashed lines) and triplet (full line) 3s → 2p lines at T = 300 K and nHe = 1.2 × 1021 cm-3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.