| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 10 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201321695 | |
| Published online | 20 November 2013 | |
Multiperiodicity, modulations and flip-flops in variable star light curves
II. Analysis of II Pegasus photometry during 1979–2010⋆
1
Department of Physics, PO Box 64, 00014 University of Helsinki,
Finland
e-mail:
marjaana.lindborg@helsinki.fi
2
Aalto University, Department of Information and Computer
Science, PO Box
15400, 00076
Aalto,
Finland
3
Tartu Observatory, 61602
Tõravere,
Estonia
4
Finnish Centre for Astronomy with ESO (FINCA), University of
Turku, Väisäläntie
20, 21500
Piikkiö,
Finland
5
Center of Excellence in Information Systems, Tennessee State
University, 3500 John A. Merritt
Blvd., Box 9501, Nashville, TN
37209,
USA
6
Leibniz-Institute for Astrophysics Potsdam,
An der Sternwarte
16, 14482
Potsdam,
Germany
Received:
14
April
2013
Accepted:
12
September
2013
Aims. According to previously published Doppler images of the magnetically active primary giant component of the RS CVn binary II Peg, the surface of the star was dominated by one single active longitude that was clearly drifting in the rotational frame of the binary system during 1994-2002; later imaging for 2004–2010, however, showed decreased and chaotic spot activity, with no signs of the drift pattern. Here we set out to investigate from a more extensive photometric dataset whether this drift is a persistent phenomenon, in which case it could be caused either by an azimuthal dynamo wave or be an indication that the binary system’s orbital synchronization is still incomplete. On a differentially rotating stellar surface, spot structures preferentially on a certain latitude band could also cause such a drift, the disruption of which could arise from the change of the preferred spot latitude.
Methods. We analyzed the datasets using the carrier fit (CF) method, which is especially suitable for analyzing time series in which a fast clocking frequency (such as the rotation of the star) is modulated with a slower process (such as the stellar activity cycle).
Results. We combined all collected photometric data into one single data
set and analyzed it with the CF method. We confirm the previously published results that
the spot activity has been dominated by one primary spotted region almost through the
entire data set and also confirm a persistent, nearly linear drift. Disruptions of the
linear trend and complicated phase behavior are also seen, but the period analysis reveals
a rather stable periodicity with
Pspot = 6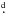 71054 ±
0
71054 ±
0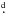 00005. After
removing the linear trend from the data, we identified several abrupt phase jumps, three
of which are analyzed in more detail with the CF method. These phase jumps closely
resemble what is called a flip-flop event, but the new spot configurations do not persist
for longer than a few months in most cases.
00005. After
removing the linear trend from the data, we identified several abrupt phase jumps, three
of which are analyzed in more detail with the CF method. These phase jumps closely
resemble what is called a flip-flop event, but the new spot configurations do not persist
for longer than a few months in most cases.
Conclusions. There is some evidence that the regular drift without phase jumps is related to the high state, while the complex phase behavior and disrupted drift pattern are related to the low state of magnetic activity. The most natural explanation of the drift is weak anti-solar (pole rotating faster than the equator) differential rotation with a coefficient k ≈ 0.002 combined with the preferred latitude of the spot structure.
Key words: stars: activity / techniques: photometric / starspots / stars: imaging
The full predicted light curve over the whole data span (Table 3) is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/559/A97
© ESO, 2013
1. Introduction
The system II Peg is one of the most extensively studied SB1 RS CVn systems; recently, surface temperature (e.g. Berdyugina et al. 1998a, 1999; Gu et al. 2003; Lindborg et al. 2011; Hackman et al. 2012) and magnetic field maps have been published (Kochukhov et al. 2013; Carroll et al. 2007, 2009). The star’s photometric light curves have also been intensively studied with time-series analysis and spot-modeling methods (see e.g. Henry et al. 1995; Rodonò et al. 2000; Siwak et al. 2010; Hackman et al. 2011; Roettenbacher et al. 2011). All longer-term light curve variations are commonly interpreted as being due to starspots (see e.g. the recent review by Strassmeier 2009), while shorter-term changes caused by flare type events, for instance, are also common in these objects (see e.g. Siwak et al. 2010). One peculiar feature reported especially by Lindborg et al. (2011) is the tendency of the magnetic activity to cluster on one primary active longitude, the position of which is linearly drifting in the orbital frame of reference of the binary system. Clustering of the spot activity on one single longitude has also been reported in other short-period eclipsing RS CVn systems, for example, by Zeilik & Budding (1987). In some previous studies of II Peg (e.g. Berdyugina et al. 1999), indications of flip flops were reported that the abrupt activity jumps from one longitude to another, separated roughly by 180 degrees, but the results of Lindborg et al. (2011) and Hackman et al. (2012) did not support this interpretation.
From comparisons with theoretical dynamo models (see e.g. Krause & Rädler 1980; Rädler 1975; Moss et al. 1995; Küker & Rüdiger 1999; Tuominen et al. 2002), the drift was preliminarily associated with an azimuthal dynamo wave of the non-axisymmetric dynamo solution, resulting from dynamo action caused by rotationally influenced turbulent convection without non-uniform rotation (so-called α2 dynamo mechanism). Typically, the dynamo models predict dynamo waves either rotating faster or slower with a constant angular frequency over time. In addition to the dynamo wave changing its position in the phase-time plot, the solutions may exhibit oscillatory behavior concerning the energy level of the mean magnetic field, reminiscent of a stellar cycle. In a recent study of Mantere et al. (2013), the modeling showed that the drift cycle length (i.e., the time required for the non-axisymmetric magnetic structure to make a full rotation in the rotational frame of reference) and the oscillation period of the magnetic energy were always connected. It has to be noted that in this particular study, only a very small fraction of the parameter space was mapped, within which solutions for which the drift cycle length and oscillation of the magnetic energy levels coincided were found to be preferred. Flip-flop-type switches have been found in dynamo models, in which relatively small amounts of differential rotation have been allowed for (so-called α2Ω modes, see e.g. Elstner & Korhonen 2005; Korhonen & Elstner 2011). In these models, flip-flops result from the competition of oscillatory axisymmetric mode and the stable non-axisymmetric mode of similar strengths.
II Peg belongs to a binary system whose rotational speed can be deduced from radial velocity measurements (e.g. Berdyugina et al. 1998b). It is well known that the tidal effects caused by the companion star will circularize the orbit of the binary system and force the rotation of the star to be synchronized to the orbital period of the binary in a time frame of a billion years after settling to the main sequence (see e.g. Zahn & Bouchet 1989). When the rotation of the star is not yet fully synchronized, that is, the rotational speed is still higher than implied by the orbital period of the binary, one would expect a systematic drift of the light curve minima when wrapped with the binary period; this constitutes the second possible explanation for the spot drift on the star’s surface. If this were the case, a persistent drift of the activity tracers should be observed, making the stellar surface and rotation visible to the observer over the whole extent of the time series – the amplitude of the spottedness or the magnetic field strength might still vary, but the drift should still be visible if this amplitude variation was removed. In contrast to the dynamo wave scenario presented above, no obvious connection between the drift versus the modulation should be visible.
A third possibility is provided by latitudinal differential rotation, that is, the angular
velocity changing as a function of latitude. Observational estimates for the differential
rotation parameter 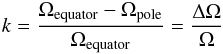 (1)for
II Peg vary from 0.005 ± 0.001 by Henry et al.
(1995), to
(1)for
II Peg vary from 0.005 ± 0.001 by Henry et al.
(1995), to 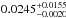 of Siwak et al. (2010), in other words, a very weak
latitudinal gradient of the angular velocity is indicated. Theoretically, rapidly rotating
late-type stars with Coriolis numbers similar to those of II Peg are predicted to show only
weak differential rotation, although specific models for giant stars seem to suggest much
stronger differential rotation in them then in main-sequence counterparts of the same
spectral type (see e.g. Kitchatinov & Rüdiger
1999). The models of Kitchatinov & Rüdiger
(2004) of giant stars in a close binary system predict the differential rotation to
be anti-solar, that is, the pole would be rotating faster than the equator, which is
attributed to the strong meridional circulation caused by large-scale thermal
inhomogeneities that drive a baroclinic effect (such as large star spots) or by tidal forces
generated by the companion. In these observational studies, the amount of differential
rotation is measured from the variations detected in the rotation period from stellar
photometry, the idea being that as the spot latitudes change, their rotation reflects the
differential rotation pattern on the stellar surface. But the photometric studies cannot
distinguish the direction of the latitudinal shear, there is, whether the pole or the
equator rotates faster.
of Siwak et al. (2010), in other words, a very weak
latitudinal gradient of the angular velocity is indicated. Theoretically, rapidly rotating
late-type stars with Coriolis numbers similar to those of II Peg are predicted to show only
weak differential rotation, although specific models for giant stars seem to suggest much
stronger differential rotation in them then in main-sequence counterparts of the same
spectral type (see e.g. Kitchatinov & Rüdiger
1999). The models of Kitchatinov & Rüdiger
(2004) of giant stars in a close binary system predict the differential rotation to
be anti-solar, that is, the pole would be rotating faster than the equator, which is
attributed to the strong meridional circulation caused by large-scale thermal
inhomogeneities that drive a baroclinic effect (such as large star spots) or by tidal forces
generated by the companion. In these observational studies, the amount of differential
rotation is measured from the variations detected in the rotation period from stellar
photometry, the idea being that as the spot latitudes change, their rotation reflects the
differential rotation pattern on the stellar surface. But the photometric studies cannot
distinguish the direction of the latitudinal shear, there is, whether the pole or the
equator rotates faster.
Intriguingly, the drift was no longer visible in the Doppler (DI) and Zeeman-Doppler images (ZDI) of Hackman et al. (2012) and Kochukhov et al. (2013), who also reported on the clear diminishing trend in the spottedness and magnetic field strength of the object. This was interpreted as the star’s activity declining toward its magnetic minimum, due to which the spot distribution on the stellar surface was postulated to be more stochastic than during the high-activity state, veiling the possible drift due to the mechanism producing it underneath. We note that the results of Carroll et al. (2007, 2009), computed from the same data with a different ZDI inversion method (Carroll et al. 2008), also indicate a reduction in the magnetic field strength between the observing seasons 2004 and 2007. The authors reported, however, that a dominant and largely unipolar field seen in 2004 changed into two distinct, large-scale bipolar structures in 2007, not completely consistent with the proposed picture of the star declining toward its magnetic minimum with less pronounced, stochastic spot activity.
 |
Fig. 1 Normalized and combined photometric data. |
Whichever the cause or persistence of the drift, this type of problem is especially suited to be analyzed with the recently developed carrier fit (CF) analysis method (Pelt et al. 2011), which is based on the idea of a continuous fitting of the time series (e.g., a light curve of a star) clocked by a certain shorter carrier period (or higher frequency) while being modulated by a longer period (or lower frequency). This method has previously been successfully applied to analyze the phase changes seen in the light curve of FK Com (Hackman et al. 2013). For II Peg, the orbital period of the binary system serves as the first guess of the carrier period, while the apparent modulation of the amplitude of the spots and/or magnetic field present the modulation period. If the drift was due to an azimuthal dynamo wave or orbital de-synchronization, we should be able to find a persistent drift period. For differential rotation, this could occur only if the spots were to persistently occur around the same latitude, which seems somewhat unlikely, although no systematic latitudinal variation has been reported yet in the object according to Lindborg et al. (2011), Hackman et al. (2012) and Kochukhov et al. (2013). Nevertheless, differential rotation is the only scenario that would naturally allow for changing drift periods associated with changes in the spot latitudes.
In this paper, we aim to investigate the drift phenomenon in detail, combining all the available photometry of the star into our analysis. The primary goal is to study whether a systematic drift period persisting over time exists with the CF method. In Sect. 2 we introduce the data used, in Sect. 3 we present a short summary of the CF method, in Sect. 4 we present our results, in Sect. 5 we compare the photometric results with earlier Doppler images, and in Sect. 6 we summarize and discuss the possible implications of the obtained results.
2. Photometric datasets
We used four different data sets for our CF analysis. The first data set (hereafter DATA1), published and analyzed by Rodonò et al. (2000), covers the years 1973–1998. The second data set (hereafter DATA2), published by Messina (2008), covers the years 1992–2004, which means that it partly overlaps DATA1. The third data set (hereafter DATA3) consists of unpublished observations with the Wolfgang-Amadeus telescope, the university of Potsdam and Vienna twin automatic photoelectric telescope (APT), which covers the years 1996–2009 and again partially overlaps the previous datasets. The fourth dataset (hereafter DATA4) was obtained with the Tennessee State University T3 0.4-m automated photometric telescope at Fairborn Observatory in Arizona, and covers the time span of 1987–2010 (see also Roettenbacher et al. 2011, for another analysis of the same dataset). These datasets were combined to collect as extensive a dataset as possible, with the densest possible coverage of observations. The combination was made by shifting the magnitudes and rescaling the amplitudes to achieve the best match in overlapping areas. The quality of the match was measured by computing mean-squared differences between magnitudes in data-point pairs where the time distance was shorter than 0.2 day. The best scaling shift and magnitude corrections were obtained by a least-squares minimization. The first six years of DATA1 (1973–1979) have gaps in time too wide for the CF analysis therefore these data were removed from the combined data set (see Fig. 1). We also divided the combined dataset into shorter segments, either to look for phase jumps or flip-flop-type events, following the ideas presented in Hackman et al. (2013), or to be able to identify the best period describing the drift of the primary light curve minimum in the orbital frame of reference.
3. CF method
Astronomical data are complicated for a straightforward Fourier analysis, because the observed light curves and spectra usually have long time gaps between observations. This makes the analysis difficult and creates false peaks due to the regularities in the gap structure of the input data (see e.g. the review by Schwarzenberg-Czerny 2003, and references therein). Pelt et al. (2011) developed a novel method for stellar light curve analysis based on the simple idea of decomposing the light curve into two separate components: a rapidly changing carrier that traces the regular part of the signal, and its slowly changing modulation. The carrier frequency can be obtained from observations (e.g. the period can be obtained from rotational velocity) or estimated from the data as a mean frequency. The smooth modulation curves are described by trigonometric polynomials or splines. Spline construction is better suited for stellar light curves with sharp phase jumps, while trigonometric polynomials can be used when relatively smooth changes are seen/expected. Although in principle, sharp phase changes can be detected with the CF method, in reality the sparseness of the data at hand often limits the capability of the method of detecting changes on very short timescales. Such very local events, for instance flare-type activity, can actually lead to local misfits in the light curve model for sparse data. For a complete description of the method we refer to Pelt et al. (2011), and for another practical application for stellar light curves to Hackman et al. (2013, analysis of FK Com); here we merely highlight the most important input quantities and properties of the method. We also stress that the CF procedure belongs to the class of explorative analysis methods; the qualitative results obtained from the phase diagrams should be quantified with more precise models with proper error estimates.
The proposed composition of the light curve is described with the following formula:
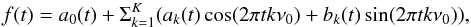 (2)where
ν0 is the carrier frequency,
a0(t) is the time-dependent mean level of the
signal, K is the total number of harmonics included in the model,
describing the overtones of the basic carrier frequency, while
ak(t) and
bk(t) are the low-frequency
signal components. For II Peg, the first guess of the carrier frequency
(2)where
ν0 is the carrier frequency,
a0(t) is the time-dependent mean level of the
signal, K is the total number of harmonics included in the model,
describing the overtones of the basic carrier frequency, while
ak(t) and
bk(t) are the low-frequency
signal components. For II Peg, the first guess of the carrier frequency
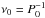 comes from considering the system to be a binary system, most likely with synchronized
orbits of the components. Therefore, we adopted the orbital period of the binary system,
P0 = 6
comes from considering the system to be a binary system, most likely with synchronized
orbits of the components. Therefore, we adopted the orbital period of the binary system,
P0 = 6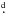 724333, estimated by
Berdyugina et al. (1998b) as the first carrier. The
next task of the analysis is to choose a suitable model for the modulators. In Pelt et al. (2011) we proposed two different types of
models based on either trigonometric or spline approximation. The II Peg light curve
contains a fairly small amount of complicated features, making the usage of the
trigonometric model adequate.
724333, estimated by
Berdyugina et al. (1998b) as the first carrier. The
next task of the analysis is to choose a suitable model for the modulators. In Pelt et al. (2011) we proposed two different types of
models based on either trigonometric or spline approximation. The II Peg light curve
contains a fairly small amount of complicated features, making the usage of the
trigonometric model adequate.
We built the trigonometric modulator model in the following way: we assumed the time
interval
[tmin,tmax] to
be the full span of our input data, based on which we defined a data period
D = C × (tmax − tmin),
where C is a so-called coverage factor, whose value must be higher than
unity. Next we constructed a truncated trigonometric series using the corresponding data
frequency, νD = 1/D, that is,
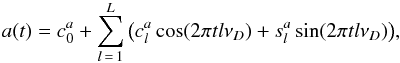 (3)and
(3)and
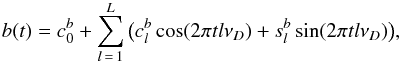 (4)where
L is the total number of harmonics used in the modulator model. The
process described by the modulators and data period D must be slow, that
is, D must be significantly longer than the carrier period
P0. The data of each set span more than several thousands of
days, due to which we concluded that 13 000 days is an appropriate value for the data
period; the corresponding coverage factors are roughly C = 1.15, well in
the range considered to be satisfactory C = 1.1...1.5 (see
Pelt et al. 2011).
(4)where
L is the total number of harmonics used in the modulator model. The
process described by the modulators and data period D must be slow, that
is, D must be significantly longer than the carrier period
P0. The data of each set span more than several thousands of
days, due to which we concluded that 13 000 days is an appropriate value for the data
period; the corresponding coverage factors are roughly C = 1.15, well in
the range considered to be satisfactory C = 1.1...1.5 (see
Pelt et al. 2011).
Next, proper estimates for the expansion coefficients were computed for every term in the series for the fixed carrier frequency ν0 and D; this is a standard linear estimation procedure and can be implemented using any standard statistical package (see Pelt et al. 2011, for a detailed description). If all coefficients (ak,bk) consist of the same number of harmonics L and we approximate separate cycles by a K-harmonic model, then the overall count of linear parameters to be fitted is N = (2 × L + 1) × (2 × K + 1). The optimal number of harmonics, K, depends on the complexity of the phase curves. The choice of the optimal number of modulator harmonics, L, is constrained by the longest gaps in the time series. Because the light curve of II Peg appears not to be very complicated, as discussed at length in Sect. 4, we found K = 3 and L = 12 adequate for the analysis of the combined data set (Stage 1). For the short segments the number of data points tends to be small and therefore we chose K = 2 (instead of K = 3) and L = 3 to reduce the number of model parameters (Stage 3).
Finally, we have found it convenient to visualize our results in the following way: we began with calculating a continuous curve estimate, ŷ(t), from the randomly spaced data set with the gaps, using a least-squares fitting scheme based on the carrier frequency. As a result, we were also able to model the gaps between the data, which allowed us to achieve a smooth picture of the long-term behavior. The continuous curve was then divided into strips, the length of each being the carrier period. Each data strip was then normalized with its extrema, so that after the normalization the data spanned the range of [−1,1]. We note that without this normalization procedure, epochs of weaker spot-activity, which show up as a weak variation in the light curve, would be drowned in the signal from strong spot-activity epochs. Finally, after normalization, we collected the strips along the time axis. To facilitate the interpretation of the plots, we did not restrict them to the interval of [0,1] over phase, but extended our phase axis to somewhat higher and lower values. At the bottom of the plots we show the time distribution of the actual observations in the form of a bar code. The black stripes are used to denote periods for which at least one observation is available, while the bright stripes represent gaps. This method of visualization allowed us to verify that the model correctly fits the data and not the gaps.
 |
Fig. 2 Continuous fit of the combined dataset from the CF analysis with carrier P0. |
4. CF analysis procedure and results
During the first stage of our investigation, we performed the CF analysis for the combined dataset (Fig. 1) as a whole. As previous photometric and spectroscopic investigations have already suggested, we found one single photometric minimum, that is, one large spotted region that dominates the light curve almost for the entire span of the data. This region often exhibits a linear downward trend in the phase diagram that is wrapped with the orbital period, indicating that it is rotating somewhat faster than the orbital period of the binary system. During some epochs, this trend is disrupted for some years, but it returns again. Therefore, we set out to determine this period, which can be thought to describe either the rotation of the spotted region on the surface of the object, or the signature of an underlying magnetic structure that feeds the surface; this constitutes the second stage of our analysis. In the third stage, we located all the epochs during which significant deviations from the drift trend can be seen. We zoomed into these epochs and performed a more detailed CF analysis on them to be able to conclude on the nature of the more complex phase-behavior occasionally seen in the object.
4.1. Stage 1: analysis of the combined dataset
We began by analyzing the whole combined dataset [DATA1,DATA2,DATA3,DATA4], that is, all
the data points in Fig. 1 excluding only the very
early points with too large gaps during 1973–1978. The CF analysis results with
P0 = 6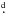 724333,
C = 1.15, number of carrier harmonics K = 3 and
modulation harmonics L = 12 is depicted in Fig. 2. The quality of the corresponding data fit can be characterized by the
determination coefficent R2 = 0.92. Table 3, available at the
CDS, contains this global CF fit (Col. 1 lists the time in HJD and Col. 2 the magnitude of
the star). However, this is not the absolutely best fit obtainable. For instance, the
model with K = 2 and L = 18 has
R2 = 0.95. Unfortunately it also shows certain artifacts
that correlate with the gaps in observations and can be considered as an overfit. The
linear downward trend in the orbital frame is clearly visible especially during the years
1995–2005 (subinterval of DATA3 and DATA4), and evidently present also during the years
1979–1988 (subinterval of DATA1 and DATA2). In the early part of the data, however, the
phase of the principal light curve minimum is alternating around the phase of the mean
trend, with seemingly regular timing. Moreover, the phase jumps seem to occur rather
abruptly.
724333,
C = 1.15, number of carrier harmonics K = 3 and
modulation harmonics L = 12 is depicted in Fig. 2. The quality of the corresponding data fit can be characterized by the
determination coefficent R2 = 0.92. Table 3, available at the
CDS, contains this global CF fit (Col. 1 lists the time in HJD and Col. 2 the magnitude of
the star). However, this is not the absolutely best fit obtainable. For instance, the
model with K = 2 and L = 18 has
R2 = 0.95. Unfortunately it also shows certain artifacts
that correlate with the gaps in observations and can be considered as an overfit. The
linear downward trend in the orbital frame is clearly visible especially during the years
1995–2005 (subinterval of DATA3 and DATA4), and evidently present also during the years
1979–1988 (subinterval of DATA1 and DATA2). In the early part of the data, however, the
phase of the principal light curve minimum is alternating around the phase of the mean
trend, with seemingly regular timing. Moreover, the phase jumps seem to occur rather
abruptly.
In the time interval of 1988–1995, the linear trend is visibly disrupted, manifested by the phase of the principal minimum staying constant in the orbital frame for these years. In 1995, however, the linear trend resumes with a period roughly equivalent to the earlier years. After 2005, a similar disruption is seen again, followed by very complex behavior at the end of the data set.
In summary, four main features can be isolated from the first stage of our analysis:
-
The data are dominated by one single light curve minimum, that is, one spotted region, almost throughout the entire span of the data.
-
There is a linear downward trend with a period faster than 6
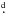 724333,
visible during 1979–1988 and 1995–2005.
724333,
visible during 1979–1988 and 1995–2005. -
Disruptions of the linear trend occur during 1988–1995 and 2005–2010.
-
Some abrupt phase jumps are seen that are not directly correlated with either the presence or absence of the linear trend.
4.2. Stage 2: finding the drift period
The next task was to estimate the period that best describes the linear trend seen in the dataset, Pspot. As already evident from the first stage of the analysis, the trend is not visible at all times of the data, meaning that the period is not completely stable.
Suitable methods for estimating light curves with significant deviations from harmonic
behavior are based on phase dispersion minimization. The Stellingwerf method (Stellingwerf 1978) is among the best known such methods
and was used in the following as a basis for the period search. However, the method needed
to be refined to be capable of dealing with a periodicity that is not completely time
independent and stable. For this purpose a more general formulation of the phase
dispersion is needed. We introduce here a variant of the statistic proposed previously by
Pelt (1983) that is hereafter referred to as
method 2. Specifically, for each trial period P we
computed the dispersion of phases wrapped with this particular period as
![\begin{eqnarray} D(P) = \frac{{\sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^N {g(t_i } } ,t_j ,P,\Delta t)[f(t_i ) - f(t_j )]^2 }}{{\sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^N {g(t_i } } ,t_j ,P,\Delta t)}}, \end{eqnarray}](/articles/aa/full_html/2013/11/aa21695-13/aa21695-13-eq45.png) (5)where
g(ti,tj,P,Δt)
is significantly greater than zero only when
(5)where
g(ti,tj,P,Δt)
is significantly greater than zero only when 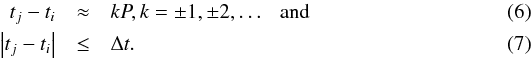 The
first condition selects only the data point (magnitude) pairs
[f(ti),f(tj)]
whose phases are approximately the same, and the second condition restricts the time
interval of the selected data points to a certain pre-selected time range
Δt. By computing D(P) for a sequence
of trial periods we obtained the phase dispersion spectra. The minima in these spectra
indicate probable periodicities; due to the normalization, the expected
D(P) value for randomly scattered phase diagrams is 2.
For the particular case when the time difference limit is longer than the full data span,
the obtained spectra practically coincide with traditional Stellingwerf spectra. By
shortening the time limit Δt, we analyzed the phase scatter for the case
when different cycles match only locally; for the present analysis, we found a
Δt of 300 days optimal. In this case the final minimum in the
D(P) spectrum indicates a certain estimate of the mean
cycle length (mean period). In this way we were able to analyze data sets that are not
coherent during the full data span, but only locally.
The
first condition selects only the data point (magnitude) pairs
[f(ti),f(tj)]
whose phases are approximately the same, and the second condition restricts the time
interval of the selected data points to a certain pre-selected time range
Δt. By computing D(P) for a sequence
of trial periods we obtained the phase dispersion spectra. The minima in these spectra
indicate probable periodicities; due to the normalization, the expected
D(P) value for randomly scattered phase diagrams is 2.
For the particular case when the time difference limit is longer than the full data span,
the obtained spectra practically coincide with traditional Stellingwerf spectra. By
shortening the time limit Δt, we analyzed the phase scatter for the case
when different cycles match only locally; for the present analysis, we found a
Δt of 300 days optimal. In this case the final minimum in the
D(P) spectrum indicates a certain estimate of the mean
cycle length (mean period). In this way we were able to analyze data sets that are not
coherent during the full data span, but only locally.
It is reasonable to compute Stellingwerf and
D(P) = D(1/ν)
spectra with a fixed step along the frequency ν. The optimal step size,
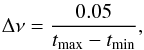 (8)limits
the phase change from one trial to the next by an upper limit of 0.05 for all pairs along
the full time span
[tmin,tmax].
The distance between neighboring periods depends on the period argument
P
(8)limits
the phase change from one trial to the next by an upper limit of 0.05 for all pairs along
the full time span
[tmin,tmax].
The distance between neighboring periods depends on the period argument
P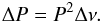 (9)This
value can be used to roughly characterize the precision of the obtained period estimates.
(9)This
value can be used to roughly characterize the precision of the obtained period estimates.
The exact error estimates and significance levels for the estimated mean periods can be computed by using either standard regression techniques, Monte Carlo type methods, the Fischer randomization technique, or bootstrap. However, we note that these are only formal error estimates. The real scatter of the mean period heavily depends on the physics involved, and to estimate it, we need significantly longer data sets than the ones available for this study. In our particular case we used the standard regression analysis method to estimate the errors of the final period. We iteratively refined the obtained period and used a correlation matrix to compute the dispersion of the refined period.
The Stellingwerf periodogram for the full dataset, plotted with the thinnest gray line in Fig. 3, shows the shallowest minimum split into several peaks. The form of the spectrum does not change when the correlation length is decreased using method 2, but the minimum deepens (second thinnest gray line). This is an indication supporting the hypothesis that the period is not completely stable. For the subset with the clearest linear trend seen in the phase diagram, the spectrum is characterized with only one clear peak in the periodogram with both methods (two thickest lines). Decreasing the correlation length again using method 2 deepens the minimum (the thickest line).
Most importantly, the best period is practically the same for both datasets analyzed with
either method. This is an indication of the trend dominating in the data, despite the
disruptions and phase jumps additionally occasionally seen in it. Therefore, we can
constrain the rotation period of the spotted region to be
Pspots = 6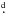 71086 ±
0
71086 ±
0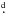 00007, the value
of the period obtained after the least-squares refinement of the initial estimate. The
phase diagram, wrapped with the new period, is shown in Fig. 4. This figure reveals quite a different picture from the phase diagram wrapped
with the orbital period – after removing the trend, the primary minimum mainly stays on
one straight line at phase 0.5, although smooth variability up and down can be seen. The
phase changes around the mean drift period during the early part of the data (1979–1990)
now look fairly similar to the fluctuations seen in the later part with a clear trend
(1995–2005). Abrupt phase jumps are more easy to identify; three major events can be seen
during 1984–1985, 1990–1991, and 2009–2010. Next, we concentrate on investigating the
phase jumps in more detail.
00007, the value
of the period obtained after the least-squares refinement of the initial estimate. The
phase diagram, wrapped with the new period, is shown in Fig. 4. This figure reveals quite a different picture from the phase diagram wrapped
with the orbital period – after removing the trend, the primary minimum mainly stays on
one straight line at phase 0.5, although smooth variability up and down can be seen. The
phase changes around the mean drift period during the early part of the data (1979–1990)
now look fairly similar to the fluctuations seen in the later part with a clear trend
(1995–2005). Abrupt phase jumps are more easy to identify; three major events can be seen
during 1984–1985, 1990–1991, and 2009–2010. Next, we concentrate on investigating the
phase jumps in more detail.
Periods derived from either the combined data or subsets with two different methods.
 |
Fig. 3 Periodograms from two different methods with two different datasets. |
 |
Fig. 4 Phase diagram with the new carrier,
Pspot = 6 |
Summary of the local CF analysis results.
4.3. Stage 3: analysis of short segments
Next, we divided the data into shorter segments and performed a “local” CF analysis (see also Hackman et al. 2013, for a similar analysis). The division of the data into segments was made according to the following rules: we started to group the data from the first point of the combined data set. The next point of the data was included in the same segment, until a gap longer than 60 days was encountered; this was found to be the absolute maximum for gap length without spoiling the CF analysis. Then the current segment was considered to be completed, and a new one started. This way, altogether 42 segments of varying length and number of data points were formed, but 19 of them contained too few points to allow for a meaningful CF analysis. The remaining segments were analyzed with the CF method using K = 2 and L = 3 and the refined carrier period Pspot. Most of the segments show very little variation in phase over time; the segments can be well described with a horizontal stripe, that is, the principal minimum remains at the same phase. As an example of practically no phase change we show SEG12 in Fig. 5, first panel; segments resembling this one are indicated with “–” (no change) in Table 2.
Only four of all the 23 segments containing enough points allowing for a local CF analysis (SEG07, SEG08, SEG14, SEG39) show clear, abrupt phase changes. In addition, two of the segments, namely SEG15 and 20, show a disrupted phase behavior that cannot well be described as phase jumps (indicated with “?” in Table 2). The two first segments showing interesting behavior (SEG07 and SEG08) are connected to the epoch of phase disturbance seen during 1984–1985. Comparing Figs. 4 and 5 (second and third upper panels), it seems evident that during 1979–1984, the activity “wobbled” around the mean phase of 0.25, whose location roughly agrees with the linear trend, that is, remains horizontal in Fig. 4. During 1984–1985, a series of more abrupt phase jumps are observed to occur, with two short-lived transitions between phases 0.2 and 0.6. After a third abrupt transition in the middle of 1985, the major part of the activity remained at the new phase of 0.6 (although hints of a secondary minimum being active at 0.25 can be seen in the global phase diagram) until 1990, the mean phase of activity again being consistent with the overall linear trend. Another phase jump can be seen in SEG14, at the end of the year 1990, when the main activity seems to have quickly reverted back to the phase of roughly 0.2, but this spot configuration appears to be unstable, reverting back to phase 0.6 via a continuous phase drift during 1992–1995. The last abrupt phase jump is seen in SEG39, close to the end of the dataset. Again, a change of roughly 0.5 in phase can be identified. We note, however, that the modeling of the very beginning or the very end of the data can be affected by the boundary effects, due to which the prominent phase jump in SEG39 must be interpreted with caution. Whether it is real or arises as an artifact because it is too close to the end point of the data will become verified as more datapoints are added to the time series.
To conclude, the characteristics of the phase jumps rather closely resemble what is called the flip-flop (Jetsu et al. 1993), that is, the activity shifts roughly 0.5 in phase within a timescale of a few months. The last jump (in SEG39) occurred very near the endpoint of the time series, therefore it is difficult to conclude about the persistence of the spot configuration after the event; only one of the other new spot configurations after a flip-flop type event, seen during 1985, seems to have persisted over a longer period of time (several years), while the others have either flipped or drifted back to the original configurations soon afterward.
 |
Fig. 5 Top row: SEG12 as an example of a segment with stable phase behavior. Lower rows: zoom-in segments in which phase changes were detected. From left to right, top to bottom, SEG07, SEG08, SEG14, SEG15, SEG20, and SEG39. |
There is a ten-year-long time interval when the abrupt phase jump activity clearly ceases to occur (1995–2005), during which only the linear drift and some wobbling around the mean phase is seen. From spectroscopy (covering the time 1994–2010 Lindborg et al. 2011; Hackman et al. 2012) and spectropolarimetry (Kochukhov et al. 2013, covering the time 2004–2010) there is some evidence of the star’s magnetic field strength weakning and the spots are more randomly distributed across the phase during the latest epoch of disturbed phase activity (2004–2010). The chosen CF visualization scheme of normalizing each stripe with its own extrema acts to hide possible amplitude variations in our photometric analysis. Therefore, we re-computed the phase diagram wrapped with Pspot without this normalization and show the result in Fig. 6. From this plot it is evident that the photometric minima are indeed deeper during the period of the most pronounced linear trend, whereas irregular phase behavior and flip-flop-type events are related to the epoch of weaker photometric minima. On the other hand, it is noteworthy that the mean photometric magnitude of the star remains approximately constant after the year 1990 (see Fig. 1), while only the strength of the variations around the mean increases during the epoch with the most pronounced linear trend. The constant mean level of the photometric magnitude suggests that the overall magnetic activity level of the star has remained unchanged, while the activity is distributed less axisymmetrically during the epoch of strong magnitude variations.
5. Comparison with recent temperature maps
In this section we compare the temperature minima obtained from Doppler imaging (DI) by Hackman et al. (2011) to the photometric results; in all, 28 surface temperature maps of the object were derived for the years 1994–2010. For comparison purposes, we plot in Fig. 7 the latitudinally averaged temperature profiles of the DI maps as a function of time, but in contrast to previous studies (see e.g. Hackman et al. 2011), we wrapped the phases with the Pspot that was found to describe the linear drift of the photometric minima. As evident from this figure, one large primary spot, seen as extensive dark patches in the color contour, was seen on the object during 1997–2002. Its phases evolve along an almost horizontal line when wrapped with Pspot. During the epochs 1994–1997 and 2004–2010 weaker spot activity is found and the spots are randomly distributed over the stellar longitude. The photometric minima from our analysis, over plotted on the DI results with black crosses, closely coincide with the DI minima for the years with pronounced spot activity, while the differences are greater for the other epochs. Compared with the previous investigation of Hackman et al. (2011), who used a different time-series analysis method for the photometric data, we find the results to agree fairly well. Therefore we conclude that the linear drift pattern is an authentic feature seen both in the DI maps and photometric data analyzed with different types of methods, persisting at least over a ten-year epoch during 1995–2005. The DI maps, on the other hand, do not show clear evidence of the very continuous phase drift seen during 2005–2009 or the abrupt phase jump detected from photometry at the end of the dataset (during 2010 in SEG39).
 |
Fig. 6 CF phase diagram without normalization. |
 |
Fig. 7 Temperature distribution over phase (y-axis) plotted as a function of time (x-axis) calculated as averages over all latitudes from the surface temperature maps obtained with Doppler imaging. The black dots indicate the phases of the photometric minima obtained from the CF analysis. The phases are wrapped with the best period describing the linear trend, Pspot using the first time-point of DI observations as the epoch. |
 |
Fig. 8 Temperature distribution over latitude (y-axis) plotted as a function of time (x-axis) calculated as averages over all longitudes from the surface temperature maps obtained with Doppler imaging. Each stripe is individually normalized so that black color represents the coolest temperature and white the hottest. |
In Fig. 8 we also show the average latitudinal distribution of the spots computed from the DI maps during 1994–2010. This figure is otherwise identical to Fig. 5 of Hackman et al. (2011), but here we normalized each stripe with its own extrema (equivalent to the CF normalization scheme) instead of a global value, enabling us to better see the seasonal variations of the spot latitudes. From this figure it is evident that during the most persistent drift, the spot latitudes show less variation than during the epoch when distrubances in the drift were detected. This finding supports the differential rotation scenario, although it cannot be regarded as conclusive evidence for it.
6. Summary and discussion
We have collected a 21-year-long photometric data set of the magnetically active primary
giant component of the RS CVn binary II Peg and analyzed this data set with the CF method,
both globally and locally. As a result, we confirm previously published results that the
spot activity was dominated by one primary spotted region almost through the entire data
set, and we also confirm a very persistent linear drift. Disruptions of the linear trend and
complicated phase behavior were also seen, but the period analysis revealed a periodicity
with Pspot = 6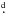 71 086 ±
0
71 086 ±
0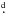 00007. After
removing the linear trend from the data, we identified several abrupt phase jumps, three of
which were analyzed with the CF method using shorter data segments. These phase jumps
closely resemble what is called a flip-flop event, that is, the spot activity changes by
roughly 0.5 in phase within months, but only one of the phase jumps leads to a stable spot
configuration that persists for several years. In other cases, flips back to or more
continuous drifts toward, the original spot configurations are seen.
00007. After
removing the linear trend from the data, we identified several abrupt phase jumps, three of
which were analyzed with the CF method using shorter data segments. These phase jumps
closely resemble what is called a flip-flop event, that is, the spot activity changes by
roughly 0.5 in phase within months, but only one of the phase jumps leads to a stable spot
configuration that persists for several years. In other cases, flips back to or more
continuous drifts toward, the original spot configurations are seen.
The comparison to Doppler-imaging temperature maps confirms the linear drift pattern with regular phase behavior for the epoch 1995–2005, during which the level of spot activity of the star has been high. During the epochs when photometric analysis shows disrupted phase behavior and phase jumps, the Doppler images show weak spots randomly distributed across the longitudes. Therefore, there is some evidence that the regular drift without phase jumps is related to the high state, while complex phase behavior and disrupted drift patterns are related to the low state of spot activity. The Zeeman-Doppler-imaging results of Kochukhov et al. (2013) indicate that the magnetic field strength of the object decreases on average since 2004. The mean photometric brightness of the object, however, has remained more or less constant since 1990, suggesting that the overall magnetic activity level has not changed considerably, although the variations around the mean have been higher during the epoch of the pronounced linear trend.
Although the periodicity describing the drift of the primary spot in the orbital frame of
reference of the binary system is stable in a statistical sense, the trend is clearly
disrupted during the epochs of complex phase behavior; this casts serious doubt on the idea
that the primary light curve minimum reflects the actual, more rapid, rotation of the
primary component of the binary system, which would indicate that the rotation rates of the
stars still remain de-synchronized by the mutual tidal forces. Moreover, practically all
dynamo models produced up to date (see e.g. Krause &
Rädler 1980; Küker & Rüdiger 1999;
Moss et al. 1995; Tuominen et al. 2002; Mantere et al. 2013)
show stable drift periods, which makes it equally hard to explain the results obtained in
this work with the azimuthal dynamo wave scenario. We note, however, that the recent models
of Mantere et al. (2013) indicate that the
oscillations in the magnetic activity level are probably connected to the cycle length of
the drift of the non-axisymmetric structures. Using the drift period
Pspot obtained in this work, an oscillation in the magnetic
energy level with a period of 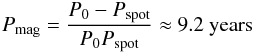 (10)is
expected. Saar & Brandenburg (1999) examined
the dependence of the rotational-to-magnetic cycle period on the inverse Rossby number
Ro-1 ≡ 4πτc/Prot,
describing the influence of rotation on the convective turbulence (with turnover time
τc) within the stellar convection zones in a large stellar
sample of late-type stars at different evolutionary stages. For II Peg the inverse Rossby
number can be approximated using an average convective turnover-time for K-subgiants of 50
days Ro-1 ≈ 94 (see e.g. Table 4 of Saar
& Brandenburg 1999, and references therein). This places the star in a
regime of the diagnostic diagram where G-K giants are observed to show a large scatter in
their rotational-to-magnetic cycle period: the majority fall on the sharp transition region
in between the active and superactive branches, on which the magnetic cycle lengths strongly
increse with respect to the rotation period, with
Pcyc/Prot
reaching values of one thousand or more. Some objects, however, also fall on the active
branch with
Pcyc/Prot of an
order of magnitude smaller. If II Peg were to belong to the class of stars transiting toward
the superactive branch, it’s magnetic cycle could be as long as 20 years, while on the
active branch it would only be on the order of two years. Our predicted cycle length would
therefore place the star in the uppermost part of the transition region.
(10)is
expected. Saar & Brandenburg (1999) examined
the dependence of the rotational-to-magnetic cycle period on the inverse Rossby number
Ro-1 ≡ 4πτc/Prot,
describing the influence of rotation on the convective turbulence (with turnover time
τc) within the stellar convection zones in a large stellar
sample of late-type stars at different evolutionary stages. For II Peg the inverse Rossby
number can be approximated using an average convective turnover-time for K-subgiants of 50
days Ro-1 ≈ 94 (see e.g. Table 4 of Saar
& Brandenburg 1999, and references therein). This places the star in a
regime of the diagnostic diagram where G-K giants are observed to show a large scatter in
their rotational-to-magnetic cycle period: the majority fall on the sharp transition region
in between the active and superactive branches, on which the magnetic cycle lengths strongly
increse with respect to the rotation period, with
Pcyc/Prot
reaching values of one thousand or more. Some objects, however, also fall on the active
branch with
Pcyc/Prot of an
order of magnitude smaller. If II Peg were to belong to the class of stars transiting toward
the superactive branch, it’s magnetic cycle could be as long as 20 years, while on the
active branch it would only be on the order of two years. Our predicted cycle length would
therefore place the star in the uppermost part of the transition region.
We now consider the option that the differential rotation of spots at more or less fixed
latitude positions would cause the persistent drift. Because the drift period is shorter
than the orbital one, this would immediately imply an anti-solar
differential rotation. The amount of differential rotation between the orbital
motion and that of the spot motions at their fixed, relatively high latitude can be then
estimated as 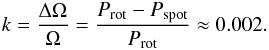 (11)Between
the pole and the equator the difference in rotation periods could be even larger, resulting
in a higher k. Nevertheless, the estimated differential rotation is
consistent with the values derived by Siwak et al.
(2010), although considerably higher than the value estimated by Henry et al. (1995). It has to be kept in mind, however,
that while our method of estimating the differential rotation is by definition based on the
spots being fixed at certain latitudes, the other methods transform detectable period
variations into differential rotation, attributing these changes to changing spot latitudes.
The most natural explanation for the disruption of the drift may be provided by the
differential rotation scenario; during the epoch of less pronounced spot activity the
longitudes and also the latitudes of the spots are far less systematic. Some, but not
conclusive, support for this is provided by the apparently average spot latitude seems to be
more stable during 1994–2002 than in 2004–2010 (Fig. 8).
(11)Between
the pole and the equator the difference in rotation periods could be even larger, resulting
in a higher k. Nevertheless, the estimated differential rotation is
consistent with the values derived by Siwak et al.
(2010), although considerably higher than the value estimated by Henry et al. (1995). It has to be kept in mind, however,
that while our method of estimating the differential rotation is by definition based on the
spots being fixed at certain latitudes, the other methods transform detectable period
variations into differential rotation, attributing these changes to changing spot latitudes.
The most natural explanation for the disruption of the drift may be provided by the
differential rotation scenario; during the epoch of less pronounced spot activity the
longitudes and also the latitudes of the spots are far less systematic. Some, but not
conclusive, support for this is provided by the apparently average spot latitude seems to be
more stable during 1994–2002 than in 2004–2010 (Fig. 8).
Even though we have been able to preliminarily distinguish weak anti-solar differential rotation as a probable source for the drift pattern seen in II Peg, this investigation poses many more questions than it has answered. Because of the small differential rotation, the α2 or α2Ω dynamo scenarios that are widely used to model these objects can still be judged to be perfectly valid tools; these models consistently show azimuthal dynamo waves both in the kinematic (velocity field given, see e.g. Mantere et al. 2013) and non-linear regimes (velocity field and differential rotation profile are solved for, see e.g. Tuominen et al. 2002). Moreover, both the predicted length of the magnetic activity cycle and the amount of differential rotation fall into sensible ranges, making it impossible to completely exclude the dynamo scenario either. The relation between the dynamo wave migration properties to the differential rotation pattern, however, has not yet been carefully studied from the dynamo models including the full dynamics, not to mention direct numerical models of giant stars with fast rotation, which are now gradually becoming possible. The final resolution of this question, must therefore, must await a more thorough theoretical and numerical investigation.
Acknowledgments
Some of the results presented in this manuscript are based on observations made with the Nordic Optical Telescope, operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias. Financial support from the Academy of Finland grants Nos. 112020, 141017 (ML) and 218159 (MJM), and financial support from the research programme “Active Suns” at the University of Helsinki (MJM and TH) are acknowledged. Astronomy at Tennessee State University has been supported by NASA, NSF, Tennessee State University, and the State of Tennessee through its Centers of Excellence programs.
References
- Berdyugina, S. V., Berdyugin, A. V., Ilyin, I., & Tuominen, I. 1998a, A&A, 340, 437 [NASA ADS] [Google Scholar]
- Berdyugina, S. V., Jankov, S., Ilyin, I., Tuominen, I., & Fekel, F. C. 1998b, A&A, 334, 863 [NASA ADS] [Google Scholar]
- Berdyugina, S. V., Berdyugin, A. V., Ilyin, I., & Tuominen, I. 1999, A&A, 350, 626 [NASA ADS] [Google Scholar]
- Carroll, T. A., Kopf, M., Ilyin, I., & Strassmeier, K. G. 2007, Astron. Nachr., 328, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, T. A., Kopf, M., & Strassmeier, K. G. 2008, A&A, 488, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carroll, T. A., Kopf, M., Strassmeier, K. G., Ilyin, I., & Tuominen, I. 2009, in Proc. IAU Symp. 259, eds. K. G. Strassmeier, A. G. Kosovichev, & J. E. Beckman, 437 [Google Scholar]
- Elstner, D., & Korhonen, H. 2005, Astron. Nachr., 326, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, S.-H., Tan, H.-S., Wang, X.-B., & Shan, H.-G. 2003, A&A, 405, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hackman, T., Mantere, M. J., Jetsu, L., et al. 2011, Astron. Nachr., 332, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Hackman, T., Mantere, M. J., Lindborg, M., et al. 2012, A&A, 538, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hackman, T., Pelt, J., Mantere, M. J., et al. 2013, A&A, 553, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, G. W., Eaton, J. A., Hamer, J., & Hall, D. S. 1995, ApJS, 97, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Jetsu, L., Pelt, J., & Tuominen, I. 1993, A&A, 278, 449 [NASA ADS] [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 1999, A&A, 344, 911 [NASA ADS] [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 2004, Astron. Nachr., 325, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Kochukhov, O., Mantere, M. J., Hackman, T., & Ilyin, I. 2013, A&A, 550, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korhonen, H., & Elstner, D. 2011, A&A, 532, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krause, F., & Rädler, K. H. 1980, Mean-field magnetohydrodynamics and dynamo theory (Oxford: Pergamon Press) [Google Scholar]
- Küker, M., & Rüdiger, G. 1999, A&A, 346, 922 [NASA ADS] [Google Scholar]
- Lindborg, M., Korpi, M. J., Hackman, T., et al. 2011, A&A, 526, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mantere, M. J., Käpylä, P. J., & Pelt, J. 2013, in Solar and Astrophysical Dynamos and Magnetic Activity, eds. A. G. Kosovichev, E. M. de Gouveia Dal Pino, & Y. Yan, Proc. IAU Symp., 294, 175 [Google Scholar]
- Messina, S. 2008, A&A, 480, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Barker, D. M., Brandenburg, A., & Tuominen, I. 1995, A&A, 294, 155 [NASA ADS] [Google Scholar]
- Pelt, J. 1983, in Statistical Methods in Astronomy, ed. E. J. Rolfe, ESA SP, 201, 37 [Google Scholar]
- Pelt, J., Olspert, N., Mantere, M. J., & Tuominen, I. 2011, A&A, 535, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rädler, K.-H. 1975, Mem. Soc. Roy. Sci. Liège, 8, 109 [NASA ADS] [Google Scholar]
- Rodonò, M., Messina, S., Lanza, A. F., Cutispoto, G., & Teriaca, L. 2000, A&A, 358, 624 [NASA ADS] [Google Scholar]
- Roettenbacher, R. M., Harmon, R. O., Vutisalchavakul, N., & Henry, G. W. 2011, AJ, 141, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Brandenburg, A. 1999, ApJ, 524, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarzenberg-Czerny, A. 2003, in Interplay of Periodic, Cyclic and Stochastic Variability in Selected Areas of the H-R Diagram, ed. C. Sterken, ASP Conf. Ser., 292, 383 [Google Scholar]
- Siwak, M., Rucinski, S. M., Matthews, J. M., et al. 2010, MNRAS, 408, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Tuominen, I., Berdyugina, S. V., & Korpi, M. J. 2002, Astron. Nachr., 323, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P., & Bouchet, L. 1989, A&A, 223, 112 [Google Scholar]
- Zeilik, M., & Budding, E. 1987, in Cool Stars, Stellar Systems and the Sun, eds. J. L. Linsky, & R. E. Stencel (Berlin: Springer-Verlag), Lect. Notes Phys., 291, 500 [Google Scholar]
All Tables
Periods derived from either the combined data or subsets with two different methods.
All Figures
 |
Fig. 1 Normalized and combined photometric data. |
| In the text | |
 |
Fig. 2 Continuous fit of the combined dataset from the CF analysis with carrier P0. |
| In the text | |
 |
Fig. 3 Periodograms from two different methods with two different datasets. |
| In the text | |
 |
Fig. 4 Phase diagram with the new carrier,
Pspot = 6 |
| In the text | |
 |
Fig. 5 Top row: SEG12 as an example of a segment with stable phase behavior. Lower rows: zoom-in segments in which phase changes were detected. From left to right, top to bottom, SEG07, SEG08, SEG14, SEG15, SEG20, and SEG39. |
| In the text | |
 |
Fig. 6 CF phase diagram without normalization. |
| In the text | |
 |
Fig. 7 Temperature distribution over phase (y-axis) plotted as a function of time (x-axis) calculated as averages over all latitudes from the surface temperature maps obtained with Doppler imaging. The black dots indicate the phases of the photometric minima obtained from the CF analysis. The phases are wrapped with the best period describing the linear trend, Pspot using the first time-point of DI observations as the epoch. |
| In the text | |
 |
Fig. 8 Temperature distribution over latitude (y-axis) plotted as a function of time (x-axis) calculated as averages over all longitudes from the surface temperature maps obtained with Doppler imaging. Each stripe is individually normalized so that black color represents the coolest temperature and white the hottest. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


