| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 10 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201220816 | |
| Published online | 01 November 2013 | |
Stellar granulation as seen in disk-integrated intensity
I. Simplified theoretical modeling⋆
1 LESIA, Observatoire de Paris, CNRS UMR 8109, UPMC, Université Denis Diderot, 5 place Jules Janssen, 92195 Meudon Cedex, France
e-mail: reza.samadi@obspm.fr
2 Zentrum für Astronomie der Universität Heidelberg, Landessternwarte, Knigstuhl 12, 69117 Heidelberg, Germany
3 GEPI, Observatoire de Paris, CNRS UMR 8111, Université Denis Diderot, 5 place Jules Janssen, 92195 Meudon Cedex, France
Received: 29 November 2012
Accepted: 4 September 2013
Context. Solar granulation has been known for a long time to be a surface manifestation of convection. The space-borne missions CoRoT and Kepler enable us to observe the signature of this phenomena in disk-integrated intensity on a large number of stars.
Aims. The space-based photometric measurements show that the global brightness fluctuations and the lifetime associated with granulation obeys characteristic scaling relations. We thus aimed at providing simple theoretical modeling to reproduce these scaling relations, and subsequently at inferring the physical properties of granulation across the Hertzsprung-Russell diagram.
Methods. We developed a simple 1D theoretical model. The input parameters were extracted from 3D hydrodynamical models of the surface layers of stars, and the free parameters involved in the model were calibrated with solar observations. Two different prescriptions for representing the Fourier transform of the time-correlation of the eddy velocity were compared: a Lorentzian and an exponential form. Finally, we compared our theoretical prediction with 3D radiative hydrodynamical (RHD) numerical modeling of stellar granulation (hereafter ab initio approach).
Results. Provided that the free parameters are appropriately adjusted, our theoretical model reproduces the observed solar granulation spectrum quite satisfactorily; the best agreement is obtained for an exponential form. Furthermore, our model results in granulation spectra that agree well with the ab initio approach using two 3D RHD models that are representative of the surface layers of an F-dwarf and a red-giant star.
Conclusions. We have developed a theoretical model that satisfactory reproduces the solar granulation spectrum and gives results consistent with the ab initio approach. The model is used in a companion paper as theoretical framework for interpretating the observed scaling relations.
Key words: convection / turbulence / Sun: granulation
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The solar surface reveals irregular cellular patterns commonly called granules. These structures were first discovered and discussed during the 19th century (see an historical review in Bray & Loughhead 1967). Their origin was first attributed by Unsöld (1930) to convective currents occuring beneath the visible photospheric layers, while their turbulent nature was first highlighted by Siedentopf (1933). Several decades later, with the advances in numerical hydrodynamical simulations, the properties of solar granulation are well explained (e.g. Muller 1999, and references therein).
Stars with effective temperatures lower than about 7000 K have an appreciable upper convective envelope and are thus expected to show – as in the Sun – granules on their surface. Because the granules evolve with time, their evolution produces small brightness fluctuations that can now be accurately monitored and measured with space-based high-precision photometry measurements performed with the MOST, CoRoT, and Kepler missions (Matthews et al. 2004; Michel et al. 2008; Kallinger & Matthews 2010; Mathur et al. 2011; Chaplin et al. 2011b). These observations reveal that the characteristic time τeff of the granules and the total brightness fluctuations σ associated with them scales as a function of the frequency νmax at which the solar-like oscillations peak (e.g., Huber et al. 2009; Kallinger & Matthews 2010; Chaplin et al. 2011b; Mathur et al. 2011; Kjeldsen & Bedding 2011). In turn, νmax is shown to scale with the cut-off frequency νc of the atmosphere, therefore mainly the pressure scale-height near the photosphere (Brown et al. 1991; Kjeldsen & Bedding 1995; Stello et al. 2009; Huber et al. 2009; Mosser et al. 2010; Belkacem et al. 2011). The observed relation between the properties of the stellar granulation and νc were explained on the basis of some simplified physical considerations (Huber et al. 2009; Kjeldsen & Bedding 2011; Mathur et al. 2011). A detailed theoretical study of the observed scaling relations is, however, lacking.
A possible theoretical approach is the one proposed by Ludwig (2006). This ab initio approach consists of modeling the stellar granulation as seen in disk-integrated intensity from the intensity emerging directly from given 3D radiative hydrodynamical (RHD) models. This numerical approach was applied by several authors (Svensson & Ludwig 2005; Ludwig et al. 2009; Mathur et al. 2011). It is very time-consuming and hence does not easily allow envisaging a large set of calculations with different surface metal abundance, for example. Furthermore, interpreting the results is not trivial, and the systematic differences obtained by Mathur et al. (2011) between observed and modeled spectra of red giants are not well understood. On the other hand, a theoretical model based on a more simplified physical approach offers the advantage of separately testing several properties of turbulent convection. In addition, it allows one to compute the granulation spectrum for a variety of stars on a large scale. Furthermore, it is possible to derive scaling relations from such a simplied theoretical model that could provide additional theoretical support for the observed scaling relations and extend the current theoretical scaling relations. We here present such a simple theoretical model of the stellar granulation as seen in disk-integrated intensity. In the companion paper (Samadi et al. 2013, hereafter Paper II), we derive theoretical scaling relations for σ and τeff from this model. Comparisons with a large sample of observed stars as well as with previously published scaling relations are reported in Paper II.
This Paper I is organized as follows: in Sect. 2, we outline our theoretical model for the stellar granulation spectrum in disk-integrated intensity and the different prescriptions adopted for modeling the properties of turbulent granules. The free parameters introduced in the theoretical model are next calibrated in Sect. 3 such that our theoretical calculations match at best the solar observations. In Sect. 4, we compare our calculations with those obtained with the ab initio approach of Ludwig (2006) using two 3D RHD models of the surface layers of an F-dwarf star and a red giant star. Finally, Sect. 5 is devoted to the conclusion.
2. Modeling of the power density spectrum
We here outline our theoretical model for the power spectrum associated with the relative variations of the bolometric flux emerging from the star in the direction of an observer, who would measure it continuously during a given duration (typically much longer than the timescale of the granulation). The detailed derivation of the model is presented in Appendix A, while the underlying approximations and assumptions are discussed in Appendix B.
F(t) is the bolometric flux toward the observer at the instant t, and we define ΔF(t) = F(t) − ⟨F⟩t as the instantaneous variation of the flux with respect to its time average, ⟨F⟩t. From now on ⟨⟩t stands for a time average. The power density spectrum (PDS) associated with the relative variation of the flux (ΔF(t)/⟨F⟩t) is hence defined by 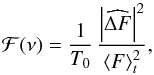 (1)where T0 is the duration of the observation, and ν a given frequency. The operator
(1)where T0 is the duration of the observation, and ν a given frequency. The operator 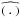 is
is 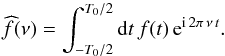 (2)We point out that with CoRoT or Kepler observations T0 is typically much longer than the granule lifetime such that the operator
(2)We point out that with CoRoT or Kepler observations T0 is typically much longer than the granule lifetime such that the operator 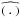 tends to the classical Fourier transform.
tends to the classical Fourier transform.
We consider a gray atmosphere. This is a necessary condition to obtain an analytical formulation for the granulation spectrum. We adopt a spherical coordinate system (r,θ,φ) with the z-axis pointing toward the observer. Accordingly, the bolometric flux received from the star at the instant t is given by 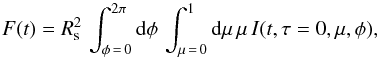 (3)where μ = cos(θ), I(t,τ,μ,φ) is the specific intensity in the direction (μ,φ), Rs the radius of the star, and τ(r) the mean optical depth
(3)where μ = cos(θ), I(t,τ,μ,φ) is the specific intensity in the direction (μ,φ), Rs the radius of the star, and τ(r) the mean optical depth 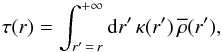 (4)where κ is the mean opacity,
(4)where κ is the mean opacity, 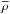 is the mean density (i.e., averaged in time and over a sphere of radius r) and the specific intensity I(τ,μ,φ) is related to the source function according to (e.g., Gray 1992, p. 114)
is the mean density (i.e., averaged in time and over a sphere of radius r) and the specific intensity I(τ,μ,φ) is related to the source function according to (e.g., Gray 1992, p. 114) 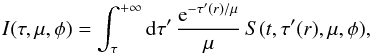 (5)where S is the source function.
(5)where S is the source function.
To proceed, we assume the local thermodynamic equilibrium (LTE) so that S = B, where B is the Planck function at the instant t and the position (τ(r),μ,φ). Note that LTE is fully justified because the region where the granules are seen most often extends to the small region around the optical depth τ ~ 1 (i.e., near the photosphere). Accordingly, and using Eqs. (3) and (5), ΔF(t) is rewritten such as 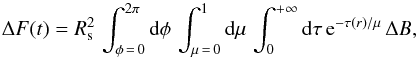 (6)where we have defined ΔB ≡ B − ⟨B⟩t.
(6)where we have defined ΔB ≡ B − ⟨B⟩t.
We neglect length-scales longer than the granulation length-scales. In that case ΔB represents the instantaneous difference between the brightness of the granules situated at position (τ(r),μ,φ) and the brightness of the material in the steady state (⟨ B ⟩ t). Finally, we assume that κρ varies at a length-scale longer than the characteristic size of the granule. From this set of assumptions, and after some calculations, Eq. (1) can be written (see details in Appendix A) 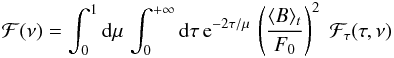 (7)with
(7)with 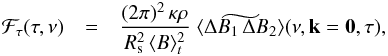 (8)where the constant F0 is given by Eq. (A.15),
(8)where the constant F0 is given by Eq. (A.15), 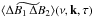 is the space and time Fourier transform of ⟨ ΔB1 ΔB2 ⟩ (see Eq. (A.13)), where k is a wavenumber, ν a frequency, and the subscripts 1 and 2 refer to two different spatial and temporal positions.
is the space and time Fourier transform of ⟨ ΔB1 ΔB2 ⟩ (see Eq. (A.13)), where k is a wavenumber, ν a frequency, and the subscripts 1 and 2 refer to two different spatial and temporal positions.
To continue we need to derive an expression for the correlation product ⟨ ΔB1 ΔB2 ⟩. To this end, we recall that B = σT4/π, where σ is the Stefan-Boltzmann constant, and introduce ΔT as the difference between the temperature of the granule and that of the surrounding medium. We further more use the quasi-normal approximation (Millionshchikov 1941) and assume that the scalar Θ ≡ ΔT/ ⟨ T ⟩ t is isotropic and behaves as a passive scalar. EΘ(k,ν) is then introduced as its associated spectrum (Lesieur 1997, Chap. V-10) and factorized into a spatial spectrum EΘ(k) and a frequency-dependent factor χk(ν) (see Eq. (A.26)). The above-mentionned set of approximations, after tedious calculations, leads us to (see details in Appendix A) 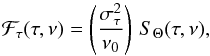 (9)where
(9)where 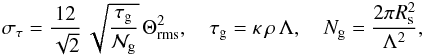 (10)Θrms the root-mean-square of Θ (Eq. (A.25)), and Λ a characteristic length (see below). Note that in Eq. (10), τg corresponds to the characteristic optical thickness of the granules, Ng to the average number of granules distributed over half of the photosphere (i.e., at r = Rs), and στ to the global brightness fluctuations associated with the granulation spectrum that one would see at the optical depth τ. The RHS of Eq. (9) involves the dimensionless source function SΘ(τ,ν), whose expression is given in Eq. (A.32). The latter depends on EΘ(k) and χk(ν).
(10)Θrms the root-mean-square of Θ (Eq. (A.25)), and Λ a characteristic length (see below). Note that in Eq. (10), τg corresponds to the characteristic optical thickness of the granules, Ng to the average number of granules distributed over half of the photosphere (i.e., at r = Rs), and στ to the global brightness fluctuations associated with the granulation spectrum that one would see at the optical depth τ. The RHS of Eq. (9) involves the dimensionless source function SΘ(τ,ν), whose expression is given in Eq. (A.32). The latter depends on EΘ(k) and χk(ν).
The adopted expression for the spatial spectrum EΘ(k) (see Eq. (A.38)) involves the length-scale Λ as well as the characteristic wavenumber kc, which separates the inertial-convective range from the inertial-conductive range. Some prescriptions are required for Λ and kc, however. We hence assume that Λ = β Hp, where Hp is the pressure scale height and β a free parameter. For kc, we adopt the prescription 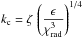 , where ζ is a free parameter introduced to exert some control on this prescription, χrad is the radiative diffusivity coefficient, and ϵ is the rate of injection of kinetic energy into the turbulent cascade.
, where ζ is a free parameter introduced to exert some control on this prescription, χrad is the radiative diffusivity coefficient, and ϵ is the rate of injection of kinetic energy into the turbulent cascade.
We turn now to the frequency component χk(ν). In a strongly turbulent medium, χk is well described by a Lorentzian function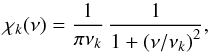 (11)where νk is by definition the half-width at half-maximum of χk(ν). The expression for νk is given in Eq. (A.45), which involves the free parameter λ. This was introduced to have some control on this definition. As an alternative for a Lorenztian function (see Appendix A.4.2), we also consider an exponential form
(11)where νk is by definition the half-width at half-maximum of χk(ν). The expression for νk is given in Eq. (A.45), which involves the free parameter λ. This was introduced to have some control on this definition. As an alternative for a Lorenztian function (see Appendix A.4.2), we also consider an exponential form ![\begin{equation} \chi_k(\nu) = { {\ln 2 } \over {2 \, {\nu_k}}} \, \exp \left [ - \left | \ln 2 \, { \nu \over \nu_k } \right | \right ] \cdot \label{EF} \end{equation}](/articles/aa/full_html/2013/11/aa20816-12/aa20816-12-eq78.png) (12)
(12)
3. Calibration using solar observations
The theoretical granulation representative of the Sun were computed on the basis of the present model using inputs extracted from a 3D hydrodynamical model of the solar surface layers. To reproduce the solar observations, we calibrated the free parameters involved in the theory.
3.1. Computation details
We computed the theoretical PDS of the granulation (ℱ) according to Eqs. (7), (9), and (10) together with Eq. (A.15) and the set of Eqs. (A.32)–(A.36). The different quantities involved in the theoretical model (stratification, convective velocity, etc.) were obtained from a 3D model in a similar way as in Samadi et al. (2003b). However, while Samadi et al. (2003b) extracted these quantities from horizontal averages at constant geometrical depth, we here performed the averages at a constant optical depth τ. This is justified because the RHS of Eq. (7) is integrated over the optical depth.
For later use, we define σ as the root-mean-square (rms) brightness fluctuations associated with a given PDS. The latter satisfies the following relation 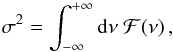 (13)where ℱ(ν) refers to a given PDS. Another important characteristic of the granulation spectrum is its associated timescale τeff, which is here defined, following Mathur et al. (2011), as the e-folding time associated with the auto-correlation function (ACF) of the relative flux variations caused by the granulation. Different PDS are next compared, in terms of their shape (i.e., ν variation), σ and τeff.
(13)where ℱ(ν) refers to a given PDS. Another important characteristic of the granulation spectrum is its associated timescale τeff, which is here defined, following Mathur et al. (2011), as the e-folding time associated with the auto-correlation function (ACF) of the relative flux variations caused by the granulation. Different PDS are next compared, in terms of their shape (i.e., ν variation), σ and τeff.
We considered a 3D model representative of the surface layers of the Sun (see details in Ludwig et al. 2009) and computed the associated theoretical PDS. This was then compared with the PDS obtained from the green channel of the SOHO/VIRGO three-channel sun-photometer (SPM, see Frohlich et al. 1997). We multiplied the original data by the instrumental function response function as derived by Michel et al. (2009) to convert the observed photometric fluctuations in terms of bolometric ones. To compare theoretical PDS with the observations, we systematically added the instrumental whited noise component, which we measured at high frequency on the observed solar spectrum.
 |
Fig. 1 Power density spectrum in ppm2/μHz as a function of frequency ν. In black: PDS obtained from the green channel of the SOHO/VIRGO three-channel sun-photometer. In red and blue: theoretical PDS of the granulation background (ℱ) computed using the quantities obtained from the solar 3D model. The red curve assumes a Lorentzian function for χk, the blue curve an exponential functional. |
3.2. Lorentzian versus exponential χk
We first assumed by default λ = 1, β = 1 and ζ = 1 and adopted a Lorentzian shape for χk (Eq. (11)). The theoretical PDS underestimates σ by a factor of about 30 and the width of the solar granulation by a factor about five (not shown). Part of this significant discrepancy is due to our prescription for Λ (Eq. (A.42)), kc (Eq. (A.43)), and νk (Eq. (A.45)). The estimation of these quantities can been controlled by the parameters β and ζ, and the product β λ, respectively. However, there is some degeneracy between ζ and β (see below). At fixed value of ζ, we then simultaneously adjusted β and β λ such that σ and the width of the spectrum best matches the observations. This led to β = 14.8 and λβ = 3.7. The resulting theoretical PDS is shown in Fig. 1. We obtained an overall satisfactory agreement between the theoretical PDS and the observations, except for the frequency variations at high frequencies.
There are several pieces of observational evidence that the granulation spectrum significantly departs at high frequencies from a Lorentzian function (e.g., Mathur et al. 2011, and references therein). Furthermore, calculations performed with the Ludwig (2006) method also confirm this general trend (Ludwig et al. 2009; Ludwig & Steffen 2012). Accordingly, we now considered the exponential function given by Eq. (12). The free parameter β and the product β λ were adjusted such that the theoretical PDS reproduces the observations best. For this we fitted the observed solar spectrum by means of the maximum-likelihood estimator (see e.g. Toutain & Appourchaux 1994; Appourchaux et al. 1998). For ζ = 1, the fit leads to β = 7.8 and β λ = 3.0. As seen in Fig. 1, we obtained an overall satisfactory agreement with the observations. In particular, the observations are much better fitted at high frequencies than when a Lorentzian function is adopted. Consequently, unless mentioned otherwise, we adopted the exponential function from now on.
Other values of the parameter ζ were also tested. For each adopted value of ζ, we have adjusted the parameter β and the product β λ such as to reproduce the solar data best. They all result in almost the same agreement with the solar observations. As for the Lorentzian χk (see Sect. 3.2), there is thus a degeneracy between the parameters β and ζ. Therefore, the observed solar granulation background does not permit one to constrain these parameters independently. However, the granules observed on the solar surface have a typical size of about 2 Mm (see e.g. Muller 1989; Roudier et al. 1991). Furthermore, the observations reported by Espagnet et al. (1993) and Hirzberger et al. (1997) suggest that kc/k0 ≈ 2. These observations accordingly favor a value of ζ of about five since this value results in kc/k0 = 1.9 and Λ = 1.7 Mm. In the following we therefore assumed ζ = 5. The corresponding value of β is 12.3, which value is within the range found by Trampedach et al. (2013), that is, 9–13.
4. Comparison with the Ludwig (2006) ab initio modeling
We compare here theoretical PDS computed with calculations performed on the basis of the Ludwig (2006) ab initio modeling assuming the same 3D hydrodynamical models in both cases. Two different 3D models were considered: a 3D model representative of the surface layers of an F-type main-sequence star (Sect. 4.1) and a second representative of the surface layers of a red giant star (Sect. 4.2). These 3D models constitute two extreme cases in the H-R diagram.
Because calculation of the PDS requires knowing the stellar radius Rs, this was obtained by matching a complete 1D standard model to the stratification of the 3D model (see details in Trampedach 1997; Samadi et al. 2008). The standard 1D model was computed using the CESAM2K code (Morel & Lebreton 2008).
4.1. F-type main-sequence stellar model
Ludwig et al. (2009) have computed two F-dwarf 3D models that included the CoRoT target HD 49933 in terms of surface metal abundance. Of these two 3D models, we considered here the one with the solar surface abundance. This model has Teff = 6725 K and log g = 4.25. We computed the theoretical PDS as detailed in Sect. 3.1. We adopted the values of the free parameters that give the best agreement between the model and the observations for the Sun (see Sect. 3). The result of the calculation is presented in Fig. 2 (top panel).
We compared the theoretical PDS with the spectrum obtained by Ludwig et al. (2009) on the basis of the ab initio method. Their calculation was based on a radius of RS,Ludwig = 1.35 R⊙, while our associated global 1D model has a radius of RS = 1.473 R⊙. To compare ours with their results, we multiplied their spectrum by (RS,Ludwig/RS)2 since the PDS is inversely proportional to the square of the radius (Ludwig 2006). The resulting PDS is shown in Fig. 2 (top panel).
 |
Fig. 2 Top: power density spectrum in ppm2/μHz as a function of frequency ν obtained for a 3D RHD model representative of an F-dwarf star (see Sect. 4.1). The black curve corresponds to the theoretical PDS obtained by Ludwig et al. (2009) on the basis of the ab initio approach, the red curve to the PDS obtained with our theoretical model using inputs extracted from the same 3D model (see Sect. 3.1). Bottom: same as the top panel for the 3D model representative of a red-giant star (see Sect. 4.2). |
The ν-variation of the PDS obtained with the ab initio approach is well reproduced. For the characteristic time τeff, our theoretical calculations result in a value of τeff 5% lower than for Ludwig et al. (2009). The rms of the global brightness fluctuations associated with their spectrum is σ = 84 ± 17 ppm. Our theoretical model results in an rms brightness fluctuation of σ = 97.4 ppm. This is about 16% higher than the result of Ludwig et al. (2009). It is worth mentioning that, consistently with the Ludwig et al. (2009) results, our model also results in a significant overestimation of the measured σ for this F-dwarf star. Furthermore, we show in Paper II that our theoretical model results for F-dwarf stars in a systematic overestimation of σ. As discussed in Paper II, this trend is very likely linked to the impact of the high level of magnetic activities on the surface convection (see also Chaplin et al. 2011a,b). We therefore emphasize that all our calculations must be rigorously considered to be valid only for stars with a low activity level.
4.2. Red giant model
We considered a 3D model of the surface layers of a red-giant star characterised by log g = 2.5 and Teff = 4964 ± 22 K (see details in Ludwig & Steffen 2012). The associated theoretical PDS is compared in Fig. 2 (bottom panel) with the PDS computed by Ludwig & Steffen (2012) on the basis on the Ludwig (2006) ab initio approach. Their calculation assumed a radius RS,Ludwig = 10 R⊙, while our associated global 1D model has a radius of Rs = 17.8 R⊙. Accordingly, we multiplied their PDS by (RS,Ludwig/Rs)2.
Except at very high frequency (ν ≳ 150 μHz), we obtain a good match between the two calculations, both in terms of amplitude and ν-variation. Our theoretical spectrum results in σ = 352 ppm, which is only 9% higher than the one obtained by Ludwig & Steffen (2012). For τeff, we obtain τeff = 1.01 × 104 s. This is 29% higher than the value derived from the Ludwig & Steffen (2012) PDS.
We note that assuming different sets of the calibrated parameters (see Sect. 3.2) has a negligible impact on the ν-variation of the PDS and a moderate effect on σ, for both the red giant and F-dwarf models. Furthermore, for both 3D models, assuming a Lorenztian function for χk(ν) instead of an exponential function, results in a considerable discrepancy at high frequency, as in the case of the Sun (not shown).
5. Conclusion
We have developed a simple 1D theoretical model for the granulation spectrum. One advantage of this model is that it can be used to compute theoretical granulation spectra on a large scale. Another benefit is that any prescription for the turbulent spectrum can been considered, in particular, different prescriptions can be tested for χk, the Fourier transform of the time correlation function of the eddy velocity at a fixed k wave-number. In this way, we have established a link between the ν-variation of the granulation spectrum in intensity with the frequency component χk.
The theoretical model was first applied to the solar case. The stratification of the surface layers of the Sun and the properties of its surface convection were obtained from a 3D hydrodynamical model of the surface layers of the Sun. Assuming default values for the free parameters involved in the theoretical model, our theoretical model strongly underestimates the quantities σ and τeff derived from the observed solar granulation spectrum. Nevertheless, the solar granulation spectrum can be well reproduced by adjusting two of the three free parameters involved in the theoretical model, while the degeneracy between the free parameters was removed by using constraints from solar images.
Two different functions for χk(ν) were tested: a Lorentzian function and an exponential one. Whatever the choice of the free parameters, the ν-variation of the solar spectrum is not reproduced at high frequencies with the Lorentzian function. Indeed, at high frequencies the theoretical spectrum decreases as ν-2, while the observations decrease much more rapidly with ν. On the other hand, adopting an exponential χk results in a much better agreement at high frequency. As discussed in Appendix C, this result confirms the previous claim by Nordlund et al. (1997) that the granules seen in the visible part of the atmosphere have a low level of turbulence.
We then compared theoretical PDS with PDS calculated on the basis of the Ludwig (2006) ab inito approach, that is from the timeseries of the intensity emerging directly from 3D hydrodynamical models of the surface layers of stars. The time-averaged properties of the surface layers were obtained from two 3D hdyrodynamical models, one representative of an F-type star and the second one for a red giant star. The theoretical PDS reproduces the main characteristics of the PDS obtained with the ab initio modeling. As in the solar case, the best agreement was obtained with an exponential χk(ν).
However, some residual differences remain between our theoretical calculations and the solar granulation spectrum as well as between our calculations and those obtained with the ab initio approach. As discussed in Appendix D, all these differences do not exhibit a severe defect of our theoretical model, however, and we conclude that the main physical assumptions of the theoretical model are validated by our different comparisons. Further theoretical developments are required to improve the modeling of the granulation background, however.
We compute in the companion paper on the basis of this theoretical model the global brightness fluctuations (σ) and the lifetime (τeff) associated with the stellar granulation for a set of stars with different spectral types and luminosity classes. This will then allow us to derive theoretical scaling laws for σ and τeff, which we then compare with Kepler observations.
Online material
Appendix A: Theoretical developments
Appendix A.1: General expression of the PDS
We establish here our general expression of the PDS, that it is Eqs. (7) and (8). We start from the term of Eq. (6), which enters in the RHS of Eq. (1). We apply the operator given by Eq. (2) on Eq. (6), it gives 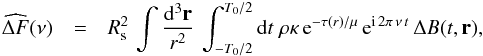 (A.1)where the space integration is performed over half of the (stellar) sphere, d3r = −dμ r2 dr dφ, and dτ = κ ρ.
(A.1)where the space integration is performed over half of the (stellar) sphere, d3r = −dμ r2 dr dφ, and dτ = κ ρ.
The extent of the region where the stellar granulation is seen is very small compared to the stellar radius Rs, such that r is almost constant over the optical depth range relevant for calculating the flux. Therefore, in very good approximation we have 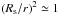 in the integrand of Eq. (A.1). Accordingly, Eq. (A.1) can be simplified as
in the integrand of Eq. (A.1). Accordingly, Eq. (A.1) can be simplified as 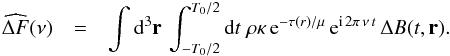 (A.2)Since
(A.2)Since 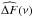 cannot be evaluated in a deterministic way but a statistical one only, we consider the square of Eq. (A.2) and average it over a large number of independent realizations. This gives
cannot be evaluated in a deterministic way but a statistical one only, we consider the square of Eq. (A.2) and average it over a large number of independent realizations. This gives 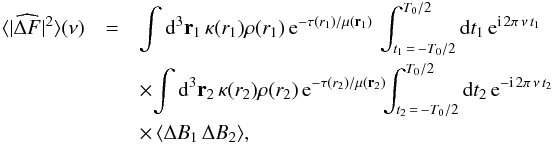 (A.3)where ΔB1 (resp. ΔB2) corresponds to the quantity ΔB evaluated at the time-space position (t1,r1) (resp. (t2,r2)).
(A.3)where ΔB1 (resp. ΔB2) corresponds to the quantity ΔB evaluated at the time-space position (t1,r1) (resp. (t2,r2)).
We then define the following new coordinates 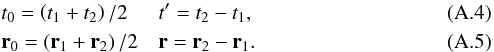 In these coordinates, r and t′ are the spatial correlation and temporal correlation lengths associated with the local properties of the turbulence, while r0 and t0 are mean space and time positions. Using the new coordinates given by Eqs. (A.4) and (A.5) in Eq. (A.6) leads to
In these coordinates, r and t′ are the spatial correlation and temporal correlation lengths associated with the local properties of the turbulence, while r0 and t0 are mean space and time positions. Using the new coordinates given by Eqs. (A.4) and (A.5) in Eq. (A.6) leads to 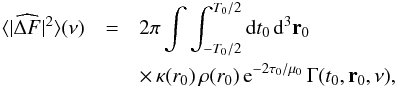 (A.6)where
(A.6)where
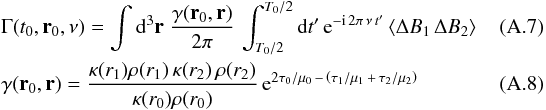 and τi = τ(ri),μi = μ(ri) with i = { 0,1,2 }.
and τi = τ(ri),μi = μ(ri) with i = { 0,1,2 }.
At this stage, a tractable expression for Eq. (A.6) calls for more assumptions. We assume that T0 is much longer than the granule lifetime. We neglect length-scales longer than the granulation length-scales. In that case ΔB represents the instantaneous difference between the brightness of the granules situated at the position (τ(r),μ,φ) and the brightness of the material in the steady state (< B > t). Accordingly, Eq. (A.6) reduces to 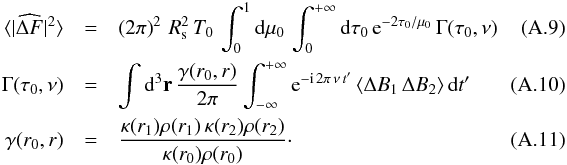 We now assume that κρ varies at a length-scale longer than the characteristic size of the granules. This assumption is discussed in Appendix B. Accordingly, γ ≃ κ(r0)ρ(r0) and Γ reduces to
We now assume that κρ varies at a length-scale longer than the characteristic size of the granules. This assumption is discussed in Appendix B. Accordingly, γ ≃ κ(r0)ρ(r0) and Γ reduces to 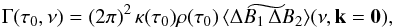 (A.12)where
(A.12)where 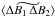 is the space and time Fourier transform of ⟨ ΔB1 ΔB2 ⟩, defined as
is the space and time Fourier transform of ⟨ ΔB1 ΔB2 ⟩, defined as 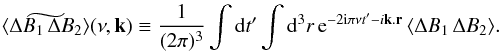 (A.13)Note that, from now on, we substitute the notation τ0 by τ.
(A.13)Note that, from now on, we substitute the notation τ0 by τ.
We now turn to the time-averaged flux ⟨ F ⟩ t. From Eqs. (3), (4), and (5) one derives 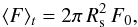 (A.14)where we have defined
(A.14)where we have defined 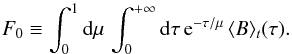 (A.15)Finally, using Eq. (A.9), Eq. (A.12) and Eq. (A.14) we derive the general expressions of Eqs. (7) and (8). The term ℱτ (Eq. (8)) stands for the PDS of the granulation as it would be seen at the optical depth τ. However, the observed PDS associated with the granulation background is given by Eq. (7) and corresponds to the sum of the spectra seen at different layers in the atmosphere, but weighted by the term e− 2τ/μ ( ⟨ B ⟩ t/F0)2.
(A.15)Finally, using Eq. (A.9), Eq. (A.12) and Eq. (A.14) we derive the general expressions of Eqs. (7) and (8). The term ℱτ (Eq. (8)) stands for the PDS of the granulation as it would be seen at the optical depth τ. However, the observed PDS associated with the granulation background is given by Eq. (7) and corresponds to the sum of the spectra seen at different layers in the atmosphere, but weighted by the term e− 2τ/μ ( ⟨ B ⟩ t/F0)2.
Appendix A.2: Source function (⟨ ΔB1 ΔB2 ⟩)
To proceed we need to derive an expression for the correlation product ⟨ ΔB1 ΔB2 ⟩. To this end, we recall that B = σT4/π, where σ is the Stefan-Boltzmann constant, and introduce ΔT as the difference between the temperature of the granule and that of the surrounding medium. We thus have 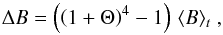 (A.16)where Θ ≡ ΔT/ ⟨ T ⟩ t. The second-order Taylor expansion of the RHS of Eq. (A.16) gives
(A.16)where Θ ≡ ΔT/ ⟨ T ⟩ t. The second-order Taylor expansion of the RHS of Eq. (A.16) gives 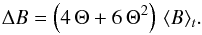 (A.17)We have neglected the third and fourth order terms in Θ. Indeed, a 3D hydrodynamical simulation of the solar surface shows that terms higher than second order contribute less than about 15% of Eq. (A.16). Accordingly,
(A.17)We have neglected the third and fourth order terms in Θ. Indeed, a 3D hydrodynamical simulation of the solar surface shows that terms higher than second order contribute less than about 15% of Eq. (A.16). Accordingly, 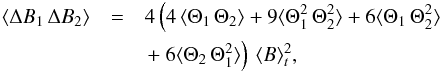 (A.18)where Θ1 ≡ Θ(r1,t1) and Θ2 ≡ Θ(r2,t2).
(A.18)where Θ1 ≡ Θ(r1,t1) and Θ2 ≡ Θ(r2,t2).
We now adopt the quasi-normal approximation (QNA). This approximation is rigorously valid for normally distributed quantities. Departure from this approximation is discussed in Appendix B. Normally distributed quantities are necessarily symmetric, such that 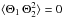 and
and 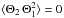 . This approximation also implies (e.g., Lesieur 1997, Chap. VII-2)
. This approximation also implies (e.g., Lesieur 1997, Chap. VII-2) 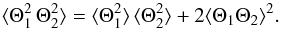 (A.19)The first term in the RHS of Eq. (A.19) does not contribute in the time Fourier domain, except at the null frequency. Accordingly,
(A.19)The first term in the RHS of Eq. (A.19) does not contribute in the time Fourier domain, except at the null frequency. Accordingly, ![\appendix \setcounter{section}{1} \begin{eqnarray} \langle \Delta B_1 \, \Delta B_2 \rangle = \left[ 16 \, \langle \Theta_1 \Theta_2 \rangle + 72 \langle \Theta_1 \Theta_2 \rangle^2 \right] \, \langle B \rangle_t^2 . \label{A_B_3} \end{eqnarray}](/articles/aa/full_html/2013/11/aa20816-12/aa20816-12-eq157.png) (A.20)Now using the Parseval-Plancherel relation, Eq. (A.20) becomes
(A.20)Now using the Parseval-Plancherel relation, Eq. (A.20) becomes ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{A_B_4} \widetilde{\langle \Delta B_1 \, \Delta B_2 \rangle} (\nu,\vec k) = \langle B \rangle_t^2 \left[ 16 \widetilde{ \langle \Theta_1 \Theta_2 \rangle} (\nu,\vec k) + 72 \, \widetilde{\cal B}_\Theta (\nu,\vec k) \right] , \end{eqnarray}](/articles/aa/full_html/2013/11/aa20816-12/aa20816-12-eq158.png) (A.21)with
(A.21)with 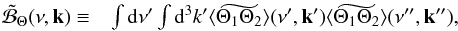 (A.22)where ν′′ = ν + ν′ and k′′ = k + k′.
(A.22)where ν′′ = ν + ν′ and k′′ = k + k′.
We assume that the scalar Θ is isotropic. Accordingly, the spatial Fourier transform of ⟨ Θ1Θ2 ⟩ (r,ν) is given by (see e.g. Lesieur 1997, Chap. V-10) 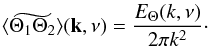 (A.23)The scalar spectrum EΘ(k,ω) is related to the scalar variance as (Lesieur 1997, Chap. V-10)
(A.23)The scalar spectrum EΘ(k,ω) is related to the scalar variance as (Lesieur 1997, Chap. V-10) 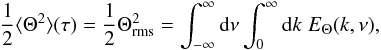 (A.24)where Θrms is by definition the rms of Θ, which is related to ΔTrms (the rms of ΔT) according to
(A.24)where Θrms is by definition the rms of Θ, which is related to ΔTrms (the rms of ΔT) according to 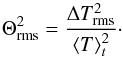 (A.25)Following Stein (1967), the scalar energy spectrum EΘ(k,ν) can be factorized into a spatial spectrum EΘ(k) and a frequency-dependent factor χk(ν) according to
(A.25)Following Stein (1967), the scalar energy spectrum EΘ(k,ν) can be factorized into a spatial spectrum EΘ(k) and a frequency-dependent factor χk(ν) according to 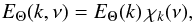 (A.26)where the frequency-dependent factor χk(ν) is normalized such that
(A.26)where the frequency-dependent factor χk(ν) is normalized such that 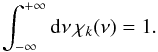 (A.27)
(A.27)
Appendix A.3: Final expression of relative flux variations
The final expression for the term ℱτ (Eq. (8)) that appears in the RHS of Eq. (7) is obtained by inserting Eq. (A.21) to (A.23) into Eq. (8), so that ![\appendix \setcounter{section}{1} \begin{equation} {\cal F}_\tau (\tau,\nu) = {{(2\pi)^2 \, \kappa \rho } \over R_{\rm s}^2} \; \left[ 16 \, \widetilde{ \langle \Theta_1 \Theta_2 \rangle} + 72 \, \tilde{\cal B}_\Theta \right] , \label{F_nu_tau_2} \end{equation}](/articles/aa/full_html/2013/11/aa20816-12/aa20816-12-eq172.png) (A.28)where the two terms in the RHS of Eq. (A.28) are considered for (τ,ν,k = 0).
(A.28)where the two terms in the RHS of Eq. (A.28) are considered for (τ,ν,k = 0).
Equation (A.28) can be further simplified by assuming that the temperature fluctuations behave as a passive scalar (see Appendix A.4.1 and the discussion in Appendix B). In that case, it can been shown that the first term in the RHS of Eq. (A.28) vanishes (see Monin & Yaglom 1971, Chap. 14.5). Accordingly, Eq. (A.28) simplifies as 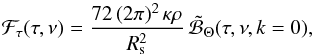 (A.29)with
(A.29)with
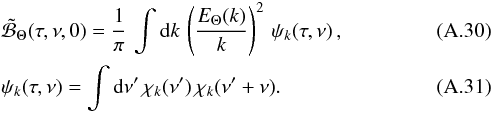 The final expression, Eq. (A.29), is recast to a more suitable form. To this end, we define the characteristic wave-number k0 = 2π/Λ where Λ is a characteristic length. We also define the characteristic frequency ν0 = 1/(2π τc) where τc is a characteristic time. Eventually, Eq. (A.29) leads to Eqs. (9), (10) where we have defined the dimensionless source function
The final expression, Eq. (A.29), is recast to a more suitable form. To this end, we define the characteristic wave-number k0 = 2π/Λ where Λ is a characteristic length. We also define the characteristic frequency ν0 = 1/(2π τc) where τc is a characteristic time. Eventually, Eq. (A.29) leads to Eqs. (9), (10) where we have defined the dimensionless source function 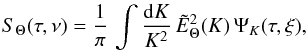 (A.32)as well as the following dimensionless quantities:
(A.32)as well as the following dimensionless quantities:
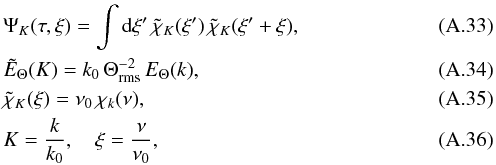 where we have defined the characteristic wavenumber k0 = 2π /Λ, and the characteristic frequency ν0 = 1/(2π τc), where τc ≡ 1/(k0 u0) is a characteristic time and u0 a characteristic velocity (see Eq. (A.40) below). Note that the dimensionless quantities
where we have defined the characteristic wavenumber k0 = 2π /Λ, and the characteristic frequency ν0 = 1/(2π τc), where τc ≡ 1/(k0 u0) is a characteristic time and u0 a characteristic velocity (see Eq. (A.40) below). Note that the dimensionless quantities 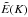 and
and 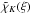 verify the following normalization conditions:
verify the following normalization conditions: 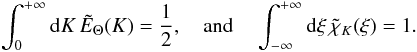 (A.37)
(A.37)
Appendix A.4: Turbulence modeling
Appendix A.4.1: Spatial spectrum
As already mentioned, it is assumed that the temperature fluctuations behave as a passive scalar (see the discussion in Appendix B). Therefore EΘ(k) is given according to (see Lesieur 1997, Chap. VI-10) 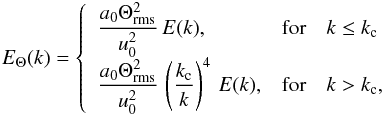 (A.38)where a0 is a normalization factor, E(k) the kinetic energy spectrum, u0 a characteristic velocity (see Eq. (A.40) below), and kc the wavenumber, which separates two characteristic ranges:
(A.38)where a0 is a normalization factor, E(k) the kinetic energy spectrum, u0 a characteristic velocity (see Eq. (A.40) below), and kc the wavenumber, which separates two characteristic ranges:
-
the inertial-convective range(k < kc). In this domain, advection of the temperature fluctuations by the turbulent velocity field dominates over the diffusion.
-
the inertial-conductive range (k > kc). In this domain, the diffusion of the temperature fluctuations dominates over advection.
We consider for E(k) the Kolmogorov spectrum, and the characteristic velocity u0 is defined such that 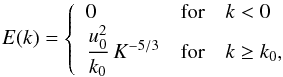 (A.39)where the characteristic velocity u0 is defined such that
(A.39)where the characteristic velocity u0 is defined such that 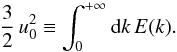 (A.40)From Eq. (A.38) and Eq. (A.39), the spacial spectrum finally becomes
(A.40)From Eq. (A.38) and Eq. (A.39), the spacial spectrum finally becomes 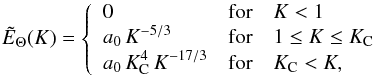 (A.41)where we have defined KC = kc/k0.
(A.41)where we have defined KC = kc/k0.
Some prescriptions are required for kc and k0. 3D RHD show that from one stellar 3D model to another, the granule size Λ scales approximately as the pressure scale-height (Hp) at the photosphere (Freytag et al. 1997). Accordingly, we assume that 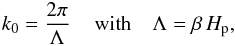 (A.42)where Λ is a characteristic length-scale, Hp the pressure scale height and β is a free parameter. Concerning the characteristic wavenumber kc, in a medium with very low Prandtl number (which is the case in the stellar medium), kc is given by (see Lesieur 1997, Chap. VI)
(A.42)where Λ is a characteristic length-scale, Hp the pressure scale height and β is a free parameter. Concerning the characteristic wavenumber kc, in a medium with very low Prandtl number (which is the case in the stellar medium), kc is given by (see Lesieur 1997, Chap. VI) 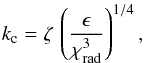 (A.43)where ζ is a free parameters introduced to exercise some control on this prescription, χrad is the radiative diffusivity coefficient, and ϵ is the rate of injection of kinetic energy into the turbulent cascade. The latter is estimated according to
(A.43)where ζ is a free parameters introduced to exercise some control on this prescription, χrad is the radiative diffusivity coefficient, and ϵ is the rate of injection of kinetic energy into the turbulent cascade. The latter is estimated according to 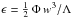 , where we have introduced the anisotropy factor
, where we have introduced the anisotropy factor 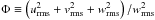 , where urms, vrms, and wrms are the rms of the three components of the velocity (horizontal and vertical ones).
, where urms, vrms, and wrms are the rms of the three components of the velocity (horizontal and vertical ones).
Appendix A.4.2: Frequency spectrum
Since in the inertial-convective range (i.e., k < kc) temperature fluctuations are dominated by advection, we assume that – at this scale range – χk(ν) is the same as the frequency spectrum associated with the velocity field, 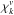 . This hypothesis tends to be supported by large eddies simulations (see e.g. Samadi et al. 2003a). Indeed, using a solar hydrodynamic simulation, Samadi et al. (2003a) have found that this property is rather well verified by the entropy fluctuations. Since entropy fluctuations are mostly dominated by temperature fluctuations, this must be the same for the temperature fluctuations. For the inertial-conductive range (k > kc): temperature fluctuations are no longer dominated by advection. However, to our knowledge, no study has been conducted yet about the properties of χk in this range. Therefore, we assume by default that in this range χk varies with ν, as do
. This hypothesis tends to be supported by large eddies simulations (see e.g. Samadi et al. 2003a). Indeed, using a solar hydrodynamic simulation, Samadi et al. (2003a) have found that this property is rather well verified by the entropy fluctuations. Since entropy fluctuations are mostly dominated by temperature fluctuations, this must be the same for the temperature fluctuations. For the inertial-conductive range (k > kc): temperature fluctuations are no longer dominated by advection. However, to our knowledge, no study has been conducted yet about the properties of χk in this range. Therefore, we assume by default that in this range χk varies with ν, as do 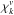 .
.
In a strongly turbulent medium, 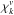 is well described by a Lorentzian function (Sawford 1991; Samadi et al. 2003a; Belkacem et al. 2010), i.e.,
is well described by a Lorentzian function (Sawford 1991; Samadi et al. 2003a; Belkacem et al. 2010), i.e., 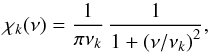 (A.44)where νk is by definition the half-width at half-maximum of χk(ν). In the framework of the Samadi & Goupil (2001) formalism, this latter quantity is evaluated as
(A.44)where νk is by definition the half-width at half-maximum of χk(ν). In the framework of the Samadi & Goupil (2001) formalism, this latter quantity is evaluated as 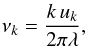 (A.45)with
(A.45)with 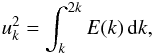 (A.46)where λ is a free parameter introduced, following Balmforth (1992), to have some control on the adopted definition for νk. We define the characteristic time τc ≡ 1/(k0 u0), which corresponds to an estimate of the lifetime of the largest eddies. Accordingly, we have ν0 = (2πτc)-1.
(A.46)where λ is a free parameter introduced, following Balmforth (1992), to have some control on the adopted definition for νk. We define the characteristic time τc ≡ 1/(k0 u0), which corresponds to an estimate of the lifetime of the largest eddies. Accordingly, we have ν0 = (2πτc)-1.
The Lorentzian χk (Eq. (A.44)) has a justification for a strongly turbulent medium. However, Georgobiani et al. (2006) have found on the basis of a 3D RHD solar model that χk decreases more rapidly with ν near the photosphere than it does in deeper layers. Accordingly, as an alternative for a Lorenztian function and following Musielak et al. (1994), we also consider for χk an exponential form ![\appendix \setcounter{section}{1} \begin{equation} \chi_k(\nu) = { {\ln 2 } \over {2 \, {\nu_k}}} \, \exp \left [ - \left | \ln 2 \, { \nu \over \nu_k } \right | \right ] \, , \label{EF2} \end{equation}](/articles/aa/full_html/2013/11/aa20816-12/aa20816-12-eq211.png) (A.47)where νk is the half-width at half-maximum. We alternatively adopted here the two different prescriptions for χk.
(A.47)where νk is the half-width at half-maximum. We alternatively adopted here the two different prescriptions for χk.
Appendix B: Approximations and assumptions
Our theoretical model is based on three major approximations and assumptions. They are discussed below.
Passive scalar assumption: it was assumed that the temperature fluctuations behave as a passive scalar. We recall that a passive scalar is a quantity that obeys an equation of diffusion (e.g., Lesieur 1997). For the temperature fluctuations, this equation of diffusion is rigorously valid when the diffusion and the Boussinesq approximations are verified and the stratification is negligible compared with the eddy size. However, all these conditions are not fulfilled in the vicinity of the photosphere where the granules are the more visible. Indeed, in this region the medium is optically thin such that the diffusion approximation does no longer hold. Furthermore, this region is characterized by a non-negligible turbulent Mach number that prevents the Boussinesq approximation from being valid. Finally, the granule sizes are typically of the order of the pressure-scale height (see below). Nevertheless, as shown by Espagnet et al. (1993) and Hirzberger et al. (1997), the spectrum, EΘ, associated with the temperature fluctuations at the surface of the Sun scales with k as predicted by Eq. (A.38), which was derived assuming that the temperature fluctuations behave as a passive scalar. This suggests that somehow the temperature fluctuations obey an equation of diffusion.
Quasi-normal approximation (QNA): the approximation of Eq. (A.19) assumes that fluctuating quantities are distributed according to a normal distribution. However, it is well known that the departure from the QNA is important in a strongly turbulent medium (Ogura 1963). Furthermore, the upper-most part of the convection zone is a turbulent convective medium composed of essentially two flows (the granules and the downdraft plumes) that are asymmetric with respect to each other. Therefore, we obviously do not deal with symmetric distribution, as it is the case for a normal distribution. With the help of a solar 3D hydrodynamical simulation, Belkacem et al. (2006) have quantified the departure from the QNA (seee also Kupka & Robinson 2007). However, by comparing 3D hydrodynamical models representative of different main-sequence stars, we have found that this departure does not vary significantly across the main sequence.
Length-scale separation: the derivation of Eq. (7) is based on the assumption that the product κρ varies at a length-scale significantly longer than the granule size. However, in the case of the Sun, for instance, the granules have a size of about 2 Mm (see e.g. Muller 1989; Roudier et al. 1991) while the pressure-scale height, Hp, is of the order of few hundred kilometers at the photosphere. Because near the photosphere the density scale-height Hρ is of the same order as Hp and even lower, our assumption does not hold near the photosphere. Nevertheless, 3D hydrodynamic models show that from a stellar model to another, the granule size scales as the pressure scale-height at the photosphere (Freytag et al. 1997; Samadi et al. 2008). Therefore, as for the QNA, we expect that the departure from our hypothesis introduces a bias that remains almost constant across the Hertzsprung-Russell diagram.
The major approximations and assumptions adopted in our model are expected to be in default near the photosphere. However, avoiding these approximations and assumptions would require additional theoretical improvements, and they constitute – at the present time – the only way for deriving an analytical model of the granulation spectrum. We also recall that our objective is to derive a simple analytical model for the interpretation of the observed scaling relations. Furthermore, provided that the three free parameters involved in the model are appropriately tuned, the theoretical model agrees reasonably well with the Ludwig (2006) 3D hydrodynamical approach (see Sect. 4).
Appendix C: Eddy-time correlation
Two different functions for χk(ν) were tested: a Lorentzian function and an exponential one. For a strongly turbulent medium, one expects a Lorentzian function (Sawford 1991; Samadi et al. 2003a; Belkacem et al. 2010). However, with this function, the theoretical granulation spectrum decreases as ν-2, while the observations decreases much more rapidly with ν. On the other hand, adopting an exponential χk results in a much better agreement at high frequency. This is because an exponential χk decreases more rapidly with frequency than does a Lorenztian χk. Finally, as in the Sun, adopting an exponential χk results in a much better match with the theoretical PDS computed with the ab initio approach for two 3D hdyrodynamical models, one representative for an F-type star and the other one for a red giant star (see Sect. 4).
According to Sawford (1991, see also Appourchaux et al. 2010, the time-Fourier transform of the Lagrangian eddy-time
correlation function is expected to tend to a Lorentzian function when the Reynolds number tends to infinity. In contrast, the less turbulent the medium (i.e., in general the lower Reynolds number), the more rapid the decrease of χk with increasing ν. This behavior is also supported for the Eulerian eddy-time correlation (χk) by hydrodynamical numerical models (see e.g. Samadi 2011). In other words, the ν variation of χk is expected to depend on the degree of turbulence. Accordingly, our result confirms that the granules, which are mainly visible near the photosphere, are less turbulent than the super-adiabatic layers situated a few hundred kilometers below the photosphere. We therefore confirm the previous claim by Nordlund et al. (1997) that the granules have a low level of turbulence. This is also consistent with the results by Georgobiani et al. (2006, see also Nordlund et al. 2009. Indeed, these authors showed that χk decreases more rapidly with ν near the surface of a solar 3D model than it does in deeper layers, where χk is close to a Lorentzian function (Samadi et al. 2003a).
Finally, the fact that the granules have a relatively low level of turbulence is probably not specific to the Sun. Indeed, the 3D RHD models of stars show that the granules have similar properties as in the Sun (e.g., Trampedach et al. 2013). Therefore, it is not surprising that the theoretical PDS computed with the ab initio approach varies with ν in a similar way as in the Sun.
Appendix D: Remaining discrepancies
Although globally satisfactory, the theoretical model does not reproduce the solar granulation spectrum perfectly. Indeed, the observed spectrum shows a kink at ν ~ 1 mHz (see Sect. 3.2). There is no consensus yet about the physical origins of this feature. Depending on the authors, it is either attributed to the occurrence of bright points (e.g., Harvey et al. 1993; Aigrain et al. 2004), the changing properties of the granules (Andersen et al. 1998), a second granulation population (Vázquez Ramió et al. 2005), and finally to faculae (Karoff 2012). A similar discrepancy was obtained by Ludwig et al. (2009) on the basis of the ab initio approach. This indicates that pure hydrodynamical approaches cannot fully account for the observed solar granulation spectrum. Nevertheless, the remaining discrepancies represent only a small fraction of the total brightness fluctuations produced by the granulation phenomenon.
The theoretical model does not perfectly reproduced the PDS obtained with the ab initio approach for the two 3D models considered in this work. For instance, a difference of less than about 15% is obtained for σ with the 3D model for an F-dwarf star and a difference less than about 30% are obtained for τeff with the 3D model for a red giant star. These differences must be attributed to the different approximations and assumptions adopted (see Appendix B above). Nevertheless, they remain of the order of the dispersion obtained between the different methods of analysis investigated by Mathur et al. (2011, see also Paper II). Because the ab initio modeling is based on a very limited set of physical hypothesis, the reasonable agreement between the two approaches shows that despite the numerous hypotheses and assumptions adopted in our theoretical model (see Appendix B), our model provides realistic results.
Acknowledgments
SOHO is a mission of international collaboration between ESA and NASA. R.S. and K.B. acknowledge financial support from the Programme National de Physique Stellaire (PNPS) of CNRS/INSU and from Agence Nationale de la Recherche (ANR, France) program “Interaction Des Étoiles et des Exoplanètes” (IDEE, ANR-12-BS05-0008). HGL acknowledges financial support by the Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject A4) of the German Research Foundation (DFG). RS thanks Frédéric Baudin for useful discussions about statistical issues.
References
- Aigrain, S., Favata, F., & Gilmore, G. 2004, in Stellar Structure and Habitable Planet Finding, eds. F. Favata, S. Aigrain, & A. Wilson, ESA SP, 538, 215 [Google Scholar]
- Andersen, B., Leifsen, T., Appourchaux, T., et al. 1998, in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, ed. S. Korzennik, ESA SP, 418, 83 [NASA ADS] [Google Scholar]
- Appourchaux, T., Gizon, L., & Rabello-Soares, M.-C. 1998, A&AS, 132, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appourchaux, T., Belkacem, K., Broomhall, A.-M., et al. 2010, A&ARv, 18, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Balmforth, N. J. 1992, MNRAS, 255, 639 [NASA ADS] [Google Scholar]
- Belkacem, K., Samadi, R., Goupil, M. J., & Kupka, F. 2006, A&A, 460, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belkacem, K., Samadi, R., Goupil, M. J., et al. 2010, A&A, 522, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belkacem, K., Goupil, M. J., Dupret, M. A., et al. 2011, A&A, 530, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bray, R. J., & Loughhead, R. E. 1967, The solar granulation [Google Scholar]
- Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991, ApJ, 368, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., Bedding, T. R., Bonanno, A., et al. 2011a, ApJ, 732, L5 [Google Scholar]
- Chaplin, W. J., Kjeldsen, H., Bedding, T. R., et al. 2011b, ApJ, 732, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Espagnet, O., Muller, R., Roudier, T., & Mein, N. 1993, A&A, 271, 589 [NASA ADS] [Google Scholar]
- Freytag, B., Holweger, H., Steffen, M., & Ludwig, H.-G. 1997, in Science with the VLT Interferometer, ed. F. Paresce (Berlin, New York: Springer Verlag), 316 [Google Scholar]
- Frohlich, C., Andersen, B. N., Appourchaux, T., et al. 1997, Sol. Phys., 170, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Georgobiani, D., Stein, R. F., & Nordlund, Å. 2006, in Solar MHD Theory and Observations: A High Spatial Resolution Perspective, eds. J. Leibacher, R. F. Stein, & H. Uitenbroek, ASP Conf. Ser., 354, 109 [Google Scholar]
- Gray, D. 1992, The observation and analysis of stellar photospheres (Cambridge University Press) [Google Scholar]
- Harvey, J. W., Duvall, Jr., T. L.,Jefferies, S. M., & Pomerantz, M. A. 1993, in GONG 1992. Seismic Investigation of the Sun and Stars, ed. T. M. Brown, ASP Conf. Ser., 42, 111 [Google Scholar]
- Hirzberger, J., Vazquez, M., Bonet, J. A., Hanslmeier, A., & Sobotka, M. 1997, ApJ, 480, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Stello, D., Bedding, T. R., et al. 2009, Communications in Asteroseismology, 160, 74 [Google Scholar]
- Kallinger, T., & Matthews, J. M. 2010, ApJ, 711, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Karoff, C. 2012, MNRAS, 421, 3170 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 2011, A&A, 529, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., & Robinson, F. J. 2007, MNRAS, 374, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Lesieur, M. 1997, Turbulence in fluids (Kluwer Academic Publishers) [Google Scholar]
- Ludwig, H. 2006, A&A, 445, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ludwig, H.-G., & Steffen, M. 2012, 3D Model Atmospheres of Red Giant Stars, eds. A. Miglio, J. Montalbán, & A. Noels (Berlin, Heidelberg: Springer Verlag), 125 [Google Scholar]
- Ludwig, H., Samadi, R., Steffen, M., et al. 2009, A&A, 506, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Hekker, S., Trampedach, R., et al. 2011, ApJ, 741, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, J. M., Kuschnig, R., Guenther, D. B., et al. 2004, Nature, 430, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Michel, E., Baglin, A., Auvergne, M., et al. 2008, Science, 322, 558 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Michel, E., Samadi, R., Baudin, F., et al. 2009, A&A, 495, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millionshchikov, M. D. 1941, Doklady Acad. Nauk SSSR, 32, 611 [Google Scholar]
- Monin, A. S., & Yaglom, A. M. 1971, Statistical Fluid mechanics: Mechanics of turbulence, ed. J. L. Lumley (Dover publications), 2 [Google Scholar]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mosser, B., Belkacem, K., Goupil, M.-J., et al. 2010, A&A, 517, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muller, R. 1989, in Solar and Stellar Granulation, eds. R. Rutten, & G. Severino (Kluwer Academic Publishers), 101 [Google Scholar]
- Muller, R. 1999, in Motions in the Solar Atmosphere, eds. A. Hanslmeier, & M. Messerotti, Astrophys. Space Sc. Lib., 239, 35 [Google Scholar]
- Musielak, Z. E., Rosner, R., Stein, R. F., & Ulmschneider, P. 1994, ApJ, 423, 474 [Google Scholar]
- Nordlund, A., Spruit, H. C., Ludwig, H.-G., & Trampedach, R. 1997, A&A, 328, 229 [NASA ADS] [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Ogura, Y. 1963, J. Fluid Mech., 16, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Roudier, T., Vigneau, J., Espagnet, O., et al. 1991, A&A, 248, 245 [NASA ADS] [Google Scholar]
- Samadi, R. 2011, in Lect. Notes Phys., 832, The Pulsations of the Sun and the Stars, eds. J.-P. Rozelot, & C. Neiner (Berlin Springer Verlag) [Google Scholar]
- Samadi, R., & Goupil, M. J. 2001, A&A, 370, 136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samadi, R., Nordlund, Å., Stein, R. F., Goupil, M. J., & Roxburgh, I. 2003a, A&A, 404, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samadi, R., Nordlund, Å., Stein, R. F., Goupil, M. J., & Roxburgh, I. 2003b, A&A, 403, 303 [Google Scholar]
- Samadi, R., Belkacem, K., Goupil, M. J., Dupret, M.-A., & Kupka, F. 2008, A&A, 489, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Samadi, R., Belkacem, K., Ludwig, H.-G., et al. 2013, A&A, 559, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sawford, B. L. 1991, Phys. Fluids, 3, 1577 [NASA ADS] [CrossRef] [Google Scholar]
- Siedentopf, H. 1933, Astron. Nachr., 247, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F. 1967, Sol. Phys., 2, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Stello, D., Chaplin, W. J., Basu, S., Elsworth, Y., & Bedding, T. R. 2009, MNRAS, 400, L80 [NASA ADS] [CrossRef] [Google Scholar]
- Svensson, F., & Ludwig, H.-G. 2005, in 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, eds. F. Favata, G. A. J. Hussain, & B. Battrick, ESA SP, 560, 979 [Google Scholar]
- Toutain, T., & Appourchaux, T. 1994, A&A, 289, 649 [NASA ADS] [Google Scholar]
- Trampedach, R. 1997, Master’s thesis, Master’s thesis, Aarhus University [Google Scholar]
- Trampedach, R., Asplund, M., Collet, R., Nordlund, Å., & Stein, R. F. 2013, ApJ, 769, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Unsöld, A. 1930, ZAp, 1, 138 [Google Scholar]
- Vázquez Ramió, H., Régulo, C., & Roca Cortés, T. 2005, A&A, 443, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Power density spectrum in ppm2/μHz as a function of frequency ν. In black: PDS obtained from the green channel of the SOHO/VIRGO three-channel sun-photometer. In red and blue: theoretical PDS of the granulation background (ℱ) computed using the quantities obtained from the solar 3D model. The red curve assumes a Lorentzian function for χk, the blue curve an exponential functional. |
| In the text | |
 |
Fig. 2 Top: power density spectrum in ppm2/μHz as a function of frequency ν obtained for a 3D RHD model representative of an F-dwarf star (see Sect. 4.1). The black curve corresponds to the theoretical PDS obtained by Ludwig et al. (2009) on the basis of the ab initio approach, the red curve to the PDS obtained with our theoretical model using inputs extracted from the same 3D model (see Sect. 3.1). Bottom: same as the top panel for the 3D model representative of a red-giant star (see Sect. 4.2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


