| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201322449 | |
| Published online | 10 October 2013 | |
An analytic distribution function for a mass-less cored stellar system in a cuspy dark-matter halo
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: breddels@astro-rug.nl
Received: 5 August 2013
Accepted: 11 September 2013
We demonstrate the existence of a distribution function that can be used to represent spherical mass-less cored stellar systems having constant mildly tangential velocity anisotropy embedded in cuspy dark-matter halos. In particular, we derived analytically the functional form of the distribution function for a Plummer stellar sphere in a Hernquist dark halo for β0 = −0.5 and for different degrees of embedding. This particular example satisfies the condition that the central logarithmic slope of the light profile γ0 > 2β0. Our models have velocity dispersion profiles similar to those observed in nearby dwarf spheroidal galaxies. Hence they can be used to generate initial conditions for a variety of problems, including N-body simulations that may represent dwarf galaxies in the Local Group.
Key words: galaxies: dwarf / galaxies: kinematics and dynamics
© ESO, 2013
1. Introduction
In the concordance ΛCDM cosmological model, galaxies are expected to be embedded in massive dark-matter halos. Recently, much emphasis has been placed on measuring and modeling the internal dynamics of dwarf spheroidal galaxies (dSph) because these systems have very high mass-to-light ratios and appear to be dark-matter dominated at all radii (see the recent reviews by Walker 2013; Battaglia et al. 2013). Particular emphasis has been placed on establishing the characteristics of the host dark-matter halos and on determining whether their properties are consistent with those expected in the context of the ΛCDM model (Stoehr et al. 2002; Strigari et al. 2010). More specifically, it is an open question whether the dSph satellites of the Milky Way could be embedded in density profiles that are centrally cusped such as the NFW profile (Navarro et al. 1996).
Much of this modeling work has been carried out using the Jeans equations in the spherical limit (e.g., Łokas 2001, 2009; Koch et al. 2007; Walker et al. 2007, 2009; Richardson & Fairbairn 2013). The general goal has been to constrain the dark-matter content (i.e., to estimate the characteristic parameters of given density profiles) by fitting the observed l.o.s. velocity distributions, and more specifically, the second and fourth moments, i.e., the dispersion and kurtosis profiles. In Jeans modeling the functional form of the velocity anisotropy needs to be specified. A fundamental limitation of this approach is that the existence of a distribution function is not guaranteed, once a solution has been found. Specifically, it is not certain that a distribution function that is positive everywhere (i.e., that it is physical) will exist.
Partly circumventing this problem, Wilkinson et al. (2002) introduced a family of parametric distribution functions that may be used to represent spherical stellar systems with anisotropic velocity ellipsoids embedded in cored dark-matter halos. More recently, the application of the Schwarzschild modeling technique to dSph has allowed considerating more general density profiles (e.g., Jardel & Gebhardt 2012; Breddels et al. 2013; Jardel et al. 2013; Breddels & Helmi 2013). In this approach the distribution functions are obtained in a numerical fashion, and by construction, they are positive everywhere. However, these distribution functions have not been given in analytic form, and it may not even be plausible to find a simple expression in the most general circumstances.
The An & Evans (2009) theorem provides an important constraint regarding distribution functions that may be associated to dSph. This theorem states that a system with a nonzero and finite central radial velocity dispersion must satisfy that the central value of the logarithmic slope of the stellar density profile γ0 and the central velocity anisotropy β0 are related through γ0 = 2β0. This implies that if the light profile is perfectly cored, as is often assumed, that is γ0 = 0, the velocity ellipsoid must be isotropic, independently of the dark-matter halo profile (which should be shallower than the singular isothermal sphere). However, if the system is cold at the center, that is σr,0 = 0, the only constraint is that γ0 > 2β0, which for cored stellar profiles is satisfied by tangentially anisotropic ellipsoids (Ciotti & Morganti 2010). Since these conditions refer to the intrinsic velocity dispersion, they do not impose strong constraints on the line-of-sight velocity dispersion (σlos), which is the observable, and one may obtain flat σlos profiles even if the system is intrinsically cold at the center.
Given the extensive modeling performed assuming cuspy dark-matter halos and cored stellar profiles, the natural question arises whether physical distribution functions that can reproduce the properties of dSph exist in such cases. For example, Evans et al. (2009) have shown that for a stellar Plummer profile with an isotropic velocity ellipsoid and a strictly constant velocity dispersion profile, the dark-matter must follow a cored isothermal sphere. We show here that this particular result cannot be generalized, and that (tracer) cored light distributions can exist in equilibrium in cuspy dark-matter halos, once the condition of constant velocity dispersion is relaxed.
In this letter, we present a distribution function that represents a mass-less stellar system having a constant anisotropy β = −1/2 following a Plummer profile embedded in a Hernquist dark-matter halo. We focus on this particular example because it is mathematically easy to manipulate, but also because it is observationally sound. The surface brightness profiles of dSph are well-fitted by Plummer models (Irwin & Hatzidimitriou 1995), and the velocity ellipsoids derived from Schwarzschild models have radially constant, if slightly negative, anisotropies (Breddels & Helmi 2013). Therefore, models such as that presented below can be used, for example, to generate initial conditions for an N-body simulation of a dwarf galaxy resembling a dSph satellite of the Milky Way.
2. Methods
2.1. Generalities
The distribution function of a spherical system in equilibrium can depend on energy E, and if the velocity ellipsoid is anisotropic, also on angular momentum L: f(E,L). It can be shown that when the distribution function takes the form f(E,L) = f1(E)L− 2β, with β = const., this β is the constant velocity anisotropy of the system.
The functional form of the energy part of the distribution function can be determined through an Abel equation, as outlined in Sect. 4.3.2 of Binney & Tremaine (2008). In that case (see their Eq. (4.67)), we may derive f1(E) from 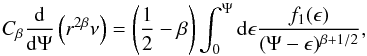 (1)where ν(r) is the density, Ψ(r) = −Φ(r) + Φ0 is the relative gravitational potential, ϵ = −E = Ψ(r) − 1/2v2 is the relative energy, and Cβ is a constant. This equation is valid for − 1/2 < β < 1/2, and might be inverted using the Abel integral to obtain an analytic expression for f1(ϵ). For β = −1, an additional derivative is needed to reach the Abel integral equation form, but the distribution function may also be derived, now from
(1)where ν(r) is the density, Ψ(r) = −Φ(r) + Φ0 is the relative gravitational potential, ϵ = −E = Ψ(r) − 1/2v2 is the relative energy, and Cβ is a constant. This equation is valid for − 1/2 < β < 1/2, and might be inverted using the Abel integral to obtain an analytic expression for f1(ϵ). For β = −1, an additional derivative is needed to reach the Abel integral equation form, but the distribution function may also be derived, now from 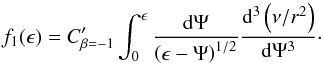 (2)These expressions are completely general, but for gravitational potentials Ψ(r) of simple mathematical form it is possible to invert and obtain r as function of Ψ, and to easily compute all corresponding derivatives.
(2)These expressions are completely general, but for gravitational potentials Ψ(r) of simple mathematical form it is possible to invert and obtain r as function of Ψ, and to easily compute all corresponding derivatives.
The case of β = −1/2 is particularly simple and yields (see Eq. (4.71) of Binney & Tremaine 2008) 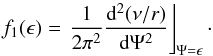 (3)If the system were self-consistent, the density and the potential would be related through the Poisson equation (see, e.g., Baes & Dejonghe 2002). However, in the case of dSph, the gravitational potential is largely determined by the dark-matter, and the stars may simply be considered as tracers. In this case, the above equations are still valid, but the density is that of the stars ν∗(r), while we may assume the potential to be that of the dark-matter only. A priori, there is no guarantee that the integral in Eq. (2) will converge for example, and that a physical solution, that is, a positive distribution function leading to a stable system, will exist for every combination of ν∗(r) and Ψ(r).
(3)If the system were self-consistent, the density and the potential would be related through the Poisson equation (see, e.g., Baes & Dejonghe 2002). However, in the case of dSph, the gravitational potential is largely determined by the dark-matter, and the stars may simply be considered as tracers. In this case, the above equations are still valid, but the density is that of the stars ν∗(r), while we may assume the potential to be that of the dark-matter only. A priori, there is no guarantee that the integral in Eq. (2) will converge for example, and that a physical solution, that is, a positive distribution function leading to a stable system, will exist for every combination of ν∗(r) and Ψ(r).
The case of β = + 1/2 is also mathematically simple (see Sect. 4.3.2 of Binney & Tremaine 2008), but for cored profiles the An & Evans (2009) theorem tells us that the resulting distribution function will be un-physical (it will have negative values), and therefore we did not consider this case in this work.
2.2. Plummer stellar sphere in a Hernquist dark halo, β = −1/2
For mathematical convenience we assumed that the gravitational potential is given by the Hernquist model (Hernquist 1990), and as explained above, it is meant to describe the (dominant) contribution of the dark-matter. Although this model is not cosmologically motivated, its density profile has the same r-1 limiting behavior in the inner regions as the NFW model. On the other hand, it has a finite mass M, and a steeper fall-off at large radii (as r-4 instead of r-3). This is also why it is often used in the literature to set up N-body simulations. The gravitational potential for the Hernquist model is 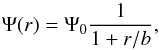 (4)where b is the scale radius, and Ψ0 = GM/b. For the stars we assumed a Plummer profile
(4)where b is the scale radius, and Ψ0 = GM/b. For the stars we assumed a Plummer profile 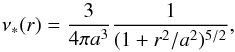 (5)where a is the Plummer scale length. Note that there are two characteristic length scales in the problem, namely a and b, and we related these using the dimensionless parameter α = a/b, and we expect that in general α ≤ 1 (i.e., that the stars are more concentrated than the dark-matter halo in which they are embedded).
(5)where a is the Plummer scale length. Note that there are two characteristic length scales in the problem, namely a and b, and we related these using the dimensionless parameter α = a/b, and we expect that in general α ≤ 1 (i.e., that the stars are more concentrated than the dark-matter halo in which they are embedded).
 |
Fig. 1 Energy part of the distribution function for a Plummer stellar sphere of scale a embedded in a Hernquist dark-matter halo of mass M and scale b, with constant velocity anisotropy β = −1/2, as given by Eq. (7). The various lines correspond to different degrees of embedding α = a/b of the stars in the (same) dark-matter halo, α = 0.01 (solid), 0.1 (dashed) and 1 (dotted). |
Using Eq. (4), we may thus express r = r(Ψ) for the Hernquist profile as 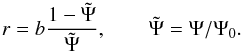 (6)The energy part of the distribution function f1(ϵ) may now be computed explicitly from Eq. (3) using Eqs. (5) and (6), and after taking the corresponding derivatives, we find
(6)The energy part of the distribution function f1(ϵ) may now be computed explicitly from Eq. (3) using Eqs. (5) and (6), and after taking the corresponding derivatives, we find 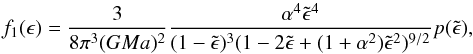 (7)where
(7)where 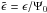 ,
, 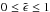 , and
, and 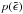 is the following polynomial:
is the following polynomial: 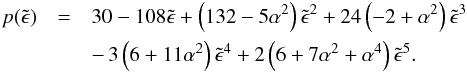 (8)
(8)
 |
Fig. 2 Velocity dispersion profiles associated to the distribution function presented in Fig. 1 for different degrees of embedding, namely α = a/b = 0.01,0.1, and 1 from top to bottom. Left column: intrinsic radial (solid) and tangential (dashed) velocity dispersions as a function of radial distance r/a. Right column: corresponding line-of-sight velocity dispersions as a function of projected distance R/a. The resulting σlos profiles are relatively flat, especially for small α, i.e., 0.01 and 0.1, and reach a finite value at the center. In general, the curves bear a good resemblance to the observed velocity dispersion profiles of stars in dSph satellites of the Milky Way, as determined in, e.g., Walker et al. (2009). |
Figure 1 shows the functional form of the distribution function f1(ϵ) for different values of α, namely α = 0.01,0.1 and 1, that is, for different degrees of embedding of the stars in the dark-matter halo. The distribution function is well-behaved, it is continuous and positive everywhere and has a positive slope, indicating that it is stable to radial modes (see Sect. 5.5 of Binney & Tremaine 2008).
We have checked that the density profile obtained by integrating this distribution function over velocity space returns the Plummer functional form. The left column of Fig. 2 shows the velocity dispersion profiles in the radial (solid) and tangential (dashed) directions for different values of α and makes explicit the dependence of the internal kinematics on the degree of embedding of the stars in the dark halo. For small α (top and middle left panels) the velocity dispersion profile is relatively flat for r > 0.1r/a. Since the properties of the halo are fixed by the mass M and the scale b, we note that the velocity dispersion has a smaller amplitude for smaller values of α, as expected.
In the right column of Fig. 2 we have plotted the resulting l.o.s. velocity dispersion profiles for the different values of α explored. It shows that these profiles are relatively flat with a projected radius over the range 0 < R/a < 2, which is similar to that probed by the observations of the kinematics of stars in the dSph satellites of the Milky Way. If we set M = 109 M⊙ and b = 2.5 kpc, the system with α = 0.01 (top panels) would have a velocity dispersion of ~2 km s-1 and a ~ 25 pc. On the other hand, if α = 0.1 (middle panels), a = 250 pc, and σlos ~ 6.3 km s-1 at the center. This case could represent systems such as Carina, Sextans, or Ursa Minor dSph for example. A more massive halo would probably be required if the aim were to represent systems such as Sculptor or Fornax, as this would allow a better match with the central value of σlos.
3. Conclusions
By example, we have demonstrated that a mass-less Plummer stellar system embedded in a Hernquist dark-matter halo constitutes a plausible physical configuration. We explicitly derived the form of the distribution function for a tangential anisotropy β = −1/2 and for different degrees of embedding of the stars, as quantified by the ratio of the scale length parameter α = a/b. This distribution function is positive for the values of α = 0.01 − 1 and also leads to a system that is stable to radial modes, as ∂f/∂ϵ > 0. The line-of-sight velocity dispersion profiles characteristic of this family of distribution functions resemble those observed for dSph and hence can be used to represent these systems. They satisfy the An & Evans (2009) theorem, namely that γ0 > 2β0, but clearly not the equality condition. We also explored the β = −1 case and found an analytic physical solution here as well, though this is more cumbersome mathematically and hence not presented here.
Acknowledgments
We are grateful to Tim de Zeeuw for encouragement and useful discussions, and to J. An and W. Evans for various interactions that led to the work presented here. We acknowledge financial support from NOVA (the Netherlands Research School for Astronomy) and the European Research Council under ERC-StG grant GALACTICA-240271.
References
- An, J. H., & Evans, N. W. 2009, ApJ, 701, 1500 [NASA ADS] [CrossRef] [Google Scholar]
- Baes, M., & Dejonghe, H. 2002, A&A, 393, 485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, G., Helmi, A., & Breddels, M. 2013 [arXiv:1305.5965] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics (Princeton University Press) [Google Scholar]
- Breddels, M. A., & Helmi, A. 2013, A&A, 558, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Breddels, M. A., Helmi, A., van den Bosch, R. C. E., van de Ven, G., & Battaglia, G. 2013, MNRAS, 433, 3173 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L., & Morganti, L. 2010, MNRAS, 408, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. W., An, J., & Walker, M. G. 2009, MNRAS, 393, L50 [NASA ADS] [Google Scholar]
- Hernquist, L. 1990, ApJ, 356, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, M., & Hatzidimitriou, D. 1995, MNRAS, 277, 1354 [NASA ADS] [CrossRef] [Google Scholar]
- Jardel, J. R., & Gebhardt, K. 2012, ApJ, 746, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Jardel, J. R., Gebhardt, K., Fabricius, M. H., Drory, N., & Williams, M. J. 2013, ApJ, 763, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Kleyna, J. T., Wilkinson, M. I., et al. 2007, AJ, 134, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Łokas, E. L. 2001, MNRAS, 327, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Łokas, E. L. 2009, MNRAS, 394, L102 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, T., & Fairbairn, M. 2013, MNRAS, 432, 3361 [NASA ADS] [CrossRef] [Google Scholar]
- Stoehr, F., White, S. D. M., Tormen, G., & Springel, V. 2002, MNRAS, 335, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Strigari, L. E., Frenk, C. S., & White, S. D. M. 2010, MNRAS, 408, 2364 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G. 2013, in Planets, Stars and Stellar Systems 5, eds. T. D. Oswalt, & G. Gilmore (Dordrecht: Springer Science+Business Media) [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2007, ApJ, 667, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2009, ApJ, 704, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkinson, M. I., Kleyna, J., Evans, N. W., & Gilmore, G. 2002, MNRAS, 330, 778 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Energy part of the distribution function for a Plummer stellar sphere of scale a embedded in a Hernquist dark-matter halo of mass M and scale b, with constant velocity anisotropy β = −1/2, as given by Eq. (7). The various lines correspond to different degrees of embedding α = a/b of the stars in the (same) dark-matter halo, α = 0.01 (solid), 0.1 (dashed) and 1 (dotted). |
| In the text | |
 |
Fig. 2 Velocity dispersion profiles associated to the distribution function presented in Fig. 1 for different degrees of embedding, namely α = a/b = 0.01,0.1, and 1 from top to bottom. Left column: intrinsic radial (solid) and tangential (dashed) velocity dispersions as a function of radial distance r/a. Right column: corresponding line-of-sight velocity dispersions as a function of projected distance R/a. The resulting σlos profiles are relatively flat, especially for small α, i.e., 0.01 and 0.1, and reach a finite value at the center. In general, the curves bear a good resemblance to the observed velocity dispersion profiles of stars in dSph satellites of the Milky Way, as determined in, e.g., Walker et al. (2009). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


