| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322262 | |
| Published online | 01 October 2013 | |
The multi-fluid pressures downstream of the solar wind termination shock
Argelander Institut für Astronomie der Universität Bonn, Abteilung f. Astrophysik und Extraterrestrische Forschung, Auf dem Huegel 71, 53121 Bonn, Germany
e-mail: msiewert@astro.uni-bonn.de
Received: 11 July 2013
Accepted: 8 August 2013
In this paper we consider a multi-fluid plasma that describes the upstream solar wind at its passage over the solar wind termination shock. In one respect, the plasma at the shock reacts like a joint fluid that is described by a single compression ratio. This ratio depends on all upstream and downstream pressures of the magnetohydrodynamic (MHD) plasma. In another respect, the distinguished plasma fluids in their downstream properties show fluid-specific reactions, thet we describe by using additional kinetic information on the plasma constituents, such as the Liouville theorem, the conservation of typical particle invariants, and the species-specific influence of the electric shock ramp. We thus obtain the resulting distribution functions of the seperate fluid particles and their associated velocity moments for the downstream region, especially their separate fluid pressures. We show that the different fluid pressures in different forms depend on the shock compression ratio and on the tilt angle between the upstream magnetic field and the shock surface normal. The dominant downstream pressures are connected with the pick-up protons and with the solar wind electrons, one dominating under some given shock conditions, the other dominating under some other shock conditions. Since the downstream distributions of solar wind protons and pick-up protons partly overlap in velocity space, we look for a joint distribution of the joint proton population in the form of a joint Kappa distribution and find that the associated Kappa index and the “Gaussian velocity width” are functions of the pick-up ion abundance, of the joint compression ratio, and of the tilt angle. Owing to the strongly heated electrons the energy-per-mass density ratio of the downstream plasma turns out to be fairly different from all that was expected up to now. This might also give a hint as to why the heliosheath plasma flow lines seen by Voyagers are different from all MHD simulations so far.
Key words: shock waves / plasmas / solar wind / Sun: heliosphere
© ESO, 2013
1. Introduction
At the latest event of the Voyager-2 crossing the solar wind termination shock, it became evident that this shock does not have the same characteristics as a classical magnetohydrodynamic (MHD) Rankine-Hugoniot shock. The entropy gain that physically should be connected with the reduced bulk velocity on the downstream side is not reflected in the thermal pressure of the downstream solar wind protons (see Richardson et al. 2008), but must at least partly reappear in shock-heated energetic pick-up protons (Decker et al. 2008). That this at least partly dissolves the problem could be shown in papers by Izmodenov & Baranov (2006), Fahr & Chalov (2008), Wu et al. (2009), Zank et al. (2010) or Chalov & Fahr (2011). Unfortunately there is no dedicated plasma instrument onboard either of the two Voyager spacecrafts that can detect protons in the “middle-energetic” keV-range, such as pick-up protons. This means that the theoretical explanations given until now cannot directly be confirmed by properties of downstream pick-up protons since this solar wind component is completely absent from Voyager data.
This situation has meanwhile encouraged additional theoretical studies that also have looked for the role of shock-heated solar wind electrons (Fahr et al. 2012; Chalov & Fahr 2013; Chashei & Fahr 2013). In these papers, it has been found that, due to the charge-specific action of the electric shock ramp on them, solar wind electrons do effectively convert upstream kinetic into downstream thermal energy, and thus on the downstream side appear as a massless, but very energetic fluid species. In any case, these theoretical endeavours have made it clear that an adequate description of the internal physics of the termination shock can only be obtained when all these different plasma species are adequately described at their passage over the shock. As a bare minimum, this asks for a multi-fluid description that takes solar wind protons, pick-up protons, and solar wind electrons reacting as separate fluids into account.
In a series of earlier papers by Fahr & Siewert (2011), Fahr et al. (2012), and Chalov & Fahr (2013), we have developed expressions for the velocity distribution function and its moments of ion and electron species immediately after the passage over the solar wind termination shock (TS). As shown there, the introduction of particle invariants and the use of Liouville’s theorem allows explicit solutions to be found for the downstream distribution functions and for their velocity moments, such as the downstream pressure of solar wind protons, solar wind electrons and pick-up protons. With these expressions, one is thus able to obtain the main contributions to the plasma pressure downstream of the shock.
In this study, we look into the individual downstream fluid pressures and their behaviour as function of the local MHD shock properties, such as the compression ratio s and the magnetic field tilt angle α, which have recently been derived by Fahr et al. (2012) and Chashei & Fahr (2013) taking an overshooting for the nonproton components of the multi-fluid shock into account. Using these results, we now look at the sum of these pressures and the resulting pressure gradients, which are very relevant for determining the plasma flow profile downstream of the shock in the inner heliosheath. While this study focusses on the immediate downstream pressure and its tangential surface gradient, the modified plasma flow profile resulting from these calculations will be the goal of a separate publication following this one.
2. Relations between upstream and downstream pressures
In this study, we assume that, as suggested for many different plasma situations by Vasyliunas (1968), Thorne & Summers (1991), Collier (1995), Collier et al. (1996), Ma & Summers (1998), Treumann (2001), Leubner (2002), Treumann et al. (2004), Yoon (2005), Yoon et al. (2005), Shizgal (2007), and especially in the recent review by Yoon et al. (2012), all distribution functions we are working with in this paper can be represented by so-called κ functions with varying parameters depending on the particle species (thermal protons, PUIs, electrons, or a distribution jointly describing all proton contributions). As we suggest, the resulting κ-values depend on the magnetic field tilt angle α and the MHD compression ratio s at the shock. Therefore, we now start briefly summarizing known properties of κ functions that we use in the following calculations.
A generic, 3D-κ function can be written as ![\begin{eqnarray} % f_\kappa(v) = \frac{n}{(\pi \sqrt{\kappa} \Theta^{2})^{3/2}} \frac{\Gamma(\kappa+1)}{\Gamma (\kappa-3/2)}\left[1+\frac{v^{2}}{\kappa\Theta^{2}}\right]^{-(\kappa+1)}\cdot \end{eqnarray}](/articles/aa/full_html/2013/10/aa22262-13/aa22262-13-eq4.png) (1)The two classical limits, κ → ∞ and
(1)The two classical limits, κ → ∞ and 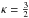 , correspond to a pure Maxwellian distribution function and a pure power law with a v-5-slope, respectively. The parameter Θ2 is the thermal width of the Gaussian core defined by (see e.g. Collier 1995; Livadiotis & McComas 2009)
, correspond to a pure Maxwellian distribution function and a pure power law with a v-5-slope, respectively. The parameter Θ2 is the thermal width of the Gaussian core defined by (see e.g. Collier 1995; Livadiotis & McComas 2009) 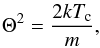 (2)with the thermal core energy kTc and the ion mass m (i.e. the proton or electron mass in this study).
(2)with the thermal core energy kTc and the ion mass m (i.e. the proton or electron mass in this study).
The pressure of the κ-distributed particle species, described as a higher velocity moment of this κ-function, is given by (see e.g. Heerikhuisen et al. 2008) 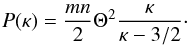 (3)
(3)
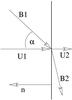 |
Fig. 1 Parameters at a typical shock. |
2.1. Pressure jumps of solar wind protons
In this study, we describe MHD shocks in the classical one-dimensional approach with the shock normal n parallel to the upstream bulk flow velocity U1 (see Fig. 1). First, we collect established properties of individual pressure jumps at MHD shocks, which is used to derive further properties of the multi-component shock system later in this paper. Beginning with the downstream pressure P2,p of solar wind protons, Fahr et al. (2012) derived the following expression that allows the downstream pressure to be expressed as a function of the upstream pressure: 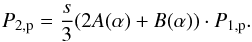 (4)Here the subscripts 1 and 2 denote upstream and downstream quantities, respectively, s = U1/U2 denotes the shock compression ratio, and the functions A(α) and B(α) are given by
(4)Here the subscripts 1 and 2 denote upstream and downstream quantities, respectively, s = U1/U2 denotes the shock compression ratio, and the functions A(α) and B(α) are given by 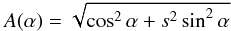 (5)and
(5)and 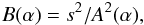 (6)where the angle α defines the inclination between the normal n and the upstream magnetic field B1.
(6)where the angle α defines the inclination between the normal n and the upstream magnetic field B1.
2.2. Pressure jumps of pick-up ions (PUIs)
Many existing studies make a clear cut between the thermal core of solar wind protons and the more energetic pick-up ion population. However, this separation is artificial, and only makes sense in the supersonic regime of the solar wind, where, to first order, thermal ions and PUIs do not interact and represent separated ion populations in velocity space. However, downstream of the TS, it is no longer possible to differentiate between a pick-up proton and an energetic solar wind proton as a different ion species, because both contributions overlap there in velocity space.
For this reason, and since all protons at the shock passage react alike, it also turns out (see Fahr et al. 2012) that the PUI downstream pressure simply deviates from the downstream solar proton pressure due to the difference already given in the upstream proton pressure, i.e. P1,pui instead of P1,p. Therefore, since PUI protons are not a physically different ion species, under the auspices given here, their downstream pressure can be derived from the same functional relation as the thermal proton pressure (Eq. (4)), as 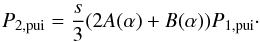 (7)It is convenient to normalise all pressures to one basic value, for which we select the upstream thermal proton pressure P1,p. Introducing the upstream PUI abundance ς = n1,pui/n1,p, Eq. (3) allows the PUI pressure to be parameterised as a function of the upstream thermal proton pressure (see Fahr et al. 2012),
(7)It is convenient to normalise all pressures to one basic value, for which we select the upstream thermal proton pressure P1,p. Introducing the upstream PUI abundance ς = n1,pui/n1,p, Eq. (3) allows the PUI pressure to be parameterised as a function of the upstream thermal proton pressure (see Fahr et al. 2012), 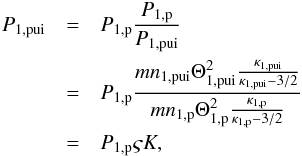 (8)where we have introduced the kappa ratio
(8)where we have introduced the kappa ratio 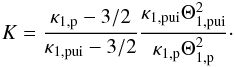 (9)Using this normalisation and Eq. (7), we can write the downstream PUI pressure as
(9)Using this normalisation and Eq. (7), we can write the downstream PUI pressure as 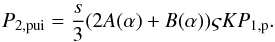 (10)The total downstream pressure P2, exerted both by thermal protons and PUIs, thus takes the simple form
(10)The total downstream pressure P2, exerted both by thermal protons and PUIs, thus takes the simple form 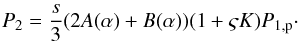 (11)It should be noted that deriving a correct representation of the upstream PUI thermal parameter Θ1,pui is a tricky problem. According to Eq. (3), the pressure of a kappa function is very sensitive to the choice of the thermal velocity Θ. No reliable (direct, indirect or extrapolated) observational data for PUI thermal velocities near the TS exists, and therefore, one has to derive this parameter from theoretical considerations. Here we have adopted the description given by Fahr (2007), who found that
(11)It should be noted that deriving a correct representation of the upstream PUI thermal parameter Θ1,pui is a tricky problem. According to Eq. (3), the pressure of a kappa function is very sensitive to the choice of the thermal velocity Θ. No reliable (direct, indirect or extrapolated) observational data for PUI thermal velocities near the TS exists, and therefore, one has to derive this parameter from theoretical considerations. Here we have adopted the description given by Fahr (2007), who found that 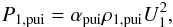 (12)where U1 is the upstream solar wind speed, and αpui is a weak function of the solar distance, which at about 100 AU is approximated by αpui(100 AU) ≃ 0.162. Making use of Eq. (3), one then obtains
(12)where U1 is the upstream solar wind speed, and αpui is a weak function of the solar distance, which at about 100 AU is approximated by αpui(100 AU) ≃ 0.162. Making use of Eq. (3), one then obtains 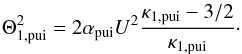 (13)which, for an adopted value of κ1,pui = 2 (i.e. a power law close to v-5 for the suprathermal tail, see Sect. 2.5) transforms into
(13)which, for an adopted value of κ1,pui = 2 (i.e. a power law close to v-5 for the suprathermal tail, see Sect. 2.5) transforms into 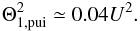 (14)
(14)
2.3. The Kappa distribution function for the joint downstream ion populations
As already pointed out, keeping two separate components for thermal solar wind and PUI protons is problematic and even physically questionable on the downstream side of the TS, where thermal and nonthermal ion distribution functions start to overlap. Therefore, we now adopt an alternative approach, where one κ distribution is used to jointly describe both proton components, depending only on one pair of parameters (κ2,j and Θ2,j) that need to be found from physical conditions. The following calculations are possible when thermal and PUI protons possess widely different kappa indices, with thermal ions characterised by a large kappa index (i.e. a distribution function very close to a Maxwellian), and PUI protons characterised by a small kappa index, essentially to a nonthermal power law.
This approach is made possible by the fact that, before crossing the TS, the thermal and nonthermal solar wind proton components are located in different regions in velocity space, while on the downstream side, this usually is no longer the case. Therefore, it is a reasonable approach to describe the downstream plasma as a single distribution function, containing both thermal and nonthermal properties, for which a κ-function is a primary choice. Following most existing studies of κ functions, we do not try to reproduce the entire microphysics resulting in this transformation; this latter point is a separate, badly understood problem of theoretical plasma physics.
We interpret the downstream thermal solar wind proton population as constituting the so-called Gaussian core of the joint Kappa distribution (see e.g. Collier 1995; Heerikhuisen et al. 2008; Livadiotis & McComas 2009), and thus can make the following “synthetic approach” towards the new distribution function: ![\begin{eqnarray} % f_{2,j}(v) &=& \frac{n_{2,j}}{(\pi \sqrt{\kappa_{2,j}}\Theta_{2,j}^{2})^{3/2}}\frac{\Gamma (\kappa_{2,j}+1)}{\Gamma (\kappa_{2,j}-3/2)}\nonumber\\ &&\times \left[1+\frac{v^{2}}{\kappa_{2,j}\Theta_{2,j}^{2}}\right]^{-(\kappa_{2,j}+1)}\cdot \end{eqnarray}](/articles/aa/full_html/2013/10/aa22262-13/aa22262-13-eq44.png) (15)Here the density n2,j is given by n2,j = n2,p + n2,pui = (1 + ς)n2,p. Since both proton components are assumed to undergo the same compression s, the downstream PUI abundance is the same as the upstream PUI abundance.
(15)Here the density n2,j is given by n2,j = n2,p + n2,pui = (1 + ς)n2,p. Since both proton components are assumed to undergo the same compression s, the downstream PUI abundance is the same as the upstream PUI abundance.
To derive the parameters Θ2,j and κ2,j, which characterise the thermal and the nonthermal parts of the joint distribution function, we start out from the pressure relation for solar wind protons (Eq. (4)) and first derive the thermal width Θ2,j of the Gaussian core through 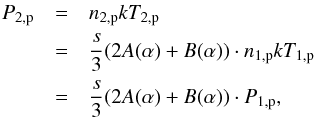 (16)which then leads to
(16)which then leads to 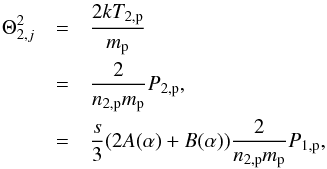 (17)where the density n1,p does not include the PUI densities because we have assumed that the thermal width is determined by the downstream thermal protons.
(17)where the density n1,p does not include the PUI densities because we have assumed that the thermal width is determined by the downstream thermal protons.
Standard upstream parameters adopted for the multi-ion mixture.
The joint Kappa index κ2,j can now be derived with the help of the pressure relation, which evidently requires the sum of the downstream solar wind proton and PUI pressures to be identical with the pressure of the joint κ-distribution, i.e. 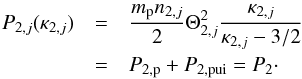 (18)Inserting the expession found for P2 (Eq. (11)) and replacing
(18)Inserting the expession found for P2 (Eq. (11)) and replacing 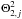 with the help of Eq. (17), we obtain
with the help of Eq. (17), we obtain 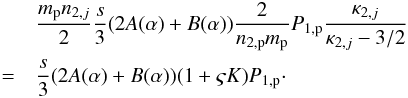 (19)Obviously, this relation can be simplified to
(19)Obviously, this relation can be simplified to 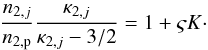 (20)Next, we make use of n2,j = n2,p + n2,pui = (1 + ς)n2,p, and obtain the equation
(20)Next, we make use of n2,j = n2,p + n2,pui = (1 + ς)n2,p, and obtain the equation 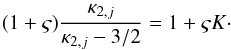 (21)This equation can now be solved to obtain the joint kappa index κ2,j,
(21)This equation can now be solved to obtain the joint kappa index κ2,j, 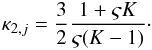 (22)Taking the limit of ς = 0 for orientation purposes, which corresponds to a vanishing PUI contribution, we obtain a value of κ2,j → ∞, i.e. the kappa function reduces to the expected Maxwellian distribution with a thermal parameter
(22)Taking the limit of ς = 0 for orientation purposes, which corresponds to a vanishing PUI contribution, we obtain a value of κ2,j → ∞, i.e. the kappa function reduces to the expected Maxwellian distribution with a thermal parameter 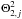 . On the other hand, for ς ≫ 1, the thermal contribution vanishes, and the distribution reduces to a pure energetic tail with a kappa index of
. On the other hand, for ς ≫ 1, the thermal contribution vanishes, and the distribution reduces to a pure energetic tail with a kappa index of 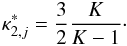 (23)The lower boundary of this value is the classical limit of κmin = 3/2; depending on the value of K (or, equivalently, the parameters κ and Θ for the upstream thermal and PUI protons), the final κ value can be slightly higher. However, under typical solar wind conditions, one obtains K ≫ 1, which means that the resulting joint κ index is very close to 3/2, which corresponds to a power law according to v-5, as has been found several times, interestingly enough (see Fisk & Gloeckler 2007).
(23)The lower boundary of this value is the classical limit of κmin = 3/2; depending on the value of K (or, equivalently, the parameters κ and Θ for the upstream thermal and PUI protons), the final κ value can be slightly higher. However, under typical solar wind conditions, one obtains K ≫ 1, which means that the resulting joint κ index is very close to 3/2, which corresponds to a power law according to v-5, as has been found several times, interestingly enough (see Fisk & Gloeckler 2007).
 |
Fig. 2 Joint κ2,j index as a function of PUI abundance for typical upstream thermal and PUI kappa values. The definition of the PUI abundance allows ς → ∞, for which κ would tend towards an asymptotic value of κ ≃ 1.5. |
Adopting the parameters given in Table 1, κ1,p = 10 and κ1,pui = 2, we obtain K = 119 and 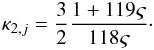 (24)This equation points to κ indices closely above 1.5, and therefore, velocity power indices only slightly steeper than −5. To demonstratre the dependence of the downstream κ2,j index on the PUI abundance, we present a plot of this function in Fig. 2, which demonstrates that the κ index is below 2 for ς > 0.05.
(24)This equation points to κ indices closely above 1.5, and therefore, velocity power indices only slightly steeper than −5. To demonstratre the dependence of the downstream κ2,j index on the PUI abundance, we present a plot of this function in Fig. 2, which demonstrates that the κ index is below 2 for ς > 0.05.
2.4. Pressure jumps for downstream electron pressures
In addition to thermal solar wind protons and PUI protons, Fahr et al. (2012) also studied the pressure contribution of electrons, which, owing to their opposite electric charges, are accelerated differently by the stationary electric shock ramp that for protons only causes the deceleration of the proton bulk flow speed. They studied the mechanism describing the behaviour of electrons, based on the conservation of the magnetic moment of the individual electrons and on an additional energy gain due to the overshooting at the TS electric ramp.
The only result from the study by Fahr et al. (2012) that we need here is the relation between the upstream and downstream electron pressures, found as ![\begin{eqnarray} % P_{2,{\rm e}}=\frac{m_{\rm p}}{m_{\rm e}}\frac{s^{2}-1}{s}\frac{U_{1}^{2}}{c_{1,{\rm e}}^{2}}\left[ \sin ^{2}\alpha A(\alpha )+\cos ^{2}\alpha B(\alpha )\right] P_{1,{\rm p}} \label{eq-p2-p1-e} \end{eqnarray}](/articles/aa/full_html/2013/10/aa22262-13/aa22262-13-eq89.png) (25)where c1,e denotes the mean thermal velocity of solar wind electrons upstream of the shock.
(25)where c1,e denotes the mean thermal velocity of solar wind electrons upstream of the shock.
Using this approach, the total pressure Π2 = P2 + P2,e, exerted jointly by all protons and electrons, yields  \nonumber\\ &&+ \frac{m_{\rm p}}{m_{\rm e}}\frac{s^{2}-1}{s}\frac{U_{1}^{2}}{c_{1,{\rm e}}^{2}} \left[ \sin ^{2}\alpha A(\alpha )+\cos ^{2}\alpha B(\alpha )\right] \Bigg]. \end{eqnarray}](/articles/aa/full_html/2013/10/aa22262-13/aa22262-13-eq92.png) (26)An alternative idea for electron thermalisation to pitchangle scattering was recently put forward by Chashei & Fahr (2013), who considered the Buneman instability modifying the behaviour of the plasma at the shock. This process was found to be independent of the magnetic field orientation; i.e. the resulting pressures would be independent of the magnetic configuration, as parameterised by the angle α. Here, we do not study this variant in greater detail, focussing on the overshooting mechanism treated as by Fahr et al. (2012) instead.
(26)An alternative idea for electron thermalisation to pitchangle scattering was recently put forward by Chashei & Fahr (2013), who considered the Buneman instability modifying the behaviour of the plasma at the shock. This process was found to be independent of the magnetic field orientation; i.e. the resulting pressures would be independent of the magnetic configuration, as parameterised by the angle α. Here, we do not study this variant in greater detail, focussing on the overshooting mechanism treated as by Fahr et al. (2012) instead.
2.5. Downstream pressures for typical parameters
Before one can calculate an all-sky pressure map at the surface of the TS, it is necessary to better understand the behaviour of the downstream pressures as a function of shock parameters, such as the magnetic field tilt angle α and the compression ratio. Unlike in our earlier studies, we here present absolute values for the downstream pressures for the entire range of magnetic field orientations.
We begin by adopting a fixed compression ratio of s = 2.5, as observed by the Voyager-2 mission (Richardson et al. 2008). For the upstream κ function parameters, we adopt the same values as those used by Fahr et al. (2012), which are reproduced in Table 1 for convenience. The resulting downstream pressures, both for the individual components and for the sum over all particle species, are presented in Fig. 3, which clearly demonstrates that the downstream pressures are strongly modulated by the shock geometry, i.e. by the magnetic field orientation. The overall behaviour pointed out by Fahr et al. (2012) is reproduced, where it was found that the pressure increase at the parallel shock is more strongly pronounced than at the perpendicular shock under an otherwise identical upstream configuration and that the thermal proton pressure contribution is negligibly small.
 |
Fig. 3 Downstream pressures as a function of the magnetic field tilt angle α for a fixed compression ratio of s = 2.5. |
However, now where we also consider pick-up ions (i.e. protons), one easily sees that, as expected, the partial pressures of the PUIs are substantially higher than the partial pressures of the thermal protons. However, the electrons still clearly dominate the total downstream pressure, exceeding pressures of heated PUIs by one magnitude. To understand this behaviour, we present enhancement factors for the individual pressure components from the upstream to the downstream sides in Fig. 4, which demonstrates that, even though the PUIs possess significantly higher pressures than the thermal solar wind ions on the downstream side, both proton components are heated by the same relative factor (see Sect. 2.2).
For an easier interpretation of the pressure ratios, we now derive additional analytical formulations for the downstream pressure ratios, normalised to the downstream proton pressure, based on the equations introduced above. From Eqs. (4) and (7), it follows that 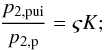 (27)this means that the amount by which the downstream PUI pressures are larger compared to the downstream solar wind proton pressures is just a function of upstream parameters, namely upstream κ parameters, upstream thermal widths Θ2 and the PUI abundance. This is not surprising, as we assumed earlier that all protons behave identically at the shock, independent of their upstream distribution function. For the standard parameters introduced in Table 1, we obtain a value of K ≃ 119, so for a typical PUI abundance of ς = 0.2, the extra pressure enhancement of PUIs with respect to downstream protons is given by
(27)this means that the amount by which the downstream PUI pressures are larger compared to the downstream solar wind proton pressures is just a function of upstream parameters, namely upstream κ parameters, upstream thermal widths Θ2 and the PUI abundance. This is not surprising, as we assumed earlier that all protons behave identically at the shock, independent of their upstream distribution function. For the standard parameters introduced in Table 1, we obtain a value of K ≃ 119, so for a typical PUI abundance of ς = 0.2, the extra pressure enhancement of PUIs with respect to downstream protons is given by  , independent of the shock geometry.
, independent of the shock geometry.
 |
Fig. 4 Pressure enhancement at the shock for individual components as a function of the magnetic field tilt angle α. |
Repeating the same calculations for the downstream electrons, we see from Eqs. (4) and (25) that 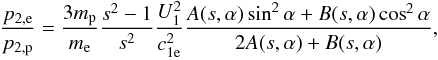 (28)which means that, unlike the PUIs, the electron pressure enhancement downstream of the shock does depend on the microphysics if the shock, as the compression ratio s and the magnetic field tilt angle α. In addition, it is possible to separate the contributions due to the shock microphysics out from those contributions due to the upstream configuration, resulting in
(28)which means that, unlike the PUIs, the electron pressure enhancement downstream of the shock does depend on the microphysics if the shock, as the compression ratio s and the magnetic field tilt angle α. In addition, it is possible to separate the contributions due to the shock microphysics out from those contributions due to the upstream configuration, resulting in 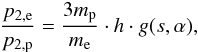 (29)with the upstream factor
(29)with the upstream factor 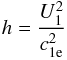 (30)and the shock factor
(30)and the shock factor 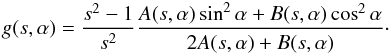 (31)The upstream factor consists of the ratio between the solar wind speed and the mean thermal electron speed, i.e. favouring a significant pressure enhancement for cold, upstream electrons and a fast upstream solar wind. For our adopted parameters, this factor takes the value h = 0.45. For completeness, we note that these definitions allow transforming Eq. (25) into
(31)The upstream factor consists of the ratio between the solar wind speed and the mean thermal electron speed, i.e. favouring a significant pressure enhancement for cold, upstream electrons and a fast upstream solar wind. For our adopted parameters, this factor takes the value h = 0.45. For completeness, we note that these definitions allow transforming Eq. (25) into 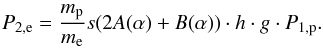 (32)The second factor, g(s,α), is a strongly nonlinear function of the shock properties that cannot be estimated easily. Therefore, we present typical values for this factor in Fig. 7, proving that this shock factor is always smaller than 1, and when no further details are known, it is a good approximation to use 0.5.
(32)The second factor, g(s,α), is a strongly nonlinear function of the shock properties that cannot be estimated easily. Therefore, we present typical values for this factor in Fig. 7, proving that this shock factor is always smaller than 1, and when no further details are known, it is a good approximation to use 0.5.
 |
Fig. 5 Pressure ratio between downstream electrons and PUIs as a function of the magnetic field tilt angle α. |
These results prove an important point, namely that the electron pressure dominates the downstream system. The downstream PUI pressure is still significantly higher than the proton pressure (by a factor of 50 − 100 depending on the PUI abundance), while the electron pressure is enhanced due to an initial acceleration at the same electric shock ramp that decelerates the proton flow (see Fahr et al. 2012), resulting in a relative pressure enhancement of the order of mp/me, which is another order of magnitude higher than the PUI pressure enhancement. This is demonstrated by the relative strength of the downstream electron-to-PUI pressures, p2,e/p2,pui, presented in Fig. 5, which easily demonstrates that the downstream electron pressure is at least one order of magnitude stronger than the next significant contribution, i.e. the PUI pressure, and therefore, the vast majority of the total downstream pressure is dominated by the electrons. We discuss the possible implications of this result in the conclusions.
To finish this part of our present study, we also investigate the impact of the compression ratio s on the pressures by evaluating total pressure (i.e. due to solar wind protons, PUI protons and electrons) downstream of the shock, while varying both the compression ratio s and the angle α. In Fig. 6, we present the joint downstream pressures for our standard parameters, demonstrating that the MHD compression ratio s strongly affects the total pressures, with higher compression ratios resulting in a nonlinear pressure increase. Since the pressure jump is a reaction to both the kinetic behaviour of the plasma at the shock and the number density change of ions, it turns out that the MHD compression (i.e. the factor s) enhances the classical heating in a nonlinear, nonpolytropic way.
 |
Fig. 6 Joint downstream pressures as a function of the magnetic field tilt angle α and varying compression ratio s. |
 |
Fig. 7 Shock factor g(s,α). |
3. The magnetic pressure and the joint multi-fluid compression ratio
Using the fluid pressures derived above, it is now possible to calculate a consistent value of the MHD compression ratio at the termination shock. In addition to the fluid plasma pressures, one also has to consider the magnetic pressure component of the field convected with the upstream solar wind across the termination shock. As it turns out from classical MHD, only the tangential magnetic field component changes across the shock, and therefore, only the magnetic pressure component tangential to the shock surface is relevant for the problem. On the upstream side, this component can be calculated with the help of Parker’s spiral field model (Parker 1958),![\begin{eqnarray} % B_{t1}^{2}/8\pi &=& \left[\left(\frac{r_{0}}{r}\right)^{2}B_{0}\cdot \left(\frac{\Omega r}{U_{1}}\cos \vartheta \right)\right]^{2}\Bigg{/}8\pi \nonumber\\ &=& \frac{B_{0}^{2}}{8\pi }\left(\frac{r_{0}}{r}\right)^{2}\left(\frac{\Omega r}{U_{1}}\cos \vartheta \right)^{2}, \end{eqnarray}](/articles/aa/full_html/2013/10/aa22262-13/aa22262-13-eq108.png) (33)with Ω denoting the solar rotation frequency, r0 = rE = 1 AU, and ϑ denoting the heliospheric latitude. At the termination shock, at r = rs, one thus has an upstream magnetic pressure of
(33)with Ω denoting the solar rotation frequency, r0 = rE = 1 AU, and ϑ denoting the heliospheric latitude. At the termination shock, at r = rs, one thus has an upstream magnetic pressure of 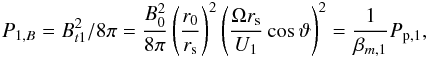 (34)where
(34)where 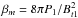 . The downstream magnetic pressure follows from elementary MHD considerations, and it turns out as
. The downstream magnetic pressure follows from elementary MHD considerations, and it turns out as 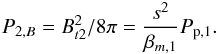 (35)Unlike previous studies, we have normalised the magnetic pressure to the upstream solar wind proton pressure as well.
(35)Unlike previous studies, we have normalised the magnetic pressure to the upstream solar wind proton pressure as well.
Since all relevant pressures have been derived, we can finally calculate the compression ratio by solving the implicit Eq. (36) above (see Fahr et al. 2012). 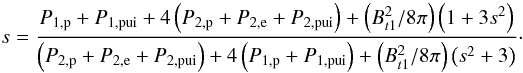 (36)In this expression, all quantities have been expressed as a function of the upstream solar wind ion pressure, meaning that we can eliminate all explicit pressures. Using Eq. (11), the sum of P2,p + P2,pui can be replaced, while Eq. (32) allows to replace P2,e, resulting in Eq. (37) (see above).
(36)In this expression, all quantities have been expressed as a function of the upstream solar wind ion pressure, meaning that we can eliminate all explicit pressures. Using Eq. (11), the sum of P2,p + P2,pui can be replaced, while Eq. (32) allows to replace P2,e, resulting in Eq. (37) (see above). 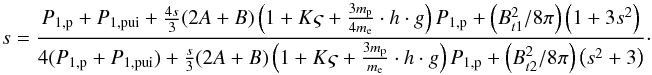 (37)Next, we can normalise the upstream pressures to P1,p. For the upstream PUI pressure, we obtain from Eqs. (4), (10), and (27) that P1,pui/P1,p = Kς, and find Eq. (38) (see above).
(37)Next, we can normalise the upstream pressures to P1,p. For the upstream PUI pressure, we obtain from Eqs. (4), (10), and (27) that P1,pui/P1,p = Kς, and find Eq. (38) (see above). 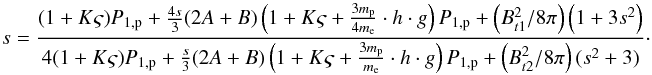 (38)Finally, Eqs. (34) and (35) allow us to formally eliminate the sole remaining absolute pressure parameter P1,p, leading to Eq. (39) (see above).
(38)Finally, Eqs. (34) and (35) allow us to formally eliminate the sole remaining absolute pressure parameter P1,p, leading to Eq. (39) (see above). 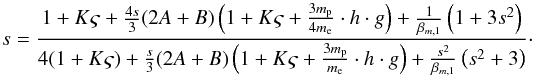 (39)Nevertheless, even though no explicit pressures remain in this equation, the parameters K and βm,1 still depend on upstream pressures; however, they are now expressed by a different set of plasma parameters that are commonly adopted in literature, offering a different approach to this problem. However, even though this expression no longer depends on absolute values for the upstream pressures, it still can only be solved numerically.
(39)Nevertheless, even though no explicit pressures remain in this equation, the parameters K and βm,1 still depend on upstream pressures; however, they are now expressed by a different set of plasma parameters that are commonly adopted in literature, offering a different approach to this problem. However, even though this expression no longer depends on absolute values for the upstream pressures, it still can only be solved numerically.
3.1. Overall all-sky results for the pressures
Before finishing this study, we give a first overview of typical, realistic all-sky results. Even though this study places emphasis on the general, PUI-enhanced multi-component shock system, it is also of interest to see how this study may impact global studies of the outer heliosphere. Since a full study of this type takes time and will exceed the limits of this paper, we did calculate one representative set of realistic all-sky parameters, demonstrating that our enhanced multi-fluid description of the solar wind termination shock does in fact result in nontrivial modifications that have to be respected in more detailed studies.
To calculate downstream pressures in the frame of our derivations, one has to adopt models for the location and geometry of the solar wind termination shock, allowing the magnetic field tilt angle α to be calculated, along with the termination shock distance rs at arbitrary positions on the sky (see e.g. Siewert et al. 2012). In the final part of this study, we adopt the models that have already been used by Fahr et al. (2011), Siewert et al. (2012, 2013): the Parker spiral model for the solar wind magnetic field (Parker 1958), with the ellipsoid heliosphere geometry based on the numerical model by Borrmann & Fichtner (2005) and later approximated analytically by Scherer & Fahr (2009); and the inner heliosheath PUI density model derived by Fahr et al. (2009) to evaluate the upstream PUI density. The latter model takes into account both integration of PUIs generated during the propagation through the inner heliosphere and also reionisation as a function of solar distance, arriving at a PUI density behaving roughly like r-1.
Our representative results are presented in Fig. 8. First, we calculated the consistent MHD compression ratio, taking the correct particle number density into account as a function of the TS distance from the Sun, a correct magnetic field geometry (based on Parker’s spiral field model, see Parker 1958), and a globally constant upstream solar wind speed of U1 = 400 km s-1. With these parameters, we obtain the MHD compression ratio presented by Fig. 8a. The other relevant parameter appearing in our pressure relations is the magnetic field tilt angle α, which we reproduce in Fig. 8b, which was calculated using the equations derived by Scherer & Fahr (2009). The resulting pressures are given by Fig. 8c.
These figures suggest that the downstream pressures are modulated by both the MHD compression ratio and the magnetic field tilt angle. However, when considering absolute pressure quantities, one also has to consider that the plasma pressure is proportional to the number density of ions; i.e., the absolute downstream pressures also scale with the TS distance, and the impact of our modified shock description cannot be estimated without a more detailed study. Finally, one must consider that the scalar absolute downstream plasma pressures themselves, which we are able to calculate with our framework, may be less relevant than their tangential pressure gradients, which serve as an important piece for any model for plasma flows in the inner heliosheath. The impact of the modified description used in this study may be much more obvious in studies that depend on the downstream TS plasma pressure as a boundary value.
Owing to these additional complications, we end our analysis at this point, but will investigate further implications of the modified downstream plasma pressures in a separate, upcoming study.
4. Conclusions
In the present paper we have shown that the solar wind termination shock can only be adequately described in all its physical properties if the multi-fluid character of the upstream plasma flow is seriously taken into account, namely, that the upstream plasma consists of at least three independent fluids, such as the solar wind protons, the pick-up protons and solar wind electrons. This abolishes the validity of the classical Rankine-Hugoniot shock relations, which now need to be replaced by a set of multi-fluid shock relations. To describe the passage of a multi-fluid plasma from upstream to downstream of the shock, two aspects of the problem have to be respected simultaneously: 1) the joint thermo- and magnetohydro- dynamic action of all fluids in determining the joint shock compression ratio s has to be correctly treated as formulated in Eq. (36), and in addition; 2) the separate species-specific changes in phasespace suffered by each of these fluids at the shock transition has to be consistently taken into account. The latter we did by conserving selected particle invariants and taking the individual, species-specific overshoot velocities into account that are enforced by the electric shock ramp.
With this procedure we can found the relevant expressions for all the fluid pressures downstream of the shock and compared them in their magnitudes in Figs. 3 to 6. It turns out that all pressures depend on the shock compression ratio s and on the tilt angle α between the shock normal and the local upstream magnetic field. While the pressures of pick-up protons and solar wind electrons are of comparable magnitudes, the solar wind proton pressure alone is of inferior magnitude. This already quantitatively explains the otherwise astonishing fact that according to Voyager-2 observations (see Richardson et al. 2008) the shocked solar wind protons for themselves still appear supersonic downstream of the shock. As we showed, however, those species that actually make the downstream plasma flow subsonic are the strongly heated pick-up protons and the strongly heated solar wind electrons. As we showed in this paper, the temperatures Te,2 of the downstream electrons are several 106K, i.e. about 10 to 20 times hotter than the downstream solar wind protons with their temperature Tp,2 ≃ 105K. This then means that the typical phase velocities of the plasma sound waves are given by (see Chen 1984) 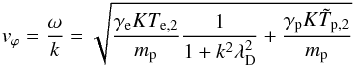 (40)where ω is the wave frequency, k = 2π/λ denotes the wavevector, and λD is the Debye length in the downstream plasma. The value
(40)where ω is the wave frequency, k = 2π/λ denotes the wavevector, and λD is the Debye length in the downstream plasma. The value 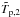 denotes the temperature of the joint proton population, including downstream pick-up ions. The quantities γe and γp are polytropic indices of electrons and protons, respectively. Perturbations with wavelengths
denotes the temperature of the joint proton population, including downstream pick-up ions. The quantities γe and γp are polytropic indices of electrons and protons, respectively. Perturbations with wavelengths 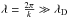 propagate at least with phase velocities of
propagate at least with phase velocities of 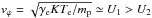 , i.e. clearly indicate the subsonic character of this downstream plasma.
, i.e. clearly indicate the subsonic character of this downstream plasma.
Thanks to the dominance in energy density by the electrons, the downstream solar wind plasma has substantially changed its physical nature. It now has nearly become a massless energy-loaded plasma dominated in its dynamics by the electron pressure. Electrostatic perturbations can now propagate along the magnetic field lines with phase velocities vϕ of the electrostatic electron oscillations which for wavevectors parallel to B, i.e.with k × B = 0, are given by 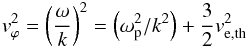 (41)i.e. at higher k-values with the very high thermal speeds of the downstream electrons of the order of ve,th ≃ U1·(mp/me). These electrostatic electron waves practically do not couple to ions, but they tend to balance out thermal electron conditions along the magnetic field lines in the heliosheath. At first order, one can thus call the heliosheath magnetic field lines “electron isothermals”.
(41)i.e. at higher k-values with the very high thermal speeds of the downstream electrons of the order of ve,th ≃ U1·(mp/me). These electrostatic electron waves practically do not couple to ions, but they tend to balance out thermal electron conditions along the magnetic field lines in the heliosheath. At first order, one can thus call the heliosheath magnetic field lines “electron isothermals”.
Concerning the fairly high temperatures of downstream electrons that we have derived in this paper and that indicate a clear downstream pressure dominance of electrons, one should perhaps caution the reader of this paper ot mention the following caveats. In our above calculations we started our numerical calculations from the assumption that on the upstream side of the termination shock solar wind electrons and solar wind protons are in thermal, i.e. in pressure equilibrium, implying that we have taken Pe,1 = Pp,1. This, however, is a fairly unsafe assumption. While we do not have any information on the thermal status of solar wind electrons upstream of the shock, we do, however, have information on the upstream solar wind proton temperatures (see Richardson et al. 2008), telling us that these amount to Tp,1 ≃ 2 × 104K. In this paper here, not knowing any better, we have assumed that upstream electrons are in pressure equilibrium with upstream solar wind protons, meaning that upstream electrons should also have the same temperature.
This, however, is a fairly problematic assumption, since solar wind protons do only arrive upstream of the shock with temperatures of about 104K, if they are effectively heated on their way out to the shock. In papers by Smith et al. (2001), Fahr & Chashei (2002), Chashei et al. (2003) or Chalov et al. (2004), it has been shown that solar wind protons on their way out to the shock are heated by MHD turbulences driven by pick-up ions. Since electrons cannot resonate with these types of low-frequency MHD waves, they do not profit from this heating process. In case of no heating, they thus had to cool off adiabatically according to Te = Te,0·(r/r0)− 4/3 bringing them to the shock with temperatures lower than the proton temperatures by a factor of about 100.
Even though a mechanism to also heat electrons at large solar distances by compressive travelling shocks has been recently discussed by Chashei & Fahr (2013), the exact efficiency of this heating has not yet been clearly quantified. At the moment, therefore, the upstream electron temperature has to be considered as an open quantity. Since, however, the downstream electron pressures scale with the uncertain upstream electron pressures, the values presented in this paper must be considered uncertain by about the same factors. Even if, however, electron downstream temperatures had to be reduced by a factor of about 50, this would nevertheless leave the downstream electrons as the pressure-dominating plasma fluid.
Acknowledgments
M. Siewert is grateful to the Deutsche Forschungsgemeinschaft for financial support granted in the framework of the project Si-1550/2-1.
References
- Borrmann, T., & Fichtner, H. 2005, Adv. Space Res., 35, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Chalov, S. V., & Fahr, H. J. 2011, Adv. Space Res., 47, 1523 [NASA ADS] [CrossRef] [Google Scholar]
- Chalov, S. V., & Fahr, H. J. 2013, MNRAS, 433, L40 [NASA ADS] [Google Scholar]
- Chalov, S. V., Alexashov, D. B., & Fahr, H. J. 2004, A&A, 416, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chashei, I. V., & Fahr, H. J. 2013, Ann. Geophys., 31, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Chashei, I. V., Fahr, H. J., & Lay, G. 2003, Adv. Space Res., 32, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, F. F. 1984, Introduction to Plasma Physics and Controled Fusion (New York: Plenum Press) [Google Scholar]
- Collier, M. R. 1995, Geophys. Res. Lett., 22, 2673 [NASA ADS] [CrossRef] [Google Scholar]
- Collier, M. R., Hamilton, D. C., Gloeckler, G., Bochsler, P., & Sheldon, R. B. 1996, Geophys. Res. Lett., 23, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Decker, R. B., Krimigus, S. M., Roelof, E. C., et al. 2008, Nature, 454, 67 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fahr, H.-J. 2007, Ann. Geophys., 25, 2649 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H. J., & Chashei, I. V. 2002, A&A, 395, 991 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H.-J., & Chalov, S. V. 2008, A&A, 490, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H.-J., & Siewert, M. 2011, A&A, 527, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H., Chashei, I. V., & Verscharen, D. 2009, A&A, 505, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H.-J., Siewert, M., McComas, D. J., & Schwadron, N. A. 2011, A&A, 531, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H.-J., Siewert, M., & Chashei, I. 2012, Ap&SS, 341, 265 [Google Scholar]
- Fisk, L. A., & Gloeckler, G. 2007, Space Sci. Rev., 130, 153 [Google Scholar]
- Heerikhuisen, J., Pogorelov, N. V., Florinski, V., Zank, G. P., & le Roux, J. A. 2008, ApJ, 682, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Izmodenov, V. V., & Baranov, V. B. 2006, ISSI Scientific Rep. Ser., 5, 67 [Google Scholar]
- Leubner, M. P. 2002, Ap&SS, 282, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Livadiotis, G., & McComas, D. J. 2009, J. Geophys. Res. (Space Phys.), 114, 11105 [Google Scholar]
- Ma, C.-y., & Summers, D. 1998, Geophys. Res. Lett., 25, 4099 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Richardson, J. D., Kasper, J. C., Wang, C., Belcher, J. W., & Lazarus, A. J. 2008, Nature, 454, 63 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Scherer, K., & Fahr, H. 2009, A&A, 495, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shizgal, B. D. 2007, Ap&SS, 312, 227 [Google Scholar]
- Siewert, M., Fahr, H.-J., McComas, D. J., & Schwadron, N. A. 2012, A&A, 539, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siewert, M., Fahr, H.-J., McComas, D. J., & Schwadron, N. A. 2013, A&A, 551, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, C. W., Matthaeus, W. H., Zank, G. P., et al. 2001, J. Geophys. Res., 106, 8253 [NASA ADS] [CrossRef] [Google Scholar]
- Thorne, R. M., & Summers, D. 1991, Phys. Fluids B, 3, 2117 [Google Scholar]
- Treumann, R. A. 2001, Ap&SS, 277, 81 [Google Scholar]
- Treumann, R. A., Jaroschek, C. H., & Scholer, M. 2004, Phys. Plasmas, 11, 1317 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyliunas, V. M. 1968, J. Geophys. Res., 73, 2839 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, P., Winske, D., Gary, S. P., Schwadron, N. A., & Lee, M. A. 2009, J. Geophys. Res. (Space Phys.), 114, 8103 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, P. H. 2005, Phys. Plasmas, 12, 042306 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, P. H., Rhee, T., & Ryu, C.-M. 2005, Phys. Rev. Lett., 95, 215003 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, P. H., Ziebell, L. F., Gaelzer, R., Lin, R. P., & Wang, L. 2012, Space Sci. Rev., 173, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., Heerikhuisen, J., Pogorelov, N. V., Burrows, R., & McComas, D. 2010, ApJ, 708, 1092 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Parameters at a typical shock. |
| In the text | |
 |
Fig. 2 Joint κ2,j index as a function of PUI abundance for typical upstream thermal and PUI kappa values. The definition of the PUI abundance allows ς → ∞, for which κ would tend towards an asymptotic value of κ ≃ 1.5. |
| In the text | |
 |
Fig. 3 Downstream pressures as a function of the magnetic field tilt angle α for a fixed compression ratio of s = 2.5. |
| In the text | |
 |
Fig. 4 Pressure enhancement at the shock for individual components as a function of the magnetic field tilt angle α. |
| In the text | |
 |
Fig. 5 Pressure ratio between downstream electrons and PUIs as a function of the magnetic field tilt angle α. |
| In the text | |
 |
Fig. 6 Joint downstream pressures as a function of the magnetic field tilt angle α and varying compression ratio s. |
| In the text | |
 |
Fig. 7 Shock factor g(s,α). |
| In the text | |
 |
Fig. 8 Shock parameters calculated consistently from Table 1 and Eq. (39). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


