| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 14 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201322135 | |
| Published online | 30 September 2013 | |
Three-dimensional non-LTE radiative transfer effects in Fe i lines
II. Line formation in 3D radiation hydrodynamic simulations
1 Max Planck Institute for Solar System Research (MPS), 37191 Katlenburg-Lindau, Germany
e-mail: holzreuter@astro.phys.ethz.ch
2 Institute of Astronomy, ETH Zentrum, 8092 Zurich, Switzerland
3 School of Space Research, Kyung Hee University, Yongin, 446-701 Gyeonggi, Republic of Korea
Received: 25 June 2013
Accepted: 8 August 2013
Here we investigate the effects of horizontal radiative transfer (RT) in combination with non-local thermodynamic equilibrum (NLTE) on important diagnostic iron lines in a realistic atmosphere. Using a snapshot of a 3D radiation-hydrodynamic (HD) simulation and a multilevel iron atom, we computed widely used Fe i line profiles at three different levels of approximation of the RT (3D NLTE, 1D NLTE, LTE). By comparing the resulting line profiles and the circumstances of their formation, we gain new insight into the importance of horizontal RT. We find that the influence of horizontal RT is of the same order of magnitude as that of NLTE, although spatially more localized. Also, depending on the temperature of the surroundings, horizontal RT is found to either weaken or strengthen spectral lines. Line depths and equivalent width may differ by up to 20% from the corresponding LTE value if 3D RT is applied. Residual intensity contrasts in LTE are found to be larger than those in 3D NLTE by up to a factor of two. When compared to 1D NLTE, we find that horizontal RT weakens the contrast by up to 30% almost independently of the angle of line of sight. While the center-to-limb variation (CLV) of the 1D and 3D NLTE contrasts have a similar form, the LTE contrast CLV shows a different run. Determination of temperatures by 1D NLTE inversions of spatially resolved observations may produce errors of up to 200 K if one neglects 3D RT. We find a linear correlation between the intensity difference of 1D and 3D NLTE and a simple estimate of the temperature in the horizontal environment of the line formation region. This correlation could be used to coarsely correct inversions done in 1D NLTE for some of the effects of horizontal RT. Horizontal RT is less important if one considers spatially averaged line profiles because local line strengthening and weakening occur with similar frequency in our HD atmosphere. Thus, the iron abundance is underestimated by 0.012 dex if calculated using 1D NLTE RT. Since effects of horizontal RT are greatest for spatially resolved quantities, the use of 3D RT is particularly important for interpreting high spatial resolution observations.
Key words: line: formation / line: profiles / radiative transfer / Sun: granulation / Sun: photosphere / Sun: atmosphere
© ESO, 2013
1. Introduction
Due to its countless spectral lines in nearly all wavelength ranges and its relatively high abundance, iron plays an important role in investigations of solar (and stellar) properties, such as temperature, elemental abundances (iron is often taken as a proxy for all metals), velocity, and magnetic fields. The rich spectrum of iron is a result of its rich and complex term structure, which also makes it difficult to achieve the proper degree of realism in the synthesis of its spectral lines. Non-local thermodynamic equilibrium (NLTE) effects have already been investigated and identified as important a considerable time ago (e.g., Athay & Lites 1972; Steenbock & Holweger 1984; Boyarchuk et al. 1985; Solanki & Steenbock 1988; Thévenin & Idiart 1999; Shchukina & Trujillo Bueno 2001). The most important NLTE effect on Fe i photospheric line formation in the Sun is so-called UV overionization, i.e., the sensitivity of Fe i to UV irradiation around 300 nm (see, e.g., Athay & Lites 1972; Rutten 1988; Shchukina & Trujillo Bueno 2001, and references therein), leading to a significant underpopulation of the Fe i levels and therefore to a weakening of many diagnostically important lines.
The complex atomic structure forces investigators to make simplifying assumptions, be it in the atomic structure or in the calculation method (e.g., the use of 1D atmospheres or the assumption of LTE) to reduce the problem to a tractable size. A series of works have focused on a maximized reproduction of the atomic structure using atoms with hundreds (Shchukina & Trujillo Bueno 2001) up to – more recently – several thousand (Mashonkina et al. 2011) levels and transitions. In addition, the advent of three-dimensional (3D) hydrodynamic (HD) and magneto-hydrodynamic (MHD) simulations of (magneto-) convection (e.g., Nordlund 1982, 1983, 1985; Stein & Nordlund 1998, 2001; Nordlund & Stein 2001; Vögler et al. 2004, 2005) has enabled a major increase in the degree of realism of the atmospheric input. Shchukina & Trujillo Bueno (2001) and Shchukina et al. (2005) were the first to combine a relatively complete atomic approach that includes NLTE with a 3D atmospheric input from a HD simulation of Asplund et al. (2000a,b) to investigate the influence of NLTE effects on the Fe i spectrum in granular and intergranular regions. However, they too had to make simplifying assumptions: by using a 1.5D approach, they neglected the influence of horizontal radiative transfer (RT).
To date, true 3D RT in combination with NLTE has only been applied to a few atomic species, such as by Kiselman & Nordlund (1995) to O i lines, Uitenbroek (2006) to Na i and Ca ii IR lines, or, more recently, Leenaarts et al. (2012) to the chromospheric Hα line, the latter showing a very strong dependence on 3D NLTE. We also suggest Leenaarts et al. (2012) for more references. So far, no publication exists that applies true 3D NLTE RT to iron lines even though the influence of horizontal RT in Fe i lines has already been impressively demonstrated some time ago by Stenholm & Stenflo (1977, 1978) within a simple flux-tube model. They showed that enhanced UV overionization due to influx of radiation from the hot walls of the flux tube leads to a significant line weakening when compared with 1D NLTE or LTE calculations. Holzreuter & Solanki (2012, hereafter Paper I) refined the investigation of Stenholm & Stenflo (1977, 1978) by using a more complex atom and a more realistic flux tube geometry (cf. Bruls & von der Lühe 2001). In Paper I we found qualitatively similar results to Stenholm & Stenflo (1977, 1978), although the picture turned out to be more complex and the line weakening less extreme.
In this work, we continue the investigation of the influence of horizontal RT on the solar Fe i spectrum by enhancing the realism of the atmosphere. Throughout this work, we use a snapshot of a 3D radiation hydrodynamic simulation computed with the MURAM code (Vögler et al. 2005). Although we do not investigate a magnetic atmosphere, the same effects as described in Paper I should also exist in a field-free atmosphere, especially at locations with strong horizontal temperature gradients. As mentioned in Paper I, we encounter not only line weakening by horizontal irradiation from hot environments, but also the inverse effect at locations where the source function of the environment is lower than that of the line-forming region itself. We show in this work that line strengthening occurs as frequently as line weakening in our HD atmosphere.
Here, we again consider the 524.71/525.02 nm and the 630.15/630.25 nm line pairs. These four lines are generally used to investigate magnetic features. The 630.15 and the 630.25 nm lines have often in the past not been considered ideal for studying convection and the like owing to their non-zero Landé factors. This view has been mitigated by the success of the Hinode SP (Kosugi et al. 2007; Tsuneta et al. 2008) also for studies unrelated to the magnetic field. Similarly, the IMaX instrument (Martínez Pillet et al. 2011) on the Sunrise mission (Solanki et al. 2010; Barthol et al. 2011) has demonstrated the usefulness of the Fe i 525.02 nm line also for nonmagnetic studies (Bello González et al. 2010; Khomenko et al. 2010; Roth et al. 2010). Another reason we used these lines was to be able to compare with an upcoming investigation based on MHD simulations.
We aim to shed more light on the quantitative differences between 1D NLTE (LTE) and 3D NLTE. We show that spatially averaged quantities such as the averaged line profile exhibit only a very minor dependence on horizontal RT, but if resolved line profiles are considered, significant differences between 1D and 3D RT line profiles may appear. This is the case for, e.g., RMS intensity contrasts in line cores. It is important to consider spatially resolved line profiles for investigations where high resolution observations are inverted.
2. Model ingredients
2.1. Radiative transfer calculations
All our calculations are done with the 3D RT code RH developed by Uitenbroek (2000) and based on the iteration scheme of Rybicki & Hummer (1991, 1992, 1994). We use a modified version (see Paper I for details) which uses monotonic parabolic Bézier integration of the source function in the integration of the short characteristics (Olson & Kunasz 1987; Kunasz & Auer 1988; Rees et al. 1989; Socas-Navarro et al. 2000) as proposed by Auer (2003).
2.2. Atomic model
f-values of our four selected lines.
We used a similar atomic model (23 levels, 33 lines, using a total of approximately 1300 wavelength points) to that used in Paper I but with the best gf-values available in the literature for the lines used in our investigation (see Table 1 for a summary). The atom was tailored to reduce the computational costs but still to represent the most important transitions for our selected lines. A test with a much larger model (121 levels, 357 lines) – kindly provided by Bruls – showed no major difference in the spectrum of the lines discussed here.
The problem of missing iron line opacity in the UV, which may lead to wrong population numbers (Bruls et al. 1992), was dealt with by artificially increasing the opacities in the relevant wavelength range as proposed by Bruls et al. (1992). We refer to Paper I for a more complete discussion.
The elastic collision rates were calculated according to the semi-classical approach of Anstee & O’Mara (1995) and Barklem & O’Mara (1997). For the iron abundance we employed a value of 7.50 (Asplund et al. 2009) for all computations.
The influence of inelastic collisions with neutral hydrogen, which is still under intense debate (see, e.g., the discussion by Mashonkina et al. 2011, and references therein), was neglected in our calculations because the formula for the calculation of the rates (Drawin 1968) is accurate within an order of magnitude only. It seems that – at least for solar conditions – the neglect does not have far reaching consequences on NLTE level populations (see e.g. Allende Prieto et al. 2004; Mashonkina et al. 2011). However, because these authors used 1D atmospheres for their argumentation, it cannot be excluded completely that in a very inhomogeneous 3D atmosphere, the influence of collisions with neutral hydrogen may at some (mainly cold) locations have some relevance.
2.3. Model atmospheres
 |
Fig. 1 Atmospheric parameters at two heights. Left: z = 0 km, i.e., at the average level of formation of the continuum. Right: z = 240 km, approximate height of the line core formation of our three selected lines. From top to bottom the hydrogen number density, nH (relative to the maximum value at that height), the vertical velocity, vz (with negative values denoting up-flows), and the temperature T are plotted. |
The input atmosphere model for our calculations was taken from a realistic 3D radiation hydrodynamic simulation. We used a snapshot from a B = 0 run of the MURAM code (Vögler et al. 2005) with an open boundary condition at the top of the atmosphere (using the so-called “fiducial layer” method, see e.g. Stein & Nordlund 1998) allowing for mass flows into or out of the cube. The original resolution of the cube was 288 × 288 × 120. The completely optically thick parts of the atmosphere sufficiently far below the photosphere (48 pixels) were cut away. The resulting 288 × 288 × 72 cube starts approximately 300 km (average 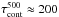 ) below the average
) below the average 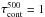 level and reaches a height of approximately 700 km above it. The spatial extent in x and y direction is 6000 km each, i.e., the cube has a constant grid spacing of approximately 21 × 21 × 15 km3. The original Cartesian geometry of the cube was directly employed also in our RT calculations. Due to the large variations in physical quantities across the cube, even a single line may be formed at rather different geometric height ranges at different (x,y)-locations. Consequently, an equidistant z-grid has proven to be favorable.
level and reaches a height of approximately 700 km above it. The spatial extent in x and y direction is 6000 km each, i.e., the cube has a constant grid spacing of approximately 21 × 21 × 15 km3. The original Cartesian geometry of the cube was directly employed also in our RT calculations. Due to the large variations in physical quantities across the cube, even a single line may be formed at rather different geometric height ranges at different (x,y)-locations. Consequently, an equidistant z-grid has proven to be favorable.
The temperature structure and the velocity fields were directly taken from the MURAM cube. The H populations (nH) of the ground level were calculated from the MURAM cube density. The population of excited levels of H were neglected. The electron densities ne were calculated by the RH code in a self consistent way. Figure 1 shows the spatial distribution of some atmospheric parameters at the average continuum formation level (z = 0 km; panels on the left) and at a height at which, roughly, the cores of the selected lines are formed (z = 240 km; panels on the right). Of course, the formation height depends strongly on x,y so that these are just illustrative heights. In Fig. 1 we see the granular structure with hot uprising granules and dense, cold downflowing intergranular lanes at the z = 0 km level. At z = 240 km, the temperature difference between still rising granular and downflowing intergranular regions is inverted, whereas the density distribution is relatively smooth. The temperature inversion takes place at heights between z = 150 km and z = 180 km.
In order to compare our 3D calculations with 1D computations we constructed plane-parallel atmospheres as in Paper I by vertically cutting the 3D cube at all (x,y)-positions. The corresponding 82 944 1D problems were solved individually. The resulting 1D population numbers were then re-transferred into a 3D cube for the final calculation of the emerging spectra (1.5D). Throughout this work we use the term 1D for the 1.5D approach.
 |
Fig. 2 Mean profiles of our three selected lines averaged over the whole x–y plane for three calculations methods (thick solid: 3D NLTE; thin solid: 1D NLTE, dashed: LTE). The thin vertical line denotes the nominal core wavelength. Note, the 1D-NLTE profiles coincide almost completely with the 3D-NLTE profiles. |
 |
Fig. 3 Map of the residual intensity of our three selected lines (top: 525.02 nm; middle: 630.15 nm; bottom: 630.25 nm) for the three different calculation methods (left: LTE; middle: 3D-NLTE; right: 1D-NLTE). |
2.4. Computational setup
For the 3D NLTE calculation, we used the standard angle set A6 of the RH code with 6 rays per octant or 48 in total. This choice is, although not ideal (see Paper I), reasonable for our case as we only want to compare different calculation methods (LTE, 3D NLTE and 1D NLTE) here. Furthermore, as the original resolution used in the HD simulation was maintained for our calculation, we expect relevant features to be larger than a single pixel and therefore a smaller angular resolution to be acceptable. The choice of 48 angles allows us to reduce the size of the numerical problem considerably. The corresponding 1D runs were done with 5 Gaussian angles.
The size of the numerical problem of a single iteration is given by the size of the atmosphere (288 × 288 × 72) times the number of rays to be calculated (48) times the number of wavelengths in the spectrum (≈1300). This circumscribes the number of formal solutions necessary per iteration (roughly 4 × 1011). The calculations were executed on a mid-scale server with four 4-threaded CPU’s, 128 GB of memory, and 5 TB of disk space. The duration of the 3D NLTE run (using 16 threads in parallel) amounted to approximately 1.5 month.
For all calculation methods, several rays of different inclination (one with μz = 1.0) were calculated throughout the cube after convergence. Along these rays, the source function and the optical depth were determined (for a selection of wavelengths only) and they were used to determine contribution functions, emergent profiles and optical path lengths as used in later sections.
3. Results
As in Paper I, our main focus lies on the differences of the spectral line profiles resulting from the three tested calculation methods (LTE, 1D NLTE, and 3D NLTE) and their origins.
3.1. Spatial variation of the residual intensity and average profiles
 |
Fig. 4 Sample cross-sections along the x-axis (at y ≈ 2500 km in Fig. 1) showing the minimal residual intensity for three lines as indicated above each panel and three methods (thick solid: 3D NLTE; thin solid: 1D NLTE, dashed: LTE). Local intensity maxima correspond to intergranular lanes (see Fig. 1). The numbered indicators on top of the panels mark x locations discussed in the text. |
The resulting average profiles of our three selected lines are presented in Fig. 2. The 1D NLTE and the 3D NLTE profiles coincide almost completely for all three lines. The LTE profiles agree fairly well too with the NLTE profiles, seemingly confirming the often-made assumption that these lines are “built in LTE”. However, some discrepancy may already be seen in the profile of the 630.25 nm line and – more strongly – in those of the 524.71/525.02 nm line pair. The good agreement between the LTE and NLTE profiles is further reduced if one considers the (resolved) line core residual intensity maps, which are given in Fig. 3. Note that the color scales used for a single line are the same for all calculation methods. Differences between the images may therefore be directly attributed to the calculation method.
The spatial variation of the residual intensity in the three lines shows considerable differences between the three methods. Thus the contrast is strongest in LTE and weakest in 3D NLTE in all three lines shown, with the difference between 1D NLTE and 3D being smaller than that between the LTE and NLTE calculations. This corroborates our findings of Paper I. However, as we do not consider a magnetic atmosphere, we expect that the effects tend to be smaller than in our flux tube/sheet model of Paper I. Also, the finite horizontal resolution of the HD cube should lead to smaller differences than in Paper I.
To provide a more quantitative view of the variability in the line profiles calculated in LTE, 1D NLTE and 3D NLTE we present, in Fig. 4, the residual intensity along a cut through the atmosphere (at y ≈ 2500 km). Some x locations on which we like to draw attention are marked with a numbered indicator on top of the individual panels.
The LTE residual intensity in the 525 nm lines (top panel) often – but not always – lies clearly below the NLTE intensities. For this line pair, the intensity difference between 1D and 3D NLTE RT is small. Significant differences are only found at a few spatially well-isolated intensity extrema (typically located near or in intergranular lanes, such as the first maximum near x = 150 km (Pos. 1), see also Fig. 1). There, the variation in the 1D NLTE intensity is often – but not always – larger. This corresponds to our findings in Paper I and those of Stenholm & Stenflo (1977). The horizontal radiation in the 3D calculation weakens lines at locations where the intensity of the environment is stronger (i.e., at local minima of I such as Pos. 2 near x ≈ 5400 km). At local intensity maxima, the environment is darker (cooler) and correspondingly, the inverse effect, i.e., a reduction of the 3D intensity, takes place (Pos. 1). As the 1D calculation neglects both types of contributions of the horizontal RT, we expect the contrast to be larger in 1D NLTE than in 3D NLTE. This can be confirmed from Fig. 3.
Note that there are locations in Fig. 4 where the above statement is obviously not valid (Pos. 3). This may be explained by the fact, that our cut along x in Fig. 4 shows only the neighborhood (in intensity) in one direction and we therefore miss part of the necessary information on the environment of the pixels in question. Thus, some of the local maxima seen in Fig. 4 are no longer maxima when considered in another direction.
In the 630 nm lines, the effect of horizontal RT is larger. The locations where the 1D NLTE and 3D NLTE differ are more numerous. Furthermore and in contrast to the lines near 520 nm, the LTE intensity can be higher or lower than the corresponding NLTE intensities. The intensity variation (contrast) is again largest in LTE, and that of 1D NLTE is larger than that of 3D NLTE, as expected. If one compares the 630.15 nm in Fig. 4 with the temperature distribution at y = 2500 km and z = 240 km in the right panel of Fig. 1, one may discover a tendency for the 1D NLTE intensity to be lower than the 3D NLTE intensity in the (colder) granular areas (Pos. 4) and to be higher than the 3D NLTE intensity in the (hotter) intergranular lanes (Pos. 1 and 5). Thus, the 3D line is weakened in the granules by the strong irradiation from its environment and strengthened in the intergranular lanes by the weaker irradiation from the colder granules. Because the lines are formed above the granular temperature inversion, the effect is reversed if compared to the case of a flux tube or sheet. However, the diversity of possible situations is large. Many locations exist where the three profiles completely coincide, while at other positions clear differences with either sign exist. The main reason for such exceptions is that irradiation from other heights (not visible in Fig. 1) may influence the line formation as well (vertical gradients of the temperature are not always well-correlated with the temperature at a given height, e.g., at z = 240 km).
3.2. Contrasts and their center-to-limb variation
 |
Fig. 5 Center-to-limb variation of the minimum residual intensity contrast of the 630.15 nm (left panel) and the 525.02 nm (right panel) lines for the three calculation methods (stars: LTE; triangles: 3D-NLTE; plus signs: 1D-NLTE). |
 |
Fig. 6 Same as Fig. 5, but for the contrast at the nominal core wavelength. Note the different contrast scales of the left and right panel. |
In the previous section, we found qualitative evidence for a strong dependence of the contrast at μ = 1.0 on the calculation method. In this section we quantify these differences for various inclinations of the line of sight (LOS) to the solar surface normal.
We begin by considering the (normalized) RMS of the residual intensity 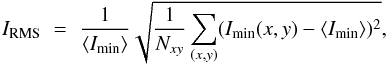 (1)with Nxy the number of grid points in the (x,y) plane, Imin the residual intensity (i.e., the minimum intensity in the line), and ⟨ Imin ⟩ its spatial average. Due to Doppler shifts this intensity refers to different wavelengths at different spatial locations. Already Fig. 3 suggested that the RMS contrast is largest in LTE. This is confirmed by Fig. 5, where the CLV of the RMS contrast of residual intensity in the 630.15 nm (left panel) and the 525.02 nm (right panel) lines are plotted.
(1)with Nxy the number of grid points in the (x,y) plane, Imin the residual intensity (i.e., the minimum intensity in the line), and ⟨ Imin ⟩ its spatial average. Due to Doppler shifts this intensity refers to different wavelengths at different spatial locations. Already Fig. 3 suggested that the RMS contrast is largest in LTE. This is confirmed by Fig. 5, where the CLV of the RMS contrast of residual intensity in the 630.15 nm (left panel) and the 525.02 nm (right panel) lines are plotted.
The contrasts in Fig. 5 increase with μ only until μ = 0.3. For larger μ they are almost independent of μ in case of the 630.15 nm line or only slightly increase with μ (525.02 nm line). The LTE contrasts are larger than the 1D NLTE contrasts at all μ, which are for Fe i 630.15 nm in turn much larger than those obtained with 3D RT. For the 525.02 nm line the 1D and 3D contrast are virtually the same for all LOS. The differences for the 630.15 nm line are surprisingly large: The 1D NLTE contrasts are 30% (μ > = 0.3) to 50% (small μ) larger than those of the 3D RT. The contrasts computed in LTE are approximately a factor of two larger than those obtained with 3D NLTE, independent of μ. The absolute values of IRMS of the 525.02 nm line are significantly higher that of 630.15 nm line. IRMS for the 630.25 nm line (not plotted) agree qualitatively well with those of the 630.15 nm line, although the differences between the three calculation methods are slightly smaller (≈20% for the difference between 1D and 3D, 50–70% for those between LTE and 3D). The larger IRMS of the 525 nm line pair is due to the large temperature sensitivity of these lines stemming from their lower excitation potential. The absolute difference between the methods and between the lines are only very weakly dependent of μ.
 |
Fig. 7 Distribution of the equivalent widths normalized to the average 3D NLTE equivalent width. Line styles for the three methods as in Fig. 4. |
We now attempt to explain the general shape of the center-to-limb variation (CLV). The plateau in the residual intensity contrast at Fig. 5 at values of μ above 0.3 and the drop in IRMS for smaller μ may be attributed to the following reasons. The variation in Imin originates mainly from horizontal temperature variations in the layers in which Imin is formed. The height of this region is only weakly dependent on the LOS angle, especially for larger μ. In addition, the temperature variation decreases only slowly with height at these heights, leading to the plateau. The drop in IRMS at μ < 0.3 is mainly caused by a geometrical effect: the structuring of the photosphere into granules and intergranular lanes with their strong temperature differences can be seen only at large μ. For small μ, we do not see this structuring anymore. The τ = 1 surface at the wavelength of the intensity minimum is then much more homogeneous and so is the temperature distribution.
A considerably different behavior is observed if instead of Imin we consider the intensity at the fixed wavelength λ0 corresponding to the nominal line core, i.e., the core wavelength of the spatially averaged profile. This case is of interest since it mimics a fixed-λ narrow-band filter. Figure 6 depicts the CLV of the intensity contrasts at the nominal line-core wavelength (λ0) of the same lines as in Fig. 5. These contrasts often (but not always) peak around μ ≈ 0.7, dropping slowly towards disc center and rather rapidly towards the limb for all methods. As in the case of Imin and for mainly the same reason, the 525.02 nm line contrast is higher than that of the 630.15 nm line, reaching values as high as 70% (note the different scales in the two panels of Fig. 6).
As in Fig. 5, the 1D NLTE contrasts for 630.15 nm in Fig. 6 (plus signs) are significantly higher than those of the 3D calculation (triangles) for all μ, whereas those of the 525.02 nm line almost coincide with each other. In Fig. 6, the LTE contrast of 630.15 nm drops off less rapidly towards lower μ than the NLTE contrasts. For μ ≥ 0.5 the LTE contrast is actually lower than the NLTE contrasts, but much larger for small μ. The same behavior, although slightly weaker, is exhibited by the 630.25 nm line (not shown here), whereas for the 525 nm lines the LTE and NLTE contrasts run more in parallel.
The difference to Fig. 5 has its origin in the strong sensitivity of the contrasts at λ0 and large μ on Doppler shifts. The strong up and downflows cause the line core to shift away from its nominal position. The nominal line core wavelength may then lay closer to the steep line flanks and already a small wavelength shift may result in a large intensity increase. The magnitude of this effect depends on how narrow the line core is. The LTE line is slightly broader (see Fig. 7) and it is formed slightly higher than the NLTE line. With increasing height, the decreasing RMS variation of the vertical velocities further reduces the LTE contrast. For small μ, however, the line is mainly sensitive to the temperature distribution at the height of formation, because the line is generally broader with less steep flanks and therefore less sensitive to the – now horizontal and more homogeneous – velocity field. Hence, the contrasts for low μ are the same in both, Figs. 5 and 6. The difference between the three calculation methods is then mainly caused by NLTE effects and horizontal RT, both of which lower the contrast.
The strong differences between contrasts resulting from the 1D and the 3D calculation even at low μ (in both, Figs. 5 and 6 may be explained by the fact that in 3D, although the observer cannot see the horizontal structuring of the granules anymore, the individual atoms emitting the observed photons still see their own environment, including the horizontal variation of the temperature and of the incident radiation. As the horizontal RT typically lowers the contrast in the line by changing the population numbers of the relevant atomic levels, the resulting emitted intensity is accordingly changed independently of the direction of the emitted photon.
The main result of this section is that the granular RMS contrasts in Fe i line cores may be very large and are strongly affected by 3D NLTE effects.
3.3. Equivalent widths, line depths and wavelength shifts
 |
Fig. 8 Distribution of the equivalent width ratios (solid: W1 - D NLTE/W3 - D NLTE; dashed: WLTE/W3 - D NLTE) for three lines as indicated on top of the panels. The short, thick vertical lines denote the average value of the two ratios. |
3.3.1. Equivalent width
We begin this section with equivalent widths, W, due to their importance for the computation of elemental abundances. Figure 7 displays the distribution of equivalent widths for the same lines and calculation methods as in Figs. 3 and 4. As was the case for the spatially averaged line profiles, the distributions look – at a first glance – quite similar, although some differences between LTE and NLTE distributions are seen. However, the similarity of the distributions can mask the rather different W at any given pixel. To quantify these differences on a pixel by pixel basis, we calculate the ratios WLTE/W3-D NLTE and W1-D NLTE/W3-D NLTE for each pixel in the whole xy plane. The histograms in Fig. 8 present the distribution of these ratios. They manifest that LTE overestimates W by roughly 10% on average. 1D NLTE also appears to overestimate W, although by a much reduced amount. However, there is a considerable spread in the ratios. The standard deviations of the plotted distributions are ≈4% for LTE/ 3D and ≈2% for 1D/3D. In extreme cases the W can differ by 10% in 1D and 3D.
The spatial distribution of the equivalent width ratios of Fig. 8 is presented in Fig. 9. The largest disagreement is – not unexpectedly – found at the edge of the granules, where large temperature and intensity gradients are found.
3.3.2. Line depth
In complete analogy to the equivalent width, differences in the line depth calculated with the three methods are of the same magnitude, i.e., typically 10%–20% between LTE and 3D NLTE (not shown here). The largest differences are again found near intergranular lanes.
3.3.3. Doppler shift
The statistical distribution of the Doppler shifts (determined by the difference between the average wavelength position of the two line flanks at half height and the nominal line core) relative to the 3D NLTE value for the 630.25 nm line are depicted in Fig. 10. The Doppler shift distributions in the other lines are of the same size or even smaller and therefore not shown here. Almost no (x,y) position shows any significant difference in the Doppler shift between any two methods. More than 80% of the 1D NLTE pixel have a Doppler shift which does not differ by more than 100 m/s from the 3D NLTE value. The distribution of the relative differences of the LTE Doppler shifts is slightly broader, which may be explained by the slightly higher opacity of the LTE line, so that it samples a somewhat higher region in the atmosphere (see, e.g., Fig. 13) and may therefore measure slightly different velocities.
3.4. Origin of the differences between 1D and 3D NLTE radiative transfer
In this section we show that the differences between 1D NLTE and 3D NLTE have their origin in the effect first described by Stenholm & Stenflo (1977), i.e., in the horizontal irradiation from hotter (or cooler) environments into the line-forming region. To see this we examine one small region of our atmosphere in more detail. We selected a set of 6 points along a cut through an intergranular lane as indicated in Fig. 11, the latter reproducing a section of 1500 × 1500 km2 of the original atmosphere. The units of the x and y axes in Fig. 11 are the same as those in Fig. 1. Every second pixel was chosen along the diagonal cut which starts at the upper left (in the following called position a) and ends at the lower right (position f in the following). The spatial distance between two such pixels amounts to approximately 55 km.
 |
Fig. 9 Map of the equivalent widths relative to the 3D-NLTE value for the same lines as in previous figures. Left: 1D-NLTE, Right: LTE. |
Figure 12 shows the profiles along the cut. The panels exhibit 1D NLTE (and LTE) profiles that differ clearly from the 3D NLTE profiles, as well as from each other. Also, the sign of the difference changes along the cut. Whereas the 3D solution gives the weakest spectral line in panels a and b, it results in the strongest line in panel d. In the other panels the results are not entirely clear-cut. We see also that LTE profiles often lie closer to the 1D NLTE profiles, but not at every location (see, e.g., panel f for an exception).
To understand the circumstances of the line formation in more detail, we have to consider the conditions at heights where the line forms. We define the line-forming region Fline(x,y) at the location (x,y) as the heights z where the line contribution function Cline(z) is larger than 20% of its maximum 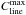 , i.e.,
, i.e., 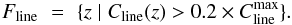 (2)We next define a temperature estimate of the environment, TEnv, whose difference to the temperature at the spatial pixel in question presumably determines magnitude and sign of the 3D RT effects. As the typical horizontal mean free path of a photon at the average heights of line core formation in the photosphere is about 100 km, we define as the environment of a point Px0,y0,z0
(2)We next define a temperature estimate of the environment, TEnv, whose difference to the temperature at the spatial pixel in question presumably determines magnitude and sign of the 3D RT effects. As the typical horizontal mean free path of a photon at the average heights of line core formation in the photosphere is about 100 km, we define as the environment of a point Px0,y0,z0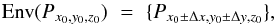 (3)with Δx = Δy = 105 km, which corresponds to a distance of 5 pixel. As the temperature TEnv of the environment at a point Px0,y0,z0, we define the average temperature of the four pixels in Env(Px0,y0,z0), i.e.,
(3)with Δx = Δy = 105 km, which corresponds to a distance of 5 pixel. As the temperature TEnv of the environment at a point Px0,y0,z0, we define the average temperature of the four pixels in Env(Px0,y0,z0), i.e., 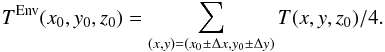 (4)The temperature difference of the environment at a point Px0,y0,z0 in the atmosphere simply becomes
(4)The temperature difference of the environment at a point Px0,y0,z0 in the atmosphere simply becomes 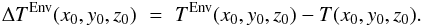 (5)Figure 13 presents the run of ΔTEnv (thick solid line on the right side of each frame) as a function of z for the same six locations as in Fig. 12. On the left side of each panel, the corresponding contribution functions of 630.25 nm (the same line as in Fig. 12) are given for the three methods (thick solid: 3D NLTE, 1D NLTE thin solid, dashed: LTE, for reference only).
(5)Figure 13 presents the run of ΔTEnv (thick solid line on the right side of each frame) as a function of z for the same six locations as in Fig. 12. On the left side of each panel, the corresponding contribution functions of 630.25 nm (the same line as in Fig. 12) are given for the three methods (thick solid: 3D NLTE, 1D NLTE thin solid, dashed: LTE, for reference only).
One easily recognizes that temperature differences of several 100 K may exist between the line-forming region and its environment. At points a, b and f, the environment is significantly hotter, at point d significantly cooler, and, in panels c und e, of similar temperature. If we compare the temperature differences in Fig. 13 with the line profiles in Fig. 12, we immediately recognize that the 1D NLTE line profiles in panels a, b and f are deeper than those calculated in 3D NLTE. In panel d however, the 3D NLTE line is clearly stronger, and in panels c and e the two profiles show only minor differences. This is exactly what one would expect from the influence of horizontal RT. Radiation from relatively hot environments weakens the 3D NLTE line profiles and colder environments may lead to the inverse effect, i.e., a strengthening of the 3D NLTE line, as in panel d. The results shown here were also reproduced by replacing the temperature with the Planck function. Because the temperature is somewhat more intuitive than the Planck function we only show the results for the temperature.
3.5. Statistical influence of horizontal radiative transfer
In Sect. 3.4 we quantified the differences between 1D NLTE and 3D NLTE discussed in the previous section, for a few sample points only, which demonstrate the basic effect. Here we consider all points of the whole atmosphere and all four computed spectral lines at the heights of line formation. In Fig. 14 we plot the two ratios (left panels: line depths D1D/D3D; right panels: equivalent widths Wλ,1D/Wλ,1D) against the average temperature difference ΔTEnv(x,y) between the line-forming region and its environment for all points (x,y) in the atmospheric model, whereas ΔTEnv(x,y) is defined as the average of all 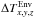 in the formation height range Fline(x,y) (see Eq. (2)). The result for Fe i 524.71 nm is not plotted since it is nearly the same as for 525.02 nm.
in the formation height range Fline(x,y) (see Eq. (2)). The result for Fe i 524.71 nm is not plotted since it is nearly the same as for 525.02 nm.
Even with our very crude definition of the environmental temperature, a clear, almost linear trend can be seen: The hotter the environment the weaker the 3D NLTE line profile and vice versa. This corresponds exactly to our results of the previous section.
For every line we may now determine the specific slopes of the line depth or Wλ ratios as a function of the temperature difference of the environment. The slope is different for every line in correspondence to their sensitivity to NLTE and horizontal RT effects. Table 2 gives the slopes of the linear regression in percentage points per 100 K temperature difference, for example, the line depth of the 630.25 nm line in 1D NLTE must be increased by 1.835% (the equivalent width by 1.521%) for every 100 K the “environment” is cooler than the line-forming region to obtain the proper 3D NLTE value. It can be seen that both the 3D line depth and Wλ decrease by approximately 1% to 2% per 100 K temperature difference in the selected lines. The zero-crossing of the regression lines is at 1.01 for both quantities, i.e., both, the 1D NLTE line depths and the equivalent widths are on average 1% larger than the corresponding 3D NLTE value.
 |
Fig. 10 Distribution of the core wavelength λmin shifts relative to the 3D NLTE value (630.25 nm line). Solid line: 1D – 3D; dashed line: LTE – 3D. Averages are indicated by the small vertical lines (as in Fig. 8). |
An improved definition of the environment could reduce the scatter in the plots. A test with other distances Δx,Δy of the four pixels confirmed that the selected distance of approximately 100 km is appropriate, but the inclusion of more pixels, possibly weighted according to their optical distance, is likely to give better correlations. However, the more sophisticated the method to determine the neighborhood, the higher are the computational costs.
Could one use such relationships as simple and still reasonably effective first order corrections of 1D NLTE values which could allow one to bypass full-blown 3D computations? Since the temperature of neighboring pixels is not known a priori in inversions, we replaced our temperature measure of the environment by the surface residual intensity of the line in the same environment. The resulting scatter plot (not shown) exhibits a very similar behavior to what is shown in Fig. 14. A possible reason is that if we assume that the lines are formed at least close to LTE, the residual intensity in the neighborhood is also a weighted measure of the temperatures in that neighborhood and therefore a similar connection between the residual intensity of the environment and the relative strength of the 3D line profile must exist.
4. Discussion
In the previous section we presented the influence of the inclusion of NLTE effects and horizontal RT on the profiles of spectral lines. We obtained these results by applying three different calculation methods (namely 3D NLTE, 1D NLTE, and LTE) on a realistic 3D model of the solar photosphere. We obtained partly substantial differences when spatially resolved quantities such as the line depth, equivalent width, etc. were considered. Spatially averaged values, however, are only rather weakly affected by horizontal RT, and although NLTE effects may have some influence, they remain small in most cases. An important exception is the RMS contrast, a global quantity that is strongly influenced by horizontal RT.
The influence of the inclusion of NLTE effects when computing spectral lines in 3D HD models has been investigated in detail by Shchukina & Trujillo Bueno (2001). Here, we therefore concentrate mainly on discussing the influence of horizontal RT.
The main reason for differences between calculations considering or neglecting horizontal RT can be generally ascribed to the effect already discussed by Stenholm & Stenflo (1977). They showed that the influx of radiation from a hot environment leads to a weakening of Fe i spectral lines (later confirmed for more realistic iron model atoms and flux-tube geometries by Bruls & von der Lühe (2001) and Holzreuter & Solanki (2012). However, in granulation (and in some flux-tube models, see Holzreuter & Solanki 2012) a full explanation requires the addition that the 3D NLTE line profile may not only be weakened by the irradiation from a hot environment, but may be strengthened if the environment is sufficiently cold. Furthermore, as the formation height of the considered lines lays slightly above the granular-intergranular temperature inversion, the over-all effect may be weaker in these lines because the contributions from both below as well as above the temperature inversion height may cancel each other.
4.1. Interpretation of contrasts
 |
Fig. 11 Enlarged subsection of the atmosphere. The color scales (T, vz) as well as the x and y axis correspond to those in Fig. 1 and 3 (residual intensity of the 630.25 nm line) respectively. The black and yellow dots indicate the positions selected in this section for a more detailed analysis. |
 |
Fig. 12 Line profiles of the 630.25 line at six different spatial positions along a cut through our model (see Fig. 11, where the cut is shown). The panels from left to right and top to bottom correspond to positions a to f along the cut, i.e., from its top-left to its bottom-right corner. Thick solid: 3D NLTE; thin solid: 1D NLTE, dashed: LTE. |
 |
Fig. 13 Thick line at right side of each panel: temperature difference, ΔT, of the line-forming region relative to its environment for the same positions as in Fig. 12. See main text for the exact definition of ΔT. Positive ΔT: the environment is hotter than the line-forming region. Lines on the left side of each panel: normalized contribution functions for the three methods indicating the heights of line formation (thick solid: 3D NLTE; thin solid: 1D NLTE, dashed: LTE). |
 |
Fig. 14 Line depth ratio D1 - D NLTE/D3 - D NLTE (left panels) and analogous ratio of equivalent width (right panels) as a function of the temperature difference to the local environment for all (x,y) positions of the hydrodynamic data cube. The point density is indicated by the colored shading in a logarithmic scale (yellow: 2, orange: 5, dark orange: 10, red: 20, etc. up to the innermost area in black with 1000+). The unit area was defined by subdividing the temperature axis into sections of 10 K and that of the EW ratio into sections 0.01. Regression lines are over-plotted and the corresponding correlation coefficients are given in the lower right corner of each frame. |
In Sect. 3.2 we found that the different levels of realism in the RT may produce very different RMS contrasts within the spectral lines. Horizontal RT reduces contrasts as strongly as NLTE effects. The two effects stack in such a way that differences of up to a factor of 2 between LTE and 3D NLTE and up to a factor of 1.5 between 1D NLTE and 3D NLTE may arise. The largest effect of horizontal RT is found in the residual intensity contrast owing to the low absolute value of the intensity. The occurrence of such strong discrepancies between different methods has an impact on the interpretation of observed contrasts, recorded in the cores of spectral lines or in spectral regions with a dense coverage by spectral lines, such as found in the UV and observed by the Sunrise filter imager (Gandorfer et al. 2011).
Spectral filters invariably have a finite width. In order to compare our calculated contrasts with those of such an observation, we convolved our calculated line profiles with Gaussian filters of different widths. Figure 15 presents the contrast after a filter tuned to the nominal line core wavelength as a function of the filter width. Black and red curves are for μ = 1.0 and μ = 0.32, respectively.
A filter as narrow as 4 pm reduces contrast considerably and filter widths of 8 pm almost halve the contrast values. However, even for filters of this width a significant difference in contrast is found between LTE and 3D NLTE amounting to a factor of 1.3 at μ = 0.32 (see Fig. 15). At double this filter width (i.e., 16 pm) the recorded radiation is dominated by the continuum, so that the contrast becomes close to the continuum contrast at this wavelength (see Danilovic et al. 2008). Since the continuum is formed in LTE, the differences between the results of the three levels of sophistication become accordingly small.
We wish to draw attention to the rather dramatic change in the CLV of the LTE contrasts as the filter width increases: the LTE contrast for larger filter width is almost the same for both μ so that CLV of the contrast is strongly distorted. In NLTE, the ratio of the contrast at μ = 1.0 to that at μ = 0.32 is reduced (from 1.8 for no spectral smoothing to 1.4 at 8 pm filter width), but remains sizable.
The contrast also depends significantly on the spatial resolution. In the past, the rule that the finer the resolution the larger the contrasts was true (Mathew et al. 2009; Wedemeyer-Böhm & Rouppe van der Voort 2009). We cannot make a testimony on whether we have reached the end of this development or not, as our HD atmosphere has only a finite resolution (21 km per pixel) too, but horizontal RT at least has some smoothing effect on such small scales so that we can speculate that the increase in contrast with resolution could flatten somewhat. However, we found in Paper I (see also Bruls & von der Lühe 2001) that very small features with large contrast may persist in magnetic atmospheres so that we must assume that we can expect some new findings when going to better resolution. We intend to expand our series of investigations to MHD atmospheres with resolutions as high as 5 km per pixel.
Because our resolution of approximately 20 km is far better than those of the best observations available today and because we do not experience any smoothing due to the point-spread function of the optical system our contrasts are much larger than observed values.
To summarize this section, we note that horizontal RT has a strong influence on the determination of contrasts and neglecting it may lead to severe errors in the interpretation of observational contrasts measured in spectral lines. Spectral filters with a width in excess of 4 pm (40 mÅ), as often used for high-resolution imaging, have a strong influence on the contrasts observed in the cores of isolated medium strong spectral lines. The CLV of the contrast may be strongly affected, whereby the effect is larger for LTE computations than in NLTE, at least for the lines considered here.
 |
Fig. 15 Influence of a (hypothetical observational) filter width (Gaussian) on the intensity contrasts at the nominal line core wavelength. The contrasts are given for two positions on the solar disc, μ = 0.32 (red) and μ = 1.00 (black), as well as our three calculation methods (asterisks: LTE; plus signs: 1D NLTE; triangles: 3D NLTE). |
4.2. The influence of horizontal radiative transfer on temperature determination
In their extensive investigation, Shchukina & Trujillo Bueno (2001) confirmed that for spatially resolved observations of Fe i spectral lines neglecting (1D) NLTE effects may influence the determination of the temperature. Such results had earlier been found by Rutten & Kostik (1982), Shchukina et al. (1990), Solanki & Steenbock (1988, for magnetic features) and others. They found, that the determined temperature obtained from the 630.15 nm line may be 100–200 K too large in granules and too small by approximately the same amount in intergranular regions. The profiles in Fig. 12 of the slightly weaker 630.25 nm line, reveal that the differences between the 3D and 1D NLTE profiles can be of the same order of magnitude as those between the 1D NLTE and LTE profiles. Hence, neglecting horizontal RT may produce errors of similar size, at least at some locations.
We find the strongest effects of horizontal RT, e.g., on the line depth or EW – as expected – at the edge of the granules, where strong horizontal temperature and density variations at heights relevant to line formation are present. These locations only partly overlap with the locations found by Shchukina & Trujillo Bueno (2001) where NLTE is important (i.e., their “granular region”). Therefore, the differences due to horizontal RT can amplify or diminish the error of neglecting NLTE in the temperature determination, as 1D NLTE effects are mainly due to the vertical structure of the atmosphere, while the effects of horizontal (3D) RT are mainly determined by the horizontal structure.
If we consider the sample profiles in Fig. 12, we would clearly assign the profile d to be in an intergranular lane (refer also to Fig. 11). If – according to the lower left panel of Fig. 14 of Shchukina & Trujillo Bueno (2001), which corresponds closely to the case in our Fig. 12d – applying LTE leads to an underestimate of the temperature by 100–200 K at such a location, one can conclude that the LTE temperature estimate at this point would be 200–400 K lower than the 3D NLTE value because the difference between the 1D and the 3D NLTE profiles is of the same magnitude as that between the LTE and 1D NLTE profiles. An analogous interpretation, but with reversed sign can be applied to panels a and b. At the very border of a granule, the LTE temperature estimate in the Fe i 630.15 nm line could be 200–400 K too high.
An example of horizontal RT reducing the error in temperature determination is illustrated in Fig. 12f, whereas Figs. 12c and e depict profiles that do not experience any change due to horizontal RT. Note also that the formation height of the considered lines lays above the granular-intergranular temperature inversion, if a weaker line would be considered, the effects of horizontal RT could have the reversed sign.
4.3. Yet another word on the iron abundance
How important is horizontal RT for abundance determinations? The strong differences between 1D and 3D NLTE in Fig. 8 may look like an alarming result for those who determine abundances by determining equivalent widths. Although differences of up to 10% at specific locations, the average ratio (vertical bars in Fig. 8) between the 1D and 3D value is at slightly more than 1.01 corresponding to a difference of approximately 1% in EW. As the curves of growth of both the 630 nm lines reaches its lowest inclination close to the actual abundance values, a small but relevant change in the iron abundance of approximately 0.012 dex may result. The same result is obtained if one considers the EW of the two spatially averaged profiles instead of the spatial average of the individual EW’s. The use of weaker lines that are less susceptible to NLTE effects may reduce the effect of neglecting horizontal RT.
Our finding is not really surprising as we consider a field-free atmosphere, where no systematic difference in density between hot and cold environments can be found. Only in an evacuated magnetic element where the hot walls can irradiate into the flux element, can the line weakening systematically dominate over the line strengthening which takes place only in a very small area in the optically much thicker walls.
5. Conclusions
This paper describes a continuation of our investigation of Paper I on the influence of horizontal radiative transfer (RT) in NLTE on diagnostically important Fe i lines. The main difference to Paper I is the replacement of the simple flux tube model atmosphere by a snapshot of a realistic 3D radiation hydrodynamic simulation (with B = 0) run of the MURAM code (Vögler et al. 2005). We kept the original resolution of 288 × 288 pixels in the xy plane which allowed us to investigate horizontal transfer in high spatial resolution (horizontal grid scale ≈20 km) spectra.
Our results confirm the line weakening influence of radiation streaming in from hot surroundings, as described by Stenholm & Stenflo (1977) and in Paper I. In the realistic field-free atmosphere considered here, we also find the inverse effect of line strengthening due to weaker irradiation from colder environments. In normal granulation, both effects occur almost equally often. This leads to a surprisingly good agreement of the spatially averaged profiles calculated in 1D NLTE with those computed in 3D NLTE. The difference to profiles computed in LTE can be quite significant, however. Furthermore, the fact that the lines considered here are formed in heights only slightly above the granular-intergranular temperature inversion may lead to a partial cancellation of the effects of horizontal RT because contributions from heights below the temperature inversion typically have a different sign than those from above it. Lines built below the temperature inversion height might have an augmented sensitivity to horizontal RT.
Shchukina & Trujillo Bueno (2001) found that NLTE effects may not be negligible even if averaged profiles calculated in LTE or NLTE agree well. Our computations show that the same can be said for the influence of horizontal RT, where significant differences to 1D NLTE in the individual profiles can be found, although the averaged profiles coincide almost completely. Equivalent widths and line depths calculated in true 3D NLTE differ mainly at spatial locations close to strong horizontal temperature gradients – as found at the boundaries of granules. These parameters in 3D NLTE may differ by up to 20% from their LTE counterparts and by up to 10% from the values obtained with 1D NLTE. The average difference between the 1D and 3D NLTE equivalent widths as well as the difference of the equivalent widths obtained by spatially averaged profiles amounts to slightly more than 1% for our atmosphere and would result in a reduction of the iron abundance of approximately 0.012 dex.
The largest influence of horizontal RT has been found in the RMS contrast of the line core intensity. While NLTE reduces the residual line contrast by approximately one third against the LTE value, we found that horizontal RT reduces the 1D NLTE contrast by another 20 to 30%, resulting in a contrast that is only roughly half of that obtained in LTE. This is valid for all distances from the limb. Contrasts measured using filters centered on the nominal wavelength of the line core depend strongly on the width of the filter. However, at all filter widths the CLV of the contrast resulting from LTE and 3D NLTE computations is different.
We have shown in detail how the temperature difference between the line-forming region and its environment systematically weakens (if the environment is hotter) or strengthens (if the environment is colder) the profiles calculated in 3D NLTE. A clear statistical correlation exists between the line weakening (strengthening) as a function of the temperature of the environment. A quantitative investigation shows that the weakening or strengthening of the 630 nm lines by horizontal RT is on the order of 1–2% of line depth or equivalent width per 100 K temperature difference to the horizontal environment of the line-forming region. A similar correlation exists also with the line intensity in the (same) neighborhood, as the line intensities are also dominated by the local temperatures as long as the line does not depart too much from LTE, which is the case for the considered lines.
Our results are of particular importance for the inversion of high resolution observations. If we invert an observation with resolution below 100 km in 1D NLTE, then our calculated profiles will locally deviate by up to several percent in line depth or equivalent width from 3D NLTE. As a consequence, temperatures obtained by such an inversion could also be wrong by several ten to a few hundred Kelvin. The aforementioned correlation between the relative environmental temperature and the 1D/3D line depth ratio could in principle be used to coarsely correct inversions done in 1D NLTE for the influence of horizontal RT. The errors in temperature between LTE and 1D NLTE also amount to 100–200 K (Shchukina & Trujillo Bueno 2001), so that locally errors up to 300–400 K can occur between LTE and 3D NLTE. However, the errors due to neglecting (1D) NLTE and due to neglecting horizontal RT can also cancel each other as enhance each other, depending on the properties of the surroundings.
The next step in this investigation of important iron lines will be the use of 3D NLTE simulations including a magnetic field. The combined influence of horizontal RT and Zeeman effect is likely to lead us to new insight into relevant RT processes in the solar photosphere. In particular, we expect to learn how well a simple flux tube model (Paper I) compares with realistic MHD simulations, with regard to line profile changes due to horizontal RT.
Acknowledgments
We are grateful to Manfred Schüssler for providing the data cubes resulting from the MURAM simulation run, as well as Han Uitenbroek for making his excellent full Stokes NLTE radiative transfer code available. Jo Bruls has provided the iron model atom and has given us many insights into NLTE effects. R. H. appreciates the flexibility of Prof. Dr. Norbert Dillier concerning the working hours at the University Hospital of Zurich. This work has been partially supported by WCU grant No. R31-10016 funded by the Korean Ministry of Education, Science and Technology. And we thank the referee for his help to improve the manuscript.
References
- Allende Prieto, C., Asplund, M., & Fabiani Bendicho, P. 2004, A&A, 423, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anstee, S. D., & O’Mara, B. J. 1995, MNRAS, 276, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Nordlund, Å., Trampedach, R., Allen de Prieto, C., & Stein, R. F. 2000a, A&A, 359, 729 [NASA ADS] [Google Scholar]
- Asplund, M., Nordlund, Å., Trampedach, R., & Stein, R. F. 2000b, A&A, 359, 743 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Athay, R. G., & Lites, B. W. 1972, ApJ, 176, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Auer, L. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 3 [Google Scholar]
- Bard, A., Kock, A., & Kock, M. 1991, A&A, 248, 315 [NASA ADS] [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 1997, MNRAS, 290, 102 [Google Scholar]
- Barthol, P., Gandorfer, A., Solanki, S. K., et al. 2011, Sol. Phys., 268, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bello González, N., Franz, M., Martínez Pillet, V., et al. 2010, ApJ, 723, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., Ibbetson, P. A., Petford, A. D., & Shallis, M. J. 1979, MNRAS, 186, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarchuk, A. A., Lyubimkov, L. S., & Sakhibullin, N. A. 1985, Astrophys., 22, 203 [Google Scholar]
- Bruls, J. H. M. J., & von der Lühe, O. 2001, A&A, 366, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruls, J. H. M. J., Rutten, R. J., & Shchukina, N. G. 1992, A&A, 265, 237 [NASA ADS] [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drawin, H.-W. 1968, Z. Phys., 211, 404 [Google Scholar]
- Gandorfer, A., Grauf, B., Barthol, P., et al. 2011, Sol. Phys., 268, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Holzreuter, R., & Solanki, S. K. 2012, A&A, 467, 695 [Google Scholar]
- Khomenko, E., Martínez Pillet, V., Solanki, S. K., et al. 2010, ApJ, 723, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Kiselman, D., & Nordlund, A. 1995, A&A, 302, 578 [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Kunasz, P., & Auer, L. H. 1988, J. Quant. Spectr. Radiat. Transf., 39, 67 [Google Scholar]
- Leenaarts, J., Carlsson, M., & Rouppe van der Voort, L. 2012, ApJ, 749, 136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez Pillet, V., Del Toro Iniesta, J. C., Álvarez-Herrero, A., et al. 2011, Sol. Phys., 268, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Mashonkina, L., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathew, S. K., Zakharov, V., & Solanki, S. K. 2009, A&A, 501, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordlund, Å. 1982, A&A, 107, 1 [Google Scholar]
- Nordlund, A. 1983, in Solar and Stellar Magnetic Fields: Origins and Coronal Effects, ed. J. O. Stenflo, IAU Symp., 102, 79 [Google Scholar]
- Nordlund, Å. 1985, Sol. Phys., 100, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, Å., & Stein, R. F. 2001, ApJ, 546, 576 [Google Scholar]
- Olson, G. L., & Kunasz, P. B. 1987, J. Quant. Spectr. Radiat. Transf., 38, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, D. E., Durrant, C. J., & Murphy, G. A. 1989, ApJ, 339, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, M., Franz, M., Bello González, N., et al. 2010, ApJ, 723, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J. 1988, in IAU Colloq. 94, Physics of Formation of Fe II Lines Outside LTE, eds. R. Viotti, A. Vittone, & M. Friedjung, Astrophys. Space Sci. Lib., 138, 185 [Google Scholar]
- Rutten, R. J., & Kostik, R. I. 1982, A&A, 115, 104 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1992, A&A, 262, 209 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1994, A&A, 290, 553 [NASA ADS] [Google Scholar]
- Shchukina, N., & Trujillo Bueno, J. 2001, ApJ, 550, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Shchukina, N. G., Shcherbina, T. G., & Rutten, R. J. 1990, in Solar Photosphere: Structure, Convection, and Magnetic Fields, ed. J. O. Stenflo, IAU Symp., 138, 29 [NASA ADS] [Google Scholar]
- Shchukina, N. G., Trujillo, B. J., & Asplund, M. 2005, ApJ, 618, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H. 2011, A&A, 529, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Socas-Navarro, H., Trujillo Bueno, J., & Ruiz Cobo, B. 2000, ApJ, 530, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., & Steenbock, W. 1988, A&A, 189, 243 [NASA ADS] [Google Scholar]
- Solanki, S. K., Barthol, P., Danilovic, S., et al. 2010, ApJ, 723, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 [NASA ADS] [Google Scholar]
- Stein, R. F., & Nordlund, A. 1998, ApJ, 499, 914 [Google Scholar]
- Stein, R. F., & Nordlund, Å. 2001, ApJ, 546, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Stenholm, L. G., & Stenflo, J. O. 1977, A&A, 58, 273 [NASA ADS] [Google Scholar]
- Stenholm, L. G., & Stenflo, J. O. 1978, A&A, 67, 33 [NASA ADS] [Google Scholar]
- Thévenin, F. 1989, A&AS, 77, 137 [NASA ADS] [Google Scholar]
- Thévenin, F. 1990, A&AS, 82, 179 [NASA ADS] [Google Scholar]
- Thévenin, F., & Idiart, T. P. 1999, ApJ, 521, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Uitenbroek, H. 2000, ApJ, 531, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Uitenbroek, H. 2006, ApJ, 639, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A., Bruls, J. H. M. J., & Schüssler, M. 2004, A&A, 421, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 503, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Atmospheric parameters at two heights. Left: z = 0 km, i.e., at the average level of formation of the continuum. Right: z = 240 km, approximate height of the line core formation of our three selected lines. From top to bottom the hydrogen number density, nH (relative to the maximum value at that height), the vertical velocity, vz (with negative values denoting up-flows), and the temperature T are plotted. |
| In the text | |
 |
Fig. 2 Mean profiles of our three selected lines averaged over the whole x–y plane for three calculations methods (thick solid: 3D NLTE; thin solid: 1D NLTE, dashed: LTE). The thin vertical line denotes the nominal core wavelength. Note, the 1D-NLTE profiles coincide almost completely with the 3D-NLTE profiles. |
| In the text | |
 |
Fig. 3 Map of the residual intensity of our three selected lines (top: 525.02 nm; middle: 630.15 nm; bottom: 630.25 nm) for the three different calculation methods (left: LTE; middle: 3D-NLTE; right: 1D-NLTE). |
| In the text | |
 |
Fig. 4 Sample cross-sections along the x-axis (at y ≈ 2500 km in Fig. 1) showing the minimal residual intensity for three lines as indicated above each panel and three methods (thick solid: 3D NLTE; thin solid: 1D NLTE, dashed: LTE). Local intensity maxima correspond to intergranular lanes (see Fig. 1). The numbered indicators on top of the panels mark x locations discussed in the text. |
| In the text | |
 |
Fig. 5 Center-to-limb variation of the minimum residual intensity contrast of the 630.15 nm (left panel) and the 525.02 nm (right panel) lines for the three calculation methods (stars: LTE; triangles: 3D-NLTE; plus signs: 1D-NLTE). |
| In the text | |
 |
Fig. 6 Same as Fig. 5, but for the contrast at the nominal core wavelength. Note the different contrast scales of the left and right panel. |
| In the text | |
 |
Fig. 7 Distribution of the equivalent widths normalized to the average 3D NLTE equivalent width. Line styles for the three methods as in Fig. 4. |
| In the text | |
 |
Fig. 8 Distribution of the equivalent width ratios (solid: W1 - D NLTE/W3 - D NLTE; dashed: WLTE/W3 - D NLTE) for three lines as indicated on top of the panels. The short, thick vertical lines denote the average value of the two ratios. |
| In the text | |
 |
Fig. 9 Map of the equivalent widths relative to the 3D-NLTE value for the same lines as in previous figures. Left: 1D-NLTE, Right: LTE. |
| In the text | |
 |
Fig. 10 Distribution of the core wavelength λmin shifts relative to the 3D NLTE value (630.25 nm line). Solid line: 1D – 3D; dashed line: LTE – 3D. Averages are indicated by the small vertical lines (as in Fig. 8). |
| In the text | |
 |
Fig. 11 Enlarged subsection of the atmosphere. The color scales (T, vz) as well as the x and y axis correspond to those in Fig. 1 and 3 (residual intensity of the 630.25 nm line) respectively. The black and yellow dots indicate the positions selected in this section for a more detailed analysis. |
| In the text | |
 |
Fig. 12 Line profiles of the 630.25 line at six different spatial positions along a cut through our model (see Fig. 11, where the cut is shown). The panels from left to right and top to bottom correspond to positions a to f along the cut, i.e., from its top-left to its bottom-right corner. Thick solid: 3D NLTE; thin solid: 1D NLTE, dashed: LTE. |
| In the text | |
 |
Fig. 13 Thick line at right side of each panel: temperature difference, ΔT, of the line-forming region relative to its environment for the same positions as in Fig. 12. See main text for the exact definition of ΔT. Positive ΔT: the environment is hotter than the line-forming region. Lines on the left side of each panel: normalized contribution functions for the three methods indicating the heights of line formation (thick solid: 3D NLTE; thin solid: 1D NLTE, dashed: LTE). |
| In the text | |
 |
Fig. 14 Line depth ratio D1 - D NLTE/D3 - D NLTE (left panels) and analogous ratio of equivalent width (right panels) as a function of the temperature difference to the local environment for all (x,y) positions of the hydrodynamic data cube. The point density is indicated by the colored shading in a logarithmic scale (yellow: 2, orange: 5, dark orange: 10, red: 20, etc. up to the innermost area in black with 1000+). The unit area was defined by subdividing the temperature axis into sections of 10 K and that of the EW ratio into sections 0.01. Regression lines are over-plotted and the corresponding correlation coefficients are given in the lower right corner of each frame. |
| In the text | |
 |
Fig. 15 Influence of a (hypothetical observational) filter width (Gaussian) on the intensity contrasts at the nominal line core wavelength. The contrasts are given for two positions on the solar disc, μ = 0.32 (red) and μ = 1.00 (black), as well as our three calculation methods (asterisks: LTE; plus signs: 1D NLTE; triangles: 3D NLTE). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


