| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322080 | |
| Published online | 14 October 2013 | |
Magnetohydrodynamics of Mira’s cometary tail
Department of Chemistry and Physics, Western Carolina University, Cullowhee, North Carolina 28723, USA
e-mail: egomez@email.wcu.edu
Received: 14 June 2013
Accepted: 26 July 2013
Aims. The asymptotic giant-branch, long-period variable star Mira exhibits a 4 parsec long cometary tail in the far-ultraviolet. We address the issue of the origin of this structure and its emission process by simulating the transition of this star from the interstellar medium to the Local Bubble, which is a tenuous, high-pressure medium.
Methods. We use the hydrodynamic and the magnetohydrodynamic modules of the PLUTO astrophysical code to carry out our simulations. We study the system without a cooling function, with a simplified exponential cooling function, and with a simplified nonequilibrium cooling function.
Results. We find evidence that magnetohydrodynamics constrain the shape of the cometary tail and explain features of its far-ultraviolet emission. We suggest an emission process that involves C0 excitation through inelastic electron collisions and a two-photon continuum to explain the luminosity of Mira’s tail.
Key words: radiation mechanisms: thermal / stars: AGB and post-AGB / ISM: magnetic fields / methods: numerical / shock waves / ISM: jets and outflows
© ESO, 2013
1. Introduction
The Dutch amateur astronomer, David Fabricius (1564–1617), recognized in 1596 that o Ceti (Mira) is a long-term variable star (Hoffleit 1997). It was surprising to find a star that could vary its brightness on a semiregular basis at that time. Even as the prototype for a class of variable stars, Mira continues to hold surprises that are a consequence of its stage in evolution, its proper motion, and its location. It is now understood that Mira is a binary system with component A undergoing an asymptotic giant branch (AGB) phase with enhanced mass loss. Mira B is less luminous and may be either a white dwarf (Sokoloski & Bildsten 2010) or a main sequence star (Karovska et al. 1997). Mira is also notable for its proper motion with respect to the interstellar medium (ISM). Mira moves at a speed of ~125 km s-1 based on a distance to Earth of 107 pc, (Knapp et al. 2003), although there is a more recent revision to the distance to 92 pc with a corresponding speed of ~106 km s-1 (van Leeuwen 2007). The Galaxy Evolution Explorer (GALEX) experiment has discovered that Mira has a tail visible in the far-ultraviolet (FUV), which covers 2° of the sky (Martin et al. 2007). At the distance given by Knapp et al. (2003), Mira appears to be surrounded by bowshock that is 0.1 pc in diameter. The tail is notably narrower than the bowshock, and it extends to about 4 pc. Spectroscopic studies suggest that knots found on the tail are shocked and ionized by post-bow-shock flow. The best fit for grism imaging of the tail is H2 emission. Martin et al. (2007) concluded that collisional excitation of H2 by hot electrons in a post shock gas must be responsible for the emission. The authors point out that this is consistent with Mira’s motion through the ISM. The knots themselves may be a record of the mass-loss history of the star, as material is stripped by the ram-pressure from the ISM.
An issue with Martin et al. (2007)’s observations is the tail’s long-lived UV emission. The total FUV luminosity of the bow shock and tail is on the order of 1032 erg s-1. Based on the motion of Mira and the GALEX observations, the authors’ estimated age of the tail is 30 kyr. If the tail is formed by material that has been stripped by ram-pressure when Mira plows through the ISM, this material should have cooled off enough, so that no UV emission would be observed. Indeed, no other AGB star has been found with a comparable cometary structure, suggesting a unique set of circumstances. In addition, numerical simulations of the cometary tail structures even extend the age of the tail. Esquivel et al. (2010) observed the appearance of vortices in their simulations of Mira’s tail, which may be the result of instabilities at the edge of the bowshock. Similar structures were found in simulations by Wareing et al. (2007) and in visible structures in the planetary nebula Sh 2-188 (Wareing et al. 2006). From the timescale of formation of such structures, Esquivel et al. (2010) conclude that the estimated age of the tail must be at least 450 kyr. However, Wareing et al. (2007) concluded earlier that the age of the tail must be 120 kyr, which is less than 450 kyr and is consistent with radio observations of the velocity of the tail material (Matthews et al. 2008).
The narrow tail is difficult to reproduce in numerical models. Wareing et al. (2007) carried out a two-wind model simulation, where the spherically symmetric AGB wind is embedded in an ISM wind in Mira’s frame of reference. They find that the structures of the tail are most likely due to turbulence rather than of a registration of the mass-loss history of Mira with the multispecies cooling function of Raymond et al. (1976). Their simulations also show a tail of the thickness of the principal bow shock that does not reproduce the extended narrow tail of Mira. However, the simulation temperatures for the outflow of 104 K appear unrealistic based on what is known from AGB winds. Villaver et al. (2012) also account for cooling, which has proven important to the morphological development of the tail. In their simulations, high density regions in the tail cool more efficiently than lower density ones. These regions would then lose thermal pressure. Thus, pressure from the ISM would narrow the tail. Their conclusion is that a narrow tail results from standard evolution of an AGB stage star with variable mass-loss.
The narrowness of the tail, however, does not by itself help explain the FUV emission. Wareing (2012) points out there is no known mechanism that drives the FUV emission without turbulent mixing of electrons with H2. One possible explanation is that Mira may have recently entered into the Local Bubble from a low-density, warm neutral medium with a temperature of 104 K, as proposed by Wareing et al. (2007). There would also be a precipitous density drop in that transition between two media, since the density of the warm neutral medium is 25 times higher than the Local Bubble. The Local Bubble, on the other hand, has a temperature of 106 K and a thermal pressure 4 times higher. When taken at an angle of 30° between the proper motion of Mira and the boundary between ISM and Local Bubble, Wareing (2012) is able to reproduce the noted “kink” in the cometary tail. The reproduced flow structure implies that Mira is traveling with a Mach 2–3 with respect to warm neutral medium. Wareing (2012) concludes that FUV emission must be thermally driven by the compression effect of the Local Bubble rather than shock heating by turbulence in the ISM.
These results have generated interest in conducting simulations of an AGB star as it crosses from a warm neutral region to a hot, tenuous medium as found in the Local Bubble. Esquivel et al. (2010) considered two models: the evolution of Mira outside of the Local Bubble in a uniform dense medium and the evolution of Mira in the Local Bubble with a hot and tenuous medium with T = 106 and density 5 × 10-2 cm-3 (Lallement et al. 2003). In the second model, the flow is subject to an ionization fraction of 1. They reproduce the narrow, 4-pc tail structure vis-à-vis the 0.1 pc bow-shock well. Their numerical model has a lower time estimate of 300 kyr due to numerical viscosity. They estimate that Mira entered the Local Bubble between 20 to 120 kyr ago. However, the tail is noticeably more turbulent than the organized outflow of the tail observed by Martin et al. (2007).
We are left with two issues in numerical modeling: how to reproduce the narrow structure of the tail while explaining its FUV emission at the same time. We make the case that both of these can be addressed by considering the magnetohydrodynamics (MHD) of the outflow from Mira as they interact with the expected shocks at the boundary between the Local Bubble and the ISM. We also argue that we must consider the asymmetric nature of the outflow. For instance, Mayer et al. (2011) report on Herschel’s observations of Mira in the IR noting that the explanation for the arc-head structures must involve some complex interactions of a bipolar jet with the ISM. Such a bipolar flow, if supersonic in its medium, could help create vortices in the cometary structures, which would provide sites for sustained electron acceleration and consequent FUV emission as these electrons become thermalized.
Here, we consider the possibility that these jets are produced in a medium with a magnetic field. We expect that MHD waves can interact with electrons and ionized hydrogen via cyclotron resonance, such that particles are scattered at high pitch angles with the field lines. Electric fields can be induced through changes in the magnetic flux producing DC currents. Ohmic losses from steady currents provide a channel by which energy stored in the jet and ISM/Local Bubble within the shocked region’s magnetic fields can heat the plasma and power the FUV emission. Thus, we conduct a set of hydrodynamic (HD) and MHD simulations with simplified cooling functions to understand the nature of the cometary structure and its emission.
2. Simulations
In our study of the Mira system, we used a two-wind model with a shock interface propagating over the computational domain. Figure 1 illustrates the general setup of the problem with the frame of reference centered on the star. The star launches a jet injected into a warm, high-density and low-pressure interstellar medium at an angle perpendicular to the direction of motion. This is meant to model the observations of Meaburn et al. (2009), where Mira exhibits a bipolar outflow of 69° ± 15° to the plane of the sky with an outflow velocity of 160 ± 10 km s-1. Raga & Cantó (2008) have likewise conducted a set of HD simulations demonstrating that a latitude-dependent wind can reproduce the double bow shock structure of Mira’s cometary head. They also suggest that axisymmetry is broken due to the misalignment between the latitudinal axis of the wind with the direction of motion of Mira. In our simulations, we keep a simpler version of Raga’s latitude-dependent wind at 90° from the direction of motion in order to keep the axisymmetric properties of the simulation setup. The jet is only injected briefly ahead of the shock front so that the dynamics here explored are those of the interaction with jet material and the shock during and after this transition.
 |
Fig. 1 Initial simulation setup for an anisotropic (jet) outflow of the star before it crosses the boundary between the Local Bubble and ISM. At this boundary, a forward shock, reverse shock, and contact discontinuity develops. |
The simulation domains span 800 × 200 cells (1.6 × 0.4 pc). We assume that the jet carries only a fraction of the estimated mass-loss rate at 10-7 M⊙ yr-1 (Mauron & Caux 1992; Ryde et al. 2000). If we assume an opening angle of the jet of θ = 5°, which carries a proportion of the total mass of θ2/4π (angle in steradians), we obtain a mass-loss rate for the jet of 7 × 10-9 M⊙ yr-1. This jet is injected in a region of 40 cells (0.08 pc) centered at 125 cells (0.25 pc) from the edge of the computational domain downstream. In our simulations we also use three levels of adaptive mesh refinement (AMR) for an equivalent grid of 6400 × 1600 cells as given by the algorithm found in Mignone et al. (2012).
Upstream from the star, we place a low-density, high-pressure medium, which would correspond to the conditions of the Local Bubble. The values of density and pressure used are from Lallement et al. (2003). This medium has a velocity that approximates Mach 3.0 in the frame of reference of the star from the values of pressure and density found on the ISM.
Once the simulation evolves, a shock develops at the boundary of the Local Bubble and the ISM, which is made of three interfaces: a forward shock that heats the ISM material, a reverse shock that heats the Local Bubble material, and a contact discontinuity between these heated media. This shock region would be expected if the Local Bubble were not in pressure equilibrium with the ISM. Eventually each one of these shock interfaces overtakes the jet of the star. Ram-pressure stripping carries jet material downstream, forming an astrosheath perpendicular to the jet.
We selected PLUTO for its ability to model high Mach-number compressible flows in astrophysical settings. This code implements a choice of Gudonov-type solvers to the Riemann problem of the decay of a shock discontinuity. We chose the Roe solver of Cargo & Gallice (1997). This code has been tested against the standard, computational fluid dynamical problems. In addition to these tests, the code has also been tested for the double Mach, strong shock reflection problem and the under-expanded jet problem, which are pertinent to the model we are testing.
The 2+1 gravity-free, MHD equations that we considered for our model evolve the primitive variables of density, ρ, fluid velocity, v = [vx,vy], and magnetic induction, B = [Bx,By,Bz], as ![\begin{eqnarray} && \frac{\partial \rho}{\partial t}+{\vec \nabla} \cdot (\rho \vec{v}) = 0 \textrm{,} \\[1mm] && \frac{\partial }{\partial t}(\rho \vec{v}) + {\vec \nabla} \cdot [\rho \vec{v}\vec{v}^{\rm T} - \vec{B}\vec{B}^{\rm T} ] + {\vec \nabla} p_{\rm t} = {\vec \nabla} \cdot \tau \textrm{,} \\[1mm] && \frac{\partial U}{\partial t} + {\vec \nabla} \cdot [\vec{v}(U+p_{\rm t})-\vec{B}(\vec{v}\cdot\vec{B})] = {\vec \nabla} \cdot {\vec \Pi}_U - \Lambda \textrm{,} \\[1mm] && \frac{\partial \vec{B}}{\partial t} - {\vec \nabla} \times (\vec{v} \times \vec{B}) = - \vec{\nabla} \times \eta \vec{J} \textrm{.} \end{eqnarray}](/articles/aa/full_html/2013/10/aa22080-13/aa22080-13-eq27.png) Here U is the total energy density; total pressure is pt = p + B2/2 accounting for the thermal and magnetic pressures; Λ is a nonideal dissipative term that accounts for optically thin, collisionally-excited radiative losses; and η is the resistive tensor. The equation of state (EOS) is ideal for a single particle species for an adiabatic index of Γ = 5/3, which allows us to write
Here U is the total energy density; total pressure is pt = p + B2/2 accounting for the thermal and magnetic pressures; Λ is a nonideal dissipative term that accounts for optically thin, collisionally-excited radiative losses; and η is the resistive tensor. The equation of state (EOS) is ideal for a single particle species for an adiabatic index of Γ = 5/3, which allows us to write 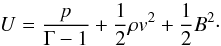 (5)In Eq. (2), we introduce the viscosity stress tensor given by
(5)In Eq. (2), we introduce the viscosity stress tensor given by ![\begin{equation} \tau = \rho \nu \left[ \vec{\nabla} v + (\vec{\nabla} v)^{\rm T} - \frac{2}{3} \tens{I} \vec{\nabla} \cdot v \right]\textrm{,} \end{equation}](/articles/aa/full_html/2013/10/aa22080-13/aa22080-13-eq34.png) (6)where ν is the kinematic viscosity and I is the identity matrix. We account for the magnetic resistivity in Eq. (3) through the flux
(6)where ν is the kinematic viscosity and I is the identity matrix. We account for the magnetic resistivity in Eq. (3) through the flux 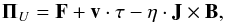 (7)where F is the thermal conduction flux. In the classical regime, the thermal conduction flux is given by Orlando et al. (2008).
(7)where F is the thermal conduction flux. In the classical regime, the thermal conduction flux is given by Orlando et al. (2008).
We define our primitive variables, so that the simulation density ρ is given in terms of the ISM density ρ0 = μHnH, where nH = 0.03 cm-3 and the pressure p is given in units of 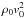 . Our jet density is equal to 5ρ0 to simulate a cooler AGB outflow to the ISM.
. Our jet density is equal to 5ρ0 to simulate a cooler AGB outflow to the ISM.
We study the cases of HD and MHD fluids both with and without cooling. We also performed simulations with explicit resistive MHD. The HD test cases are two dimensional in a Cartesian system of 800 × 200 cells with 6.17 × 1015 cm on each side. This yields a computational domain equivalent to 1.6 × 0.4 pc. Magnetic monopole control is dealt with the 8-wave MHD formulation. Where we study cooling, we invoke simplified exponential cooling function of the form 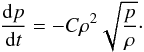 (8)The constant C is
(8)The constant C is 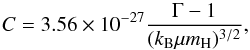 (9)where Γ is the adiabatic constant, kB is Boltzmann’s constant, μ is the mean molecular weight, and mH is the mass of the hydrogen atom.
(9)where Γ is the adiabatic constant, kB is Boltzmann’s constant, μ is the mean molecular weight, and mH is the mass of the hydrogen atom.
PLUTO also includes a simplified model for radiative cooling that evolves only the hydrogen ionization fraction. This is the simplified nonequilibrium cooling model (SNEq). A full description of this model is given by Teşileanu et al. (2008) and references therein. The SNEq simulates the emission of 17 lines, the two-photon continuum, and ionization/recombination radiative losses, but only the ionization of H is evolved in the integration. The other ion abundances are fixed through charge-transfer to the H ionization. Teşileanu et al. (2008) find that the SNEq cannot represent radiative losses accurately above 3 × 104 K because it lacks higher ionization stages. This may give us a limit to the validity of some of our simulations. However, Teşileanu et al. (2008) found that even the simple cooling function SNEq is a much better approximation than losses from a tabulated cooling process for a preliminary dynamical study at lower temperatures, such as the one found in Raymond et al. (1976). This also reduces the computational costs of our simulations.
Where we use the MHD modules, the magnetic field is given in units of 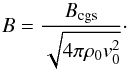 (10)The B-field of the ISM and the Local Bubble is initially set at B ≈ 5 μG, which is the expected value for an ordered field in the pertinent region (Wielebinski & Krause 1993). The field for the jet itself is in equipartition with its pressure. This is because weak magnetic fields can be amplified under the presence of an external mechanism (i.e., the passage of Mira into the Local Bubble) to reduce the compressional effect of shock waves in a field, so that it reaches a value of B2/(8π) ~ p (Helfer 1953). The orientation of both of these fields is along the y-axis perpendicular to the direction of the main shock.
(10)The B-field of the ISM and the Local Bubble is initially set at B ≈ 5 μG, which is the expected value for an ordered field in the pertinent region (Wielebinski & Krause 1993). The field for the jet itself is in equipartition with its pressure. This is because weak magnetic fields can be amplified under the presence of an external mechanism (i.e., the passage of Mira into the Local Bubble) to reduce the compressional effect of shock waves in a field, so that it reaches a value of B2/(8π) ~ p (Helfer 1953). The orientation of both of these fields is along the y-axis perpendicular to the direction of the main shock.
3. Results
We completed a set of simulations for a stellar outflow as it transitions from a warm dense medium to a hot tenuous medium using a HD model (with and without cooling) and an MHD model (with and without cooling). Figure 2 shows the simulations shortly after the shock has overtaken the stellar jet. We see a shock front as a region of high density that gradually overtakes the star. The jet from the star is pushed back by the shock and upstream wind. There is a streamline flow over the jet that creates a vortex of low pressure and density immediately behind the jet (0.3 pc in the simulation scale). If we think of Mira’s tail as a record not only of mass loss but also of the conditions in the ISM-Local Bubble, we can identify regions on the tail that hold structures that represent different dynamical epochs in Mira’s trajectory. For instance there is a loop of ejected material located 22′ north of Mira, which extends 6.3′ west from the north-south path of Mira’s tail in the UV images from Martin et al. (2007). This structure is similar to the one observed in the simulation.
Farther down, ram-pressure stripped material creates a high-pressure, high-density region at the axis of the simulation and the base of the shock (0.7 pc). Earlier in the simulation, this region at the base of the shock had a higher density and pressure than that of the shock structure. Thus, material begins to propagate upward perpendicular to the shock velocity vector. There is an analogous structure in Mira’s tail. About 31′ north of Mira there is a beam-like feature 9′24′′ west of the north-south cometary tail. We claim that this feature is a shock structure in the transition region from the ISM to the Local Bubble. This shock has been enriched with ram-stripped material as per the simulations. Wareing (2012) has noted that this region is a “kink” in the tail, which the author has modeled as a region of ISM-Local Bubble transition. Although this could be the main shock between the Local Bubble and the ISM, it is possible that the Local Bubble has been carved out of the ISM by at least one, if not more SNe, and that multiple shock regions could mark the boundary of the Local Bubble in the process of expansion. If so, this would help explain the gaps in the tail (at 1°10′ and 1°27′), which could either be previous shock encounters or represent a period of low mass ejection by Mira.
We also need to explain the gross structure of the shocked region of the HD vs. MHD simulations. Consider the formulation of de Hoffmann & Teller (1950) in the shock frame, where v1 is the flow speed into the shock and v2 is the flow out (on the opposite side.) Thus the total pressure for a non-relativistic perpendicular shock to B is given by 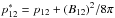 . When applied to the Rankine-Hugoniot equations, one obtains
. When applied to the Rankine-Hugoniot equations, one obtains ![\begin{equation} v_1-v_2=\left[ (p_2^*-p_1^*) \left( \frac{1}{\rho_1}-\frac{1}{\rho_2} \right) \right]\cdot \end{equation}](/articles/aa/full_html/2013/10/aa22080-13/aa22080-13-eq64.png) (11)The consequence of this relation is that there is a greater velocity difference between the upstream and the downstream flows from the shock. It follows then that the region of shocked material (between the forward and reverse shock) would be larger in the MHD case. This also allows for a larger region of expansion for high pressure material close to the axis of the simulation. The effect of having a magnetic field is to enrich the main shock structure with multiple magnetosonic shocks propagating perpendicularly to the direction of the main shock. Each is enriched with a substantial fraction of the density of the jet (see Fig. 2). It is important to note that there is little effect of cooling in the MHD simulation, as the magnetic pressure component supports these structures even when there is a loss of hydrodynamic pressure as shown in Fig. 3.
(11)The consequence of this relation is that there is a greater velocity difference between the upstream and the downstream flows from the shock. It follows then that the region of shocked material (between the forward and reverse shock) would be larger in the MHD case. This also allows for a larger region of expansion for high pressure material close to the axis of the simulation. The effect of having a magnetic field is to enrich the main shock structure with multiple magnetosonic shocks propagating perpendicularly to the direction of the main shock. Each is enriched with a substantial fraction of the density of the jet (see Fig. 2). It is important to note that there is little effect of cooling in the MHD simulation, as the magnetic pressure component supports these structures even when there is a loss of hydrodynamic pressure as shown in Fig. 3.
 |
Fig. 2 2D hydrodynamic simulations showing the density in units of 7.9 × 10-25 gm/cm3 (ISM densities). The top corresponds to a hydrodynamic simulation without cooling. The second shows the simulation with a powerlaw cooling. The third shows a magnetohydrodynamic simulation without cooling. The bottom figure corresponds to an MHD simulation with a power law cooling. The figures correspond to 30, 26, 31 and 31 kyrs after Mira has entered the Local Bubble. |
 |
Fig. 3 2D hydrodynamic simulations showing the pressure in units of 6.6 × 10-13 erg/cm3 (ISM densities). The top corresponds to a hydrodynamic simulation without cooling. The second shows the simulation with a powerlaw cooling. The third shows a magnetohydrodynamic simulation without cooling. The bottom figure corresponds to an MHD simulation with a power law cooling. The figures correspond to 30, 26, 31 and 31 kyr after Mira has entered the Local Bubble. |
As the main shock propagates away from the jet, we see that ram-pressure stripped material of high density in its wake forms turbulent filaments close to the axis of the simulation. The turbulence is also clear in Fig. 4, which shows the density, pressure and x-velocity of the system at 61 kyr of evolution. The jet of the star has ejected turbulent, high-density vortices into the tenuous medium, which extend 0.3 pc from the injection point. For comparison, this bend is reminiscent of the head-tail structure found in FR I radio sources like NGC 1265. This is far too large a structure from what is seen by GALEX or IR observations. In its wake, we see turbulent filamentary structures akin to those found by Esquivel et al. (2010).
 |
Fig. 4 2D hydrodynamic simulation with no cooling after 61 kyr showing the logarithm of density in units of 7.9 × 10-25 gm/cm3 and logarithm of pressure in units of 6.6 × 10-13 erg/cm3. |
Once exponential cooling is included, we obtain a more condensed system. Figure 5 shows the simulation density after an integration of 61 kyr. The shock has exited the computational domain and left a narrower astrosheath. As expected, the cooling has allowed the stripped high-density gas filaments to condense into narrower structures in pressure balance with the Local Bubble medium. The jet material has condensed two high density knots about 10-2 pc wide. The cometary tail has become less turbulent but is also less substantial.
 |
Fig. 5 2D hydrodynamic simulation with simplified exponential cooling after 61 kyr showing the logarithm of density in units of 7.9 × 10-25 gm/cm3 and logarithm of pressure in units of 6.6 × 10-13 erg/cm3. |
 |
Fig. 6 2.5D magnetohydrodynamic simulation with resistivity and simplified exponential cooling after 88 kyr showing the logarithm of density in units of 7.9 × 10-25 gm/cm3 (ISM density) and logarithm of pressure in units of 6.6 × 10-13 erg/cm3. The jet is Mach 0.75. |
We also conducted a set of MHD simulations without any cooling, which are not shown. The results showed a very narrow sheet with no turbulence and a smooth magnetic field structure that connected the jet outflow with the shock even after t > 50 kyrs. We regard this set of simulations as physically unrealistic as we expect significant radiative losses from thermalized electrons interacting with ions. Thus, we need to account for cooling and resistivity in the flow.
Figure 6 shows an MHD simulation with resistivity and simplified exponential cooling at 88 kyr after the shock has passed over the jet. Here we see dense filaments that extend 1 pc downstream from the jet and almost 0.4 pc from the axis. These remain connected to the jet. The filaments lie at the boundary between alternating low and high pressure sheets.
Figure 7 shows an MHD simulation with resistivity and SNEq after 79 kyr. The filaments end in dense globules of low pressure. The filamentary structure is narrower with a maximum extent of 0.2 pc from the simulation axis. In SNEq, the filaments have less pressure support and thus are more confined. The temperature of the jet and the filaments have a value of 104 K, which helps justify a posteriori the use of SNEq. However, the Local Bubble medium has a temperature in excess of 106 K, which the module is not able to simulate properly. Nevertheless, this medium has low density, so it seems unlikely that radiative losses are important. The issue then becomes what to make of the boundary between the filaments and the medium.
 |
Fig. 7 2.5D magnetohydrodynamic simulation with resistivity and simplified, non-equilibrium cooling after 79 kyr showing the logarithm of density in units of 7.9 × 10-25 gm/cm3 (ISM densities) and logarithm of pressure in units of 6.6 × 10-13 erg/cm3. The jet is Mach 0.75. |
4. Discussion
Previous simulations by Wareing et al. (2007) and Esquivel et al. (2010) show that the tail structures in the hot, low-density medium of the Local Bubble are very turbulent unlike the collimated appearance of the observed tail. When we compare our simulations of HD with an MHD with cooling, we find the MHD filamentary structure much more akin to the collimated structure of the jet. We even find that we can reproduce the filament found at 22′ north of Mira, which is not found in previous simulations.
Wareing et al. (2007) have noted that their simulated temperatures dropped rapidly along the tail, which means that the driving mechanism for the FUV emission may be no longer present to support emission through the extended lifetime and length of the tail. We did not extend our simulations through the length of the tail but do see that the temperature of the filaments remains constant up to 1.5 pc in the MHD-SNEq case. In Fig. 9, we observe the temperature profile over the axis of the tail. Dips in the profile correspond to high-density, low temperature filaments. Peaks correspond to gaps in the filaments where the low-density, high-pressure Local Bubble medium shows through. We can compare this to the HD-Exponential Cooling simulation where we are left with a sparse set of nodules for which emission could take place because of the anisotropy in Mira’s material ejection. Figure 8 shows this in the temperature profile along the axis.
The simulations also demonstrate how one could have extended emission from the tail. Wareing (2012) concludes that the passage into the Local Bubble may lead to reheating of tail material via over-pressure. Thus the FUV emission would be thermally driven by compression effect rather than bow-shock heating. To this picture we want to add that MHD provides a means by which jet kinetic energy and magnetic energy in the shock can be converted into FUV emission. Even when resistivity is included in MHD simulations, we do not see a precipitous drop in the temperature meaning that the cooling lifetime is longer than the dynamical time. We conclude that emission can be sustained through the first few pc after the tail has crossed a shock. Indeed ohmic losses provide one channel by which thermal energy in the tail interact with shock magnetic fields to heat the plasma and power the FUV emission.
We then face the issue of the nature of the emission process. As seen in Figs. 9 and 8, even the cool, high-density filaments have temperatures of ~104 K, which is at the point of disassociation for molecular hydrogen. Yet, it is electron collisions with H2 that is claimed to be the mechanism for UV emission. Given the temperature, we can suggest an alternative emission process through C0 excitation through electron impact.
 |
Fig. 8 Temperature versus distance from the edge of the grid for an HD simulation with exponential cooling. |
 |
Fig. 9 Temperature versus distance from the edge of the grid for an MHD simulation with SNEq cooling. |
Let us consider the CI3P–1D transition and an ionization rate that gives the electron density compared to the particle density as ne ~ n = 1 cm-3. We assume that the fractional abundance of C in terms of hydrogen is n(C0)/n = 4 × 10-4, the cosmic abundance, given by Aller (1961). We are also given an electron temperature of Te ≈ 104 K. With the radiative cooling rate integrated over the spectrum as given by Flower et al. (1986) (and references therein), we thus have 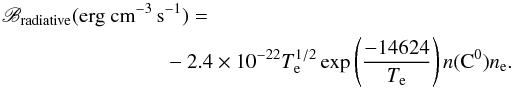 (12)We obtain a luminosity per unit volume of 6 × 10-25 erg cm-3 s-1. This is a lower limit. The temperatures in the simulations can go higher, and we can expect some mixing of Local Bubble electrons with the electrons in the shock and filament region. We also expect a higher ratio for the fractional abundance of C in the AGB ejecta.
(12)We obtain a luminosity per unit volume of 6 × 10-25 erg cm-3 s-1. This is a lower limit. The temperatures in the simulations can go higher, and we can expect some mixing of Local Bubble electrons with the electrons in the shock and filament region. We also expect a higher ratio for the fractional abundance of C in the AGB ejecta.
We now consider the total luminosity of Mira’s cometary shock region with a volume of 0.4 × 0.4 × 1 pc. Over this volume, the total luminosity is L~ 2 × 1030 erg s-1 , which is within the order of magnitude of the luminosity of the bow shock region given by Martin et al. (2007). It is also true that the SNEq simulates the emission of the two-photon continuum, which includes the FUV spectrum. A more complete analysis with detailed evolution of multi-ion species is needed to understand this process and will be the subject of more research.
5. Conclusions
We conducted a numerical simulation study of the 4-degree cometary tail of the AGB star Mira to explain its FUV emission. We used a two-wind model with a shock interface. To carry out our simulations, we used the PLUTO code with adaptive mesh refinement with an asymmetric stellar outflow from Mira when it transitions from a warm dense medium of the ISM to a hot tenuous medium of the Local Bubble. The simulations were carried out using a HD model and an MHD model. We considered each case with and without cooling. Where cooling was considered, we invoked a simplified exponential cooling function or an SNEq model. The resistivity was also utilized to account for the coupling of shock magnetic energy to thermal energy. Here, we considered the case of ram-pressure stripped material that has been ejected after Mira has entered the Local Bubble.
In both cooling and noncooling HD simulations we find that ram-pressure stripped material forms highly turbulent filaments with a morphology that is at odds with the observed morphology of Mira’s tail. In contrast, we are able to reproduce the arching filaments and dense nodules with an MHD-SNEq simulation. We also find that these filaments are too hot for H2 molecules to exist. Thus, we suggest an alternative emission process through C0 excitation through inelastic electron collisions. Using our simulation data and the known parameters of Mira’s tail, we expect a luminosity of L~ 2 × 1030 erg s-1 through this process.
Acknowledgments
This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number OCI-1053575.
References
- Aller, L. H. 1961, The Abundances of the Elements (Interscience Publishers) [Google Scholar]
- Cargo, P., & Gallice, G. 1997, J. Comput. Phys., 136, 446 [NASA ADS] [CrossRef] [Google Scholar]
- de Hoffmann, F., & Teller, E. 1950, Phys. Rev., 80, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Esquivel, A., Raga, A. C., Cantó, J., et al. 2010, ApJ, 725, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau-des Forêts, G., & Hartquist, T. W. 1986, MNRAS, 218, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Helfer, H. L. 1953, ApJ, 117, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffleit, D. 1997, JAAVSO, 25, 115 [Google Scholar]
- Karovska, M., Hack, W., Raymond, J., & Guinan, E. 1997, ApJ, 482, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Knapp, G. R., Pourbaix, D., Platais, I., et al. 2003, A&A, 403, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Welsh, B. Y., Vergely, J. L., et al. 2003, A&A, 411, 447 [EDP Sciences] [Google Scholar]
- Martin, D. C., Seibert, M., Neill, J. D., et al. 2007, Nature, 448, 780 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Matthews, L. D., Libert, Y., Gérard, E., Le Bertre, T., & Reid, M. J. 2008, ApJ, 684, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Mauron, N., & Caux, E. 1992, A&A, 265, 711 [NASA ADS] [Google Scholar]
- Mayer, A., Jorissen, A., Kerschbaum, F., et al. 2011, A&A, 531, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meaburn, J., López, J. A., Boumis, P., et al. 2009, A&A, 500, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Zanni, C., Tzeferacos, P., et al. 2012, ApJS, 198, 7 [Google Scholar]
- Orlando, S., Bocchino, F., Reale, F., et al. 2008, ApJ, 678, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Raga, A. C., & Cantó, J. 2008, ApJ, 685, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, J. C., Cox, D. P., & Smith, B. W. 1976, ApJ, 204, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Ryde, N., Gustafsson, B., Eriksson, K., et al. 2000, ApJ, 545, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Sokoloski, J. L., & Bildsten, L. 2010, ApJ, 723, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Teşileanu, O., Mignone, A., & Massaglia, S. 2008, A&A, 488, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data, Astrophysics and Space Science Library (Dordrecht: Springer), 350 [Google Scholar]
- Villaver, E., Manchado, A., & García-Segura, G. 2012, ApJ, 748, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Wareing, C. J. 2012, ApJ, 748, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Wareing, C. J., O’Brien, T. J., & Zijlstra, A. A. 2006, MNRAS, 366, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Wareing, C. J., Zijlstra, A. A., O’Brien, T. J., & Seibert, M. 2007, ApJ, 670, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Wielebinski, R., & Krause, F. 1993, A&AR, 4, 449 [Google Scholar]
All Figures
 |
Fig. 1 Initial simulation setup for an anisotropic (jet) outflow of the star before it crosses the boundary between the Local Bubble and ISM. At this boundary, a forward shock, reverse shock, and contact discontinuity develops. |
| In the text | |
 |
Fig. 2 2D hydrodynamic simulations showing the density in units of 7.9 × 10-25 gm/cm3 (ISM densities). The top corresponds to a hydrodynamic simulation without cooling. The second shows the simulation with a powerlaw cooling. The third shows a magnetohydrodynamic simulation without cooling. The bottom figure corresponds to an MHD simulation with a power law cooling. The figures correspond to 30, 26, 31 and 31 kyrs after Mira has entered the Local Bubble. |
| In the text | |
 |
Fig. 3 2D hydrodynamic simulations showing the pressure in units of 6.6 × 10-13 erg/cm3 (ISM densities). The top corresponds to a hydrodynamic simulation without cooling. The second shows the simulation with a powerlaw cooling. The third shows a magnetohydrodynamic simulation without cooling. The bottom figure corresponds to an MHD simulation with a power law cooling. The figures correspond to 30, 26, 31 and 31 kyr after Mira has entered the Local Bubble. |
| In the text | |
 |
Fig. 4 2D hydrodynamic simulation with no cooling after 61 kyr showing the logarithm of density in units of 7.9 × 10-25 gm/cm3 and logarithm of pressure in units of 6.6 × 10-13 erg/cm3. |
| In the text | |
 |
Fig. 5 2D hydrodynamic simulation with simplified exponential cooling after 61 kyr showing the logarithm of density in units of 7.9 × 10-25 gm/cm3 and logarithm of pressure in units of 6.6 × 10-13 erg/cm3. |
| In the text | |
 |
Fig. 6 2.5D magnetohydrodynamic simulation with resistivity and simplified exponential cooling after 88 kyr showing the logarithm of density in units of 7.9 × 10-25 gm/cm3 (ISM density) and logarithm of pressure in units of 6.6 × 10-13 erg/cm3. The jet is Mach 0.75. |
| In the text | |
 |
Fig. 7 2.5D magnetohydrodynamic simulation with resistivity and simplified, non-equilibrium cooling after 79 kyr showing the logarithm of density in units of 7.9 × 10-25 gm/cm3 (ISM densities) and logarithm of pressure in units of 6.6 × 10-13 erg/cm3. The jet is Mach 0.75. |
| In the text | |
 |
Fig. 8 Temperature versus distance from the edge of the grid for an HD simulation with exponential cooling. |
| In the text | |
 |
Fig. 9 Temperature versus distance from the edge of the grid for an MHD simulation with SNEq cooling. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


