| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A70 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321365 | |
| Published online | 04 October 2013 | |
Radiative forces on macroscopic porous bodies in protoplanetary disks: laboratory experiments
Faculty of Physics, University of Duisburg-Essen, Lotharstr. 1, 47057 Duisburg, Germany
e-mail: gerhard.wurm@uni-due.de
Received: 26 February 2013
Accepted: 31 July 2013
In optically thin parts of protoplanetary disks photophoresis is a significant force not just for dust grains, but also for macroscopic bodies. The absolute strength on the supposedly highly porous objects is not known in detail as yet. We set up a low pressure torsion balance and studied photophoretic forces down to 100 nN on plates at a light flux of 100 W/m2. We investigated the dependence on plate dimensions and on ambient pressure and considered the influence of channels through the plates. As samples for full (no channel) plates we used tissue with 2 mm thickness and circular shape with diameters of 10 mm, 30 mm and 50 mm. The influence of channels was probed on rectangular-shaped circuit boards of 35 mm × 35 mm area and 1.5 mm thickness. The number of channels was 169 and 352. The pressure was varied over three decades between 0.001 and 1 mbar. At low pressure, the absolute photophoretic force is proportional to the cross section of the plates. At high pressure, gas flow through the channels enhances the photophoretic force. The pressure dependence of the radiative force can (formally) be calculated by photophoresis on particles with a characteristic length. We derived two characteristic length scales l depending on the plate radius r1, the channel radius r2, and the thickness of the plate, which equals the length of the channel d as l = r0.35 × d0.65. The highest force is found at a pressure pmax = 15 × l-1 Pa mm. In total, the photophoretic force on a plate with channels can be well described by a superposition of the two components: photophoresis due to the overall size and cross section of the plate and photophoresis due to the channels, both with their characteristic pressure dependencies. We applied these results to the transport of large solids in protoplanetary disks and found that the influence of porosity on the photophoretic force can reverse the inward drift of large solids, for instance meter-sized bodies, and push them outward within the optically thin parts of the disk.
Key words: solid state: refractory / accretion, accretion disks / hydrodynamics / methods: laboratory / protoplanetary disks / planets and satellites: formation
© ESO, 2013
1. Introduction
For the past several years photophoretic forces have been considered to influence particle transport in protoplanetary disks (Krauss & Wurm 2005; Wurm & Krauss 2006; Herrmann & Krivov 2007; Krauss et al. 2007; Mousis et al. 2007; Takeuchi & Krauss 2008; Wurm & Haack 2009b,a; Moudens et al. 2011; von Borstel & Blum 2012; de Beule et al. 2013). Whenever particles embedded in a gaseous environment are illuminated and absorb some of the radiation, the temperature gradient along the particle and the interaction with gas molecules leads to a force that – in most cases – is directed away from the light source. A particle motion induced by such radiometric forces is commonly called photophoresis (Ehrenhaft 1918; Rohatschek 1995).
The strength of photophoresis on cm-size particles is easily demonstrated by a Crookes radiometer (Crookes 1874) and can be a factor of 100 higher than stellar gravity for 1 Pa pressure (Krauss & Wurm 2005). Supported by photophoresis, large bodies drifting inward would slow down or even reverse motion close to the inner edge of a disk and move outward as shown below.
Unfortunately, the complexity of photophoresis increases with the complexity of particle shapes. Large objects in protoplanetary disks for instance are highly porous (Meisner et al. 2012). Collisions of larger aggregates might also lead to macroporosity of large objects (Kothe et al. 2013). The question therefore is how such large complex bodies react when they are subjected to photophoresis. Is an individual constituent of an aggregate important, or does the whole aggregate set the radiative force at a given ambient gas pressure? Do large pores or channels through an aggregate increase or decrease the photophoretic force, and if so, in which pressure range?
Temperature gradients across a particle can lead to thermal creep (gas flow) through channels (Alexeenko et al. 2006; Vargo et al. 1999; Knudsen 1909; Muntz et al. 2002; Han et al. 2007). This increases the photophoretic force on the particle in certain pressure ranges that have been studied for instance by Kuepper et al. (2013) under microgravity or in this work. This paper is a first attempt at quantifying the influence of channels of a given size through a larger body on the photophoretic force in a systematic way. The idea of photophoresis for large (macro)-porous bodies is sketched in Fig. 1 (see text below for details of the specific regimes sketched).
 |
Fig. 1 Idea of photophoretic force enhancement by channels and macro pores, a) low pressure: only the real cross-sectional area counts, individual molecule collisions and momentum transfer; b) intermediate pressure: thermal creep in channels leads to increase of pressure at warm side; c) high pressure: thermal creep only acts close to the inner channel walls; pressure increase can be balanced more easily by back flow through the center part of the channel; d) thermal creep in more realistic porous bodies in protoplanetary disks (dust aggregates, chondrule aggregates, larger rubble piles). |
To quantify this we set up a torsion balance to measure the photophoretic force on cm-size plates with and without channels and characterized the pressure dependence of the photophoretic force. In a first application we show the significance of pores for transport in protoplanetary disks.
2. Photophoresis
Photophoresis for spherical particles has been considered in detail for the whole range of ambient pressure from the free molecular flow regime at low pressure to hydrodynamic flow at high pressure (Beresnev et al. 1993; Rohatschek 1995). Spherical particles have the advantage that only one size, the particle radius a enters. A semi-empirical description for photophoresis over the whole pressure range has been worked out by Rohatschek (1995) for a perfectly absorbing sphere given as 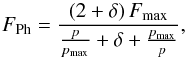 (1)with
(1)with
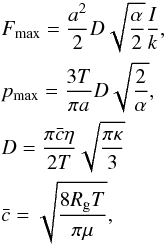 (2)where a is the particle radius, I is the radiant flux density, T is the gas temperature, p is the gas pressure, k is the thermal conductivity of the particle, α is the thermal accomodition coefficient, which is often assumed to be 1, η is the viscosity of the gas, κ is the thermal creep coefficient, which has a value of 1.14 (Rohatschek 1995), Rg is the universal gas constant, and μ is the molar mass of the gas particles. δ is a free parameter on the order of | δ | ≤ 1 to connect the low-pressure and high-pressure range in different models. For different experimental settings it can be regarded as a free empirical parameter. However, it mostly influences the width of the transition around pmax. It does not change the position of the maximum, though.
(2)where a is the particle radius, I is the radiant flux density, T is the gas temperature, p is the gas pressure, k is the thermal conductivity of the particle, α is the thermal accomodition coefficient, which is often assumed to be 1, η is the viscosity of the gas, κ is the thermal creep coefficient, which has a value of 1.14 (Rohatschek 1995), Rg is the universal gas constant, and μ is the molar mass of the gas particles. δ is a free parameter on the order of | δ | ≤ 1 to connect the low-pressure and high-pressure range in different models. For different experimental settings it can be regarded as a free empirical parameter. However, it mostly influences the width of the transition around pmax. It does not change the position of the maximum, though.
 |
Fig. 2 Sketch of the pendulum setup. |
The transition occuring at pmax can also be illustrated in another way. For this we refer to the Knudsen number, which is defined as Kn = λ/a, where λ is the mean free path of the gas molecules. It ist not immediately evident in Eq. (2), but the pressure pmax roughly coincides with Kn = 1. Therefore, the strongest effect is given at a pressure where the mean free path of the gas molecules equals the size of the particles. This view leads to a more natural division in low- and high-pressure region. The right hand part of the denominator in Eq. (1) or pmax/p dominates at a pressure much lower than pmax or Kn ≫ 1 and the two first terms in the denominator become negligible. The force is proportional to the pressure in that case. D, which is present in the nominator in Fmax and in the denominator in pmax, cancels out. If δ is assumed to be 0, Eq. (1) using Eq. (2) simplifies to 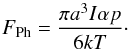 (3)The size dependence a3 in Eq. (3) has two components. a2 is showing the proportionality to the cross-section for a spherical particle. This factor can be understood at low pressure or large Knudsen numbers (Fig. 1a) as only the individual impacting gas molecule counts whose number increases linearly with cross-section; or a2 for a spherical particle. Another a-dependence in Eq. (3) comes from the temperature difference that develops from the illumination between front and back side. The thicker the particle, the larger the temperature difference, and the larger the difference in momentum transferred by gas molecules at the different cold and warm sides. To a first order the temperature difference and therefore the force is proportional to the thickness or a for a spherical particle.
(3)The size dependence a3 in Eq. (3) has two components. a2 is showing the proportionality to the cross-section for a spherical particle. This factor can be understood at low pressure or large Knudsen numbers (Fig. 1a) as only the individual impacting gas molecule counts whose number increases linearly with cross-section; or a2 for a spherical particle. Another a-dependence in Eq. (3) comes from the temperature difference that develops from the illumination between front and back side. The thicker the particle, the larger the temperature difference, and the larger the difference in momentum transferred by gas molecules at the different cold and warm sides. To a first order the temperature difference and therefore the force is proportional to the thickness or a for a spherical particle.
At high pressure net motion of gas molecules in the vicinity of a particle surface occurs. In general there is a net flow of gas from the cold side to the warm side of a non-equilibrated particle along the surface (see Fig. 1b). This is called thermal creep and also leads to a force on a particle. The fundamental physics for this force is challenging and has been debated. However, it was shown recently that the gas density builds up on the warm side due to this gas flow and pushes the particle toward the cold side (Ketsdever et al. 2012) (1b).This high-pressure region of the photophoretic force can also be approximated with respect to the ambient pressure dependence. The first term in the denominator in Eq. (1) or p/pmax dominates at a pressure much higher than pmax, the other two terms are negligible and the force decreases with pressure as 1/p in that case. The decrease with ambient pressure arises because the thickness of the layer along the surface for which thermal creep occurs is on the order of the mean free path. This constantly diminishes at higher pressure. A back flow close to this layer can equilibrate the system more easily at high pressure (Fig. 1c). This already leads to the second group of particles, which have been studied over the past 100 years, the plates (Ketsdever et al. 2012). For plates a similar pressure dependence as in Eq. (1) has been suggested, that is, in the free molecular flow regime the pressure enters linearly (~p) (Ketsdever et al. 2012). In the hydrodynamic regime it enters as ~1/p. However, for plates the maximum force pressure is not straightforward to define because it is a priori unclear which size enters, or in other words, the question might be which value to use for the Knudsen number marking the transition.
The plate diameter is relatively large compared with the thickness, and choosing one value or the other will change the Knudsen number by one or more orders of magnitude. The situation even deteriorates for a plate with channels that introduce another size, namely the diameter of the channel.
Experiments dedicated to the pressure dependence of radiative forces on plates have been carried out by Selden et al. (2009). The authors measured a transition (maximum force) at 4 to 6 × 10-3 mbar for plates heated not by light, but electrically. Two circular plates with diameters of 8.6 and 11.1 cm, and a rectangular plate with the same surface area as the bigger disk with dimensions of 7.62 × 12.7 cm2 were studied, all with a thickness of 0.95 cm. As seen below, the ambient force maxima pressure found by these authors fits the characteristic size defined by our experiments here.
The photophoretic force is low at very low as well as at very high pressure. However, the important point is that it has a maximum at an ambient pressure related to typical size scales of a particle. If there are several prominent size scales that vary by orders of magnitude, photophoretic forces will have different maxima. A significant force can still be related to an inner size scale (pore) at a given pressure even if the overall size of an aggregate would suggest only a small contribution.
3. Experiments
We carried out experiments similar to those of Selden et al. (2009), but heated the samples by light and extended the studies to plates with channels.
3.1. Setup
To measure the photophoretic forces we developed a torsion balance inside a vacuum chamber that could be evacuated down to 1 × 10-3 mbar. The pendulum was fixed with an electric magnet and when switched off, a camera recorded its movement. A marker at the end of the pendulum was observed to trace its motion. Image analysis and averging over the marker pixels gives the deflection of the pendulum at a given time to a precision of 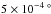 . Knowing the elastic modulus of the torsion wire and the moment of inertia, we can calculate the force acting on the sample by measuring the acceleration of the pendulum. We determined the parameters of the pendulum prior to the experiments. With this setup we reached a resolution of 100 nN. A sketch of the setup is given in Fig. 2.
. Knowing the elastic modulus of the torsion wire and the moment of inertia, we can calculate the force acting on the sample by measuring the acceleration of the pendulum. We determined the parameters of the pendulum prior to the experiments. With this setup we reached a resolution of 100 nN. A sketch of the setup is given in Fig. 2.
The sample was illuminated by a halogen lamp. The light was shaped by a single lens to achieve a uniform parallel light flux across the plates. The flux density at the position of the sample was measured to about 100 W/m2. To adjust the pressure we used a metering valve, beginning at the lowest pressure and increasing the pressure inside the camber.
3.2. Samples
3.2.1. Tissue plates
As seen from Eqs. (2) and (3) the photophoretic force depends on the thermal conductivity of the particle or plate. In general, porous materials have low thermal conductivity. Tissue plates were chosen as one sample because they are easy to handle but still have a low thermal conductivity due to their porosity. The circular plates had radii of 10, 30, and 50 mm. A microscopic view ot the tissue samples is given in Fig. 3. The individual fibres can be seen at microscopic resolution. The samples were also initially chosen in view of a potential effect of these pores on the photophoretic force. The porosity might influence the gas flow (i.e., act like channels) but the fibers of the tissue are so irregular and irregularly spaced that we did not find a well-defined pressure dependence due to the pores here, but only focused on the effect of the total plate size of the tissue.
3.3. Circuit boards
We then used two rectangular samples of circuit board with a grid of well-defined channels but reasonably low thermal conductivity. The two samples had dimensions of 35 × 35 mm2 and a thickness of 1.5 mm. The plates had 169 and 352 channels of 1 mm diameter to study the effect of well-defined channels on the photophoretic force. The plates were painted black to achieve a uniform light absorption. They are shown in Fig. 4.
4. Results
4.1. Tissue plates
The pressure-dependent force on the tissue plates is plotted in Fig. 5.
 |
Fig. 3 Microscope image of a tissue plate. |
 |
Fig. 4 Samples made of circuit board. Their dimensions are 35 × 35 × 1.5 mm3. |
 |
Fig. 5 Pressure dependence of the photophoretic force on the tissue plates. |
Selden et al. (2009) discussed the pressure dependence of the photophoretic force in terms of force per area or force per edge. The photophoretic force per area is depicted in Fig. 6. At low pressure, as expected and in agreement with Selden et al. (2009), we found a linear increase with pressure of a constant force per area.
 |
Fig. 6 Pressure dependence of the photophoretic force per area on the tissue plates. The dotted line shows the linear dependency for low pressure. |
The photophoretic force per perimeter is shown in Fig. 7. The two largest samples converge at high pressure with a force per perimeter now decreasing linearly with pressure (dotted line). This also agrees with the results by Selden et al. (2009). While the third plate converged well with the other two plates at low pressure for the force per area, it is somewhat shifted to lower values here. It has to be noted that this was the smallest plate. Because of its nature the tissue is somewhat compressible, which might be a reason for the shift. We therefore attribute the deviation to the specific sample. This is probably no general trend with plate size, but we cannot specify this in more detail at this point.
 |
Fig. 7 Pressure dependence of the photophoretic force per perimeter on the tissue plates; The line shows a linear dependency at high pressure for the two large samples converging. |
For a spherical particle the photophoretic force depends on the pressure according to Eq. (1). Here, pmax for a spherical particle depends inversely on the radius of the sphere. To test if a plate can be described by a typical size as well, we used Eq. (1) and determined a pressure pmax of the maximum force (Fig. 8). Despite the two different size scales present in a plate (diameter and thickness), the fit describes the transition regime very well.
 |
Fig. 8 Pressure dependence fitted by Eq. (1) (dotted line). Only data points with at least two thirds of the peak value were considered for the fit (solid line) to reduced the chance of including other effects (convection, etc.). |
4.2. Circuit boards
The data on the circuit boards are displayed in Fig. 9. At pressure higher than 10-1 mbar the force on the plate with the larger number of channels is significantly increased. To separate the contributions from the whole plate and the channels, we took the following approach:
We first calculated the difference between the two channel plates. We attributed this difference (increase) to the presence of 183 more channels in the second plate. We considered that a whole plate (not available for measurements) would also differ by the contributions of 169 channels to the plate with 169 channels. Therefore, we constructed an artificial dataset for a whole plate without channels, subtracting the difference again (in detail 169/183 of it) from the dataset of the 169-channel plate. These data were fitted by Eq. (1) in analogy to the tissue plates. This whole procedure was only carried out to obtain the best value for the pressure at the force maximum due to the total plate size. We then assumed the resulting pressure to be fixed to describe the pressure dependence on the total plate size for the two channel plates.
We added a second function according to Eq. (1) to model the contribution of the channels. Because the channels in the two plates have the same dimensions and only differ in their number, the position of the pressure for the maximum force should be the same in both cases and only the absolute value of the force should vary. With these assumptions we gained the overall fits plotted in Fig. 9. The channels give an additional force at a different pressure.
 |
Fig. 9 Forces measured for channel plates (F169 and F352) and extrapolated to a channel-less plate (F0). The thick lines are the sum of the associated thin lines of the two component fits. The thick solid line is the fit of the extrapolated force for a plate without channels. |
The magnitude of the two contributions can be compared with the plate area and the perimeter length of the according samples, which is listed in Table 1. For the total cross-section the channel cross-sections are subtracted from the total plate area. For the perimeter every channel perimeter is added to the outer perimeter of the plate.
Relations between force maxima, cross sections, and perimeters.
The low-pressure maximum Fmax,P scales with the plate cross-section. Here, the only influence of the channels is to decrease the total cross-section. The total perimeter is not important in the low-pressure data. The magnitude of the force attributed to the channels Fmax,C scales linearly with the number of channels. The higher the number of channels, the stronger the force.
4.3. Pressure of maximum force
The data give different values of the pressure at which the force is at maximum. The position of the maximum force differs stongly with changing dimensions of the samples. We estimate here if a potential systematic description of the maximum force pressure is possible. The following data points of different sized samples can be considered:
-
cylindrical tissue plates;
-
square circuit boards;
-
cylindrical channels within the circuit boards;
-
data on square plates reported by Selden et al. (2009);
-
two data points from glass plates consisting of sintered microspheres studied in microgravity experiments by Kuepper et al. (2013).
We began with the most simple relation known for spherical particles, given as pmax ~ a-1, where a is the particle radius (Rohatschek 1995). Because non-spherical particles do not have a single dimension, but the fits describing them are consistent with the description based on a single parameter, i.e. pmax, there should be one characteristic length l, so that pmax ~ l-1.
For the cylindrical plates there are two dimensions to consider, radius and thickness. To maintain the overall dimension of a length and obtain a comparable quantity we used a weighted geometric mean of radius r and thickness d with the form 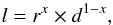 (4)where 0 < x < 1 is a parameter to deduce from the experimental data. The plates are rectangular, but Selden et al. (2009) found that the force on circular plates and rectangular plates with the same area are subject to the same force, therefore we used the radius of a circle with the same area. For the size for the plates consisting of sintered glass spheres by Kuepper et al. (2013) we used the total plate radius. For the channel size of the sintered plate we used the radius of the constituent spheres, which approximately equals the typcial size of the pores. This is not quite as well defined in dimensions as the channels in our experiments. The fitted parameters did not change significantly, when we left these data out. In total, a value of x = 0.35 was obtained by a least-squares fit, as depicted in Fig. 10.
(4)where 0 < x < 1 is a parameter to deduce from the experimental data. The plates are rectangular, but Selden et al. (2009) found that the force on circular plates and rectangular plates with the same area are subject to the same force, therefore we used the radius of a circle with the same area. For the size for the plates consisting of sintered glass spheres by Kuepper et al. (2013) we used the total plate radius. For the channel size of the sintered plate we used the radius of the constituent spheres, which approximately equals the typcial size of the pores. This is not quite as well defined in dimensions as the channels in our experiments. The fitted parameters did not change significantly, when we left these data out. In total, a value of x = 0.35 was obtained by a least-squares fit, as depicted in Fig. 10.
 |
Fig. 10 Maximum forces pressure for various samples with respect to the characteristic length. The solid line is a fit of the form pmax = 1/l. The dashed line shows the calculated position of the maximum force by Eq. (2). triangles: data taken from Selden et al. (2009); diamonds: data taken from Kuepper et al. (2013). |
For the given experimental data we derive the fit 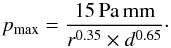 (5)From Eq. (2) we can obtain the position of the maximum force for spherical particles, and using the calculated characteristic length, we can compare this with our measurements. For these calculations we used T = 296 K, R = 8.3 J/(mol K), M = 29 g/mol and η = 1.8 × 10-5 Pa s. In this case the calculated proportionality constant is 19.4 Pa mm.
(5)From Eq. (2) we can obtain the position of the maximum force for spherical particles, and using the calculated characteristic length, we can compare this with our measurements. For these calculations we used T = 296 K, R = 8.3 J/(mol K), M = 29 g/mol and η = 1.8 × 10-5 Pa s. In this case the calculated proportionality constant is 19.4 Pa mm.
Obviously, the photophoretic forces on plates and channels can (at least formally) be clearly quantified by one scheme for a characteristic size. Especially for the channels considered as kind of inverse plates this was not necessarily to be expected.
5. Motion of large porous bodies in protoplanetary disks
The experiments show that in the simplest version the photophoretic force on large and highly porous bodies is a superposition of two photophoretic forces:
-
a force related to the total size;
-
a force related to the pores or building-block size.
The important point is that both forces have the characteristic pressure dependence related to the relevant size and their strength peaks at different pressure, and, therefore, it peaks at different radial distances to the star. The scaling of both forces relative to each other, fs, will depend on the details of the inner structure of the porous bodies. These findings can be applied to protoplanetary disks if the force is written as the sum of two equations of the Rohatschek type (Eq. (1)). For the subsequent application we assumed the parameter δ, which is small, to be 0 and introduced the above-mentioned scale factor fs to describe the fraction of the force attributed to the pores related to the force attributed to the total size, or 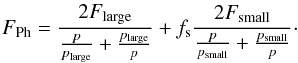 (6)Here, large refers to the overall size of the body. Small relates to the pore size or size of the building blocks. Other parameters can be taken from Eq. (2).
(6)Here, large refers to the overall size of the body. Small relates to the pore size or size of the building blocks. Other parameters can be taken from Eq. (2).
To see the significance of each of the two components and the difference introduced by porosity we considered the drift of large bodies in a protoplanetary disk caused by photophoretic force, gravity, and gas drag. We mostly followed the work by Weidenschilling (1977).
The difference of the transversal motion of the gas with respect to Keplerian speed can be considered in terms of a residual gravity for solids Δg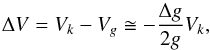 (7)where Vk is the Kepler velocity and Vg the gas velocity. For a disk where the pressure (locally) decreases by a power law p = p0r− n, the residual gravitational acceleration can be expressed as
(7)where Vk is the Kepler velocity and Vg the gas velocity. For a disk where the pressure (locally) decreases by a power law p = p0r− n, the residual gravitational acceleration can be expressed as 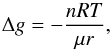 (8)where μ is the molecular weight of the gas and R the gas constant. Note that Δg < 0 means inward drift. When we add photophoresis, we obtain a radial acceleration
(8)where μ is the molecular weight of the gas and R the gas constant. Note that Δg < 0 means inward drift. When we add photophoresis, we obtain a radial acceleration 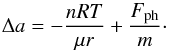 (9)In equilibrium, this acceleration on a particle is balanced by the gas drag force FD. The radial inward drift velocity u and the transversal drift velocity w with respect to the gas add to the total relative motion with respect to the gas of
(9)In equilibrium, this acceleration on a particle is balanced by the gas drag force FD. The radial inward drift velocity u and the transversal drift velocity w with respect to the gas add to the total relative motion with respect to the gas of 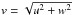 . Following Weidenschilling (1977) this is
. Following Weidenschilling (1977) this is 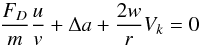 (10)and
(10)and 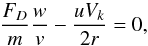 (11)which yields for u
(11)which yields for u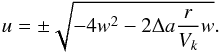 (12)Inserting Eq. (12) into Eq. (11), one obtains an equation for w. This equation depends on the assumed drag law for FD. The drag law itself depends on the solution of the equation. To solve this consistently, the solutions for all drag laws were calculated and the appropriate solution was chosen. Table 2 summarizes the used drag laws and the conditions for their validity. There are two modifications with respect to the aproach Weidenschilling (1977) used.
(12)Inserting Eq. (12) into Eq. (11), one obtains an equation for w. This equation depends on the assumed drag law for FD. The drag law itself depends on the solution of the equation. To solve this consistently, the solutions for all drag laws were calculated and the appropriate solution was chosen. Table 2 summarizes the used drag laws and the conditions for their validity. There are two modifications with respect to the aproach Weidenschilling (1977) used.
First, for some parameters, the drift velocities and Reynolds numbers become high. To smooth the transition between the Epstein to the Newtonian regime we calculated the point where both drag forces are equal and located the transition there. Second, for some parameters no self-consistent solution was obtained when the Reynolds number was only slightly larger than 1. This is also due to the choice of four drag forces, which do not connect smoothly. In this cases the Stokes regime was used even though the Reynolds number increased to 40. These adaptations do not change the basic results.
Drag laws.
We used these equations to calculate the radial drift velocity of bodies of 1 cm, 1 dm, 1 m, and 10 m. Without photophoresis and applying the Weidenschilling (1977) nebula model we obtained the same results as Weidenschilling (1977), except that our two modifications smooth the transition regions between different drag regimes (not plotted here). Using the minimum mass solar nebula by Hayashi et al. (1985), we derived Figs. 11 and 12. In this first application we fixed the small size scale at 1 mm radius, which in view of abundant mm-chondrules in primitive meteorites is at least one reasonable choice and useful as an example to show the influence of the pore size scale.
 |
Fig. 11 Drift of different sized non-porous bodies in protoplanetary disks (minimum mass solar nebula). Dashed line: without photophoresis, solid line: with photophoresis. |
 |
Fig. 12 Drift of differently sized bodies including porosity. Upper dashed line: non-porous bodies including photophoresis (as Fig. 11), lower lines: with second photophoretic term attributed to the pores. We assumed the photophoretic strength ratio fs to be 0.1 or 1. |
As can be seen, introducing porosity has a strong effect. At 1 AU, for instance, it can change the sign of the drift and move meter-sized bodies outward, which are otherwise often considered to be problematic because of their large inward drift. This concept holds for other sizes as well. A ten-meter-body, however, is not influenced much by photophoresis, regardless of wheather it has mm-pores.
We note that these calculations are only applicable in optically thin environments. This might occur at later times, before disk dispersal, but probably the gas density is also lower then. The other active photophoretic site is close to the illuminated inner edge of protoplanetary disks, where photophoresis is always acting. In this case photophoresis and pores will lead to a sorting of bodies in the transition zone between optically thin and optically thick outward parts of the disk. However, the calculations clearly show the strength of photophoresis itself and especially the effect of the pores, which for instance supports meter-sized bodies, which are assumed to drift fastest without photophoretic support.
6. Conclusions
With measurements of the force acting on plates with a torsion balance, we were able to quantify the photophoretic force and to distinguish the photophoretic force on the whole plate from an additional force caused by channels within the plate. The magnitudes of both contributions scale with the areas of the whole plate and the area covered by the channels.
The position of the pressure at which the photophoretic force is at maximum depends on the geometric properties. For spherical particles studied in the past it is proportional to r-1 (Rohatschek 1995). We found that we can use the same simple inverse dependency, but attributing a characteristic length l to the plates and channels. This length combines the radius of the plate (channel) and the thickness as pmax ~ r-0.35 × d-0.65. The photophoretic force reaches its maximum roughly at the pressure for which the mean free path equals the characteristic length.
The measurements reported here are a first step toward modeling photophoretic transport of larger bodies in protoplanetary disks, that is at the inner edge of a disk. Because larger bodies are often ruble piles consisting of smaller units, the strength of the photophoretic force will depend on the structure of these bodies. Application to the minimum mass solar nebula showed that porosity, ideally simulated by channel plates in our experiments, can lead to a significant increase in the photophoretic force at low pressure even if the total size of the body would suggest the photophoretic force to decrease. An instructive example is the motion of meter-sized bodies – assumed to drift inward – which can be reversed by photophoretic motion, but only if porosity is taken into account.
Acknowledgments
This work is based on DFG funded projects within the research group FOR 759 and the priority program SPP 1385. Access to parabolic flights, providing data here, has been granted by ESA education within the “Fly your thesis program 2012”. We also thank the referee for the thoughtful review of this paper.
References
- Alexeenko, A. A., Gimelshein, S. F., Muntz, E. P., & Ketsdever, A. D. 2006, Int. J. Therm. Sci., 45, 1045 [CrossRef] [Google Scholar]
- Beresnev, S., Chernyak, V., & Fomyagin, G. 1993, Phys. Fluids, 5, 2043 [Google Scholar]
- Crookes, W. 1874, Proc. Phys. Soc. London, 1, 35 [CrossRef] [Google Scholar]
- de Beule, C., Kelling, T., Wurm, G., Teiser, J., & Jankowski, T. 2013, ApJ, 763, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenhaft, F. 1918, Ann. Phys., 361, 81 [CrossRef] [Google Scholar]
- Han, Y.-L., Phillip Muntz, E., Alexeenko, A., & Young, M. 2007, Nanoscale Microscale Thermophys. Eng., 11, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C., Nakazawa, K., & Nakagawa, Y. 1985, in Protostars and Planets II, eds. D. C. Black, & M. S. Matthews, 1100 [Google Scholar]
- Herrmann, F., & Krivov, A. V. 2007, A&A, 476, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ketsdever, A., Gimelshein, N., Gimelshein, S., & Selden, N. 2012, Vacuum, 86, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Knudsen, M. 1909, Ann. Phys., 336, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Kothe, S., Blum, J., Weidling, R., & Güttler, C. 2013, Icarus, 225, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Krauss, O., & Wurm, G. 2005, ApJ, 630, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Krauss, O., Wurm, G., Mousis, O., et al. 2007, A&A, 462, 977 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuepper, M., Duermann, C., & de Beule, C. G. W. 2013, MST, submitted [Google Scholar]
- Meisner, T., Wurm, G., & Teiser, J. 2012, A&A, 544, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moudens, A., Mousis, O., Petit, J.-M., et al. 2011, A&A, 531, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mousis, O., Petit, J.-M., Wurm, G., et al. 2007, A&A, 466, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muntz, E. P., Sone, Y., Aoki, K., Vargo, S., & Young, M. 2002, J. Vac. Sci. Technol. A: Vac. Surf. Films, 20, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Rohatschek, H. 1995, J. Aerosol Sci., 26, 717 [CrossRef] [Google Scholar]
- Selden, N., Ngalande, C., Gimelshein, S., et al. 2009, Phys. Rev. E, 79, 041201 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, T., & Krauss, O. 2008, ApJ, 677, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Vargo, S. E., Muntz, E. P., Shiflett, G. R., & Tang, W. C. 1999, J. Vac. Sci. Technol., 17, 2308 [NASA ADS] [CrossRef] [Google Scholar]
- von Borstel, I., & Blum, J. 2012, A&A, 548, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Wurm, G., & Haack, H. 2009a, in Cosmic Dust – Near and Far, eds. T. Henning, E. Grün, & J. Steinacker, ASP Conf. Ser., 414, 509 [Google Scholar]
- Wurm, G., & Haack, H. 2009b, Meteor. Planet. Sci., 44, 689 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wurm, G., & Krauss, O. 2006, Icarus, 180, 487 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Idea of photophoretic force enhancement by channels and macro pores, a) low pressure: only the real cross-sectional area counts, individual molecule collisions and momentum transfer; b) intermediate pressure: thermal creep in channels leads to increase of pressure at warm side; c) high pressure: thermal creep only acts close to the inner channel walls; pressure increase can be balanced more easily by back flow through the center part of the channel; d) thermal creep in more realistic porous bodies in protoplanetary disks (dust aggregates, chondrule aggregates, larger rubble piles). |
| In the text | |
 |
Fig. 2 Sketch of the pendulum setup. |
| In the text | |
 |
Fig. 3 Microscope image of a tissue plate. |
| In the text | |
 |
Fig. 4 Samples made of circuit board. Their dimensions are 35 × 35 × 1.5 mm3. |
| In the text | |
 |
Fig. 5 Pressure dependence of the photophoretic force on the tissue plates. |
| In the text | |
 |
Fig. 6 Pressure dependence of the photophoretic force per area on the tissue plates. The dotted line shows the linear dependency for low pressure. |
| In the text | |
 |
Fig. 7 Pressure dependence of the photophoretic force per perimeter on the tissue plates; The line shows a linear dependency at high pressure for the two large samples converging. |
| In the text | |
 |
Fig. 8 Pressure dependence fitted by Eq. (1) (dotted line). Only data points with at least two thirds of the peak value were considered for the fit (solid line) to reduced the chance of including other effects (convection, etc.). |
| In the text | |
 |
Fig. 9 Forces measured for channel plates (F169 and F352) and extrapolated to a channel-less plate (F0). The thick lines are the sum of the associated thin lines of the two component fits. The thick solid line is the fit of the extrapolated force for a plate without channels. |
| In the text | |
 |
Fig. 10 Maximum forces pressure for various samples with respect to the characteristic length. The solid line is a fit of the form pmax = 1/l. The dashed line shows the calculated position of the maximum force by Eq. (2). triangles: data taken from Selden et al. (2009); diamonds: data taken from Kuepper et al. (2013). |
| In the text | |
 |
Fig. 11 Drift of different sized non-porous bodies in protoplanetary disks (minimum mass solar nebula). Dashed line: without photophoresis, solid line: with photophoresis. |
| In the text | |
 |
Fig. 12 Drift of differently sized bodies including porosity. Upper dashed line: non-porous bodies including photophoresis (as Fig. 11), lower lines: with second photophoretic term attributed to the pores. We assumed the photophoretic strength ratio fs to be 0.1 or 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


