| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 11 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201220763 | |
| Published online | 27 September 2013 | |
The achromatic chessboard, a new concept of a phase shifter for nulling interferometry
V. Experimental demonstration and performance
1 LESIA, UMR 8109 CNRS, Observatoire de Paris, UVSQ, Université Paris-Diderot, 5 place J. Janssen, 92195 Meudon, France
e-mail: daniel.rouan@obspm.fr
2 LUTH, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jules Janssen, 92195 Meudon, France
3 GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jules Janssen, 92195 Meudon, France
Received: 19 November 2012
Accepted: 2 May 2013
Context. To find evidence one day of life on extra solar planets, one will have to directly detect photons of the exoplanet to obtain spectra and to look for specific spectroscopic features. One possible technique is dark fringe interferometry with several telescopes in space. This type of interferometry requires an achromatic π phase shift in one arm of an interferometer. We have already presented a concept of a quasi-achromatic phase shifter that is made of two cellular mirrors in which each cell position and phase shift is specific, so that the behavior of the null depth as a function of the wavelength is flat within a broad range.
Aims. We want to experimentally validate this concept of an achromatic phase shifter and measure its performance in two different cases: a transmissive mask, which is made in bulk optics that are machined with ion etching and a reflective one, which is made by using a commercial segmented deformable mirror that is properly controlled.
Methods. We assembled a dedicated optical bench, nicknamed DAMNED, to assess the concept and characterize its performance in the visible and to determine the limitations of this phase shifter. We analyze its performance by comparing the experimental results with a numerical instrument model.
Results. We tested several transmissive masks and a reflective one. We reached an attenuation of about 2 × 10-3 with a white source (Δλ = 430 to 830 nm) that proved to be the actual achromatic behavior of the phase shifter, despite its modest value. Extrapolated to mid-IR, its performance would be within typical specifications of a space mission as Darwin.
Key words: astrobiology / instrumentation: interferometers / techniques: high angular resolution / techniques: interferometric / planets and satellites: detection / planets and satellites: atmospheres
© ESO, 2013
1. Introduction
Today, more than 800 exoplanets have been discovered. If most of them are between Uranus and Jupiter’s size, some are definitely rocky planets while very few are in the habitable zone (HZ). Because of biases in detection methods, planets that are both rocky and in HZ are exceptional (von Braun et al. 2011). Only a handful of them have been directly detected and only in very specific situations, either when the planet is young and still very hot or when the hosting star is indeed a brown dwarf (Schneider et al. 2011). It is a known fact that it is extremely difficult to directly detect an exoplanet that orbits a star. The reasons are (i) that the planet is very close to the star where the typical angular distance to the star is on the order of 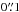 and (ii) that the contrast is very high, on the order of 10 millions in the infrared and 10 billions in the visible, as in the case of the Earth/Sun system. An additional huge challenge and potentially a rewarding one is to determine if a planet does shelter life. One piece of widely accepted evidence of its presence would be the simultaneous detection of H2O, CO2, O3 in the planet’s atmosphere. Coupling a low resolution spectrometer and a multi-telescopes Bracewell nulling interferometer (Bracewell 1978) in a space experiment in the mid-IR (6–18 μm) is one of the paths, which has been proposed since 1993 (Léger et al. 1996) for searching those potential life signatures. The space mission Darwin is probably the most advanced concept in this respect (Cockell et al. 2009). In the simplest version of the nulling interferometer, a π phase shift is added on one arm of a Michelson interferometer, so the fringe pattern projected on the sky exhibits a central dark fringe, which is common to all wavelengths. An on-axis star at the center of this dark fringe would thus be extinguished, while a putative planet orbiting the star can coincide with a bright fringe (a transmitting area on the sky) for a proper baseline between telescopes and hopefully, can be directly detected.
and (ii) that the contrast is very high, on the order of 10 millions in the infrared and 10 billions in the visible, as in the case of the Earth/Sun system. An additional huge challenge and potentially a rewarding one is to determine if a planet does shelter life. One piece of widely accepted evidence of its presence would be the simultaneous detection of H2O, CO2, O3 in the planet’s atmosphere. Coupling a low resolution spectrometer and a multi-telescopes Bracewell nulling interferometer (Bracewell 1978) in a space experiment in the mid-IR (6–18 μm) is one of the paths, which has been proposed since 1993 (Léger et al. 1996) for searching those potential life signatures. The space mission Darwin is probably the most advanced concept in this respect (Cockell et al. 2009). In the simplest version of the nulling interferometer, a π phase shift is added on one arm of a Michelson interferometer, so the fringe pattern projected on the sky exhibits a central dark fringe, which is common to all wavelengths. An on-axis star at the center of this dark fringe would thus be extinguished, while a putative planet orbiting the star can coincide with a bright fringe (a transmitting area on the sky) for a proper baseline between telescopes and hopefully, can be directly detected.
Among the numerous technical challenges of such a space mission, a major one is to realize a π phase shift on a broad wavelength range. Several concepts were already proposed to solve this problem. We previously presented a new concept for providing such a functionality, which allows a simple and symmetric design of the interferometer, with only one device per beam in Paper I (Rouan & Pelat 2008) and Paper II (Pelat et al. 2010). This is based on a pair of square cellular mirrors that looks like chessboards. Each cell has a thickness that introduces a phase shift of (2k + 1)π or of 2kπ on the fraction of the wave plane it reflects for a given central wavelength. The number of cells, their position and thickness are constrained by a mathematical scheme such that the behavior of the null depth as a function of wavelength, which is expressed as the ratio of intensities at the recombined focus with and without the phase shifter, is flat within a broad range, as shown in Sect. 2. We developed in Papers I and II the theoretical grounds for which the achromatic phase shifter is based. We considered especially two-telescope interferometers and studied the two situations of the optical setup, where the pupils of the two telescopes are exactly superimposed (known as on-axis recombination) or where recombination occurs at the focal plane (known as multi-axis recombination).
In Paper I, we examined the basic principles and several solutions of chessboard patterns in terms of the distribution of the individual phase shifts between cells. We concluded that there was a preferred one providing the deepest null depth. In Paper II, the mathematical formalism was established in more details to reach an analytical expression, and the question of distribution of cells in the X-Y directions was also studied. We showed that an optimum pattern for each one of the two configurations was fulfilling some criterium on minimizing the intensity of the scattered light around the nulled area. The main purpose of this paper is now to present the experimental setup that we developed to validate the concept and to demonstrate that the chessboard nuller is working and can reach performances that are well understood. Some of the material that appears here was presented at two SPIE conferences and in the proceedings of those conferences (Papers III and IV: Pickel et al. 2010, 2012). However, the result was preliminary, and we thought it was more consistent to gather a unique paper with all the aspects related to the experimental demonstrator, even at the price of some repetition. What is essentially new in this paper is the deeper analysis of the results obtained with the transmissive chessboard and the completely new results related to the reflexive setup using a segmented deformable mirror (SDM).
We will first present in Sect. 2 a more compact and straightforward demonstration of the functioning of the device than what was established in Papers I and II. In Sect. 3, the experimental setup, nicknamed DAMNED (Dual Achromatic Mask for Nulling Experimental Demonstrator), is described. In Sect. 4, the results are presented and analyzed. Since the question of the theoretical bandwidth that one can ultimately achieve using the chessboard phase shifter is related to its actual performance, we added an appendix, where this quantity is established with regards the star-to-planet contrast.
2. The achromatic chessboard principle in a nutshell
In a 2-telescope Bracewell interferometer, a π phase shift must be added in one arm. This can be achieved for a given wavelength λo by using some device that introduces just an optical path difference (opd ) of λo/2; it can be as simple as a dielectric plate. For a point source exactly on-axis (the star) and the assumption of a perfect interferometer, the electric field after recombination is equal to (1 + z) with 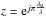 , where λ is the observing wavelength, and λo is a reference wavelength. We note that the maximum amplitude is 2. If
, where λ is the observing wavelength, and λo is a reference wavelength. We note that the maximum amplitude is 2. If 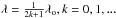 , then the amplitude is null, and the star is fully extinguished. In other words, z = −1 is a root of the nulling function (1 + z), and we have a nulling effect around z = −1. To strengthen the nulling effect, we proposed to design a device for which z = −1 is a multiple root of order n of the nulling function. Under that assumption, the nulling function is (1 + z)n that is very flat around z = −1 (i.e. λ = λo at the first spectral order), because the first n terms of its Taylor series will be zero. In other words the star will be strongly attenuated on a large bandwidth around λo. We demonstrate in Appendix A that the nulling bandwidth, when considering the unavoidable attenuation of the planet, is (
, then the amplitude is null, and the star is fully extinguished. In other words, z = −1 is a root of the nulling function (1 + z), and we have a nulling effect around z = −1. To strengthen the nulling effect, we proposed to design a device for which z = −1 is a multiple root of order n of the nulling function. Under that assumption, the nulling function is (1 + z)n that is very flat around z = −1 (i.e. λ = λo at the first spectral order), because the first n terms of its Taylor series will be zero. In other words the star will be strongly attenuated on a large bandwidth around λo. We demonstrate in Appendix A that the nulling bandwidth, when considering the unavoidable attenuation of the planet, is (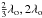 ) for the first spectral order. We now show how to construct the corresponding chessboards.
) for the first spectral order. We now show how to construct the corresponding chessboards.
When developing (1 + z)n using the binomial formula, two kinds of terms appear: some are in z2k + 1, and some are in z2k. The first ones correspond to an opd λo/2(modλo) and the second to an opd λo(modλo). The coefficient of each term (i.e., 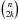 or
or 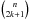 ), as given by the binomial formula, gives the number of cells associated with a given k. One can check that the total number of cells required is
), as given by the binomial formula, gives the number of cells associated with a given k. One can check that the total number of cells required is 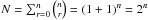 . If we now assign all the λo(modλo) cells to a chessboard on one arm and all the λo/2(modλo) cells to the chessboard of the other arm, we still have a Bracewell nulling interferometer at λo but with the desired property of producing an amplitude varying as (1 + z)n. This is because this expression is precisely the sum of all elementary complex amplitudes. To have two square shaped chessboards of 2m × 2m cells per chessboard (for a total of 2 × 2m × 2m), n must be odd, where n = 2m + 1. We call m the order of the chessboards, which is also the order of the interferometer constructed with them. We note that m = 0 corresponds to the classical Bracewell interferometer and m = 1 to the interferometer with 2 chessboards of 2 × 2 cells each, etc.
. If we now assign all the λo(modλo) cells to a chessboard on one arm and all the λo/2(modλo) cells to the chessboard of the other arm, we still have a Bracewell nulling interferometer at λo but with the desired property of producing an amplitude varying as (1 + z)n. This is because this expression is precisely the sum of all elementary complex amplitudes. To have two square shaped chessboards of 2m × 2m cells per chessboard (for a total of 2 × 2m × 2m), n must be odd, where n = 2m + 1. We call m the order of the chessboards, which is also the order of the interferometer constructed with them. We note that m = 0 corresponds to the classical Bracewell interferometer and m = 1 to the interferometer with 2 chessboards of 2 × 2 cells each, etc.
For different values of m, we computed the theoretical attenuation of a point source: the results are shown in Fig. 1. Each curve gives the attenuation around λo = 650 nm with m varying from 0 to 5. As expected for a given null depth, the spectral bandwidth increases when m increases. In our experiment, we tested two types of chessboards, a reflective one whose order is m = 2 (green curve in Fig. 1) and a transmissive one whose order is m = 3 (dark blue curve). The structure of both pairs of phase shifters is shown in Fig. 2, where the numbering on each cell is the phase shift in units of π.
 |
Fig. 1 Theoretical attenuation (null depth) of an on-axis point source versus wavelength for a perfect chessboard device designed for the central wavelength of 650 nm. The different curves correspond to the order of the chessboard from m = 0, which is pure Bracewell (dark), to m = 5 (light blue). |
 |
Fig. 2 The two patterns of phase chessboards used in DAMNED: the upper pattern corresponds to a reflective mask synthetized using a SDM and the lower pattern to a transmissive mask made in bulk optics my engraving a transparent plate. In both cases, φ = 0mod 2π (even) cells are on the left and φ = πmod 2π (odd) cells are on the right. The numbering on each cell is the phase shift in units of π. |
3. Experimental setup
The first goal of the bench is to check if a destructive interference can be produced by using the chessboard phase mask as a π phase shifter in a Bracewell interferometer and to measure its depth on an artificial star. The second goal is to estimate its performance in terms of achromaticity.
3.1. Basic choices for the configuration, use of a single-mode fiber optics
The first choice was to make the demonstration in the visible range, because on-the-shelf components and detectors are available only in this domain at reasonable prices. We also wanted to avoid a cryogenic setup that would be much more complex to handle and to modify with the advent of new findings or issues. The drawback of course, is that specifications on the opd between shells is more difficult to meet.
For the sake of simplicity, we have decided to use the multi-axis solution for the interferometric recombination: it presents the advantage of avoiding the delicate use of semi-reflecting plates to superimpose the beams. This means that the interferometric pattern is the point spread fonction (PSF) of the pupil modulated by fringes with the central fringe being a dark one. On the other hand, the putative planet that would correspond to a constructive interference would produce the same fringe pattern but would be just shifted by half a fringe separation (bright central fringe). Trying to separate the planet signal from the star signal in the darkest fraction of the central stellar fringe would correspond to a terrible loss of the planet flux. One possible solution to obtain a gain on the useful planetary signal is then to make the recombination on the head of a single-mode fiber optics (SMFO), which offers the property of realizing the sum of the electric field on its head. Because the amplitude of the stellar light follows an odd distribution in the direction of the baseline, the sum performed by the SMFO is null on any interval centered on the axis of symmetry and thus materializes the nulling. The planet fringe system is even in amplitude and the integral, at least on the complete central fringe, is positive, as illustrated in Fig. 3. This scheme was first proposed by Wallner et al. (2004) and demonstrated experimentally by Haguenauer & Serabyn (2006) and Buisset (2006). We decided to make use of this property due to the simplicity of its implementation.
Another important simplification, directly related to the previous one, is that we did not try to make an actual interferometer with a long baseline, but we chose to work with the two pupils that are placed side-by-side. This offers the advantage that we can use a single collimated beam of a reasonable diameter to illuminate the two pupils, and this is not a real limitation considering the main goal which is the validation of the quasi-achromatic nulling by the chessboard.
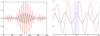 |
Fig. 3 Principle of nulling recombination on a single-mode fiber: on the left are the superimposed fringe pattern of a classical interferometer (black) and of a Bracewell interferometer (red). The amplitude of the black line is smaller on purpose, since it is supposed to correspond to the planet amplitude. On the right, a close-up of the central part of the fringes is shown with a shaded area that delineates the core of the single-mode optics which achieves the summation of the electric field it receives. The anti symmetric character of the Bracewell fringes (star signal) leads to the nulling effect, while the symmetry of the planetary electric field preserves the signal. |
The null depth is defined as the ratio of the minimum intensity coupled into the SMFO to the maximum value of the non-nulling situation. One produces the non-nulled star by just using a rectangular diaphragm instead of the phase shifter. The chessboard and the rectangular diaphragm are the same size.
By moving the head of a SMFO in the image plane – i.e. at the focus of a parabola – and measuring the flux at each position, one obtains a convolution of the diffraction amplitude by the core of the fiber optics. At the exact center of the dark fringe, the electric field is odd, so all the light is, in principle, extinguished within the SFMO. In a way, this method allows to obtain a map, which looks like the PSF produced by the interferometer that features the chessboard at the focus of the parabola, with a better sampling and with better dynamics than a direct image obtained on a CCD camera. To illustrate this, one can compare Figs. 9 (reconstructed map) and 11 (direct image).
3.2. Chessboard realization
The transmissive chessboards were manufactured by the “Pôle Instrumental du GEPI” in the Observatoire de Paris. The 2 × (8 × 8) cells were engraved by chemistry-assisted ion-etching on a glass plate (4.8 mm × 9.6 mm) with a deposit of chromium on the border to delineate the transmissive area. The plain diaphragm is an identical non-engraved rectangular glass plate with the same chromium deposit.
The reflective chessboards are synthetized by means of a 12 × 12 deformable electrostatic segmented mirror from Boston Micro-machines controlled by an electronic module provided by the same manufacturer. The 300 μm actuators of the segmented mirror can shape a rectangle of 8 × 4 actuators, according to the opd pattern of Fig. 2 (1.2 mm × 2.4 mm), or two separated 4 × 4 squares (with up to four actuators of separation). The non-nulling configuration is obtained with the same area of actuators but with a surface as flat as possible. The stroke of each actuator is not very large (typically 1.5 μm) but compatible with the 4λo/2 maximum difference of levels of the 4 × 8 cells configuration.
3.3. Optical bench
The experimental setup was designed to measure rapidly the two images that are required to calculate the attenuation, in order to limit the effect of possible drifts. The setup is versatile enough to use either transmissive (Fig. 4) or reflective chessboards (Fig. 5). A picture of the setup is shown in Fig. 6.
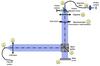 |
Fig. 4 Optical scheme of DAMNED for the transmissive setup. |
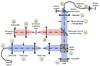 |
Fig. 5 Optical scheme of DAMNED for the reflexive setup using a SDM. |
 |
Fig. 6 Optical bench DAMNED. The blue and red lines indicate the travel of the beam for the main measuring channel and for the strioscopic channel, respectively. See Figs. 4, 5, and text for the details on the different components and their numbering. |
-
The source ① is either a laser diode (λ = 635 nm) or a white laser and is linked to fiber optics. It is placed at the object focal plane of an off-axis parabola ② (focal length f1 = 520 mm).
-
The collimated beam is directed to the segmented mirror ⑥ after reflection on a beam splitter ⑤. This segmented mirror is made of 12 × 12 actuators, which can be moved in piston with an accuracy better than 1 nm, and produces the order 2 chessboards of 8 × 4 actuators.
-
The rectangle pattern of actuators is selected. Two lenses ④ are used to image the proper diaphragm ③ (rectangle or two separate squares) on the mirror.
-
The segmented mirror ⑥ reflects the beam back to the beam splitter ⑤.
-
The beam reaches a motorized plate ⑦ with three positions: one that is free when using the segmented mirror, one for a transmissive chessboards, and one for a non-engraved rectangular glass plate diaphragm.
-
The collimated beam reaches a second high optical quality off-axis parabola ⑧ (focal length f = 240 mm), which focuses it on the core of a SMFO ⑨ . The fiber has a core of 2.5 μm and is single mode for λ > 430 nm. Two piezoelectric motors are used to move the SMFO in x and y by steps as small as 10 nm. By moving the fiber, the nulling pattern produced by the chessboards can be reconstructed and their performances can be measured.
-
The other end of this SMFO is placed at the object focal plane of a lens ⑩. A filter or/and an optical density can be placed in the collimated beam. Four 20 nm bandpass filters are used to measure the chromatism effects on the null.
-
Eventually, the intensity is measured using a CCD camera that is placed slightly out of focus from a lens. The effects of the CCD flat-field in the intensity estimation is limited by this lack of focus. The defocus allows the use of not too short exposure times at high flux levels.
When using the transmissive configuration (Fig. 4), the motorized plate ⑦ puts in place the transmissive chessboard, and the SDM is replaced by a plane mirror ⑥. Both the rectangular diaphragm ③ and the two lenses ④ are removed.
3.4. Control of the segmented mirror
 |
Fig. 7 Structure of the spatial filter used to remove low spatial frequency in the strioscopic setup used to flatten the SDM. |
As each actuator of the SDM is controlled in open loop, their relative z-position is not accurate enough, despite the resolution, which can be of one nanometer. To measure the relative actuators’ positions and correct them, a strioscopic method is used. The strioscopic optical path is shown in red in Figs. 5 and 6 and described in the following:
-
The rectangular diaphragm ③ and the two lenses ④ are optional,and they can be removed to observe the complete surface of themirror.
-
After the reflection on the segmented mirror ⑥ and the beam splitter ⑤, a movable plane mirror ⑪ reflects the beam to switch between the strioscopy mode and the measurement mode.
-
A lens ⑫ (focal length f = 500 mm) is placed, so that the segmented mirror is at its object focal plane.
-
In the image focal plane ⑬, a cross-shaped mask (Fig. 7) is placed to filter the spatial frequencies.
-
A second lens ⑭ (focal length f′ = 300 mm) is placed, so that the cross-shaped mask is at its object focal plane.
-
The CCD camera ⑮ is positioned in the image focal plane of the last lens.
The strioscopy technique produces the modulus of the derivative of the wavefront phase. With this setup, the surface of the mirror can be analyzed, and the absolute value of the relative position between two adjacent actuators can be evaluated by measuring the flux at the transition. The left image of Fig. 8 shows a picture of the segmented mirror surface without the spatial filter, and one can hardly distinguish the actuators. The center image of Fig. 8 shows the same but with the spatial filter mask: the transitions between adjacent actuators can be seen clearly. The flux in the transition area is proportional to the difference of altitude between the actuators.
To control the position of the actuators and synthesize the chessboards, the surface needs to be flattened. From an arbitrary reference actuator, the adjacent actuator is flattened by minimizing the flux on the transition between them (Fig. 8). The process is repeated with the next adjacent actuator and iterated until all the actuators have been flattened. To minimize the propagation of the error, different ways to chain the flattening have been evaluated: the most precise is first flattening the central row, starting on both right and left directions from the central actuator, and then by flattening all the columns, starting from the actuators of the central row on both up and down directions. The result of the flattened mirror surface is shown in the bottom image Fig. 8. An accuracy of 3.3 nm has been achieved.
 |
Fig. 8 Images of the segmented mirror surface. Upper left: without the spatial filter of Fig. 7 put in place. Upper right: with the spatial filter but with the same voltage (135 V) applied to all actuators, so that they are at about half stroke. Bottom: applying the flattenning procedure (see text). Note that the contrast has been artificially enhanced in each case. |
From the flattened position, the chessboard can be easily synthesized by applying a proper voltage map to move each actuator to its z-position.
3.5. Control of the whole bench and measurement procedure
The CCD camera and most of the mechanisms on the bench have been interfaced to a computer through standard commercial input/output electronic boards – thanks to an integrated GUI interface and the development of control scripts – so that the different phases of a measurement session can be scheduled in an automatic way, allowing a fair reproducibility.
A standard session at a given wavelength consists of: i) an introduction in the beam of the plain diaphragm; ii) an acquisition of a series of CCD dark frames by inserting a small shutter at the output of the SMFO that is linked to the light source; iii) an acquisition of a series of CCD frames after removing the shutter; iv) a small displacement of the head of the SMFO in x and/or y by controlling the piezo; v) going to step ii) until the scan is complete; vi) resetting the position of the SFMO and the introduction of the chessboard in the beam; and repeating ii) to v).
The integration time of the CCD camera is automatically adjusted to avoid saturation. Aperture photometry on the area of the pixels that are illuminated by the out-of-focus spot produces the flux measurement used to evaluate the null depth.
4. Results
4.1. Transmissive phase shifter
Several transmissive chessboard masks have been manufactured and tested when the depth of the cells (measured with a “measuring machine”) were within the specifications. They all were specified for a central wavelength λo = 650 nm. We note that the theoretical bandwidth for this wavelength for a chessboard of infinite order is (433–1300) nm.
In the following, we present the results obtained with the most accurately manufactured device. The measured dispersion of depths (1σ) is typically 15 nm within one given level, and the difference of the mean depth of a given level with the specified value is typically 20 nm.
The maps of the null depth produced by the chessboards in two narrow-band filters, which are centered at 560 and 650 nm, and in a broad band filter whose bandpass is 450–840 nm, are shown on the left of Fig. 9. One can clearly see the dark fringe between two lobes. Using a set of routines in Yorick, specifically developed to simulate the performance of the experiment, we were able to simulate a realistic chessboard with the actual cells thicknesses. We observe (Fig. 9, right) that the simulation gives a result close to the measurements, especially since the asymmetry in intensity between the two lobes and their slight relative shift are correctly reproduced. We conclude that there are probably no major contributions to the loss of performance that we did not identify. It is not straightforward to ascribe the asymmetry to one of the aberrations produced when the wavefront propagates through the nonperfect chessboard.
Table 1 displays the results in terms of null depth at different wavelengths, where each one is defined by a narrow-band filter of Δλ = 20 nm. The last entry corresponds to a measurement without any filter: this means that the wavelength range was defined by the response of the camera, the transmission of the SMFO, and the spectral characteristics of the white source. We estimate this range to be 450 to 840 nm. In Fig. 10, the corresponding value of null depth and several curves taken from the simulation are plotted. These experimental results prove that a fair degree of achromaticity of the nulling is reached thanks to the chessboards phase shifter. In particular, the last entry shows that we have a significant attenuation for a white source (450–840 nm). This is clearly much better that the one that would be produced by a unique dielectric plate phase shifter in the same narrow band: for instance, one would expect a bandpass of only 70 nm for a comparable null depth of 8 × 10-3 in a perfect interferometer. In Fig. 10, the measured null depth at different wavelengths is compared to the simulations, assuming two methods for the flux measurement. The most interesting result is probably the one obtained without any filter that shows the very significant null depth on a broad band.
Despite that those performances appear modest compared to a goal of a few 10-6 in null depth, one should not forget that this null depth would increase in the mid-infrared, assuming the same manufacturing accuracy. This domain of wavelength is precisely the one where nulling interferometry is meaningful. For instance, assuming an identical manufacturing uncertainty of 20 nm rms on the depths of the seven levels of engraving1 for a mean wavelength of 10 μm, the null depth should be of the order of 6.3 × 10-6, which is practically equal to the required specification. Clearly, a first conclusion of those measurements is that a chessboard phase shifter in bulk optics could legitimately be considered for a mid-infrared nulling interferometer.
 |
Fig. 9 Upper right: simulated image at λ = 560 nm of the nulled PSF, which considers the measured phase unaccuracy on the transmissive chessboard. Upper left: the measured PSF obtained by scanning the SMFO. One pixel corresponds to one step of displacement of the SMFO of 200 nm. Middle panel: same as upper panel but at the wavelength of 650 nm. Lower panel: same as upper panel but in a broad wavelength range of about 450–840 nm. |
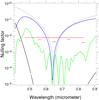 |
Fig. 10 Measured null depth of the transmissive chessboard phase mask in different broadband filters (colored segments of line), which include the large band of 470–830 nm. The black line is the theoretical performance of a perfect component and the green line is the simulated null depth of the real device when the minimum of the fringe pattern is used. The blue line which is the same quantity when using just the central pixel value as the measure, assumes that the fiber will be placed there and not moved (as it would likely be in the case of a space experiment). The dotted line gives the nulling depth for a perfect Bracewell interferometer. |
 |
Fig. 11 Images at different wavelengths of the fringe pattern; they were obtained by direct imaging on a CCD camera of the Fizeau recombined focus. The label at top of each image gives the wavelength. The last image corresponds to no filter. |
Measured null depth in different broadband filters for one of the transmissive chessboard phase mask we manufactured.
4.2. Reflective phase shifter
Since the manufacturing process of a transmissive device in bulk optics cannot be improved by a significant factor, this pushed us to mitigate the problem of the accuracy of the individual cell phase shift by using a SDM instead of a transmissive mask, since nanometric control is in principle possible for the former.
With this type of device, our expectation is to control the position of each actuator with better accuracy and to also have the capability of a feedback after a first measurement to improve the nulling by small adjustments.
Starting from the configuration of a flattened mirror, as described in Sect. 3.4, we synthesize chessboards with a central wavelength of λo = 635 nm by applying a matrix of offset voltages which is based on the average voltage/piston characteristic given by the manufacturer. We first made a series of measurement with the same protocol as in the case of the transmissive mask that is by scanning the head of the SMFO at the focus of the imaging parabola. The result was, however, disappointing, and we rapidly identified that the problem was the much larger size of the PSF because of the reduced size of the chessboard mask (actually the SDM): there is a factor of 4 between the two cases. This translated into a strong loss of signal when using the SMFO and also a difficulty to locate precisely the dark fringe by scanning, since the separation between the lobes was out of the range of the xy piezo actuators.
Of course, one could think to reduce the parabola focal length, but the cost of a new, fast parabola was beyond our budget. We concluded that the method was no longer adapted to this new situation and decided to make an evaluation of the nulling efficiency directly on the image of the fringe pattern at the focus of the parabola, by assessing the darkness of the central fringe compared to the central bright fringe seen when the SDM is made flat. For this purpose, we added a few optical elements to obtain the direct diffraction image produced by the interferometer. This provided the additional advantage to check in real time if the actuators were effectively at a level close to their theoretical piston value by looking at the symmetry of the pattern; this check was done before starting a several hours measurement sequence. This proved to be a real asset.
The very first measurements we obtained are displayed in Fig. 11: clearly, the dark central fringe is present at all wavelengths and symmetric. It is also present in the no-filter image. The overall aspect of the image also looks more satisfactory than with the transmissive chessboard: less shear between the lobes and there is a lower difference in intensity between the peak values of the lobes. Table 2 and Fig. 12 summarize the results on the null depth measured at different wavelengths. The red curve is the ratio of the minimum pixel on the dark fringe, when the SDM is shaped along the chessboard design, to the maximum pixel on the bright fringe when the SDM is flat (constructive case). This ratio represents extinction of an on-axis star that is the null depth. As far as planet detection is concerned, a more pertinent quantity (blue curve) is defined which uses another constructive case for the reference. It is obtained by adding a λo/2 opd to one pupil of the chessboard (as it would be the case for a planet). The maximum pixel on the bright fringe is also taken as the reference. One notes that at 650 nm which is close to the central wavelength (635 nm) and at 740 nm, the performance is better than with the transmissive phase mask, although this is no longer true at the two extreme wavelengths, 560 and 830 nm. This reduced bandpass of the nulling performance is however consistent with the fact that the order of the mask is only 2, instead of 3 for the transmissive one.
Two other tests were done with the SDM. In the first one we simulated a configuration closer to a real interferometer, in contrast to having just two telescopes side-by-side, by using a synthesized chessboard on square pupils, which are separated by one or more cells. Figure 13 shows the image obtained without any filter, when the separation is 4 cells (1.2 mm): the fringe pattern is squeezed, as expected, and the lobes around the central dark fringe are well balanced, despite that the image appears more distorted than in the previous case. We suspect that it is the delicate positioning of the physical diaphragm that is responsible of this distortion.
In the second test, we conducted an experiment that is probably the most robust demonstration of the achromatic character of the phase shifter. Instead of using different filters, we fixed the wavelength, using a diode laser as a source (635 nm), and we scanned the voltages applied to the cells so that at each step the chessboard pattern produced is the one corresponding to a given λo. Since there are no exchanges of filters during the sequence, the stability of the experiment should be better. Figure 14 shows the result in terms of the null depth related to λo. The behavior appears quite smooth, and a useful bandpass of 380 nm is derived when considering a null depth of 10-2.
The precise z-position of each actuator is not well mastered in this preliminary phase, and obviously, there are several points on which we can work as a means to improve the performance, to begin with a better calibration of the voltage/piston response of each cell of the SDM, and to determine a finer use of the information given by the strioscopy setup in order to adjust more accurately the piston. A new phase has been started recently to implement those improvements.
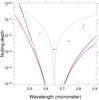 |
Fig. 12 Null depth measured in four narrowband filters using the reflexive chessboard phase mask (short segments of line). The curves give the theoretical null depth of a perfect component. The red color refers to a null depth based on a non-nulling reference produced by a flattened chessboard; the blue color refers to a reference produced by adding a λo/2 opd to one pupil of the chessboard: it measures a star-to-planet contrast ratio than a null depth (see text). The dotted line gives the nulling depth for a perfect Bracewell interferometer. |
Measured null depth in different narrow band filters, when using the reflective chessboard phase mask synthesized with the SDM.
 |
Fig. 13 Images without any filter of the fringe pattern, when the two pupils on the SDM are separated by 4 cells (1.2 mm). |
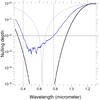 |
Fig. 14 Blue line: measured null depth, when the wavelength is fixed (laser diode) and the piston of the cells on the SDM is scanned to maintain a nulling phase pattern at each step for the reference wavelength, as indicated on the horizontal axis. The bandpass at a null depth level of 10-2 is indicated by the horizontal straight line. Solid black line: null depth in a perfect case. Dotted line: nulling depth for a perfect Bracewell interferometer. |
4.3. Interpretation of the measurements
Compared to the theoretical performance of a perfect device (black curve in Figs. 10, 12, and 14), the measured performance is of course much lower. However, our simulations, when considering a realistic device, do reproduce to some extent this loss of performance, which should thus be ascribed to the manufacturing error in the cells thickness. This was expected (see Pelat et al. 2010), and we do confirm by those measurements that the chessboards performance is quite sensitive to the errors on cells thicknesses.
One can give an analytical justification and estimation of this effect that is similar to the analysis of a wavefront perturbated by atmospheric turbulence. Let us consider the Fresnel vector (phasor) associated with the even chessboard: it is the sum of the Fresnel vectors of each cell. In an orthogonal X-Y frame, the two projections of this sum have amplitudes that can be written as: 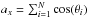 and
and 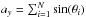 ,
,
where θi is the angle between the Fresnel vector associated with the cell i and the real axis; θi thus translates the manufacturing phase error. Since the error θi is small those expressions reduce to
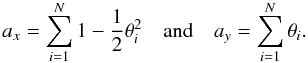 Assuming that θi is normally distributed with a variance
Assuming that θi is normally distributed with a variance 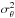 , we can derive the statistical mean and variances of ax and ay:
, we can derive the statistical mean and variances of ax and ay:
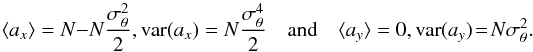 For the odd chessboard, the expressions are the same, but of course, the Fresnel vector is opposite. When recombining the two beams, for instance, at the focus of the parabola, the resulting complex amplitude A = aeven + aodd has a statistical mean and variance of
For the odd chessboard, the expressions are the same, but of course, the Fresnel vector is opposite. When recombining the two beams, for instance, at the focus of the parabola, the resulting complex amplitude A = aeven + aodd has a statistical mean and variance of
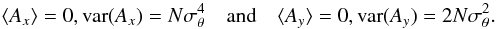 Finally, the intensity I, which is the squared modulus of the amplitude, is a stochastic variable that has for mean and variance:
Finally, the intensity I, which is the squared modulus of the amplitude, is a stochastic variable that has for mean and variance:
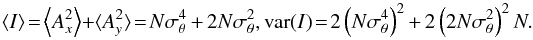 Since
Since 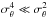 , this expression reduces to
, this expression reduces to 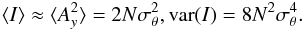 (1)The null depth, which is the ratio of the intensities with and without phase shifter, is then a stochastic variable f of mean and variance:
(1)The null depth, which is the ratio of the intensities with and without phase shifter, is then a stochastic variable f of mean and variance: 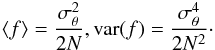 (2)Since each Fresnel vector that is associated with one chessboard is the sum of many Fresnel vectors, we can use the central limit theorem to state that Ay is a normal random variable and thus, conclude that the statistical distribution of
(2)Since each Fresnel vector that is associated with one chessboard is the sum of many Fresnel vectors, we can use the central limit theorem to state that Ay is a normal random variable and thus, conclude that the statistical distribution of 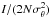 follows a χ2 law with one degree of freedom. The standard deviation of this distribution function is equal to its mean times
follows a χ2 law with one degree of freedom. The standard deviation of this distribution function is equal to its mean times 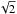 , which implies that large variations of I must be observed from one realization of a device to another. This is what our simulations gives: from one simulated pair of chessboards with a random manufacturing error on each cell to another one, the null depth can vary by several orders of magnitude. This comes as a surprise in the first instance but is simply a consequence of the χ2 law with one degree of freedom. To illustrate this, let us compute the ratio of the nulling depth f for the worst case (larger f) scenario to the best case (lower f) scenario on a set of 20 devices. We find a median value for this ratio equal to 2570 on 1000 realizations of this set.
, which implies that large variations of I must be observed from one realization of a device to another. This is what our simulations gives: from one simulated pair of chessboards with a random manufacturing error on each cell to another one, the null depth can vary by several orders of magnitude. This comes as a surprise in the first instance but is simply a consequence of the χ2 law with one degree of freedom. To illustrate this, let us compute the ratio of the nulling depth f for the worst case (larger f) scenario to the best case (lower f) scenario on a set of 20 devices. We find a median value for this ratio equal to 2570 on 1000 realizations of this set.
Concerning the transmissive chessboard we have measured the best component among those manufactured by the Pôle instrumental du GEPI, using a profilometer. We obtained a standard deviation of 15 nm on the thickness of the cells (relative to the nominal value) belonging to a same floor, while the step between two levels is 712 nm. This translates into σθ = 0.0662 radians. However, there is an additional dispersion of the thickness difference between levels (realtive to the nominal value) that amounts to 20 nm rms and that produces a more severe effect, since all cells of a given level have a correlated error. It is not straightforward to establish the proper expression that takes this correlation into account, since the number of cells per level varies largely from one to another. Roughly, one can say that the null depth should stand somewhere around 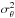 /(Nlevels − 2) instead of around
/(Nlevels − 2) instead of around 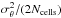 . We justify the use of (Nlevels − 2) instead of Nlevels because two of the levels exhibits only 2 cells each. Using this last expression, we deduce that the null depth should be of the order of 1.5 × 10-3. This value is smaller by a factor of three than the actual measured performance summarized in Table 1 and in Fig. 10 for the most accurate component we tested. This analytical expression provides a lower limit of the null depth on average. Other causes, such as non-perfect alignment and centering on the single mode fiber, can further reduce the effectiveness of the nulling. We do not yet have a similar estimate of the uncertainty on the actual piston of each actuator of the SDM; however, the previous generic analysis will, of course, be applicable when a safe estimate will become available.
. We justify the use of (Nlevels − 2) instead of Nlevels because two of the levels exhibits only 2 cells each. Using this last expression, we deduce that the null depth should be of the order of 1.5 × 10-3. This value is smaller by a factor of three than the actual measured performance summarized in Table 1 and in Fig. 10 for the most accurate component we tested. This analytical expression provides a lower limit of the null depth on average. Other causes, such as non-perfect alignment and centering on the single mode fiber, can further reduce the effectiveness of the nulling. We do not yet have a similar estimate of the uncertainty on the actual piston of each actuator of the SDM; however, the previous generic analysis will, of course, be applicable when a safe estimate will become available.
5. Conclusion and prospects
We present an experimental setup of a genuine nulling interferometer that features a new concept of an achromatic phase shifter. This concept is based on the design of an optical chessboard with cells that introduce a peculiar pattern of phase shifts to produce a complex amplitude at the recombined focus, which has a root of order n at λ = λo and thus leads to a flattening of the null depth versus wavelength that is equivalent to a broadening of the achromatic bandpass.
A first series of measurements was done using a transmissive chessboard made in bulk optics as the π phase shifter. The most important result is that those tests demonstrated the validity of the concept. They also confirmed numerical simulations that indicate that our phase shifter is very sensitive to the cells’s thickness error to a level such that manufacturing a performing device in bulk optics is probably too challenging in the visible. By extrapolating the measured performance to the mid-infrared on the other hand, the null depth would be practically within the required specification for an earth-like planet detection, provided that a same manufacturing accuracy is reachable. To go around this problem in our visible demonstrator, we decided to switch to a controlled SDM for the synthesis of the phase chessboard with the hope that the piston on an actuator can be controlled with an accuracy better than 1 nm. We present the very first results here using reflective chessboards that are synthesized with a SDM from Boston micro-machines. They appear to be very encouraging, since they confirm the achromatic behavior of the chessboard phase shifter and open the door to a series of new tests made possible thanks to the versatility offered by the control of all cells independently. We identified several points where the null depth could be improved, such as in a better positioning of the actuators, through a trial and error method. Thanks to the easy control of the mirror, we plan to do many more tests. For example, we plan to do a modulation between different nulling configurations for a better determination of the bias. We expect to produce more new results within the coming year.
Baudoz et al. (2006) quote an accuracy of 0.5% on the step thickness when prototyping the three four-quadrant phase mask coronagraphs designed for λ = 10 to 15 μm, which equip the MIRI-JWST instrument. For instance this leads to 25 nm accuracy for the 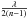 step required by four-quadrant coronagraph for ZnSe (optical index = 2.4) at λ = 15 μm.
step required by four-quadrant coronagraph for ZnSe (optical index = 2.4) at λ = 15 μm.
Acknowledgments
CNES and CNRS funded the Ph.D. grant of D. Pickel. We thank the anonymous referee for his(her) careful reading of the manuscript which leads to a significant improvement of the paper. Thanks are extended to the team at Pole Instrumental du GEPI, who manufactured carefully the transmissive chessboards.
References
- Baudoz, P., Boccaletti, A., Riaud, P., et al. 2006, PASP, 118, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Bracewell, R. N. 1978, Nature, 274, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Buisset, C. 2006, in ESA SP, 621, 102 [Google Scholar]
- Cockell, C. S., Herbst, T., Léger, A., et al. 2009, Exp. Astron., 23, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Haguenauer, P., & Serabyn, E. 2006, Appl. Opt., 45, 2749 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., Mariotti, J. M., Mennesson, B., et al. 1996, Icarus, 123, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Pelat, D., Rouan, D., & Pickel, D. 2010, A&A, 524, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickel, D., Rouan, D., Pelat, D., et al. 2010, in SPIE Conf. Ser., 7739, 62 [Google Scholar]
- Pickel, D., Rouan, D., Pelat, D., et al. 2012, in SPIE Conf. Ser., 8442, 7 [Google Scholar]
- Rouan, D., & Pelat, D. 2008, A&A, 484, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Braun, K., Boyajian, T. S., Kane, S. R., et al. 2011, ApJ, 729, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Wallner, O., Perdigues Armengol, J. M., & Karlsson, A. L. 2004, in SPIE Conf. Ser., 5491, ed. W. A. Traub, 798 [Google Scholar]
Appendix A: The contrast bandwidth
This appendix addresses the question of planet detection, bearing in mind that it is not enough to have a good null depth for an on-axis star but the planet should not be too significantly extinguished. Therefore, a more pertinent quantity than the null depth is the star to planet intensity ratio which is noted as | ρ | 2 and called contrast.
The determination of the theoretical bandwidth 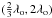 has been carried out in Paper II (Pelat et al. 2010), but using the simplification that an opd of δ = λo/2 on one pupil, which is introduced to simulate the planet case, is seen as a constant phase shift of π, as the chessboards order goes to infinity. This nonobvious fact, which holds true as far as the star/planet ratio is concerned, certainly needs a justification.
has been carried out in Paper II (Pelat et al. 2010), but using the simplification that an opd of δ = λo/2 on one pupil, which is introduced to simulate the planet case, is seen as a constant phase shift of π, as the chessboards order goes to infinity. This nonobvious fact, which holds true as far as the star/planet ratio is concerned, certainly needs a justification.
To give substance to this assertion, let us consider a device, where an on-axis star is seen with the amplitude A∗ = (1 + z)n, z = ejφ, φ = πλo/λ. We recall that our nulling interferometers of order m are designed for n = 2m + 1 in such a way that we can arrange the phase shifters in two square chessboards both containing 2m × 2m cells. The planet is seen as an off-axis object which is considered on the same intensity as the star of the system to avoid the introduction of a star/planet factor that has no significance as far as the bandwidth is concerned. We then compare the amplitudes and intensities of a star seen on-axis relative to the same star seen off-axis. The off-axis star is seen presenting a supplementary opd of δ = λo/2 on the center of one pupil and zero on the other. This can be on the odd or on the even pupil.
To perform the computations more easily, two simplifications, both stemming from the consideration that the size of the pupils is much smaller than the baseline, are made.
-
1.
We consider a hypothetical super-Michelson interferometer,where the effects of all cells are added on-axis. That is the phaseshifts induced by the positioning of the cells on the pupil plane areneglected. (Note that the exact analytical computation has beendone in Paper II.)
-
2.
Because of the tilt of the off-axis waveplane, the opd s are not constant on the pupil’s plane. Nevertheless, we shall neglect this effect. In other words, we consider only a piston of λo/2 on one pupil (either the even or the odd one). Under a condition of constructive interferences, this approximation is of little consequence.
This piston will induce a phase shift of φδ = 2π(λo/2)/λ, or φδ = φ. Therefore, the complex amplitude on the even or odd pupil is multiplied by z. Without this piston (on-axis star), the amplitude at the exit of the even pupil is given by ![\appendix \setcounter{section}{1} \begin{eqnarray} \tfrac{1}{2}\left[(1+z)^n+(1-z)^n\right], \end{eqnarray}](/articles/aa/full_html/2013/10/aa20763-12/aa20763-12-eq114.png) (A.1)which retains only the terms of even powers of
(A.1)which retains only the terms of even powers of 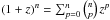 ; at the exit of the odd one, the amplitude is
; at the exit of the odd one, the amplitude is ![\appendix \setcounter{section}{1} \begin{eqnarray} \frac{1}{2}\left[(1+z)^n-(1-z)^n\right], \end{eqnarray}](/articles/aa/full_html/2013/10/aa20763-12/aa20763-12-eq116.png) (A.2)which retains only the terms of odd powers of (1 + z)n. Therefore, the amplitude
(A.2)which retains only the terms of odd powers of (1 + z)n. Therefore, the amplitude  of the off-axis star, when piston is on the even pupil, is given by
of the off-axis star, when piston is on the even pupil, is given by ![\appendix \setcounter{section}{1} \begin{eqnarray*} A'_* &=&\frac{1}{2}z \left[(1+z)^n+(1-z)^n\right] + \frac{1}{2}\left[(1+z)^n-(1-z)^n\right]\\ &=&\frac{1}{2} \left[(1+z)^{n+1}-(1-z)^{n+1}\right], \end{eqnarray*}](/articles/aa/full_html/2013/10/aa20763-12/aa20763-12-eq119.png) and when the piston is on the odd pupil
and when the piston is on the odd pupil ![\appendix \setcounter{section}{1} \begin{eqnarray*} A'_* &=&\frac{1}{2}\left[(1+z)^n+(1-z)^n\right] + \tfrac{1}{2}z\left[(1+z)^n-(1-z)^n\right]\\ &=&\frac{1}{2}\left[(1+z)^{n+1}+(1-z)^{n+1}\right]. \end{eqnarray*}](/articles/aa/full_html/2013/10/aa20763-12/aa20763-12-eq120.png) Let us define
Let us define 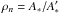 . For a planet having an intensity i⊕ relative to its star, a relevant performance indicator of nulling efficiency is the star/planet intensity ratio. This value is equal to | ρn | 2/i⊕. When closer it is to zero, the nulling interferometer is the more efficient. We have
. For a planet having an intensity i⊕ relative to its star, a relevant performance indicator of nulling efficiency is the star/planet intensity ratio. This value is equal to | ρn | 2/i⊕. When closer it is to zero, the nulling interferometer is the more efficient. We have
Behavior of | ρn | 2 at the edges of the bandwidths, where p = nmod 4.
 |
Fig. A.1 Contrast provided by the phase-shifter devices as measured by | ρn | 2. The plot starts from n = 1 for a Bracewell setup (black curve) and continue up to n = 10. A piston of λo/2 is applied on the even pupil. |
![\appendix \setcounter{section}{1} \begin{eqnarray} \rho_n=\frac{A_*}{A'_*}=\frac{(1+z)^n}{\frac{1}{2}\left[(1+z)^{n+1}\pm(1-z)^{n+1}\right]}\cdot \end{eqnarray}](/articles/aa/full_html/2013/10/aa20763-12/aa20763-12-eq134.png) (A.3)Within the interval φ ∈ (π/2,3π/2)mod 2π, (1 − z) is not equal to zero; therefore, one can write
(A.3)Within the interval φ ∈ (π/2,3π/2)mod 2π, (1 − z) is not equal to zero; therefore, one can write ![\appendix \setcounter{section}{1} \begin{eqnarray} \rho_n =\frac{1}{1-z}\frac{\biggl(\dfrac{1+z}{1-z}\biggr)^n}{\dfrac{1}{2}\Bigl[\biggl(\dfrac{1+z}{1-z}\biggr)^{n+1}\pm\!1\Bigr]}\cdot \end{eqnarray}](/articles/aa/full_html/2013/10/aa20763-12/aa20763-12-eq137.png) (A.4)As shown in Paper II, (1 + z)/(1 − z) is the stereographic projection on the imaginary axis of the affix z toward the complex (1,0). One gets (1 + z)/(1 − z) = jcot(φ/2), which is a complex whose modulus is less than 1 within the interval considered. For a given φ, such that
(A.4)As shown in Paper II, (1 + z)/(1 − z) is the stereographic projection on the imaginary axis of the affix z toward the complex (1,0). One gets (1 + z)/(1 − z) = jcot(φ/2), which is a complex whose modulus is less than 1 within the interval considered. For a given φ, such that 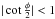 , the quantity ρn vanishes as
, the quantity ρn vanishes as 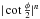 , when n goes to infinity. Therefore
, when n goes to infinity. Therefore
 |
Fig. A.3 Contrast when adopting, for the off-axis object, a supplementary constant phase of π applied indifferently on either the odd or the even pupil. The bandwidth derived from these curves do not differ significantly from those computed with the Figs. A.1 and A.2 curves. |
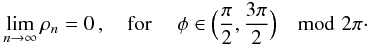 (A.5)This equation defines a principal bandwidth of (π/2,3π/2) or
(A.5)This equation defines a principal bandwidth of (π/2,3π/2) or 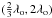 , as claimed in Paper II. Outside this bandwidth, when
, as claimed in Paper II. Outside this bandwidth, when ![\hbox{$\phi\in[0,\frac{\pi}{2})\cup(\frac{3\pi}{2},2\pi]\mod2\pi$}](/articles/aa/full_html/2013/10/aa20763-12/aa20763-12-eq147.png) , one gets
, one gets ![\appendix \setcounter{section}{1} \begin{eqnarray} \rho_n =\frac{2}{1+z}\frac{1}{\Bigl[1\pm\biggl(\dfrac{1-z}{1+z}\biggr)^{n+1}\Bigr]}, \end{eqnarray}](/articles/aa/full_html/2013/10/aa20763-12/aa20763-12-eq148.png) (A.6)where (1 − z)/(1 + z) = jtan(φ/2) is a complex of modulus <1. The limit of the intensity ratio (contrast), which retains only the term
(A.6)where (1 − z)/(1 + z) = jtan(φ/2) is a complex of modulus <1. The limit of the intensity ratio (contrast), which retains only the term 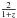 on ρn that does not depend upon n, is therefore given by
on ρn that does not depend upon n, is therefore given by 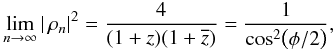 (A.7)where
(A.7)where 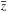 is the complex conjugate of z. The greatest possible contrast is equal to 2 near the extremities of the bandwidths. Exactly at these extremities, where z = ± j, one gets
is the complex conjugate of z. The greatest possible contrast is equal to 2 near the extremities of the bandwidths. Exactly at these extremities, where z = ± j, one gets 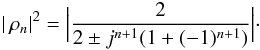 (A.8)The behavior of | ρn | 2 at the edges of the bandwidth depends on the rest of n + 1 modulo 4. This is summarized on Table A.1, where we have set n = 4k + p.
(A.8)The behavior of | ρn | 2 at the edges of the bandwidth depends on the rest of n + 1 modulo 4. This is summarized on Table A.1, where we have set n = 4k + p.
We have plotted | ρn | 2 in Figs. A.1 and A.2 for a λo/2 piston applied on the odd and the even pupil respectively. The curves have been computed for ten values of n, starting from n = 1 for a Bracewell to n = 10. We have also plotted in Fig. A.3 the approximation adopted in Paper II. This was where the piston is supposed to induce a constant phase shift of π on all wavelengths within the bandwidth. While this seems like a crude approximation, it is equivalent to the consideration that sin2(φ/2) ≈ 1 on the (π/2,3π/2)mod 2π intervals. Therefore it has little influence on the practical bandwidth approximation, as shown on the figure.
All Tables
Measured null depth in different broadband filters for one of the transmissive chessboard phase mask we manufactured.
Measured null depth in different narrow band filters, when using the reflective chessboard phase mask synthesized with the SDM.
All Figures
 |
Fig. 1 Theoretical attenuation (null depth) of an on-axis point source versus wavelength for a perfect chessboard device designed for the central wavelength of 650 nm. The different curves correspond to the order of the chessboard from m = 0, which is pure Bracewell (dark), to m = 5 (light blue). |
| In the text | |
 |
Fig. 2 The two patterns of phase chessboards used in DAMNED: the upper pattern corresponds to a reflective mask synthetized using a SDM and the lower pattern to a transmissive mask made in bulk optics my engraving a transparent plate. In both cases, φ = 0mod 2π (even) cells are on the left and φ = πmod 2π (odd) cells are on the right. The numbering on each cell is the phase shift in units of π. |
| In the text | |
 |
Fig. 3 Principle of nulling recombination on a single-mode fiber: on the left are the superimposed fringe pattern of a classical interferometer (black) and of a Bracewell interferometer (red). The amplitude of the black line is smaller on purpose, since it is supposed to correspond to the planet amplitude. On the right, a close-up of the central part of the fringes is shown with a shaded area that delineates the core of the single-mode optics which achieves the summation of the electric field it receives. The anti symmetric character of the Bracewell fringes (star signal) leads to the nulling effect, while the symmetry of the planetary electric field preserves the signal. |
| In the text | |
 |
Fig. 4 Optical scheme of DAMNED for the transmissive setup. |
| In the text | |
 |
Fig. 5 Optical scheme of DAMNED for the reflexive setup using a SDM. |
| In the text | |
 |
Fig. 6 Optical bench DAMNED. The blue and red lines indicate the travel of the beam for the main measuring channel and for the strioscopic channel, respectively. See Figs. 4, 5, and text for the details on the different components and their numbering. |
| In the text | |
 |
Fig. 7 Structure of the spatial filter used to remove low spatial frequency in the strioscopic setup used to flatten the SDM. |
| In the text | |
 |
Fig. 8 Images of the segmented mirror surface. Upper left: without the spatial filter of Fig. 7 put in place. Upper right: with the spatial filter but with the same voltage (135 V) applied to all actuators, so that they are at about half stroke. Bottom: applying the flattenning procedure (see text). Note that the contrast has been artificially enhanced in each case. |
| In the text | |
 |
Fig. 9 Upper right: simulated image at λ = 560 nm of the nulled PSF, which considers the measured phase unaccuracy on the transmissive chessboard. Upper left: the measured PSF obtained by scanning the SMFO. One pixel corresponds to one step of displacement of the SMFO of 200 nm. Middle panel: same as upper panel but at the wavelength of 650 nm. Lower panel: same as upper panel but in a broad wavelength range of about 450–840 nm. |
| In the text | |
 |
Fig. 10 Measured null depth of the transmissive chessboard phase mask in different broadband filters (colored segments of line), which include the large band of 470–830 nm. The black line is the theoretical performance of a perfect component and the green line is the simulated null depth of the real device when the minimum of the fringe pattern is used. The blue line which is the same quantity when using just the central pixel value as the measure, assumes that the fiber will be placed there and not moved (as it would likely be in the case of a space experiment). The dotted line gives the nulling depth for a perfect Bracewell interferometer. |
| In the text | |
 |
Fig. 11 Images at different wavelengths of the fringe pattern; they were obtained by direct imaging on a CCD camera of the Fizeau recombined focus. The label at top of each image gives the wavelength. The last image corresponds to no filter. |
| In the text | |
 |
Fig. 12 Null depth measured in four narrowband filters using the reflexive chessboard phase mask (short segments of line). The curves give the theoretical null depth of a perfect component. The red color refers to a null depth based on a non-nulling reference produced by a flattened chessboard; the blue color refers to a reference produced by adding a λo/2 opd to one pupil of the chessboard: it measures a star-to-planet contrast ratio than a null depth (see text). The dotted line gives the nulling depth for a perfect Bracewell interferometer. |
| In the text | |
 |
Fig. 13 Images without any filter of the fringe pattern, when the two pupils on the SDM are separated by 4 cells (1.2 mm). |
| In the text | |
 |
Fig. 14 Blue line: measured null depth, when the wavelength is fixed (laser diode) and the piston of the cells on the SDM is scanned to maintain a nulling phase pattern at each step for the reference wavelength, as indicated on the horizontal axis. The bandpass at a null depth level of 10-2 is indicated by the horizontal straight line. Solid black line: null depth in a perfect case. Dotted line: nulling depth for a perfect Bracewell interferometer. |
| In the text | |
 |
Fig. A.1 Contrast provided by the phase-shifter devices as measured by | ρn | 2. The plot starts from n = 1 for a Bracewell setup (black curve) and continue up to n = 10. A piston of λo/2 is applied on the even pupil. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 but with a piston of λo/2 applied on the odd pupil. |
| In the text | |
 |
Fig. A.3 Contrast when adopting, for the off-axis object, a supplementary constant phase of π applied indifferently on either the odd or the even pupil. The bandwidth derived from these curves do not differ significantly from those computed with the Figs. A.1 and A.2 curves. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


