| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220560 | |
| Published online | 07 October 2013 | |
Orbits and masses in the young triple system TWA 5 ⋆
1
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
e-mail: koehler@mpia.de
2
Universitäts-Sternwarte München,
Ludwig-Maximilians-Universität, Scheinerstr. 1, 81679
München,
Germany
3
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748
Garching bei München,
Germany
4
Institute for Astronomy, University of Hawaii,
34 Ohia Ku Str., Pukalani, HI
96768,
USA
Received: 15 October 2012
Accepted: 25 August 2013
Aims. We aim to improve the orbital elements and determine the individual masses of the components in the triple system TWA 5.
Methods. Five new relative astrometric positions in the H band were recorded with the adaptive optics system at the Very Large Telescope (VLT). We combine them with data from the literature and a measurement in the Ks band. We derive an improved fit for the orbit of TWA 5Aa-b around each other. Furthermore, we use the third component, TWA 5B, as an astrometric reference to determine the motion of Aa and Ab around their center of mass and compute their mass ratio.
Results. We find an orbital period of 6.03 ± 0.01 years and a semi-major axis of 63.7 ± 0.2 mas (3.2 ± 0.1 AU). With the trigonometric distance of 50.1 ± 1.8 pc, this yields a system mass of 0.9 ± 0.1 M⊙, where the error is dominated by the error of the distance. The dynamical mass agrees with the system mass predicted by a number of theoretical models if we assume that TWA5 is at the young end of the age range of the TW Hydrae association. We find a mass ratio of MAb/MAa = 1.3-0.4+0.6 , where the less luminous component Ab is more massive. This result is likely to be a consequence of the large uncertainties due to the limited orbital coverage of the observations.
Key words: stars: low-mass / brown dwarfs / stars: fundamental parameters / stars: individual: TWA 5 / binaries: close / celestial mechanics
© ESO, 2013
1. Introduction
The mass is the most important parameter for the structure and evolution of a star. Therefore, empirical mass determinations are crucial for our understanding of stellar astrophysics. In particular, this is the case for low-mass pre-main-sequence (PMS) stars and brown dwarfs, where a number of evolutionary models with different mass predictions exist (e.g., D’Antona & Mazzitelli 1997; Baraffe et al. 1998; Palla & Stahler 1999; Siess et al. 2000; Tognelli et al. 2011). Binary stars are the only way to measure stellar masses directly without relying on theoretical models. They are therefore valuable test cases for theoretical PMS tracks.
The TW Hydrae association is one of the closest associations of young stars with a median distance of 56 pc (Weinberger et al. 2013). Its members have been shown to be young (~5–15 Myr), based on lithium abundance tests and their positions in the H-R diagram (Weintraub et al. 2000, and references therein). The TW Hydrae association is therefore an ideal region for studying spatially resolved PMS binaries.
The object TWA 5 is one of the five original members of the TW Hydrae association identified by Kastner et al. (1997). It is composed of at least three components: a pair of low-mass stars; TWA 5Aa-b, which had a separation of 55 mas when it was discovered by Macintosh et al. (2001); and a brown dwarf companion, TWA 5B, located about 2′′ away (Webb et al. 1999). Konopacky et al. (2007) presented an orbital solution for the inner binary with a period of 5.94 ± 0.09 years and a semi-major axis of 66 ± 5 mas, which results in a binary system mass of 0.71 ± 0.14 M⊙ (for a distance of 44 pc).
In this paper, we present new relative astrometric measurements collected between 2007 and 2013. The binary has completed two full orbits since its discovery in 2000 and one orbit since the work of Konopacky et al. (2007). We combine the new data with data from the literature to derive an improved orbit solution. Furthermore, Weinberger et al. (2013) published new results for the parallax of TWA 5, which significantly changes and improves the mass estimates from orbit determinations.
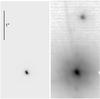 |
Fig. 1 Image of TWA 5Aa/b and TWA 5B taken with NACO in January 2012. North is up and east is to the left. Both panels show the same image with a linear scale on the left and with a logarithmic scale on the right to unveil the low-mass companion TWA 5B. |
2. Observations and data reduction
The first new observations were taken in 2007 and 2008 in the course of a different project and have been retrieved from the archive of the European Southern Observatory (ESO). The data was recorded with NAOS/Conica (NACO for short), the adaptive optics, near-infrared camera at the ESO Very Large Telescope (VLT) on Cerro Paranal, Chile (Rousset et al. 2003; Lenzen et al. 2003). The Ks photometric filter with a central wavelength of 2.18 μm was used. The resulting diffraction limit is λ/D = 56 mas.
In 2011, we started monitoring the orbital motion of TWA 5. The observations were also carried out with NACO but in the H-band filter with a central wavelength of 1.66 μm, which gives a smaller diffraction limit of 43 mas. We used the S13 camera, which provides a field of view of ~13.6″ × 13.6″. To allow the use of speckle-interferometric algorithms (see below), we employed the cube-mode of CONICA and recorded many exposures with short integration times of 0.2 s each. One cube contained typically ~100 images. Eight cubes at different positions on the detector chip were taken at each epoch.
The NACO images were sky subtracted with a median sky image, and bad pixels were replaced by the median of the closest good neighbors. Figure 1 shows an example of the result. The separation of the binary is close to the diffraction limit, which makes it difficult to disentangle the point spread functions of the two components in the images. Therefore, we used our software for speckle interferometry (see e.g. Köhler et al. 2000). In this program, the modulus of the complex visibility (i.e., the Fourier transform of the object brightness distribution) is determined from power spectrum analysis. The phase is computed using the Knox-Thompson algorithm (Knox & Thompson 1974) and from the bispectrum (Lohmann et al. 1983). Examples of the results are presented in Figs. 2 and 3.
For the deconvolution of speckle images, an unresolved star is required to calibrate the point spread function (PSF). Initially, we used TWA 5B for this purpose, since it is present in all our frames and well separated from TWA 5A so that the PSFs do not overlap. In principle, TWA 5B is an ideal PSF reference, since it lies within the isoplanatic patch and was observed simultaneously with TWA 5A. However, it is much fainter, which results in a high noise level in the visibilities.
 |
Fig. 2 Modulus of the visibility of TWA 5Aa/b observed through the Ks filter in July 2007 and June 2008. The data points show the measurements, and the line in the plot for 2007 is the result of a fit of a binary model to the data. The line in the plot for 2008 does not show a fit to the data but shows the visibility for the position computed from the orbit. The separation predicted at this date is too small to be resolved, which is confirmed by the data. |
 |
Fig. 3 Modulus of the visibility of TWA 5Aa/b observed through the H filter between 2011 and 2013. The data points show the measurements and the lines are the results of fits of binary models to the data. |
Starting with our own observations in 2011, we observed the binary HIP 56620 immediately after TWA 5 to calibrate the pixel scale and orientation. We tried using the brighter component of HIP 56620 to deconvolve the speckle-images of TWA 5A. Although the observations were not intended for this, we found that the reconstructed visibilities are significantly less noisy than those based on TWA 5B. Therefore, we used the visibilities deconvolved with HIP 56620 for the astrometric measurement.
The final complex visibility was computed by averaging moduli and phases derived from the eight data cubes. The parameters of the binary (separation, position angle, and flux ratio) are determined by a multidimensional least-squares fit of a binary model to the complex visibility. Uncertainties were estimated by fitting each of the individual visibilities computed from one of the eight data cubes. The standard deviation of the results were adopted as the error of the relative positions.
In 2007, the separation of the binary was smaller than the diffraction limit λ/D = 56 mas of the observations but larger than λ/2D. This means that the first minimum of the visibility but not the following maximum was measured (see Fig. 2). As a result, the position derived from these measurements has a larger uncertainty than the other observations.
The visibilities measured in June 2008 show no clear sign of binarity. This is not surprising, since the expected separation at the time of the observations is about 14 mas, which is significantly smaller than λ/2D in the Ks-band. The line in the lower right panel in Fig. 2 shows the visibility of the binary at the position predicted by the orbit we derive in Sect. 3. The data indicates that the binary is partially resolved and that the separation might be a bit larger than predicted. However, we do not regard this as a resolved measurement and do not use it in the orbit fit.
To measure the relative positions of TWA 5A and B, we used the starfinder program (Diolaiti et al. 2000). The program does not recognize that TWA 5A is a binary. Since TWA 5Aa and Ab have comparable brightness, the measured position is not centered on the brighter component but refers to the combined center of light of Aa and Ab.
2.1. Astrometric calibration
Since the observations in 2007 and 2008 were not intended for high-precision astrometry, no special measurements for the calibration of the plate scale and orientation of the camera were taken. We resorted to images of fields in the Orion Trapezium that had been taken for a different project in October 2007. These observations were done in the Ks filter, which is the same as the observations of TWA 5 in 2007 and 2008. We reduced the images of the Trapezium in the same way as the images of the science target. The starfinder program was used to measure the positions of the cluster stars on the detector. The pixel positions were compared to the coordinates given in Close et al. (2012), which in turn are based on HST-positions of a few cluster stars. We computed the mean pixel scale and orientation of NACO from a global fit of all star positions. The scatter of values derived from star pairs were used to estimate the errors. The pixel scale was determined as (13.271 ± 0.013) mas/pixel. The position angle (PA) of the vertical axis of the detector was (0.43 ± 0.10)° (measured from north to east).
During our astrometric monitoring program in 2011 to 2013, images of the Hipparcos-binary HIP 56620 were taken. However, we found that its relative position in January 2011 was significantly different from the position measured by Hipparcos about 20 years earlier (see Appendix A). Furthermore, we found a systematic change of the position with time, which led us to the conclusion that the relative position of HIP 56620 is not stable enough to serve for the astrometric calibration of NACO.
Therefore, we decided to rely on the Trapezium cluster for the calibration of all our observations. Two data sets are available from the ESO archive that were recorded on 30 January 2011 and 2 January 2012. The average pixel scale resulting from these data was (13.285 ± 0.013) mas/pixel, and the average PA of the y-axis of the images was (0.81 ± 0.1)° (measured from north to east)1. These values were used to calibrate our measurements. The errors of the calibration were added to the errors of the measurements when we computed the relative positions.
The calibrated positions of TWA 5Ab relative to TWA 5Aa are listed in Table 1 with data taken from the literature. Table 2 contains the positions of TWA 5B relative to the photocenter of A. They agree well with the result of Weinberger et al. (2013).
Astrometric measurements of TWA 5 Aa-b.
3. Orbit of TWA 5Aa-b
We estimated the orbital parameters of TWA 5Aa-b by fitting orbit models to the observations listed in Table 1. We used a grid-search for eccentricity e, period P, and time of periastron T0, a procedure used previously (e.g., Köhler et al. 2008, 2012). At each grid point, the Thiele-Innes elements were determined by a linear fit to the observational data using singular value decomposition. From the Thiele-Innes elements, the semi-major axis a, the angle between node and periastron ω, the position angle of the line of nodes Ω, and the inclination i were computed.
Since the orbit of TWA 5Aa-b is already well known (Konopacky et al. 2007), only a small range of parameter values had to be scanned: 100 points within 0.5 ≤ e < 1.0, 100 points within 5.8 yr ≤ P < 6.3 yr, and initially 200 points for T0 distributed over one orbital period. After the initial scan over T0, the best estimate for T0 was improved by re-scanning a narrower range of T0 centered on the minimum that was found in the coarser scan. This grid refinement was repeated until the step size was less than one day.
We improved the results of the grid-search with a Levenberg-Marquardt
χ2 minimization algorithm (Press et al. 1992) that fits for all 7 parameters simultaneously. The simple
approach would be to use the orbital elements with the minimum
χ2 found with the grid-search. However, initial test runs
showed that the algorithm does not converge on the global minimum. For the same reason, we
did not use the previously published orbit solution as a starting point. To make sure we
find the global minimum value of χ2, we decided to use all
orbits resulting from the grid-search as starting points that had
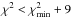 . The number 9 was chosen arbitrarily to
avoid starting from orbits that are obviously bad. The orbit with the global minimum
χ2 found by the Levenberg-Marquardt fit is shown in Fig. 4, and its elements are listed in Table 3. To convert the semi-major axis from mas to AU, we used
the new trigonometric distance of 50.1 ± 1.8 pc (Weinberger et al. 2013).
. The number 9 was chosen arbitrarily to
avoid starting from orbits that are obviously bad. The orbit with the global minimum
χ2 found by the Levenberg-Marquardt fit is shown in Fig. 4, and its elements are listed in Table 3. To convert the semi-major axis from mas to AU, we used
the new trigonometric distance of 50.1 ± 1.8 pc (Weinberger et al. 2013).
Astrometric measurements of TWA 5B relative to the photocenter of TWA 5A.
 |
Fig. 4 The orbit of component TWA 5Ab around Aa. The observed positions are marked by their error ellipses and lines connecting the observed and calculated position at the time of the observations. The dash-dotted line indicates the line of nodes and the solid line the periastron. The crosses mark the expected positions at the beginning of the years 2008 to 2013. |
We compute χ2 with the formula
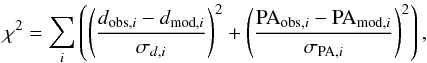 where d and PA are separations
and position angles2, respectively,
σd and σPA are
their respective errors, while the indices, obs and mod, mark the observations and model
predictions. The sum is computed over the observations.
where d and PA are separations
and position angles2, respectively,
σd and σPA are
their respective errors, while the indices, obs and mod, mark the observations and model
predictions. The sum is computed over the observations.
The two rightmost columns in Table 1 list the differences of d and PA between the observations and the model. Most of the differences are less than 2σ. The biggest outlier is the separation in January 2012. We inspected the raw data and found that the peak of the PSF was so bright that it reached into the non-linear regime of the detector. This might influence the position of the center of light and therefore cause a bias in our measurement. Therefore, we decided to omit the data point of January 2012 from our orbit fit. This changes the reduced χ2 from 3.5 to 2.1, the semi-major axis from 3.1 to 3.2 AU, and the system mass from 0.80 to 0.90 M⊙.
Errors of the orbital elements were determined by studying the
χ2 function around its minimum. The uncertainty for each
parameter corresponded to the point where 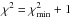 . The reduced χ2
of our fit was 2.1, a bit more than one would expect for a good fit. This indicated that
some of the errors might have been underestimated. To avoid underestimating the errors of
the orbital elements as well, we rescaled the errors of the observations so that the minimum
χ2 was 1. Although some of the observations showed larger
deviations from the model than others, we had no reason to trust any of the measurements
less than the others. Therefore, we multiplied all observational errors by the same factor
. The reduced χ2
of our fit was 2.1, a bit more than one would expect for a good fit. This indicated that
some of the errors might have been underestimated. To avoid underestimating the errors of
the orbital elements as well, we rescaled the errors of the observations so that the minimum
χ2 was 1. Although some of the observations showed larger
deviations from the model than others, we had no reason to trust any of the measurements
less than the others. Therefore, we multiplied all observational errors by the same factor
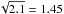 . The errors of the orbital elements in Table
3 were based on χ2
computed with these scaled measurement errors, while the deviations between model and
observations listed in Table 1 were computed with the
original measurement errors.
. The errors of the orbital elements in Table
3 were based on χ2
computed with these scaled measurement errors, while the deviations between model and
observations listed in Table 1 were computed with the
original measurement errors.
Estimating the error of the mass required a special procedure. The mass itself was computed using Kepler’s third law (M = a3/P2, Kepler 1619). The semi-major axis a and the period P are usually strongly correlated. To obtain a realistic estimate for the mass error, we did not use standard error propagation. Instead, we considered a set of orbital elements where the semi-major axis was replaced by the mass. This is possible because Kepler’s third law gives an unambiguous relation between the two sets of elements. With the mass being one of the orbital elements, we treated it as one of the independent fit parameters and determined its error in the same way as for the other parameters.
Parameters of the best orbital solution.
To check whether our error estimates for the orbital elements are reasonable, we employed the jackknife method. We removed one epoch of our set of observations and repeated the orbit fit with the remaining data. This was repeated for all observations with the exception of May 2002 and December 2003. These two points are the sole measurements in the north- and southwestern sections of the orbits. The standard deviations of the orbital elements resulting from this set of orbit fits are comparable in size to the error estimates obtained by χ2-analysis. The most important disparities are the errors of the semi-major axis, where the jackknife method yields an error of ±0.95 mas, and the system mass with a fit-error of ±0.037 M⊙. However, if the error of the distance is included, the total error of the mass is ±0.1 M⊙, which is the same as the error obtained by χ2-analysis.
4. Orbit of TWA 5B and mass ratio Aa/Ab
The orbit of components TWA 5Aa and Ab around each other allows us to determine only the combined mass of TWA 5Aa and Ab (which we will abbreviate as Aa and Ab from now on). To compute the individual masses, we need to know the mass ratio q, which can be computed if the position of the center of mass (CM) of Aa and Ab is known. Unfortunately, we cannot observe the CM directly. However, we know that TWA 5B is in orbit around the CM of Aa and Ab and that Aa and Ab are in orbit around their CM. The CM is always on the line between Aa and Ab, and its distance from Aa is the constant fraction3, f = q/(1 + q), of the separation of Aa and Ab. With this information, the relative positions of TWA 5Aa, Ab, and B are sufficient to solve for the orbit of TWA 5B and the mass ratio Aa/Ab.
We follow the method that we used previously to derive individual masses in the triple systems T Tauri and LHS 1070 (Köhler et al. 2008, 2012). The position of the CM of Aa and Ab is described in two ways: first, it is on a Kepler-orbit around TWA 5B, which is described by seven orbital elements (for the mathematical description of the Kepler-orbit, it is irrelevant whether we put the CM or TWA 5B in the center). Second, the position of the CM can be computed from the observed positions of Aa and Ab, and the mass ratio (which is treated as a free parameter). Standard error propagation is used to obtain an error estimate for this position. To compute χ2, we compare the position of the CM from the orbit around TWA 5B to the position derived from the observations. Our model has therefore eight free parameters: the seven elements, which describe the orbit of the CM of Aa+Ab around B, and the parameter f = q/(1 + q). We chose to use the parameter f instead of the mass ratio q, since f is confined to the range 0 to 1, while q is a number between 0 and infinity. Therefore, f is better suited to a grid search.
We have only five two-dimensional measurements of the relative position of TWA 5B. The PA
changed by less than 2° over the course of the observations. These data do not constrain the
orbit very well. Furthermore, the system mass of the best-fitting orbit model is
6.4 M⊙, which is much too high for TWA 5. To improve the
situation, we also use our knowledge of the total system mass. Our orbit fit for TWA 5Aa-b
yielded a combined mass of TWA 5Aa and Ab of 0.9 ± 0.1 M⊙.
TWA 5B is a brown dwarf (Webb et al. 1999); its mass
cannot be higher than ~0.1 M⊙. To compute
χ2 in our orbit fit, we add a term of the form
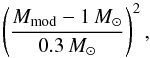 where Mmod is the
total system mass of the model. We adopted a large error of
0.3 M⊙ for our mass estimate, since we want the orbit fit to
be constrained mainly by the astrometric data. We repeated the fit with mass errors of 1, 3,
and 10 M⊙ to see how it affects the system mass determined by
the fit results. Only a mass error of 10 M⊙ leads to a small
change of the system mass from 1.1 to 1.3 M⊙. Changing the
mass error had no effect on the mass ratio.
where Mmod is the
total system mass of the model. We adopted a large error of
0.3 M⊙ for our mass estimate, since we want the orbit fit to
be constrained mainly by the astrometric data. We repeated the fit with mass errors of 1, 3,
and 10 M⊙ to see how it affects the system mass determined by
the fit results. Only a mass error of 10 M⊙ leads to a small
change of the system mass from 1.1 to 1.3 M⊙. Changing the
mass error had no effect on the mass ratio.
 |
Fig. 5 The motion of component TWA 5B relative to Aa. The observed positions are marked by their error ellipses and lines connecting the observed and calculated position at the time of the observations. The dashed line is the Kepler-orbit around the center of mass of Aa and Ab. The solid line is our best fit for the motion of B relative to Aa. The dotted line is the best fit if the mass ratio Aa/Ab is fixed at 1 or equal masses. |
Parameters of the best orbital solution for A–B.
 |
Fig. 6 The motion of component TWA 5B relative to Aa. Note that this is a combination of the orbit of B and the orbit of Aa, which are both around the CM of Aa/Ab. The error bars are the measurements, the solid line is the best fit with the mass ratio Ab/Aa as a free parameter. The dotted line shows the best-fitting orbit if the mass ratio is fixed at 1 or for equal masses of Aa and Ab. |
The fitting procedure is similar to that used for the orbit of Aa-Ab, except that the grid-search is carried out in four dimensions: eccentricity e, period P, time of periastron T0, and the fractional mass f. Singular value decomposition was used to fit the Thiele-Innes constants, which give the remaining orbital elements. It is worth noting that the orbital elements in this fit describe the orbit of the A-B binary, only the fractional mass f refers to the pair Aa-Ab.
The four dimensional grid ranged from 0.3 to 0.7 in f, 0 to 0.25 in e, and 100 to 3000 years in P. The grid in T0 started with 100 points distributed uniformly over one orbital period. Similar to the fit for the orbit of Aa-Ab, the grid in T0 was refined until the grid spacing was less than one day.
The parameters of the orbit with the globally minimum χ2 are
listed in Table 4. To estimate the errors, we
employed the same method as in Sect. 3. We vary one
parameter to find the point where 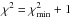 . Since
. Since
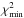 is smaller than 1, the measurement errors
were used without scaling. The motion of TWA 5B relative to component Aa is shown in Figs.
5 and 6.
is smaller than 1, the measurement errors
were used without scaling. The motion of TWA 5B relative to component Aa is shown in Figs.
5 and 6.
The reduced χ2 of 0.4 is surprisingly low, considering that the fit is essentially based on the same data as the fit for the inner orbit. However, five astrometric positions correspond to ten measurements, just two more than the eight parameters of the fit. This means that our capability to detect inconsistencies in the data is limited.
The mass ratio of 1.3 means that the component Ab is more massive than Aa. Since Aa is brighter, one would expect it to be more massive, resulting in a mass ratio slightly below 1. However, the uncertainties of our fit are large. A mass ratio of 0.9 is within the 68.3% confidence interval of our fit. The uncertainties are caused by the incomplete orbital coverage of our observations (see Fig. 5). All our measurements of the position of TWA 5B have been collected when Ab was in the northeast section of its orbit. An observation in 2010, when Ab was in the southwest part of its orbit, would have helped to measure the diameter of the astrometric wobble of Aa around the CM. Thanks to the period of Aa-Ab, this part of the orbit will be reached again in 2015/2016.
 |
Fig. 7 Mass vs. age for the models with the same luminosity as TWA 5Aa and Ab. The error bars indicate the measured age and system mass of TWA 5A. The first panel shows the combined mass of Aa and Ab, while the second and third panel show the individual masses of Aa and Ab, respectively. |
5. Comparison to theoretical models
The aim of dynamical mass determinations is to test the predictions of theoretical PMS. The simplest way to do this would be to pick a model with the measured mass, and compare the predicted brightness at the age and distance of the object to the measured brightness. However, theoretical models follow the evolution of individual stars, while our orbit yields the system mass, which is the sum of the masses MAa + MAb. Individual masses computed with the mass ratio derived in Sect. 4 have larger uncertainties and are therefore less useful for comparing to theoretical predictions (see below).
For now, we can go the other way: we take the resolved bolometric luminosities (Konopacky et al. 2007, who derived them from H-band magnitudes and bolometric corrections for PMS stars). We compute absolute luminosities with the new trigonometric distance (Weinberger et al. 2013). Then, we find the corresponding theoretical models for TWA 5Aa and Ab, interpolating between tracks with different masses if necessary. Finally, we compare the sum of the predicted masses to the dynamical system mass derived here.
The first panel in Fig. 7 shows the system mass as a function of age predicted by the models of Baraffe et al. (1998), Palla & Stahler (1999), Siess et al. (2000), and Tognelli et al. (2011). Overplotted is the system mass of TWA 5A resulting from our orbit fit and the age of the TW Hydrae association. The age is well constrained to be 5–15 Myr by a number of methods (Weintraub et al. 2000, and references therein).
At first glance, all the models reproduce the data fairly well; most of them are within 1σ. The models of Baraffe et al. (1998) predict a younger age or higher mass but also reasonably agree with the data.
The second and third panel in Fig. 7 show similar plots for the individual masses. The mass of TWA 5Aa is lower than predicted, while the mass of Ab is in good agreement with the models. However, one should keep in mind that both masses are anti-correlated since the sum of both has to be 0.9 ± 0.1 M⊙ (note that the binary mass has been determined by the fit for the inner orbit and is in no way correlated with q). Therefore, a mass of Aa at the upper end of the error bar corresponds to a mass MAb at the lower end, which would also be different from the model predictions.
The models agree with the dynamical mass only if the age of TWA 5A is at the young end of the age range for the TW Hydrae association. By placing TWA 5A in an HR diagram, Weinberger et al. (2013) found an age of 9–11 Myr. With this age, the models predict a mass that is clearly higher than our dynamical mass. The cause for this discrepancy is not clear, but we note that the HRD would give a younger age and lower masses if TWA 5 was cooler than the temperature derived from its spectral type. A temperature of ~3500 K would yield results that agree with the dynamical mass.
6. Conclusions and outlook
We present new relative positions of TWA 5Aa and Ab and derive new orbital elements from them. The system mass of 0.9 ± 0.1 M⊙ resulting from the new orbit is larger than the mass estimate previously obtained (Konopacky et al. 2007) due to the larger distance based on the trigonometric parallax by Weinberger et al. (2013). With the new distance, the orbit of Konopacky et al. (2007) yields a mass of 1.0 ± 0.2 M⊙. The uncertainty of the mass determination resulting from the new orbit fit is substantially smaller than before. The uncertainty of the orbit fit is negligible compared to the uncertainty of the distance. This situation will improve when the astrometric satellite Gaia delivers precise parallaxes.
We used the third component TWA 5B as astrometric reference to measure the individual motion of TWA 5Aa and Ab around their center of mass. From this, we can derive the mass ratio of Aa and Ab and hence individual masses of the two components. Unfortunately, our relative measurements of TWA 5Aa, Ab, and B cover only the northeast section of the inner orbit, resulting in large uncertainties for the mass ratio. It will reduce the errors significantly if the system is observed again in 2015/2016, when component Ab is in the southwest part of its orbit.
A comparison of the dynamical mass(es) with those predicted by a number of theoretical models shows that all models considered are in reasonable agreement with the data. The errors of the mass and age determinations are still too large to distinguish between the models.
Dynamically, this system is an interesting case because it might be in Kozai resonance (Kozai 1962). This would explain the high eccentricity of the inner orbit. An analysis of its dynamics will be published elsewhere (Beust et al., in prep.).
As a secondary result, our data demonstrate that astrometric observations with NACO could be affected by a scatter in the instrument’s orientation of 0.1–0.2° with occasional larger jumps that can be explained by technical interventions. The cause for the random scatter could not be clarified with only one dataset at hand. To guarantee high-precision astrometry, it would require astrometric standards being present within the observed field of view. If no standards in the field are available, a calibration field should be observed shortly before or after the science target.
The difference in orientation measured in 2007 can be explained by one or more technical interventions on NACO in 2008 (Kervella et al. 2013).
It is also possible to compute χ2 from the relative position in x and y. This results in a different χ2 unless correlations between x and y are considered. We expect d and PA to be uncorrelated, since their errors are mostly caused by different effects (changes in pixel scale and rotation of the camera).
The parameter f is often called fractional mass (Heintz 1978), since it is the secondary star’s fraction of the total mass in a binary. It is useful in our case because it also describes the fractional offset of the CM from Aa, which is the separation Aa–CM divided by the separation Aa–Ab.
References
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Brandeker, A., Jayawardhana, R., & Najita, J. 2003, AJ, 126, 2009 [NASA ADS] [CrossRef] [Google Scholar]
- Close, L. M., Puglisi, A., Males, J. R., et al. 2012, ApJ, 749, 180 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., & Mazzitelli, I. 1997, Mem. Soc. Astron. Italiana, 68, 807 [Google Scholar]
- Diolaiti, E., Bendinelli, O., Bonaccini, D., et al. 2000, A&AS, 147, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heintz, W. D. 1978, Double Stars, Geophysics and Astrophysics Monographs No. 15 (Dordrecht, Holland: D. Reidel Publishing Company) [Google Scholar]
- Kastner, J. H., Zuckerman, B., Weintraub, D. A., & Forveille, T. 1997, Science, 277, 67 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kervella, P., Mérand, A., Petr-Gotzens, M. G., Pribulla, T., & Thévenin, F. 2013, A&A, 552, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knox, K. T., & Thompson, B. J. 1974, ApJ, 193, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, R., Kunkel, M., Leinert, C., & Zinnecker, H. 2000, A&A, 356, 541 [NASA ADS] [Google Scholar]
- Köhler, R., Ratzka, T., Herbst, T. M., & Kasper, M. 2008, A&A, 482, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Köhler, R., Ratzka, T., & Leinert, C. 2012, A&A, 541, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Konopacky, Q. M., Ghez, A. M., Duchêne, G., McCabe, C., & Macintosh, B. A. 2007, AJ, 133, 2008 [NASA ADS] [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, W., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Proc., 4841, 944 [Google Scholar]
- Lohmann, A. W., Weigelt, G., & Wirnitzer, B. 1983, Appl. Opt., 22, 4028 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Macintosh, B., Max, C., Zuckerman, B., et al. 2001, in Young Stars Near Earth: Progress and Prospects, eds. R. Jayawardhana, & T. Greene, ASP Conf. Ser., 244, 309 [Google Scholar]
- Palla, F., & Stahler, S. W. 1999, ApJ, 525, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., & ESA 1997, The Hipparcos and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA Hipparcos Space Astrometry Mission, ESA SP 1200 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in C, 2nd edn. (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, in Adaptive Optical System Technologies II, eds. P. L. Wizinowich, & D. Bonaccini, SPIE Proc., 4839, 140 [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
- Tognelli, E., Prada Moroni, P. G., & Degl’Innocenti, S. 2011, A&A, 533, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Webb, R. A., Zuckerman, B., Platais, I., et al. 1999, ApJ, 512, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberger, A. J., Anglada-Escudé, G., & Boss, A. P. 2013, ApJ, 762, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Weintraub, D. A., Saumon, D., Kastner, J. H., & Forveille, T. 2000, ApJ, 530, 867 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Astrometric calibration
One of the more challenging tasks when doing astrometry with NACO is the astrometric calibration, which is the determination of the precise pixel scale and orientation of the detector at the time of the observation. During our astrometric monitoring program of TWA 5 in 2011 to 2013, images of the Hipparcos-binary HIP 56620 (separation 3.390″, position angle 240.8°, Perryman & ESA 1997) were taken. To check whether the relative position of HIP 56620 has changed in the 20 years since the Hipparcos mission, we calibrated NACO with a set of images of the Orion Trapezium cluster taken on 30 January 2011. Following the procedure described in Sect. 2.1, we obtained a pixel scale of (13.281 ± 0.007) mas/pixel and a PA of (0.80 ± 0.02)°. With this calibration, we find that the separation of HIP 56620 on 27 January 2011 was (3.397 ± 0.002)″, and the PA was (240.27 ± 0.12)°. This position is significantly different from the position measured by Hipparcos about 20 years earlier.
Figure A.1 shows separation and position angle of HIP 56620 from all our observations in detector coordinates (separation in pixels, position angle measured counterclockwise from the y-axis of the images).
First, we note that the separation measured in the J-band is always larger by about 0.15% than the separation measured in H. It is unlikely that the positions of the photocenter of the stars depend on the wavelength. Instead, this shift can be explained by chromatic aberration of the optics in CONICA (R. Lenzen, priv. comm.). This means that the pixel scale of NACO is wavelength-dependent, albeit on a scale that has to be considered only for high-precision astrometry. To achieve the best precision, the pixel scale should always be calibrated in the same filter as the observations of the science target.
Second, we see a systematic change in both separation and position angle between May 2011 and January 2013. Orbital motion of the binary might be an explanation, except that the point in January 2011 does not follow the trend. The orbital period is far too long to explain this sudden change.
 |
Fig. A.1 Relative position of the components of HIP 56620 on the NACO detector. The position angle is in detector coordinates and measured counterclockwise from the y-axis. |
Third, HIP 56620 was observed twice on 17 January 2013 due to the scheduling of our observations by ESO. These are two independent observations with a new acquisition and optimization of the AO system. The separation measured in the two observations differs by about 0.1%, and the position angle by 0.17°. There is no difference between the observations that could explain this shift. Therefore, we believe that this represents the intrinsic precision of an astrometric observation of a binary with NACO. Unless some sources that can be used for calibration are within the field-of-view of the binary, the observations require moving the telescope from the calibration field
to the science target, which causes changes of the calibration parameters that are similar to our two observations of HIP 56620 on 17 January 2013.
Since we do not know the true separation and position angle of HIP 56620 during our observations, we decided not to use it for the astrometric calibration. Instead, our calibration is based on two data sets of the Trapezium cluster in Orion (Sect. 2.1). Observations of clusters have the advantage that they contain more than one star pair, which reduces the risk of undetected outliers. As an estimate for the errors of the calibration parameters, we adopt an error of 0.013 mas/pixel for the pixel scale and 0.1° for the orientation. This is larger than the scatter of the calibration measurements but closer to the systematic uncertainties of astrometric observations with NACO discussed in the previous paragraph.
All Tables
All Figures
 |
Fig. 1 Image of TWA 5Aa/b and TWA 5B taken with NACO in January 2012. North is up and east is to the left. Both panels show the same image with a linear scale on the left and with a logarithmic scale on the right to unveil the low-mass companion TWA 5B. |
| In the text | |
 |
Fig. 2 Modulus of the visibility of TWA 5Aa/b observed through the Ks filter in July 2007 and June 2008. The data points show the measurements, and the line in the plot for 2007 is the result of a fit of a binary model to the data. The line in the plot for 2008 does not show a fit to the data but shows the visibility for the position computed from the orbit. The separation predicted at this date is too small to be resolved, which is confirmed by the data. |
| In the text | |
 |
Fig. 3 Modulus of the visibility of TWA 5Aa/b observed through the H filter between 2011 and 2013. The data points show the measurements and the lines are the results of fits of binary models to the data. |
| In the text | |
 |
Fig. 4 The orbit of component TWA 5Ab around Aa. The observed positions are marked by their error ellipses and lines connecting the observed and calculated position at the time of the observations. The dash-dotted line indicates the line of nodes and the solid line the periastron. The crosses mark the expected positions at the beginning of the years 2008 to 2013. |
| In the text | |
 |
Fig. 5 The motion of component TWA 5B relative to Aa. The observed positions are marked by their error ellipses and lines connecting the observed and calculated position at the time of the observations. The dashed line is the Kepler-orbit around the center of mass of Aa and Ab. The solid line is our best fit for the motion of B relative to Aa. The dotted line is the best fit if the mass ratio Aa/Ab is fixed at 1 or equal masses. |
| In the text | |
 |
Fig. 6 The motion of component TWA 5B relative to Aa. Note that this is a combination of the orbit of B and the orbit of Aa, which are both around the CM of Aa/Ab. The error bars are the measurements, the solid line is the best fit with the mass ratio Ab/Aa as a free parameter. The dotted line shows the best-fitting orbit if the mass ratio is fixed at 1 or for equal masses of Aa and Ab. |
| In the text | |
 |
Fig. 7 Mass vs. age for the models with the same luminosity as TWA 5Aa and Ab. The error bars indicate the measured age and system mass of TWA 5A. The first panel shows the combined mass of Aa and Ab, while the second and third panel show the individual masses of Aa and Ab, respectively. |
| In the text | |
 |
Fig. A.1 Relative position of the components of HIP 56620 on the NACO detector. The position angle is in detector coordinates and measured counterclockwise from the y-axis. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


