| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 15 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201321068 | |
| Published online | 13 August 2013 | |
Direction dependent background fitting for the Fermi GBM data
1 Eötvös University, 1053 Budapest, Hungary
e-mail: zsolt.bagoly@elte.hu
2 MTA CSFK Konkoly Observatory, 1121 Budapest, Hungary
3 Argelander-Institute für Astronomie der Universität Bonn, 53121 Bonn, Germany
4 Bolyai Military University, 1581 Budapest, Hungary
Received: 8 January 2013
Accepted: 6 June 2013
Context. We present a method for determining the background of the gamma-ray bursts (GRBs) of the Fermi Gamma-ray Burst Monitor (GBM) using the satellite positional information and a physical model. Since the polynomial fitting method typically used for GRBs is generally only indicative of the background over relatively short timescales, this method is particularly useful in the cases of long GRBs or those that have autonomous repoint request (ARR) and a background with much variability on short timescales.
Aims. Modern space instruments, like Fermi, have some specific motion to survey the sky and catch gamma-ray bursts in the most effective way. However, GBM bursts sometimes have highly varying backgrounds (with or without ARR), and modelling them with a polynomial function of time is not efficient – one needs more complex, Fermi-specific methods. This article presents a new direction dependent background fitting method and shows how it can be used for filtering the lightcurves.
Methods. First, we investigate how the celestial position of the satellite may have influence on the background and define three underlying variables with physical meaning: celestial distance of the burst and the detector’s orientation, the contribution of the Sun and the contribution of the Earth. Then, we use multi-dimensional general least square fitting and Akaike model selection criterion for the background fitting of the GBM lightcurves. Eight bursts are presented as examples, of which we computed the duration using background fitted cumulative lightcurves.
Results. We give a direction dependent background fitting (DDBF) method for separating the motion effects from the real data and calculate the duration (T90, T50, and confidence intervals) of the nine example bursts, from which two resulted an ARR. We also summarize the features of our method and compare it qualitatively with the official GBM Catalogue.
Conclusions. Our background filtering method uses a model based on the physical information of the satellite position. Therefore, it has many advantages compared to previous methods. It can fit long background intervals, remove all the features caused by the rocking behaviour of the satellite, and search for long emissions or not-triggered events. Furthermore, many parts of the fitting have now been automatised, and the method has been shown to work for both sky survey mode and ARR mode data. Future work will provide a burst catalogue with DDBF.
Key words: gamma-ray burst: general / methods: data analysis / instrumentation: detectors / gamma rays: diffuse background
© ESO, 2013
1. Introduction
NASA’s Fermi Gamma-ray Space Telescope has an orbit of altitude ~565 km and period of ~96 min. It carries two main instruments on board. The Large Area Telescope’s (LAT) energy range (20 MeV − 300 GeV) overlaps the energy range of the Gamma-ray Burst Monitor (GBM, 8 keV − 40 MeV). GBM consists of two types of detectors: 12 sodium iodide (NaI) and 2 bismuth germanate-oxide (BGO) detectors (Meegan et al. 2009).
The primary observation mode of Fermi is sky survey mode. This enables the LAT to monitor the sky systematically, whilst maintaining an uniform exposure. In this mode, the entire sky is observed for ~30 min per 2 orbits. If a sufficiently bright GRB is detected by GBM, an autonomous repoint request (ARR) may be issued. This will cause the satellite to slew, so that the burst’s coordinates (calculated by the GBM) stay within the field of view of the LAT for ~2 h (Fitzpatrick et al. 2011). However, this repositioning right after the trigger results in rapid and high background rate variations of the GBM lightcurves – sometimes even during the burst, which is the most important time of the observation. Therefore, it is crucial to have a filtering method, which is capable of correcting for the background variations caused by the ARR.
To date, GBM has triggered on 1000 GRBs (GCN 2013), (Fermi-Timeline-Posting 2013). Only a small fraction (~70 GRBs) resulted an ARR (Paciesas 2013, priv. comm.). The relatively low rate of ARR’s is due to the GBM trigger that has to meet certain criteria (such as high peak flux) before an ARR occurs. When we started to analyse GRBs detected by GBM, we found that several non-ARR bursts have a background variation of the same order of magnitude as the burst itself. As we will show, one can find connection between these background rates and the actual position and orientation of the satellite. Therefore it is necessary to use the directional information to filter the background not only for ARR but also for many non-ARR cases.
Here, we present the effect of the slew and how it is represented in the measured data of the GBM. We summarize why the usual background subtraction methods are inefficient in most cases, especially for the long bursts, as seen in Sect. 2. Then, we introduce variables based on the position of the satellite related to the Earth and the Sun (Sect. 3) and use them with the time variable to fit a general multi-dimensional linear function to the background (Sect. 4). Our method is called direction dependent background fitting (DDBF).
We also present examples where we compute the duration (T90 and T50) from our background-filtered lightcurves and show that the DDBF method can be used for both the Sky Survey and ARR observations (Sect. 5). Confidence levels and a comparison to the GBM catalogue are given in Sect. 6.
 |
Fig. 1 Lightcurve of the Fermi burst 091030.613 measured by the 3rd GBM-detector without any background filtering with 1-s bins. The grey line is a fitted polynomial function of time of order 3 for the ranges of [− 200:− 20] and [38:200] s, which does not seem to be a correct model for this whole background. Reduced chi-square statistics are given in the top right corner (Szécsi et al. 2012a). |
2. Difficulties with the Fermi background
2.1. Lightcurves with unpredictably varying background
The lightcurve for GBM trigger 091030.613 is shown in Fig. 1 in the energy range ~11–980 keV. This burst did not result in an ARR (GCN 2013). We decided to use the sum of the channels except for the highest and lowest, where the detector’s efficiency drops, so the signal is statistically stronger. Since we are only interested in the duration information of the bursts, we use the high time resolution data (CTIME, see Sect. 3 for the detailed description) and sum of the channels. We note that, however, the analysis can be done using either different channels or the high spectral resolution data files (CSPEC), so spectral information can be obtained (see Szécsi et al. 2012b).
In Fig. 1, the burst is clearly visible above the background, but the background is varying so rapidly and to such an extent that one can question the usefulness of fitting and subtracting a simple polynomial function of order 3 (grey line in Fig. 1). This situation is typical in the case of Fermi, as can be seen in the examples in Sect. 5.2. Especially when a long burst occurs, the background rate can change too quickly for analyses without some knowledge about the satellite position and the gamma sources on the sky. In the following, we are investigating for possible background sources. We will see that one can find a correspondence between the gamma background and the celestial orientation of the satellite. Furthermore, both the Sun and the Earth limb have a contribution, given that they move in and out of the field of view because of the rocking motion of the satellite. Based on these physical conditions, we are constructing a background model and a fitting algorithm, both of which give us a more effective method for filtering the motion effects. Since the method is based on the actual directional information of the satellite, it is possible to analyse bursts for which an ARR was issued.
2.2. Previous methods
In the BATSE era, it was sufficient to fit a low-order polynomial in the function of time for most cases. It was because BATSE has had a fixed orientation and has not been able to change it during a burst. As a result, sources moving in and out of the field of view could not play an important role on a shorter timescale, and all the backgrounds could be subtracted by fitting a time-dependent low-order (up to 3) polynomial (Koshut et al. 1996; Sakamoto et al. 2008; Varga et al. 2005).
In the Fermi era, this situation has however fundamentally changed. To present this on our example above, we fitted a simple 3rd-order polynomial function of time shown with a grey line in Fig. 1. The fitting was done by using only a selected short time interval around the burst, which is a common method of the BATSE era. This fit may be sufficient around the burst prompt emission, but is sufficient only there. It is clear that the background cannot be well modelled with this simple function over a long timescale. Moreover, an incidental longtime emission would be overlooked.
Fitting higher order polynomials of time could be suggested. We rule out this solution because of two reasons. First, these fittings show polynomial instabilities in the burst interval, as we have seen it in our early experiments; namely, we got high order, low amplitude oscillations of these fittings during the interval of the burst. Second, we wanted to take into consideration that the main cause of the complicated background is well known (namely the rocking motion of the satellite). Indeed, we use physically defined underlying variables, as we will show in Sect. 4, and with them, we fit higher order multidimensional functions. As a conclusion, time-dependent polynomial fittings may have been sufficient for the BATSE data but Fermi-data cannot be analysed that way due to the rapid motion of the satellite: we need a Fermi specific method.
Such a method was presented by Fitzpatrick et al. (2011). They estimated the background successfully with the rates from adjacent days, when the satellite was at the same geographical coordinates. This solution is only applicable when the satellite is in sky survey mode and cannot be used if an ARR occurred. If an ARR is accepted, this technique cannot be employed.
3. Investigation of possible background sources
3.1. Orientation of NaI detectors
As we mentioned above, Fermi uses a complex algorithm to optimize the observation of the gamma-ray sky. In sky survey mode, the satellite rocks around the zenith within ± 50°, and the pointing alternates between the northern and southern hemispheres each orbit (Meegan et al. 2009; Fitzpatrick et al. 2011).
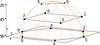 |
Fig. 2 Setup of the 12 NaI detectors of GBM given in the Spacecraft Coordinates (see Meegan et al. 2009). The zenith angle of the detectors in degrees is marked. This design is built in order to cover the whole visible part of the sky with the GBM. (The figure is based on Table 1. of Meegan et al. 2009. Notations “a” and “b” mean the 10th and 11th NaI detectors, respectively.) |
The set-up of the instruments on-board is well known from the literature (Meegan et al. 2009). The 12 NaI detectors are placed in such a way that the entire unocculted sky is observable with them at the same time, as seen in Fig. 2. Fermi has a proper coordinate system, whose Z axis is given by the LAT main axis. From now on, we only analyse the data of the NaI detectors; the BGO detectors will be considered in a future work.
The Fermi data set is available from the web for the GBM’s 12 NaI detectors1. The positional information of the spacecraft is contained in the LAT data (called Spacecraft Data2). The GBM data, which we use in our analysis (called CTIME), are available at 8 energy channels with 0.064-s and 0.256-s resolution (for triggered and non-triggered mode, respectively). The position data is available in 30-s resolution.
 |
Fig. 3 Orientation of the 12 NaI detectors on the sky (in the second equatorial system), during the pre- and post-1000 s around the burst 091030.613. To show the direction with time, we marked the starting points of every line with a small star. The Sun’s position is marked with big sphere. The burst position is marked with diamond. |
The 30-s Spacecraft Data were evenly proportioned to 0.256-s and 0.064-s bins using linear interpolation, to correspond to the CTIME data of non-triggered and triggered mode, respectively. We created a 3D-plot from this data using the known orientation of the 12 NaI detectors given in the Spacecraft coordinate system. Figure 3 shows the detectors’ orientation (path) on the sky during the pre- and post-1000 s around the trigger of 091030.613 (lightcurve was shown in Fig. 1).
The catalogue location for the GRB is shown with a diamond (α = 260.72°, δ = 22.67°, see Paciesas et al. 2012). Since we wanted to know the position of the detectors on the sky, we needed to transform the proper coordinate system of the Fermi shown in Fig. 2 to the general (second) equatorial system, since the burst’s position was given in the latter. In addition, we plot the celestial angle between the 3rd detector (black line in Fig. 3) and the burst 091030.613 (marked with a diamond in Fig. 3) against time in Fig. 4.
 |
Fig. 4 Celestial distance of the 3rd GBM detector and the Fermi-burst 091030.613 as a function of time. It is worth comparing this figure to Fig. 1. |
At this point, we have to mention the effect of the NaI detectors’ characteristics. Figure 12 from Meegan et al. (2009) shows the angular dependence of a NaI detector effective area: the angular response for the flat crystal is approximately cosine. For this reason, we define our first underlying variable as the cosine of the celestial angle between the detector and the burst (as it is shown in Fig. 4). We will find further underlying variables in Sects. 3.2 and 3.3.
However, the NaI characteristics are also energy dependent: The dependence of the transmissivity on the angle of incidence is more important at higher than at lower energies. Furthermore, a detector has two small sensitivity peaks around − 150 and 150 degrees, which means that they can detect photons coming under the plane of the crystal. We consider these features by allowing higher orders when performing the fits seen in Sect. 4.
If we compare Figs. 4 to 1, it is clear that the unpredictable variation in the background is connected to the orientation of the detector in question. We can also examine other bursts (see Sect. 5.2. for more examples). However, we cannot state a clear relation between the angle and the lightcurve.
3.2. Earth
The satellite’s Z axis (the direction of the LAT) is pointing to the opposite direction of the Earth, when it is possible. Due to the rocking behavior, GBM detectors’ orientation are, however, towards the Earth-limb from time to time.
The Earth-limb is notable from the board of Fermi. At an altitude of ~565 km, it corresponds to an aperture of ~134° when fully in the FoV. Therefore, we have to consider the effect of the Earth-limb when analysing the data of the GBM detectors. There are terrestrial gamma-ray flashes (brief bursts of gamma-radiation that are thought to be associated with lightning in the upper atmosphere); furthermore, gamma-rays of the GRB’s scatter on the atmosphere. The main contributor in our background model is the latter. Terrestrial gamma-ray flashes have a duration of only tens of milliseconds (Briggs et al. 2010) and are too short to have a significant effect.
We presume therefore that the detected background also depends on how much sky the Earth-limb shields from the detector’s FoV. To measure this, we define the Earth-occulted sky rate as the rate of the Earth-covered sky correlated to the size of the FoV. As Fermi has a proper motion, the Earth-occulted sky rate is a function of time, satellite position, and orientation. Based on spherical geometrical computations given in Appendix A, we can get the Earth-occulted sky rate as a function of the aperture of the Earth-limb and the maximum altitude of the Earth seen from the Fermi. The Earth-occulted sky rate is plotted in Fig. 5 as a function of time.
 |
Fig. 5 Earth-occulted sky rate for the 3rd GBM detector as a function of time during the GRB 091030.613. (The Earth-occulted sky rate is zero, if the Earth-limb is out of the FoV.) |
We can see the same effect like above: there is some noticeable connection between the lightcurve in Fig. 1 and the Earth-occulted sky rate in Fig. 5.
3.3. Sun
One of the main contributors of the gamma-ray sky is the Sun. Flares and other eruptive solar events produce gamma rays in addition to those created by cosmic rays striking the Suns gas. If we are looking for a complete model of the background, we need to consider the contribution of the Sun as well.
The Sun’s position is known from ephemeris tables for the day of the burst. We do not need more precise data than one day, because the time interval around the burst is only 2000 s in our analysis, and the position of the Sun does not change significantly during that time.
We compute the celestial distance (i.e. the angle) between the detector’s direction and the Sun’s position. This parameter is shown in Fig. 6. The Sun’s position is also shown in the Fig. 3 with a yellow circle.
 |
Fig. 6 Celestial distance of the 3rd GBM detector and the Sun as a function of time during the GRB 091030.613. The dashed line shows the 0 level (under this the Sun and the detector close in an angle larger than 90°). It is worth comparing this figure to Fig. 1. |
Comparing Figs. 1 to 6, one can see a connection between them. It is interesting to take notice of the fact that when the Sun’s angle is larger then 90° (the cosine is lower that 0) around 600 s, the background rate in Fig. 1 drops. It shows a further correspondence of the background and the direction of the satellite towards to the Sun.
3.4. Other gamma sources
It is known today that the gamma-ray sky is not dark (Ackermann et al. 2012). Apart from the gamma-ray bursts, the terrestrial flashes, and the Sun’s activity, there are also additional gamma-ray sources. Some examples include the gamma-rays produced when cosmic rays collide with gas in the Milky Way and the contribution from individual galactic sources, such as pulsars and other transient sources. As an extragalactic counterpart, we see collective radiation from galaxies that we are not detecting directly and gamma-rays from jets of active galaxies.
All this gamma-background has to be paid respect to. Rather than consider each contributing source individually, we introduce them into our model by allowing higher order terms when constructing the basis function of the general least square problem in Sects. 4.1 and 4.2. Furthermore, we use the method of singular value decomposition and Akaike model selection described in Sects. 4.3 and 4.4 for choosing the contributing ones, since the net effect of all these sources is hard to compute at every second.
4. Background subtraction
In Sect. 3, we have found three variables, which contribute to the variation in the background (see Figs. 4–6). They may help extend the polynomials of time that are only usable in some short intervals around the bursts. These three variables contain physical information of the background, because they are suggested by the actual position and orientation of the satellite.
However, we cannot quantify the contribution from the various sources at any given time. As we know that they have an influence on the background, we can fit a theoretical function of these physical underlying variables. Therefore, we fit and subtract the background using the three defined variables (burst position, Sun, and Earth) and the time variable, on a higher degree.
At this point, the following question may arise: why is the burst location needed? If a curve contains no burst for sure, there is no sense of using the burst position as an underlying variable. In that case, we would probably need to use only the Sun and the Earth (maybe implement the position of some other gamma-sources as well).
The reason why we use the burst position when there is a burst in the data is that the burst itself is a gamma source. Of course, it does not produce gamma photons at a constant level, but transiently. It is possible, nevertheless, that a not yet identified long emission would be enhanced (or weakened) because the satellite moved toward (or away of) the burst. To analyse (or sometimes even detect) emission coming from the astrophysical source outside of the main burst interval, it is needed to identify the fluctuations of the background rate caused by the change in the distance between the detector and the burst.
Next, we summarize the method of general least square for multidimensional fits, the algorithm of singular value decomposition, its numerical solution, and the Akaike model selection criterion for choosing the best model. Since we use underlying variables, which are calculated based on the actual direction and orientation of the satellite, we call this method direction dependent background fitting (DDBF).
4.1. General least square
For simplifying the explanation, we will use the following notation:
yi = counts per bin;
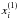 = celestial distance between burst and detector orientation (Fig. 4);
= celestial distance between burst and detector orientation (Fig. 4);
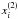 = celestial distance between Sun and detector orientation (Fig. 6);
= celestial distance between Sun and detector orientation (Fig. 6);
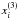 = rate of the Earth-uncovered sky (Fig. 5);
= rate of the Earth-uncovered sky (Fig. 5);
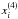 = time.
= time.
We have a set of datapoints (xi,yi), where the components of xi are 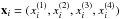 , while i = 1...N.
, while i = 1...N.
We use the general least square method (Press et al. 1992) for a multidimensional fit (since xi has more than one component). The theoretical value of y(xi) can be expressed with functions of xi, known as the basis functions Xk(xi): 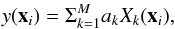 (1)where the weights ak are the model parameters that we need to estimate from the data (k = 1...M). Note that the basis functions Xk(xi) can be nonlinear functions of xi (this is why the method is called generalized), but the model depends only linearly on its parameters ak.
(1)where the weights ak are the model parameters that we need to estimate from the data (k = 1...M). Note that the basis functions Xk(xi) can be nonlinear functions of xi (this is why the method is called generalized), but the model depends only linearly on its parameters ak.
The maximum likelihood estimate of the model parameters ak is obtained by minimizing the quantity 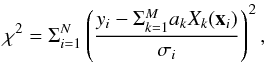 (2)which is known as the chi-square statistics or chi-square function.
(2)which is known as the chi-square statistics or chi-square function.
One can write the chi-square function in a matrix equation form as well. For that, it is useful for defining the design matrix A (N × M, N ≥ M) of the fitting problem. Since the measured values of the dependent variable do not enter the design matrix, we may also define the vector b. The components of A and b are defined to be the following: 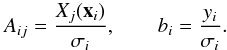 (3)From now, we set σi = const.
(3)From now, we set σi = const.
In terms of the design matrix A and the vector b, the chi-square function can be written as 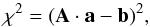 (4)and we need an a that minimizes this function, so the derivatives of χ2 with respect of the components of [a] k = ak are zeros. That leads us to the equation for a:
(4)and we need an a that minimizes this function, so the derivatives of χ2 with respect of the components of [a] k = ak are zeros. That leads us to the equation for a: 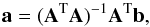 (5)where AT means the transpose of A, and the expression (ATA)-1AT are called generalized inverse or pseudoinverse of A. The best technique of computing pseudoinverse is based on singular value decomposition (SVD), which we describe in Sect. 4.3. We first specify the general method written above for the case of the Fermi GBM lightcurves in the following section.
(5)where AT means the transpose of A, and the expression (ATA)-1AT are called generalized inverse or pseudoinverse of A. The best technique of computing pseudoinverse is based on singular value decomposition (SVD), which we describe in Sect. 4.3. We first specify the general method written above for the case of the Fermi GBM lightcurves in the following section.
4.2. Multidimensional fit
Equation (1) describes a hypersurface, and it is a generalization of fitting a straight line to the data. Very simple backgrounds may be fitted well with first degree hypersurface (hyperplane) of the four variables described as 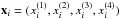 :
: 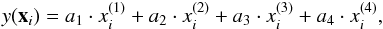 (6)where the basis functions are
(6)where the basis functions are 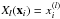 , respectively, and the design matrix simply consists of the components of xi with
, respectively, and the design matrix simply consists of the components of xi with 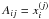 .
.
 |
Fig. 7 The 2-dimensional hypersurface of a 3rd degree fitting to a Fermi lightcurve is shown. The fitted variables ( |
For the most complicated Fermi backgrounds, higher degree of the variables are needed, however. One can illustrate the lightcurve data yi and the fitted hypersurface y(xi) using the two variables 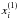 and
and 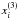 , which are both of 3rd degree on a 3D plot, as seen in Fig. 7. The design matrix of this problem is
, which are both of 3rd degree on a 3D plot, as seen in Fig. 7. The design matrix of this problem is ![\begin{equation} \mathbf{A}= \left(\begin{array}{cccccc} x^{(1)}_1 & (x^{(1)}_1)^2 & x^{(3)}_1 & (x^{(3)}_1)^2 & x^{(1)}_1\cdot x^{(3)}_1 & 1 \\[1mm] x^{(1)}_2 & (x^{(1)}_2)^2 & x^{(3)}_2 & (x^{(3)}_2)^2 & x^{(1)}_2 \cdot x^{(3)}_2 & 1 \\[1mm] ... & & & & & \\[1mm] x^{(1)}_N & (x^{(1)}_N)^2 & x^{(3)}_N & (x^{(3)}_N)^2 & x^{(1)}_N \cdot x^{(3)}_N & 1 \end{array}\right). \label{eq:design2} \end{equation}](/articles/aa/full_html/2013/09/aa21068-13/aa21068-13-eq52.png) (7)Since we would like to have a method for all the cases of Fermi-bursts (whether it is simple, complicated, non-ARR, or ARR), we define our model to be comprehensive. Let us have y(xi) as the function of
(7)Since we would like to have a method for all the cases of Fermi-bursts (whether it is simple, complicated, non-ARR, or ARR), we define our model to be comprehensive. Let us have y(xi) as the function of 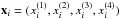 of order 3, so the basis functions Xk(xi) (and columns of the design matrix) consist of every possible products of the components
of order 3, so the basis functions Xk(xi) (and columns of the design matrix) consist of every possible products of the components 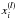 up to order 3. That means that we have M = kmax = 35 basis functions and a1, a2...a35 as free parameters. We are sure that we do not need so many free parameters to describe a simple background, and although a complicated or ARR background may require more free parameters, 35 is too much in every practical case. Therefore, we decrease the number of free parameters using SVD in the next section.
up to order 3. That means that we have M = kmax = 35 basis functions and a1, a2...a35 as free parameters. We are sure that we do not need so many free parameters to describe a simple background, and although a complicated or ARR background may require more free parameters, 35 is too much in every practical case. Therefore, we decrease the number of free parameters using SVD in the next section.
4.3. Singular value decomposition
In Sect. 4.1, we showed that the least square problem can be solved by computing the pseudoinverse of the design matrix A. For this purpose, we used Singular Value Decomposition (SVD), since SVD is robust and very stable numerically (Long 2005; Press et al. 1992).
The SVD takes an N × M matrix A and factors it into A = USVT. In this expression, U and V are N × N and M × M orthogonal matrices, respectively, and S is an N × M diagonal matrix. The columns of U and V are the eigenvectors of AAT and ATA, respectively. Furthermore, S contains the square roots of the eigenvalues of AAT and ATA (both have the same eigenvalues, but different eigenvectors). These eigenvalues (diagonal elements in S) are called the singular values, si.
In overdetermined cases (N ≥ M), the last N − M singular values, however, are zeros, so we may consider only U as an N × M matrix, V as an M × M matrix, and S as M × M (it is called economic SVD).
If U and V enter the SVD decomposition of A as described above, one can show easily (using the orthogonalithy of U and V) that the pseudoinverse of A can be obtained as 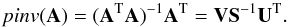 (8)SVD is implemented in several numerical software. In our work, we used Octave’s SVD function3, known as the svd, and pseudoinversion function, known as the pinv (Long 2005).
(8)SVD is implemented in several numerical software. In our work, we used Octave’s SVD function3, known as the svd, and pseudoinversion function, known as the pinv (Long 2005).
Computing the pseudoinverse, we need the reciprocal of the singular values in the diagonals of S-1, and there is a problem with this. The size of a singular value tells you exactly how much influence the corresponding rows and columns of U and V have over the original matrix A. We can find the exact value of A by multiplying USVT. If we, however, remove (for example) the last columns of U and V and the final singular value, we are removing the least important data. If we then multiplied these simpler matrices, we would only get an approximation to A but one which still contains all but the most insignificant information. This means that SVD allows us to identify linear combinations of variables that do not contribute much to reducing the chi-square function of our data set.
The singular values are usually arranged in the order of size with the first being the largest and most significant. The corresponding columns of U and V are therefore also arranged in importance. If a singular value is tiny, very little of the corresponding rows and columns get added into the matrix A when it is reconstructed by SVD. If we compute the pseudoinverse of A, the reciprocals of the tiny and not important singular values will be unreasonably huge and enhance the numerical roundoff errors as well.
This problem can be solved defining a limit value, below which reciprocals of singular values are set to zero. It means that the resulted matrix is an approximation of the real pseudoinverse, but we only omit information of the less interest.
With Eq. (1), we can define models of any number of variables and of arbitrary degree. In our case, we define models with four underlying variables of degree 3. Therefore, we have M = 35 free fitting parameters, as described above in Sect. 4.2. We do not know how many and which ones of these parameters have real importance in the variation in the background, but SVD can give us the answer trivially: pseudoinverse should be done by omitting the singular values which do not contribute so much.
The only question that remains is where this limit should be when singular values are not so important. We find an answer to that question in Sect. 4.4 using model selection criteria.
4.4. Model selection
Model selection is usually based on some information criterion. We use the Akaike information criterion (AIC) method to distinguish between different models to the data (Akaike 1974). However, we note here that AIC has to be used with caution, especially in the most complicated cases of backgrounds (see examples in Sect. 5.2).
We first assume that we have M models so that the kth model has k free parameters (k = 1...M). When the deviations of the observed values from the model are normally and independently distributed, every model has a value AICk so that 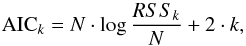 (9)where RSSk is the residual sum of squares from the estimated model (
(9)where RSSk is the residual sum of squares from the estimated model (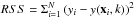 ), N is the sample size, and k is the number of free parameters to be estimated. The first term of Eq. (9) measures the goodness of fit (discrepancy between observed values and the values expected under the model in question), the second term penalizes the free parameters. Given any two estimated models, the model with the lower value of AICk is the one to be preferred. Given many models, the one with lowest AICk will be the best choice: It has as many free parameters as needed but not more. Note that we do not use AIC for deciding how good the fit is but only for choosing one model over the another. The goodness of fit is given by the chi-square statistics defined by Eq. (2).
), N is the sample size, and k is the number of free parameters to be estimated. The first term of Eq. (9) measures the goodness of fit (discrepancy between observed values and the values expected under the model in question), the second term penalizes the free parameters. Given any two estimated models, the model with the lower value of AICk is the one to be preferred. Given many models, the one with lowest AICk will be the best choice: It has as many free parameters as needed but not more. Note that we do not use AIC for deciding how good the fit is but only for choosing one model over the another. The goodness of fit is given by the chi-square statistics defined by Eq. (2).
So far, we defined a complex model with 35 free parameters and, therefore, the design matrix A has 35 singular values (see Sect. 4.2). However, we know that we can omit some of the tiny singular values when computing the pseudoinverse of A – the ones, which are not necessary to the best fit of the gamma background. Thus, we take a loop over the pseudoinverse operation and decrease the omitted number (that is, increase the used number) of singular values in every step. Furthermore, we also compute the AICk in every step with k being the number of singular values not omitted. In that way, the number of singular values, which minimize the AICk as a function of k will be the best choice when calculating the pseudoinverse, so we get the most useful estimation of the model parameters a (let us remember that singular values are sorted in decreasing order, so the last and not important ones will be penalized by the second term of AIC).
At this point, we return to the Fermi’s GRB 091030.613 presented in Sects. 2 and 3 and follow the method of general least square, as described above. We compute AICk for every k = 1...35. This function is shown in Fig. 8.
 |
Fig. 8 Akaike information criterion for model selection. Model with 14 singular values is selected. (First and last five singular values are usually too high, so we do not show them.) |
Based on the AIC, the model with 14 singular values is the best choice. We present the result of the fitting with this model in Sect. 5.
4.5. Features of DDBF
One cornerstone of the fitting algorithm DDBF described above is the definition of the boundaries that decide the interval of the burst and the intervals of the background. In this work, we follow the common method of using user-selected time intervals (Paciesas et al. 2012).
Unlike in Paciesas et al. (2012), usage of the position data gives us the possibility of fitting the whole background of the CTIME file instead of selecting two or three small fractions around the burst. This notable feature has two important consequences.
First, the user has to select only the two boundaries before and after the burst; the other boundaries of the background intervals are inherently at the beginning and at end of the CTIME datafile. This reduces the error factor put into the DDBF method by the user compared to the method of Paciesas et al. (2012).
Second, one can easily detect a possible long emission coming from the astrophysical source. Since this emission has nothing to do with the direction and orientation of the satellite, the signal consequently has to be present in the lightcurve after the background filtering. (The opposite is also true: a signal after the burst could be considered a long emission when the user defines two short background intervals, although it was caused by the motion of the satellite. One example for this case is presented in Sect. 5.2.2.)
In the case of the GRB 091030.613, we used a burst-interval between − 20 and 38 s before and after the burst, respectively (see Sect. 5, Fig. 9). This means that the data of this time interval were omitted when fitting to the background. Other than that, the whole CTIME lightcurve were fitted.
It is one of our future plans to create a self-consistent method, which can automatically define these intervals based on a self-consistent iteration algorithm, so the user’s presence would be unnecessary and the method would be totally automatic.
5. Results
5.1. Direction dependent fit and T90 for GRB 091030.613
In this section, we present the result of the DDBF for the GRB 091030.613 (the one that we showed in Fig. 1 and noted that there are difficulties with its background fitting).
 |
Fig. 9 Fitted background of the lightcurve of the Fermi burst 091030.613 measured by the 3rd GBM detector. Fitting was done by DDBF method (Szécsi et al. 2012a,c), using 14 non-zero singular values according to AIC. Reduced chi-square statistics is shown in the top right corner. |
 |
Fig. 10 Cumulative lightcurve of the Fermi burst 091030.613 by the 3rd GBM detector. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. (Model with 14 singular values was selected, as seen in Fig. 8.) |
The DDBF method is a good alternative for the polynomial fitting of time for two reasons. First, the background model consists of astrometric computations of astrophysical objects, and the fitting variables have physical meanings. This property is missing when one uses simple polynomial fitting of time; however, Fermi’s complex motion prefers to have a more detailed model for the background sources.
Second, using the polynomial fitting of time, one has to define two short time intervals before and after the burst, which can be well described by a polynomial function (see Sect. 4.5). Usually, these intervals have to be short enough and defined precisely to get a correct fit. DDBF can fit all the 2000-s data of the CTIME (and CSPEC) files. Therefore, we are also able to study long emissions or precursors.
Figure 10 shows the cumulative lightcurve from which we computed the durations (Szécsi et al. 2012b). Horizontal lines were computed by averaging the cumulated background levels before and after the burst: These are the levels of 0% and 100% of total cumulated counts.
We note that these levels were selected by the user for the Fermi GBM Catalogue. Since they only fitted some short intervals around the burst using time-dependent polynomials, this step could not been automatised (Paciesas et al. 2012). With DDBF, however, we fit all the 2000 s of the CTIME file (except for the burst in the middle) using direction dependent underlying variables. Our method gives us cumulative lightcurves, where the resulting levels are tightly distributed around a constant value, and therefore, the automation (calculating the average of the levels) is possible.
Between the levels of 0% and 100%, 19 equally heightened points mark every 5% of their cumulated counts (the first and last are fixed where the lightcurves step over and below the levels before and after). T90 is computed by subtracting the value corresponding to 5% from the value corresponding to 95%.
The Fermi GBM Catalogue reports 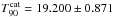 s. Our result is
s. Our result is 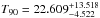 s. We always give confidence intervals instead of error bars with the T90 values, since the DDBF method is complicated: the error estimation needs further considerations. See Sect. 6 for details.
s. We always give confidence intervals instead of error bars with the T90 values, since the DDBF method is complicated: the error estimation needs further considerations. See Sect. 6 for details.
This result does not depend on the spectrum or the detector response matrix, because we summed up the channels of the CTIME files. However, the DDBF can be used for every channel separately (as it was done in Szécsi et al. 2012b) and can also be used with CSPEC data to obtain spectral information.
5.2. Examples
We began with the observation that many of Fermi bursts (even in non-ARR cases) have a varying background corresponding to the actual direction of the satellite. Thus, our idea was to use this directional information in the filtering algorithm. We created a method, which is able to separate this background from the lightcurves. Now, we want to demonstrate the effectiveness of our method, so we present examples here, with each having an extreme background.
These examples were purposely chosen to demonstrate how powerful DDBF can be and to give an overall impression about the cases for which it can be used in and the advantages and the difficulties it carries. Two of the examples below are ARR bursts (Sects. 5.2.5 and 5.2.7). In general, we would like to draw attention to the connection between the direction dependent underlying variables and the variability features of the lightcurve: the correlation between them are undeniable in every single case (even in no-ARR cases).
In each example, we present figures of the original lightcurves for one of the triggered detectors, summarizing the counts of the effective range of channels of CTIME file. On these lightcurves, we plot the fitted theoretical background with a solid line and the reduced chi-square statistics in the top right corner. Then, we show the absolute value of the direction dependent underlying variables (in one graph), and the AICk as a function of used singular values.
As a final result, we show the cumulative lightcurves, which we used to compute the T90 values. We also give the preliminary 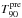 from the gamma-ray coordinates network (GCN 2013), and the
from the gamma-ray coordinates network (GCN 2013), and the 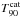 from the catalogue computed and published by the GBM team (Paciesas et al. 2012). We give confidence intervals of the computed T90s (and T50s as well). The description of how these confidence intervals were computed is in Sect. 6.
from the catalogue computed and published by the GBM team (Paciesas et al. 2012). We give confidence intervals of the computed T90s (and T50s as well). The description of how these confidence intervals were computed is in Sect. 6.
It is important to note, however, that only long GRBs were analysed here. The reason of this is that short bursts usually are not influenced by the fast motions of the satellite. During one short burst, the background does not change so much that DDBF should be used. Furthermore, short bursts are better analysed using the time tagged events (TTE) data type instead of CTIME (and CSPEC), and therefore, they are not presented here.
Since we want to present how effective our method is, we show the detector having the highest background variability without filtering in every case. However, it is possible to combine the same analysis for a number of bright detectors for each burst to reduce the error. It will be a part of a future work to create a catalogue of the durations of the Fermi bursts using DDBF, in which we will use more than one detector’s data. Here, we present the method with only one triggered detector for each case.
5.2.1. GRB 090102.122
GRB 090102.122 is an example where no fast motion was carried out, and therefore, no high background rate variation is taken place. This burst had no ARR. The lightcurve is simple in the sense that a time dependent polynomial function could possibly be used to fit it properly. However, we present DDBF results only to show that the method works in these simple cases as well. The AIC chose 9 singular values, and one can see in the information criterion plot that more values than this are punished by the AIC: Too many free parameters would cause the fitted curve to have unnecessary loops fitted to the noise of the background. The Fermi catalogue reports 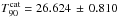 s (Paciesas et al. 2012). Detector “a” was analysed here.
s (Paciesas et al. 2012). Detector “a” was analysed here.
 |
Fig. 11 Top: lightcurve of the Fermi GRB 090102.122 as measured by the triggered GBM detector “a” and the fitted background with a grey line. Burst interval (s): [− 5:35]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
 |
Fig. 12 Cumulative lightcurve of GRB 090102.122. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
Around − 150 s in the lightcurve, there is a peak, which cannot be explained by the physical underlying variables. This causes a little hump in the cumulative lightcurve in Fig. 12. (Furthermore, the same peak can be seen in the lightcurves of the other triggered detector.) It is out of the scope of this article to decide whether it is a pre-burst or another instrumental effect, however, we emphasize again that DDBF can also be used for finding pre-bursts or long emissions. We measured 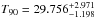 s.
s.
5.2.2. GRB 090113.778
The Fermi catalogue reports 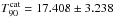 s (Paciesas et al. 2012) and this is a no-ARR case. Detector “0” was analysed here (Szécsi et al. 2012c). This lightcurve in Fig. 23 has some extra counts around 400 and 600 s. Both of them can be explained with the variation in the underlying variables: around 400 s, the Earth limb was out of the FoV and then it came back and peaked at 600 s until the Sun’s position changed significantly. Both of these could cause the extra counts. The best chosen model with 12 singular values could fit these peaks (see the big and small loops in the fitted lightcurve at 400 and 600 s). Since the underlying variables are based on the motion of the satellite, it follows that these two peaks are probably not astrophysical effects. They do not come from the GRB but from the combined effect of the background sources in the surroundings: the Earth and the Sun. It is important to note that a statement like that could not be made using the traditional method of polynomial fitting of time.
s (Paciesas et al. 2012) and this is a no-ARR case. Detector “0” was analysed here (Szécsi et al. 2012c). This lightcurve in Fig. 23 has some extra counts around 400 and 600 s. Both of them can be explained with the variation in the underlying variables: around 400 s, the Earth limb was out of the FoV and then it came back and peaked at 600 s until the Sun’s position changed significantly. Both of these could cause the extra counts. The best chosen model with 12 singular values could fit these peaks (see the big and small loops in the fitted lightcurve at 400 and 600 s). Since the underlying variables are based on the motion of the satellite, it follows that these two peaks are probably not astrophysical effects. They do not come from the GRB but from the combined effect of the background sources in the surroundings: the Earth and the Sun. It is important to note that a statement like that could not be made using the traditional method of polynomial fitting of time.
After the background subtraction, the cumulative lightcurve (Fig. 14) is noisy because this burst was not so intense with only ~1800 counts, while other examples have 10 000−20 000 counts. Our result is 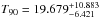 s.
s.
5.2.3. GRB 090618.353
The Fermi catalogue reports 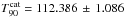 s (Paciesas et al. 2012). No ARR was taken.
s (Paciesas et al. 2012). No ARR was taken.
The data from detector “7” were analysed here. Nevertheless, we should note that detector “4” has so many counts that almost any kind of background model seems to be good enough to compute T90 when using detector “4”. We still choose to present detector “7” here, because we can show our method working in a more complicated case.
Now we may be used to the fact that quickly varying underlying variables (which correspond to fast motion of the satellite) cause a quick change in the lightcurve background at the same time. This burst had no ARR, but the satellite started to rotate according to the fast change of the underlying variables after the trigger. At this point, the lightcurve is changing more quickly than before. The fitted grey line (chi-square statistics are 1.009) pursue this change, and results in a duration of 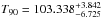 s.
s.
5.2.4. GRB 090828.099
GRB 090828.099 was detected by the GBM on 28 August 2009 at 02:22:48.20 UT (GCN 2013, 9844). The first GBM catalogue reported 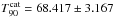 s (Paciesas et al. 2012). This is a non-ARR case. The data from detector “5” was analysed here.
s (Paciesas et al. 2012). This is a non-ARR case. The data from detector “5” was analysed here.
 |
Fig. 13 Top: lightcurve of the Fermi GRB 090113.778 as measured by the triggered GBM detector 0’ and the fitted background with a grey line. Burst interval: [− 20:40]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
 |
Fig. 14 Cumulative lightcurve of GRB 090113.778. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
 |
Fig. 15 Top: lightcurve of the Fermi GRB 090618.353 as measured by the triggered GBM detector “7” and the fitted background with a grey line. Burst interval: [− 20:130]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
 |
Fig. 16 Cumulative lightcurve of GRB 090618.353. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
 |
Fig. 17 Top: lightcurve of the Fermi GRB 090828.099 as measured by the triggered GBM detector “5” and the fitted background with a grey line. Burst interval: [− 10:80]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
 |
Fig. 18 Cumulative lightcurve of GRB 090828.099. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
The AIC gives us the model with 7 singular values. This is also a simple background. Only the first 300−400 s are influenced by the fast motion, but DDBF could filter this effect. The duration computed with the DDBF is 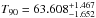 s.
s.
5.2.5. GRB 091024.372 and .380
This case deserves attention because an ARR was caused by this burst. The GBM was triggered twice on GRB 091024: the first time at 08:55:58.47 UT (GRB 091024.372) and the second time at 09:06:29.36 UT (GRB 091024.380). The GCN 10114 reports: “This burst was detected by Swift and the Fermi Gamma-ray Burst Monitor with a first emission interval lasting ~50 s and a second emission interval starting ~630 s after trigger and lasting more than 400 s. The spacecraft performed a repointing maneuver for this burst which resulted in pointed observation for 5 h starting ~350 s after [the second] trigger.” (GCN 2013, 10114).
Additionally, Gruber et al. (2011) performed a detailed analysis of this burst and its optical afterglow. Here, we show DDBF duration results separately for the two triggers. Further investigation is needed to analyse the total ~1020 s of this extreme long burst as a whole with DDBF. This will be provided in a future work.
Figure 19 shows the CTIME data of the first trigger (.372) using the triggered detector “8”. The second burst episode after 630 s can also be recognized in the lightcurve by the naked eye (however, the satellite changed its position at the time of this second trigger, so this emission looks less intensive here in detector “8”). On the other hand, one can notice that the underlying variables do not show any variability at this time interval. Qualitatively this means that something is happening there which is not coming from our modelled sources (Earth or Sun). This can be shown more quantitatively, if one considers that another local minimum can be seen at 15 which are close to the global minimum at 20, which AIC determines for this fit. Here the models with too many free parameters considered the second burst as a background noise and tried to filter it with these polynomial loops. Indeed, the fitted curve shows several loops, especially at the interval of the second burst.
We can draw two lessons from all of this. First, one has to use AIC with caution. Sometimes, the preferred singular value is not the one AIC gives, if there is another one close enough. In the case of the first emission (.372), there are no loops on the fitted curve, when one uses only 15 singular values (the second local minimum of the AIC). Fortunately, the final T90 result does not change much (less than 1% in this case). Second, one needs to pay more attention to too many singular values (we would say more than 20, based on our other examples), especially if there is an additional local minimum in AIC close to the chosen one. This can mean that something is happening that cannot be well modelled and may be an astrophysical process. We already mentioned that DDBF can be used to detect long emissions: this is clearly such a case. Our final result for the first emission (.372) is 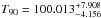 s.
s.
 |
Fig. 19 Top: lightcurve of the Fermi GRB 091024.372 as measured by the triggered GBM detector “8” and the fitted background with a grey line. Burst interval: [− 19:119]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
 |
Fig. 20 Cumulative lightcurve of GRB 091024.372. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
The second burst emission is after 630 s in Fig. 19. As we already mentioned, this second emission resulted a second trigger from the GBM (.380), which is shown in Fig. 21 using the data of the triggered detector “9”. Here, the first trigger is visible at − 630 s. However, it is less intensive, since detector “9” was not triggered with the first emission.
This second burst was so long (GBM Catalogue reported 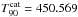 s, Paciesas et al. 2012) that we needed to reconsider the best model given by AIC. The minimum of AIC as a function of the used singular values is at 11, but this model has a large polynomial loop in the burst interval and is, therefore, useless. Although this is understandable, longer burst intervals lead to shorter fitted backgrounds (and thus, a large amount of information can be lost), it implies that the information criterion has to be used with caution, especially in extreme cases. In this case, we chose the model with 7 singular values. This model fits the background considerably well according to our experience, and is supported by the information criterion: the smallest local minimum is at 7.
s, Paciesas et al. 2012) that we needed to reconsider the best model given by AIC. The minimum of AIC as a function of the used singular values is at 11, but this model has a large polynomial loop in the burst interval and is, therefore, useless. Although this is understandable, longer burst intervals lead to shorter fitted backgrounds (and thus, a large amount of information can be lost), it implies that the information criterion has to be used with caution, especially in extreme cases. In this case, we chose the model with 7 singular values. This model fits the background considerably well according to our experience, and is supported by the information criterion: the smallest local minimum is at 7.
The ARR was issued at 09:12:14.28 UT, ~970 s after the first trigger (.372) and ~350 s after the second trigger (.380) (Gruber et al. 2011). A small change in the underlying variables at 350 s in Fig. 21 can be seen, but the ARR slew was not too large, since the source was already at 15 degrees from the LAT boresight. Nonetheless, the effect of the ARR is represented by the fitted model, as seen by the small knot of the grey line at 350−400 s in Fig. 21. As for the cumulative lightcurve in Fig. 22, the first emission at − 630 s is present with a non-significant sign, otherwise our result of 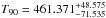 s agrees with the GBM Catalogue.
s agrees with the GBM Catalogue.
 |
Fig. 21 Top: lightcurve of the Fermi GRB 091024.380 as measured by the triggered GBM detector “9” and the fitted background with a grey line. Burst interval: [− 200:600]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion, the smallest local minimum of 7 singular values is used here. See Sect. 4.4. |
 |
Fig. 22 Cumulative lightcurve of GRB 091024.380. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
5.2.6. GRB 100130.777
The Fermi GRB 100130B was detected by the GBM on 10 January 2010 at 18:38:35.46 UT. The GBM GRB Catalogue presented 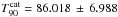 s (Paciesas et al. 2012). We analyse the data of triggered NaI detector “8” using DDBF.
s (Paciesas et al. 2012). We analyse the data of triggered NaI detector “8” using DDBF.
 |
Fig. 23 Top: lightcurve of the Fermi GRB 100130.777 as measured by the triggered GBM detector “8” and the fitted background with a grey line. Burst interval: [− 30:90]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
 |
Fig. 24 Cumulative lightcurve of GRB 100130.777. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
Although the background does not change extremely during the ~80 s of the burst, it is a good example to present the contribution of the celestial position of the satellite to the actual level of the background. If one takes a look at Fig. 23, one can see that the variation in the lightcurve has a connection to the variation in the underlying variables.
AIC gives us a best model of 17 singular values. After the background subtraction, the cumulative lightcurve (Fig. 24) gives us 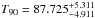 s. For error estimation, see Sect. 6.
s. For error estimation, see Sect. 6.
5.2.7. GRB 100414.097
This GRB also had an ARR event. Quoting the GCN report 10595: “at 02:20:21.99 UT on 14 April 2010, the Fermi Gamma-Ray Burst Monitor triggered and located GRB 100414A. The Fermi Observatory executed a maneuver following this trigger and tracked the burst location for the next 5 h, subject to Earth-angle constraints.” (GCN 2013, 10595).
In this case, we chose to analyse a non-triggered detector (detector “5”). Because this burst was so intensive and bright, the triggered detectors show totally negligible background rate variations compared to the brightness of the burst. Since we want to demonstrate that our method works in very complicated cases as well, we analyse a lower signal-to-noise detector. Evidently, DDBF can also fit the data of the bright triggered detectors well.
 |
Fig. 25 Top: lightcurve of the Fermi GRB 100414.097 as measured by the non-triggered GBM detector “5” and the fitted background with a grey line. Burst interval: [− 20:30]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
 |
Fig. 26 Cumulative lightcurve of GRB 100414.097. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
The GBM Catalogue reports a duration of T90 = 26.497 ± 2.073 s. According to the GCN 10594 and 10610, this burst also triggered the LAT and the Suzaku Wide-band All-sky Monitor (WAM) (GCN 2013, 10594, 10610).
As we already mentioned above, singular values that are too high (≳20) deserve attention. In this case, the AIC chose 21 singular values. This 21 singular value model describes the background well. The only exception is the extra count rate around 600 s, which is also clearly noticeable in the cumulative lightcurve. More detailed analysis of the spectral features of this event are needed to determine if this event is caused by the burst or not. Given that there were additional observations by the LAT and by the Suzaku WAM which do not report long emission, we expect that this was a local event at the GBM caused by cosmic rays or another possible transient source, which could be filtered by using different energy channels. Our result is 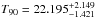 s.
s.
Final T90 and T50 results.
6. Confidence intervals
The DDBF method described above is too complicated to give a simple expression for the error of T90 using general rules of error propagation. We therefore decided to give confidence intervals corresponding to 68% (approximately 1σ level). For this, we use Monte Carlo (MC) simulations. We simulate the data with Poisson noise: assuming that counts are given by a Poisson process, we exchange our input data to one coming from a random Poisson distribution. In the case of a Poisson distribution, which is parametrised by the mean rate (λ), the expected value is given by λ. We therefore replace each datapoint with a value drawn from a Poisson distribution with a mean equal to the datapoint in question.
DDBF was repeated for 1000 MC simulated data. The distribution of the Poisson-modified T90 and T50 values are shown in Figs. 27 and 28 for GRB 091030.613, respectively.
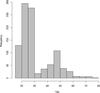 |
Fig. 27 Distibution of the T90 obtained from the MC simulated data for Fermi burst 091030.613 (Szécsi et al. 2012c). |
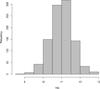 |
Fig. 28 Distibution of the T50 obtained from the MC simulated data for the Fermi burst 091030.613 (Szécsi et al. 2012c). |
Figure 27 shows two significant peaks around 22 and 47 s. The first peak at 22 s corresponds to the measured T90 value. However, the measured T90 value is systematically longer in some cases of the Poisson noise simulation, because this burst has a little pulse around 47 s (see Figs. 9 and 10), and T90 is sensitive for this kind of uncertainties. In Fig. 28., there is, however, no sign of this second peak: T50 is more robust and less likely to be influenced by these fluctuations (Szécsi et al. 2012c).
Final results of T90s and T50s with confidence intervals are given in Table 1 for the bursts mentioned in Sect. 5.2.
6.1. Comparison with the Fermi GBM Catalogue
In Table 1, we also show the 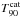 s and
s and 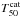 s of the Fermi GBM Catalogue (Paciesas et al. 2012) for comparison.
s of the Fermi GBM Catalogue (Paciesas et al. 2012) for comparison.
At this point, we need to give some notes about the differences between the method of the Catalogue and DDBF. First of all, we only used one detector when we measured the duration, whilst the Catalogue used the sum of the brightest detectors.
On the other hand, there are further differences between the Catalogue’s method and the DDBF. As we mentioned in Sect. 5, our method solved the problem of automatizing the identification of the 0% and 100% levels of cumulated counts, so the user do not need to define them by hand. This disposes of one possible error source.
Additionally, using direction dependent variables produced the possibility of fitting the whole CTIME background (only the burst has to be taken off in the middle). This reduces the error of the user selected background intervals and, on the other hand, makes the automatic detection of a long emission possible. See Sect. 4.5. for more details.
With respect to the error estimation of the Catalogue, they followed the method developed for the BATSE data by Koshut et al. (1996), which uses the variance of the 0% and 100% levels of cumulated counts as a basis for the error estimates (Paciesas et al. 2012). We decided to avoid this method (as we avoid the use of time-dependent polynomial methods developed for the BATSE, as seen in Sect. 2), and give an alternative solution with Monte Carlo simulation of the data in Sect. 6. This choice is based on our belief that the DDBF is too complicated, and using the error estimation of Koshut et al. (1996) would underestimate the real error of our method.
Furthermore, we give different higher and lower confidence intervals. In our experience, many bursts show different amounts of uncertainties at the starting point than at the finishing point. One demonstrative example is the T90 value of GRB 091030.613: the MC modified distribution in Fig. 27 is clearly not symmetric. Therefore, it would be an oversimplification to give only one value as an error bar or confidence interval. For more examples, see Szécsi et al. (2012c).
Given all of these facts, it follows that a comparison with the Fermi GBM Catalogue data is not meaningful in a quantitative sense at the moment. It is currently under way to process all Fermi bursts with DDBF and publish an alternative catalogue, in which we will use the combined data of the detectors. Unfortunately, we cannot say anything about the robustness of our method until we finish processing a significant number of bursts. Once it is done, we will provide an overall statistical comparison between the two dataset together with our catalogue.
7. Summary and conclusion
Since the commonly used background filtering methods are not efficient for many cases of the Fermi, we developed a new technique based on the motion and orientation of the satellite known as the the direction dependent background fitting (DDBF) method.
The DDBF technique considers the position of the burst, the Sun and the Earth. Based on this information on position, we computed physically meaningful underlying variables and fitted a four dimensional hypersurface on the background. Singular value decomposition and AIC were used to reduce the number of free parameters. More research may be required to find a more suitable model dimension reducing criterion.
The background model was subtracted from the measured data, resulting in background-free lightcurves. These lightcurves can be used to perform statistical surveys. We showed the efficiency of our DDBF method computing durations of some very complicated cases. We also calculated confidence intervals for our duration values corresponding to 1σ level.
We summarized some of the main differences between DDBF and the background estimation method of the GBM Catalogue and decided not to give a quantitative comparison at this point. Our plan is to process the combined data of the detectors with DDBF for every Fermi burst and produce an alternative catalogue. This future work will also contain the statistically relevant comparison of the official GBM Catalogue and the DDFB Catalogue which has yet to come.
The DDBF method has the advantage of considering only variables with physical meanings and it fits all the 2000 s CTIME data well as opposed to the currently used method. These features are indeed necessary when analysing long GRBs, where motion effects can influence the background rate in a very extreme way. Therefore, not only Sky Survey but also ARR mode GRB’s can be analysed, and possible long emission can be detected.
Furthermore, there seems to be no reason why DDBF could not be used for other sources than GRBs. The method only considers the background levels before and after the event; therefore, the event itself has no influence to the resulted background model, even if it is very bright. Nevertheless, the duration can play a role in its applicability. Events that are comparably long to the 2000 s data file could be problematic. The DDBF is not necessary for short events, as the effects of the motion of the spacecraft are negligible: one may use the time dependent polynomial fitting for short GRBs. However, DDBF is able to discover long emissions or prebursts, as we have shown in Sect. 5.2. Therefore, DDBF could be used to verify the final result in the case of short bursts as well.
In summary, celestial position plays an important role in the Fermi data set. If one wants to filter the background more efficiently and in a physically more comprehensible way, one has to use this information. Utilizing this principle, we have created the DDBF method. In future work, DDBF will be used to create a catalogue of the durations of the Fermi GBM GRBs.
The High Energy Astrophysics Science Archive Research Center (HEASARC): legacy.gsfc.nasa.gov
LAT Photon, Event, and Spacecraft Data Query: http://Fermi.gsfc.nasa.gov/cgi-bin/ssc/LAT/LATDataQuery.cgi
GNU Octave: http://www.gnu.org/software/octave/
Acknowledgments
This study was supported by the Hungarian OTKA-77795 grant, by OTKA/NKTH A08-77719 and A08-77815 grants (Z.B.). D.Sz. is grateful to Péter Veres for the introduction to the field of the GRB data analysis and for all the useful explanations and to Áron Szabó for highlighting the mathematical basics of the statistical methods and for his patience and advices. We would like to express our gratitude to William Paciesas for his generous help with the ARR cases. Additionally, thanks to David Gruber for his comments concerning GRB 091024 and for all the discussions and inspirations. Special thanks to Gerard Fitzpatrick for the language editing. We also thank the anonymous Referee for the especially constructive remarks and suggestions. D.Sz. has been supported by the “Lendület-2009” Young Researchers’s Program of the Hungarian Academy of Sciences and the OTKA-NIH Grant MB0C 81013.
References
- Ackermann, M., Ajello, M., Atwood, W. B., et al. 2012, ApJ, 750, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Akaike, H. 1974, IEEE Transactions on Automatic Control, 19, 716 [Google Scholar]
- Briggs, M. S., Fishman, G. J., Connaughton, V., et al. 2010, JGR, 115, 7323 [CrossRef] [Google Scholar]
- Fermi-Timeline-Posting 2013, Fermi Science Support Center, http://fermi.gsfc.nasa.gov/ssc/observations/timeline/posting/arr/ [Google Scholar]
- Fitzpatrick, G., et al. 2011, Fermi Symposium Proc., eConf C110509 [Google Scholar]
- GCN 2013, The Gamma Ray Coordinates Network, gcn.gsfc.nasa.gov [Google Scholar]
- Gruber, D., Krühler, T., Foley, S., et al. 2011, A&A, 528, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koshut, T., Paciesas, W., Kouveliotou, C., et al. 1996, ApJ, 463, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Long, P. 2005, Introduction to Octave, Department of Engineering, University of Cambridge [Google Scholar]
- Meegan, C., Lichti, G., Bhat, P. N., et al. 2009, ApJ, 702, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Paciesas, W. S., Meegan, C. A., von Kienlin, A., et al. 2012, 199, 18 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannerty, B. P. 1992, Numerical Recipes in C: The Art of Scientific Computing (New York: Cambridge University Press) [Google Scholar]
- Sakamoto, T., Barthelmy, S. D., Barbier, L., et al. 2008, ApJS, 175, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Szécsi, D., Bagoly, Z., Horváth, I., et al. 2012a, Acta Polytech., 52, 43 [NASA ADS] [Google Scholar]
- Szécsi, D., Bagoly, Z., Balázs, L. G., Veres, P., & Kóbori, J. 2012b, Proc. of Fermi/Swift GRB Conference, Munich, PoS(GRB 2012)051 [Google Scholar]
- Szécsi, D., Bagoly, Z., Kóbori, J., et al. 2012c, Fermi Symposium Proc., eConf C121028 [arXiv:1303.3141] [Google Scholar]
- Varga, B., Horváth, I., & Balázs, L. G. 2005, Il Nuovo Cimento C, 28, 861 [NASA ADS] [Google Scholar]
Appendix A: Earth in the FoV
In Sect. 3.2, we defined one of the underlying variables as the Earth-occulted sky rate – i.e., the Earth-uncovered sky correlated to the size of the detector’s field of view (FoV). Here, we present the computations.
Let us have R as the radius of Earth and h as the altitude of the satellite. (The actual h during the burst is known from the LAT spacecraft data file.) The aperture σ of the cone constituted by the Earth-limb seen from the board of satellite is 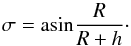 (A.1)Angular dependence of the detector effective area is assumed to be constant, so the FoV of one GBM detector is 2π sterad. However, more precise calculations could be done knowing the real characteristics (Meegan et al. 2009).
(A.1)Angular dependence of the detector effective area is assumed to be constant, so the FoV of one GBM detector is 2π sterad. However, more precise calculations could be done knowing the real characteristics (Meegan et al. 2009).
When the Earth-limb is totally in the FoV, the Earth-covered area is computed by integrating on a spherical surface as follows, 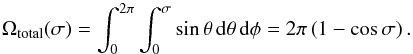 (A.2)Equation (A.2) means the solid angle of a cone of aperture σ.
(A.2)Equation (A.2) means the solid angle of a cone of aperture σ.
If only a fraction of the Earth-limb is in the FoV, then Ω = Ω(σ,ρ) is smaller then Ωtotal and is a function of the maximum altitude of the Earth-limb ρ as well. In this case, we have to separate the area in the FoV to two parts, which are marked with light grey and dark grey in Fig. A.1.
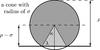 |
Fig. A.1 Earth limb seen onboard from the Fermi. Detector can only see the coloured parts above the solid horizontal black line. |
We can calculate the dark grey surface the same way as above. Using 2π − 2κ, instead of 2π when integrating with respect to φ, we find that 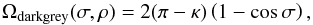 (A.3)where κ is a function of ρ and σ. It is easy to see that the light grey triangle in Fig. A.1 is a spherical triangle, since its every side is a geodetic curve. Therefore, κ can be calculated from the Napiers pentagon:
(A.3)where κ is a function of ρ and σ. It is easy to see that the light grey triangle in Fig. A.1 is a spherical triangle, since its every side is a geodetic curve. Therefore, κ can be calculated from the Napiers pentagon: 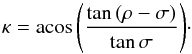 (A.4)Then, we calculate the light grey surface. The area of a spherical triangle is given by the Girard formule:
(A.4)Then, we calculate the light grey surface. The area of a spherical triangle is given by the Girard formule: 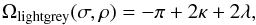 (A.5)where λ = acos (cos(ρ − σ)sinκ) from the Napiers pentagon.
(A.5)where λ = acos (cos(ρ − σ)sinκ) from the Napiers pentagon.
Thus, the surface above the black line is the sum of the light grey and dark grey parts: ![\appendix \setcounter{section}{1} \begin{eqnarray} \Omega^{\sigma<\rho}(\sigma,\rho)&=&2\left[\pi - \acos{\left(\frac{\tan{(\rho-\sigma)}}{\tan{\sigma}}\right)}\right] \left(1-\cos{\sigma}\right) \notag\\ &&-\pi + 2 \acos{\left(\frac{\tan{(\rho-\sigma)}}{\tan{\sigma}}\right)} \notag\\ &&+2\acos{\left(\cos{(\rho-\sigma)} \cdot \sin\acos{ \frac{\tan{(\rho-\sigma)}}{\tan{\sigma}} }\right)} \cdot \label{eq:Osr2} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21068-13/aa21068-13-eq169.png) (A.6)Equation (A.6) has to be modified a little bit when ρ < σ: in this case, the horizontal solid black line is over the half of the circle, and the light grey triangle has to be subtracted from the integral calculated from (A.2) with 2κ instead of 2π:
(A.6)Equation (A.6) has to be modified a little bit when ρ < σ: in this case, the horizontal solid black line is over the half of the circle, and the light grey triangle has to be subtracted from the integral calculated from (A.2) with 2κ instead of 2π: ![\appendix \setcounter{section}{1} \begin{eqnarray} \Omega^{\rho<\sigma}(\sigma,\rho)&=&2\left[\acos{\left(\frac{\tan{(\sigma-\rho)}}{\tan{\sigma}}\right)}\right] \left[1-\cos{\sigma}\right] +\pi \notag\\ &&- 2 \acos{\left(\frac{\tan{(\sigma-\rho)}}{\tan{\sigma}}\right)} \notag\\ &&- 2\acos{\left(\cos{(\sigma\!-\!\rho)} \cdot \sin\acos{\left(\frac{\tan{(\sigma\!-\!\rho)}}{\tan{\sigma}}\right)}\right)}. \label{eq:Osr1} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21068-13/aa21068-13-eq172.png) (A.7)
(A.7)
We plot Eqs. (A.6) and (A.7) as a function of ρ for σ = π/3, as seen in Fig. A.2. Equations (A.6) and (A.7) give us Eq. (A.2), when ρ = 2σ, and have no meaning when ρ < σ or ρ > 2σ. Therefore, we define an underlying variable x(3) (called the Earth-occulted sky rate, see Sects. 3.2 and 4.1) the following way: 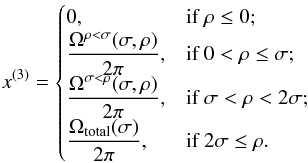 (A.8)Note that we divided by 2π because we assumed that FoV of the detector is 2π sterad. In that way, we get the rate of the Earth-limb to the FoV. We computed expression (A.8) for every second of the lightcurve and use it as an underlying variable in Sect. 3.2.
(A.8)Note that we divided by 2π because we assumed that FoV of the detector is 2π sterad. In that way, we get the rate of the Earth-limb to the FoV. We computed expression (A.8) for every second of the lightcurve and use it as an underlying variable in Sect. 3.2.
All Tables
All Figures
 |
Fig. 1 Lightcurve of the Fermi burst 091030.613 measured by the 3rd GBM-detector without any background filtering with 1-s bins. The grey line is a fitted polynomial function of time of order 3 for the ranges of [− 200:− 20] and [38:200] s, which does not seem to be a correct model for this whole background. Reduced chi-square statistics are given in the top right corner (Szécsi et al. 2012a). |
| In the text | |
 |
Fig. 2 Setup of the 12 NaI detectors of GBM given in the Spacecraft Coordinates (see Meegan et al. 2009). The zenith angle of the detectors in degrees is marked. This design is built in order to cover the whole visible part of the sky with the GBM. (The figure is based on Table 1. of Meegan et al. 2009. Notations “a” and “b” mean the 10th and 11th NaI detectors, respectively.) |
| In the text | |
 |
Fig. 3 Orientation of the 12 NaI detectors on the sky (in the second equatorial system), during the pre- and post-1000 s around the burst 091030.613. To show the direction with time, we marked the starting points of every line with a small star. The Sun’s position is marked with big sphere. The burst position is marked with diamond. |
| In the text | |
 |
Fig. 4 Celestial distance of the 3rd GBM detector and the Fermi-burst 091030.613 as a function of time. It is worth comparing this figure to Fig. 1. |
| In the text | |
 |
Fig. 5 Earth-occulted sky rate for the 3rd GBM detector as a function of time during the GRB 091030.613. (The Earth-occulted sky rate is zero, if the Earth-limb is out of the FoV.) |
| In the text | |
 |
Fig. 6 Celestial distance of the 3rd GBM detector and the Sun as a function of time during the GRB 091030.613. The dashed line shows the 0 level (under this the Sun and the detector close in an angle larger than 90°). It is worth comparing this figure to Fig. 1. |
| In the text | |
 |
Fig. 7 The 2-dimensional hypersurface of a 3rd degree fitting to a Fermi lightcurve is shown. The fitted variables ( |
| In the text | |
 |
Fig. 8 Akaike information criterion for model selection. Model with 14 singular values is selected. (First and last five singular values are usually too high, so we do not show them.) |
| In the text | |
 |
Fig. 9 Fitted background of the lightcurve of the Fermi burst 091030.613 measured by the 3rd GBM detector. Fitting was done by DDBF method (Szécsi et al. 2012a,c), using 14 non-zero singular values according to AIC. Reduced chi-square statistics is shown in the top right corner. |
| In the text | |
 |
Fig. 10 Cumulative lightcurve of the Fermi burst 091030.613 by the 3rd GBM detector. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. (Model with 14 singular values was selected, as seen in Fig. 8.) |
| In the text | |
 |
Fig. 11 Top: lightcurve of the Fermi GRB 090102.122 as measured by the triggered GBM detector “a” and the fitted background with a grey line. Burst interval (s): [− 5:35]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
| In the text | |
 |
Fig. 12 Cumulative lightcurve of GRB 090102.122. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
| In the text | |
 |
Fig. 13 Top: lightcurve of the Fermi GRB 090113.778 as measured by the triggered GBM detector 0’ and the fitted background with a grey line. Burst interval: [− 20:40]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
| In the text | |
 |
Fig. 14 Cumulative lightcurve of GRB 090113.778. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
| In the text | |
 |
Fig. 15 Top: lightcurve of the Fermi GRB 090618.353 as measured by the triggered GBM detector “7” and the fitted background with a grey line. Burst interval: [− 20:130]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
| In the text | |
 |
Fig. 16 Cumulative lightcurve of GRB 090618.353. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
| In the text | |
 |
Fig. 17 Top: lightcurve of the Fermi GRB 090828.099 as measured by the triggered GBM detector “5” and the fitted background with a grey line. Burst interval: [− 10:80]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
| In the text | |
 |
Fig. 18 Cumulative lightcurve of GRB 090828.099. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
| In the text | |
 |
Fig. 19 Top: lightcurve of the Fermi GRB 091024.372 as measured by the triggered GBM detector “8” and the fitted background with a grey line. Burst interval: [− 19:119]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
| In the text | |
 |
Fig. 20 Cumulative lightcurve of GRB 091024.372. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
| In the text | |
 |
Fig. 21 Top: lightcurve of the Fermi GRB 091024.380 as measured by the triggered GBM detector “9” and the fitted background with a grey line. Burst interval: [− 200:600]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion, the smallest local minimum of 7 singular values is used here. See Sect. 4.4. |
| In the text | |
 |
Fig. 22 Cumulative lightcurve of GRB 091024.380. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
| In the text | |
 |
Fig. 23 Top: lightcurve of the Fermi GRB 100130.777 as measured by the triggered GBM detector “8” and the fitted background with a grey line. Burst interval: [− 30:90]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
| In the text | |
 |
Fig. 24 Cumulative lightcurve of GRB 100130.777. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
| In the text | |
 |
Fig. 25 Top: lightcurve of the Fermi GRB 100414.097 as measured by the non-triggered GBM detector “5” and the fitted background with a grey line. Burst interval: [− 20:30]. Bottom left: underlying variables (absolute values). See Sect. 3. Bottom right: Akaike information criterion. See Sect. 4.4. |
| In the text | |
 |
Fig. 26 Cumulative lightcurve of GRB 100414.097. Horizontal lines are drawn at 0% and 100% of total cumulated counts; dots mark every 5%. |
| In the text | |
 |
Fig. 27 Distibution of the T90 obtained from the MC simulated data for Fermi burst 091030.613 (Szécsi et al. 2012c). |
| In the text | |
 |
Fig. 28 Distibution of the T50 obtained from the MC simulated data for the Fermi burst 091030.613 (Szécsi et al. 2012c). |
| In the text | |
 |
Fig. A.1 Earth limb seen onboard from the Fermi. Detector can only see the coloured parts above the solid horizontal black line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



