| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 5 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321025 | |
| Published online | 30 August 2013 | |
The dependence of the parallel and perpendicular mean free paths on the rigidity of the solar energetic particles: Theoretical model versus observations
1
Key Laboratory of Ionospheric Environment, Institute of Geology and
Geophysics, Chinese Academy of Sciences,
100029
Beijing,
PR China
e-mail: hqhe@mail.iggcas.ac.cn; wanw@mail.iggcas.ac.cn
2
Beijing National Observatory of Space Environment, Institute of
Geology and Geophysics, Chinese Academy of Sciences, 100029
Beijing, PR
China
3
Key Laboratory of Solar Activity, National Astronomical
Observatories, Chinese Academy of Sciences, 100012
Beijing, PR
China
Received:
1
January
2013
Accepted:
21
June
2013
Context. The dependence of the parallel and perpendicular mean free paths on the particle rigidity is an important topic in the studies of the diffusion and propagation of charged energetic particles in a large-scale turbulent magnetic field.
Aims. In this work, we investigate the dependence of the parallel and perpendicular mean free paths on the rigidity of solar energetic particles (SEPs) by means of both the theoretical model and spacecraft observations with regard to several typical SEP events.
Methods. A direct method developed by previous studies and derived from the focused transport equation and Taylor-Green-Kubo (TGK) formulation is applied to explicitly determine the parallel and perpendicular mean free paths of SEPs in a turbulent and spatially varying magnetic field.
Results. We find that the parallel and perpendicular mean free paths, λ∥ and λ⊥, of energetic protons monotonically decrease with increasing particle rigidity, and the ratio λ⊥/λ∥ monotonically increases with particle rigidity, when the magnetic turbulence is weak. Taking a series of typical SEP events together, it can also be seen that the ratio λ⊥/λ∥ of the perpendicular to the parallel mean free paths remains in the range of 0.001−0.2.
Key words: interplanetary medium / magnetic fields / solar-terrestrial relations / Sun: coronal mass ejections / Sun: flares / Sun: particle emission
© ESO, 2013
1. Introduction
The diffusion mechanism of charged energetic particles in the interstellar and interplanetary space remains one of the fundamental problems of long-standing importance in the fields of modern astrophysics and heliophysics. Theoretically, a better understanding of this problem is essential for studying the acceleration, transport, and modulation of charged energetic particles in the turbulent magnetic fields.
Generally, the diffusion tensor of charged energetic particles in the turbulent magnetic fields can be separated into two parts: a symmetric part, consisting of parallel diffusion along and perpendicular diffusion across the average magnetic field and an asymmetric component, known as the drift effect. For the transport of solar energetic particles (SEPs), the parallel diffusion and perpendicular diffusion are usually considered. Due to its evident importance in the transport process of charged energetic particles, the parallel diffusion has been extensively investigated (e.g., Jokipii 1966; Bieber et al. 1994; Teufel & Schlickeiser 2002; He & Qin 2011). Nevertheless, the perpendicular diffusion has been an enigmatic problem in the community for a long time until some observational results were recently reported (e.g., Dwyer et al. 1997; Zhang et al. 2003). This placed strong constraints on the numerical simulations (e.g., Giacalone & Jokipii 1999; He et al. 2011; Qin et al. 2011) and the theoretical investigations (e.g., Matthaeus et al. 2003; Shalchi et al. 2004; He & Wan 2012b). By implementing a series of elaborate numerical calculations, He et al. (2011) found that the perpendicular diffusion has a very important influence on the propagation of SEPs in the heliosphere, particularly when a spacecraft is not directly connected to the acceleration regions either on the Sun or near the coronal mass ejection driven shocks by the interplanetary magnetic field lines.
Although significant progress has been achieved toward a better understanding of the diffusion mechanisms through several decades of efforts in the community by using spacecraft observations and theoretical modeling, a lot of challenging questions still remain. One issue is the lack of a simple and computationally tractable model of the diffusion coefficients or mean free paths, which is significant to theoretical investigations and practical applications, especially for space weather forecasting. Bieber et al. (1995) and Zank et al. (1998) presented approximate evaluations for the values of the parallel mean free path (see Eqs. (5)−(9) in Pei et al. 2010). Hinted by Shalchi (2011) recently, He & Wan (2012a) provided a direct method to quickly and explicitly determine the spatially dependent parallel mean free path of SEPs with adiabatic focusing. Furthermore, He & Wan (2012b) presented a direct approach to investigate the spatially dependent perpendicular mean free path of SEPs in a turbulent and spatially varying magnetic field, in light of the results in He & Wan (2012a).
The dependence of the parallel and perpendicular mean free paths on the rigidity of SEPs transporting in the interplanetary magnetic field is a very appealing subject in research, and it attracts a number of authors (e.g., Palmer 1982; Bieber et al. 1994; Giacalone 1998; Dröge 2000; He & Wan 2012a,b). Specifically, Palmer (1982) compiled together a large amount of SEP events, which were evaluated at only one or very few rigidities, and claimed that the dependence of the observed parallel mean free paths on the particle rigidity is flat. Namely, the parallel mean free paths of SEPs are roughly independent of particle rigidity. However, Bieber et al. (1994) revisited the Palmer consensus and pointed out that the proton parallel mean free paths monotonically increase with increasing particle rigidity, when individual SEP events are considered separately. Giacalone (1998) recompiled the results of Bieber et al. (1994) to include an unusual SEP event serving as a counterexample, which was taken from Ma Sung & Earl (1978) and displayed a monotonically decreasing dependence of the parallel mean free paths on the increasing particle rigidity. Additionally, Dröge (2000) investigated several SEP events and stated that a uniform shape of the functional form of the rigidity dependence, which only alters its absolute height for different cases, can account for all observations. Most recently, He & Wan (2012a) showed that the dependence of the parallel mean free paths derived from a direct method on the particle rigidity agrees well with the Palmer consensus band and the results of Bieber et al. (1994). In addition, He & Wan (2012b) used the direct approach to investigate the dependence of the perpendicular mean free path λ⊥ and its ratio λ⊥/λ∥ to the parallel mean free path on the particle rigidity to show that λ⊥ monotonically increases with the particle rigidity, while λ⊥/λ∥ monotonically decreases with increasing particle rigidity.
With combination of theoretical model and spacecraft observations, we focus on a series of typical SEP events, which serve as demonstrating examples in this article, to investigate the dependence of the parallel and perpendicular mean free paths on the rigidity of SEPs. We find that the parallel and perpendicular mean free paths of energetic protons monotonically decrease with increasing particle rigidity, and the ratio λ⊥/λ∥ monotonically increases with increasing particle rigidity, when the magnetic turbulence is weak. Therefore, a small value of δB/B can explain the occasionally observed decreasing dependence of the mean free paths on the particle rigidity (Ma Sung & Earl 1978). To our knowledge, this is the first time that this phenomenon has been obtained in the theoretical investigations. Additionally, it can be seen that the ratio λ⊥/λ∥ of the perpendicular to the parallel mean free paths remains in the range 0.001−0.2, when taking a series of typical SEP events together. In Sect. 2, we first represent a brief description of the direct methods, which were developed by He & Wan (2012a) and He & Wan (2012b) to explicitly determine the spatially dependent parallel and perpendicular mean free paths of SEPs with adiabatic focusing. The practical implications of the direct methods for the space weather forecasting of SEP events are also summarized in this section. In Sect. 3, we analyze the dependence of the parallel and perpendicular mean free paths on the particle rigidity in several selected SEP events and compare the predictions of the direct methods to the observational determination results, which are adopted from previous works. A summary of our results is provided in Sect. 4.
2. Direct methods for determining the mean free paths
2.1. Formulation
The focused transport equation that governs the gyrophase-averaged distribution function
f(x,μ,t) of SEPs can be written as (e.g.,
He et al. 2011; Shalchi 2011) 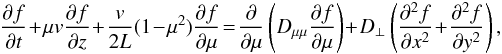 (1)where
z is the coordinate along the average magnetic field line,
μ is the pitch-angle cosine of particles, t is the
time, v is the particle velocity,
Dμμ is the pitch-angle diffusion
coefficient, D⊥ is the perpendicular diffusion coefficient,
and L is the adiabatic focusing length of the heliospheric magnetic
field. Based on Eq. (1), Shalchi (2011) derived an exact formula for the
parallel mean free path with adiabatic focusing. Motivated by the works of Shalchi (2011) and Burger et al. (2008), recently, He & Wan
(2012a,b) presented direct methods to
quickly and explicitly determine the spatially dependent parallel and perpendicular mean
free paths of SEPs with an adiabatic focusing effect. We show here a brief description of
the direct methods. For a detailed description of the methods, please refer to He & Wan (2012a,b). The formulation of the direct methods can be briefly written as
(1)where
z is the coordinate along the average magnetic field line,
μ is the pitch-angle cosine of particles, t is the
time, v is the particle velocity,
Dμμ is the pitch-angle diffusion
coefficient, D⊥ is the perpendicular diffusion coefficient,
and L is the adiabatic focusing length of the heliospheric magnetic
field. Based on Eq. (1), Shalchi (2011) derived an exact formula for the
parallel mean free path with adiabatic focusing. Motivated by the works of Shalchi (2011) and Burger et al. (2008), recently, He & Wan
(2012a,b) presented direct methods to
quickly and explicitly determine the spatially dependent parallel and perpendicular mean
free paths of SEPs with an adiabatic focusing effect. We show here a brief description of
the direct methods. For a detailed description of the methods, please refer to He & Wan (2012a,b). The formulation of the direct methods can be briefly written as
![\begin{equation} \lambda_{\parallel}=\frac{3L^{3}}{\lambda_{\parallel,0}^{2}}\left[\frac{\lambda_{\parallel,0}}{L}-\tanh\left(\frac{\lambda_{\parallel,0}}{L}\right)\right],\label{mfp} \end{equation}](/articles/aa/full_html/2013/09/aa21025-13/aa21025-13-eq16.png) (2)
(2)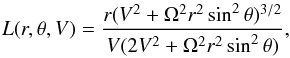 (3)and
(3)and ![\begin{equation} \lambda_{\perp}=\left[a^{2}\frac{q-1}{2q}\sqrt{\pi}\frac{\Gamma(\frac{q}{2}+1)}{\Gamma(\frac{q}{2}+\frac{1}{2})}l_{\rm 2D}\frac{\delta B_{\rm 2D}^{2}}{B^{2}}\right]^{\frac{2}{3}}(3\lambda_{\parallel})^{\frac{1}{3}}.\label{pmfp} \end{equation}](/articles/aa/full_html/2013/09/aa21025-13/aa21025-13-eq18.png) (4)In the above
equations, λ∥ ,0 is the parallel mean free
path of SEPs without adiabatic focusing, r is the radial distance from
the center of the Sun, θ is the co-latitude measured from the rotation
axis of the Sun, V is the solar wind speed, Ω is the angular rotation
velocity of the Sun, a is a constant chosen to be
(4)In the above
equations, λ∥ ,0 is the parallel mean free
path of SEPs without adiabatic focusing, r is the radial distance from
the center of the Sun, θ is the co-latitude measured from the rotation
axis of the Sun, V is the solar wind speed, Ω is the angular rotation
velocity of the Sun, a is a constant chosen to be
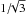 ,
q is the inertial range spectral index, l2D
and
,
q is the inertial range spectral index, l2D
and 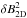 are the
bendover scale and the variance of the two-dimensional component of the turbulence,
respectively, and B is the strength of the average magnetic field in a
particular spatial position in the heliosphere.
are the
bendover scale and the variance of the two-dimensional component of the turbulence,
respectively, and B is the strength of the average magnetic field in a
particular spatial position in the heliosphere.
As indicated by He & Wan (2012b) in the
theoretical investigations with typical parameter regimes, it can be drawn that
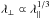 .
This relation was also shown in the work of Bieber et al.
(2004), who found that a perpendicular mean free path increasing monotonically
with the parallel mean free path is a robust feature of the nonlinear guiding center
(NLGC) model (Matthaeus et al. 2003). This is
contradictory to the field line random walk (FLRW) description but agrees with simulations
and with common practice in modulation modeling. On the other hand, the numerical results
of Minnie et al. (2009) showed that the
perpendicular mean free path saturates at a particular value determined by the box size
L, in a finite domain with finite box size.
.
This relation was also shown in the work of Bieber et al.
(2004), who found that a perpendicular mean free path increasing monotonically
with the parallel mean free path is a robust feature of the nonlinear guiding center
(NLGC) model (Matthaeus et al. 2003). This is
contradictory to the field line random walk (FLRW) description but agrees with simulations
and with common practice in modulation modeling. On the other hand, the numerical results
of Minnie et al. (2009) showed that the
perpendicular mean free path saturates at a particular value determined by the box size
L, in a finite domain with finite box size.
It should be noted that the expressions of the direct methods presented above are derived from the focused transport equation and Taylor-Green-Kubo (TGK) formulation (e.g., Kubo 1957). By putting the observed physical quantities corresponding to the interplanetary conditions into the direct methods, we can explicitly determine both the parallel and the perpendicular mean free paths of SEPs. Some previous works (e.g., Dröge 2000) determined the parallel mean free path of SEPs using the simulation method, by fitting the time profiles of both flux and anisotropy between spacecraft observations and numerical simulations of the transport of SEPs. Recently, Pei et al. (2010) also discussed the heliospheric values of the parallel and perpendicular mean free paths using theoretical models and evaluated turbulence parameters. The approach used by Pei et al. (2010) especially with regard to the model of spatially varying turbulence parameters is complementary to our results in the current paper. In principle, a global model of heliospheric turbulence is important to the determinations of mean free paths and drift scale, although the development of this realistic turbulence model in accord with multipoint observations is a challenging problem.
2.2. Practical implications
As we know, the charged energetic particles, including SEPs and galactic cosmic rays (GCRs), are a health risk for the astronauts working in space and damage the electronic components on satellites. Therefore, it is very important to predict the transport process and space-time evolution of these kinds of energetic particles, especially in the current space science and technology era. To quickly and accurately predict the transport process and space-time evolution of SEPs before they arrive at the spacecraft or enter Earth’s orbit, it is crucial to develop a sufficiently efficient forecasting module based on physical quantitative descriptions of the diffusion processes. This task has become a focus of international space weather and space physics research.
From the formulae given in Sect. 2.1, we only need some observable quantities concerning the physical properties of SEPs and interplanetary conditions, such as the solar wind and the turbulent magnetic field, to determine the parallel and perpendicular mean free paths of SEPs. This natural advantage of the direct methods enables us to explicitly and quickly obtain the spatially dependent parallel and perpendicular mean free paths of SEPs without applying the time-consuming numerical simulations of the particle propagation.
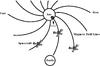 |
Fig. 1 Sketch to show the scenario of space weather forecasting for SEP events. The spirals correspond to interplanetary magnetic field lines, along and across which the SEPs transport diffusively in the solar-terrestrial space. The realistic physical parameters observed before a specific solar event by the in-situ spacecraft can be used to quickly determine the parallel and perpendicular mean free paths, with which we can further obtain the intensity and evolution of SEPs at a particular location in the interplanetary space. |
 |
Fig. 2 Parallel mean free paths of solar energetic protons vs. particle rigidity for several typical SEP events, which were analyzed in two or more energy channels. The different symbols denote the observational determinations from different SEP events. This figure is adapted from Bieber et al. (1994) and Giacalone (1998). See text for source references. |
Generally speaking, the variation magnitudes of the interplanetary conditions, such as the solar wind speed and the large-scale turbulent magnetic field, are relatively small during a time range of several hours, which is a typical time period spent by the SEPs transporting in the interplanetary space from the surface of the Sun to the spacecraft or about 1 AU, namely, the Earth’s orbit. Therefore, we can utilize the realistic physical parameters as inputs observed before a specific solar event by a series of in-situ spacecraft spreading in the interplanetary medium to quickly determine the spatially dependent parallel and perpendicular mean free paths. We can then further obtain the intensity and evolution of SEPs at a particular location in the interplanetary space. By simultaneously evaluating the flux profiles of different kinds of particles with different energies, we can predict the total radiation dose in a particular spatial position in the heliosphere during the forthcoming SEP event. The scenario of space weather forecasting for SEP events is schematically illustrated in Fig. 1.
Relevant physical parameters and their values used in the theoretical model to determine the parallel and perpendicular mean free paths for every SEP event.
3. The rigidity dependence of the mean free paths
In this section, we will investigate the rigidity dependence of the parallel and perpendicular mean free paths of SEPs. First, we represent the classical observational results of the parallel mean free paths in Fig. 2, which was first compiled by Bieber et al. (1994) and then recompiled by Giacalone (1998). Here, Fig. 2 is an adaptation of Fig. 4 from Bieber et al. (1994) and Fig. 2 from Giacalone (1998). In Fig. 2, we see that there are two or more energy channels for every case of the six SEP events. Specifically, the triangles and crosses denote the SEP events of 1980 March 25 and 1979 June 9, respectively, of which both are adopted from Kallenrode (1993). The circles and diamonds indicate the SEP events of 1977 December 27 and 1977 November 22, respectively, of which both were analyzed by Beeck et al. (1987). The squares show the SEP event of 1978 April 11, which is taken from Valdés-Galicia et al. (1988). The asterisks denote the SEP event of 1970 March 29, which are adopted from Ma Sung & Earl (1978) and are shown here as a counterexample (Giacalone 1998). As we can see in the Fig. 2, the majority of the observational determination results illustrate that the parallel mean free path monotonically increases with increasing particle rigidity. However, there are also some particular cases, which display a monotonically decreasing dependence of the parallel mean free path with increasing particle rigidity, such as in the 1970 March 29 SEP event. In general, the functional form of the rigidity dependence shows variable absolute heights for different SEP events.
 |
Fig. 3 Fitting results of the theoretical model predictions to the observational determinations for the selected SEP events displayed in Fig. 2. The types of symbols (with colors) corresponding to different SEP events are the same as those in Fig. 2. The solid curves with different colors in three panels indicate the predictions of the theoretical model for the corresponding SEP events. Top: parallel mean free paths from the theoretical model in comparison with the observational determinations from spacecraft measurements of solar energetic protons in the SEP events. Middle: perpendicular mean free paths calculated from the corresponding parallel mean free paths. Bottom: ratios of the perpendicular to the parallel mean free paths. |
Fitting the theoretical models to the spacecraft observations poses a challenge to the modeling and simulations of the diffusion processes of charged energetic particles. On the other hand, we need these fittings to verify the theoretical models and to investigate the inherent physical mechanisms in the diffusion processes. Figure 3 shows the fitting results of the direct methods presented in Sect. 2 to the observational determinations of the parallel mean free paths for the six SEP events displayed in Fig. 2. The types of symbols (with colors) in Fig. 3 corresponding to different SEP events are the same as those in Fig. 2. The solid curves with different colors in three panels indicate the predictions of the theoretical model for the corresponding SEP events. We briefly describe here the locations of the spacecraft that observed the particular SEP events when the charged energetic particles arrived. During the 1980 March 25 SEP event, the Helios 1 spacecraft was located at heliocentric radial distance r = 0.91 AU and co-latitude θ = 93.0°. The Helios 2 was located at heliocentric distance r = 0.67 AU and co-latitude θ = 88.2° when the energetic particles of the 1979 June 9 SEP event arrived. The ISEE 1 was located at the positions of r = 1.0 AU, θ = 92.4° and r = 1.0 AU, θ = 88.0°, during the SEP events of 1977 December 27 and 1977 November 22, respectively. The 1978 April 11 SEP event was observed by Helios 2, which was located at r = 0.49 AU and θ = 96.3°. The fitting results of this SEP event are taken from He & Wan (2012b). The SEP event of 1970 March 29 was observed by IMP 4 and IMP 5, of which both were approximately located at r = 1.0 AU and θ = 96.7° when the particles arrived. We list these realistic quantities in Table 1. Other relevant physical parameters such as the solar wind speed and the turbulence strength of the magnetic field, that we use in the calculations for every SEP event are also explained in Table 1. Note that the values of the physical parameters used in the calculations are approximately evaluated according to the spacecraft measurements during the corresponding SEP events. We utilize the slab/two-dimensional composite magnetic turbulence model, in which the turbulence energy in the slab and two-dimensional modes is in the ratio of 20:80 and believed to agree with solar wind observations (Bieber et al. 1996).
As displayed in the top panel of Fig. 3, the
theoretical model shows remarkable agreement with the observational determinations of the
parallel mean free paths. By using the realistic physical parameters concerning the
properties of SEPs and interplanetary conditions as inputs, we reproduce the rigidity
dependence of the parallel mean free paths for every SEP event. Therefore, it is justified
that the direct methods presented in Sect. 2 (see also He
& Wan 2012a,b) are reliable and
helpful tools in theoretical investigations and space weather research. For the
justification of the perpendicular mean free path, please refer to Fig. 9 of He & Wan (2012b), who have shown that the
theoretical results of the perpendicular mean free path agree well with the observational
determinations. In addition, we can see that the shapes and slopes of the rigidity
dependence of the parallel mean free paths for different SEP events are more or less
distinct from each other, especially for the 1970 March 29 SEP event, which serves as a
counterexample. This finding poses important modifications to the claim by Dröge (2000) that “a uniform shape of the functional form
of the rigidity dependence, which varies only in absolute height for different events, can
explain all observations”. Noticeably in Fig. 3, the
functional form of the rigidity dependence alters its absolute level from one event to
another, which agrees with the result of Dröge (2000).
According to the findings in He & Wan
(2012a,b), the parallel mean free path
λ∥ monotonically decreases with increasing magnetic turbulence
strength, while the perpendicular mean free path λ⊥
monotonically increases with the magnetic turbulence strength. Combined with Table 1, we can see that the shapes, slopes, and absolute
heights of the rigidity dependence of the parallel and perpendicular mean free paths are
mainly determined by the strength and geometry, such as in the parameters of
lslab, l2D, and
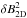 of the turbulent
magnetic field. Therefore, the physical parameters of
δB/B,
lslab, l2D, and
of the turbulent
magnetic field. Therefore, the physical parameters of
δB/B,
lslab, l2D, and
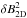 would be key proxies
in the spacecraft observations to characterize the scattering conditions and the transport
processes of charged energetic particles, including SEPs in the heliosphere. Most
interestingly, the parallel and perpendicular mean free paths of energetic protons
monotonically decrease with increasing particle rigidity, when the magnetic turbulence is
weak, such as in the case where
δB/B = 0.1 during the 1970 March 29 SEP
event. To our knowledge, this is the first time that this phenomenon has been obtained in
the theoretical investigations. Although the prediction of the theoretical model does not
completely fit the observational results for the 1970 March 29 SEP event, the qualitative
agreement between the theoretical model and the observational determinations can be
evidently seen. Therefore, we can explain the occasionally observed decreasing rigidity
dependence of the mean free paths presented in Ma Sung
& Earl (1978).
would be key proxies
in the spacecraft observations to characterize the scattering conditions and the transport
processes of charged energetic particles, including SEPs in the heliosphere. Most
interestingly, the parallel and perpendicular mean free paths of energetic protons
monotonically decrease with increasing particle rigidity, when the magnetic turbulence is
weak, such as in the case where
δB/B = 0.1 during the 1970 March 29 SEP
event. To our knowledge, this is the first time that this phenomenon has been obtained in
the theoretical investigations. Although the prediction of the theoretical model does not
completely fit the observational results for the 1970 March 29 SEP event, the qualitative
agreement between the theoretical model and the observational determinations can be
evidently seen. Therefore, we can explain the occasionally observed decreasing rigidity
dependence of the mean free paths presented in Ma Sung
& Earl (1978).
The perpendicular mean free path λ⊥ and its ratio λ⊥/λ∥ to the parallel mean free path corresponding to the particular SEP events are displayed in the middle and bottom panels, respectively. As one can see in the panels, the perpendicular mean free path λ⊥ for every SEP event displays a relatively weak rigidity dependence, and the ratio λ⊥/λ∥ monotonically decreases with increasing particle rigidity (see also He & Wan 2012b) for most SEP events with the interesting exception of the 1970 March 29 SEP event, in which the ratio λ⊥/λ∥ monotonically increases with increasing particle rigidity. As we know, the value or magnitude of the ratio λ⊥/λ∥ is one of the most enigmatic puzzles in heliospheric studies. Taking all of the SEP events together in the bottom panel of Fig. 3, we can see that the ratio λ⊥/λ∥ approximately spans a variation range of 0.001−0.2.
4. Summary and conclusions
The rigidity dependence of the parallel and perpendicular mean free paths of charged energetic particles, including SEPs, in the large-scale turbulent magnetic fields, is a very important and engaging topic in the community. Although understanding of this topic has made considerable progress in recent years, there still lacks an effective theoretical model with a simple and computationally tractable form to simultaneously investigate the rigidity dependence of the parallel and perpendicular mean free paths of SEPs in an event-to-event view. In the current paper, we focus on this interesting topic by combining the direct methods for determining the spatially dependent parallel and perpendicular mean free paths with adiabatic focusing presented by He & Wan (2012a,b), respectively, with spacecraft observation results that concern several selected SEP events analyzed by previous authors. The theoretical model shows encouraging agreement with the observational results and basically reproduces the rigidity dependence of the parallel mean free paths for several typical SEP events including a counterexample. This indicates that the direct methods are useful in the theoretical investigations and helpful in the space weather forecasting. The main conclusions of our results in this article are summarized below.
The rigidity dependence of the parallel and perpendicular mean free paths and their ratio varies in absolute height for different SEP events. Generally, we have found the following: when the other physical parameters are the same and when SEPs transport with stronger turbulence in the magnetic field, the rigidity dependence of the parallel mean free path displays a lower absolute level, and the rigidity dependence of the perpendicular mean free path has a higher absolute level.
The shapes, slopes, and absolute heights of the rigidity dependence of the parallel and
perpendicular mean free paths and their ratio are dominantly determined by the strength and
topology in parameters, such as lslab,
l2D, and 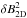 of the turbulent
magnetic field. Therefore, the physical quantities of
δB/B, lslab,
l2D, and
of the turbulent
magnetic field. Therefore, the physical quantities of
δB/B, lslab,
l2D, and 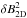 can be seen as
the crucial proxies in the spacecraft measurements to characterize the scattering conditions
and the transport processes of charged energetic particles, including SEPs in the
interplanetary space.
can be seen as
the crucial proxies in the spacecraft measurements to characterize the scattering conditions
and the transport processes of charged energetic particles, including SEPs in the
interplanetary space.
When the magnetic turbulence is weak, the parallel and perpendicular mean free paths of energetic protons monotonically decrease with increasing particle rigidity, and the ratio λ⊥/λ∥ monotonically increases with increasing particle rigidity. Therefore, a small value of δB/B can explain the occasionally observed decreasing rigidity dependence of the mean free paths (Ma Sung & Earl 1978).
Taking a series of typical SEP events together, it can be seen that the ratio λ⊥/λ∥ of the perpendicular to the parallel mean free paths remains in the range 0.001−0.2. Our results would provide valuable constraints on the diffusion theories and diffusion models.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under grants NNSFC 41204130 and NNSFC 41131066, the National Important Basic Research Project under grant 2011CB811405, the Chinese Academy of Sciences under grant KZZD-EW-01-2, the China Postdoctoral Science Foundation under grants 2011M500381 and 2012T50131, the Open Research Fund of Key Laboratory of Solar Activity, Chinese Academy of Sciences, and the Key Laboratory of Random Complex Structures and Data Science, CAS. H.-Q. He gratefully acknowledges the support of K.C.Wong Education Foundation.
References
- Beeck, J., Mason, G. M., Hamilton, D. C., et al. 1987, ApJ, 322, 1052 [NASA ADS] [CrossRef] [Google Scholar]
- Bieber, J. W., Matthaeus, W. H., Smith, C. W., et al. 1994, ApJ, 420, 294 [Google Scholar]
- Bieber, J. W., Burger, R. A., & Matthaeus, W. H. 1995, in Proc. 24th Int. Cosmic Ray Conf., 4, 694 [Google Scholar]
- Bieber, J. W., Wanner, W., & Matthaeus, W. H. 1996, J. Geophys. Res., 101, 2511 [Google Scholar]
- Bieber, J. W., Matthaeus, W. H., Shalchi, A., & Qin, G. 2004, Geophys. Res. Lett., 31, L10805 [Google Scholar]
- Burger, R. A., Krüger, T. P. J., Hitge, M., & Engelbrecht, N. E. 2008, ApJ, 674, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Dröge, W. 2000, ApJ, 537, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Dwyer, J. R., Mason, G. M., Mazur, J. E., et al. 1997, ApJ, 490, L115 [Google Scholar]
- Giacalone, J. 1998, Space Sci. Rev., 83, 351 [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 1999, ApJ, 520, 204 [Google Scholar]
- He, H.-Q., & Qin, G. 2011, ApJ, 730, 46 [NASA ADS] [CrossRef] [Google Scholar]
- He, H.-Q., & Wan, W. 2012a, ApJ, 747, 38 [NASA ADS] [CrossRef] [Google Scholar]
- He, H.-Q., & Wan, W. 2012b, ApJS, 203, 19 [NASA ADS] [CrossRef] [Google Scholar]
- He, H.-Q., Qin, G., & Zhang, M. 2011, ApJ, 734, 74 [Google Scholar]
- Jokipii, J. R. 1966, ApJ, 146, 480 [Google Scholar]
- Kallenrode, M.-B. 1993, J. Geophys. Res., 98, 19037 [NASA ADS] [CrossRef] [Google Scholar]
- Kubo, R. 1957, J. Phys. Soc. Japan, 12, 570 [Google Scholar]
- Ma Sung, L. S., & Earl, J. A. 1978, ApJ, 222, 1080 [NASA ADS] [CrossRef] [Google Scholar]
- Matthaeus, W. H., Qin, G., Bieber, J. W., & Zank, G. P. 2003, ApJ, 590, L53 [Google Scholar]
- Minnie, J., Matthaeus, W. H., Bieber, J. W., Ruffolo, D., & Burger, R. A. 2009, J. Geophys. Res., 114, A01102 [NASA ADS] [CrossRef] [Google Scholar]
- Palmer, I. D. 1982, Rev. Geophys. Space Phys., 20, 335 [Google Scholar]
- Pei, C., Bieber, J. W., Breech, B., et al. 2010, J. Geophys. Res., 115, A03103 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, G., He, H.-Q., & Zhang, M. 2011, ApJ, 738, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A. 2011, ApJ, 728, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A., Bieber, J. W., & Matthaeus, W. H. 2004, ApJ, 604, 675 [Google Scholar]
- Teufel, A., & Schlickeiser, R. 2002, A&A, 393, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valdés-Galicia, J. F., Wibberenz, G., Quenby, J. J., et al. 1988, Sol. Phys., 117, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., Matthaeus, W. H., Bieber, J. W., & Moraal, H. 1998, J. Geophys. Res., 103, 2085 [Google Scholar]
- Zhang, M., Jokipii, J. R., & McKibben, R. B. 2003, ApJ, 595, 493 [Google Scholar]
All Tables
Relevant physical parameters and their values used in the theoretical model to determine the parallel and perpendicular mean free paths for every SEP event.
All Figures
 |
Fig. 1 Sketch to show the scenario of space weather forecasting for SEP events. The spirals correspond to interplanetary magnetic field lines, along and across which the SEPs transport diffusively in the solar-terrestrial space. The realistic physical parameters observed before a specific solar event by the in-situ spacecraft can be used to quickly determine the parallel and perpendicular mean free paths, with which we can further obtain the intensity and evolution of SEPs at a particular location in the interplanetary space. |
| In the text | |
 |
Fig. 2 Parallel mean free paths of solar energetic protons vs. particle rigidity for several typical SEP events, which were analyzed in two or more energy channels. The different symbols denote the observational determinations from different SEP events. This figure is adapted from Bieber et al. (1994) and Giacalone (1998). See text for source references. |
| In the text | |
 |
Fig. 3 Fitting results of the theoretical model predictions to the observational determinations for the selected SEP events displayed in Fig. 2. The types of symbols (with colors) corresponding to different SEP events are the same as those in Fig. 2. The solid curves with different colors in three panels indicate the predictions of the theoretical model for the corresponding SEP events. Top: parallel mean free paths from the theoretical model in comparison with the observational determinations from spacecraft measurements of solar energetic protons in the SEP events. Middle: perpendicular mean free paths calculated from the corresponding parallel mean free paths. Bottom: ratios of the perpendicular to the parallel mean free paths. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


