Table 3
Mean (and median) observed kinematic properties for low-z comparison samples from the literature.
| Sample | SFR | v | σ | v/σ | R eff | M dyn |
| [M⊙ yr-1] | (km s-1) | (km s-1) | (kpc) | (1010M⊙) | ||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) |
|
|
||||||
| Spiral | 1.8 ± 0.4 (0.7) | 162 ± 7 (143) | 24 ± 0.5 (24) | 7.0 ± 0.3 (6.3) | 5.5 ± 0.3 (4.8) | 11.5 ± 1.5 (4.9) |
|
|
||||||
| E/S0 | 0.12 ± 0.04 (0.08) | 47 ± 4 (44) | 162 ± 9 (163) | 0.34 ± 0.03 (0.34) | 2.9 ± 0.3 (2.4) | 13.8 ± 3.2 (6.9) |
|
|
||||||
| LBA | 26.7 ± 7.1 (17.0) | 67 ± 11 (63) | 71 ± 6 (67) | 0.95 ± 0.11(1.1) | 1.4 ± 0.1 (1.5) | 1.0 ± 0.2 (1.0) |
Notes. Column (1): low-z sample: spiral sample is
drawn from Epinat et al. (2010), E/S0 from
Cappellari et al. (2007) and LBAs from
Gonçalves et al. (2010). Column (2): star
formation rate (SFR). For spirals, it has been derived using only 50 objects, for
which the SFRs have been computed from Hα measurements by James et al. (2004) using Salpeter IMF (Salpeter 1955) and applying the Kennicutt et al. (1994) relation. For E/S0
galaxies we considered the SFR computed in Shapiro
et al. (2010) for a subsample of 13 sources using the
Spitzer/IRAC data at 8.0 μm. They have
calibrated this relation from the Yun et al.
(2001) relation between SFR and radio continuum. If the Kennicutt (1998) SFR-Hα
conversion is applied to calibrate the 8.0 μm SFR estimator, the
SFR would lower by ~13% (see Wu et al. 2005).
For the LBAs, the star formation rates are measured by Gonçalves et al. (2010) from combined Hα and
MIPS 24 μm data using Kroupa
(2008) IMF. The resulting SFRs are lower by a factor of ~1.5 compared to a
Salpeter (1955) IMF. Column (3): observed
velocity amplitude obtained as follows: for spirals, it is the observed maximum
rotational velocity; for the E/S0 sample it is the luminosity-weighted squared
velocity (i.e., 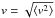 )
within 1 Reff; for LBAs the velocity amplitude has been
defined as the vshear in this work. Column (4): velocity
dispersion derived as follows: for spirals, it is the (uniformly weighted) mean
velocity dispersion; for E/S0s it is the luminosity-weighted squared velocity
dispersion (i.e.,
)
within 1 Reff; for LBAs the velocity amplitude has been
defined as the vshear in this work. Column (4): velocity
dispersion derived as follows: for spirals, it is the (uniformly weighted) mean
velocity dispersion; for E/S0s it is the luminosity-weighted squared velocity
dispersion (i.e., 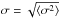 )
within 1 Reff; for LBAs the velocity dispersion is the
average velocity dispersion of each spaxel, weighted by flux. Column (5): dynamical
ratio determined as the ratio between the values shown in Cols. (3) and (4). Column
(6): effective radius for the different samples. For spirals it has been derived as
half of the optical radius (Ropt) associated with the
isophotal level at 25 mag arcsec-2 in the B-band, where
Ropt = 1.9 × Reff (see
Epinat et al. 2009); for E/S0 the
half-light radius is measured in the I-band from WFPC2/HST images;
for LBAs the effective radius was derived by selecting N spaxels
with S ! N > 6 such that
)
within 1 Reff; for LBAs the velocity dispersion is the
average velocity dispersion of each spaxel, weighted by flux. Column (5): dynamical
ratio determined as the ratio between the values shown in Cols. (3) and (4). Column
(6): effective radius for the different samples. For spirals it has been derived as
half of the optical radius (Ropt) associated with the
isophotal level at 25 mag arcsec-2 in the B-band, where
Ropt = 1.9 × Reff (see
Epinat et al. 2009); for E/S0 the
half-light radius is measured in the I-band from WFPC2/HST images;
for LBAs the effective radius was derived by selecting N spaxels
with S ! N > 6 such that
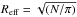 (see Law et al. 2007). Column (7): dynamical
mass determined as follows: for spirals we compute the total mass using the formula
employed in their paper for rotation-dominated objects; we compute the dynamical
masses for E/S0 using the formula
Kσ2Reff/G
as explained in Cappellari et al. (2006);
finally, the dynamical masses of LBAs have been derived in Gonçalves et al. (2010) using the formula
5σ2Reff/G.
(see Law et al. 2007). Column (7): dynamical
mass determined as follows: for spirals we compute the total mass using the formula
employed in their paper for rotation-dominated objects; we compute the dynamical
masses for E/S0 using the formula
Kσ2Reff/G
as explained in Cappellari et al. (2006);
finally, the dynamical masses of LBAs have been derived in Gonçalves et al. (2010) using the formula
5σ2Reff/G.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


