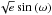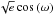EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 556 (August 2013) A&A, 556 (2013) A133 Full HTML
Highlight
Free Access
Issue
A&A
Volume 556, August 2013
Article Number A133
Number of page(s) 10
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201321871
Published online 08 August 2013

© ESO, 2013

1. Introduction

Brown dwarfs are abundant in the Galaxy (Basri 2000) and appear to form like stars (Luhman 2012) but are not massive enough to sustain hydrogen fusion. Along with very low-mass stars, they are referred to as ultracool dwarfs (spectral type M7 and later, Kirkpatrick 2005) that have masses in the range of approximately 0.01–0.1 times the mass of the Sun (M⊙). They bridge the mass gap between planets and stars and provide us with a critical test of our understanding of planet and star formation. Observations of binary systems offer the opportunity for detailed studies and a handful of small-separation (≲1 AU) ultracool binaries (i.e. both components are ultracool dwarfs) have been characterised (Lane et al. 2001; Bouy et al. 2004; Zapatero Osorio et al. 2004; Close et al. 2005; Dupuy et al. 2010) using spectroscopy (Basri & Martín 1999), eclipse photometry (Stassun et al. 2006), astrometry (Dahn et al. 2008), and gravitational microlensing (Choi et al. 2013). Many systems have been discovered using direct imaging, so they tend to be widely separated (≳1 AU) and to have components of similar brightness and nearly equal masses, which means high secondary/primary mass ratios q = M2/M1 (e.g. Martin et al. 1999a; Bouy et al. 2003; Close et al. 2003). Because of the associated long orbital periods of ≳10 years, it is tedious to obtain dynamical mass and eccentricity constraints from orbital motion measurements of these wide systems (e.g. Konopacky et al. 2010).

Ultracool binaries and binary stars with Sun-like primaries show differences in the distributions of mass ratio and orbital separation (Burgasser et al. 2007) that may be signatures of distinct formation mechanisms (Whitworth et al. 2007; Thies & Kroupa 2008; Goodwin 2013). Most of the known systems have high mass ratios and are widely separated, which is attributable in part to the sensitivity limitations of the respective observing techniques. Consequently, the occurrence and configurations of small-separation ultracool binaries with low mass ratios are uncertain. This includes extrasolar planets that are common around Sun-like stars (Mayor et al. 2011) but that have so far not been found around brown dwarfs. Two very low-mass stars are known to host Earth-mass planets (Kubas et al. 2012; Muirhead et al. 2012), and radial velocity and direct imaging surveys could exclude a large population of giant planets >1 Jupiter mass (MJ) in close orbits <0.05 AU and at wide separations ≳2 AU around ultracool dwarfs (Blake et al. 2010; Stumpf et al. 2010).

Astrometric measurements determine the positions of stars in the plane of the sky and make it possible to discover and characterise multiple stellar systems through the detection of orbital motion. Low-mass systems containing brown dwarfs and extrasolar planets are difficult to study in this way because they are faint, and the signatures of orbital motion have typical amplitudes smaller than one milli-arcsecond (mas) (Black & Scargle 1982), which is a challenging figure for currently available instruments. However, astrometric measurements of 50–100 micro-arcseconds (μas) precision were demonstrated by Lazorenko (2006); Lazorenko et al. (2007, 2009, 2011) using ground-based optical imaging with an 8 m-class telescope. To exploit this capability, we have initiated a planet-search survey around ultracool dwarfs that will be described in detail in a forthcoming paper. Here, we report the first result of this survey: the detection and characterisation of a low-mass companion to an ultracool dwarf.

2. Observations and data reduction

We observed the nearby ultracool dwarf DENIS-P J082303.1-491201 (Phan-Bao et al. 2008, spectral type L1.5, hereafter DE0823−49) with the FORS2 (Appenzeller et al. 1998) seeing-limited optical camera of the Very Large Telescope on 14 epochs between October 2010 and January 2013. The observations were separated by typically one month during the seasonal windows, and at each epoch we obtained 25 consecutive I-band images of the target field located close to the southern Galactic plane and containing several hundred reference stars with brightnesses of approximately 17th–22nd magnitude, thus similar to DE0823−49 having an I-band magnitude of mI = 17.1. The position of the target relative to the local grid of reference stars was determined using an improved version of the methods described in Lazorenko et al. (2009, 2011). The dense stellar field is used to correct for atmospheric image motion, optical distortions introduced by the telescope and camera system, and systematic displacement errors at the level of one-thousandth of a detector pixel. One central element of the method relies on averaging the turbulence occurring in the Earth’s atmosphere above the telescope over its 8.2 m aperture.

The relative positions of reference stars are free to vary between frames due to proper motion and parallax. Additionally, they are affected by differential chromatic refraction that displaces “blue” stars towards zenith and “red” stars in the opposite direction. This displacement is typically 1–10 mas and can be computed using a star’s colour index (Lazorenko 2006, Eq. (19)); however, a better correction can be obtained by modelling it with a free parameter (Lazorenko et al. 2011). The typical epoch precision of the astrometric observations was 0.1–0.2 mas, comparable to our observations of the ultracool dwarf VB 10 (Lazorenko et al. 2011), and this allowed us to accurately monitor the sky-projected motion of DE0823−49. After accounting for proper and parallactic motion, an additional signal was detected with a much larger amplitude than the measurement precision. The astrometric data were therefore searched for evidence of orbital motion and processed with a Bayesian analysis package consisting of a genetic algorithm followed by a Markov chain Monte Carlo (MCMC) analysis.

3. Orbit adjustment and parameter estimation

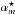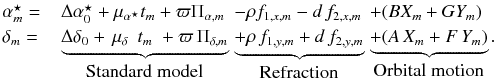The target’s astrometric motion is modelled with the prescription Eq. (1), where αm⋆\hbox{$\alpha^{\star}_m$} and δm are the astrometric measurements relative to the grid of reference stars in right ascension (RA) and declination (Dec), respectively, in frame m taken at time tm (Lazorenko et al. 2011; Sahlmann et al. 2011) \begin{eqnarray} \label{axmodel} \small \begin{array}{ll@{\hspace{1mm}}l@{\hspace{1mm}}l} \alpha^{\star}_{m} = & \Delta \alpha^{\star}_0 + \mu_{\alpha^\star} t_m + \varpi \Pi_{\alpha,m} &- \rho f_{1,x,m}- d \,f_{2,x,m} &+ (B X_m + G Y_m)\\ \delta_{m} = & \underbrace{\Delta \delta_0 + \,\mu_\delta \, \; t_m \;+ \varpi \, \Pi_{\delta,m}}_{\mbox{Standard model} } &\underbrace{+ \rho \,f_{1,y,m}+ d \,f_{2,y,m}}_{\mbox{Refraction}} &\underbrace{+ (A \, X_m + F \, Y_m)}_{\mbox{Orbital motion}}. \end{array} \end{eqnarray}(1)The standard astrometric model consists of coordinate offsets Δα0⋆,Δδ0\hbox{$\Delta\alpha^{\star}_0, \Delta\delta_0$}, the target’s proper motions μα⋆,μδ, and the parallactic motion expressed as the product of relative parallax ϖ and the parallax factors Πα,Πδ. This parallax is not absolute because it is measured relative to the reference stars that are not located at infinite distances, which makes a parallax correction necessary (Sect. 3.4). We require reference stars to have zero parallax on average and about half of the reference stars therefore have negative parallaxes.

Differential chromatic refraction is modelled with the parameters ρ and d whose values depend on the star’s colour. The parameter d is necessary because the observations were obtained with the telescope’s longitudinal atmospheric dispersion compensation mechanism (Avila et al. 1997), which improves the image quality and has one degree of freedom, which is the average zenith angle zL of an observation. 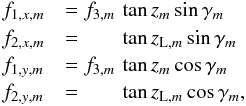The factors \begin{eqnarray} \label{eq:x} \begin{array}{ll@{\hspace{0mm}}l} f_{1,x,m} &= f_{3,m}\,\, &\tan z_m \sin \gamma_m\\ f_{2,x,m} &= &\tan z_{{\rm L},m} \sin \gamma_m\\ f_{1,y,m} &= f_{3,m}\,\, &\tan z_m \cos \gamma_m\\ f_{2,y,m} &= &\tan z_{{\rm L},m} \cos \gamma_m, \end{array} \end{eqnarray}(2)where z is the zenith angle and γ is the angle between the direction to zenith and the y-axis (declination), depend on ambient temperature Ta in degree Celsius and pressure Pa in hPa f3,m=(1−Ta,m−11273+11)(1+Pa,m−744744)·\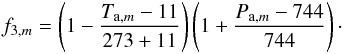begin{eqnarray} \label{eq:xx} f_{3,m} = \left(1-\frac{T_{{\rm a},m}-11}{273+11}\right)\left(1+\frac{P_{{\rm a},m}-744}{744}\right)\cdot \end{eqnarray}(3)Finally, orbital motion is modelled as a Keplerian two-body system, where A,B,F,G are the Thiele-Innes constants (that map the barycentric orbit semimajor axis a1, the argument of periastron ω, the inclination i, and the ascending node Ω), and Xm,Ym are the elliptical-rectangular coordinates that depend on eccentricity e and eccentric anomaly E. The time-dependent eccentric anomaly 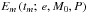Emtm(; e,M0,P)\hbox{$E_m\left(t_m;\,e,M_{0},P\right)$} is also a function of the mean anomaly M0 and the orbital period P. There are thus 14 free parameters.

The astrometry data and the parameters needed to apply the model function Eq. (1) are given in Table 1, available at the CDS, which contains the following information for the 281 individual frames. Column 1 lists the epoch number, Col. 2 gives the modified Julian date of the observation, Cols. 3–6 give the relative astrometry and uncertainties (α⋆, σα⋆, δ, σδ), Cols. 7 and 8 list the parallax factors, Cols. 9–12 give the factors f1,x,m, f2,x,m, f1,y,m, f2,y,m, and Col. 13 lists the covariance.

3.1. Genetic algorithm

The genetic algorithm is designed to efficiently, yet comprehensively, probe a large parameter space and to identify the best set of parameters. We divided the 14 free parameters into the two groups of linear and non-linear parameters on the basis of their appearance in Eq. (1). The genetic part of the algorithm probes the non-linear parameters of the Keplerian equations, namely the eccentricity, the mean anomaly, and the period, whereas the remaining 11 linear parameters (Δα0⋆,Δδ0,μα⋆,μδ,ϖ,A,B,F,G,ρ,d\hbox{$\Delta\alpha^{\star}_0, \Delta\delta_0, \mu_{\alpha^\star}, \mu_\delta, \varpi, A,B,F,G,\rho, d$}) are obtained using a standard least-square fit. Initial guesses for the orbital period are obtained from a generalised Lomb-Scargle periodogram and the set of best solutions is retrieved using the Bayesian formalism by maximising log (Posterior) = log (Likelihood × Priors). The list of priors used to build the merit function is given in Table 2.

Table 2

Parameters probed by the genetic algorithm.

3.2. Markov chain Monte Carlo

Posterior sampling using the genetic algorithm is efficient at identifying the best solution but it does not lead to a statistically reliable sample that can be used to obtain robust parameter distributions and determine confidence intervals. We therefore sample the posterior distributions using a MCMC analysis with Metropolis-Hastings. MCMC posterior sampling (Andrieu & Thoms 2008) is a commonly implemented method, for instance in exoplanet research (Gregory 2005a,b; Collier Cameron et al. 2007; Pollacco et al. 2008). We start the MCMC by drawing several chains (typically 5) from the last chromosome generation of the genetic algorithm to compare their convergence. The step sizes are derived according to the rms of 95% of the last population obtained by the genetic algorithm. The astrometric model is no longer split into linear and non-linear parameters, but instead all 14 parameters are probed with the different set of priors listed in Table 3. Two additional nuisance parameters are added to take potential signals into account that are not accounted for by the model (Pollacco et al. 2008). Those terms affect both the likelihood and the priors. We use uniform priors for all parameters except for P, a1, and ϖ, for which modified Jeffreys priors are preferred (Gregory 2005b). We use ecosω\hbox{$\sqrt{e}\cos{\omega}$} and esinω\hbox{$\sqrt{e}\sin{\omega}$} as free parameters that translate into a uniform prior in eccentricity (Anderson et al. 2011). The mean longitude λ0 = M0 + ω is preferred over the mean anomaly or the date of periastron passage because it is not degenerate at low eccentricities. A large number of MCMC iterations allows us to retrieve a statistically reliable posterior distribution and the marginal parameter distributions.

Table 3

Parameters probed by the MCMC.

3.3. MCMC results

We run the MCMC for 107 iterations and the statistics are derived on the last 7.5 × 106 elements. A characteristic of the reduction procedure is that astrometric measurements taken within one epoch are correlated and the corresponding covariance matrix has non-zero off-diagonal entries. In practice, however, their effect is taken into account by the nuisance parameters, and we therefore work with a diagonal covariance matrix (see Appendix A). The marginal parameter distributions corresponding to the astrometric data of DE0823−49 are shown in Fig. 1. Most parameters show a nearly Gaussian distribution. Joint marginal parameter distributions are represented in Fig. 2 and used to identify correlations between different sets of parameters. The parameters show no significant correlation with the exception of a weak correlation between the parallax and the barycentric orbit semi-major axis. The median values and the 1-σ confidence intervals of the adjusted parameters are given in Table 4.

The coordinate offsets Δα0⋆,Δδ0\hbox{$\Delta\alpha^{\star}_0, \Delta\delta_0$} are relative to the target’s position at the reference date. An additional noise (nuisance parameter) of 0.16 mas and 0.12 mas in RA and Dec, respectively, is required for the model adjustment. We separately list the rms of the 281 individual frame residuals (σO − C) and the rms of the 14 epoch-averaged residuals (σO − C,Epoch = 0.330 mas). The latter is slightly higher than the mean epoch uncertainty of 0.188 mas. The excess noise originates primarily in the RA measurements (0.410 mas rms compared to 0.221 mas rms of Dec measurements) and is attributable to the presence of a background star located 1–0.7″ west on the target’s projected trajectory. The angular separation of both objects decreases with time to the point that it degrades the photocentre measurement especially in the second and third observation seasons (Fig. 4a,b). 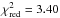This is also reflected in the reduced chi-squared value χred2=3.40\hbox{$\chi^2_\mathrm{red}=3.40$} that significantly exceeds unity. For Dec measurements, χred,δ2=1.62\hbox{$\chi^2_\mathrm{red, \delta}=1.62$} is better and comparable to χred,ref2=1.72±0.48\hbox{$\chi^2_\mathrm{red,ref}=1.72\pm 0.48$} (rms) for bright reference stars. The fit quality of DE0823−49 in Dec is thus equal to that of distant reference stars.

Table 4

Physical and orbital parameters of the DE0823−49 system.

3.4. Parallax correction

thumbnail Fig. 3

Astrometric motion of DE0823−49 and its barycentric orbit. Panel a) shows proper and parallactic motion relative to the field of reference stars. The astrometric observations and the model are shown as black circles and grey curve, respectively. The black arrow indicates the direction and amplitude of the proper motion over one year. Panel b) is a close-up of the barycentric orbit caused by the gravitational pull of the orbiting brown dwarf. Observations with s.e.m. error bars and the best-fit model are shown as black circles and grey curve, respectively. The barycentre and periastron position are marked with a cross and an open square, respectively, and the dotted line represents the line of nodes.

Because the target’s motion is measured relative to reference stars that are not located at infinite distance, a correction term has to be applied to convert relative parallax ϖ to absolute parallax ϖabs. There are three strategies to performing the parallax correction: (1) tie the reference frame to extragalactic and therefore quasi-absolute references; (2) determine photometric distances to the reference stars (Vrba et al. 2004; Faherty et al. 2012); (3) use a Galactic model to estimate the distances of field stars (Andrei et al. 2011; Dupuy & Liu 2012). Ideally, the parallax correction uncertainty should be smaller than the parallax precision, which in our case is <0.1 mas. Inspection of the target field revealed that extragalactic sources that could be securely identified were extended objects and their photocentres can therefore not be measured with sufficient accuracy. The first method is thus not applicable. The second method relies on obtaining V − K colours of reference stars, for instance those included in the NOMAD catalogue (Zacharias et al. 2004). For DE0823−49, the number of usable stars is restricted to ten, which led to poor results so we discarded the second method, too.

For the third method, we used a model of the Galaxy (Robin et al. 2003) to obtain a synthetic sample of stars in a 10′ × 10′ field centred on the target and selected the magnitude range covered by the reference stars used for determining the parallax. The measured magnitude distribution is closely matched by the model (Fig. B.1a). In our model adjustments, negative parallaxes are allowed and thus the measured parallax distribution appears shifted towards lower values relative to the model parallax distribution. The average value of this shift corresponds to the parallax correction. We discarded the tenth percentile of largest and smallest parallaxes, i.e. only data located between the two dashed lines in Fig. B.1b were considered, and we obtained a parallax correction of Δϖ =  + 0.062 ± 0.038 mas (s.e.m. using 283 stars) to be added to the relative parallax of DE0823−49. Its value is low and comparable to its uncertainty, which is expected because the reference stars are faint (17th–22nd mag in I-band) and therefore located at large distances. The correction corresponds to an average distance of the reference stars of ~16 kpc, which is compatible with the extent of the Galaxy. (DE0823−49 is located towards the Vela constellation.) We have tested the Galactic model method with a brighter target of our astrometric survey, for which 21 reference stars could be used to apply the photometric distance method. The results of both methods agreed, thus validating our approach.

thumbnail Fig. 4

Orbital motion of DE0823−49 as a function of time. The orbital signature in right ascension (panel a)) and declination (panelc)) is shown, where black symbols show epoch average values and grey symbols indicate the individual frame measurements. Panels b) and d) show the observed minus calculated residuals of epoch averages.

3.5. Primary mass estimation

We cannot measure the mass of DE0823−49 directly so have to rely on an indirect estimate obtained from spectro-photometric measurements, the absolute parallax, and an age estimate in combination with evolutionary models of substellar and stellar objects. We compared the optical spectrum of DE0823−49 (Phan-Bao et al. 2008) to spectral standards from Martín et al. (1999b) and found that the gravity-sensitive Na I equivalent width of 3.4 ± 0.5  Å and the TiO band around 8400 Å indicate that the object is intermediate between the “old” L1 spectral standard DENIS-P J1441-0945 and the “young” L1 standard G 196-3 B (Fig. C.1, see also Fig. 3 of Martín et al. 2010). DE0823−49 shows a hint of Li absorption but the low signal-to-noise prevents us from claiming a detection on the basis of this spectrum alone. We therefore adopted an age range of 0.6–3 billion years (Gyr) for DE0823−49. The tangential velocity of 15 km s-1 for DE0823−49 is comparable to the values of M7-L2 dwarfs in the field (Schmidt et al. 2007), having an estimated age range of 2–4 Gyr. DE0823−49 is a photometrically calm object with no noticeable activity. We monitored its brightness relative to field stars over the observation timespan and found that photometric fluctuations do not exceed the typical measurement uncertainty of ±0.004 mag.

Optical and infrared photometric measurements of DE0823−49 were retrieved from the catalogues 2MASS (Skrutskie et al. 2006; J, H, K bands) and DENIS (Phan-Bao et al. 2008; I,H,K bands). Absolute magnitudes were obtained on the basis of the measured absolute parallax. The BT-Settl models (Chabrier et al. 2000; Allard et al. 2012) were linearly interpolated in mass for a given age to determine the best-fit mass using a least-square minimisation taking the magnitude and parallax uncertainties into account. The formal errors of this procedure were very small (<0.5%), and we adopted a constant 10% mass uncertainty instead to account for potential model inaccuracies (see e.g. Dupuy et al. 2009). An alternative mass-estimation method using the bolometric luminosity is discussed in Appendix C and yields similar results. The mass estimate of DE0823−49 at 1 Gyr is 0.075 ± 0.007   M⊙, and in the age range of 0.6 − 10 Gyr the corresponding mass lies in the range of 0.067 − 0.079  M⊙ with essentially no mass variation for ages older than 3 Gyr. Follow-up spectroscopy is required to confirm the youth indicators of DE0823−49 and to obtain a refined age estimate.

4. Orbit and companion mass of DE0823−49

Proper and parallactic motion of the target are hundreds and tens of mas, respectively (Fig. 3a), and are superimposed on the orbital motion with an amplitude of several mas (Fig. 3b). The parallax determines the target’s distance, thus allowing us to convert angular measurements to linear quantities, and the orbital parameters yield information on the physical properties of the binary system. For the estimated age range of 0.6 − 3 Gyr, DE0823−49 has a mass in the range of 0.067 − 0.079   M⊙, thus encompassing the theoretical hydrogen burning mass limit of ~0.075 M⊙ assuming solar metallicity. DE0823−49 is therefore either a very low-mass star or a brown dwarf, an ambiguity that leaves our main finding unaffected.

The parallactic motion of DE0823−49 reveals the system’s distance of 20.77 ± 0.08 parsec from Earth, in agreement with an earlier photometric estimate by Phan-Bao et al. (2008) but determined with a relative precision of 0.4%. Our measurements show that DE0823−49 moves on a photocentric orbit with a semimajor axis of 4.61-0.13+0.15\hbox{$4.61_{-0.13}^{+0.15}$} mas and a period of 246.4 ± 1.4 days (Table 4). The orbit is eccentric (0.35-0.06+0.07\hbox{$0.35_{-0.06}^{+0.07}$}) and is observed with an inclination of 56.6-2.0+1.9\hbox{$56.6_{-2.0}^{ +1.9}$}°(Fig. 3b). Using the photocentric semimajor axis as an approximation of the barycentric orbit size, we estimated the secondary mass and the I-band magnitude difference between primary and secondary of ΔmI = 5.1 − 8.4 in the 0.6 − 3 Gyr age range. We therefore assumed that the companion’s light contribution is negligible and that the barycentric orbit coincides with the photocentric orbit. The system’s mass ratio lies in the range of 0.355–0.380 and is determined by the semimajor axis and the primary mass estimate, where the age uncertainty dominates the mass ratio uncertainty. The corresponding companion mass is 26.7–29.4 MJ and falls into the mass range of giant planets and low-mass brown dwarf companions around Sun-like stars (Sahlmann et al. 2011). Figure 2 shows an overview of known ultracool binaries and the particular location occupied by DE0823−49 with a relative separation of 0.36 ± 0.01 AU.

5. Discussion and conclusions

The discovery of the DE0823−49 system is unusual in the context of the known ultracool binary population because it has a particularly low mass ratio and is located in a sparsely populated region of the separation – mass-ratio plane shown in Fig. 5. Ultracool binaries were previously found primarily in nearly equal mass configurations (q ≳ 0.7) and with a separation distribution peaked at ~1–10 AU (Fig. 5), in contrast to solar-type and M dwarf binaries that show a flat mass-ratio distribution for q ≳ 0.2 and a separation distribution peaked at ~25–35 AU (Raghavan et al. 2010; Janson et al. 2012).

The sharp decline in the number of ultracool binaries with separations ≲1 AU coincides with the typical resolution limit of current telescopes that impedes detection of these binaries with the most successful method of direct imaging, which is most sensitive to systems with nearly equal masses because of the favourable brightness contrast. Radial velocity observations are sensitive to small separation binaries but merely yield a lower limit to the mass ratio, when assuming the primary mass can be estimated, in particular for low mass-ratio systems that constitute single-lined spectroscopic binaries (Joergens & Müller 2007; Blake et al. 2008). Observations aimed at detecting unresolved binaries through differences in the components’ spectra (Burgasser et al. 2010) may identify binaries like DE0823−49. Gravitational microlensing events were used to discover two binaries seen close to DE0823−49 in Fig. 5 (Choi et al. 2013). Those systems are located at large distances from Earth (400 and 2000 parsec) and have low total masses (0.025 and 0.034 M⊙) compared to DE0823−49 with M1 + M2 ≃ 0.10  M⊙. Microlensing events typically yield unrepeatable snapshots and therefore the eccentricities and orbital periods of those binaries will remain unknown. However, the recent discovery of these three systems indicate that small-separation binaries with low mass ratios may not be as rare as previously thought.

thumbnail Fig. 5

Separations and mass ratios of very low-mass binaries. Panel a) shows the mass ratio as a function of separation for 108 very low-mass binaries (M1 + M2 < 0.2  M⊙, Sect. D). The location of the DE0823−49 binary is indicated with a black diamond and uncertainties are smaller than the symbol size. Binaries with separations <100 AU are shown, where the separation is either given by the the orbit’s semimajor axis or, in most cases, the actual observed projected separation of directly imaged binaries. Error bars are not shown for clarity of display. Symbols indicate the respective detection method: diamonds, astrometry; squares, radial velocity; triangles, gravitational microlensing; star, eclipse photometry; circles, direct imaging or spectroscopy. For radial velocity systems with unknown mass ratio, the range of possible values is indicated. Panel b) shows the distribution in separation. The two smallest separation binaries are a short period spectroscopic binary (Basri & Martín 1999) and an eclipsing binary (Stassun et al. 2006). Panel c) shows the distribution in mass ratio. The two systems with mass ratios smaller than DE0823−49 are a planetary mass companion detected through microlensing (Kubas et al. 2012) and a directly imaged companion to a young brown dwarf (Chauvin et al. 2004).

With our observational procedures and reduction methods we have demonstrated the capability of ground-based optical astrometry to achieve 200 μas astrometry on faint optical sources over a large field of view (a few arcminutes). For ultracool dwarfs, the astrometric performance of FORS2 is therefore comparable to what is expected from the Gaia space astrometry mission (e.g. Mignard 2011). This opens a new window to the parameter space of low mass ratios and small-to-intermediate separations of ultracool binaries. Astrometric surveys will contribute to the comprehensive characterisation of ultracool binaries by measuring their frequency at separations of ~0.1–10 AU, estimated in the range of 1–30% (Guenther & Wuchterl 2003; Basri & Reiners 2006; Joergens 2008; Blake et al. 2010), and by refining their eccentricity distribution. The observational evidence will help resolve the question of whether ultracool binaries form like stellar binaries (Thies & Kroupa 2008; Parker & Goodwin 2011). In addition to its sensitivity to companions, astrometry yields a direct measurement of the target’s distance from the Earth that is essential for understanding the physics of ultracool dwarfs. The parallax accuracy achieved here allows distance determinations at an unprecedented precision for ground-based optical astrometry, thus removing distances as a dominant source of uncertainty in the modelling of ultracool dwarfs. Finally, the astrometric performance demonstrated here is sufficient for discovering the planetary companions of nearby ultracool dwarfs with masses as low as one Neptune mass at separations ≳0.4 AU.

Online material

thumbnail Fig. 1

Marginal parameter distributions for DE0823−49 obtained from 7.5 × 106 MCMC iterations. In each panel, the dashed line indicates the median value of the respective parameter identified by the x-coordinate lable. Y-coordinate units are arbitrary and indicate relative occurrence.

thumbnail Fig. 2

Joint marginal distribution of several parameters for DE0823−49 obtained from 7.5 × 106 MCMC iterations. In each panel, contour lines represent the 1, 2, and 3σ confidence intervals of the joint distribution. Sub-panels show the marginal distributions. The top-left panel represents the joint distribution of the parameters esin(ω)\hbox{$\sqrt{e} \sin{(\omega)}$} andecos(ω)\hbox{$ \sqrt{e} \cos{(\omega)}$} with grey circles representing eccentricity values of 0.125, 0.25, 0.5, 0.75, and 1.0.

Appendix A: Data covariance

Due to the reduction procedure, the individual frame measurements within one epoch are not independent but are instead subject to correlated noise of equal magnitude in RA and Dec. Therefore, the corresponding covariance matrix contains non-zero off-diagonal elements and has a block-diagonal form with the nominal uncertainties on the diagonal and the covariance amplitude on the off-diagonal elements for each epoch. The covariance between data taken at different epochs is always zero. Because consideration of the covariances is expensive in computation time, we neglect the off-diagonal terms of the covariance matrix to run the principal part of the MCMC. We quantified the effect of considering the full covariance matrix by running an MCMC with fewer (105) iterations. The results in both cases are statistically indistinguishable because the parameter standard deviations are equivalent and the differences in the median parameter values are less than σ/10. The only significant difference is a smaller resulting nuisance parameter in RA (sα) when considering the full covariance matrix (0.08 mas compared to 0.16 mas with a diagonal covariance matrix), indicating that this parameter sensibly accounts for additional signals in the form of correlated noise. We conclude that the off-diagonal terms of the covariance matrix can be neglected when employing the analysis methods presented here.

Appendix B: Comparison with Galaxy model

Figure B.1 illustrates how we use a model of the Galaxy to determine the parallax correction Δϖ.

thumbnail Fig. B.1

Using a galaxy model to determine the parallax correction. Cumulative distribution of magnitudes (panel a)) and parallaxes (panel b)) for the 283 reference stars of DE0823−49. The model and measured data are shown in grey and black, respectively.

Appendix C: Primary mass estimation using bolometric luminosity

As a consistency check, we used the method of Sect. 3.5 restricted to the three 2MASS bands and compared the results to a method that relies on an estimation of the bolometric luminosity. We converted 2MASS magnitudes to the MKO system using updated colour transformations (Carpenter 2001)1 and bolometric corrections (Liu et al. 2010) to obtain the luminosity, and we assumed an uncertainty of one spectral type subclass. The corresponding mass at a given age was found by interpolating the BT-Settl models. Differences between J, H, K are negligible, and we used their average. The resulting masses lie a few percent higher than the estimation with the previous method, but both methods yield compatible results within the adopted 10% uncertainty. At 1 Gyr the alternative mass estimate is 0.079 ± 0.001, where the error reflects only the uncertainty in spectral type. In the age range of 0.6–10 Gyr, the alternative mass range is 0.072 − 0.081  M⊙.

thumbnail Fig. C.1

Comparison of the optical spectra of DE0823−49 from Phan-Bao et al. (2008) (solid), the “old” L1 dwarf DENIS-P J1441-0945 (dashed), and the “young” L1 dwarf G 196-3 B (dotted), both from Martín et al. (1999b). The relevant spectral features are labelled.

Appendix D: Compilation of very low-mass binary systems

The sample of binaries shown in Fig. 5 was constructed on the basis of the compilation at vlmbinaries.org. Because its last update was in July 2009, we searched the literature for new systems and revised parameters. We added 24 systems from Choi et al. (2013), Burgasser et al. (2011), Allers et al. (2010), Gelino & Burgasser (2010), Liu et al. (2010, 2011), Kraus & Hillenbrand (2012), Gelino et al. (2011), Chauvin et al. (2012), Geyer et al. (1988), Phan-Bao et al. (2006), Allers et al. (2009), and Burgasser et al. (2009), and we updated system parameters, when applicable, using the compilations of Liu et al. (2010), Dupuy & Liu (2011), and Kraus & Hillenbrand (2012).

Acknowledgments

J.S., D.S., M.M., D.Q., and S.U. thank the Swiss National Science Foundation for supporting this research. E.M. was supported by the Spanish Ministerio de Economia y Competitividad through grant AyA2011-30147-C03-03 and thanks the Geosciences Department at the University of Florida for a visiting appointment. J.S. thanks T. Dupuy for sharing his VLM binary compilation and kindly acknowledges support as a visitor at the Centro de Astrobiología in Villanueva de la Cañada (Madrid). We thank N. Phan-Bao for making the spectrum of DE0823−49 available to us. We thank the ESO staff for efficiently scheduling and executing our observations. This publication makes use of the Very-Low-Mass Binaries Archive housed at http://www.vlmbinaries.org and of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.

References

  1. Allard, F., Homeier, D., & Freytag, B. 2012, Roy. Soc. Lond. Philosoph. Trans. Ser. A, 370, 2765 [Google Scholar]
  2. Allers, K. N., Liu, M. C., Shkolnik, E., et al. 2009, ApJ, 697, 824 [NASA ADS] [CrossRef] [Google Scholar]
  3. Allers, K. N., Liu, M. C., Dupuy, T. J., & Cushing, M. C. 2010, ApJ, 715, 561 [NASA ADS] [CrossRef] [Google Scholar]
  4. Anderson, D. R., Collier Cameron, A., Hellier, C., et al. 2011, ApJ, 726, L19 [NASA ADS] [CrossRef] [Google Scholar]
  5. Andrei, A. H., Smart, R. L., Penna, J. L., et al. 2011, AJ, 141, 54 [NASA ADS] [CrossRef] [Google Scholar]
  6. Andrieu, C., & Thoms, J. 2008, Statistics and Computing, 18, 343 [Google Scholar]
  7. Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
  8. Avila, G., Rupprecht, G., & Beckers, J. M. 1997, in SPIE, 2871 [Google Scholar]
  9. Basri, G. 2000, ARA&A, 38, 485 [NASA ADS] [CrossRef] [Google Scholar]
  10. Basri, G., & Martín, E. L. 1999, AJ, 118, 2460 [Google Scholar]
  11. Basri, G., & Reiners, A. 2006, AJ, 132, 663 [Google Scholar]
  12. Black, D. C., & Scargle, J. D. 1982, ApJ, 263, 854 [NASA ADS] [CrossRef] [Google Scholar]
  13. Blake, C. H., Charbonneau, D., White, R. J., et al. 2008, ApJ, 678, L125 [NASA ADS] [CrossRef] [Google Scholar]
  14. Blake, C. H., Charbonneau, D., & White, R. J. 2010, ApJ, 723, 684 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bouy, H., Brandner, W., Martín, E. L., et al. 2003, AJ, 126, 1526 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bouy, H., Duchêne, G., Köhler, R., et al. 2004, A&A, 423, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Burgasser, A. J., Reid, I. N., Siegler, N., et al. 2007, Protostars and Planets V, 427 [Google Scholar]
  18. Burgasser, A. J., Dhital, S., & West, A. A. 2009, AJ, 138, 1563 [NASA ADS] [CrossRef] [Google Scholar]
  19. Burgasser, A. J., Cruz, K. L., Cushing, M., et al. 2010, ApJ, 710, 1142 [NASA ADS] [CrossRef] [Google Scholar]
  20. Burgasser, A. J., Bardalez-Gagliuffi, D. C., & Gizis, J. E. 2011, AJ, 141, 70 [NASA ADS] [CrossRef] [Google Scholar]
  21. Carpenter, J. M. 2001, AJ, 121, 2851 [NASA ADS] [CrossRef] [Google Scholar]
  22. Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
  23. Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2004, A&A, 425, L29 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  24. Chauvin, G., Faherty, J., Boccaletti, A., et al. 2012, A&A, 548, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Choi, J.-Y., Han, C., Udalski, A., et al. 2013, ApJ, 768, 129 [NASA ADS] [CrossRef] [Google Scholar]
  26. Close, L. M., Siegler, N., Freed, M., & Biller, B. 2003, ApJ, 587, 407 [NASA ADS] [CrossRef] [Google Scholar]
  27. Close, L. M., Lenzen, R., Guirado, J. C., et al. 2005, Nature, 433, 286 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  28. Collier Cameron, A., Wilson, D. M., West, R. G., et al. 2007, MNRAS, 380, 1230 [NASA ADS] [CrossRef] [Google Scholar]
  29. Dahn, C. C., Harris, H. C., Levine, S. E., et al. 2008, ApJ, 686, 548 [NASA ADS] [CrossRef] [Google Scholar]
  30. Dupuy, T. J., & Liu, M. C. 2011, ApJ, 733, 122 [NASA ADS] [CrossRef] [Google Scholar]
  31. Dupuy, T. J., & Liu, M. C. 2012, ApJS, 201, 19 [NASA ADS] [CrossRef] [Google Scholar]
  32. Dupuy, T. J., Liu, M. C., & Ireland, M. J. 2009, ApJ, 692, 729 [NASA ADS] [CrossRef] [Google Scholar]
  33. Dupuy, T. J., Liu, M. C., Bowler, B. P., et al. 2010, ApJ, 721, 1725 [NASA ADS] [CrossRef] [Google Scholar]
  34. Faherty, J. K., Burgasser, A. J., Walter, F. M., et al. 2012, ApJ, 752, 56 [NASA ADS] [CrossRef] [Google Scholar]
  35. Gelino, C. R., & Burgasser, A. J. 2010, AJ, 140, 110 [NASA ADS] [CrossRef] [Google Scholar]
  36. Gelino, C. R., Kirkpatrick, J. D., Cushing, M. C., et al. 2011, AJ, 142, 57 [NASA ADS] [CrossRef] [Google Scholar]
  37. Geyer, D. W., Harrington, R. S., & Worley, C. E. 1988, AJ, 95, 1841 [NASA ADS] [CrossRef] [Google Scholar]
  38. Goodwin, S. P. 2013, MNRAS, 430, L6 [NASA ADS] [Google Scholar]
  39. Gregory, P. C. 2005a, ApJ, 631, 1198 [NASA ADS] [CrossRef] [Google Scholar]
  40. Gregory, P. C. 2005b, Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with Mathematica Support (Cambridge University Press) [Google Scholar]
  41. Guenther, E. W., & Wuchterl, G. 2003, A&A, 401, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Janson, M., Hormuth, F., Bergfors, C., et al. 2012, ApJ, 754, 44 [NASA ADS] [CrossRef] [Google Scholar]
  43. Joergens, V. 2008, A&A, 492, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Joergens, V., & Müller, A. 2007, ApJ, 666, L113 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kirkpatrick, J. D. 2005, ARA&A, 43, 195 [NASA ADS] [CrossRef] [Google Scholar]
  46. Konopacky, Q. M., Ghez, A. M., Barman, T. S., et al. 2010, ApJ, 711, 1087 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kraus, A. L., & Hillenbrand, L. A. 2012, ApJ, 757, 141 [NASA ADS] [CrossRef] [Google Scholar]
  48. Kubas, D., Beaulieu, J. P., Bennett, D. P., et al. 2012, A&A, 540, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Lane, B. F., Zapatero Osorio, M. R., Britton, M. C., Martín, E. L., & Kulkarni, S. R. 2001, ApJ, 560, 390 [NASA ADS] [CrossRef] [Google Scholar]
  50. Lazorenko, P. F. 2006, A&A, 449, 1271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Lazorenko, P. F., Mayor, M., Dominik, M., et al. 2007, A&A, 471, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Lazorenko, P. F., Mayor, M., Dominik, M., et al. 2009, A&A, 505, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Lazorenko, P. F., Sahlmann, J., Ségransan, D., et al. 2011, A&A, 527, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Liu, M. C., Dupuy, T. J., & Leggett, S. K. 2010, ApJ, 722, 311 [NASA ADS] [CrossRef] [Google Scholar]
  55. Liu, M. C., Delorme, P., Dupuy, T. J., et al. 2011, ApJ, 740, 108 [NASA ADS] [CrossRef] [Google Scholar]
  56. Luhman, K. L. 2012, ARA&A, 50, 65 [NASA ADS] [CrossRef] [Google Scholar]
  57. Martin, E. L., Brandner, W., & Basri, G. 1999a, Science, 283, 1718 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  58. Martín, E. L., Delfosse, X., Basri, G., et al. 1999b, AJ, 118, 2466 [NASA ADS] [CrossRef] [Google Scholar]
  59. Martín, E. L., Phan-Bao, N., Bessell, M., et al. 2010, A&A, 517, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, in press [arXiv:1109.2497] [Google Scholar]
  61. Mignard, F. 2011, Adv. Space Res., 47, 356 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  62. Muirhead, P. S., Johnson, J. A., Apps, K., et al. 2012, ApJ, 747, 144 [NASA ADS] [CrossRef] [Google Scholar]
  63. Parker, R. J., & Goodwin, S. P. 2011, MNRAS, 411, 891 [NASA ADS] [CrossRef] [Google Scholar]
  64. Phan-Bao, N., Forveille, T., Martín, E. L., & Delfosse, X. 2006, ApJ, 645, L153 [NASA ADS] [CrossRef] [Google Scholar]
  65. Phan-Bao, N., Bessell, M. S., Martín, E. L., et al. 2008, MNRAS, 383, 831 [NASA ADS] [CrossRef] [Google Scholar]
  66. Pollacco, D., Skillen, I., Collier Cameron, A., et al. 2008, MNRAS, 385, 1576 [NASA ADS] [CrossRef] [Google Scholar]
  67. Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Sahlmann, J., Ségransan, D., Queloz, D., et al. 2011, A&A, 525, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Schmidt, S. J., Cruz, K. L., Bongiorno, B. J., Liebert, J., & Reid, I. N. 2007, AJ, 133, 2258 [NASA ADS] [CrossRef] [Google Scholar]
  71. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  72. Stassun, K. G., Mathieu, R. D., & Valenti, J. A. 2006, Nature, 440, 311 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  73. Stumpf, M. B., Brandner, W., Joergens, V., et al. 2010, ApJ, 724, 1 [NASA ADS] [CrossRef] [Google Scholar]
  74. Thies, I., & Kroupa, P. 2008, MNRAS, 390, 1200 [NASA ADS] [CrossRef] [Google Scholar]
  75. Vrba, F. J., Henden, A. A., Luginbuhl, C. B., et al. 2004, AJ, 127, 2948 [NASA ADS] [CrossRef] [Google Scholar]
  76. Whitworth, A., Bate, M. R., Nordlund, Å., Reipurth, B., & Zinnecker, H. 2007, Protostars and Planets V, 459 [Google Scholar]
  77. Zacharias, N., Monet, D. G., Levine, S. E., et al. 2004, BAAS, 36, 1418 [Google Scholar]
  78. Zapatero Osorio, M. R., Lane, B. F., Pavlenko, Y., et al. 2004, ApJ, 615, 958 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 2

Parameters probed by the genetic algorithm.

In the text
Table 3

Parameters probed by the MCMC.

In the text
Table 4

Physical and orbital parameters of the DE0823−49 system.

In the text

All Figures

thumbnail Fig. 3

Astrometric motion of DE0823−49 and its barycentric orbit. Panel a) shows proper and parallactic motion relative to the field of reference stars. The astrometric observations and the model are shown as black circles and grey curve, respectively. The black arrow indicates the direction and amplitude of the proper motion over one year. Panel b) is a close-up of the barycentric orbit caused by the gravitational pull of the orbiting brown dwarf. Observations with s.e.m. error bars and the best-fit model are shown as black circles and grey curve, respectively. The barycentre and periastron position are marked with a cross and an open square, respectively, and the dotted line represents the line of nodes.
In the text
thumbnail Fig. 4

Orbital motion of DE0823−49 as a function of time. The orbital signature in right ascension (panel a)) and declination (panelc)) is shown, where black symbols show epoch average values and grey symbols indicate the individual frame measurements. Panels b) and d) show the observed minus calculated residuals of epoch averages.
In the text
thumbnail Fig. 5

Separations and mass ratios of very low-mass binaries. Panel a) shows the mass ratio as a function of separation for 108 very low-mass binaries (M1 + M2 < 0.2  M⊙, Sect. D). The location of the DE0823−49 binary is indicated with a black diamond and uncertainties are smaller than the symbol size. Binaries with separations <100 AU are shown, where the separation is either given by the the orbit’s semimajor axis or, in most cases, the actual observed projected separation of directly imaged binaries. Error bars are not shown for clarity of display. Symbols indicate the respective detection method: diamonds, astrometry; squares, radial velocity; triangles, gravitational microlensing; star, eclipse photometry; circles, direct imaging or spectroscopy. For radial velocity systems with unknown mass ratio, the range of possible values is indicated. Panel b) shows the distribution in separation. The two smallest separation binaries are a short period spectroscopic binary (Basri & Martín 1999) and an eclipsing binary (Stassun et al. 2006). Panel c) shows the distribution in mass ratio. The two systems with mass ratios smaller than DE0823−49 are a planetary mass companion detected through microlensing (Kubas et al. 2012) and a directly imaged companion to a young brown dwarf (Chauvin et al. 2004).
In the text
thumbnail Fig. 1

Marginal parameter distributions for DE0823−49 obtained from 7.5 × 106 MCMC iterations. In each panel, the dashed line indicates the median value of the respective parameter identified by the x-coordinate lable. Y-coordinate units are arbitrary and indicate relative occurrence.
In the text
thumbnail Fig. 2

Joint marginal distribution of several parameters for DE0823−49 obtained from 7.5 × 106 MCMC iterations. In each panel, contour lines represent the 1, 2, and 3σ confidence intervals of the joint distribution. Sub-panels show the marginal distributions. The top-left panel represents the joint distribution of the parameters esin(ω)\hbox{$\sqrt{e} \sin{(\omega)}$} andecos(ω)\hbox{$ \sqrt{e} \cos{(\omega)}$} with grey circles representing eccentricity values of 0.125, 0.25, 0.5, 0.75, and 1.0.
In the text
thumbnail Fig. B.1

Using a galaxy model to determine the parallax correction. Cumulative distribution of magnitudes (panel a)) and parallaxes (panel b)) for the 283 reference stars of DE0823−49. The model and measured data are shown in grey and black, respectively.
In the text
thumbnail Fig. C.1

Comparison of the optical spectra of DE0823−49 from Phan-Bao et al. (2008) (solid), the “old” L1 dwarf DENIS-P J1441-0945 (dashed), and the “young” L1 dwarf G 196-3 B (dotted), both from Martín et al. (1999b). The relevant spectral features are labelled.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.