| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A146 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321739 | |
| Published online | 09 August 2013 | |
Energetic-particle-flux decreases related to magnetic cloud passages as observed by the Helios 1 and 2 spacecraft
1
Space Research Group, Universidad de Alcalá,
28801
Madrid,
Spain
e-mail:
juanjo.blanco@uah.es
2
Institut für Experimentelle und Angewandte Physik, Christian
Albrechts Universität zu Kiel, 24118
Kiel,
Germany
Received: 19 April 2013
Accepted: 1 July 2013
It has been observed that a magnetic cloud (MC) can affect the propagation conditions of solar energetic particles and low-energy cosmic rays. This effect is commonly observed as a decrease in the energetic-particle fluxes, which are partially excluded from the interior of the cloud. The twin spacecraft Helios 1 and Helios 2 explored the inner heliosphere between 0.29 AU and 1 AU from the mid 1970s to early 1980s. The E6 Experiment onboard Helios is the energetic-particle detector able to measure electrons, protons and alphas in the range of 300 keV/n to >50 MeV/n. It has been shown previously that, in absence of strong solar-particle events, the single detector rates of the E6 anti-coincidence and saphire Cherenkov detectors are sensitive to cosmic rays with rigidities above GV. Because their statistical precision is in the order of hundreds of counts per second, both detectors are very well suited for studying the short-term decreases observed in their count rates during magnetic cloud passages. A total of 35 magnetic clouds have been identified at the Helios locations. Nineteen of them were free of solar energetic-particle contamination. This subset led us to investigate the effect of magnetic clouds on the galactic cosmic ray (GCR) flux. The depth of the decreases are studied in terms of the solar wind and magnetic field properties of the magnetic cloud. We found dependences with the MC magnetic field strength, magnetic rigidity and with the MC time of flight, with the latter supporting the idea of magnetically closed MCs, i.e. with the two legs rooted in the Sun. We also studied MC properties and found evidence of MC expansion during its journey through the inner heliosphere.
Key words: Sun: coronal mass ejections (CMEs) / solar-terrestrial relations / solar wind / Sun: particle emission / astroparticle physics
© ESO, 2013
1. Introduction
The twin spacecraft Helios 1 and Helios 2 explored the inner heliosphere from about 0.29 AU to 1 AU in the 1970s. Onboard the spacecraft in situ instruments measured, among other properties, the solar wind, the heliospheric magnetic field, and energetic particles. Given the close approach to the Sun, revisiting these data is ideally suited for stating the expected environmental context for the planned future missions toward the inner heliosphere, for example Solar Orbiter or Solar Probe Plus. Galactic cosmic rays (GCRs) and solar energetic particles (SEPs) were measured by the experiment E6 (Kunow et al. 1977). The short-term effect of the solar wind on GCRs as observed by instruments onboard the spacecraft has been intensely studied. Helios 1 and 2 were especially important in the development of this task because of their orbits, their long operational life and their sensors, which were suitable to monitor GCRs and SEPs. Different authors have used the counts of the anti-coincidence sensor of E6 to study the low-energy GCR component variations caused by interaction with solar wind structures and solar activity (Cane et al. 1994, 1997; Richardson et al. 1996). According to these authors, this anti-coincidence detector (A detector) gave a large statistics of particles above 60 MeV/n, enough to follow tiny variations in response to embedded structures in solar wind. Nevertheless, strong contamination of SEP may be expected at these energies during solar violent episodes such as flares and coronal mass ejections (CMEs), and interplanetary events such as shocks and interplanetary CMEs (ICMEs).
Magnetic clouds (MCs) are structures observed in the solar wind that are characterized by a smooth magnetic field rotation, a relative high magnetic field intensity, and low temperature, (Burlaga et al. 1981). These MCs used to be detected in one third of the ICMEs, and they have been observed at solar distances of between 0.3 AU (Bothmer & Schwenn 1998) and 4 AU (Burlaga & Behannon 1982).
It has been commonly observed that ICMEs are able to drive shock waves in front of them. ICMEs have an observable effect on GCRs. During their passage, decreases in energetic particle fluxes are measured in a very wide energy range. These decreases were first observed by ground-based detectors and were termed Forbush decreases (FDs; Forbush 1938). They are characterized by a sharp decrease followed by a slow recovery phase. The whole event can last some days. Both the ICME and the driven shock have an impact on the ground-based count rate; they produce a two-step FD (Barnden 1973). However, the two-step model has recently been revised by Jordan et al. (2011), who concluded that it should be discarded because small magnetic field structures can play an important role in shaping the observed FD shape. These ground-level observations show that ICMEs can affect the GCR propagation with energies of up to some GeV. The shape of the FD is determined by the shock, the ICME, the MC, and small magnetic structures. Also, as pointed out by Blanco et al. (2013), it is determined by the region of the ICME, which sweeps the Earth, and the ICME’s deceleration from Sun to Earth. These decreases are also observed by instruments onboard the spacecraft. They have been deeply studied looking for the key signature responsible for these decreases. The MC size, the magnetic field intensity, speed, or shock strength and shock speed have been some of the main candidates to be correlated with the magnitude of these decreases (Cane 1993; Cane et al. 1994, 1997; Richardson et al. 1996). A complete statistical study of the FD-shock-ICME relationship is given in Richardson & Cane (2011), where the authors analysed ICMEs and GCR decreases for a period of fourteen years (1995–2009) using measurements from spacecraft at 1 AU and neutron monitors. They concluded that MCs are magnetically closed structures and that the depth of the GCR decrease depends on the ICME time of flight.
ICMEs with or without MCs and driven shocks are not the only solar wind structures able to produce decreases in the energetic-particle fluxes. Stream interaction regions also have an important effect on energetic-particle fluxes. They induce decreases that are different in shape, duration, and depth from those produced by ICMEs. The decreases induced by stream interaction regions are generally speaking larger/longer, more shallow and sometimes recur following the solar rotation (Richardson et al. 1996; Heber et al. 1998).
In this work we analyse the count rate decreases of energetic particles detected by E6 onboard Helios 1 and 2. First, we show the energy threshold for the A detector and the Cherenkov detector (C detector) by comparing them with the response of the stack of silicon detectors to energetic particles. Second, we revise the E6 measurements from 1975 to 1980, looking for decreases in the count rate in the A and C detectors, and selecting those with clear MC signatures. Finally, we study the effect of these MCs on the GCR background and the MC properties in the inner heliosphere.
2. Instrumentation
The cosmic ray experiment E6 onboard Helios 1 and Helios 2 was designed to measure energetic nucleons above 1.7 MeV/n and electrons above 0.3 MeV. Their early results showed their scientific relevance thanks to their privileged observation points (Kunow et al. 1977). In addition to E6, the Helios payload was composed of different instruments with the goal of performing in situ measurements of the magnetic field and solar wind by means of the flux-gate magnetometer (E2; Rosenbauer et al. 1977) and the plasma experiment (E1; Neubauer et al. 1977), respectively. Fifteen-minutes averaged data from E6 are used in this work. Magnetic field 15-min averaged measurements in solar ecliptic coordinates (SSE) and 1-h averaged solar wind data were also used.
The cosmic ray experiment (E6) was composed of a stack of five silicon detectors (D1 to D5), one sapphire Cerenkov (C) detector at the stack bottom and an anti-coincidence (A) scintillator that surrounds the whole array of detectors (Kunow et al. 1977). Detectors A and C could provide simple counts of energetic particles above a threshold of energy, but the A and C detectors had a different energy threshold. In Fig. 1 a comparison of the response of the A (black circles) and C (red triangles) detectors with the channel of protons with energy higher than 50 MeV (green squares) is shown. The figure shows an FD observed by Helios 1 on 12 May 1978. Fifteen-minutes averaged data were normalized by the mean count rate (Cmean) calculated during the stable period previous to the event. The expression (C(t)/Cmean) ∗ 100 was used to make them comparable. The >51 MeV channel is highly fluctuating during this event, but a clear decrease in its count rate is observed. These fluctuations can be attributed to the low statistics of this channel (about 0.75 c/s). The decrease is also observed in the A detector count rate. A double-peaked enhancement is measured before the beginning of the FD. Because of the high statistics of the A detector (300 c/s) this enhancement has to be considered a real effect. The C detector count rate shows the FD, but only one small enhancement is detected. The C detector statistics is high enough (90 c/s) to assume that this behaviour is real. It is clear that A detector has a response to particles with energies below 50 MeV/n from Fig. 1. The C detector shows a similar response to those observed for the >50 MeV channel. This observation experimentally supports that the C and A detectors had different energy thresholds. This is also confirmed in Figs. 3 and 5. Moreover, both detectors have a high enough statistics to provide reliable measurements by counting energetic particles, especially compared with silicon detectors designed to provide energetic particle measurements. The mean value of the A and C count rates are more than three orders of magnitude higher than those of the compared energetic channel. In previous works (Cane et al. 1994, 1997; Richardson et al. 1996), counts from the A detector have been used to study GCR because of its high count rate (about 300 c/s), but the C detector has a count rate high enough to follow the GCR variations (about 90 c/s) as well, and comparing them provides some additional information about the energy of the incident particles.
 |
Fig. 1 Normalized count rates of A (red triangles) and C (black circles) and protons with energy higher than 50 MeV (green squares). Normalized count rates have been calculated using the expression (C(t)/Cmean) ∗ 100. |
3. Data analysis
The count-rate background in these two detectors is mostly produced by GCRs that filled up the heliosphere. We searched for observable short-term decreases in the count rate of the Helios A and C detectors from 1975 to 1980. These decreases measured by spacecraft are often named FD (Richardson & Cane 2011) in a similar way to the decreases observed by ground-level detectors (Forbush 1938). We assumed in this work that a decrease in C detector of more than 4% with respect to the previous background count-rate level is an FD. Once an FD is confirmed, solar wind conditions and interplanetary magnetic field were analysed looking for the MC signatures proposed by Burlaga et al. (1981), i.e. smooth magnetic field rotation, low temperature and high magnetic field strength, with clear evidence of flux ropes according to the model of MC proposed by Hidalgo & Nieves-Chinchilla (2012). This MC model was used as fit function to the measured magnetic field with the aim to confirm a flux rope structure, to establish the flux rope limits and so the MC limits, and to determine the MC orientation. Fifty-three FDs were recorded, but only in thirty-five of them we found a clear flux rope structure and MC signatures, i.e. the 66% of the FDs observed by E6 could be associated with an MC passage. We point out that only two MCs showed no clear signatures of a shock wave preceding the MC passage. The complete set of events is listed in Table 1.
MC list.
Bothmer & Schwenn (1998) compiled a list of 42 MCs in 1975–1980. Only 24 of them (57%) produced decreases in the C detector below 4%. This percentage is similar to the 60% reported by Cane et al. (1997), but higher than the 34% reported by Jordan et al. (2011). This discrepancy arises because Jordan et al. (2011) analysed a set of ICMEs both with and without an MC inside an ICME, while in this work we focus on MCs. The comparison is an even poorer match for the 25% obtained by Blanco et al. (2013) from a pool of 59 shock-driving ICMEs from January 1997 to September 2006. Still, in this list only 24 MCs were detected and eight of them (33%) produced an observable FD at ground-level neutron monitors. All events in Blanco et al. (2013) were recorded at 1 AU while the events presented in this work were detected at heliocentric distances below 1 AU. This clear difference could be explained if the MC location plays a role for the FD depth, which deeper when the MC is closer to Sun.
Cane et al. (1997) pointed out, SEP can overlap the low-energy population of GCR and mask the effect of an MC on GCR background. To avoid this, the 35 events were split into four categories according to the observed behaviour of the measured count rates in the A and C detectors. The first category is type 1, where the C and A detector count rate show no previous or simultaneous enhancements. In this case we assumed that the FD is free of solar energetic-particle contamination. The second category is type 1*, where the A detector shows enhancements due to solar energetic-particles, but the C detector does not. The third category is type 2, where consecutive decreases in the A and C detectors are observed, and type 3 is the fourth category where a strong solar energetic-particle contamination is observed in both detectors.
3.1. Type 1
We named type 1 the MCs associated to count-rate decreases measured by the A and C detectors simultaneously. This implies that solar energetic-particles are not observed by these two detectors and so contamination due to solar energetic-particles is not expected. The FD observed on 7 January 1975 (Fig. 2) is an example of a type 1 event. The decrease is initiated in coincidence with the arrival of an interplanetary shock at doy 6:22 h:32 min, which was followed by an ICME six hours later. An MC characterized by a smooth magnetic field rotation, a maximum magnetic field of 18 nT with low temperature and a speed decrease from 700 at MC nose to 500 km s-1 at its rear was detected in the ICME. Helios 1 was located at 0.923 AU. The MC boundaries are marked by the vertical lines at doys 7:05 h:51 min and 7:17 h:38 min, where the MC magnetic structure is underlined by the continuous lines that are the result of fitting the MC model to the measured magnetic field. Both A and C detectors show the same behaviour. The number of counts begins to decrease when the driven shock (vertical dotted line in Fig. 2) arrives at the spacecraft location. Afterwards, the decrease becomes sharper at the MC nose arrival (see the first vertical solid line in Fig. 2). The counts show a decrease higher than 10%. The recovery phase starts during the MC passage, and finally, the previous level in counts is recovered after the MC passage (see the second vertical solid line in Fig. 2). This decrease was observed during a gradual event, as can be appreciated in the E6 lower-energy channels, but no clear decreases were noticed in the solar energetic-particle fluxes (fifth panel of Fig. 2). For this event, this effect, i.e. decrease in cosmic rays without similar response in solar energetic particle, may be explained by the argument that this MC alone is not an effective barrier for particles accelerated by the shock at energies above some MeV/n, while the GCRs are affected by the whole structure shock-sheath-MC.
 |
Fig. 2 Type 1 example. Decrease observed by Helios 1 during an IMC passage on January 1975. From top to bottom: density, temperature, solar wind speed, magnetic field components, the 3.77–12.72 MeV proton channel, and the 1.69–3.68 MeV/n alpha channel from the cosmic ray experiment (E6), normalized count rate in A and C detectors and magnetic field strength. Vertical lines mark the shock position (dotted line) and MC boundaries (solid lines) and the overplotted solid lines in fourth panel are the fit lines from the MC model. |
3.2. Type 1*
An event was catalogued as type 1* when the A detector shows enhancements in the count rate and the C detector does not. These events are contaminated with solar energetic particles with energies that are in principle lower than 50 MeV/n. Although the C detector counts show a clear decrease in coincidence with the MC passage, some solar contamination cannot be discarded in this detector. An example of this type 1* is shown in Fig. 3. An MC preceded by a shock wave arrived at the Helios 1 location at 0.45 AU on May 1979. The MC was embedded in a gradual event and a clear decrease in alphas of 1.69–3.68 MeV/n and protons of 3.77–12.72 MeV could be observed with the MC arrival. In coincidence with the decrease in protons and alphas, an abrupt decrease in the C detector is also noticed. These decreases began at the MC sheath, i.e. the turbulent region between the shock and the MC. This event was catalogued as type 1* because of the enhancement in the A count rate observed during the shock passage. This enhancement could also imply some contamination of shock-accelerated particles in the A detector count rate. For this particular event, the MC seems to be a barrier to the particles accelerated by the shock. From the comparison with the type 1 example, three direct differences are observed: their heliospheric location, their magnetic field strength, and their speed. The ICME presented as an example of type 1 was located at almost 1 AU with a magnetic field maximum of roughly 20 nT and a speed of about 750 km s-1, while the ICME presented as an example of type 1* was located at 0.45 AU with a magnetic field higher than 90 nT and a speed in the order of 500 km s-1.
 |
Fig. 3 Type 1* example. Decrease observed by Helios 1 during an MC passage on May 1979. The panel distribution is identical to that shown in Fig. 2. |
3.3. Type 2
An event was defined as type 2 when consecutive decreases in the A and C detectors were noted. These events seem to be only a more complex version of type 1, where two or more different agents produce observable FDs in both detectors. As an example, the event observed on January 29, 1977 at a heliodistance of 0.94 AU is plotted in Fig. 4. The shock produced the initial decrease 12 h before the MC passage. Then, the counts showed a slight recovery and a new decrease just when the MC nose arrived. A third decrease beyond the MC limits is observed without any clear evidence of another structure in the solar wind. Clear enhancements of the solar energetic particles in SEP fluxes are not observed.
3.4. Type 3
This type of event is characterized by an observable enhancement in the count rate of A and C, associated to strong, and very energetic SEP events. In such cases a strong SEP contamination is expected in both detectors. In some cases this contamination is so high that the effect of MC on GCR flux is completely masked. Because of that, only for clear signatures of decreases higher than 4%, the event was included in the list. On 12 May 1978 a type 3 event was detected by Helios 1 at 0.42 AU (Fig. 5). Twenty-four hours before the shock and the MC passage, a strong increment in the A and C count rates was observed during a SEP event. After the peak, a long decrease was measured, lasting until the shock and MC detection. The shock arrival was observed with a solar wind speed step of 300 km s-1 and a very sharp enhancement in magnetic field intensity. Previously to the MC arrival, the A detector showed several peaks. These peaks were not observed in the C detector, supporting the idea of multiple solar particle injections at energies lower than 50 MeV/n. A pronounced decrease in the C detector marks the MC nose. This is not as clear in the A detector counts. Just after the MC passage, another large jump in solar wind speed of about 100 km s-1, probably related to a stream interaction region, was detected. These two speed jumps and the MC seem a sandwich-like structure. A strong interaction between the rear part of the MC and the fast solar wind stream marked by the second speed step may hide the expected solar wind signatures for an MC. This strengthened the assumption that the C detector can be used an additional signature of an MC passage even when a strong solar particle contamination exists.
 |
Fig. 4 Type 2 example. Decrease observed by Helios 1 during an MC passage on January 1977. The panel distribution is identical to that shown in Fig. 2. |
4. Results
Nineteen events were catalogued as type 1 (Table 1). All of them were preceded by a shock except in two cases. The mean percentage decrease in the C detector was about 10%. In most cases, the FD began with the shock arrival and the MC was observed during the recovery phase. The count-rate background was recovered after the MC passage. These events are often accompanied by an increase of low-energy particles measured by the E6. However, decreases in low-energy channels of protons and alphas are not usually appreciated in coincidence with those observed in the C detector. This observation can be interpreted by assuming two different energetic-particle populations, a solar component with energies in the order of few MeV, accelerated locally by the shock and efficiently diffused (and trapped) inside the MC by a mechanism depending on the particle pitch angle and rigidity, as suggested in Rodríguez-Pacheco et al. (2003), and a cosmic ray component that is slowly coming into the ICME by diffusion, as proposed by Richardson & Cane (2011). The mean values of velocity (446 km s-1), MC diameter (0.15 AU) and magnetic field intensity (49 nT) were obtained.
Six decreases were considered to be of type 1* (Table 1). An A detector increase usually coincided with the shock arrival. The deepest point in the FD was observed by both detectors simultaneously and normally during the MC passage. The mean MC speed is 491 km s-1, the mean field 57 nT and the mean MC section is 0.14 AU. The magnetic field is higher and the speed is slightly faster than that measured for type 1.
Three of the compiled events showed two or more consecutive decreases in the count rate of the A and C detectors and were catalogued as type 2. Two of them consisted of a shock, detected more than 12 h before the MC passage. Both the shock and the MC produced separated decreases in the background of particles above 50 MeV/n with similar depths. Moreover, the level of the background was almost recovered between both structures. The deeper part of decreases was reached during the MC passage, as for type 1, and the recovery phase ended after the trailing boundary of the MC had passed the spacecraft location. The third one showed two consecutive decreases, the first one apparently related to a flux rope, but without the solar wind features that identify an MC, and the second one related to an MC.
Seven events were recorded as type 3 (Table 1). The C detector showed a normalized count rate lower than the A detector and faster recovery phases in all events probably because of a higher-energy threshold and so lower contamination due to SEPs. This is an additional evidence of the different response of the A and C detectors to particle energy. A noticeable change in the count rate shape was detected at the shock passage, which was clearer during the MD arrival. Still, the quantification of the total decrease is very difficult because of the strong influence of solar energetic particles. This implies that no reliable conclusions can be drawn by analysing these decreases. Since the FD is still visible, it provides an additional signature for determining the MC boundaries. Type 3 events are characterized by a mean MC speed of 615 km s-1, a magnetic strength of 57 nT, and a section size of 0.16 AU. The most relevant feature of type 3 is the MC mean speed which is 200 km s-1 higher than those computed for the others. These seven events were included in the subset of events with decreases >7% investigated by Cane et al. (1994). According to the authors, these seven decreases were associated with ejecta, but two of them did not show evidence of an MC. These decreases were observed on 9 April 1978 and 12 May 1978. On the other hand, these two events do not appear as MCs in the list of Bothmer & Schwenn (1998). We detected clear evidence of a flux rope after fitting the MC model to the events. For this reason we included them in our list of MCs that produced FD in the A and C detectors. We previously analysed the event observed in May 1978 (Fig. 5) as an example of type 3 in detail.
 |
Fig. 5 Type 3 example. Decrease observed by Helios 1 during an MC passage on May 1978. The panel distribution is identical to that shown in Fig. 2. |
4.1. Forbush decreases and MC properties
After classifying the 35 compiled events into the four groups described above, our goals are to study the dependences between the decreases in the C detector and the MC properties and after that, the MC properties themselves in the inner heliosphere. To achieve the first aim, we excluded the type 3 events from our analysis because of the expected strong contamination by SEPs.
First of all, we considered possible corrections in the C count rate due to the MC orientations. Cane et al. (1994) analysed the effect on energetic particles with energies >60 MeV/n of an ejecta detected by Helios 1, Helios 2, and IMP 8 on 9 March 1978 (this ejecta is not included in our list). They concluded that the clear differences in the FD shape and depth could be explained by assuming that spacecraft followed different paths through the ejecta and one of the spacecraft traversed the ejecta partially. Blanco et al. (2013) analysed a pool of FDs detected by neutron monitors and produced by ICMEs with MCs and ICMEs with flux ropes. These authors showed that MCs are more effective than flux ropes in producing deeper FDs. Because the flux ropes were mostly aligned along the ICME legs, they concluded that the spacecraft path through ICME can affect the FD strength because the spacecraft is observing different regions of the ICME.
We only considered MCs with complete magnetic field rotations. Here, complete means that the MC topology can be fitted to the Hidalgo and Nieves-Chinchilla model (Hidalgo & Nieves-Chinchilla 2012) and it could be expected that the spacecraft observes equivalent ICME regions. If this assumption was applicable, no clear dependences with the MC orientation were supposed to be found. The orientation of the MC axis can be estimated using the results inferred from the model. The decrease percentages in the C detector were plotted versus longitude angle (Fig. 6a) and elevation angle (Fig. 6b) in the SSE coordinate system. It is clear from this figure that there is no dependence on the MC axis orientation. This result can be expected when the energetic-particle population is isotropic, as the case for the cosmic-ray population. Even when some solar particle component is present, for instance type 1*, no clear dependence with MC orientation is observed. The same applies to type 3 events although they are not shown in Fig. 6. Because of this observation, no corrections taking into account the MC orientation are required when analysing the C detector decreases in terms of MC properties.
 |
Fig. 6 Decrease in the C detector versus MC longitude (a) and elevation (b) angles. Red circles, blue up triangles and green down triangles represent Type 1, 1*, and 2, respectively. |
 |
Fig. 7 Decrease in C detector versus MC magnetic field intensity (a), MC speed (b), MC associated rigidity (c) and distance to Sun (d). Red circles, blue up triangles and green down triangles represent Type 1, 1*, and 2, respectively. The solid black lines represent the linear fit to type 1. |
The decreases in the C detector are due to the change in the transport conditions of the energetic particles above 50 MeV/n. These transport conditions are strongly affected by variations in both intensity and direction of the magnetic field, therefore magnetic turbulence, shocks, MCs and interaction regions are real candidates to produce FDs. In this work we focus on the MC role as an agent that can exclude these particles from its inner region, and we revise different MC parameters such as magnetic field intensity, speed, size, rigidity or time of flight, which can be relevant agents for the FD strength.
We compiled the higher value of the magnetic field measured in the MC structure defined by their flux rope signatures for the magnetic field intensity. In Fig. 7a, the growing trend of the decrease in the count rate with field intensity is plotted. The continuous line represents the linear fit to type 1. A Pearson coefficient (Pc) of 0.66 is found. This trend is clear for type 2 and not as clear for type 1*, where solar particles contamination can be expected according to the definition of type 1*. This growing trend was previously reported by Cane (1993) using observations at 1 AU.
A growing trend is also observed when plotting the C count rate against the MC speed for the role of speed in producing FD (Fig. 7b). The Pc is 0.42 in this case. This is in fact a poor correlation. Richardson & Cane (2011) give a correlation of 0.64 considering ICMEs with and without MCs. Blanco et al. (2013) obtained a linear correlation of 0.71 between the decrease percentage and the MC speed. These two statistics were performed on a pool of events detected a 1 AU. The discrepancy between our result and these previous ones can be explained because the effect of the MC location is not taken into account when all measurements are acquired at 1 AU. Therefore, the MC speed itself cannot explain the observed decreases.
If MCs are closed magnetic structures, at least locally, it is expected that the rigidity of incoming particles may be an important factor for the depth of the decrease. This assumption is tested in Fig. 7c. Here we assumed that it is possible to define an associated rigidity with an MC as the rigidity of a particle affected by the MC field with a gyroradii equal to the MC diameter. To compute this parameter, we considered the MC section diameter, which is estimated taking into account the spacecraft entrance and exit times in the MC, its speed and the magnetic field intensity in the MC. The associated rigidity was then calculated using the expression R = rBc, where r is the MC diameter, B is the magnetic field intensity and c is the speed of light. A clear growing trend is again observed in type 1 and 2, as can bee seen with the help of the linear fit line (Pc = 0.66). This trend is lost for type 1*. Again we point out that the SEP presence can contaminate the counts in the C detector. This seems to indicate that under some circumstances, solar energetic particles can enter an MC easier than cosmic rays with the same rigidity.
In previous paragraphs, the FD depth was analysed in terms of local parameters of MCs such as orientation, field strength, speed, and rigidity. A clear dependence on the local MC orientation was not found, neither was a good correlation with the MC speed. But better correlations were found with respect the magnetic field strength and rigidity. This may confirm that locally, MCs work as closed magnetic structures that prevent incoming GCRs.
The range of heliocentric distances sampled by Helios (from 0.3 to 1 AU) led us to check the effect of the MC location on the inner heliosphere on FDs (Fig. 7d). In principle, some dependence is expected because the GCR flux increases with the distance to Sun. Although the depth of the FDs diminished with the heliocentric distance, only a poor correlation (Pc = 0.41) was found.
The low correlation coefficients of these trends and the short list of events (nineteen type 1 events) can put into doubt whether such trends are real. To test this hypothesis a Student t test was performed. We found that the trends of magnetic field and rigidity have a confidence level higher than 95%. The confidence levels for speed and heliocentric distance, are lower than the previous ones but higher than 90% and 85%, respectively.
Globally, an MC is considered to be closed when both ends are connected to the Sun. Counterstreaming electrons were used to confirm whether MC are closed structures from a global point of view. Shodhan et al. (2000) found that less than 50% of the MCs at 1 AU are consistent with flux ropes with both legs connected to the Sun. These authors pointed out a dependence between close flux and MC size as well, where the closer the flux, the larger the MC.
According to this idea, of MCs as globally closed magnetic structures, GCR can be used as a probe to infer to which degree the MC is closed. As has been pointed out by Richardson & Cane (2011), MCs may be an effective barrier to exclude GCR, but some of them can enter MCs by different mechanisms, for example by diffusion. Assuming a roughly constant GCR diffusion rate, the depth of FDs probably decreases as the MC time into solar wind grows. To test this assumption, the decrease in C count rate is represented against the time of flight of the MCs. This time was estimated assuming that the MC speed is constant. We multiplied this speed by the observed MC distance to the Sun. The result is presented in Fig. 8. A clear descending relationship is observed in this plot. Longer travel times are related with smaller decreases. The obtained linear correlation for type 1 events is –0.64. The decreasing trend of the count-rate percentage with heliocentric distance (Fig. 7d), and a roughly constant speed with the distance to the Sun (Fig. 9) support the assumption that the dependence of the FD depth with the MC time of flight is a real MC lifetime effect.
This result does not contradict the findings by Shodhan et al. (2000) about closed MCs. One of the selection criteria applied in this work was that an FD has to be observed by the C detector. This criterion can introduce a bias in our statistic. Assuming that FDs are evidence of closed MCs, only the 57% of the MCs in the list of Bothmer & Schwenn (1998) are MCs with their feet anchored in the Sun. This percentage roughly agree with that obtained by Shodhan et al. (2000) using counterstreaming electrons as sign of closed MCs.
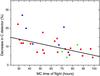 |
Fig. 8 Decrease in the C detector versus MC time of flight. Red circles, blue up triangles, and green down triangles represent type 1, 1*, and 2, respectively. The solid line represents a linear fit to type 1. |
Since this is a statistical process, longer travel times will increase the number of cosmic ray particles that manage to enter the closed MC loops. Yet, this result itself does not exclude other causes such as changes in the effectiveness of an MC as a barrier for GCRs as can be inferred from the decreasing slope when the MC magnetic flux is represented versus its heliocentric distance (Fig. 9c). This loss in effectiveness as a magnetic barrier could be consistent with the eroded MC proposed by Ruffenach et al. (2012), where some reconnection processes, are supposed to occur at the MC nose.
As we commented above, the decrease in the count rate of GCRs at low energies, above 50 MeV/n, can be used as additional signature of the MC to those proposed by Burlaga et al. (1981). Using this criterion, we identified 35 MCs at different heliocentric distances from the Helios 1 and 2 measurements. According to the behaviour of the count rates by the A and C detectors, we divided them into four categories.
 |
Fig. 9 MC properties versus solar distance. From top to bottom, diameter of the MC cross section, magnetic field intensity, magnetic flux, and MC speed. Red circles, blue up triangles, green down triangles, and violet squares represent type 1, 1*, 2, and 3, respectively. The continuous line in the upper panel represents the relationship between the radial width and the solar distance proposed by Savani et al. (2012), W = 0.14R + 0.04 . |
In the following paragraphs, we address the question whether this classification can find out differences among these types regarding the general properties of an MC. Their section diameter, magnetic field intensity, magnetic flux, and the speed are represented versus the s/c heliocentric distance in Fig. 9. Types 1, 1*, 2, and 3 are represented by red circles, blue up triangles, green down triangles, and violet squares, respectively. It is clear that the MC properties seem to be independent of the event classification, except for the MC speed, because the MCs catalogued as type 3 are faster. This allows us to consider all events in the same category when studying MC properties.
Two results are readily inferred from Figs. 9a and 9b. The size of MCs grows and the magnetic field intensity is reduced with distance to the Sun. We estimated the MC size from the diameter of the MC section computed from the spacecraft time in the MC multiplied by the MC speed. Both results can be explained assuming an MC expansion because of a weakening of the magnetic field and so a lower magnetic pressure when the MC moves away from the Sun. Recently, Gulisano et al. (2010) asserted that the MC expansion does exist and distinguished between two types of expansion, local and global. But, after checking the MC magnetic flux (Fig. 9c), the previous assumption of an expanding MC is not companied by magnetic flux conservation and a decreasing trend with distance is noticed. According to this, magnetic flux is not conserved during MC expansion. At this point, we have to remember that we are analysing different MCs, which makes it very difficult to infer definite individual conclusions such as magnetic flux conservation from this statistical study. Moreover, different works warn about the strong deformation that the MC section can suffer when it travels through the heliosphere. This deformation produces noncircular cross-sections (Riley & Crooker 2004; Owens et al. 2006; Owens 2008). Savani et al. (2011) obtained a ratio of the transverse width and the radial width of 6. They pointed out that the strongest deformation occurs close to the Sun and the aspect ratio remains roughly constant after overtaking the Venus orbit. We clarify that we assumed a circular cross-section to estimate the magnetic flux. If deformation is important, the computed magnetic flux could be underestimated, questioning the decreasing magnetic flux calculated for MCs at different solar distances. To compare the circular cross-section approach with deformed cross-sections, we plotted the linear relationship of the radial width and distance to the Sun proposed by Savani et al. (2012), W = 0.14R + 0.04 (continuous line in the upper panel of Fig. 9). This relationship seems to work better at heliodistances of between 0.3 and 0.6 AU than at larger distances, therefore it is difficult to confirm whether it works at 1 AU. We can guess that the transverse width could be inclined with respect to the Sun-Earth line because of the MC interaction with the solar wind. These effects make an analysis of the magnetic flux transported by the MCs more difficult.
Finally, the dependence with solar distance (Fig. 9d) is not observed for the MC speed. This observation implies that any deceleration process in an MC probably occurs below 0.3 AU. The temptation of arguing that the acceleration of the MC between 0.3 and 1 AU is not enough significant to be observed is very strong, but again, because this is a statistical study, individual conclusions cannot be conclusive. Especially when different works point out that deceleration in CMEs is observed and after comparing the CME emergence speed with the speed of its counterpart MC at 1 AU, some acceleration probably exists along the MC path from the Sun to the Earth (Vršnak 2001; Blanco et al. 2013).
5. Conclusions
We have analysed a pool of 35 MCs selected by the criteria of a short-term decrease in the count rate of energetic particles with an energy higher than 50 MeV/n and the observation of a flux rope structure. We showed that this short-term decrease can be used as a complementary signature of an MC without introducing a bias in the final selection.
The 68% of the decreases in C detector higher than 4% were associated to an MC. In almost all of them (98%) a preceding shock was detected. This supports the main role of both shock and MC in producing FDs. Another important observation is the non-dependence of FD characteristics on the MC orientation. This implies an isotropic GCR flux coming in the MC without favoured entrance directions. This strengthens the argument of the MCs as closed magnetic structures.
The FD depth is linearly related to the magnetic field strength of the MC by a correlation factor of 0.66 and to the MC associated rigidity by a factor of 0.66. However, a poor linear relationship with the MC speed (Pc = 0.42) was found. On the other hand, a negative linear relationship (Pc = −0.64) was found with
the time of flight of the MC. This could imply an almost constant incoming rate of GCR into MC. All these correlations were obtained for MCs classified as type 1.
Our analysis of MC properties showed that the MC diameter grows with the distance to the Sun, confirming the MC expansion during its travel in the interplanetary medium. The MC magnetic field intensity diminishes with the heliocentric distance, as expected for an expanding magnetic structure. But, the MC magnetic flux also decreases, implying an expansion mode without constant magnetic flux. This result cannot be correct if the MC cross-section is strongly deformed between 0.3 to 1 AU. For this cross-section deformation, the comparison of the MC diameter assuming a circular section with a deformed cross-section drives us to the conclusion that the cross-section transverse width could be tilted with respect to the Sun-Earth line as a consequence of the MC interaction with the solar wind.
Finally, the MC speed does not show a clear dependence on the distance to the Sun. If this observation is confirmed, the deceleration process has to take place at closer distances to the Sun than <0.3 AU.
Acknowledgments
We acknowledge to the Coordinated Data Analysis Web (CDAWeb) for the use of data. This work has been supported by the grants JCCM PPII10-0150-6529 and AYA2011-29727-C02-01.
References
- Barnden, L. R. 1973, in International Cosmic Ray Conference, 2, 1277 [Google Scholar]
- Blanco, J. J., Catalán, E., Hidalgo, M. A., et al. 2013, Sol. Phys., 284, 167 [Google Scholar]
- Bothmer, V., & Schwenn, R. 1998, Ann. Geophys., 16, 1 [Google Scholar]
- Burlaga, L. F., & Behannon, K. W. 1982, Sol. Phys., 81, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res., 86, 6673 [Google Scholar]
- Cane, H. V. 1993, J. Geophys. Res., 98, 3509 [NASA ADS] [CrossRef] [Google Scholar]
- Cane, H. V., Richardson, I. G., von Rosenvinge, T. T., & Wibberenz, G. 1994, J. Geophys. Res., 99, 21429 [NASA ADS] [CrossRef] [Google Scholar]
- Cane, H. V., Richardson, I. G., & Wibberenz, G. 1997, J. Geophys. Res., 102, 7075 [NASA ADS] [CrossRef] [Google Scholar]
- Forbush, S. E. 1938, Phys. Rev., 54, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Gulisano, A. M., Démoulin, P., Dasso, S., Ruiz, M. E., & Marsch, E. 2010, A&A, 509, A39 [Google Scholar]
- Heber, B., Bothmer, V., Dröge, W., et al. 1998, J. Geophys. Res., 103, 4809 [NASA ADS] [CrossRef] [Google Scholar]
- Hidalgo, M. A., & Nieves-Chinchilla, T. 2012, ApJ, 748, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Jordan, A. P., Spence, H. E., Blake, J. B., & Shaul, D. N. A. 2011, J. Geophys. Res., 116, 11103 [NASA ADS] [CrossRef] [Google Scholar]
- Kunow, H., Witte, M., Wibberenz, G., et al. 1977, J. Geophys. Z. Geophys., 42, 615 [Google Scholar]
- Neubauer, F. M., Beinroth, H. J., Barnstorf, H., & Dehmel, G. 1977, J. Geophys. Z. Geophys., 42, 599 [Google Scholar]
- Owens, M. J. 2008, J. Geophys. Res. (Space Physics), 113, 12102 [NASA ADS] [CrossRef] [Google Scholar]
- Owens, M. J., Merkin, V. G., & Riley, P. 2006, J. Geophys. Res. (Space Physics), 111, 3104 [Google Scholar]
- Richardson, I. G., & Cane, H. V. 2011, Sol. Phys., 270, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, I. G., Wibberenz, G., & Cane, H. V. 1996, J. Geophys. Res., 101, 13483 [Google Scholar]
- Riley, P., & Crooker, N. U. 2004, ApJ, 600, 1035 [Google Scholar]
- Rodríguez-Pacheco, J., Cid, C., Blanco, J. J., & Sequeiros, J. 2003, Sol. Phys., 213, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbauer, H., Schwenn, R., Marsch, E., et al. 1977, J. Geophys. Z. Geophys., 42, 561 [Google Scholar]
- Ruffenach, A., Lavraud, B., Owens, M. J., et al. 2012, J. Geophys. Res. (Space Physics), 117, 9101 [Google Scholar]
- Savani, N. P., Owens, M. J., Rouillard, A. P., et al. 2011, ApJ, 732, 117 [Google Scholar]
- Savani, N. P., Davies, J. A., Davis, C. J., et al. 2012, Sol. Phys., 279, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Shodhan, S., Crooker, N. U., Kahler, S. W., et al. 2000, J. Geophys. Res., 105, 27261 [Google Scholar]
- Vršnak, B. 2001, Sol. Phys., 202, 173 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Normalized count rates of A (red triangles) and C (black circles) and protons with energy higher than 50 MeV (green squares). Normalized count rates have been calculated using the expression (C(t)/Cmean) ∗ 100. |
| In the text | |
 |
Fig. 2 Type 1 example. Decrease observed by Helios 1 during an IMC passage on January 1975. From top to bottom: density, temperature, solar wind speed, magnetic field components, the 3.77–12.72 MeV proton channel, and the 1.69–3.68 MeV/n alpha channel from the cosmic ray experiment (E6), normalized count rate in A and C detectors and magnetic field strength. Vertical lines mark the shock position (dotted line) and MC boundaries (solid lines) and the overplotted solid lines in fourth panel are the fit lines from the MC model. |
| In the text | |
 |
Fig. 3 Type 1* example. Decrease observed by Helios 1 during an MC passage on May 1979. The panel distribution is identical to that shown in Fig. 2. |
| In the text | |
 |
Fig. 4 Type 2 example. Decrease observed by Helios 1 during an MC passage on January 1977. The panel distribution is identical to that shown in Fig. 2. |
| In the text | |
 |
Fig. 5 Type 3 example. Decrease observed by Helios 1 during an MC passage on May 1978. The panel distribution is identical to that shown in Fig. 2. |
| In the text | |
 |
Fig. 6 Decrease in the C detector versus MC longitude (a) and elevation (b) angles. Red circles, blue up triangles and green down triangles represent Type 1, 1*, and 2, respectively. |
| In the text | |
 |
Fig. 7 Decrease in C detector versus MC magnetic field intensity (a), MC speed (b), MC associated rigidity (c) and distance to Sun (d). Red circles, blue up triangles and green down triangles represent Type 1, 1*, and 2, respectively. The solid black lines represent the linear fit to type 1. |
| In the text | |
 |
Fig. 8 Decrease in the C detector versus MC time of flight. Red circles, blue up triangles, and green down triangles represent type 1, 1*, and 2, respectively. The solid line represents a linear fit to type 1. |
| In the text | |
 |
Fig. 9 MC properties versus solar distance. From top to bottom, diameter of the MC cross section, magnetic field intensity, magnetic flux, and MC speed. Red circles, blue up triangles, green down triangles, and violet squares represent type 1, 1*, 2, and 3, respectively. The continuous line in the upper panel represents the relationship between the radial width and the solar distance proposed by Savani et al. (2012), W = 0.14R + 0.04 . |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


