| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A150 | |
| Number of page(s) | 11 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201321286 | |
| Published online | 09 August 2013 | |
SWEET-Cat: A catalogue of parameters for Stars With ExoplanETs
I. New atmospheric parameters and masses for 48 stars with planets⋆,⋆⋆
1
Centro de Astrofísica, Universidade do Porto,
Rua das Estrelas,
4150-762
Porto,
Portugal
e-mail:
nuno@astro.up.pt
2
Departamento de Física e Astronomia, Faculdade de Ciências,
Universidade do Porto, Rua do Campo
Alegre, 4169-007
Porto,
Portugal
3
UJF – Grenoble 1/CNRS-INSU, Institut de Planétologie et
d’Astrophysique de Grenoble (IPAG) UMR 5274, Grenoble
38041,
France
4
Instituto de Astrofísica de Canarias, 38200, La Laguna, Tenerife, Spain
5
Departamento de Astrofísica, Universidad de La
Laguna, 38206, La
Laguna, Tenerife,
Spain
6
Observatoire de Genève, Université de Genève,
51 ch. des Maillettes,
1290
Sauverny,
Switzerland
Received: 13 February 2013
Accepted: 27 June 2013
Context. Thanks to the importance that the star-planet relation has to our understanding of the planet formation process, the precise determination of stellar parameters for the ever increasing number of discovered extra-solar planets is of great relevance. Furthermore, precise stellar parameters are needed to fully characterize the planet properties. It is thus important to continue the efforts to determine, in the most uniform way possible, the parameters for stars with planets as new discoveries are announced.
Aims. In this paper we present new precise atmospheric parameters for a sample of 48 stars with planets. We then take the opportunity to present a new catalogue of stellar parameters for FGK and M stars with planets detected by radial velocity, transit, and astrometry programs.
Methods. Stellar atmospheric parameters and masses for the 48 stars were derived assuming local thermodynamic equilibrium (LTE) and using high-resolution and high signal-to-noise spectra. The methodology used is based on the measurement of equivalent widths for a list of iron lines and making use of iron ionization and excitation equilibrium principles. For the catalogue, and whenever possible, we used parameters derived in previous works published by our team, using well-defined methodologies for the derivation of stellar atmospheric parameters. This set of parameters amounts to over 65% of all planet host stars known, including more than 90% of all stars with planets discovered through radial velocity surveys. For the remaining targets, stellar parameters were collected from the literature.
Results. The stellar parameters for the 48 stars are presented and compared with previously determined literature values. For the catalogue, we compile values for the effective temperature, surface gravity, metallicity, and stellar mass for almost all the planet host stars listed in the Extrasolar Planets Encyclopaedia. This data will be updated on a continuous basis. The compiled catalogue is available online. The data can be used for statistical studies of the star-planet correlation, as well as for the derivation of consistent properties for known planets.
Key words: planetary systems / stars: solar-type / stars: abundances / catalogs
Based on observations collected at ESO facilities under programs 088.C-0892(A), 089.C-0444(A), 090.C-0146(A) (FEROS spectrograph, 2.2-m ESO-MPI telescope, La Silla), 380.C-0083(A), and 083.C-0174(A) (UVES spectrograph, ESO VLT Kueyen telescope, Paranal).
The catalogue is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/556/A150
© ESO, 2013
1. Introduction
The study of extrasolar planetary systems is steadily becoming a mature field of research. To date, over 850 extra-solar planets have been discovered around solar-type stars1. Most of these were found thanks to the incredible precision achieved by today’s radial velocity and photometric transit techniques. In addition to the dozens of giant planets detected, these efforts are adding to the lists the first planets that may be rocky in nature like our Earth (e.g. Léger et al. 2009; Batalha et al. 2011; Dumusque et al. 2012). To these we should add a plethora of additional candidates announced as part of space-based transit surveys like Kepler (Batalha et al. 2013). Overall, these discoveries are showing that planets are ubiquitous around solar-type stars (e.g. Mayor et al. 2011; Howard et al. 2012).
The strong increase in the number of known planetary systems is allowing astronomers to analyse in a statistically significant way the properties of the newfound worlds (see e.g. Udry & Santos 2007). In addition, a combination of different techniques and methods is also giving us the possibility to explore the planetary properties, including the study of their atmospheres and internal structure (e.g. Valencia et al. 2010; Cowan & Agol 2011; Demory et al. 2012).
A key aspect to this progress is the characterization of the planet host stars. Several reasons exist for this. For instance, precise (or if possible, accurate) stellar radii are critical if we want to measure precise values for the radius of a transiting planet (see e.g. Torres et al. 2012). The determination of stellar radii depends in turn on the quality of the derived stellar parameters such as the effective temperature.
The chemical composition of a planet, both its interior and atmosphere, is also likely to be related to the chemical composition of the proto-stellar cloud, reflected in the composition of the stellar atmosphere (Guillot et al. 2006; Fortney et al. 2007; Bond et al. 2010). The precise derivation of stellar chemical abundances thus gives us important clues to understanding the planets and their observed properties.
Furthermore, a number of studies have pointed towards the existence of a strong relation between the properties and frequency of the newfound planets and those of their host stars. In this respect, the well known correlation between the stellar metallicity and the frequency of giant planets is a good example. Large spectroscopic studies (e.g. Santos et al. 2001, 2004b; Fischer & Valenti 2005; Sousa et al. 2011b; Mayor et al. 2011; Mortier et al. 2013a) confirmed the initial suspicions (Gonzalez 1997; Santos et al. 2000a) of a positive correlation between the probability of finding a giant planet and the metal content of the stars. This strong correlation even prompted new planet search surveys based on metal-rich samples (e.g. Tinney et al. 2003; Fischer et al. 2004; Da Silva et al. 2006). Although positively increasing the planet detection rate, these surveys biased the samples towards metal-rich stars, a bias that has to be taken into account when studying the metallicity-planet correlation.
Curiously, this strong metallicity-giant planet correlation was not found for the lowest mass planets (Sousa et al. 2011b; Mayor et al. 2011; Buchhave et al. 2012). Both results, however, are in full agreement with the expectations from the most recent models of planet formation based on the core-accretion paradigm (e.g. Mordasini et al. 2012, and discussion therein).
Although the general metallicity-giant planet correlation is reasonably well established, many details are still missing that may hold the clue to new and important details concerning planet formation. For example, the exact shape of the metallicity-planet correlation is still debated (Santos et al. 2004b; Johnson et al. 2010; Mortier et al. 2013a). The understanding of this issue may be critical to point out the mechanisms responsible for the formation of giant planets across the whole metallicity range (e.g. Matsuo et al. 2007), or to the understanding of the frequency of planets in the Milky Way. The role of the abundances of other elements is also being discussed (e.g. Adibekyan et al. 2012a) with some curious trends being a strong matter of debate concerning e.g. the abundances of the light element lithium (Israelian et al. 2009; Baumann et al. 2010; Sousa et al. 2010; Ghezzi et al. 2010b) or specific trends including other elemental abundances (e.g. Ramírez et al. 2010; González Hernández et al. 2010).
A role in the formation of giant planets has also been assigned to stellar mass. It is now widely accepted that the frequency of giant planets orbiting M dwarfs is considerably lower than that found for FGK dwarfs (Bonfils et al. 2005b, 2013; Endl et al. 2006), at least regarding the short-period domain (Neves et al. 2013). Higher mass stars, on the other hand, seem to have a higher frequency of orbiting giant planets (Lovis & Mayor 2007; Johnson et al. 2007a). This result is expected from the models of planetary formation following the core-accretion paradigm (Laughlin et al. 2004; Ida & Lin 2005; Kennedy & Kenyon 2008);see however Kornet et al. (2005) and Boss (2006). We note that this correlation may be related to the different trend in stellar metallicity that has been suggested to exist for intermediate mass giant stars with planets (Pasquini et al. 2007; Ghezzi et al. 2010a; Hekker & Meléndez 2007).
Finally, it is important to note that the role of stellar properties (metallicity and temperature) on the formation of different architectures of planetary systems has also been addressed. Among these, suspicions have been raised concerning the metallicity-orbital period relation (e.g. Queloz et al. 2000; Sozzetti 2004; Santos et al. 2003; Beaugé & Nesvorný 2013; Dawson & Murray-Clay 2013). Hot-Jupiters have often been identified as orbiting particularly metal-rich stars (however this trend has not been confirmed from a statistical point of view). More recently, the temperature and age of the star has been linked with the alignement of the stellar spin-orbital plane angle (Winn et al. 2010; Triaud 2011; Albrecht et al. 2012), a result that hints at the mechanisms responsible for the migration of hot-Jupiters.
Paramount to the discussion of all these issues is the correct determination of stellar parameters like the effective temperature, the stellar metallicity, and the stellar mass. Since accurate values for these are usually not possible2, it is critical that at least uniform sets of stellar parameters exist. Unfortunately this is not always the case, with different teams making use of different methods (line-lists, model atmospheres, methodologies) to derive the atmospheric properties of the host stars. In many cases, comparisons have shown that the differences are residual (see e.g. Sousa et al. 2008), but in other cases the discrepancies have significant impact on the knowledge of the planet parameters (for a recent discussion on the possible offsets see Torres et al. 2012).
In this paper we present new atmospheric parameters and masses for a sample of 48 stars with planets. The atmospheric parameters were derived in local thermodynamic equilibrium (LTE) from a uniform analysis, and making use of high-resolution and high signal-to-noise (S/N) spectra. These values are then included in a new catalogue of stellar parameters for stars with planets that we have called SWEET-Cat, also presented in this paper. The catalogue, available online, represents an effort to compile a set of data that is usually not found together in the literature. The baseline parameters in the catalogue are also compared with the ones listed in other compilations or catalogues. This comparison provides the reader (in particular the exoplanet community) with the possibility to understand the typical errors (including systematic) that exist in the values of parameters for stars with planets published in the literature.
In the next sections we present the sample of 48 stars discussed in this paper and their stellar parameters. We then present the content of the catalogue, the different sources of stellar parameters used, and some considerations about future improvements.
2. New parameters for 48 planet hosts
Stellar atmospheric parameters and masses for the 48 planet hosts presented in this paper.
The sample of 48 stars consists of dwarfs of spectral type F, G, or K that are known to be orbited by a planet found by the radial velocity method (according to the online catalogue http://www.exoplanet.eu). The list of stars is presented in Table 1.
As mentioned above, the parameters were derived from the analysis of high-resolution and high S/N spectra. The spectra were gathered through observations made by our team and by the use of the ESO archive. In total, six different spectrographs were used: FEROS (2.2 m ESO/MPI telescope, La Silla, Chile), FIES (Nordic Optical Telescope, La Palma, Spain), HARPS (3.6 m ESO telescope, La Silla, Chile), SARG (TNG Telescope, La Palma, Spain), SOPHIE (1.93 m telescope, OHP, France), and UVES (VLT Kueyen telescope, Paranal, Chile). The characteristics of each spectrograph and the number of stars observed are listed in Table 2. We note that the use of different spectrographs is not expected to introduce significant systematic differences in the derived stellar parameters, as can be seen from previous studies (e.g. Santos et al. 2004b).
The spectra were reduced and extracted using the available pipelines or IRAF3. The spectra were then corrected for radial velocity with the IRAF task DOPCOR. Individual exposures of multiple observed stars with the same instrument were co-added using the task SCOMBINE in IRAF.
From the spectra, we derived the atmospheric stellar parameters (effective temperature Teff, surface gravity log g, microturbulence ξ, and metallicity [Fe/H]) and the masses as described in Sect. 3.2.1. The followed procedure is based on the equivalent widths of Fe i and Fe ii lines, and iron excitation and ionization equilibrium, assumed in Local Thermodynamic Equilibrium (LTE). Herefore, the 2002 version of MOOG4 (Sneden 1973), a grid of ATLAS plane-parallel model atmospheres (Kurucz 1993) and the iron linelist of Sousa et al. (2008) are used. For stars cooler than 5200 K (as initially derived with the Sousa et al. line list) we re-derived and adopted the parameters using the line list of Tsantaki et al. (2013), specially suitable for cool stars. Stellar masses and their errors were computed with the corrected calibration of Torres et al. (2010) as discussed in Sect. 3.2.1.
To measure the equivalent widths of the iron lines, the code ARES is used (automatic routine for line equivalent widths in stellar spectra; Sousa et al. 2007). The input parameters for ARES, are the same as in Sousa et al. (2008), except for the rejt parameter, which determines the calibration of the continuum position. Since this parameter strongly (and mostly) depends on the S/N of the spectra, different values are needed for each spectrum. In this study, the S/N values were derived for each spectrum using the IRAF routine BPLOT. Three spectral regions are used: [5744 Å, 5747 Å], [6047 Å, 6053 Å] and [6068 Å, 6076 Å]. The final S/N of the spectra measured in the region around 6000 Å is in most cases above 100 (see Table 1). We note also that these values are probably underestimated because the identification of regions completely absent of absorption lines is not straightforward5.
The rejt parameter was then set by visual inspection for ten different spectra with different S/N values (representable for the whole sample). Therejt parameters for the remaining spectra were then derived by a simple interpolation of these values. This method ensures a uniform usage of therejt parameter, since we otherwise do not have access to a uniform source for the S/N as in Sousa et al. (2008). The final dependence of therejt parameter to the S/N is the same as in Mortier et al. (2013b).
Spectrograph details: resolving power and spectral ranges.
Table 1 lists the derived stellar atmospheric parameters for the 48 planet hosts. These dwarf stars cover wide ranges of effective temperature, surface gravity, microturbulence, metallicity, and mass: 4510–6732 K, 4.02–4.81 dex, 0.32–2.03 km s-1, −0.62–0.5 dex, and 0.77–1.42 M⊙, respectively. Mean error bars of 42.7 K, 0.09 dex, 0.07 km s-1, 0.03 dex, and 0.08 M⊙ are obtained. The errors on the atmospheric parameters were derived as in Santos et al. (2004b). Errors in the mass were computed as described in Sect. 3.2.1. The uniformity of our analysis minimizes possible systematic errors in the final parameters.
In Figs. 1–3 we compare our baseline parameters for our 48 stars (green symbols) with those listed in the Extrasolar Planets Encyclopaedia (Schneider et al. 2011), exoplanets.org (Wright et al. 2011), and the NASA Exoplanet Archive6. As can be seen from the plots, in general the parameters agree well with previously published values. A few outliers exist, however, in particular concerning the stellar metallicity (up to ~0.3 dex).
 |
Fig. 1 Comparison between our baseline stellar parameters with those listed in the Extrasolar Planets Encyclopaedia for the same stars. Only stars with planets detected by radial velocity surveys are included. Green triangles denote the 48 stars whose parameters are presented in this paper. The dotted line represents a 1:1 relation, and the full line a linear fit to the data. Typical error bars are shown on the upper-left part of each panel. |
 |
Fig. 2 Same as Fig. 1 but for the data from exoplanets.org (Wright et al. 2011). |
3. The SWEET catalogue
As mentioned above, the parameters derived in this paper were added to other values in the literature into a new catalogue of stellar parameters for stars with planets. This catalogue is presented in this paper.
The complete list of the fields in the catalogue is listed in Table 3. A more detailed description of each field is given in the following sections.
3.1. Identification and basic data
At the time that this paper was being written, the Extrasolar Planets Encyclopaedia listed 889 planets in 694 planetary systems7, most of them discovered by radial velocity or transit surveys. Owing to its completeness and tradition, we decided to use this database as a starting point for the catalogue.
For each planet host star listed in the Encyclopaedia having been detected by radial velocity, astrometry, or transit measurements, we compiled a series of basic information. In this first version of the catalogue we decided to exclude direct imaging planets (most of them around early-type stars), planets discovered using the microlensing technique (because of the difficulty in characterizing the host stars), as well as degenerated stars (e.g. pulsars hosting planetary systems detected by timing techniques). For the remaining stars (i.e. those listed in the Encyclopaedia as radial velocity, transiting, or astrometry planet hosts), we compiled the following basic information:
 |
Fig. 3 Same as Fig. 1 but for the data from the NASA Exoplanet Archive. Transiting planets and radial-velocity planets are denoted by crosses and dots, respectively. |
-
name of the star: although we adopted the Encyclopaedia name,for all cases where the star has an HD number, this isalso listed;
-
coordinates: right ascensions and declinations were compiled from the SIMBAD astronomical database. We adopted the ICRS coordinates (J2000). Coordinates that were not available were left blank;
-
V magnitudes for all targets were also compiled from SIMBAD whenever possible. Exceptions where no V magnitudes were listed in SIMBAD (for some Kepler and WASP candidates mostly) were taken directly from the Encyclopaedia. The V magnitudes are meant to serve as reference, and not to be used for accurate physical calculations;
-
parallax values were compiled from SIMBAD whenever these exist. For cases where the parallax is not available, we computed a spectroscopic parallax using the estimated stellar parameters (for details on the method we point to Sousa et al. 2011a). A few parallaxes for M dwarfs were also taken from the literature.
List of fields in the catalogue and description (when necessary).
3.2. Atmospheric parameters and masses
The determination of accurate stellar atmospheric parameters is a huge matter of debate. Several methodologies have been explored to derive effective temperatures, surface gravities, or stellar metallicities, with clear differences in the resulting zero point or scale (for references and discussions see Sousa et al. 2008; Casagrande et al. 2010; Torres et al. 2012). In other words, it is at present very difficult to point towards any accurate sources of stellar parameters. As a consequence, any catalogue of stellar parameters for stars with planets should probably focus, whenever possible, on uniformity, i.e. on precision rather than accuracy.
With this in mind, in the next sections we describe our baseline sources for the stellar parameters. We note, however, that the catalogue is updated on a regular basis, and the sources of parameters may change over time. The philosophy behind the catalogue will be maintained.
The parameters compiled from these baseline sources are derived using a homogeneous analysis (i.e. as homogeneous as possible, meaning that they were derived by our team using the best possible uniform methodology). We will call these baseline parameters for the rest of the paper, in contrast to parameters compiled from other literature sources. All together, at the present time, we have baseline parameters for more than 65% of all planet host stars, including 87% of all radial velocity survey planet hosts (over 95% if we just include dwarf stars).
We should note that these baseline parameters are the closest that we can have to a homogeneous set of data; however, the term homogeneous should be read with some caution. Parameters derived for different stars, using different data sets (from different spectrographs), cannot be seen as fully homogeneous. For instance, although in most of the cases we use the same baseline line-list to derive stellar parameters (see below), the final line-list is always a sub-sample of this, because some spectrographs have spectral gaps, or simply due to the exclusion of some specific lines, in a case by case analysis, owing to the presence of cosmic rays. Furthermore, the continuum position used when measuring line equivalent widths is subject to errors that depend on the S/N of the data, for example. These facts will produce systematic offsets between the parameters derived for the different stars. However, in the large majority of the cases these offsets are expected to be very small and within the error bars of the individual parameters(see Sousa et al. 2008, where a comparison with the parameters derived for a common set of stars using two line-lists, one which is a sub-sample of the other, is presented). Finally, we cannot exclude systematic effects when comparing the analysis for stars of significantly different temperature or evolutionary stage (e.g. Santos et al. 2009). These effects are difficult to quantify, but can be at least partially solved when using appropriate line-lists and methodologies (see e.g. Tsantaki et al. 2013; Mortier et al. 2013b).
When we used data from other literature, care was taken to critically compile what we considered to be the best values, i.e. the ones that seem to give the best guarantee of uniformity with respect to our baseline parameters. Individual references are shown in the online catalogue. We are not, however, in a position to guarantee the uniformity of these results with respect to our baseline parameters, even if in many cases the parameters compare well with ours for stars we have in common (see below).
Again, it is important to add a word of caution. We are not saying here that the parameters derived by other authors are not uniform (among themselves) or that they are not of high quality, only that their consistency with respect to our baseline values is more difficult to ensure.
We decided not to include in the table an estimate for the stellar radius. First, because this can be computed directly from the other fields (see e.g. Santos et al. 2004a). Secondly, because for transit host stars, uniform values for this quantity have been compiled by other groups in other catalogues (e.g. Southworth 2012).
In the next sections we will describe the baseline methods used to derive what we call baseline stellar parameters, including the values for the 48 stars presented above. We also present comparisons of our baseline parameters with those presented in other catalogues and the literature. These comparisons provide a reference for the typical systematic errors existing in the stellar parameters for stars with planets derived by different teams using different, or sometimes similar methodologies.
3.2.1. FGK stars from radial velocity surveys
The most productive radial velocity planet search surveys concentrated their efforts on the search for planets around solar-type, FGK dwarfs or sub-giants (for some examples see e.g. Udry et al. 2000; Mayor et al. 2003; Marcy et al. 2005; Johnson et al. 2007b). Furthermore, because of astrophysical constraints imposed by active young stars, most of these targets are old, slow rotators (Saar & Donahue 1997; Santos et al. 2000b; Paulson et al. 2002), with thousands of well-defined weak metallic lines in their spectra. This makes them ideal targets for a standard spectroscopic analysis using iron line equivalent widths and ionization and excitation equilibrium principles (see Santos et al. 2004b; Sousa et al. 2008; and Tsantaki et al. 2013, for details on the methodology).
For more than ten years our team has been collecting and compiling high-resolution spectra to derive uniformly stellar parameters and chemical abundances for stars with planetary mass companions discovered by radial velocity surveys (e.g. Santos et al. 2001, 2004b, 2005; Sousa et al. 2008, 2011b,a; Tsantaki et al. 2013). This lead us to use our own parameters to establish the baseline for the whole catalogue. We note that in several cases, the parameters derived by our team have not been published in dedicated papers, but rather have been included in the discovery papers (for recent examples see Boisse et al. 2012; Marmier et al. 2013).
The choice of this baseline methodology for the derivation of stellar parameters is anchored on the extremely good agreement with the values found by methods that are usually considered to be standard. For instance, the temperatures are in very good agreement with those derived using the infrared flux method (IRFM; see e.g. Blackwell & Shallis 1977; Casagrande et al. 2010, and references therein) and interferometry, both at the low (Tsantaki et al. 2013) and high temperature (Sousa et al. 2008) regimes. This result can be seen in Fig. 4 where baseline temperature values are compared with those derived using both the IRFM and interferometry. The differences are very small, with an offset of −32 and 34 K for the comparison with the IRFM and interferometry results, respectively (differences are in the sense other−ours). These offsets are mostly independent of the temperature, and cannot be directly attributed to any of the methods used. For more details see Tsantaki et al. (2013) and references therein.
 |
Fig. 4 Comparison of the effective temperatures derived using the baseline methodology in the catalogue with values derived using the IRFM and interferometry. As in Tsantaki et al. (2013). |
 |
Fig. 5 Comparison between the masses for FGK dwarfs derived using the Padova isochones and the Torres et al. (2010) calibration. The solid line represents the 1:1 relation and the dotted line a quadratic fit. |
To keep uniformity, for all FGK dwarfs with baseline atmospheric parameters, stellar masses have been derived using a uniform method. For simplicity, we computed them with the calibration of Torres et al. (2010), using as input our spectroscopic parameters; however, the following small correction was applied. The values derived using this calibration are, in general, similar to the ones obtained using the web interface based on the Padova isochrones (da Silva et al. 2006)8 – see comparison in Fig. 5. However, a general offset is present that is a function of stellar mass. This offset was already discussed in Torres et al. (2010). In order to correct for this offset, we fitted a quadractic function to the plot in Fig. 5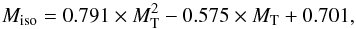 (1)where Miso and MT denote the stellar masses derived using the Padova isochrones and the Torres et al. calibration, respectively. This equation was used to correct for the mass values listed in the catalogue.
(1)where Miso and MT denote the stellar masses derived using the Padova isochrones and the Torres et al. calibration, respectively. This equation was used to correct for the mass values listed in the catalogue.
Errors in the stellar mass were also computed using the corrected Torres et al. calibration. The values were derived by means of a Monte Carlo analysis, where in each case 10 000 random values of effective temperature, surface gravity, and stellar metallicity were drawn assuming a Gaussian distribution from the derived uncertainties. The resulting mass distribution is used to derive the central value (the mass) and the 1-sigma uncertainty. The intrinsic error in the Torres et al. calibration was also quadratically added to the final uncertainly.
In Figs. 1–3 we compare our baseline parameters for stars detected in the context of radial velocity surveys with those listed in the Extrasolar Planets Encyclopaedia (Schneider et al. 2011), exoplanets.org (Wright et al. 2011), and the NASA Exoplanet Archive9.The general trends show good agreement, though some systematic effects are present. In Table 4 we present the coefficients of the linear fits to the data. These may be used to correct for the systematic trends. No fit was done for the comparison of metallicities with the data from the NASA Exoplanet Archive because this only has metallicities for a minority of the stars listed. We note also that several important outliers appear in the plots. This shows the need for a careful and uniform derivation of stellar parameters in any case-by-case analysis of stars with planets. Finally, we note that in several cases the parameters listed in the first two catalogues mentioned above were taken from our own sources, a fact that contributes to the improvement of the agreement seen in the plots.
As mentioned above, for FGK dwarfs which do not have baseline spectroscopic parameters, stellar parameters were compiled from the literature. Whenever possible, we used sources for which the stellar parameters compare well with our own values (e.g. the SPOCS catalogue, Valenti & Fischer 2005) – see Sousa et al. (2008) for a comparison.
3.2.2. FGK stars with transiting planets
For all FGK stars with transiting planets for which we could obtain a high-resolution spectrum, atmospheric parameters and masses were derived using the same methodology described in the previous section. As before, most of these parameters have already been published in dedicated papers (e.g. Santos et al. 2006; Ammler-von Eiff et al. 2009, see also Mortier et al., in prep.) or in planet discovery papers where the spectroscopic analysis was done by our team (see Santerne et al. 2012, for a recent example). This guarantees the best possible uniformity of the results.
For stars with transiting planets, surface gravities were also derived using the information coming from transit light curves. Indeed, surface gravities are typically very difficult to determine accurately through spectroscopy. For stars with a transiting planet, however, the surface gravity can be determined more directly. Purely from transit photometry, the stellar density can be calculated from the Seager & Mallén-Ornelas (2003)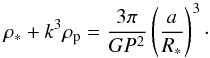 (2)Since the constant coefficient k is usually small, the second term on the left is negligible. All parameters on the right come directly from transit light curves (in the present paper these were taken directly from transit analysis papers in the literature). With this stellar density, combined with the effective temperature and metallicity from the spectroscopic analysis, the surface gravity can be determined through isochrone fitting (see e.g. Sozzetti et al. 2007). As presented in Mortier et al. (in prep.), for this step, we used the PARSEC isochrones (Bressan et al. 2012) and a χ2 minimization process for the fitting.
(2)Since the constant coefficient k is usually small, the second term on the left is negligible. All parameters on the right come directly from transit light curves (in the present paper these were taken directly from transit analysis papers in the literature). With this stellar density, combined with the effective temperature and metallicity from the spectroscopic analysis, the surface gravity can be determined through isochrone fitting (see e.g. Sozzetti et al. 2007). As presented in Mortier et al. (in prep.), for this step, we used the PARSEC isochrones (Bressan et al. 2012) and a χ2 minimization process for the fitting.
The temperatures and metallicities derived using the ionization and excitation equilibrium of iron lines have been shown to be mostly independent of the adopted surface gravity (Torres et al. 2012). This is due to the relatively low sensitivity of Fe i lines (used to constrain the temperature and metallicity) to changes in log g. For example, if we derive the effective temperature and metallicity for the Sun using the adopted methodology and line-lists, but fix log g to 3.0 (a strong ~1.5 dex difference), the derived effective temperature and metallicity values are only ~250 K and ~0.10 dex higher, respectively, than the adopted solar values. As such, the temperatures and metallicities derived with our adopted spectroscopic method can be used as reference values even if the derived spectroscopic surface gravities differ from those derived using the transit light curve (and the stellar density; see Sozzetti et al. 2007). A more detailed discussion of this issue will be presented in Mortier et al. (in prep.).
As mentioned above, the effective temperatures derived by the adopted methodology are in very good agreement with those derived by the IRFM. This implies that the stellar radii that we can derive using these parameters are probably as accurate as one can guarantee.
 |
Fig. 6 Same as Fig. 1 but for the data from the homogeneous part of the TEPCat catalogue (Southworth 2012). In the lower panel, crosses denote surface gravities derived using the transit light curve. |
In Fig. 6 we compare our baseline parameters for FGK stars with transiting planets with those presented in the homogeneous table of the TEPCat catalogue (Southworth 2012)10. On the log g plot (lower panel), crosses denote a comparison with our surface gravities derived using the transit light curve, while dots denote a comparison with our purely spectroscopic values. X-axis error bars refer to the typical spectroscopic uncertainties. Because of the very good agreement, we decided not to present any fits for the log g comparison. For all the parameters compared, the results show again a good agreement. There is, however, a small offset on the metallicities between the two samples, and perhaps more important, a general trend on the temperature scales. This temperature scale difference may lead to the derivation of significant different values for the planetary radii (in particular for the higher temperature stars). The dispersion in the log g comparison denotes the higher errors present in the pure spectroscopic analysis.
Whenever we did not have access to a high-resolution spectrum (mostly for planets detected as part of the Kepler and WASP surveys), priority was given to studies and compilations such as the TEPCat catalogue (Southworth 2012, for transiting planets). For the remaining stars, planet discovery papers were often used as the source for the stellar parameters. In some cases, the methodologies used are similar to the ones adopted for the majority of the stars in our catalogue.
3.2.3. Giant and evolved stars
The determination of stellar parameters for cool, giant stars is a matter of strong debate in the literature, with several authors raising doubts about the zero point of the metallicity scale in these objects (e.g. Taylor & Croxall 2005; Cohen et al. 2008; Santos et al. 2009, 2012). Although the exact reasons are still not clear, these problems may have even lead to a significant discrepancy in studies done by different authors concerning the metallicity-giant planet correlation in giants (see debate in Pasquini et al. 2007; Hekker & Meléndez 2007; Ghezzi et al. 2010a).
To guarantee the maximum degree of homogeneity in the parameter scale used in the present paper, we decided to adopt as baseline the recent study by Mortier et al. (in prep.) where the parameters for 71 evolved stars with planets were derived using the same iron line ionization and excitation equilibrium method used for the study of FGK dwarfs. For the remaining stars, values were compiled from the literature, both from the discovery papers or from other compilations/catalogues (e.g. Luck & Heiter 2007; Soubiran et al. 2010).
Finally, since the mass calibration presented in Torres et al. (2010) is not valid for giant stars, the masses for all stars with log g values lower than ~4.0 were derived using the Padova isochrones (da Silva et al. 2006).
3.2.4. M-dwarfs stars
The derivation of M-dwarf atmospheric parameters is a challenging task. Owing to the difficulty in deriving precise values for the effective temperature and metallicity based on spectral fitting procedures (e.g. Valenti et al. 1998; Woolf & Wallerstein 2005; Bean et al. 2006; Önehag et al. 2012), most determinations of their values are based on calibrations using colors (Bonfils et al. 2005a; Johnson & Apps 2009; Casagrande et al. 2008; Schlaufman & Laughlin 2010; Neves et al. 2012) or spectroscopic indices (e.g. Terrien et al. 2012; Rojas-Ayala et al. 2012; Mann et al. 2013; Neves et al. 2013).
For reasons of consistency, in this paper we used the photometric calibration of Neves et al. (2012) as our baseline to measure the metallicity. In the case where HARPS spectra were available, however, the parameters were derived using the new Neves et al. (2013) spectroscopic calibration. Both Neves et al. (2012) and Neves et al. (2013) calibrations use the same metallicity scale, thus assuring uniformity in the results. The [Fe/H] uncertainties of the two calibrations are assumed to be 0.20 and 0.10 dex, respectively. The metallicity scale used compares very well with other estimates from the literature (see e.g. Neves et al. 2012).
 |
Fig. 7 Comparison of the effective temperatures (left) and metallicities (right) for M dwarfs listed in this catalogue with values obtained in the literature using other calibrations. See text for details. |
Effective temperatures for all the stars in this paper, except for the case of the Kepler stars (see below), were derived using the calibrations based on the V − J, V − H, and V − K colors presented in Casagrande et al. (2008). These are based on the multiple optical infrared technique (MOITE) method which is an optical extension of the IRFM (Blackwell & Shallis 1977). For the cases where HARPS spectra were available, the spectroscopic calibration of Neves et al. (2013) was used instead. This calibration used the Casagrande parameters as baseline, meaning that all values are on the same scale and have the same accuracy. The uncertainty in Teff for the Casagrande et al. (2008) was computed by adding the propagation of the errors of the V and infrared photometry (Skrutskie et al. 2006) taken to calculate the calibrations with the estimated error of the calibration (150 K). We assume an error of 150 K for the Neves et al. (2013) relation.
The stellar masses were derived using the K-band empirical calibration of Delfosse et al. (2000). Mass uncertainties are estimated to be 10%. The surface gravities were derived using Newton’s law from the mass and the radius derived using the empirical relations of Boyajian et al. (2012). We estimate a 10% uncertainty for the radii measurements. The uncertainties of the surface gravity are calculated by propagating the errors of the mass and radius. Parallaxes were taken from SIMBAD except when otherwise mentioned.
Given the differences in the methodologies used to derive stellar parameters for FGK stars (see above) and those used here for M dwarfs, we cannot guarantee that the parameters derived for these latter are on the same scale as those derived for the FGK dwarfs. However, our choice gives us some confidence that the values for their parameters are homogeneous between themselves.
In Fig. 7 we compare the metallicity and effective temperature values derived using the methodology described above with those presented by other authors or derived using other calibrations. As denoted in the insets, different symbols denote different sources: Casagrande et al. (2008, C08), Rojas-Ayala et al. (2012, RA12), Boyajian et al. (2012, BOY12) concerning the effective temperatures, and Bonfils et al. (2005a, B05), Schlaufman & Laughlin (2010, SL10), Önehag et al. (2012, O12), Terrien et al. (2012, T12), and Rojas-Ayala et al. (2012, RA12) concerning metallicities. The results show that in general, and on average, the values used in this catalogue are reasonably well correlated with those derived in the literature (or derived using specific calibrations). The major difference concerns the effective temperatures, for which our values agree very well with the ones derived using the Casagrande et al. (2008) IRFM calibration, but present a significant offset with respect to other literature values, specially for the lower temperature stars. The agreement with the Casagrande et al. determinations come with no surprise, since our temperature scale was calibrated using their values as reference. In Table 5 we list the average offsets between the different sets of data as well as the number of stars used for the comparison shown in Fig. 7. All values denote the differences in the sense literature − this work.
For Kepler M stars, due to the difficulty in gathering either high resolution-spectra or reliable photometry, we opted to take the parameters from the TEPCAT catalogue (Southworth 2012), directly from the discovery papers, or from updated papers from the Kepler team.
3.2.5. General comments and the online catalogue
In Fig. 8 we plot the distribution of effective temperatures, metallicities, surface gravities, and masses that are listed in our catalogue. Besides the whole distribution, we also plot the histogram for the sample of FGK stars with derived baseline stellar parameters, as well as the subsample of FGK stars with planets discovered using the radial velocity method.
Mean offsets and number of stars used to compare the metallicity and temperature scales for M-dwarfs.
 |
Fig. 8 Histograms with the distributions of different stellar parameters in our catalogue. |
The complete table with compiled stellar parameters for planet host stars is available online at https://www.astro.up.pt/resources/sweet-cat. The html version is available for download as an ascii file with all the fields. Improvements on this online table will be done on a continuous basis.
4. Conclusions
In this paper we present new spectroscopic atmospheric parameters and masses for a sample of 48 stars with planets discovered in the context of different radial velocity planet search programs.
These parameters are then included in a new catalogue of stellar parameters for FGK and M stars with planets. The stellar parameters in this catalogue are compiled from literature sources in a way that optimizes the uniformity of the values, making them more suitable for statistical studies of stars with planets. The catalogue will be updated as new planet hosts appear in the literature. We will also continue our effort to determine on a regular basis uniform stellar parameters from high-resolution and high S/N spectra. New parameter values may be added to the catalogue even before a paper is published to present them.
At the time this paper was being published, the parameters listed in the catalogue came from literature sources, both published and to be published soon. Without all these studies the present compilation would not have been possible. Although we do not encourage it, we understand that for simplicity the user may wish to cite only the present paper if using the catalogue in a statistical way. We strongly suggest, however, that in studies of individual stars the original source of the parameters is also cited.
In its present form, the catalogue presents basic parameters as well as a compilation of atmospheric parameters and masses for all planet host stars known. In the future the catalogue may be expanded to add additional stellar parameters of interest, such as the projected rotational velocity (v sini), the rotational period, and the chromospheric activity level (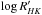 ). Furthermore, we are also considering compiling chemical abundances for elements other than iron as long as uniform sources exist (e.g. Adibekyan et al. 2012b).
). Furthermore, we are also considering compiling chemical abundances for elements other than iron as long as uniform sources exist (e.g. Adibekyan et al. 2012b).
For an updated table we point to http://www.exoplanet.eu
Acknowledgments
We would like to thank Paulo Peixoto for the rapid construction of the web page with the online catalogue. This work has made use of the SIMBAD database. This work was supported by the European Research Council/European Community under the FP7 through Starting Grant agreement number 239953 and by Fundação para a Ciência e a Tecnologia (FCT) in the form of grant reference PTDC/CTE-AST/098528/2008. E.D.M., S.G.S., V.N., and V.Zh.A. also acknowledge the support from FCT in the form of fellowship references SFRH/BPD/76606/2011, SFRH/BPD/47611/2008, SFRH/BD/60688/2009, and SFRH/BPD/70574/2010. G.I. acknowledges financial support from the Spanish Ministry project MICINN AYA2011-29060.
References
- Adibekyan, V. Z., Delgado Mena, E., Sousa, S. G., et al. 2012a, A&A, 547, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012b, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albrecht, S., Winn, J. N., Johnson, J. A., et al. 2012, ApJ, 757, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Ammler-von Eiff, M., Santos, N. C., Sousa, S. G., et al. 2009, A&A, 507, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batalha, N. M., Borucki, W. J., Bryson, S. T., et al. 2011, ApJ, 729, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Baumann, P., Ramírez, I., Meléndez, J., Asplund, M., & Lind, K. 2010, A&A, 519, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bean, J. L., Benedict, G. F., & Endl, M. 2006, ApJ, 653, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Beaugé, C., & Nesvorný, D. 2013, ApJ, 763, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Boisse, I., Pepe, F., Perrier, C., et al. 2012, A&A, 545, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bond, J. C., O’Brien, D. P., & Lauretta, D. S. 2010, ApJ, 715, 1050 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2005a, A&A, 442, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Forveille, T., Delfosse, X., et al. 2005b, A&A, 443, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boss, A. P. 2006, ApJ, 644, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Casagrande, L., Flynn, C., & Bessell, M. 2008, MNRAS, 389, 585 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, J. G., Huang, W., Udalski, A., Gould, A., & Johnson, J. A. 2008, ApJ, 682, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006a, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Da Silva, R., Udry, S., Bouchy, F., et al. 2006b, A&A, 446, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, R. I., & Murray-Clay, R. A. 2013, ApJ, 767, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
- Demory, B.-O., Gillon, M., Seager, S., et al. 2012, ApJ, 751, L28 [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Endl, M., Cochran, W. D., Kürster, M., et al. 2006, ApJ, 649, 436 [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., Laughlin, G., Butler, R. P., et al. 2004 [arXiv:astro-ph/0409107] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Ghezzi, L., Cunha, K., Schuler, S. C., & Smith, V. V. 2010a, ApJ, 725, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Ghezzi, L., Cunha, K., Smith, V. V., & de la Reza, R. 2010b, ApJ, 724, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G. 1997, MNRAS, 285, 403 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Israelian, G., Santos, N. C., et al. 2010, ApJ, 720, 1592 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., & Meléndez, J. 2007, A&A, 475, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, A. W., Marcy, G. W., Bryson, S. T., et al. 2012, ApJS, 201, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2005, ApJ, 626, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Israelian, G., Delgado Mena, E., Santos, N. C., et al. 2009, Nature, 462, 189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Johnson, J. A., & Apps, K. 2009, ApJ, 699, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Butler, R. P., Marcy, G. W., et al. 2007a, ApJ, 670, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Fischer, D. A., Marcy, G. W., et al. 2007b, ApJ, 665, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Kornet, K., Bodenheimer, P., Różyczka, M., & Stepinski, T. F. 2005, A&A, 430, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. 1993, R. Kurucz CD-ROM No. 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory), 13 [Google Scholar]
- Laughlin, G., Bodenheimer, P., & Adams, F. C. 2004, ApJ, 612, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Lovis, C., & Mayor, M. 2007, A&A, 472, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luck, R. E., & Heiter, U. 2007, AJ, 133, 2464 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, A. W., Brewer, J. M., Gaidos, E., Lépine, S., & Hilton, E. J. 2013, AJ, 145, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G., Butler, R. P., Fischer, D., et al. 2005, Prog. Theor. Phys. Suppl., 158, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Marmier, M., Ségransan, D., Udry, S., et al. 2013, A&A, 551, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuo, T., Shibai, H., Ootsubo, T., & Tamura, M. 2007, ApJ, 662, 1282 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., Klahr, H., & Henning, T. 2012, A&A, 541, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Santos, N. C., Sousa, S., et al. 2013a, A&A, 551, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Santos, N. C., Sousa, S. G., et al. 2013b, A&A, submitted [Google Scholar]
- Neves, V., Bonfils, X., Santos, N. C., et al. 2012, A&A, 538, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neves, V., Bonfils, X., Santos, N. C., et al. 2013, A&A, 551, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Önehag, A., Heiter, U., Gustafsson, B., et al. 2012, A&A, 542, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasquini, L., Döllinger, M. P., Weiss, A., et al. 2007, A&A, 473, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paulson, D. B., Saar, S. H., Cochran, W. D., & Hatzes, A. P. 2002, AJ, 124, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Mayor, M., Weber, L., et al. 2000, A&A, 354, 99 [NASA ADS] [Google Scholar]
- Ramírez, I., Asplund, M., Baumann, P., Meléndez, J., & Bensby, T. 2010, A&A, 521, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2012, ApJ, 748, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Santerne, A., Díaz, R. F., Moutou, C., et al. 2012, A&A, 545, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2000a, A&A, 363, 228 [NASA ADS] [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2000b, A&A, 361, 265 [NASA ADS] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2001, A&A, 373, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., Mayor, M., Rebolo, R., & Udry, S. 2003, A&A, 398, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Bouchy, F., Mayor, M., et al. 2004a, A&A, 426, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004b, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., Mayor, M., et al. 2005, A&A, 437, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Pont, F., Melo, C., et al. 2006, A&A, 450, 825 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Lovis, C., Pace, G., Melendez, J., & Naef, D. 2009, A&A, 493, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Lovis, C., Melendez, J., et al. 2012, A&A, 538, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlaufman, K. C., & Laughlin, G. 2010, A&A, 519, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. 1973, Ph.D. Thesis, Austin, Univ. of Texas [Google Scholar]
- Soubiran, C., Le Campion, J.-F., Cayrel de Strobel, G., & Caillo, A. 2010, A&A, 515, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Sousa, S. G., Fernandes, J., Israelian, G., & Santos, N. C. 2010, A&A, 512, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., et al. 2011a, A&A, 526, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Udry, S. 2011b, A&A, 533, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J. 2012, MNRAS, 426, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Sozzetti, A. 2004, MNRAS, 354, 1194 [CrossRef] [Google Scholar]
- Sozzetti, A., Torres, G., Charbonneau, D., et al. 2007, ApJ, 664, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, B. J., & Croxall, K. 2005, MNRAS, 357, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Terrien, R. C., Mahadevan, S., Bender, C. F., et al. 2012, ApJ, 747, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Tinney, C. G., Butler, R. P., Marcy, G. W., et al. 2003, ApJ, 587, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Torres, G., Fischer, D. A., Sozzetti, A., et al. 2012, ApJ, 757, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Triaud, A. H. M. J. 2011, A&A, 534, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsantaki, M., Sousa, S. G., Adibekyan, V. Z., et al. 2013, A&A, 555, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udry, S., Mayor, M., Naef, D., et al. 2000, A&A, 356, 590 [NASA ADS] [Google Scholar]
- Udry, S., & Santos, N. 2007, ARA&A, 45, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia, D., Ikoma, M., Guillot, T., & Nettelmann, N. 2010, A&A, 516, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Valenti, J. A., Piskunov, N., & Johns-Krull, C. M. 1998, ApJ, 498, 851 [Google Scholar]
- Winn, J. N., Fabrycky, D., Albrecht, S., & Johnson, J. A. 2010, ApJ, 718, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Woolf, V. M., & Wallerstein, G. 2005, MNRAS, 356, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Fakhouri, O., Marcy, G. W., et al. 2011, PASP, 123, 412 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Stellar atmospheric parameters and masses for the 48 planet hosts presented in this paper.
Mean offsets and number of stars used to compare the metallicity and temperature scales for M-dwarfs.
All Figures
 |
Fig. 1 Comparison between our baseline stellar parameters with those listed in the Extrasolar Planets Encyclopaedia for the same stars. Only stars with planets detected by radial velocity surveys are included. Green triangles denote the 48 stars whose parameters are presented in this paper. The dotted line represents a 1:1 relation, and the full line a linear fit to the data. Typical error bars are shown on the upper-left part of each panel. |
| In the text | |
 |
Fig. 2 Same as Fig. 1 but for the data from exoplanets.org (Wright et al. 2011). |
| In the text | |
 |
Fig. 3 Same as Fig. 1 but for the data from the NASA Exoplanet Archive. Transiting planets and radial-velocity planets are denoted by crosses and dots, respectively. |
| In the text | |
 |
Fig. 4 Comparison of the effective temperatures derived using the baseline methodology in the catalogue with values derived using the IRFM and interferometry. As in Tsantaki et al. (2013). |
| In the text | |
 |
Fig. 5 Comparison between the masses for FGK dwarfs derived using the Padova isochones and the Torres et al. (2010) calibration. The solid line represents the 1:1 relation and the dotted line a quadratic fit. |
| In the text | |
 |
Fig. 6 Same as Fig. 1 but for the data from the homogeneous part of the TEPCat catalogue (Southworth 2012). In the lower panel, crosses denote surface gravities derived using the transit light curve. |
| In the text | |
 |
Fig. 7 Comparison of the effective temperatures (left) and metallicities (right) for M dwarfs listed in this catalogue with values obtained in the literature using other calibrations. See text for details. |
| In the text | |
 |
Fig. 8 Histograms with the distributions of different stellar parameters in our catalogue. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


