| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201220939 | |
| Published online | 31 July 2013 | |
Competition of rotation and stratification in flux concentrations
1 Nordita, KTH Royal Institute of Technology and Stockholm University, Roslagstullsbacken 23, 10691 Stockholm, Sweden
2 Department of Astronomy, AlbaNova University Center, Stockholm University, 10691 Stockholm, Sweden
3 Department of Mechanical Engineering, Ben-Gurion University of the Negev, POB 653, 84105 Beer-Sheva, Israel
4 Department of Radio Physics, N. I. Lobachevsky State University of Nizhny Novgorod, Russia
Received: 17 December 2012
Accepted: 29 May 2013
Context. In a strongly stratified turbulent layer, a uniform horizontal magnetic field can become unstable and spontaneously form local flux concentrations due to a negative contribution of turbulence to the large-scale (mean-field) magnetic pressure. This mechanism, which is called negative effective magnetic pressure instability (NEMPI), is of interest in connection with dynamo scenarios in which most of the magnetic field resides in the bulk of the convection zone and not at the bottom, as is often assumed. Recent work using mean-field hydromagnetic equations has shown that NEMPI becomes suppressed at rather low rotation rates with Coriolis numbers as low as 0.1.
Aims. Here we extend these earlier investigations by studying the effects of rotation both on the development of NEMPI and on the effective magnetic pressure. We also quantify the kinetic helicity resulting from direct numerical simulations (DNS) with Coriolis numbers and strengths of stratification comparable to values near the solar surface and compare it with earlier work at smaller scale separation ratios. Further, we estimate the expected observable signals of magnetic helicity at the solar surface.
Methods. To calculate the rotational effect on the effective magnetic pressure we consider both DNS and analytical studies using the τ approach. To study the effects of rotation on the development of NEMPI we use both DNS and mean-field calculations of the three-dimensional hydromagnetic equations in a Cartesian domain.
Results. We find that the growth rates of NEMPI from earlier mean-field calculations are well reproduced with DNS, provided the Coriolis number is below 0.06. In that case, kinetic and magnetic helicities are found to be weak and the rotational effect on the effective magnetic pressure is negligible as long as the production of flux concentrations is not inhibited by rotation. For faster rotation, dynamo action becomes possible. However, there is an intermediate range of rotation rates where dynamo action on its own is not yet possible, but the rotational suppression of NEMPI is being alleviated.
Conclusions. Production of magnetic flux concentrations through the suppression of turbulent pressure appears to be possible only in the uppermost layers of the Sun, where the convective turnover time is less than two hours.
Key words: magnetohydrodynamics (MHD) / hydrodynamics / turbulence / Sun: dynamo
© ESO, 2013
1. Introduction
In the Sun, magnetic fields are produced by a large-scale dynamo (see, e.g., Moffatt 1978; Parker 1979; Krause & Rädler 1980; Zeldovich et al. 1983; Ossendrijver 2003; Brandenburg & Subramanian 2005a). Although many details of this process remain subject to debate, it seems relatively clear that rotation enhances the efficiency of the dynamo if the Coriolis parameter is not very large. In the absence of rotation and shear, only small-scale magnetic fields are generated by what is often referred to as small-scale dynamo action (see, e.g., Zeldovich et al. 1990; Brandenburg & Subramanian 2005a). Rotation leads to an α effect (Steenbeck et al. 1966) if there is also stratification in density or turbulent intensity. The α effect can produce mean magnetic field and net magnetic flux.
Stratification leads to yet another effect that does not produce magnetic flux but merely concentrates it locally by what is now referred to as negative effective magnetic pressure instability (NEMPI). Direct numerical simulations (DNS) of Brandenburg et al. (2011a) have shown in surprising detail many aspects of NEMPI that were previously seen in mean-field simulations (MFS) of Brandenburg et al. (2010) and that have been anticipated based on analytical studies for some time (Kleeorin et al. 1989, 1990, 1993, 1996; Kleeorin & Rogachevskii 1994; Rogachevskii & Kleeorin 2007).
The main physics of this effect is connected with the suppression of turbulent pressure by a weak mean magnetic field that is less than the equipartition field. At large Reynolds numbers, the resulting reduction of the turbulent pressure is larger than the added magnetic pressure from the mean magnetic field itself, so that the effective magnetic pressure that accounts for turbulent and nonturbulent contributions becomes negative. In a strongly stratified layer, i.e., a layer in which the density varies much more rapidly with height than the magnetic field does, this leads to an instability that is analogous to Parker’s magnetic buoyancy instability, except that there the magnetic field varies more rapidly with height than the density does. Because the effective magnetic pressure is negative, magnetic structures are negatively buoyant and sink, which has been seen in the DNS of Brandenburg et al. (2011a).
One of the main successes of recent comparative work between DNS and MFS is the demonstration of a high degree of predictive power of MFS. The examples include details regarding the shape and evolution of structures, the dependence of their depth on the magnetic field strength, and the dependence of the growth rate on the scale separation ratio. Recent MFS of Losada et al. (2012; hereafter LBKMR) have shown that in the presence of even just weak rotation the growth rate of NEMPI is significantly reduced. Expressed in terms of the Coriolis number, Co = 2Ω/urmskf, where Ω is the angular velocity, urms is the rms velocity of the turbulence, and kf is the wavenumber of the energy-carrying eddies, the critical value of Co was predicted to be as low as 0.03. Although this value does not preclude the operation of NEMPI in the upper parts of the Sun, where Co is indeed small (about 10-4 at the surface), it does seem surprisingly low, which raises questions regarding the accuracy of MFS in this case. The purpose of the present paper is therefore to compare MFS of LBKMR with DNS of the same setup. It turns out that, while we do confirm the basic prediction of LBKMR, we also resolve an earlier noticed discrepancy in the growth rates between DNS and MFS in the absence of rotation (see the appendix of Kemel et al. 2012a). Indeed, in the particular case of a magnetic Reynolds number of 18 and a scale separation ratio of 30, the formation of structures is unusually strong and the averaged stratification changes significantly to affect the determination of the effective magnetic pressure. However, by restricting the analysis to early times, we obtain coefficients that are not only in better agreement with an earlier formula of Brandenburg et al. (2012a) with a smaller scale separation ratio but also give MFS results that agree better with our new DNS.
The DNS are used primarily to compute the growth rates and magnetic field structures during the saturated state without invoking the mean-field concept. By contrast, the τ approach (Orszag 1970; Pouquet et al. 1976; Kleeorin et al. 1990; Rogachevskii & Kleeorin 2004) is used to determine the dependence of mean-field coefficients on the rotation rate. This can also be done with DNS (Kemel et al. 2012a). Here we apply those calculations to the case with rotation.
We recall that we adopt here an isothermal stratification and an isothermal equation of state. This is done because the effect that we are interested in exists even in this simplest case, where temperature and pressure scale height are constant. Nonisothermal setups have been studied at the mean-field level both with (Käpylä et al. 2012, 2013) and without (Brandenburg et al. 2010) entropy evolution included. In a stably stratified layer, entropy evolution leads to an additional restoring force and hence to internal gravity waves (Brunt-Väisälä oscillations) that stabilize NEMPI (Käpylä et al. 2012). Thus, by using both isothermal stratification and an isothermal equation of state, we recover a situation that is similar to an adiabatic layer, except that the temperature and hence the pressure scale height decrease with height.
The system we are thus dealing with is governed by the combined action of rotation and stratification. In principle, such systems have been studied many times before, for example, to determine the α effect in mean-field dynamo theory (Krause & Rädler 1980; Brandenburg & Subramanian 2005a). The difference to earlier work is the big scale separation ratio, where the domain is up to 30 times larger than the scale of the energy-carrying eddies. As mentioned, stratification and rotation lead to kinetic helicity and an α effect. We therefore also quantify here the amount of kinetic helicity produced and ascertain whether this leads to observable effects in the resulting magnetic structures. We use here the opportunity to explore the feasibility of determining the magnetic helicity spectrum from measurements of the magnetic correlation tensor along a longitudinal strip.
We begin by discussing first the basic equations to determine the effective magnetic pressure from DNS and the τ approach (Sect. 2), compare growth rates for MFS and DNS (Sect. 4), and turn then to the measurement of kinetic and magnetic helicity from surface measurements (Sect. 5) before concluding in Sect. 6.
2. The model
We consider DNS of an isothermally stratified layer (Brandenburg et al. 2011a; Kemel et al. 2012a) and solve the equations for the velocity U, the magnetic vector potential A, and the density ρ in the presence of rotation Ω,
where D/Dt = ∂/∂t + U·∇ is the advective derivative, ν is the kinematic viscosity, η is the magnetic diffusivity due to Spitzer conductivity of the plasma, 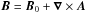 is the magnetic field,
is the magnetic field, 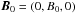 is the imposed uniform field, J = ∇ × B/μ0 is the current density, μ0 is the vacuum permeability,
is the imposed uniform field, J = ∇ × B/μ0 is the current density, μ0 is the vacuum permeability, 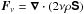 is the viscous force,
is the viscous force, 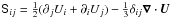 is the traceless rate-of-strain tensor. The angular velocity vector Ω is quantified by its scalar amplitude Ω and colatitude θ, such that Ω = Ω( − sinθ,0,cosθ). As in LBKMR, z corresponds to radius, x to colatitude, and y to azimuth. The forcing function f consists of random, white-in-time, plane, nonpolarized waves with a certain average wavenumber kf. The turbulent rms velocity is approximately independent of z with
is the traceless rate-of-strain tensor. The angular velocity vector Ω is quantified by its scalar amplitude Ω and colatitude θ, such that Ω = Ω( − sinθ,0,cosθ). As in LBKMR, z corresponds to radius, x to colatitude, and y to azimuth. The forcing function f consists of random, white-in-time, plane, nonpolarized waves with a certain average wavenumber kf. The turbulent rms velocity is approximately independent of z with 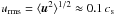 . The gravitational acceleration g = (0,0, − g) is chosen such that k1Hρ = 1, so the density contrast between bottom and top is exp(2π) ≈ 535 in a domain − π ≤ k1z ≤ π. Here,
. The gravitational acceleration g = (0,0, − g) is chosen such that k1Hρ = 1, so the density contrast between bottom and top is exp(2π) ≈ 535 in a domain − π ≤ k1z ≤ π. Here, 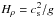 is the density scale height and k1 = 2π/L is the smallest wavenumber that fits into the cubic domain of size L3. In most of our calculations, structures develop whose horizontal wavenumber kx is close to k1. We adopt Cartesian coordinates (x,y,z), with periodic boundary conditions in the x- and y-directions and stress-free, perfectly conducting boundaries at the top and bottom (z = ± Lz/2). In all cases, we use a scale separation ratio kf/k1 of 30, a fluid Reynolds number Re ≡ urms/νkf of 36, and a magnetic Prandtl number PrM = ν/η of 0.5. The magnetic Reynolds number is therefore ReM = PrMRe = 18. The value of B0 is specified in units of the volume-averaged value
is the density scale height and k1 = 2π/L is the smallest wavenumber that fits into the cubic domain of size L3. In most of our calculations, structures develop whose horizontal wavenumber kx is close to k1. We adopt Cartesian coordinates (x,y,z), with periodic boundary conditions in the x- and y-directions and stress-free, perfectly conducting boundaries at the top and bottom (z = ± Lz/2). In all cases, we use a scale separation ratio kf/k1 of 30, a fluid Reynolds number Re ≡ urms/νkf of 36, and a magnetic Prandtl number PrM = ν/η of 0.5. The magnetic Reynolds number is therefore ReM = PrMRe = 18. The value of B0 is specified in units of the volume-averaged value 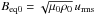 , where ρ0 = ⟨ ρ ⟩ is the volume-averaged density, which is constant in time. As in earlier work, we also define the local equipartition field strength
, where ρ0 = ⟨ ρ ⟩ is the volume-averaged density, which is constant in time. As in earlier work, we also define the local equipartition field strength 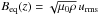 . In our units, k1 = cs = μ0 = ρ0 = 1. In addition to visualizations of the actual magnetic field, we also monitor
. In our units, k1 = cs = μ0 = ρ0 = 1. In addition to visualizations of the actual magnetic field, we also monitor 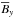 , which is an average over y and a certain time interval Δt. Time is sometimes specified in terms of turbulent-diffusive times
, which is an average over y and a certain time interval Δt. Time is sometimes specified in terms of turbulent-diffusive times 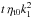 , where ηt0 = urms/3kf is the estimated turbulent diffusivity.
, where ηt0 = urms/3kf is the estimated turbulent diffusivity.
The simulations are performed with the Pencil Code1, which uses sixth-order explicit finite differences in space and a third-order accurate time-stepping method. We use a numerical resolution of 2563 mesh points.
We compare with and extend earlier MFS of LBKMR, where we solve the evolution equations for mean velocity 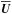 , mean density
, mean density 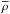 , and mean vector potential
, and mean vector potential 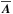 , in the form
, in the form
where 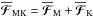 , with
, with ![\begin{equation} \meanrho \, \meanFFFF_{\rm M} = -\half\nab\left[(1-q_{\rm p})\meanBB^2\right] \label{efforce} \end{equation}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq60.png) (7)being the mean-field magnetic pressure force, and
(7)being the mean-field magnetic pressure force, and 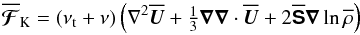 (8)is the total (turbulent plus microscopic) viscous force. Here,
(8)is the total (turbulent plus microscopic) viscous force. Here, 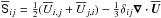 is the traceless rate-of-strain tensor of the mean flow and qp is approximated by (Kemel et al. 2012b)
is the traceless rate-of-strain tensor of the mean flow and qp is approximated by (Kemel et al. 2012b) 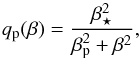 (9)which is only a function of the ratio
(9)which is only a function of the ratio 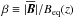 . Here, β⋆ and βp are coefficients that have been determined from previous numerical simulations in the absence of rotation (Brandenburg et al. 2012a). In Eq. (7) we have taken into account that the mean magnetic field is independent of y, so the mean magnetic tension vanishes.
. Here, β⋆ and βp are coefficients that have been determined from previous numerical simulations in the absence of rotation (Brandenburg et al. 2012a). In Eq. (7) we have taken into account that the mean magnetic field is independent of y, so the mean magnetic tension vanishes.
The strength of gravitational stratification is characterized by the nondimensional parameter 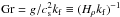 (Brandenburg et al. 2012b). Another important nondimensional parameter is the Coriolis number, Co = 2Ω/urmskf. Alternatively, we normalize the growth rate of the instability by a quantity
(Brandenburg et al. 2012b). Another important nondimensional parameter is the Coriolis number, Co = 2Ω/urmskf. Alternatively, we normalize the growth rate of the instability by a quantity 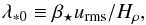 (10)which is motivated by the analytic results of LBKMR and the finding that NEMPI is suppressed when 2Ω ≳ λ∗ 0.
(10)which is motivated by the analytic results of LBKMR and the finding that NEMPI is suppressed when 2Ω ≳ λ∗ 0.
3. Effective magnetic pressure
In this section we study the effect of rotation on the function qp(β). We consider first the results of DNS and turn then to an analytical treatment.
3.1. Numerical results
In the MFS of LBKMR, we assumed that 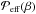 does not change significantly with Co in the range considered. With DNS we can compute
does not change significantly with Co in the range considered. With DNS we can compute 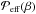 by calculating the combined Reynolds and Maxwell stress for a run with and a run without an imposed magnetic field. This allows us to compute qp(β) using Eq. (17) of Brandenburg et al. (2012a):
by calculating the combined Reynolds and Maxwell stress for a run with and a run without an imposed magnetic field. This allows us to compute qp(β) using Eq. (17) of Brandenburg et al. (2012a): ![\begin{equation} \qp=-2 \left. \left[\meanrho\,(\overline{u_x^2}-\overline{u_{0x}^2}) +\half\overline{\bb^2}-\overline{b_x^2} \right] \right/ \meanBB^2, \end{equation}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq73.png) (11)where the subscripts 0 indicate values obtained from a reference run with B0 = 0. This expression does not take into account small-scale dynamo action, which can produce finite background magnetic fluctuations b0. The effective magnetic pressure is then determined using the equation
(11)where the subscripts 0 indicate values obtained from a reference run with B0 = 0. This expression does not take into account small-scale dynamo action, which can produce finite background magnetic fluctuations b0. The effective magnetic pressure is then determined using the equation ![\hbox{$\Peff(\beta)=\half[1-\qp(\beta)]\beta^2$}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq76.png) . The result is plotted in Fig. 1 for three values of Co during an early time interval when structure formation is still weak, and the background stratification remains unchanged, so that the result is not yet affected. We note that even in the Co = 0.13 case, in which the instability is no longer so prominent, we have to restrict ourselves to early times, since the negative effective magnetic pressure affects the background stratification and hence the pressure changes at later times. The resulting profiles of
. The result is plotted in Fig. 1 for three values of Co during an early time interval when structure formation is still weak, and the background stratification remains unchanged, so that the result is not yet affected. We note that even in the Co = 0.13 case, in which the instability is no longer so prominent, we have to restrict ourselves to early times, since the negative effective magnetic pressure affects the background stratification and hence the pressure changes at later times. The resulting profiles of 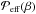 are virtually the same for all three values of Co. We also compare the resulting profiles with those from Eq. (9) for different combinations of β⋆ and βp. It turns out that the curves for different values of Co are best reproduced for β⋆ = 0.44 and βp = 0.058.
are virtually the same for all three values of Co. We also compare the resulting profiles with those from Eq. (9) for different combinations of β⋆ and βp. It turns out that the curves for different values of Co are best reproduced for β⋆ = 0.44 and βp = 0.058.
 |
Fig. 1 Normalized effective magnetic pressure, |
3.2. Theoretical predictions
We now compare the values with theoretical predictions for qp(β). We take into account the feedback of the magnetic field on the turbulent fluid flow. We use a mean-field approach, whereby velocity, pressure, and magnetic field are separated into mean and fluctuating parts. We also assume vanishing mean motion. The strategy of our analytic derivation is to determine the Ω dependencies of the second moments for the velocity 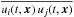 , the magnetic field
, the magnetic field 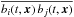 , and the cross-helicity tensor
, and the cross-helicity tensor 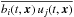 , where b are fluctuations of magnetic field produced by tangling of the large-scale field. To this end we use the equations for fluctuations of velocity and magnetic field in rotating turbulence, which are obtained by subtracting equations for the mean fields from the corresponding equations for the actual (mean plus fluctuating) fields.
, where b are fluctuations of magnetic field produced by tangling of the large-scale field. To this end we use the equations for fluctuations of velocity and magnetic field in rotating turbulence, which are obtained by subtracting equations for the mean fields from the corresponding equations for the actual (mean plus fluctuating) fields.
3.2.1. Governing equations
The equations for the fluctuations of velocity and magnetic fields are given by 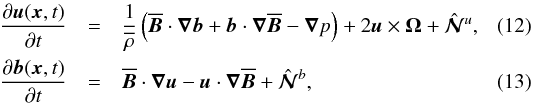 where Eq. (12) is written in a reference frame rotating with constant angular velocity Ω,
where Eq. (12) is written in a reference frame rotating with constant angular velocity Ω, 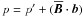 are the fluctuations of total pressure, p′ are the fluctuations of fluid pressure,
are the fluctuations of total pressure, p′ are the fluctuations of fluid pressure, 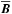 is the mean magnetic field, and
is the mean magnetic field, and 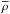 is the mean fluid density. For simplicity we neglect effects of compressibility. The terms
is the mean fluid density. For simplicity we neglect effects of compressibility. The terms 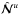 and
and 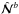 , which include nonlinear and molecular viscous and dissipative terms, are given by
, which include nonlinear and molecular viscous and dissipative terms, are given by 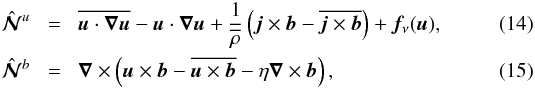 where
where 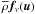 is the molecular viscous force and j = ∇ × b/μ0 is the fluctuating current density. To eliminate the pressure term from the equation of motion (12), we calculate ∇ × (∇ × u). Then we rewrite the obtained equation and Eq. (13) in Fourier space.
is the molecular viscous force and j = ∇ × b/μ0 is the fluctuating current density. To eliminate the pressure term from the equation of motion (12), we calculate ∇ × (∇ × u). Then we rewrite the obtained equation and Eq. (13) in Fourier space.
3.2.2. Two-scale approach
We apply the two-scale approach and express two-point correlation functions in the following form: 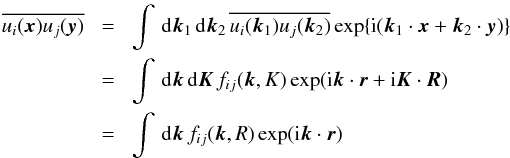 (16)(see, e.g., Roberts & Soward 1975). Here and elsewhere, we drop the common argument t in the correlation functions,
(16)(see, e.g., Roberts & Soward 1975). Here and elsewhere, we drop the common argument t in the correlation functions, 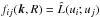 , where
, where 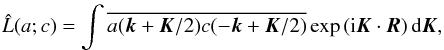 with the new variables R = (x + y)/2, r = x − y, K = k1 + k2, k = (k1 − k2)/2. The variables R and K correspond to the large scales, while r and k correspond to the small scales. This implies that we have assumed that there exists a separation of scales, that is, the turbulent forcing scale ℓf is much smaller than the characteristic scale LB of inhomogeneity of the mean magnetic field.
with the new variables R = (x + y)/2, r = x − y, K = k1 + k2, k = (k1 − k2)/2. The variables R and K correspond to the large scales, while r and k correspond to the small scales. This implies that we have assumed that there exists a separation of scales, that is, the turbulent forcing scale ℓf is much smaller than the characteristic scale LB of inhomogeneity of the mean magnetic field.
3.2.3. Equations for the second moments
We derive equations for the following correlation functions: 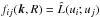 ,
, 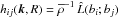 , and
, and 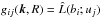 . The equations for these correlation functions are given by
. The equations for these correlation functions are given by
Hereafter we have omitted the R-argument in the correlation functions and neglected terms ~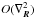 , and εijn is the fully antisymmetric Levi-Civita tensor. In Eqs. (17)–(19), the terms
, and εijn is the fully antisymmetric Levi-Civita tensor. In Eqs. (17)–(19), the terms 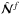 ,
, 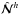 , and
, and 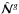 are determined by the third moments appearing due to the nonlinear terms; the source terms
are determined by the third moments appearing due to the nonlinear terms; the source terms 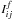 ,
, 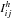 , and
, and 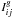 , which contain the large-scale spatial derivatives of the mean magnetic and velocity fields, are given by Eqs. (A3)–(A6) in Rogachevskii & Kleeorin (2004). These terms determine turbulent magnetic diffusion and effects of nonuniform mean velocity on the mean electromotive force.
, which contain the large-scale spatial derivatives of the mean magnetic and velocity fields, are given by Eqs. (A3)–(A6) in Rogachevskii & Kleeorin (2004). These terms determine turbulent magnetic diffusion and effects of nonuniform mean velocity on the mean electromotive force.
For the derivation of Eqs. (17)–(19) we use an approach that is similar to that applied in Rogachevskii & Kleeorin (2004). We take into account that in Eq. (19) the terms with tensors that are symmetric in i and j do not contribute to the mean electromotive force because ℰm = εmji gij. We split all tensors into nonhelical, hij, and helical, 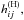 parts. The helical part of the tensor of magnetic fluctuations
parts. The helical part of the tensor of magnetic fluctuations 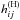 depends on the magnetic helicity, and the equation for
depends on the magnetic helicity, and the equation for 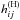 follows from magnetic helicity conservation arguments (see, e.g., Kleeorin & Rogachevskii 1999; Brandenburg & Subramanian 2005a, and references therein).
follows from magnetic helicity conservation arguments (see, e.g., Kleeorin & Rogachevskii 1999; Brandenburg & Subramanian 2005a, and references therein).
3.2.4. The τ-approach
The second-moment Eqs. (17)–(19) include the first-order spatial differential operators applied to the third-order moments M(III). To close the system, we express the set of the third-order terms 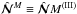 through the lower moments M(II). We use the spectral τ approximation, which postulates that the deviations of the third-moment terms,
through the lower moments M(II). We use the spectral τ approximation, which postulates that the deviations of the third-moment terms, 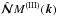 , from the contributions to these terms afforded by the background turbulence,
, from the contributions to these terms afforded by the background turbulence, 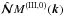 , are expressed through similar deviations of the second moments:
, are expressed through similar deviations of the second moments: 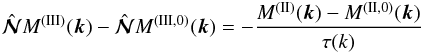 (20)(Orszag 1970; Pouquet et al. 1976; Kleeorin et al. 1990; Rogachevskii & Kleeorin 2004), where τ(k) is the scale-dependent relaxation time, which can be identified with the correlation time of the turbulent velocity field for large Reynolds numbers. The quantities with the superscript (0) correspond to the background turbulence (see below). We apply the spectral τ approximation only for the nonhelical part hij of the tensor of magnetic fluctuations. A justification for the τ approximation in different situations has been offered through numerical simulations and analytical studies (see, e.g., Brandenburg et al. 2004; Brandenburg & Subramanian 2005b, 2007; Rogachevskii et al. 2011).
(20)(Orszag 1970; Pouquet et al. 1976; Kleeorin et al. 1990; Rogachevskii & Kleeorin 2004), where τ(k) is the scale-dependent relaxation time, which can be identified with the correlation time of the turbulent velocity field for large Reynolds numbers. The quantities with the superscript (0) correspond to the background turbulence (see below). We apply the spectral τ approximation only for the nonhelical part hij of the tensor of magnetic fluctuations. A justification for the τ approximation in different situations has been offered through numerical simulations and analytical studies (see, e.g., Brandenburg et al. 2004; Brandenburg & Subramanian 2005b, 2007; Rogachevskii et al. 2011).
3.2.5. Solution of equations for the second moments
We solve Eqs. (17)–(19) neglecting the sources 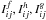 with the large-scale spatial derivatives. The terms with the large-scale spatial derivatives, which determine the turbulent magnetic diffusion, can be taken into account by perturbations. We subtract from Eqs. (17)–(19) the corresponding equations written for the background turbulence using the spectral τ approximation. We assume that the characteristic time of variation of the second moments is substantially larger than the correlation time τ(k) for all turbulence scales. This allows us to get a stationary solution for the equations for the second-order moments, M(II). Thus, we arrive at the following steady-state solution of Eqs. (17)–(19):
with the large-scale spatial derivatives. The terms with the large-scale spatial derivatives, which determine the turbulent magnetic diffusion, can be taken into account by perturbations. We subtract from Eqs. (17)–(19) the corresponding equations written for the background turbulence using the spectral τ approximation. We assume that the characteristic time of variation of the second moments is substantially larger than the correlation time τ(k) for all turbulence scales. This allows us to get a stationary solution for the equations for the second-order moments, M(II). Thus, we arrive at the following steady-state solution of Eqs. (17)–(19):
![\begin{eqnarray} && f_{ij}({\bm k}) = L_{ijmn}^{-1} \left[f_{mn}^{(0)}({\bm k}) + i \tau ({\bm k} \cdot \overline{\bm B}) \Phi_{mn}({\bm k})\right] , \label{B17}\\ && h_{ij}({\bm k}) = - i \tau({\bm k} \cdot \overline{\bm B}) \Phi_{ij}({\bm k}), \label{B18}\\ && g_{ij}({\bm k}) = i \tau ({\bm k} \cdot \overline{\bm B}) D_{im}^{-1} \left[f_{mj}({\bm k}) - h_{mj}({\bm k})\right]. \label{B19} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq141.png) We have assumed that there is no small-scale dynamo in the background turbulence. Here, the operator
We have assumed that there is no small-scale dynamo in the background turbulence. Here, the operator 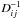 is the inverse of the operator
is the inverse of the operator 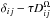 (Rädler et al. 2003) and the operator
(Rädler et al. 2003) and the operator 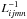 is the inverse of the operator
is the inverse of the operator 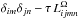 (Elperin et al. 2005). These operators are given by
(Elperin et al. 2005). These operators are given by ![\begin{eqnarray} && D_{ij}^{-1} = \chi(\psi) \, (\delta_{ij} + \psi \, \varepsilon_{ijm} \, \hat k_m + \psi^2 \, k_{ij}) \nonumber\\ && \phantom{D_{ij}^{-1}} = \delta_{ij} + \psi \, \varepsilon_{ijm} \, \hat k_m - \psi^2 \, P_{ij} + O(\psi^3), \label{B12}\\ && L_{ijmn}^{-1}({\bm \Omega}) = \half [B_1 \, \delta_{im} \delta_{jn} + B_2 \, k_{ijmn} + B_3 \, (\varepsilon_{imp} \delta_{jn} \nonumber\\ && \phantom{L_{ijmn}^{-1}({\bm \Omega}) =} + \varepsilon_{jnp} \delta_{im}) \hat k_p + B_4 \, (\delta_{im} k_{jn} + \delta_{jn} k_{im}) \nonumber\\ && \phantom{L_{ijmn}^{-1}({\bm \Omega}) =} + B_5 \, \varepsilon_{ipm} \varepsilon_{jqn} k_{pq} + B_6 \, (\varepsilon_{imp} k_{jpn} + \varepsilon_{jnp} k_{ipm}) ] \nonumber\\ && \phantom{L_{ijmn}^{-1}({\bm \Omega})} = \delta_{im} \delta_{jn} + \psi \, (\varepsilon_{imp} \delta_{jn} + \varepsilon_{jnp} \delta_{im}) \hat k_p - \psi^2 (\delta_{im} P_{jn} \nonumber\\ && \phantom{L_{ijmn}^{-1}({\bm \Omega}) =} + \delta_{jn} P_{im} - 2 \varepsilon_{imp} \varepsilon_{jqn} k_{pq}) + O(\psi^3), \label{B14} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq146.png)
where 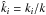 , χ(ψ) = 1/(1 + ψ2), ψ = 2τ(k) (k·Ω)/k, B1 = 1 + χ(2ψ), B2 = B1 + 2 − 4χ(ψ), B3 = 2ψ χ(2ψ), B4 = 2χ(ψ) − B1, B5 = 2 − B1 and B6 = 2ψ [χ(ψ) − χ(2ψ)], Pij(k) = δij − kikj/k2, δij is the Kronecker tensor.
, χ(ψ) = 1/(1 + ψ2), ψ = 2τ(k) (k·Ω)/k, B1 = 1 + χ(2ψ), B2 = B1 + 2 − 4χ(ψ), B3 = 2ψ χ(2ψ), B4 = 2χ(ψ) − B1, B5 = 2 − B1 and B6 = 2ψ [χ(ψ) − χ(2ψ)], Pij(k) = δij − kikj/k2, δij is the Kronecker tensor.
We use the following model for the homogeneous and isotropic background turbulence: 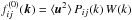 , where W(k) = E(k)/8πk2, the energy spectrum is
, where W(k) = E(k)/8πk2, the energy spectrum is 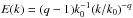 , k0 = 1/ℓf, and the length ℓf is the maximum scale of turbulent motions. The turbulent correlation time is τ(k) = C τ0 (k/k0)− μ, where the coefficient C = (q − 1 + μ)/(q − 1). This value of the coefficient C corresponds to the standard form of the turbulent diffusion coefficient in the isotropic case, i.e., ηT = ⟨ u2 ⟩ ∫τ(k) E(k) dk = τ0 ⟨ u2 ⟩ /3. Here the time
, k0 = 1/ℓf, and the length ℓf is the maximum scale of turbulent motions. The turbulent correlation time is τ(k) = C τ0 (k/k0)− μ, where the coefficient C = (q − 1 + μ)/(q − 1). This value of the coefficient C corresponds to the standard form of the turbulent diffusion coefficient in the isotropic case, i.e., ηT = ⟨ u2 ⟩ ∫τ(k) E(k) dk = τ0 ⟨ u2 ⟩ /3. Here the time 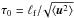 and
and 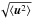 is the characteristic turbulent velocity in the scale ℓf. For the Kolmogorov’s type background turbulence (i.e., for a turbulence with a constant energy flux over the spectrum), the exponent μ = q − 1 and the coefficient C = 2. In the case of a turbulence with a scale-independent correlation time, the exponent μ = 0 and the coefficient C = 1. Motions in the background turbulence are assumed to be nonhelical.
is the characteristic turbulent velocity in the scale ℓf. For the Kolmogorov’s type background turbulence (i.e., for a turbulence with a constant energy flux over the spectrum), the exponent μ = q − 1 and the coefficient C = 2. In the case of a turbulence with a scale-independent correlation time, the exponent μ = 0 and the coefficient C = 1. Motions in the background turbulence are assumed to be nonhelical.
where Ψ = 2τ2(k·cA)2, 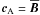 /
/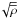 , and we have taken into account that
, and we have taken into account that 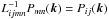 . After the integration in k space, we obtain the magnetic tensor hij in physical space:
. After the integration in k space, we obtain the magnetic tensor hij in physical space: 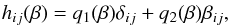 (28)where
(28)where 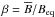 , and the functions q1(β) and q2(β) are given in Appendix A. We consider the case in which angular velocity is perpendicular to the mean magnetic field. The results can easily be generalized to the case of the arbitrary angle between the angular velocity and the mean magnetic field.
, and the functions q1(β) and q2(β) are given in Appendix A. We consider the case in which angular velocity is perpendicular to the mean magnetic field. The results can easily be generalized to the case of the arbitrary angle between the angular velocity and the mean magnetic field.
The contribution of turbulence to the mean-field magnetic pressure is given by the function qp(β) = [q1(β) − q2(β)]/β2: ![\begin{eqnarray} q_{\rm p}(\beta) &=& {1 \over 12 \beta^2} \Big[A_1^{(0)}(0) - A_1^{(0)}(4\beta) - A_2^{(0)}(4\beta) \nonumber\\ && -~ 2(\Omega \tau_0)^2 \Big(A_1^{(2)}(0) - 4C_1^{(2)}(0) - 10 A_1^{(2)}(4\beta) \nonumber\\ && +~ 40 C_1^{(2)}(4\beta) + {9 \over 2 \pi} \left[\bar A_1(16\beta^2) -4 \bar C_1(16\beta^2) \right] \Big) \Big], \label{B25} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq183.png) (29)where the functions
(29)where the functions 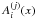 ,
, 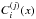 ,
, 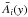 ,
, 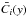 , and their asymptotics are given in Appendix A. Following earlier work (Brandenburg et al. 2012a), we now define a magnetic Reynolds number based on the scale ℓf = 2π/kf, which is related to the ReM defined earlier via Rm = 2πReM. For
, and their asymptotics are given in Appendix A. Following earlier work (Brandenburg et al. 2012a), we now define a magnetic Reynolds number based on the scale ℓf = 2π/kf, which is related to the ReM defined earlier via Rm = 2πReM. For 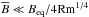 , the function qp(β) is given by
, the function qp(β) is given by 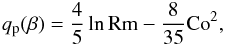 (30)and for
(30)and for 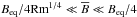 the function qp(β) is given by
the function qp(β) is given by 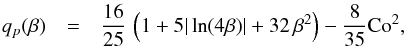 (31)where Co = 2Ωτ0. This shows that for the values of Co of interest (Co ≤ 0.06), the correction to qp is negligible (below 10-3), which is in agreement with the numerical findings in Fig. 1.
(31)where Co = 2Ωτ0. This shows that for the values of Co of interest (Co ≤ 0.06), the correction to qp is negligible (below 10-3), which is in agreement with the numerical findings in Fig. 1.
4. Coriolis effects of NEMPI in DNS and MFS
4.1. DNS and comparison with MFS
 |
Fig. 2 Dependence of λ/λ∗ 0 on 2Ω/λ∗ 0 for DNS (red dashed line), compared with MFS (i) where qp0 = 20 and βp = 0.167 (black solid line), and MFS (ii) where qp0 = 32 and βp = 0.058 (blue dash-dotted line). In this case no growth was found for Co ≥ 0.03. In all cases we have B0/Beq0 = 0.05. |
 |
Fig. 3 yt-averaged |
We have performed DNS for different values of Co and calculated the growth rate λ; see Fig. 2. It turns out that λ shows a decline with increasing values of Co that is similar to the one seen in the MFS of LBKMR, who used qp0 = 20 and βp = 0.167 (corresponding to β⋆ = 0.75). While some growth is still possible for Co = 0.13 and 0.66, the field begins to attain systematic variations in the z direction that are more similar to those in a dynamo. In that case, we would have to deal with a coupled system, and a direct comparison with the NEMPI growth rate would not be possible. We return to this issue later in Sect. 5.1.
In Fig. 2 we compare the growth rate with the MFS of LBKMR, who used qp0 = 20 and βp = 0.167 (corresponding to β⋆ = 0.75). This set of parameters is based on a fit by Kemel et al. (2012a) for kf/k1 = 30 and ReM = 18. We note that the growth rates for the MFS are about three times larger than those of the DNS. As explained in the introduction, this might be caused by an inaccurate estimate of the mean-field coefficients for these particular values of kf/k1 and ReM. Indeed, according to Eq. (22) of Brandenburg et al. (2012a), who used kf/k1 = 5, these parameters should be qp0 = 32 and βp = 0.058 (corresponding to β⋆ = 0.33) for ReM = 18. This assumes that these parameters are independent of the value of kf, which is not true either; see Kemel et al. (2012a). To clarify this question, we now perform 3D MFS with this new set of parameters. Those results are also shown in Fig. 2. It turns out that with these parameters the resulting growth rates are indeed much closer to those of the DNS, suggesting that the former set of mean-field coefficients might indeed have been inaccurate. As alluded to in the introduction, this could be because NEMPI is very strong for kf/k1 = 30 and leads to inhomogeneous magnetic fields. For these fields, the usual determination of mean-field coefficients, as used by Brandenburg et al. (2012a), is no longer valid because for inhomogeneous magnetic fields there would be additional terms in the parametrization for the mean Reynolds-Maxwell stress (cf. Kemel et al. 2012c). We note that for this comparison we have kept the value of λ∗ 0 in the normalization of both axes unchanged. However, if we accept that the correct value of β⋆ is not 0.75, but 0.33, the graphs for DNS and MFS (ii) would almost coincide with that for DNS (i).
 |
Fig. 4 Evolution of B1/Beq for runs of which three are shown in Fig. 3. The three horizontal lines correspond to the approximate values of B1/Beq in the three rows of Fig. 3. |
 |
Fig. 5 By at the periphery of the computational domain for Co = 0.006 (left), 0.03 (middle), and 0.06 (right) at the same times as in Fig. 3. The x,y,z coordinates are indicated in the middle frame. We note the strong surface effect for Co = 0.03 in the last time frame. |
In Fig. 3 we show the yt-averaged  for Co = 0.006, 0.03, and 0.06 at different times. When comparing results for different rotation rates, one should take into account that the growth rates become strongly reduced. Indeed, in the last row of Fig. 3 we chose the times such that the amplitude of NEMPI is comparable for Co = 0.006 and 0.03. However, for Co = 0.06 we ran much longer and the amplitude of NEMPI is here even larger; see Fig. 4, where we show B1/Beq, which is the normalized magnetic field strength for the horizontal wavenumber k = k1 in the top layers with 2 ≤ k1z ≤ 3. It is clear that the formation of structures through NEMPI remains more strongly confined to the uppermost layers as we increase the value of Co. Even for Co = 0.13, there is still noticeable growth of structures, which is different from what is seen in MFS; see Fig. 2.
for Co = 0.006, 0.03, and 0.06 at different times. When comparing results for different rotation rates, one should take into account that the growth rates become strongly reduced. Indeed, in the last row of Fig. 3 we chose the times such that the amplitude of NEMPI is comparable for Co = 0.006 and 0.03. However, for Co = 0.06 we ran much longer and the amplitude of NEMPI is here even larger; see Fig. 4, where we show B1/Beq, which is the normalized magnetic field strength for the horizontal wavenumber k = k1 in the top layers with 2 ≤ k1z ≤ 3. It is clear that the formation of structures through NEMPI remains more strongly confined to the uppermost layers as we increase the value of Co. Even for Co = 0.13, there is still noticeable growth of structures, which is different from what is seen in MFS; see Fig. 2.
These figures show the generation of structures that begin to sink subsequently. However, for Co = 0.03 and larger, this sinking is much less prominent. Instead, the structures remain confined to the surface layers, which is seen more clearly in visualizations of By at the periphery of the computational domain for Co = 0.03; see Fig. 5, which is for approximately the same times as Fig. 3.
 |
Fig. 6 Results of MFS of LBKMR showing By at the periphery of the computational domain for Co = + 0.03 in the LBKMR case (left) and with the new set of parameters (right) at the same time. (The range in By/B0 shown here is larger than that shown in LBKMR.) |
 |
Fig. 7 By at the periphery of the computational domain for Co = 0.006 and θ = 45° (upper row) and 90° (lower row), at three different times (from left to right). The x,y,z coordinates are indicated in the middle frame. |
To our surprise, the large-scale structures still remain independent of the y-direction, which is clearly at variance with results of the corresponding MFS. In Fig. 6 we reproduce a result similar to that of LBKMR for Co = ± 0.03. Even at other angles such as θ = 45° and 90°, no variation in the y-direction is seen; see Fig. 7. The reason for this discrepancy between DNS and the corresponding MFS is not yet understood. Furthermore, the confinement of structures to the surface layers, which is seen so clearly in DNS, seems to be absent in the corresponding MFS.
4.2. Comparison of the 2D and 3D data of LBKMR
The apparent lack of y dependence of the large-scale magnetic field in the DNS shows that this contribution to the magnetic field is essentially two-dimensional. In the lower panel of Fig. 5 of LBKMR, a comparison between 2D and 3D MFS was shown for Co ≈ 0.01 as a function of latitude. At the pole, the normalized growth rates were λ/λ∗ 0 ≈ 0.07 and 0.14 for 2D and 3D MFS, respectively. This difference is smaller for smaller values of Co, but it increases with increasing values of Co; see Fig. 8. We note that the 2D result in this figure supersedes that of Fig. 3 of LBKMR, here λ was determined from the amplification of the total magnetic field (which includes the imposed field) rather than from the deviations of the magnetic field from the imposed one. This resulted in a four times smaller estimate of λ. Furthermore, the critical value of Co, above which NEMPI shuts off, is now delayed by a factor of about 2–3.
 |
Fig. 8 Dependence of λ/λ∗ 0 on 2Ω/λ∗ 0 in the 3D and 2D cases for θ = 0° (corresponding to the pole). |
The plot in Fig. 8 has been done for the more optimistic set of mean-field parameters (qp0 = 20 and βp = 0.167), but the essential conclusions that the growth rates in 2D and 3D are similar should not depend on this. The remaining differences between DNS and MFS regarding the lack of y dependence of the mean field and the confinement of structures to the surface layers might be related to the absence of mean-field transport coefficients other than qp, ηt, and νt. By and large, however, the agreement between DNS and MFS is remarkably good in that the predicted decline of NEMPI at rather modest rotation rates is fully confirmed by DNS.
5. Kinetic and magnetic helicity
By adding rotation to our strongly stratified simulations, we automatically also produce kinetic helicity. In this section we quantify this, compare the helicity with earlier work, and address the question whether this might lead to observable effects. All results presented in this section are based on time series, with error bars being estimated as the largest departure from any one-third of the full time series.
5.1. Helicity production
In turbulence, the presence of rotation and stratification gives rise to kinetic helicity and an α effect (Krause & Rädler 1980; Brandenburg et al. 2013). As a measure of kinetic helicity, we determine the normalized helicity as 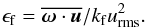 (32)In Fig. 9 we compare our present runs at kf/k1 = 30 with those of Brandenburg et al. (2012b) at kf/k1 = 5 showing ϵf versus Gr Co. For our present runs (red filled symbols), kinetic helicity is clearly very small, which is a consequence of the small value of Co. Compared with earlier runs at kf/k1 = 5, which gave ϵf ≈ 2 Gr Co, the present ones show about twice as much helicity. Interestingly, for rapid rotation the relative kinetic helicity declines when the product Gr Co is larger than about 0.5. The maximum value of ϵf that can be reached is about 0.3. In a fully periodic domain, dynamo action would be possible when ϵf > (kf/k1)-1, which is 0.2 in this case. However, because of stratification and boundaries, the onset is delayed and no dynamo action has been found in the simulations of Brandenburg et al. (2012b). However, in the present case, dynamo action is possible for ϵf > 1/30, which leads to a Beltrami-like magnetic field with variation in the z direction. Dynamo action is demonstrated in the absence of an imposed field, which leads to slightly smaller values of ϵf for the same value of Gr Co (see blue symbols in Fig. 9). The case Co = 0.33 is close to marginal and the field is slowly decaying, which is in agreement with the expected position of the marginal line.
(32)In Fig. 9 we compare our present runs at kf/k1 = 30 with those of Brandenburg et al. (2012b) at kf/k1 = 5 showing ϵf versus Gr Co. For our present runs (red filled symbols), kinetic helicity is clearly very small, which is a consequence of the small value of Co. Compared with earlier runs at kf/k1 = 5, which gave ϵf ≈ 2 Gr Co, the present ones show about twice as much helicity. Interestingly, for rapid rotation the relative kinetic helicity declines when the product Gr Co is larger than about 0.5. The maximum value of ϵf that can be reached is about 0.3. In a fully periodic domain, dynamo action would be possible when ϵf > (kf/k1)-1, which is 0.2 in this case. However, because of stratification and boundaries, the onset is delayed and no dynamo action has been found in the simulations of Brandenburg et al. (2012b). However, in the present case, dynamo action is possible for ϵf > 1/30, which leads to a Beltrami-like magnetic field with variation in the z direction. Dynamo action is demonstrated in the absence of an imposed field, which leads to slightly smaller values of ϵf for the same value of Gr Co (see blue symbols in Fig. 9). The case Co = 0.33 is close to marginal and the field is slowly decaying, which is in agreement with the expected position of the marginal line.
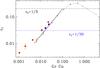 |
Fig. 9 Relative kinetic helicity spectrum as a function of Gr Co for Gr = 0.03 with Co = 0.03, 0.06, 0.13, 0.49, and 0.66 (red and blue symbols) compared with results from earlier simulations of Brandenburg et al. (2012b) for Gr = 0.16 (small dots connected by a dotted line). The solid line corresponds to ϵf = 2Gr Co. The two horizontal dash-dotted lines indicate the values of |
 |
Fig. 10 Visualization of Bx and By for the run with Co = 0.5 showing dynamo action. We note the clear signature of a Beltrami field showing variation in the z direction. |
In Fig. 10 we show visualizations of Bx and By for a run with Co = 0.5 showing dynamo action. We note the approximate phase shift of 90° between Bx and By, which has been seen in earlier simulations of α2-type dynamo action from forced turbulence (Brandenburg 2001). As alluded to in Sect. 4.1, the possibility of dynamo action might be responsible for the continued growth found in DNS for Co ≥ 0.13. Visualizations of the yt-averaged 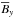 for Co = 0.13 and 0.31 show that structures with variation in the x direction still emerge in front of a new component that varies strongly in the z direction and that becomes stronger as the value of Co is increased.
for Co = 0.13 and 0.31 show that structures with variation in the x direction still emerge in front of a new component that varies strongly in the z direction and that becomes stronger as the value of Co is increased.
Our results for Co = 0.13 and 0.31 might be examples of a dynamo coupled to NEMPI. Such coupled systems are expected to have an overall enhancement of growth. This possibility, which is not included in the present mean-field model, has recently been demonstrated in spherical geometry (Jabbari et al. 2013) by coupling an α2 dynamo to NEMPI. Looking at Fig. 2, we conclude that for Co ≥ 0.13 the coupled system with NEMPI and dynamo instability is excited in a case where the dynamo alone would not be excited and that the growth rate begins to be larger than that of NEMPI alone. Obviously, more work in that direction is necessary.
 |
Fig. 11 Comparison of yt-averaged |
5.2. Surface diagnostics
As a consequence of the production of kinetic helicity, the magnetic field should also be helical. However, since magnetic helicity is conserved, and was zero initially, it should remain zero, at least on a dynamical time scale (Berger 1984). This condition can be obeyed if the magnetic field is bi-helical, i.e., with opposite signs of magnetic helicity at large and small wavenumbers (Seehafer 1996; Ji 1999). We now ask whether signatures of this could in principle be detected at the solar surface. To address this question, we use our simulation at intermediate rotation speed with Co = 0.03, where magnetic flux concentrations are well developed at the surface of the domain, and compare the helicity with a larger value of 0.13.
Measuring magnetic helicity is notoriously difficult because it involves the magnetic vector potential, which is gauge dependent. However, under the assumption of homogeneity and isotropy, the Fourier transform of the magnetic correlation tensor is 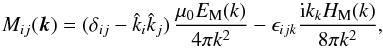 (33)where
(33)where 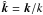 is the unit vector of k and EM(k) and HM(k) are magnetic energy and magnetic helicity spectra, which obey the realizability condition 2μ0EM(k) ≥ k | HM(k) |. Here, the factor 2 in front of EM(k) is just a consequence of the factor 1/2 in the definition of energy. Matthaeus et al. (1982) used the solar wind data from Voyager II to determine HM(k) from the in situ measurements of B, while Brandenburg et al. (2011b) applied the technique to measuring HM(k) at high heliographic latitudes, where HM(k) is finite and turned out to be bi-helical. We now adopt the same method using Fourier transforms in the y direction. In the Sun, this corresponds to measuring B along a 2π ring at a fixed polar latitude, where one might have a chance to observe the full circumference at the same time. In Fig. 12 we show the result for three values of Co.
is the unit vector of k and EM(k) and HM(k) are magnetic energy and magnetic helicity spectra, which obey the realizability condition 2μ0EM(k) ≥ k | HM(k) |. Here, the factor 2 in front of EM(k) is just a consequence of the factor 1/2 in the definition of energy. Matthaeus et al. (1982) used the solar wind data from Voyager II to determine HM(k) from the in situ measurements of B, while Brandenburg et al. (2011b) applied the technique to measuring HM(k) at high heliographic latitudes, where HM(k) is finite and turned out to be bi-helical. We now adopt the same method using Fourier transforms in the y direction. In the Sun, this corresponds to measuring B along a 2π ring at a fixed polar latitude, where one might have a chance to observe the full circumference at the same time. In Fig. 12 we show the result for three values of Co.
 |
Fig. 12 Normalized magnetic helicity spectra for different values of the Coriolis number, Co. In all panels, the same range is shown, but for Co = 0.66 the normalized helicity exceeds this range and reaches − 0.05. |
It turns out that HM(k) is compatible with zero for our intermediate value of Co. For faster rotation (Co = 0.13), HM(k) is negative at large wavenumbers (k ≫ kf) and positive (but still compatible with zero within error bars) at intermediate wavenumbers (0.15 < k/kf < 0.6). For k/kf < 0.15, the magnetic helicity is again negative. However, the error bars are large and rotation is already so fast that structure formation via NEMPI is impossible. It is therefore unclear whether meaningful conclusions can be drawn from our results.
In the northern hemisphere of the Sun, a bi-helical spectrum is expected where magnetic helicity is negative on all scales except the largest ones, where the α effect operates. This sense is reversed in the solar wind far from the Sun (Brandenburg et al. 2011b). This has also been seen in simulations of magnetic ejecta from a dynamo-active sphere (Warnecke et al. 2011), which may be explained by a diffusive magnetic helicity transport (Warnecke et al. 2012).
5.3. Energy and helicity spectra
 |
Fig. 13 Kinetic and magnetic energy and helicity spectra computed from the full 3D data set for Co = 0.03. Positive (negative) values of spectral helicity are indicated with filled (open) symbols. We note the enhancement of spectral power at the smallest wavenumber of the domain, k1. |
To put the above considerations in relation to the actual helicity content, we now compare with the magnetic and kinetic energy and helicity spectra computed from the fully 3D data set; see Fig. 13. The magnetic and kinetic helicity spectra are normalized by k/2 and 1/2k, respectively, so that one can estimate how much the absolute values of these spectra are below their maximum possible values given by the corresponding realizability conditions, | HM | k/2 ≤ EM and | HK | /2k ≤ EK, respectively.
The spectra show that, while the velocity and magnetic fields have significant helicity only at the largest scale, they remain clearly below their maximum possible values. At large scales (small k), both helicities are negative (indicated by open symbols), but the magnetic helicity is predominantly positive at wavenumbers slightly below kf. This is consistent with Fig. 12, which also shows positive values, although only in the case of faster rotation (Co = 0.13). Below the forcing scale, both energy spectra show a k3/2 spectrum, which is shallower than the white noise spectrum (k2) and similar to what has been seen in helically driven dynamos (Brandenburg 2001). We also note the uprise of magnetic and kinetic power at the smallest wavenumber (k = k1), which is again similar to helically driven dynamos. However, it is here not as strong as in the dynamo case.
6. Conclusions and discussion
The present work has confirmed the rather stringent restrictions of LBKMR, showing that NEMPI is already suppressed for rather weak rotation (Co ≳ 0.03). This demonstrates the predictive power of those earlier MFS. On the other hand, it also shows that the consideration of the mere existence of a negative effective magnetic pressure is not sufficient. We knew already that sufficiently strong stratification and scale separation are two important necessary conditions. In this sense, the existence of NEMPI might be a more fragile phenomenon that the existence of a negative magnetic pressure, which is fairly robust and can be verified even in absence of stratification (Brandenburg et al. 2010). For the rather small Coriolis numbers considered here, no measurable change of qp was seen in the simulations, which is in agreement with our theory predicting that the change is of the order Co2.
Applied to the Sun with Ω = 2 × 10-6 s-1, the strong sensitivity of the instability to weak rotation implies that NEMPI can only play a role in the uppermost layers, where the correlation time is shorter than Co/2Ω ≈ 2 hours. Although this value might change with a changing degree of stratification, this would be surprising as it would exclude even the lower parts of the supergranulation layer, where τ is of the order of one day. On the other hand, we have to keep in mind that our conclusions, which are based on isothermal models, should be taken with care. It would therefore be useful to extend the present studies to polytropic layers where the scale height varies with depth. We also note that weak rotation (Co = 0.03) enhances the surface appearance. At the same time, as we argued in Sect. 4.1, the sinking of structures becomes less prominent, which suggests that they might remain confined to the surface layers. However, preliminary MFS do not indicate a significant dependence of the eigenfunction on Co for values below 0.1. Our interpretation, if correct, would therefore need to be a result of nonlinearity.
If we were to apply NEMPI to the formation of active regions in the Sun, we should keep in mind that the scale of structures would be 6–8 pressure scale heights (Kemel et al. 2012a). At the depth where the turnover time is about two hours, we estimate the rms velocity to be about 500 m/s, so the scale height would be about 3 Mm, corresponding to a NEMPI scale of at least 20 Mm. This might still be of interest for explaining plage regions in the Sun. Clearly, more work using realistic models would be required for making more conclusive statements.
Regarding the production of kinetic helicity and the possible detection of a magnetic helicity spectrum, our results suggest that the relative magnetic helicity cannot be expected to be more than about 0.01. This is a consequence of correspondingly low values of kinetic helicity. We find that the normalized kinetic helicity is given by ϵf ≈ 2Gr Co. For the Sun, we expect Gr = (kfHρ)-1 ≈ 0.16, which agrees with what is used in our simulations; thus there is not much room for more optimistic estimates. In this connection we should note that in Kemel et al. (2012a) the value of kfHρ (= Gr-1) was estimated based on stellar mixing length theory, using ℓmix = αmixHp for the mixing length with αmix ≈ 1.6 being an empirical parameter. For isentropic stratification, the pressure scale height Hp is related to Hρ via γHp ≈ Hρ. With kf = 2π/ℓmix we obtain kfHρ = 2π γ/αmix ≈ 2π, so Gr = (kfHρ)-1 ≈ 0.16. We note here that, owing to a mistake, we underestimated the value of kfHρ by a factor of 2.6. This factor also has an enhancing effect on the growth rate of NEMPI. The correct value should then be larger and would now be clearly faster than the turbulent–diffusive rate. Furthermore, as we have shown here, at the point where NEMPI begins to be suppressed by rotation, effects related to dynamo action reinforce the concentration of flux, even though the dynamo alone would not yet be excited. In this sense, the stringent restrictions of LBKMR from MFS appear now less stringent in DNS. It might be hoped that this new feature can eventually be reproduced by MFS, such as those of Jabbari et al. (2013) that take the α effect into account.
Acknowledgments
We thank Koen Kemel for helpful comments concerning the influence of magnetic structure formation on the measurement of qp0 and βp in DNS and an anonymous referee for useful suggestions that have led to improvements in the presentation and a more thorough analysis. This work was supported in part by the European Research Council under the AstroDyn Research Project No. 227952, by the Swedish Research Council under the project grants 621-2011-5076 and 2012-5797 (IRL, AB), by EU COST Action MP0806, by the European Research Council under the Atmospheric Research Project No. 227915, and by a grant from the Government of the Russian Federation under contract No. 11.G34.31.0048 (NK, IR). We acknowledge the allocation of computing resources provided by the Swedish National Allocations Committee at the Center for Parallel Computers at the Royal Institute of Technology in Stockholm and the National Supercomputer Centers in Linköping, the High Performance Computing Center North in Umeå, and the Nordic High Performance Computing Center in Reykjavik.
References
- Berger, M. 1984, Geophys. Astrophys. Fluid Dyn., 30, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A. 2001, ApJ, 550, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005a, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005b, A&A, 439, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2007, Astron. Nachr., 328, 507 [Google Scholar]
- Brandenburg, A., Käpylä, P., & Mohammed, A. 2004, Phys. Fluids, 16, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2010, Astron. Nachr., 331, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Kemel, K., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2011a, ApJ, 740, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Subramanian, K., Balogh, A., & Goldstein, M. L. 2011b, ApJ, 734, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Kemel, K., Kleeorin, N., & Rogachevskii, I. 2012a, ApJ, 749, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Rädler, K.-H., & Kemel, K. 2012b, A&A, 539, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A., Gressel, O., Käpylä, P. J., et al. 2013, ApJ, 762, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Elperin, T., Golubev, I., Kleeorin, N., & Rogachevskii, I. 2005, Phys. Rev. E, 71, 036302 [NASA ADS] [CrossRef] [Google Scholar]
- Jabbari, S., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2013, A&A, in press [arXiv:1302.5841] [Google Scholar]
- Ji, H. 1999, Phys. Rev. Lett., 83, 3198 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J., Brandenburg, A., Kleeorin, N., Mantere, M. J., & Rogachevskii, I. 2012, MNRAS, 422, 2465 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J., Brandenburg, A., Kleeorin, N., Mantere, M. J., & Rogachevskii, I. 2013, Solar and Astrophysical Dynamos and Magnetic Activity, eds. A. G. Kosovichev, E. M. de Gouveia Dal Pino, & Y. Yan, Proc. IAU Symp., 294 [arXiv:1211.2962] [Google Scholar]
- Kemel, K., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2012a, Solar Phys., DOI:10.1007/s11207-012-0031-8 [Google Scholar]
- Kemel, K., Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2012b, Astron. Nachr., 333, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Kemel, K., Brandenburg, A., Kleeorin, N., & Rogachevskii, I. 2012c, Phys. Scripta [arXiv:1208.0517] [Google Scholar]
- Kleeorin, N., & Rogachevskii, I. 1994, Phys. Rev. E, 50, 2716 [NASA ADS] [CrossRef] [Google Scholar]
- Kleeorin, N., & Rogachevskii, I. 1999, Phys. Rev. E, 59, 6724 [NASA ADS] [CrossRef] [Google Scholar]
- Kleeorin, N., Mond, M., & Rogachevskii, I. 1993, Phys. Fluids B, 5, 4128 [NASA ADS] [CrossRef] [Google Scholar]
- Kleeorin, N., Mond, M., & Rogachevskii, I. 1996, A&A, 307, 293 [NASA ADS] [Google Scholar]
- Kleeorin, N. I., Rogachevskii, I. V., & Ruzmaikin, A. A. 1989, Sov. Astron. Lett., 15, 274 [NASA ADS] [Google Scholar]
- Kleeorin, N. I., Rogachevskii, I. V., & Ruzmaikin, A. A. 1990, Sov. Phys. JETP, 70, 878 [Google Scholar]
- Krause, F., & Rädler, K.-H. 1980, Mean-field magnetohydrodynamics and dynamo theory (Oxford: Pergamon Press) [Google Scholar]
- Losada, I. R., Brandenburg, A., Kleeorin, N., Mitra, D., & Rogachevskii, I. 2012, A&A, 548, A49 (LBKMR) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthaeus, W. H., Goldstein, M. L., & Smith, C. 1982, Phys. Rev. Lett., 48, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Moffatt, H. K. 1978, Magnetic field generation in electrically conducting fluids (Cambridge: Cambridge University Press) [Google Scholar]
- Orszag, S. A. 1970, J. Fluid Mech., 41, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Ossendrijver, M. 2003, A&A Rev., 11, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1979, Cosmical magnetic fields (New York: Oxford University Press) [Google Scholar]
- Pouquet, A., Frisch, U., & Léorat, J. 1976, J. Fluid Mech., 77, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Rädler, K.-H., Kleeorin, N., & Rogachevskii, I. 2003, Geophys. Astrophys. Fluid Dyn., 97, 249 [Google Scholar]
- Roberts, P. H., & Soward, A. M. 1975, Astron. Nachr., 296, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Rogachevskii, I., & Kleeorin, N. 2004, Phys. Rev. E, 70, 046310 [NASA ADS] [CrossRef] [Google Scholar]
- Rogachevskii, I., & Kleeorin, N. 2007, Phys. Rev. E, 76, 056307 [NASA ADS] [CrossRef] [Google Scholar]
- Rogachevskii, I., Kleeorin, N., Käpylä, P. J., & Brandenburg, A. 2011, Phys. Rev. E, 84, 056314 [NASA ADS] [CrossRef] [Google Scholar]
- Seehafer, N. 1996, Phys. Rev. E, 53, 1283 [Google Scholar]
- Steenbeck, M., Krause, F., & Rädler, K.-H. 1966, Z. Naturforsch., 21a, 369 [Google Scholar]
- Warnecke, J., Brandenburg, A., & Mitra, D. 2011, A&A, 534, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warnecke, J., Brandenburg, A., & Mitra, D. 2012, J. Spa. Weather Spa. Clim., 2, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeldovich, Ya. B., Ruzmaikin, A. A., & Sokoloff, D. D. 1983, Magnetic fields in astrophysics (New York: Gordon & Breach) [Google Scholar]
- Zeldovich, Ya. B., Ruzmaikin, A. A., & Sokoloff, D. D. 1990, The Almighty Chance (Singapore: Word Scientific Publ) [Google Scholar]
Appendix A: The identities used in Sect. 3.2 for the integration in k-space
To integrate over the angles in k-space in Sect. 3.2, we used the following identities (Rogachevskii & Kleeorin 2004, 2007):
![\appendix \setcounter{section}{1} \begin{eqnarray} &&\bar K_{ij} = \int {k_{ij} \sin \theta \over 1 + a \cos^{2} \theta} \,{\rm d}\theta \,{\rm d}\varphi = \bar A_{1} \delta_{ij} + \bar A_{2} \beta_{ij} , \label{C22} \\[1mm] && \bar K_{ijmn} = \int {k_{ijmn} \sin \theta \over 1 + a \cos^{2} \theta} \,{\rm d}\theta \,{\rm d}\varphi = \bar C_{1} (\delta_{ij} \delta_{mn} + \delta_{im} \delta_{jn} \nonumber \\[1mm] && \phantom{\bar K_{ijmn} =} + \delta_{in} \delta_{jm}) + \bar C_{2} \beta_{ijmn} + \bar C_{3} (\delta_{ij} \beta_{mn} + \delta_{im} \beta_{jn} + \delta_{in} \beta_{jm} \nonumber \\[1mm] &&\phantom{\bar K_{ijmn} =} + \delta_{jm} \beta_{in} + \delta_{jn} \beta_{im} + \delta_{mn} \beta_{ij}) , \label{C24}\\[1mm] &&\bar H_{ijmn}(a) = \int {k_{ijmn} \sin \theta \over (1 + a \cos^{2} \theta)^{2} } \,{\rm d}\theta \,{\rm d}\varphi \nonumber \\[1mm] &&\phantom{\bar H_{ijmn}(a)} = - \biggl( {\partial \over \partial b } \int {k_{ijmn} \sin \theta \over b + a \cos^{2} \theta} \,{\rm d}\theta \,{\rm d}\varphi \biggr)_{b=1} \nonumber \\[1mm] &&\phantom{\bar H_{ijmn}(a)}= \bar K_{ijmn}(a) + a {\partial \over \partial a} \bar K_{ijmn}(a) , \label{C23} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq286.png) where
where 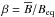 ,
, 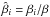 ,
, 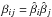 , and
, and ![\appendix \setcounter{section}{1} \begin{eqnarray} &&\bar A_{1} = {2 \pi \over a} \biggl[(a + 1) {\arctan (\sqrt{a}) \over \sqrt{a}} - 1 \biggr] , \nonumber\\[1mm] &&\bar A_{2} = - {2 \pi \over a} \biggl[(a + 3) {\arctan (\sqrt{a}) \over \sqrt{a}} - 3 \biggr] , \nonumber\\[1mm] &&\bar C_{1} = {\pi \over 2a^{2}} \biggl[(a + 1)^{2} {\arctan (\sqrt{a}) \over \sqrt{a}} - {5 a \over 3} - 1 \biggr] , \nonumber\\[1mm] &&\bar C_{2} = \bar A_{2} - 7 \bar A_{1} + 35 \bar C_{1} , \nonumber\\[1mm] &&\bar C_{3} = \bar A_{1} - 5 \bar C_{1} . \label{P22} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq290.png) (A.4)In the case of a ≪ 1 these functions are given by
(A.4)In the case of a ≪ 1 these functions are given by ![\appendix \setcounter{section}{1} \begin{eqnarray*} &&\bar A_{1}(a) \sim {4 \pi \over 3} \biggl(1 - {1 \over 5} a \biggr) , \quad \bar A_{2}(a) \sim - {8 \pi \over 15} a , \\[1mm] &&\bar C_{1}(a) \sim {4 \pi \over 15} \biggl(1 - {1 \over 7} a \biggr) \cdot \end{eqnarray*}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq292.png) In the case of a ≫ 1 these functions are given by
In the case of a ≫ 1 these functions are given by ![\appendix \setcounter{section}{1} \begin{eqnarray*} &&\bar A_{1}(a) \sim {\pi^{2} \over \sqrt{a}} - {4 \pi \over a} , \quad \bar A_{2}(a) \sim - {\pi^{2} \over \sqrt{a}} + {8 \pi \over a} , \\[1mm] &&\bar C_{1}(a) \sim {\pi^{2} \over 4 \sqrt{a}} - {4 \pi \over 3 a} \cdot \end{eqnarray*}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq294.png) The functions
The functions 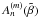 are given by
are given by ![\appendix \setcounter{section}{1} \begin{eqnarray} && A_{n}^{(0)}(\tilde \beta) = {3 \tilde \beta^{2} \over \pi} \int_{\tilde \beta}^{\tilde \beta{\rm Rm}^{1/4}} {\bar A_{n}(X^{2}) \over X^{3}} \,{\rm d} X , \label{X26}\\[1mm] && A_{n}^{(2)}(\tilde \beta) = {3 \tilde \beta^{6} \over \pi} \int_{\tilde \beta}^{\tilde \beta{\rm Rm}^{1/4}} {\bar A_{n}(X^{2}) \over X^{7}} \,{\rm d} X , \label{X27}\\[1mm] && \int_0^1 \bar A_{n}(a(\bar \tau)) \bar \tau^m \, {\rm d}\bar \tau = {2 \pi \over 3} A_{n}^{(m)}(\tilde \beta) , \label{X28} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq296.png)
and similarly for 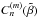 , where
, where ![\hbox{$a = [\tilde \beta u_{0} k \tau(k) / 2]^{2}$}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq298.png) ,
, 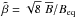 , and
, and 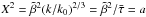 . The explicit form of the functions
. The explicit form of the functions 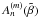 and
and 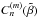 for m = 0; 2 are given by
for m = 0; 2 are given by ![\appendix \setcounter{section}{1} \begin{eqnarray} A_{1}^{(0)}(\tilde \beta) &=& {1 \over 5} \biggl[2 + 2 {\arctan \tilde \beta \over \tilde \beta^3} (3 + 5 \tilde \beta^{2}) - {6 \over \tilde \beta^{2}} - \tilde \beta^{2} \ln {\rm Rm} \nonumber \\[1mm] & & - 2 \tilde \beta^{2} \ln \biggl({1 + \tilde \beta^{2} \over 1 + \tilde \beta^{2} \sqrt{\rm Rm}}\biggr) \biggr] , \label{X40}\\[1mm] A_{2}^{(0)}(\tilde \beta) &=& {2 \over 5} \biggl[2 - {\arctan \tilde \beta \over \tilde \beta^3} (9 + 5 \tilde \beta^{2}) + {9 \over \tilde \beta^{2}} - \tilde \beta^{2} \ln {\rm Rm} \nonumber \\[1mm] & & - 2 \tilde \beta^{2} \ln \biggl({1 + \tilde \beta^{2} \over 1 + \tilde \beta^{2} \sqrt{\rm Rm}}\biggr) \biggr] , \label{X41}\\[1mm] A_{1}^{(2)}(\tilde \beta) &=& {2 \over 63} \biggl[1 + 3 {\arctan \tilde \beta \over \tilde \beta^3} (7 + 9 \tilde \beta^{2}) - {21 \over \tilde \beta^{2}} - {3 \tilde \beta^{2} \over 2} M(\tilde \beta) \biggr] , \label{X42}~~~~~~~~~~~~\\[1mm] C_{1}^{(2)}(\tilde \beta) &=& {1 \over 33} \biggl[{2 \over 21} + {\arctan \tilde \beta \over \tilde \beta^5} \biggl({99 \over 14}\tilde \beta^{4} + 11 \tilde \beta^{2} + {9 \over 2}\biggl) \nonumber ~~~~~~~~~~~~\\[1mm] & & - {19 \over 2\tilde \beta^{2}} - {9 \over 2\tilde \beta^{4}} - {\tilde \beta^{2} \over 7} M(\tilde \beta) \biggr] , \end{eqnarray}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq302.png) where
where 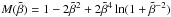 . Here we have taken into account that Rm ≫ 1. For
. Here we have taken into account that Rm ≫ 1. For 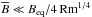 , these functions are given by
, these functions are given by ![\appendix \setcounter{section}{1} \begin{eqnarray*} A_{1}^{(0)}(\tilde \beta) &\sim& 2 - {1 \over 5} \tilde \beta^{2} \ln {\rm Rm}, \\ A_{2}^{(0)}(\tilde \beta) &\sim& - {2 \over 5} \tilde \beta^{2} \biggl[\ln {\rm Rm} + {2 \over 15}\biggr] , \\ A_{1}^{(2)}(\tilde \beta) &\sim& {2 \over 3}\biggl(1 - {3 \over 10} \tilde \beta^{2}\biggr) , \quad A_{2}^{(2)}(\tilde \beta) \sim - {2 \over 5} \tilde \beta^{2} , \\ C_{1}^{(2)}(\tilde \beta) &\sim& {2 \over 15} \biggl(1 - {3 \over 14} \tilde \beta^{2}\biggr) \cdot \end{eqnarray*}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq306.png) For
For 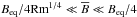 , these functions are given by
, these functions are given by ![\appendix \setcounter{section}{1} \begin{eqnarray*} A_{1}^{(0)}(\tilde \beta) &\sim& 2 + {2 \over 5} \tilde \beta^{2} \biggl[2 \ln \tilde \beta - {16 \over 15} + {4 \over 7} \tilde \beta^{2} \biggr] , \\ A_{2}^{(0)}(\tilde \beta) &\sim& {2 \over 5} \tilde \beta^{2} \biggl[4 \ln \tilde \beta - {2 \over 15} - 3 \tilde \beta^{2} \biggr] \cdot \end{eqnarray*}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq307.png) Other functions in this case have the same asymptotics as in the case of
Other functions in this case have the same asymptotics as in the case of 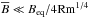 . For B ≫ Beq/4, these functions are given by
. For B ≫ Beq/4, these functions are given by 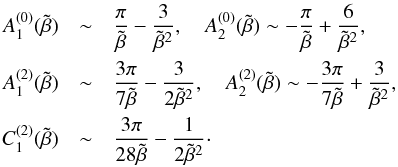 The functions q1(β) and q2(β) are given by
The functions q1(β) and q2(β) are given by
All Figures
 |
Fig. 1 Normalized effective magnetic pressure, |
| In the text | |
 |
Fig. 2 Dependence of λ/λ∗ 0 on 2Ω/λ∗ 0 for DNS (red dashed line), compared with MFS (i) where qp0 = 20 and βp = 0.167 (black solid line), and MFS (ii) where qp0 = 32 and βp = 0.058 (blue dash-dotted line). In this case no growth was found for Co ≥ 0.03. In all cases we have B0/Beq0 = 0.05. |
| In the text | |
 |
Fig. 3 yt-averaged |
| In the text | |
 |
Fig. 4 Evolution of B1/Beq for runs of which three are shown in Fig. 3. The three horizontal lines correspond to the approximate values of B1/Beq in the three rows of Fig. 3. |
| In the text | |
 |
Fig. 5 By at the periphery of the computational domain for Co = 0.006 (left), 0.03 (middle), and 0.06 (right) at the same times as in Fig. 3. The x,y,z coordinates are indicated in the middle frame. We note the strong surface effect for Co = 0.03 in the last time frame. |
| In the text | |
 |
Fig. 6 Results of MFS of LBKMR showing By at the periphery of the computational domain for Co = + 0.03 in the LBKMR case (left) and with the new set of parameters (right) at the same time. (The range in By/B0 shown here is larger than that shown in LBKMR.) |
| In the text | |
 |
Fig. 7 By at the periphery of the computational domain for Co = 0.006 and θ = 45° (upper row) and 90° (lower row), at three different times (from left to right). The x,y,z coordinates are indicated in the middle frame. |
| In the text | |
 |
Fig. 8 Dependence of λ/λ∗ 0 on 2Ω/λ∗ 0 in the 3D and 2D cases for θ = 0° (corresponding to the pole). |
| In the text | |
 |
Fig. 9 Relative kinetic helicity spectrum as a function of Gr Co for Gr = 0.03 with Co = 0.03, 0.06, 0.13, 0.49, and 0.66 (red and blue symbols) compared with results from earlier simulations of Brandenburg et al. (2012b) for Gr = 0.16 (small dots connected by a dotted line). The solid line corresponds to ϵf = 2Gr Co. The two horizontal dash-dotted lines indicate the values of |
| In the text | |
 |
Fig. 10 Visualization of Bx and By for the run with Co = 0.5 showing dynamo action. We note the clear signature of a Beltrami field showing variation in the z direction. |
| In the text | |
 |
Fig. 11 Comparison of yt-averaged |
| In the text | |
 |
Fig. 12 Normalized magnetic helicity spectra for different values of the Coriolis number, Co. In all panels, the same range is shown, but for Co = 0.66 the normalized helicity exceeds this range and reaches − 0.05. |
| In the text | |
 |
Fig. 13 Kinetic and magnetic energy and helicity spectra computed from the full 3D data set for Co = 0.03. Positive (negative) values of spectral helicity are indicated with filled (open) symbols. We note the enhancement of spectral power at the smallest wavenumber of the domain, k1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray} &&{\DD\UU\over\DD t}=-2\OO\times\UU -\cs^2\nab\ln\rho+{1\over\rho}\JJ\times\BB+\ff+\grav+\FF_\nu,\\[2mm] &&{\partial\AAA\over\partial t}=\UU\times\BB+\eta\nabla^2\AAA,\\[2mm] &&{\partial\rho\over\partial t}=-\nab\cdot\rho\UU, \end{eqnarray}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq12.png)
![\begin{eqnarray} \label{dUmean} &&{\partial\meanUU\over\partial t}=-\meanUU\cdot\nab\meanUU-2\OO\times\meanUU -\cs^2\nab\ln\meanrho+\grav+\meanFFFF_{\rm MK}, \\[1mm] &&{\partial\meanAA\over\partial t}=\meanUU\times\meanBB-(\etat+\eta)\meanJJ, \\[1mm] &&{\partial\meanrho\over\partial t}=-\meanUU\cdot\nab\meanrho -\meanrho\nab\cdot\meanUU, \end{eqnarray}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq58.png)
![\begin{eqnarray} && {\partial f_{ij}({\bm k}) \over \partial t} = i({\bm k} \cdot \overline{\bm B}) \Phi_{ij} + L_{ijmn}^{\Omega} f_{mn} + I^f_{ij} + \hatNN_{ij}^f , \label{B6} \\[1mm] && {\partial h_{ij}({\bm k}) \over \partial t} = - i({\bm k}\cdot \overline{\bm B}) \Phi_{ij} + I^h_{ij} + \hatNN_{ij}^h , \label{B7} \\[1mm] && {\partial g_{ij}({\bm k}) \over \partial t} = i({\bm k} \cdot \overline{\bm B}) [f_{ij}({\bm k}) - h_{ij}({\bm k}) - h_{ij}^{(H)}] \nonumber\\ && \qquad\qquad +~ D_{jm}^{\Omega}({\bm k}_2)g_{im}({\bm k}) + I^g_{ij} + \hatNN_{ij}^g , \label{B8} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq113.png)
![\begin{eqnarray*} &&\Phi_{ij}({\bm k}) = \meanrho^{-1}\, [g_{ij}({\bm k}) - g_{ji}(-{\bm k})], \\[1mm] &&D_{ij}^{\Omega}({\bm k}) = 2 \varepsilon_{ijm} \Omega_n k_{mn}, \\[1mm] &&L_{ijmn}^{\Omega} = D_{im}^{\Omega}({\bm k}_1) \, \delta_{jn} + D_{jn}^{\Omega}({\bm k}_2) \, \delta_{im} . \end{eqnarray*}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq114.png)
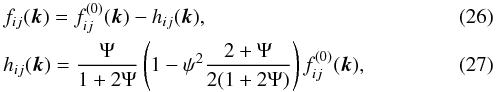
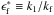
![\appendix \setcounter{section}{1} \begin{eqnarray} && q_1(\beta) = {1 \over 12} \Big[A_1^{(0)}(0) - A_1^{(0)}(4\beta) - \half A_2^{(0)}(4\beta) \nonumber\\ && \phantom{q_1(\beta) =} - (\Omega \tau_0)^2 \Big(A_1^{(2)}(0) - 2C_1^{(2)}(0) - 10 A_1^{(2)}(4\beta) \nonumber\\[0.5mm] && \phantom{q_1(\beta) =} + 20 C_1^{(2)}(4\beta) + {9 \over 2 \pi} \left[\bar A_1(16\beta^2) -2 \bar C_1(16\beta^2) \right] \Big) \Big], \label{B23}~~~~~~~~~~~\\[0.5mm] && q_2(\beta) = {1 \over 12} \Big[\half A_2^{(0)}(4\beta) + (\Omega \tau_0)^2 \Big(A_1^{(2)}(0) - 6C_1^{(2)}(0) \nonumber\\[0.5mm] && \phantom{q_2(\beta) =} - 10 A_1^{(2)}(4\beta) + 60 C_1^{(2)}(4\beta) + {9 \over 2 \pi} \big[\bar A_1(16\beta^2) \nonumber\\[0.5mm] &&\phantom{q_2(\beta) =} -6 \bar C_1(16\beta^2) \big] \Big) \Big]. \label{B24} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20939-12/aa20939-12-eq311.png)