| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201220913 | |
| Published online | 31 July 2013 | |
Induced rotational excitation of the fluoromethylidynium 12CF+ and 13CF+ through collision with helium
1 Laboratoire de Spectroscopie Atomique Moléculaire et Applications, Faculté des Sciences, Université Tunis el Manar, 2092 Tunis, Tunisie
e-mail: yosra-aji@hotmail.fr
2 Université Paris-Est, Laboratoire Modélisation et Simulation Multi-Échelle, MSME UMR 8208 CNRS, 5 Bd Descartes, 77454 Marne-La-Vallée, France
Received: 14 December 2012
Accepted: 11 June 2013
Aims. The present paper focuses on the calculation of the collision rate coefficients for rotational excitation of the 12CF+ and its isotopologue 13CF+ by He for temperature ranging from 10 to 300 K.
Methods. A two-dimentional (2D) potential energy surface (PES) of the CF+(X1Σ+)-He(1S) system is calculated at the ab initio coupled cluster with single, double, and perturbative triple excitation level of theory with the aug-cc-pV5Z basis set. The basis set superposition errors were taken into account in our computation. Dynamical calculations of state-to-state rotational integral cross sections of the CF+ by collision with He were performed using the close-coupling method.
Results. The PES presents a global minimum of ~212 cm-1 below the CF+-He dissociation limit. Collisional cross sections among the first 11 rotational levels of CF+ were calculated for total energies up to 1500 cm-1. Downward rate coefficients between the rotational levels were calculated for temperature ranging from 10 to 300 K. A propensity toward an even parity of ΔJ is observed.
Key words: molecular data / molecular processes / ISM: molecules
© ESO, 2013
1. Introduction
It was reported that the Herschel, SOFIA, and ALMA observatories gave high spectral resolution observations on molecular emission in the submillimeter and far-infrared domains. These observations, supplemented by molecular modeling, are powerful tools to investigate the physical and chemical conditions of astrophysical objects. Most of these observations require accurate knowledge about collisional processes that occur in the interstellar medium (ISM). To achieve the best precision required in astrophysics, a fully quantum mechanical treatment of the collision dynamics is recommended, in addition to experimental investigations. Many experimental and theoretical studies of the collision-inducing rotational energy transfer have been performed in the last four decades. Particularly, the collisional rate coefficients with the most abundant interstellar species, H, H2, and He, have been shown to be of great astrophysical importance (Wernli et al. 2006; Kłos et al. 2007; Lique & Spielfiedel 2007; Guillon et al. 2008; Buffa et al. 2009; Lique et al. 2009, 2010; Dubernet et al. 2009; Najar et al. 2009; Sarrasin et al. 2010).
The significant abundance of H2 in the ISM implies that this molecule is the primary collision partner for any other species. The major gas component in ISM, H2(j = 0), is electronically equivalent to the He atom. Astronomers usually estimated the rate coefficients for the collisions with para-H2(j = 0) from those obtained by collision with He (Schöier et al. 2005). The studies reported by Wernli et al. 2006, Lique et al. (2008), and Dumouchel et al. (2010) indicated that the use of the scaled factor of 1.4 to deduce the rate coefficients of the collision with para-H2(j = 0) from those corresponding to the collision with He provides the correct magnitude order. This was showen to be unlikely for charged species. For instance, for the HCO+ system, the last approximation can be used to estimate the collisional rates with H2 from those with He, but the factor scaling will be between 2 and 4 (Monteiro 1985).
The results of the study on the chemistry of fluorine, which was reported by Neufeld et al. (2005), predicted that CF+ ion is the second most abundant fluorine-bearing molecule in the ISM after HF; it’s formation from the reaction of HF with C+ (the dominant reservoir of gas-phase carbon) follows these two equations:  The first detection of CF+ in the photo-dissociation regions (PDR) was toward the Orion Bar (Neufeld et al. 2006), showing spatially extended emission in the 1–0, 2–1, and 3–2 rotational transitions. The observations of Nagy et al. (2012) extended the observed CF+ transitions in this region up to the 5–4 transition and the line intensity is consistent with the previously observed transitions.
The first detection of CF+ in the photo-dissociation regions (PDR) was toward the Orion Bar (Neufeld et al. 2006), showing spatially extended emission in the 1–0, 2–1, and 3–2 rotational transitions. The observations of Nagy et al. (2012) extended the observed CF+ transitions in this region up to the 5–4 transition and the line intensity is consistent with the previously observed transitions.
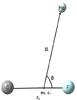 |
Fig. 1 Definition of the body-fixed Jacobi coordinates system for the CF+-He complex. |
The C-containing species were also demonstrated to be of great astrophysical significance because they may provide information on the 13C/12C ratio. To improve the knowledge on the fluorine interstellar chemistry, Cazzoli et al. (2010) recorded accurate rest frequencies for future radioastronomical observations. In their studies, they improved the accuracy of the CF+ spectroscopic parameters available in the literature. They also provided the spectroscopic parameters of 13CF+ for the first time. Recently, they extended their previous work using THz measurements to provide accurate and reliable higher frequencies (Cazzoli et al. 2012). Their measurements enabled the prediction of rotational transitions with a good accuracy, up to 2.0–2.5 THz.
From a spectroscopic point of view, the most recent studies of CF+ did not consider the hyperfine structure because the experiments were not able to resolve the hyperfine components (Cazzoli et al. 2010). Recently, Guzmán et al. (2012a) detected the J = 1–0 and J = 2–1 rotational lines of CF+ with a high signal-to-noise ratio toward the PDR and core positions in the Horsehead. In contrast to other mm lines in the Horsehead, the CF+J = 1–0 (102.587 GHz) line is double-peaked. They applied a high-level quantum chemical calculation to determine the hyperfine splitting and pointed out a constant of 7.6 × 10-6 cm-1 as a value for the fluorine spin rotation (Guzmán et al. 2012b). This low computed value of the spin rotation constant confirmed the nonobservations of the hyperfine splitting in the experiments performed by Cazzoli et al. (2010).
In the present work, we focus on the study of the rotational (de-)excitation rate coefficients of 12CF+ and 13CF+ by collision with He using quantum mechanical calculations. A new accurate ab initio two-dimentional potential energy surface (PES) is provided. The computation of pure rotational cross sections is performed using the close-coupling (CC) method for rotational levels below J = 10 and for total energy up to 1500 cm-1. The collisional rate coefficients are obtained by averaging these cross sections over a Maxwell-Boltzmann velocity distribution at low temperatures ranging from 10 to 300 K. In our calculations, the hyperfine structure is neglected.
This paper is organized as follows: Sect. 2 describes the ab initio calculations of the PES. The dynamical calculation results are presented and discussed in Sect. 3. A comparison between 12CF+-He and 13CF+-He collisional data is included in the last subsection. Concluding remarks are given in Sect. 4.
2. Potential energy surface
In this work the vibrational excitation is expected to be negligible because we are interested in studying low-temperature collisions. As a consequence, the collision partners may be considered as rigid. To perform our calculations, we describe the van der Waals CF+-He system by Jacobi coordinates (r,R,θ). As shown in Fig. 1, r is the internuclear distance of CF+ frozen at its experimental equilibrium geometry r = re = 2.1812 bohr (Kawaguchi & Hirota 1985), R is the distance between the He atom and the mass center (m.c.) of CF+, and θ is the angle between the two distance vectors. The collinear CF+...He corresponds to θ = 0°.
The interaction energy of the CF+-He system is calculated using the coupled cluster with single, double, and perturbative triple excitation (CCSD(T)) method (Hampel et al. 1992) as it is implemented in the MOLPRO molecular package (Werner et al. 2002) in connection with the aug-cc-pV5Z basis set of Dunning (1989). The use of the monoconfigurational CCSD(T) approach is verified because the weight of the dominant configuration (1a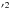 2a
2a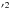 3a
3a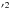 4a
4a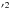 5a′21a
5a′21a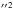 6a
6a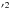 7a
7a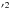 ) for the ground state is greater than 0.96 for all orientations. The basis set superposition errors (BSSE) were corrected in all geometries using the Boys & Bernardi (1970) counterpoise procedure. The distance R was varied by step of 0.25 bohr between 3 and 15 bohr and then by step of 1 bohr between 15 and 25 bohr. The value of θ was varied from 0 to 180° with a uniform step size of 15°. The PES was constructed with 767 ab initio geometries treated in the Cs symmetry group.
) for the ground state is greater than 0.96 for all orientations. The basis set superposition errors (BSSE) were corrected in all geometries using the Boys & Bernardi (1970) counterpoise procedure. The distance R was varied by step of 0.25 bohr between 3 and 15 bohr and then by step of 1 bohr between 15 and 25 bohr. The value of θ was varied from 0 to 180° with a uniform step size of 15°. The PES was constructed with 767 ab initio geometries treated in the Cs symmetry group.
 |
Fig. 2 Cuts of the PES for angle values θ = 0°, θ = 90°, and θ = 180° as a function of the distance R. |
In Fig. 2 we represented three cuts of the PES, which are V(re, RCF+...He, θ = 0°), V(re, RCF+ ⊥ He, θ = 90°), and V(re, RHe...CF+, θ = 180°), where RCF+...He is the value of R for an approach of He towards F atom and RHe...CF+ is that for He towards C atom. For θ = 0° the minimum is located at RCF+...He ~ 6 bohr with a depth well of –116.55 cm-1; for θ = 90° the minimum is at RCF+ ⊥ He ~ 5.25 bohr with a depth of –201.099 cm-1, and for θ = 180° it is found to be –79.55 cm-1 at RHe...CF+ ~ 7.25 bohr. Thus, the global minimum is placed near the perpendicular position. The He approach on the F side leads to a deeper minimum than on the C side. In fact, the electronic cloud of the CF+ molecule is shifted to the fluorine atom as it is more electronegative than that of carbon.
 |
Fig. 3 Contour plot of the PES (in cm-1) of CF+(X1 ∑ +)-He(1S) as a function of R and θ (re = 2.1812 bohr). The zero of energy is taken as that of the CF+–He asymptote. |
Figure 3 displays the contours plot of this potential. The interaction energy has a global minimum of –212.192 cm-1 at R = 5.17 bohr and θ = 99.4°.
We are interested in comparing our PES with that of CH+-He system studied by Hammami et al. (2008a). This comparison is based on three aspects:
-
1.
The interaction of two ions (CF+ and CH+, which both have the carbon atom in common) by collision with the He atom.
-
2.
The repartition of the positive charge in CF+ and CH+ molecules is concentrated on the carbon atom.
-
3.
The shapes of CF+-He and CH+-He PESs are very similar.
Indeed, more than 85% of the positive charge for both ions is almost concentrated on the carbon atom (see Table 1). Moreover, the CH+-He PES owns a minimum of 537 cm-1 at the position of R = 4.05 bohr and θ = 84° (Hammami et al. 2008a), which is a very similar minimum position to that of CF+-He. To compare these minimum positions, we represent in Fig. 4 the Jacobi coordinates referring to the mass center (R,θ) and the charge center (R′, θ′) of CF+-He (left-hand panel) and CH+-He (right-hand panel) van der Waals systems at their global minimum positions. Here, re is the internuclear distance of CF+ and CH+ fixed at their equilibrium values of the ground state, re(CF+) = 2.1812 bohr, and re(CH+) = 2.1371 bohr. From this figure, one can clearly see that both minima occur at a very similar Jacobi angle (θ′(CF+-He)= 86,5° and θ′(CH+-He)= 86°) if we refer to the molecules’ charge centers. Not surprisingly the R′ coordinates are in the order 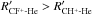 ; this stems from the fact that CH+much strongly attracts the atom He than does CF+. This behavior is also observed when comparing the well depths of the two PES. In fact, the CH+-He potential well is deeper than the CF+-He one.
; this stems from the fact that CH+much strongly attracts the atom He than does CF+. This behavior is also observed when comparing the well depths of the two PES. In fact, the CH+-He potential well is deeper than the CF+-He one.
Distribution of positive charge on the CF+ and CH+ molecules.
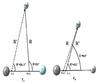 |
Fig. 4 Jacobi coordinates for the CF+-He and CH+-He systems at the global minimum positions m.c. and c.c. are, respectively, the mass and charge center of the diatomic molecules. |
In the framework of the long-range approximation, the energy contribution to the interaction between the CF+ molecule with a permanant dipole moment μCF+ and the apolar He atom with a polarisability αHe = 1.38 D is reduced to the induction part, which is expressed as 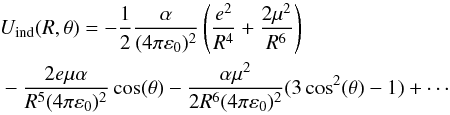 (3)The long-range part of our potential was studied by comparing the ab initio PES with the analytical expression (Eq. (3)). For θ = 90° this expression is reduced to
(3)The long-range part of our potential was studied by comparing the ab initio PES with the analytical expression (Eq. (3)). For θ = 90° this expression is reduced to 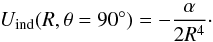 (4)Figure 5 depicts the variation of the long-range ab initio and analytical potential energies for θ = 90°, showing a good agreement between the two sets of data.
(4)Figure 5 depicts the variation of the long-range ab initio and analytical potential energies for θ = 90°, showing a good agreement between the two sets of data.
 |
Fig. 5 Comparison between the long range ab initio and analytical potential energies for θ = 90°. |
Before starting dynamical calculations, an analytic expansion of the PES is required as input for MOLSCAT package (Hutson et al. 1994). Thus, our PES is expanding in terms of Legendre polynomials and is expressed as 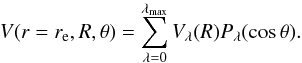 (5)From an ab initio grid containing 13 values of θ, we were able to include terms up to λmax = 12. To test the potential expansion, we started from the 13 values of θ for each radial distance R and deduced 19 ones using the cubic spline subroutine. These values were then fitted with the same procedure using 19 terms of Vλ(R). The dependence on R of the dominant coefficients Vλ(R) are showed in Fig. 6. Over the entire grid, the mean relative difference between the fitted and ab initio data is lower than 1% (see Table 2).
(5)From an ab initio grid containing 13 values of θ, we were able to include terms up to λmax = 12. To test the potential expansion, we started from the 13 values of θ for each radial distance R and deduced 19 ones using the cubic spline subroutine. These values were then fitted with the same procedure using 19 terms of Vλ(R). The dependence on R of the dominant coefficients Vλ(R) are showed in Fig. 6. Over the entire grid, the mean relative difference between the fitted and ab initio data is lower than 1% (see Table 2).
 |
Fig. 6 Vλ expansions of the interaction PES (λ = 0,1,2,3) as a function of the Jacobi coordinate R. |
From all the foregoing results, we deduced that the collisional calculations may be carried out for R starting from 3 bohr, which provides sufficiently repulsive potential for all orientations. During the scattering calculations, an interpolation was performed to obtain Vλ(R) at other values of R using the POTENL routine implemented in the MOLSCAT program. For large distances R > 25 bohr, this routine extrapolates Vλ(R) parameters by an inverse exponent expansion such as 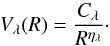 (6)It takes into account the latest values of Vλ(R) to obtain the Cλ and ηλ coefficients for each λ value. It gives, for example, η(λ = 0) = 4.14, η(λ = 1) = 5.12, and η(λ = 2) = 6.19. These values are in good agreement with the expression of the long-range potential given in Eq. (3).
(6)It takes into account the latest values of Vλ(R) to obtain the Cλ and ηλ coefficients for each λ value. It gives, for example, η(λ = 0) = 4.14, η(λ = 1) = 5.12, and η(λ = 2) = 6.19. These values are in good agreement with the expression of the long-range potential given in Eq. (3).
Potential energies obtained from ab initio calculations and the corresponding fitted values obtained from the Vλ coefficients.
MOLSCAT parameters used in our calculations.
 |
Fig. 7 Collision excitation cross sections of 12CF+ (upper panel) and 13CF+ (middle panel) by He as a function of the kinetic energy for transitions 0–J′ with J′ = 1–4. The comparison is given in the lower panel. |
 |
Fig. 8 Collisional excitation cross sections of 12CF+ and 13CF+ by He as a function of J′ for selected collision energies. |
3. Dynamical calculations
3.1. Cross sections
In this work, we are interested in studying the rotational excitation of 12CF+ and 13CF+ by collision with He at low temperature (T ≤ 300 K) for values of J ranging from 0 to 10 and a total energy up to 1500 cm-1, where J denotes the rotational angular momentum of the CF+ molecule. The rotational levels of CF+ may be computed with the usual expansion using the spectroscopic constants Be and De reported in Table 3. To calculate the cross sections, we use the quantum mechanical CC approach of Arthurs & Dalgarno (1960) implemented in the MOLSCAT code. To account for resonances during the calculation, we carefully spanned the energy range as follows: for E < 100 cm-1 the energy step was set to 0.1 cm-1; for 100 cm-1 ≤ E < 200 cm-1 to 0.2 cm-1; for 200 cm-1 ≤ E < 500 cm-1 to 1 cm-1; for 500 cm-1 ≤ E < 1000 cm-1 to 5 cm-1, and for 1000 cm-1 ≤ E ≤ 1500 cm-1 to 10 cm-1. In addition, we set Jmax = 15 for E < 200 cm-1, Jmax = 17 for 200 cm-1 ≤ E < 500 cm-1, and Jmax = 20 for E ≥ 500 cm-1. These values were fixed after performing some convergence tests. The maximum value of the total angular momentum Jtot was set large enough to ensure the convergence of the cross sections to be within 0.01 Å2 for elastic transitions and 0.001 Å2 for inelastic ones; typically, at 100 cm-1, Jtot = 63, at 500 cm-1, Jtot = 133, at 1000 cm-1, Jtot = 175, and at 1500 cm-1, Jtot = 203. The coupled equations were solved using the propagator of Manolopoulos (1986).
Dynamical calculations for the 13CF+-He system were performed at the same levels of theory using the 12CF+ PES, taking into account the displacement of the mass center with the change of the reduced mass and the spectroscopic constant Be and De.
Figure 7 presents the collisional excitation cross sections of 12CF+ and 13CF+ by He as a function of the kinetic energy for transitions from the ground level (J = 0) to J′ = 1–4 rotational levels. As one can see, the cross sections present several resonances (shape and Feshbach), particularly at low kinetic energies. This typical behavior for cross sections was pointed out by different studies (Smith et al. 1979; Christoffel & Bowman 1983; Lique et al. 2007; Hammami et al. 2008a,b,c; Nkem et al. 2009). These resonances are precisely detected in our calculated cross sections. This can be attributed to the small value of the rotational constant Be in comparison to that employed in the studies cited above. At high energy, we note the disappearance of these resonances: they do not exist for transitions involving energy levels with high ΔJ. The fine energy grid used at low energies was necessary for a good description of these resonances.
For propensity rules, we note that the 0–1 transition is dominant only at very low energies, i.e., from 0 to 15 cm-1. It should be noticed that a strong propensity towards an even parity of ΔJ transitions is also observed for almost the entire range of energies. The same rules were found for the CH+-He system. To compare the cross sections of 12CF+and 13CF+ by collision with He, we represented them in Fig. 7 (lower panel) as a function of kinetic energy for 0–1 and 0–2 transitions. This figure shows clearly that the cross sections exhibit almost the same trends for both systems, with a slight change due to the reduced mass and rotational constant difference between both isotopes. Figure 8 displays the dependance of cross sections on the rotational levels J′ from the ground state (J = 0) for both systems and for selected energies E = 100, 500, and 1000 cm-1. From this figure, we deduced that the general trends discussed above remain valid.
3.2. Collision rate coefficients
The rate coefficients are obtained by averaging the cross sections over a Maxwell-Boltzmann distribution of kinetic energies expressed as 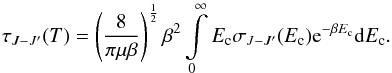 (7)
(7)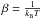 , where kB is the Boltzmann constant and T is the kinetic temperature, Ec is the relative kinetic energy (which is the difference between the total (E) and rotational (EJ) energies), and μ is the reduced mass (its values for 12CF+-He and 13CF+-He systems are given in Table 3).
, where kB is the Boltzmann constant and T is the kinetic temperature, Ec is the relative kinetic energy (which is the difference between the total (E) and rotational (EJ) energies), and μ is the reduced mass (its values for 12CF+-He and 13CF+-He systems are given in Table 3).
 |
Fig. 9 Calculated downward rate coefficients as a function of kinetic temperature for the collision of 12CF+and 13CF+ with He for transitions J–0 (upper panel) and J–1 (middle panel), and for astronomers observed transitions for 12CF+ (lower panel). |
 |
Fig. 10 Calculated downward rate coefficients for the collisions of 12CF+ and 13CF+ with He for J–J′ transitions with J′ = 0 (upper panel) and J′ = 1 (lower panel) for selected kinetic temperature. |
The downward rate coefficients for 12CF+ and 13CF+ by collision with He for J ranging from 0 to 10 at selected temperatures will be reported online at the BASECOL1 (Dubernet et al. 2013) and LAMDA2 (Schöier et al. 2005) data bases.
We displayed in Fig. 9 the collision rates of 12CF+-He and 13CF+-He as a function of the temperature. All curves in this figure are smoothly varying functions with the increase of kinetic temperature. There is a significant variation of rate coefficients at low temperatures. Figure 10 illustrates the variation of downward rate coefficients as a function of J for J − J′ transitions with J′ = 0 (upper panel) and J′ = 1 (lower panel) for selected temperatures T = 20, 100, and 300 K. According to this figure, it is important to note that the rate of collision confirms the already noted propensity towards even parity of ΔJ transitions obtained with cross sections, except for 1–0 transition. In fact, the CF+-He PES is practically symmetrical relative to θ = 90°, and the largest (in magnitude) of the anisotropic terms (λ > 0) in the radial coefficients Vλ corresponds to λ = 2. Otherwise, as one can see from Table 4, the energy spacing between the ground state and the first rotational one is very small compared to the other ones. This may be the main effect that promotes 1–0 transition. This behavior confirms all the results discussed and concluded in cross sections indicated above. The even propensity rule was found to be similar to that obtained for the CH+-He. This feature is due to the shape of CH+-He PES, which is already similar to that obtained in our study.
Rotational levels of 12CF+ and 13CF+ molecules.
Comparison between 12CF+-He and 13CF+-He cross sections.
3.3. Comparison between 12CF+ and 13CF+ collisional data
The Computation of collisional data for isotopologue species differs by the reduced mass, the rotational constants, and the position of the mass center. These effects significantly alter the data for the H/D substitutions, such as H2/D2 (Flower & Roueff 1999; Flower 1999), NH/ND (Dumouchel et al. 2012), H2O/D2O (Faure et al. 2004, 2012), and DCO+/HCO+ (Buffa 2012), but not for the 12C/13C, 14N/15N, and 16O/18O ones (Wickham-Jones et al. 1987; Yang et al. 1992; Reid et al. 1997). In the present work we have taken into account the displacement of the mass center in the calculation of the PES and used the 13CF+ rotational constant and its corresponding reduced mass. To show the influence of each effect on the collisional data, we calculated the CF+-He cross sections using the 12CF+-He PES with the 12CF+ rotational structure, the 12CF+-He PES with the 13CF+ rotational structure, and the 13CF+-He PES with the 13CF+ rotational structure. The results are presented in Table 5 for E = 100 and 500 cm-1. From Table 5, it can be seen that cross sections are very sensitive to the displacement of mass center and to the change of the rotational structure because the results obtained by the different sets of calculations differ significantly. In contrast, the cross sections calculated with the same rotational structure and two different PESs are increasingly close. This confirms that the displacement of mass center has an effect on collisional data. The latter, however, is not as important as the change of the rotational structure. Indeed, for most of the transitions the relative average error between the calculated cross sections using 12CF+-He PES and two different rotational structures of 12CF+ and 13CF+ molecules (~12%) is almost higher than those calculated with the same rotational structure of 13CF+ and two different 12CF+-He and 13CF+-He PESs (~3.8%), mainly for transitions with high rotational levels J, when the energy spacings between the 12CF+ and 13CF+ rotational levels is large (see Table 4).
From this table it can be seen that the small spacing between 12CF+ and 13CF+ levels leads to a small difference in the cross section values and the rate coefficients ones. This behavior is clearly seen in Fig. 7 (lower panel), which shows the same intensity and trends detected for the energy variation of 12CF+-He and 13CF+-He cross sections. A good agreement between both isotopologues rate coefficients is observed in the two upper panels of Figs. 9 and 10. The slight difference obtained can be mainly due to the three effects cited above.
The 13CF+-He rates are found to be slightly lower than those of 12CF+-He. This may be due to the energy spacing between the rotational levels of each molecule affected by the difference of the rotational constants. Indeed, for a given energy and transition the Ece− βEc factor in (Eq. (7)) is found to be weaker in the case of 13CF+. Furthermore, the difference between 12CF+-He and 13CF+-He rate coefficients can be attributed to the small effect of the reduced mass values in the Boltzmann factors (Eq. (7)). From Figs. 8 and 10, one can see that the propensity rules are found to be identical for both isotopologues.
4. Summary and conclusion
In the present study, a reliable ab initio PES for the CF+-He complex is computed using the CCSD(T) method with the aug-cc-pV5Z basis set for all atoms. A comparison of our PES with that of Hammami et al. (2008a) is mentioned, e.g., the shape of the CF+-He PES is found to be very similar to that of the CH+-He system. The results of a quantum mechanical CC calculation of integral cross sections for transitions between the lower rotational levels of CF+ induced by collision with He are reported. For 13CF+-He system, dynamical calculations were performed from a translation of 12CF+ mass center.
Up to T = 300 K, downward rate coefficients were obtained by averaging the cross sections over a Maxwell-Boltzmann distribution of the kinetic energy. The comparison between the 12CF+-He and 13CF+-He collisional data indicates the same trends and a very close order of magnitude. The slight discrepancies between both sets of data are explained mainly by the difference in the rotational structure and the displacement of the associated potential interaction with He.
A strong propensity towards even ΔJ transition is observed for cross sections and rate coefficients. Similar conclusions were found in the study of the CH+-He complex.
These results are very useful for astophysical observations as well as for experiments. The use of our rates to interpret CF+ observations could have important consequences on the understanding of fluorine chemistry in the ISM.
From rotational rate coefficients obtained in this work, it will be feasible to compute the hyperfine rate coefficients using the approach described by Faure & Lique (2012). This approach is well adapted to both closed- and open-shell linear rigid rotors with 1Σ or 2Σ electronic symmetry colliding with electrons, He, or para H2(j = 0).
Acknowledgments
We would like to acknowledge M. Hochlaf, N. Jaidane, N. Feautrier, and F. Lique for their continuing interest in this work and the fruitful discussions. Thanks to A. Ben Fredj and J. J. Fifen for their interesting remarks.
References
- Agúndez, M., Goicoechea, J. R., Cernicharo, J., & Roueff, E. 2010, ApJ, 713, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Arthurs, A. M., & Dalgarno, A. 1960, Proc. R. Soc. Lond. A, 256, 540 [Google Scholar]
- Boys, S. F., & Bernardi, F. 1970, Mol. Phys., 19, 533 [Google Scholar]
- Buffa, G. 2012, MNRAS, 421, 719 [NASA ADS] [Google Scholar]
- Buffa, G., Dore, L., & Meuwly, M. 2009, MNRAS, 397, 1909 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoli, G., Puzzarini, C., & Lapinov, A. V. 2004, ApJ, 611, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoli, G., Cludi, L., Puzzarini, C., & Gauss, J. 2010, A&A, 509, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazzoli, G., Cludi, L., Buffa, G., & Puzzarini, C. 2012, ApJS, 203, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Christoffel, K. M., & Bowman, J. M. 1983, J. Chem. Phys., 78, 3952 [NASA ADS] [CrossRef] [Google Scholar]
- Dubernet, M.-L., Daniel, F., Grosjean, A., & Lin, C. Y. 2009, A&A, 497, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubernet, M.-L., Alexander, M. H., Ba, Y. A., et al. 2013, A&A, 553, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumouchel, F., Faure, A., & Lique, F. 2010, MNRAS, 406, 2488 [NASA ADS] [CrossRef] [Google Scholar]
- Dumouchel, F., Kłos, J., Toboła, R., et al. 2012, J. Chem. Phys., 137, 114306 [NASA ADS] [CrossRef] [Google Scholar]
- Dunning, T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., & Lique, F. 2012, MNRAS, 425, 740 [Google Scholar]
- Faure, A., Gorfinkiel, J. D., & Tennyson, J. 2004, MNRAS, 347, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., Valiron, P., Wernli, M., et al. 2005, J. Chem. Phys., 122, 221102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Faure, A., Wiesenfeld, L., Scribano, Y., & Ceccarelli, C. 2012, MNRAS, 420, 699 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Flower, D. R. 1999, J. Phys. B, 32, 1755 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., & Roueff, E. 1999, J. Phys. B, 32, 3399 [NASA ADS] [CrossRef] [Google Scholar]
- Jankowski, P., & Szalewicz, K. 2005, J. Chem. Phys., 123 104301. [Google Scholar]
- Hammami, K., Owono Owono, L. C., Jaidane, N., & Ben Lakhdar, Z. 2008a, J. Mol. Struct. (THEOCHEM), 853, 18 [Google Scholar]
- Hammami, K., Nkem, C., Owono Owono, L. C., Jaidane, N., & Ben Lakhdar, Z. 2008b, J. Chem. Phys., 129, 204305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hammami, K., Owono Owono, L. C., Jaidane, N., & Ben Lakhdar, Z. 2008c, J. Mol. Struct. (THEOCHEM), 860, 45 [Google Scholar]
- Hampel C., Peterson K. A., & Werner, H.-J. 1992, Chem. Phys. Lett., 190, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hutson, J. M., & Green, S. 1994, MOLSCAT computer code, version 14, Collaborative Computational Project No. 6, Science and Engineering Research Council, UK [Google Scholar]
- Guillon, G., Stoecklin, T., Voronin, A., & Halvick, P. 2008, J. Chem. Phys., 129, 10430 [Google Scholar]
- Guzmán, V., Pety, J., Gratier, P., et al. 2012a, A&A, 543, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzmán, V., Roueff, E., Gauss, J., et al. 2012b, A&A, 548, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawaguchi, K., & Hirota, E. 1985, J. Chem. Phys., 83, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Kłos, J., Lique, F., & Alexander, M. H. 2007, Chem. Phys. Lett., 445, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Lique, F., & Spielfiedel, A. 2007, A&A, 462, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lique, F., Senent, M.-L., Spielfiedel, A., & Feautrier, N. 2007, J. Chem. Phys., 126, 164312 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lique, F., Toboła, R., Kłos, J., et al. 2008, A&A, 478, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lique, F., van der Tak, F. F. S., Kłos, J., Bulthuis, J., & Alexander, M. H. 2009, A&A, 493, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lique, F., Spielfiedel, A., Feautrier, N., et al. 2010, J. Chem. Phys., 132, 024303 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Manolopoulos, D. E. 1986, J. Chem. Phys., 85, 6425 [NASA ADS] [CrossRef] [Google Scholar]
- Monteiro, T. 1985, MNRAS, 214, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Nagy, Z., van der Tak, F. F. S., Ossenkopf, V., et al. 2013, A&A, 550, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Najar, F., Ben Abdallah, D., Jaidane, N., et al. 2009, J. Chem. Phys., 130, 204305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Neufeld, D. A., Wolfire, M. G., & Schilke, P. 2005, ApJ, 628, 260 (NWS05) [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Schilke, P., Menten, K. M., et al. 2006, A&A, 454, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nkem, C., Hammami, K., Manga, A., et al. 2009, J. Mol. Struct. (THEOCHEM), 901, 220 [CrossRef] [Google Scholar]
- Plummer, G. M., Anderson, T., Herbst, E., & DeLucia, F. C. 1986, J. Chem. Phys., 84, 2427 [NASA ADS] [CrossRef] [Google Scholar]
- Sarrasin, E., Ben Abdallah, D., Wernli, M., et al. 2010, MNRAS, 404, 518 [NASA ADS] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, L. N., Malik, D. J., & Secrest, D. 1979, J. Chem. Phys., 71, 4502 [NASA ADS] [CrossRef] [Google Scholar]
- Stoecklin, T., & Voronin, A. 2008, Eur. Phys. J. D, 46, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramazani, S., Frankcombe, T. J., Andersson, S., & Collins, M. A. 2009, J. Chem. Phys., 130, 244302 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, J. P., Thakkar, A. J., Barnes, P. W., et al. 1997, J. Chem. Phys., 107, 2329 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Ossenkopf, V., Nagy, Z., et al. 2012, A&A, 537, 10 [Google Scholar]
- Werner, H.-J., Follmeg, B., & Alexander, M. H. 1988, J. Chem. Phys., 89, 3139 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H.-J., Knowles, P. J., & Almöf, J. 2002, MOLPRO, a package of ab initio programs, University College Cardiff Consultants Limited, see http://www.molpro.net [Google Scholar]
- Wernli, M., Valiron, P., Faure, A., et al. 2006, A&A, 446, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wickham-Jones, C. T., Williams, H. T., & Simpson, C. J. S. M. 1987, J. Chem. Phys., 87, 5294 [NASA ADS] [CrossRef] [Google Scholar]
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, X., Kim, E. H., & Wodtke, A. M. 1992, J. Chem. Phys., 96, 5111 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Potential energies obtained from ab initio calculations and the corresponding fitted values obtained from the Vλ coefficients.
All Figures
 |
Fig. 1 Definition of the body-fixed Jacobi coordinates system for the CF+-He complex. |
| In the text | |
 |
Fig. 2 Cuts of the PES for angle values θ = 0°, θ = 90°, and θ = 180° as a function of the distance R. |
| In the text | |
 |
Fig. 3 Contour plot of the PES (in cm-1) of CF+(X1 ∑ +)-He(1S) as a function of R and θ (re = 2.1812 bohr). The zero of energy is taken as that of the CF+–He asymptote. |
| In the text | |
 |
Fig. 4 Jacobi coordinates for the CF+-He and CH+-He systems at the global minimum positions m.c. and c.c. are, respectively, the mass and charge center of the diatomic molecules. |
| In the text | |
 |
Fig. 5 Comparison between the long range ab initio and analytical potential energies for θ = 90°. |
| In the text | |
 |
Fig. 6 Vλ expansions of the interaction PES (λ = 0,1,2,3) as a function of the Jacobi coordinate R. |
| In the text | |
 |
Fig. 7 Collision excitation cross sections of 12CF+ (upper panel) and 13CF+ (middle panel) by He as a function of the kinetic energy for transitions 0–J′ with J′ = 1–4. The comparison is given in the lower panel. |
| In the text | |
 |
Fig. 8 Collisional excitation cross sections of 12CF+ and 13CF+ by He as a function of J′ for selected collision energies. |
| In the text | |
 |
Fig. 9 Calculated downward rate coefficients as a function of kinetic temperature for the collision of 12CF+and 13CF+ with He for transitions J–0 (upper panel) and J–1 (middle panel), and for astronomers observed transitions for 12CF+ (lower panel). |
| In the text | |
 |
Fig. 10 Calculated downward rate coefficients for the collisions of 12CF+ and 13CF+ with He for J–J′ transitions with J′ = 0 (upper panel) and J′ = 1 (lower panel) for selected kinetic temperature. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


