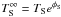| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | L10 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201321541 | |
| Published online | 15 July 2013 | |
Rapid cooling of Cassiopeia A as a phase transition in dense QCD
Institute for Theoretical Physics, J. W. Goethe University,
60438
Frankfurt am Main,
Germany
e-mail:
sedrakian@th.physik.uni-frankfurt.de
Received:
21
March
2013
Accepted:
19
June
2013
We present a model of the compact star in Cassiopea A that accounts for its unusually fast cooling behavior. This feature is interpreted as an enhancement in the neutrino emission triggered by a transition from a fully gapped, two-flavor, color-superconducting phase to a crystalline phase or an alternative gapless, color-superconducting phase. By fine-tuning a single parameter – the temperature of this transition – a specific cooling scenario can be selected that fits the Cas A data. Such a scenario requires a massive M ~ 2 M⊙ star and is, therefore, distinctive from models invoking canonical 1.4 M⊙ mass star with nucleonic pairing alone.
Key words: dense matter / stars: neutron / pulsars: general
© ESO, 2013
1. Introduction
Recently, an unprecedented fast cooling of the compact star in Cassiopeia A (Cas A) – the youngest known supernova remnant in Milky Way – was inferred from the Chandra observations over a period of ten years (Heinke & Ho 2010; Shternin et al. 2011). The age of the object 330 yr is tentatively deduced from the association of the remnant with the supernova SN 1680. This age estimate is confirmed through kinematical estimates. The fits to the surface temperature of the star suggest that the thermal soft X-ray spectrum originates in a nonmagnetized carbon atmosphere at temperature ~2. × 106 K and emitting region of 8−17 km.
Hadronic models of compact stars have been invoked to fit the data by assuming a canonical 1.4 M⊙ mass neutron star. The proposed models include those that attribute the Cas A cooling to a star that (a) undergoes a transition to a superfluid state in the baryonic core, which is accompanied by an enhancement of the cooling due to Cooper pair-breaking processes (Page et al. 2011; Shternin et al. 2011). These models appear to be the most natural ones, since they do not require “exotic” physics, and the parameter values are within their accepted range. In another model, (b), the star experiences thermal relaxation in the core that is slower than commonly accepted owing to low thermal conductivity (Blaschke et al. 2012). In addition, the relation between surface and core temperature used in these simulations is fitted to slowly cooling stars and deviates from the relation used in the models in the previous item, (a). An alternative model suggests that the star (c) undergoes rotationally induced compression that triggers a rapid Urca cooling in the center of the star (Negreiros et al. 2013). This model requires a significant fine tuning of the parameters and assumes an initial spin of the star in the millisecond range, which has not been observed in young neutron stars so far.
Recent observations of PSR J1614-2230 and PSR J0348+0432 lend firm evidence that equilibrium sequences of neutron stars contain massive ~2 M⊙ members (Demorest et al. 2010; Antoniadis et al. 2013). Models that predict quark matter in such massive compact stars in color-superconducting states have been studied extensively (Alford et al. 2005a; Klähn et al. 2007; Ippolito et al. 2008; Knippel & Sedrakian 2009; Kurkela et al. 2010; Bonanno & Sedrakian 2012). Color superconductivity is important; otherwise, the unpaired quarks cool a star by neutrino emission rapidly to temperatures well below those observed in Cas A (Page et al. 2000; Alford et al. 2005b; Anglani et al. 2006; Grigorian et al. 2005; Hess & Sedrakian 2011).
The true ground state of QCD is not known at densities relevant for compact stars. At relevant densities, the strong coupling αS ~ 1, that is, the perturbation theory, is not useful. Furthermore, because of β-equilibrium and strange quark mass, the Fermi-surfaces of up- and down-quarks are shifted apart. As a consequence, there are modifications to the standard Bardeen-Cooper-Schrieffer (BCS) picture of pairing. The non-BCS pairing may lead to one of the possible gapless two-flavor phases (Shovkovy & Huang 2003; Müther & Sedrakian 2003; Shovkovy et al. 2005) or, for example, to the crystalline color-superconducting phase (Alford et al. 2001; Casalbuoni et al. 2005; Giannakis et al. 2005; Rajagopal & Sharma 2006; Gatto & Ruggieri 2007; Mannarelli et al. 2007; Sedrakian & Rischke 2009; Huang & Sedrakian 2010; Anglani et al. 2013). The crystalline-color-superconductivity comes in several variants, which differ by the way the translational symmetry is broken by the condensate of Cooper pairs carrying finite momentum. Below we use results obtained for the so-called Fulde-Ferrell phase (hereafter FF phase), which is simple to model, but is general enough to preserve a key feature of the crystalline phases, namely the existence of gapless modes on the Fermi surfaces of quarks (Alford et al. 2001; Sedrakian & Rischke 2009; Huang & Sedrakian 2010).
 |
Fig. 1 Upper panel: phase diagram of color-superconducting quark matter in the temperature (T) and isospin imbalance α = (nd − nu)/(nu + nd) plane, where nd and nu are the number densities of d and u flavors of quarks. The arrows schematically show the path in the phase diagram during the cooling of a star. Lower panel: phase diagram of the same phases, but in the temperature and baryon density (nB) plane for matter in β-equilibrium with electrons. |
Proto-neutron stars emerge from supernova explosions with temperatures T ~ 50 MeV and nearly isospin symmetric matter in the core. After the initial fast cooling to T ~ 0.1 MeV, the core reaches its asymptotic state, which is highly isospin asymmetric. The initial fast temperature drop is followed by much slower cooling to temperatures of about 10 keV over the following 104−105 years. Initially, the high-temperature and low-isospin quark matter core is in the perfect two-flavor, color-superconducting (hereafter 2SC) state where the Fermi surfaces of the up- and down-quarks are completely gapped. As the star cools and the β-equilibrium is established, the 2SC phase becomes unstable, because the asymptotic ground state of quark matter corresponds to the class of gapless and/or crystalline two-flavor, color-superconducting phases mentioned above. This is illustrated in the top panel of Fig. 1, where we show the phase diagram of the FF and 2SC phases in the temperature and flavor-asymmetry plane, adapted from Sedrakian & Rischke (2009).
During the early evolution of the star, the matter traverses from the upper lefthand corner of the phase diagram (i.e. from unpaired, almost isospin symmetric matter) to the righthand lower corner, which corresponds to the cold FF phase and large isospin asymmetry. The phase diagram of the same phases in the density-temperature plane and under β-equilibrium is shown in the lower panel of Fig. 1, which is adapted from Huang & Sedrakian (2010). These figures are only shown to illustrate the structure and topology of the phase diagram. The magnitude of the critical temperature of transition from the 2SC phase to the crystalline color-superconducting or similar gapless phase will be treated as a free parameter. Our fits to Cas A below show that it must be smaller than the values obtained from theoretical models.
In this work we conjecture that the rapid cooling of Cas A can be understood as a phase transition from the perfect 2SC phase to a crystalline/gapless, color-superconducting state. Thus, somewhat counterintuitively, the rapid cooling is the result of a phase transition within the phase diagram of dense QCD from one to another color-superconducting phase. This transition can be characterized by two parameters, the critical transition temperature T∗ and the transient “widths” w. The parameter w encodes the finite time scale of the transition. In general T∗ will depend on a number of factors, such as the nucleation history of the superconducting phase, geometry of the superconducting regions, dynamics and order of the phase transition, etc. Furthermore, because of the density dependence of the critical temperature T∗ in the stellar interior, this phase transition will not occur everywhere in the quark core, but gradually within some shells. Therefore, the values of T∗ and w will be determined by the local conditions in shells. We expect that the transition is not instantaneous, because it takes place via propagation of the phase-separation fronts rather than a coherent instantaneous transition.
The equilibrium model calculations give Tc ~ 10 MeV in a particular (Nambu-Jona-Lasinio Lagrangian based) model, see Fig. 1. But the absolute value of the gap strongly depends on the model. It may differ from the equilibrium critical temperature of phase transition for dynamical reasons. (Supercooled state in electronic superconductor are observed, where the system remains in the initial unpaired state below the equilibrium critical transition temperature Tc, because of the finite time scales of the phase transition process.) These considerations motivate our treatment of T∗ as a free parameter that will be used to fit our cooling model to the Cas A data. The slope of the transient can be chosen separately by the choice of the parameter w prior to the fit procedure. The simulations below will be carried out assuming a density independent T∗. The density dependence seen in Fig. 1 arises from the dependence of the density of states at the Fermi-level alone; the coupling constants of the model are density-independent. In general, the strong coupling constant of QCD “runs” with density (energy), therefore, the density dependence of T∗ may be more complicated than in the model above. The possible density dependence of T∗ will smooth out the transition to the crystalline phase, which is taken into account phenomenologically in the parameter w.
A preliminary report of the present study was given elsewhere (Sedrakian 2013).
2. Modeling cooling processes
Our cooling model is described in Hess & Sedrakian (2011), where the details of the microscopic input and the method of solution can be found. Here we describe the extension of this model, which allows us to account for the phase transition between the phases in a phenomenological manner.
Quark matter consisting of two light u and d flavors of
quarks cools predominantly via the beta decay (Urca) reactions
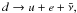 and u + e → d + ν, where
e stands for electron, and ν and
and u + e → d + ν, where
e stands for electron, and ν and
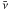 represent electron neutrino and antineutrino. For unpaired quarks and to leading order in
the strong coupling constant αS, the emissivity
of the process per quark color was calculated by Iwamoto
(1980),
represent electron neutrino and antineutrino. For unpaired quarks and to leading order in
the strong coupling constant αS, the emissivity
of the process per quark color was calculated by Iwamoto
(1980), 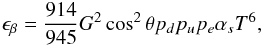 (1)where
G is the weak coupling constant, θ the Cabibbo angle,
and where pd,
pu, and
pe are the Fermi momenta of down quarks, up
quarks, and electrons.
(1)where
G is the weak coupling constant, θ the Cabibbo angle,
and where pd,
pu, and
pe are the Fermi momenta of down quarks, up
quarks, and electrons.
Quark pairing modifies the temperature dependence of process (1). In the BCS-type superconductors, the process is suppressed almost
linearly for T ≃ Tc and exponentially for
T ≪ Tc, where Tc
is the critical temperature. In gapless superconductors the emergence of the new scale
δμ = (μd − μu)/2,
where μu,d are the chemical potentials of light
quarks, leads to two qualitatively different possibilities, which are distinguished by the
value of the dimensionless parameter
ζ = Δ0/δμ, where
Δ0 is the gap in the limit δμ = 0 (Jaikumar et al. 2006). When
ζ > 1, the entire Fermi surface is gapped.
Consequently, when the thermal smearing of the Fermi surface ~T is much
smaller than the gap, no excitation can be created out of the Fermi sphere. When
ζ < 1, particles can be excited from the gapless
regions of the Fermi sphere. For the FF phases the shift in the chemical potential is
replaced by the anti-symmetric in the flavor part of the single particle spectrum of up- and
down-quarks,
ϵu/d;
i.e.,
δμ → ]ϵd(Q) − ϵu(Q)] /2,
where Q is the total momentum of a Cooper pair. In the case of
a single plane-wave crystalline phase, the spectrum depends on the magnitude of the vector
Q alone. The asymptotic behavior of the ζ
parameter discussed above permits us to use an interpolation formula that covers the
asymptotic limits and does not require detailed modeling of the physics of the underlying
phase (Jaikumar et al. 2006)
![\begin{eqnarray} \epsilon^{\rm rg}_{\beta}(\zeta;T\le T_{\rm c}) = 2f(\zeta) \epsilon_{\beta}, \quad f(\zeta) = \frac{1}{\exp[(\zeta-1)\frac{\delta\mu}{T}-1]+1}, \end{eqnarray}](/articles/aa/full_html/2013/07/aa21541-13/aa21541-13-eq49.png) (2)where
the factor two is the number of colors.
(2)where
the factor two is the number of colors.
Because the 2SC pairing pattern breaks the SU(3) color symmetry, one of the quark colors
(say, the blue color) is not involved in that pairing. The strength and the flavor content
of pairing among blue quarks is model dependent (Alford et
al. 2003; Schmitt et al. 2003; Schmitt 2005; Aguilera et
al. 2005, 2006; Aguilera 2007). It is likely that cross-flavor (blue-up and blue-down)
pairing is suppressed by a large mismatch between the Fermi surfaces of the up and down
quarks. Pairing is expected in the color 6S and
flavor 3S channel, which is same-flavor and
same-color pairing, so is not affected by the flavor asymmetry (Alford et al. 2003). However, the pairing in this channel vanishes in the
chiral limit, when the mass of blue quarks vanishes. Pairing due to alternative mechanisms
is not excluded, besides those studied so far. Quite generally, single-flavor and/or color
pairings have gaps in the range of 10−100 keV, which are much smaller than the gaps emerging
from 2SC-type pairing. Since there are no definitive theoretical predictions about the
pairing in the blue sector, we assume that the neutrino emissivity of blue quarks is
suppressed exponentially by the pairing gap, as is the case for nucleonic matter. Therefore,
we simply parameterize the modifications of the Urca process on blue quarks as in the case
of baryonic matter: 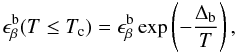 (3)where Δb is the
pairing gap for the blue color quarks. Note that
(3)where Δb is the
pairing gap for the blue color quarks. Note that 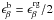 owing to the different numbers of
colors involved. Several studies used similar parameterizations (Grigorian et al. 2005; Hess &
Sedrakian 2011). Furthermore, we choose to work with a pairing gap
Δb = 100 keV, which leads to blue quarks not affecting the cooling dynamics or
the fits to Cas A data; i.e., they only play a passive role. The effect of lower values of
this gap on the cooling is discussed elsewhere (Hess
& Sedrakian 2011).
owing to the different numbers of
colors involved. Several studies used similar parameterizations (Grigorian et al. 2005; Hess &
Sedrakian 2011). Furthermore, we choose to work with a pairing gap
Δb = 100 keV, which leads to blue quarks not affecting the cooling dynamics or
the fits to Cas A data; i.e., they only play a passive role. The effect of lower values of
this gap on the cooling is discussed elsewhere (Hess
& Sedrakian 2011).
 |
Fig. 2 Left panel. Dependence of the redshifted surface
temperature (logarithmic scale) on time for the values of the transition temperature
T∗ (in MeV) indicated in the plot and for fixed width
w = 0.2 MeV. We also show the same dependence for
T∗ = 0.093 and w = 0.3
(dash-double-dotted line) and w = 0.1 (double-dash-dotted line). The
underlying model is the 1.93 M⊙ compact star model of
Knippel & Sedrakian (2009).
Right panel. Dependence of the redshifted surface temperature (in
units of 106 K) on time for the same model. The points with error bars show
the Cas A data, and the solid lines are fits to these data by variation of
T∗ for fixed width w = 0.2 MeV. The
redshifted temperature measured by a distant observer is obtained as
|
In addition to neutrino emissivities, we need to model the specific heat of the quark
phases. For the inhomogeneous red-green condensate, the critical temperature changes with
δμ (Hess & Sedrakian 2011)
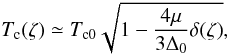 (4)where
μ = (μd + μu)/2,
Δ0 = Δ(ζ = 0),
Tc0 = Tc(ζ = 0),
and
δ(ζ) = (nd − nu)/(nd + nu).
The fully gapped and gapless regimes behave differently; in the presence of gapless modes,
the specific heat has a linear dependence on the temperature. A phenomenological way to
model this behavior is given by the relation
(4)where
μ = (μd + μu)/2,
Δ0 = Δ(ζ = 0),
Tc0 = Tc(ζ = 0),
and
δ(ζ) = (nd − nu)/(nd + nu).
The fully gapped and gapless regimes behave differently; in the presence of gapless modes,
the specific heat has a linear dependence on the temperature. A phenomenological way to
model this behavior is given by the relation
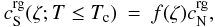 (5)where
(5)where
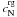 is the
specific heat of red-green unpaired quarks and
is the
specific heat of red-green unpaired quarks and 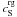 is the
specific heat of pair-correlated quarks. To compute the specific heats of the electrons and
unpaired quarks, we assume that each form noninteracting, ultrarelativistic gas.
is the
specific heat of pair-correlated quarks. To compute the specific heats of the electrons and
unpaired quarks, we assume that each form noninteracting, ultrarelativistic gas.
Finally, we need the relation between the temperature of the isothermal interior and the
surface, which can be written as (Gudmundsson et al.
1983; Potekhin et al. 1997)
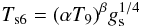 (6)where
Ts6 is the surface temperature in units of 106 K,
T9 the isothermal core temperature in units of 109
K, α and β are constants that depend on the composition of
the star’s atmosphere, gs is the surface gravity in units of
1014 cm s-2. For the present model with
M/M⊙ = 1.93 and
R = 13.32 km we find gs = 1.91. We assume
β = 0.55, which lies between the values for the purely-iron
(β = 0.5) and fully accreted (β = 0.61) envelope. We
adopt the value α = 18.1, which is appropriate for a accreted envelope
(Potekhin et al. 1997). The fit results are
sensitive to the β parameter, but not to the α parameter.
(6)where
Ts6 is the surface temperature in units of 106 K,
T9 the isothermal core temperature in units of 109
K, α and β are constants that depend on the composition of
the star’s atmosphere, gs is the surface gravity in units of
1014 cm s-2. For the present model with
M/M⊙ = 1.93 and
R = 13.32 km we find gs = 1.91. We assume
β = 0.55, which lies between the values for the purely-iron
(β = 0.5) and fully accreted (β = 0.61) envelope. We
adopt the value α = 18.1, which is appropriate for a accreted envelope
(Potekhin et al. 1997). The fit results are
sensitive to the β parameter, but not to the α parameter.
3. Simulation results
The key idea of our model is that the transition occurs from the fully gapped (perfect) 2SC
phase to some type of crystalline/gapless phase. A particular realization of this scenario
would be a transition to single plane wave crystalline phase (the FF phase). We model this
transition phenomenologically by adopting temperature dependent (and, therefore,
time-dependent) parameter ζ(T). (Hess & Sedrakian (2011) assume constant ζ, so
phase transitions of the type discussed here were excluded in their study from the outset).
The temperature dependence of this parameter is modeled such that one obtains
ζ > 1 for
T > T∗, whereas
ζ < 1 for
T < T∗. The
ζ(T) function is modeled by the simply law
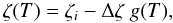 (7)where
ζi is the initial value, Δζ
the constant change in this function, and the function
g(T) affects the transition from the initial value
ζi to the asymptotic final value
ζf = ζi − δζ.
The transition is conveniently modeled by the following function
(7)where
ζi is the initial value, Δζ
the constant change in this function, and the function
g(T) affects the transition from the initial value
ζi to the asymptotic final value
ζf = ζi − δζ.
The transition is conveniently modeled by the following function
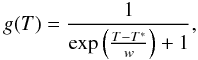 (8)which allows us to
control the temperature of transition, fixed by T∗, and the
smoothness of the transition, fixed by width w.
(8)which allows us to
control the temperature of transition, fixed by T∗, and the
smoothness of the transition, fixed by width w.
The cooling simulations were carried out using the model of Hess & Sedrakian (2011), which solves the general relativistic equations
of cooling in spherical symmetry (see also Glen &
Sutherland 1980). The time evolution is carried out for the quantity
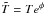 , where
T is the local temperature and φ is related to the
temporal component of the metric tensor as
g00 = e2φ.
, where
T is the local temperature and φ is related to the
temporal component of the metric tensor as
g00 = e2φ.
The lefthand panel of Fig. 2 shows the cooling evolution of M = 1.93 M⊙ model of a compact star for several values of T∗ and fixed w = 0.2 MeV. In addition, the figure shows the effect of keeping T∗ constant and varying of w. Evidently the drop in the temperature is smoother in the case of larger w. Once a suitable value of w, which fits the slope of the transient, is assumed, one can proceed to fit the data by choosing the temperature T∗. It is seen that for a specific value of T∗ the cooling curve passes through the location of Cas A in the log T −log t plane. The righthand panel of Fig. 2 shows the observed evolution of Cas A for the same value of w and two (fine-tuned) values of T∗. The numerical values of gaps in the red-green and blue channels Δ0 = 60 MeV and Δb = 0.15 MeV were used in the simulations. The critical temperature of the same-color pairing of the blue quarks satisfies the condition Tcb = Δb/1.76 > T∗, which implies that blue quarks have no effect on the dynamics of the transition process. In case of low critical temperatures of blue quark pairing, a compact star will rapidly cool via neutrino emission on time scales t ≤ 300 yr below the temperature of Cas A, which obviously will preclude any fit to the data.
In closing, it should be stressed that the data can be fitted by choosing a range of combinations of w and T∗ parameters, the first of which encodes unknown physics of dynamics of the phase transition and the density dependence of critical temperature. Therefore, even though some fine tuning of T∗ is required to fit the data, the actual range of T∗ by which the data can be fitted is in fact much broader. Better understanding of these factors, as well as of the magnitude of the critical temperature, are required in order to constraint the range of these parameters.
4. Conclusions
We have demonstrated that the rapid cooling of Cas A can be understood as a phase transition from the perfect two-flavor, color-superconducting phase to a gapless/crystalline phase. Counterintuitively, the phase transition occurs within the phase diagram of dense QCD and reflects the ordering of various superconducting phases in the temperature, density, and isospin spaces. This idea is supported qualitatively by the structure of the phase diagram of the dense QCD at densities and temperatures relevant to the cooling evolution of compact stars.
We have shown that the data can be fitted by adjusting a single parameter – the phase transition temperature – at a fixed value of transient time scale, which encodes the dynamics of the transition. A further important assumption is that there is no interference from the blue quarks, so that the temperature of the model is above the Cas A temperature for t ≤ 300 yr, which is an obvious requirement for any successful fit to data in the absence of internal heating.
The present model implies that only massive compact stars undergo the rapid temperature drop observed in Cas A, for only massive members of compact star sequences contain (color-superconducting) quark matter in their interiors. It also implies that massive compact stars that are older than Cas A are invisible in X-rays with modern instruments. Our model thus differs from the alternatives, which invoke nucleonic pairing and pair-breaking processes (Page et al. 2011; Shternin et al. 2011) or slow thermal relaxation (Blaschke et al. 2012) and also work for low-mass mass neutron stars. Rotation is unimportant for our modeling as opposed to the model of Negreiros et al. (2013). It is evident that the various models can be distinguished through their distinctive features in case further observational information becomes available. Clearly, it would be premature to conclude that the Cas A behavior is direct evidence of superfluidity for any particular type of superfluid in neutron star interiors.
Acknowledgments
The author is grateful to M. Alford, H. Grigorian, D. Hess, X.-G. Huang, K. Rajagopal, D. H. Rischke, A. Schmitt, and I. Wasserman for useful discussions and correspondence. This work is partially supported though a collaborative research grant of the Volkswagen Foundation (Hannover, Germany).
References
- Aguilera, D. N. 2007, Ap&SS, 308, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilera, D. N., Blaschke, D., Buballa, M., & Yudichev, V. L. 2005, Phys. Rev. D, 72, 034008 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilera, D. N., Blaschke, D., Grigorian, H., & Scoccola, N. N. 2006, Phys. Rev. D, 74, 114005 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M., Bowers, J. A., & Rajagopal, K. 2001, Phys. Rev. D, 63, 074016 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M. G., Bowers, J. A., Cheyne, J. M., & Cowan, G. A. 2003, Phys. Rev. D, 67, 054018 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M., Braby, M., Paris, M., & Reddy, S. 2005a, ApJ, 629, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M., Jotwani, P., Kouvaris, C., Kundu, J., & Rajagopal, K. 2005b, Phys. Rev. D, 71, 114011 [NASA ADS] [CrossRef] [Google Scholar]
- Anglani, R., Nardulli, G., Ruggieri, M., & Mannarelli, M. 2006, Phys. Rev. D, 74, 074005 [NASA ADS] [CrossRef] [Google Scholar]
- Anglani, R., Casalbuoni, R., Ciminale, M., et al. 2013 [arXiv:1302.4264] [Google Scholar]
- Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 448 [Google Scholar]
- Blaschke, D., Grigorian, H., Voskresensky, D. N., & Weber, F. 2012, Phys. Rev. C, 85, 022802 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanno, L., & Sedrakian, A. 2012, A&A, 539, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casalbuoni, R., Gatto, R., Ippolito, N., Nardulli, G., & Ruggieri, M. 2005, Phys. Lett. B, 627, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gatto, R., & Ruggieri, M. 2007, Phys. Rev. D, 75, 114004 [NASA ADS] [CrossRef] [Google Scholar]
- Giannakis, I., Hou, D.-F., & Ren, H.-C. 2005, Phys. Lett. B, 631, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Glen, G., & Sutherland, P. 1980, ApJ, 239, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Grigorian, H., Blaschke, D., & Voskresensky, D. 2005, Phys. Rev. C, 71, 045801 [NASA ADS] [CrossRef] [Google Scholar]
- Gudmundsson, E. H., Pethick, C. J., & Epstein, R. I. 1983, ApJ, 272, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Heinke, C. O., & Ho, W. C. G. 2010, ApJ, 719, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Hess, D., & Sedrakian, A. 2011, Phys. Rev. D, 84, 063015 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, X.-G., & Sedrakian, A. 2010, Phys. Rev. D, 82, 045029 [NASA ADS] [CrossRef] [Google Scholar]
- Ippolito, N. D., Ruggieri, M., Rischke, D. H., Sedrakian, A., & Weber, F. 2008, Phys. Rev. D, 77, 023004 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, N. 1980, Phys. Rev. Lett., 44, 1637 [Google Scholar]
- Jaikumar, P., Roberts, C. D., & Sedrakian, A. 2006, Phys. Rev. C, 73, 042801 [NASA ADS] [CrossRef] [Google Scholar]
- Klähn, T., Blaschke, D., Sandin, F., et al. 2007, Phys. Lett. B, 654, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Knippel, B., & Sedrakian, A. 2009, Phys. Rev. D, 79, 083007 [NASA ADS] [CrossRef] [Google Scholar]
- Kurkela, A., Romatschke, P., Vuorinen, A., & Wu, B. 2010 [arXiv:1006.4062] [Google Scholar]
- Mannarelli, M., Rajagopal, K., & Sharma, R. 2007, Phys. Rev. D, 76, 074026 [NASA ADS] [CrossRef] [Google Scholar]
- Müther, H., & Sedrakian, A. 2003, Phys. Rev. D, 67, 085024 [NASA ADS] [CrossRef] [Google Scholar]
- Negreiros, R., Schramm, S., & Weber, F. 2013, Phys. Lett. B, 718, 1176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Page, D., Prakash, M., Lattimer, J. M., & Steiner, A. W. 2000, Phys. Rev. Lett., 85, 2048 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Page, D., Prakash, M., Lattimer, J. M., & Steiner, A. W. 2011, Phys. Rev. Lett., 106, 081101 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Potekhin, A. Y., Chabrier, G., & Yakovlev, D. G. 1997, A&A, 323, 415 [NASA ADS] [Google Scholar]
- Rajagopal, K., & Sharma, R. 2006, Phys. Rev. D, 74, 094019 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, A. 2005, Phys. Rev. D, 71, 054016 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, A., Wang, Q., & Rischke, D. H. 2003, Phys. Rev. Lett., 91, 242301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sedrakian, A. 2013, PoS (Confinment X), 251 [Google Scholar]
- Sedrakian, A., & Rischke, D. H. 2009, Phys. Rev. D, 80, 074022 [NASA ADS] [CrossRef] [Google Scholar]
- Shovkovy, I., & Huang, M. 2003, Phys. Lett. B, 564, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Shovkovy, I. A., Rüster, S. B., & Rischke, D. H. 2005, J. Phys. G Nuclear Phys., 31, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Shternin, P. S., Yakovlev, D. G., Heinke, C. O., Ho, W. C. G., & Patnaude, D. J. 2011, MNRAS, 412, L108 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Upper panel: phase diagram of color-superconducting quark matter in the temperature (T) and isospin imbalance α = (nd − nu)/(nu + nd) plane, where nd and nu are the number densities of d and u flavors of quarks. The arrows schematically show the path in the phase diagram during the cooling of a star. Lower panel: phase diagram of the same phases, but in the temperature and baryon density (nB) plane for matter in β-equilibrium with electrons. |
| In the text | |
 |
Fig. 2 Left panel. Dependence of the redshifted surface
temperature (logarithmic scale) on time for the values of the transition temperature
T∗ (in MeV) indicated in the plot and for fixed width
w = 0.2 MeV. We also show the same dependence for
T∗ = 0.093 and w = 0.3
(dash-double-dotted line) and w = 0.1 (double-dash-dotted line). The
underlying model is the 1.93 M⊙ compact star model of
Knippel & Sedrakian (2009).
Right panel. Dependence of the redshifted surface temperature (in
units of 106 K) on time for the same model. The points with error bars show
the Cas A data, and the solid lines are fits to these data by variation of
T∗ for fixed width w = 0.2 MeV. The
redshifted temperature measured by a distant observer is obtained as
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.