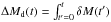| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201321500 | |
| Published online | 25 June 2013 | |
Effect of the toroidal magnetic field on the runaway instability of relativistic tori
1
Astronomical Institute, Academy of Sciences,
Boční II 1401,
14100
Prague,
Czech Republic
e-mail:
hamersky@astro.cas.cz
2
Charles University in Prague, Faculty of Mathematics and Physics,
V Holešovičkách 2,
18000
Prague, Czech
Republic
Received:
18
March
2013
Accepted:
16
May
2013
Aims. Runaway instability operates in fluid tori around black holes. It affects systems close to the critical (cusp overflowing) configuration. The runaway effect depends on the radial profile l(R) of the angular momentum distribution of the fluid, on the dimension-less spin a of the central black hole (|a| ≤ 1), and other factors, such as self-gravity. Previously it was demonstrated that for the power-law dependence of the radial angular momentum profile, l(R) ∝ Rq, non-magnetized tori always become runaway stable for a sufficiently high positive value of q. Here we discuss the role of runaway instability within a framework of an axially symmetric model of perfect fluid endowed with a purely toroidal magnetic field.
Methods. The gradual accretion of material over the cusp transfers the mass and angular momentum onto the black hole, thereby changing the intrinsic parameters of the Kerr metric. We studied the effect of the plasma parameter β (ratio of gas to magnetic pressure) and other parameters of the model on the evolution of critical configurations that are just on the verge of cusp overflow.
Results. By contributing to the total pressure, the magnetic field causes small departures from the corresponding non-magnetic configuration in the early phases of accretion. However, we show that the toroidal magnetic component inside an accretion torus does not change the frequency of its oscillations significantly. We identify these oscillations as the radial epicyclic mode in our example. Nevertheless, these weak effects can trigger the runaway instability even in situations when the purely hydrodynamical regime of the torus is stable. On the other hand, in most cases the stable configuration remains unaffected, and the initial deviations gradually decay after several orbital periods. We show examples of the torus evolution depending on the initial magnetization β, the slope q, and the spin a.
Conclusions. The toroidal magnetic field plays a more important role in the early phases of the accretion process until the perturbed configuration finds a new equilibrium or disappears because of the runaway instability.
Key words: accretion, accretion disks / black hole physics / instabilities
© ESO, 2013
1. Introduction
Toroidal equilibria of perfect fluid in permanent rotation were introduced a long time ago as an initial step on the way towards an astrophysically realistic description of accretion of gaseous material onto a black hole in active galactic nuclei and black hole binaries (Fishbone & Moncrief 1976; Abramowicz et al. 1978; Pugliese et al. 2013). These axially symmetric and stationary solutions are subject to various types of instability (e.g., Abramowicz & Fragile 2013). Here we concentrate on a global type of instability caused by an overflow of material over the cusp of a critical equipotential surface (Daigne & Mochkovitch 1997; Abramowicz et al. 1998; Korobkin et al. 2013). It was suggested that this may lead to specific features that should be observable in the radiation emitted from an accreting black-hole system (Zanotti et al. 2003).
The effect of the mentioned instability can be catastrophic under certain conditions. In particular, a black-hole torus becomes runaway unstable if the angular momentum profile within the torus does not rise sufficiently fast with radius (Abramowicz et al. 1998; Lu et al. 2000). The role of general relativity effects on the runaway mechanism was studied in Font & Daigne (2002) in the context of gamma-ray burst sources. These authors found that by allowing the mass of the black hole to grow by accretion, the disc becomes unstable. However, the parameter space of the problem is much richer than what could be taken into account in early works. For example, the self-gravity of the fluid tends to act against the stability of non-accreting tori (Goodman & Narayan 1988; Masuda et al. 1998; Montero et al. 2010; Korobkin et al. 2011). Furthermore, the spin parameter can play a role for accretion onto a rotating black hole. In astrophysically realistic models, an interplay of mutually competing effects have to be taken into account.
The role of magnetic fields is known to be essential for accretion. Even the Rayleigh-stable tori (Seguin 1975) with a radially increasing profile, dl / dR > 0, become dynamically unstable because of turbulence in the presence of a weak magnetic field (Balbus & Hawley 1991). Here we aim to clarify the simpler question of the global stability of a rotationally symmetric black-hole accretion tori, taking into account the effect of a large-scale (organized) magnetic field that obeys the same axial symmetry. Komissarov (2006) has developed a suitable analytical (toy) model of such a magnetized torus described by a polytropic equation of state in Kerr metric. In this model the magnetic field only enters the equilibrium solution for the torus as an additional pressure-like term (Pugliese & Montani 2013).
We employed this solution as an initial configuration, which we then perturbed and evolved numerically by using a two-dimensional numerical scheme (HARM; see Gammie et al. 2003). A complementary approach in the context of gamma-ray bursts has been developed in Barkov & Baushev (2011), who adopted the same initial configuration of an axially symmetric magnetized torus, which they evolved taking self-gravity and neutrino cooling mechanisms into account. Although the basic idea behind the runaway instability has been well-known since the early papers (see Abramowicz et al. 1983; Wilson 1984) – it is connected with the existence of the innermost stable circular orbit around black holes in general relativity – an interplay of different effects makes the discussion rather complex, and so simplified models have their value for understanding the runaway mechanism in astrophysically realistic systems.
Assuming axial symmetry is a useful simplification to explore the origin of runaway instability, although it is a far too strong constraint for any realistic model of an accreting system. Moreover, a purely toroidal structure of the magnetic field and complete negligence of radiative cooling are an over-simplification, which we adopt in this paper. However, these assumptions allow us to concentrate on the particular type of the above-mentioned relativistic instability while non-axisymmetric modes are suppressed. It also helps us to proceed systematically through the parameter space of the model to reveal the dependence on black-hole spin and the magnetic field strength as they act concurrently within the relativistic scheme. In this respect our work is complementary to three-dimensional simulations (e.g., Korobkin et al. 2013; McKinney et al. 2012), which are more complete and, at the same time, more difficult to comprehend.
In Sect. 2 we summarize our approach to magnetized tori and the numerical scheme used in our simulations. Then we present our results by comparing properties of magnetized and non-magnetized accretion tori that are subject to a weak perturbation from the equilibrium state. In Sect. 3 we discuss our results and give a brief conclusion.
2. Axisymmetric accretion of magnetized fluid tori
2.1. Initial configuration
The magnetized ideal fluid can be described by the energy-momentum tensor (e.g., Anile 1989)
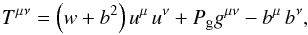 (1)where
w is the specific enthalpy, Pg is the gas
pressure, and bμ is the projection of the
magnetic field vector
(b2 = bμbμ).
(1)where
w is the specific enthalpy, Pg is the gas
pressure, and bμ is the projection of the
magnetic field vector
(b2 = bμbμ).
From the energy-momentum tensor conservation, 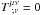 , it
follows for a purely axially rotating fluid (Abramowicz et
al.1978, 2013)
, it
follows for a purely axially rotating fluid (Abramowicz et
al.1978, 2013) 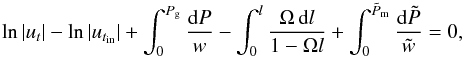 (2)where
ut is the covariant component of the
four-velocity (subscript “in” corresponds to the inner edge of the torus),
Ω = uϕ / ut
is the angular velocity and
l = − uϕ / ut
is the angular momentum density.
(2)where
ut is the covariant component of the
four-velocity (subscript “in” corresponds to the inner edge of the torus),
Ω = uϕ / ut
is the angular velocity and
l = − uϕ / ut
is the angular momentum density.
The specific enthalpy,
w ≡ ρ + Pg + U,
can be expressed in terms of the internal energy density U, the rest-mass
density ρ, and two contributions to the total pressure,
P(ρ) = Pg + Pm,
where Pg is the gas (thermodynamical) part and
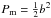 is the magnetic
part. The last term introduces the effect of the magnetic field in the context of our
model and the tilde denotes
is the magnetic
part. The last term introduces the effect of the magnetic field in the context of our
model and the tilde denotes 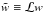 ,
,
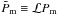 , where
, where
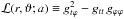 is a combination of
metric terms, in our case the known function of radius, latitude, and spin of the Kerr
metric.
is a combination of
metric terms, in our case the known function of radius, latitude, and spin of the Kerr
metric.
By assuming a suitable equation of state and the rotation law of the fluid, Eq. (2)can be integrated to obtain the structure of equipotential surfaces of the equilibrium configuration. The last term on the left-hand side of Eq. (2)was assumed to be zero in the original solution (Abramowicz et al. 1978), but Komissarov (2006) noticed that its special form allows us to take a purely toroidal magnetic field readily into consideration. The two contributions are assumed to be proportional to each other.
Non-vanishing components of the magnetic vector
bμ are 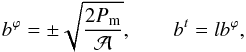 (3)with
(3)with
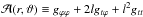 .
To solve Eq. (2) and construct the torus,
one needs to constrain the angular momentum profile
l(R). In this way, we obtain the stationary
non-accreting configuration, where all viscous effects are neglected. Therefore, accretion
can proceed only due to the relativistic cusp overflow.
.
To solve Eq. (2) and construct the torus,
one needs to constrain the angular momentum profile
l(R). In this way, we obtain the stationary
non-accreting configuration, where all viscous effects are neglected. Therefore, accretion
can proceed only due to the relativistic cusp overflow.
For constant angular momentum density, Eq. (2)can be solved analytically as well as in the magnetic case by imposing
proportionality 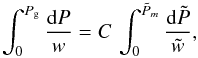 (4)where C
is a constant that sets the mutual relation between hydrodynamic and magnetic effects.
Since C determines the mutual relation between the hydrodynamic and the
magnetic pressure components, its value indirectly influences also the magnetization ratio
β (the equipartion state is reached for β near unity,
whereas β ≫ 1 represents a sub-equipartion magnetic field). Indeed, the
thermodynamic and the magnetic pressure terms and the total pressure are directly
proportional to each other. This leads to the solution for total pressure in the form
(4)where C
is a constant that sets the mutual relation between hydrodynamic and magnetic effects.
Since C determines the mutual relation between the hydrodynamic and the
magnetic pressure components, its value indirectly influences also the magnetization ratio
β (the equipartion state is reached for β near unity,
whereas β ≫ 1 represents a sub-equipartion magnetic field). Indeed, the
thermodynamic and the magnetic pressure terms and the total pressure are directly
proportional to each other. This leads to the solution for total pressure in the form
![\begin{equation} P= A {\kappa}^{-3}\left[ \left( \frac{{u_{t_{\rm in}}}}{{u_t}} \, \exp{\int_0^l\frac{\Omega \mathrm{d}l}{1-\Omega l}} \right)^{\tilde{C}}-1 \right]^4 , \label{Sol5} \end{equation}](/articles/aa/full_html/2013/07/aa21500-13/aa21500-13-eq31.png) (5)where
A = 0.0039 and
(5)where
A = 0.0039 and 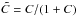 are constants, and
P = κργ
is the assumed form of equation of state with the polytropic index
γ = 4 / 3 (Abramowicz
& Fragile 2013).
are constants, and
P = κργ
is the assumed form of equation of state with the polytropic index
γ = 4 / 3 (Abramowicz
& Fragile 2013).
We focus on critical tori that develop the relativistic cusp at the inner edge, R = Rin, where the angular momentum is equal to the Keplerian angular momentum at the corresponding radius in the common equatorial plane of the black hole and the torus (ϑ = π / 2). The mass accretion can either bring the system out of the critical configuration and stabilise it with an updated set of model parameters and a modified profile of angular momentum, or the accretion process continues in a runaway mode and leads to a complete destruction of the torus.
 |
Fig. 1 Stationary distribution of mass across the meridional section of the equilibrium non-magnetised torus in Kerr metric (a = 0.3; the case of a purely hydrodynamical torus). The top panel shows the shape and the density structure in the poloidal coordinates as defined in the HARM code (Gammie et al. 2003), and the same configuration is drawn for Boyer-Lindquist coordinates in the bottom panel. See the text for details. |
An exemplary profile of such a torus is shown in Fig. 1, where contours of constant mass density are constructed from the analytical
form of the solution (5). The contours are
over-plotted on top of the colour-coded density structure. The black hole is located
towards the left side of the plot; the coordinates are defined in such a way that the
entire left edge of the plot corresponds to the location of the outer horizon at
r = r+. The bottom panel shows the same
configuration in Boyer-Lindquist coordinates (r,ϑ). The torus surface
extends from the inner rim at r = 4.5 up to the outer boundary at
r = 8.4 in the equatorial plane, y = 0. The right edge
is at x = 15; Cartesian coordinates are derived from Boyer-Lindquist
coordinates,
x2 + y2 = r2
(x = rsinϑ,
y = rcosϑ) and scaled with units of
GM / c2. The colour bar is
scaled logarithmically with values of normalised rest-mass density
ρ(x,y) relative to its maximum value
ρc at the torus centre
(x = Rc = 6.3, y = 0). In
the bottom panel the horizon is located at 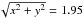 , so it is hidden behind
the left border of the graph.
, so it is hidden behind
the left border of the graph.
We notice that the constant density and pressure contours from Eq. (5) correspond accurately to the colour scale of the image. Since the latter is based on a direct output from the numerical code, we can be confident that the computed structure and the necessary transformations of the coordinates are correct. This is a reassuring check before we embark on the time evolution of a perturbed configuration, where the analytical calculation is not available.
Let us note that the HARM code (Gammie et al. 2003) defines radial and latitudinal coordinates in a way that helps resolving the plunging region near above the black-hole horizon. On the other hand, the sharp inner cusp of the critical configuration is revealed more clearly in standard Boyer-Lindquist coordinates. Figure 1 compares the torus structure in both types of coordinates.
 |
Fig. 2 Schematic graph of the angular momentum radial profile of the material inside the accretion torus. At the inner edge (Rin = 4.5GM / c2) of the matter configuration the angular momentum is equal to the Keplerian value, l = lK(Rin). The relativistic Keplerian angular momentum distribution first decreases with the radius, passes through a minimum, and then grows ∝ R1 / 2 asymptotically at large radii. The constant value, l = const., corresponds to the marginally stable configuration, which has been often discussed in the context of geometrically thick discs. The radially growing profile (q > 0) improves the stability of the accretion flow. |
2.2. Time evolution of perturbed configuration
We assume that the above-described initial stationary state is pushed out of equilibrium. This leads to the capture of a small amount of material by the black hole, which increases the black-hole mass, and so the accretion occurs. Abramowicz et al. (1998) argued that tori with radially increasing angular momentum density are more stable. Therefore, we started with q > 0 (see Fig. 2) and concentrated on the influence of the magnetic field on the accretion rate.
The algorithm of the numerical experiment proceeds as follows. At the initial step the
mass of the black hole was increased by a small amount, typically by about few percent.
After the time step δt, the elementary mass δM and
angular momentum
δL = l(Rin) δM
are accreted across the horizon, ![\hbox{$r=r_+\equiv[1+\sqrt{1-a^2}]\,GM/c^2$}](/articles/aa/full_html/2013/07/aa21500-13/aa21500-13-eq61.png) . The mass
increase δM is computed as a difference of the mass of torus
. The mass
increase δM is computed as a difference of the mass of torus
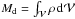 at t and t + δt, where
at t and t + δt, where
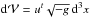 is taken over the spatial
volume occupied by the torus. The corresponding elementary spin increase is
δa = l δM / (M + δM).
Therefore, at each step of the simulation we updated the model parameters by the
corresponding low values of mass and angular momentum changes:
M → M + δM,
a → a + δa. The inner cusp moves
accordingly.
is taken over the spatial
volume occupied by the torus. The corresponding elementary spin increase is
δa = l δM / (M + δM).
Therefore, at each step of the simulation we updated the model parameters by the
corresponding low values of mass and angular momentum changes:
M → M + δM,
a → a + δa. The inner cusp moves
accordingly.
 |
Fig. 3 Torus mass, Md(t), relative to the black-hole mass as a function of time. The initial rapid accretion rate results in a drop of Md that becomes partially stabilised during the subsequent evolution. Time is given in dimensionless units of GM / c3. The orbital period is close to its Keplerian value near the inner edge, i.e. about Δt(R) ≃ 100 for the material near R = Rin. Top panel: the case of spin a = 0.1 is shown for different values of magnetisation parameters β = 3 (dashed), β = 80 (dotted), and β → ∞ (i.e. a non-magnetized case; solid line). Bottom panel: as above, but for a = 0.9. |
We employed geometrized units, setting the speed of light and the gravitational constant
equal to unity, c = G = 1. This implies the scaling of
various quantities with the central black-hole mass M. However, the mass
as well as the spin parameter evolve gradually (adiabatically) as the accretion of
material proceeds from the torus,
M ≡ M(t),
a ≡ a(t). Corresponding quantities in
physical units are obtained by the following conversions:
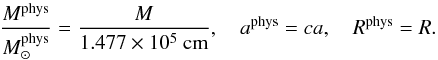 (6)Also,
(6)Also,
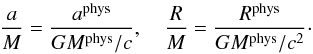 (7)To obtain the frequency
in physical units [Hz], one uses the relation
κphys = cκ. The geometrized frequencies are
scaled by M-1. Therefore, their numerical values must be
multiplied by the factor
(7)To obtain the frequency
in physical units [Hz], one uses the relation
κphys = cκ. The geometrized frequencies are
scaled by M-1. Therefore, their numerical values must be
multiplied by the factor 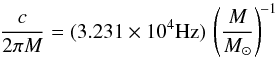 (8)to
find the frequency in [Hz].
(8)to
find the frequency in [Hz].
Figure 3 shows the dependence of the torus mass on time for different values β of the ratio between thermodynamical and magnetic pressure (plasma parameter), β ≡ Pg / Pm, for a torus with the radially increasing distribution of angular momentum, l(R) = lK, R = Rin [1 + ϵ(R − Rin)] q with q > 0, 0 < ϵ ≪ 1. This means that the reference level of the angular momentum density is set to l = const. = lK(Rin), motivated by the standard theory of thick accretion discs, where the constant value is a limit for stability. A radially growing profile then helps to stabilise the configuration.
Unless stated otherwise, we set q = 1,
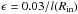 for definiteness of examples in
the simulations. At the inner edge of the torus the angular momentum equals the Keplerian
value, and for higher radii it grows to super-Keplerian rotation, taking into account the
specific shape of the relativistic Keplerian angular momentum (e.g., Abramowicz & Fragile 2013). Furthermore, following the von
Zeipel theorem, in the vertical direction along the constant
R = const. surface within the torus, the angular
momentum is defined by its value in the equatorial plane. The topology of these surfaces
is cylindrical except for relativistic deviations that are important only at very small
radii (Chakrabarti 1991).
for definiteness of examples in
the simulations. At the inner edge of the torus the angular momentum equals the Keplerian
value, and for higher radii it grows to super-Keplerian rotation, taking into account the
specific shape of the relativistic Keplerian angular momentum (e.g., Abramowicz & Fragile 2013). Furthermore, following the von
Zeipel theorem, in the vertical direction along the constant
R = const. surface within the torus, the angular
momentum is defined by its value in the equatorial plane. The topology of these surfaces
is cylindrical except for relativistic deviations that are important only at very small
radii (Chakrabarti 1991).
From the graph we see that the amount of accreted mass is generally larger for smaller β. The plot also shows that the overall gradually decreasing trend is superposed with fast oscillations. After the initial drop of the torus mass (given by the magnitude of the initial perturbation, δM ≃ 0.01M) phases of enhanced accretion change with phases of diminished or zero accretion.
 |
Fig. 4 Time evolution of density levels in four snapshots of the poloidal section (x,y) across the accretion torus (x = 0 is the symmetry axis). This example starts from the critical equilibrium configuration, which is perturbed at the initial moment of time. At this moment the Keplerian orbital time at the inner cusp, R = 5 GM / c2, corresponds to TKep = 70 GM / c3. Subsequently, accretion across the inner edge takes place onto the black hole (the outer horizon is at the left side of the panel). This process proceeds in an oscillatory manner, interchanging the phases of fast and diminishing accretion rate. The plasma magnetization parameter is set to β = 25 (sub-equipartion pressure of the magnetic field), the black-hole spin a = 0.1 (slow rotation of the black hole) in this example. The same colour scale as in Fig. 1. Geometrized units are used, where the length is scaled with respect to the gravitational radius, GM / c2, and time is scaled by GM / c3. |
The oscillatory behaviour can be traced by the position of the torus centre, which we discuss below. It resembles the eigenfrequency modes that were proposed as a model for quasi-periodic oscillations in some X-ray binaries (Rezzolla et al. 2003; Montero & Zanotti 2012). A similar accretion history is found also for higher spin values, i.e., closer to extreme rotation, although we always assumed |a| < 1 (we did not consider the possibility of a naked singularity, but see Stuchlík et al.2011, for a recent discussion of such a possibility).
Figure 4 shows levels of mass density at different time moments. Four frames exhibit the changing torus structure during the accretion process. (a) The first frame corresponds to the initial equilibrium state; no mass overflow takes place and the mass distribution just fills the critical surface. (b) The next frame shows the perturbed configuration where the inner edge is pushed slightly outwards, which pushes the torus out of its initial steady-state. (c) The third frame captures the moment when the accretion drops, and finally, (d) in the last frame the mass transfer onto the black hole is completely interrupted, although the configuration is not exactly stable (accretion is then restored and the cycle continues). We carried out these simulations for a different angular momentum dependence on radius to reveal the above-mentioned effect of the l(R) profile.
 |
Fig. 5 Md(t), mass of the torus, normalised with respect to the starting mass at the initial moment of the simulation, Md(0), is plotted as a function of time for different values of q = 0.6 (dotted), 0.8 (dot-dashed), 1.0 (dashed), 1.1 (solid). Top panel: a = 0.3; bottom panel: a = 0.9. For small q and small a the torus is unstable and its mass becomes quickly accreted onto the black hole, whereas higher values of the slope of the angular moment distribution and fast spin of the black hole tend to stabilise the system against the initial perturbation (accretion stops at a certain moment). |
 |
Fig. 6 Top panel: time to accrete half of the total mass of the torus as a function of q (plasma parameter β = 3). In agreement with the graph of Md(t) in Fig. 5 we notice a higher rate of accretion (shorter accretion half-time) for lower values of q. Bottom panel: the dependence of accretion half-time on the plasma magnetization parameter β is shown; the power-law index of the angular moment radial profile is set to a fixed value q = 1.1. |
 |
Fig. 7 Oscillation of the torus centre R = Rc (top panel; radius is expressed in geometrized units GM / c2 on the vertical axis), and of the central density ρ = ρc (bottom panel); density is relative to its peak value at the centre, ρc = ρ(Rc). The solid line is for a non-magnetized case (β ≫ 1), the dotted line denotes the magnetized configuration (β = 3). |
Figure 5 is complementary to Fig. 3. In Fig. 5 we compare several cases of different angular momentum profiles, as characterised by the slope q. One can see that the accretion rate is higher than in the previous example. This plot also confirms that for higher q the amount of accreted mass is diminished, in agreement with prior studies. In fact, for cases with indices q = 0.6 and q = 0.8 almost the whole torus is accreted. For q = 1.0, almost 96% of the initial torus mass is accreted, while for q = 1.1 it becomes 88% of the initial mass. A comparison between the two panels of Fig. 5 confirms the general trend, which shows that tori are more stable for higher spin values, i.e., closer to the extremely co-rotating black hole (a → 1) for otherwise similar parameters. We also followed the oscillations of the point of maximal mass density inside the torus (the torus centre); it shows a behaviour consistent with the above-described evolution of the accreted mass.
Figure 6 studies the dependence of accretion rate by plotting the half-mass accretion time as a function of q and β. Furthermore, Fig. 7 compares the magnetized vs. non-magnetized tori for the same spin (a = 0.3). In the top panel we show the time dependence of the radial coordinate of the point with the highest mass density R = Rc (hence the highest pressure) of these two tori, and in the bottom panel the dependence of the highest mass density is captured as a function of time. In the limit of a non-magnetised slender torus (Rc ≫ 1) these oscillations correspond to the situation that has been treated previously by analytical methods (Blaes et al. 2006). Although the amplitude of Rc oscillations is quite small in these examples (because the oscillations were initiated by a weak perturbation and the torus centre is relatively far from the black hole), the outer layers of the torus are affected more significantly and can be accreted across the inner edge.
In these simulations we neglected self-gravitation of the torus (Goodman & Narayan 1988; Karas et al. 2004). However, when the mass and angular momentum are accreted by the black hole, its parameters M and a are obviously changed. Hence, even for non-selfgravitating tori we need to update the parameters of Kerr space-time metric to achieve a consistent description. In our scheme we changed M and a at each time step, according to accreted mass and its angular momentum content. Then we can watch how this updating influences the accretion process, namely, oscillations of the torus centre, torus mass, and other characteristics. Figure 8 plots the dependence of the central mass density on time for a l(R) ∝ Rq profile for the non-magnetized case. In an analogous way, we examined the role of different initial perturbations δM(t = 0).
From these illustrations one can deduce that for a sufficiently steep slope q the torus becomes stabilised with respect to runaway accretion. The steeper q, the longer oscillation period. The (weak) initial perturbation does not significantly influence the oscillation period, only the oscillation amplitude is affected. Qualitatively identical conclusions are obtained for a slightly different value of the polytropic gas index. As mentioned above, the results presented here were computed for γ = 4 / 3; we also computed the same set of plots for γ = 5 / 3 with very similar results, while the model is more sensitive to relatively weak variations of q.
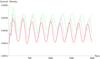 |
Fig. 8 Central mass density for the fixed angular momentum a = 0.5 of the black hole and varying index of the angular momentum profile of matter in the torus: q = 0.9, 1.0, and 1.1. Vanishing magnetisation (β ≫ 1) in this example. |
Finally, two additional plots reveal the changing parameters of the torus and the black hole in the course of accretion. Figure 9 compares the positions of the torus cusp and the torus centre as functions of the accreted mass for different initial values of spin a = 0.3, 0.5, and 0.7. The evolution of metric parameters M and a has a stabilising effect because the critical surface moves inward, so this case corresponds to the situation when the accretion rate and other characteristics oscillate. It does not lead to the runaway behaviour, which is also reflected in the gradually decreasing cusp radius. On the other hand, the solid line is related to the case when the accreted mass contains less angular momentum, and so the impact of increasing the black-hole mass is stronger than the effect of increasing the spin. In this case updating the metric parameters results in tori that tend to be more unstable. The mutual relation between the two radii, i.e. Rcusp vs. Rc, provides information about the size of the torus as it changes by loosing material onto the black hole and moving in radius, while the black hole grows.
Naturally, the mean centre of the torus, R = Rc, moves along with the above-mentioned gradual evolution of the inner cusp, R = Rcusp, by the mass transfer from the torus onto the black hole. The torus centre obviously satisfies Rc(t) > Rcusp(t) > r+(t) at each moment of the evolution. However, the exact mutual relation between these radii depends on details of the particular case, namely, the density and the angular momentum distribution within the torus. Therefore, both the mean Rc and the mean Rcusp can either approach the centre or recede towards a larger distance, depending on whether the torus shrinks and eventually becomes accreted onto the black hole (which is the case of runaway accretion) or if the partially accreted structure becomes stabilised against more mass transfer and stays away from the black hole. Naturally, the centre radius is influenced also by the fact that the black hole itself evolves its mass and spin.
Figure 10 shows the oscillation frequency of the torus, as determined from a sequence of our numerical solutions with different position of the torus centre. The frequency varies gradually in this graph, along with the black-hole dimensionless spin a. Again, this change can be seen as a result of accretion of the material from the torus onto the black hole, which modifies the model parameters including the black-hole spin and the torus centre (as well as the corresponding torus mass, Md, and other characteristics of the system, as explained above). This dependence allows us to unambiguously identify the relevant oscillation mode. We confirm a very precise agreement between the resulting curve in Fig. 10 and the theoretical formula for the radial epicyclic oscillation κ ≡ κ(M,a) (e.g. Kato et al. 2008, see Eq. (2.105)). The difference between the numerically determined value and the analytical formula for the radial epicyclic frequency is less than 1 per cent, and so the two dependencies are practically indistinguishable in the plot.
Naturally, to achieve a consistent solution, the parameters need to be evolved during the accretion process. Nevertheless, we checked that the above-mentioned point about the metric parameters does not influence the oscillation period of a globally stable configuration, i.e., until the perturbation itself remains weak. In other words, while the position of the torus centre and the magnitude of central density differ at a level of several percent between different simulations, the agreement about the oscillation frequency is typically one order of magnitude better.
We recall a useful scheme (see Table 1 in Font & Daigne 2002) that summarises a competing role of different agents that influence the stability of geometrically thick accretion tori near black holes. These are partly real physical effects (such as the angular moment profile of the accreted material, rotation of the black hole, and self-gravity), and partly reflect the impact of approximations that are employed to describe the system (such as the Newtonian versus pseudo-Newtonian versus general-relativistic models). As mentioned above, radially growing angular momentum and fast rotation of the black hole tend to stabilise the system against the runaway instability, while self-gravity acts instead against stability. Therefore we can also include the magnetic field as another ingredient into the discussion of stability. However, as demonstrated also above in this paper, with the increasing number of different factors and the interplay of mechanisms taken into account, the whole pictures becomes more complicated than when one had restricted the discussion to the competition of just two or three degrees of freedom. In the end the outcome of the analysis can depend on detailed values of the parameters, e.g. q vs. a. Moreover, especially the magnetic field can develop different geometrical structures on vastly different scales, and so it may be difficult or impossible to characterise the role of magnetic field on the runaway stability in a simple way.
 |
Fig. 9 Evolution of the characteristic radii during the process of mass transfer from the
accretion torus onto the black hole. Left panel: the mean radius
R = Rcusp(t) of the
cusp (i.e. the inner edge of the critical overflowing configuration) as a function
of the mass accreted from the torus onto the black hole, computed by integrating
|
In our highly simplified scheme we showed that the effect of the toroidal test magnetic field (embedded in a prescribed manner into the polytropic fluid) just adds to the internal pressure of the fluid. Hence it basically enhances the instability in a similar way as any other contribution that can enhance the pressure above the equilibrium value.
3. Discussion and conclusions
Within the framework of an axially symmetric magnetized fluid torus model we have extended the previous results on the onset of runaway instability of relativistic configurations near a rotating black hole. We concentrated on systems with radially increasing angular momentum density that are threaded by a purely toroidal magnetic field. We neglected self-gravity of the gaseous material (the mass of the torus was set to be at most several percent of the black-hole mass), nevertheless, we allowed for a gradual change of the Kerr metric mass and spin parameters by accretion over the inner edge. The angular momentum distribution within the torus was also allowed to evolve, starting from the initial power-law profile. The mass transfer influences the location of the cusp of the critical configuration, which can lead to the runaway instability.
If the profile of the angular momentum increases sufficiently fast with radius (typically, for q ≳ 0.8), the initial perturbation becomes stabilised by accretion of a small amount of material, whereas for small q the instability causes rapid accretion of the torus. The intensity of the threaded magnetic field influences the process of stabilisation or destruction of the torus because, within the framework of the adopted model, the magnetic pressure adds directly to the gas pressure (plasma parameter β ≳ 1).
 |
Fig. 10 Oscillation frequency of the torus as a function of the black-hole dimensionless spin a from the numerical simulation (assuming 0 ≤ a ≤ 1, q = 1). Different runs differ from each other by the radial position of the centre of the accretion torus, and therefore the oscillation frequency also varies. The functional dependence agrees with the radial epicyclic mode. |
The process of accretion is not perfectly monotonic, instead, there are changing phases of enhanced accretion rate and phases where the mass of torus remains almost constant. The overall gradual decrease of the torus mass is superposed with oscillations that can be seen by following the central density variations on the dynamical time-scale and the position of the centre of the torus. The oscillation amplitude is sensitive to the initial perturbation, but the frequency is not, namely, a small change of the metric coefficients does not affect the oscillation frequency.
The toroidal magnetic field plays a more important role in the early phases of the accretion process until the perturbed configuration finds a new equilibrium or disappears because of the runaway instability. If the oscillations become stabilised with time, no significant differences occur from the corresponding non-magnetized case, even when β is near unity (equipartition) and the accreted fraction of the torus material is significant.
Acknowledgments
We thank an anonymous referee for helpful suggestions. We acknowledge support from the student project of the Charles University (GAUK 139810; J.H.) and the collaboration project between the Czech Science Foundation and Deutsche Forschungsgemeinschaft (GACR-DFG 13-00070J; V.K.). The Astronomical Institute has been operated under the program RVO:67985815.
References
- Abramowicz, M. A., & Fragile, P. C. 2013, Foundations of Black Hole Accretion Disk Theory, Living Rev. Relativity, 16, 1 [Google Scholar]
- Abramowicz, M. A., Jaroszyński, M., & Sikora, M. 1978, A&A, 63, 221 [NASA ADS] [Google Scholar]
- Abramowicz, M. A., Calvani, M., & Nobili, L. 1983, Nature 302, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M. A., Karas, V., & Lanza, A. 1998, A&A, 331, 1143 [NASA ADS] [Google Scholar]
- Anile, A. M. 1989, Relativistic Fluids and Magneto-Fluids (Cambridge: Cambridge University Press) [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Barkov, M. V., & Baushev, A. N. 2011, New Astron., 16, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Blaes, O., Arras, P., & Fragile, P. C. 2006, MNRAS, 369, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarti, S. K. 1991, MNRAS, 250, 7 [NASA ADS] [Google Scholar]
- Daigne, F., & Mochkovitch, R. 1997, MNRAS, 285, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Fishbone, L. G., & Moncrief, V. 1976, ApJ, 207, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Font, J. A., & Daigne, F. 2002, ApJ, 581, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F., McKinney, J. C., & Tóth, G. 2003, ApJ, 589, 444 [Google Scholar]
- Goodman, J., & Narayan, R. 1988, MNRAS, 231, 97 [NASA ADS] [Google Scholar]
- Karas, V., Huré, J.-M., & Semerák, O. 2004, CQG, 21, R1 [Google Scholar]
- Kato, S., Fukue, J., & Mineshige, S. 2008, Black-Hole Accretion Disks (Kyoto: Kyoto University Press) [Google Scholar]
- Komissarov, S. S. 2006, MNRAS, A&A, 368, 993 [Google Scholar]
- Korobkin, O., Abdikamalov, E., Schnetter, E., Stergioulas, N., & Zink, B. 2011, PRD, 83, 043007 [NASA ADS] [CrossRef] [Google Scholar]
- Korobkin, O., Abdikamalov, E., Stergioulas, N., et al. 2013, MNRAS, 431, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, Y., Cheng, K. S., Yang, L. T., & Zhang, L. 2000, MNRAS, 314, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Masuda, N., Nishida, S., & Eriguchi, Y. 1998, MNRAS, 297, 1139 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., Tchekhovskoy, A., & Blandford, R. D., 2012, MNRAS, 423, 3083 [NASA ADS] [CrossRef] [Google Scholar]
- Montero, P. J., & Zanotti, O. 2012, MNRAS, 419, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Montero, P. J., Font, J. A., & Shibata, M. 2010, Phys. Rev. Lett., 104, 191101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Noble, S. C., Gammie, C. F., McKinney, J. C., & Del Zanna, L. 2006, ApJ, 641, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Pugliese, D., & Montani, G. 2013, Eur. Lett., 101, 19001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pugliese, D., Montani, G., & Bernardini, M. G. 2013, MNRAS, 428, 952 [Google Scholar]
- Rezzolla, L., Yoshida, S., & Zanotti, O. 2003, MNRAS, 344, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Seguin, F. H. 1975, ApJ, 197, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Stuchlík, Z., Hledík, S., & Truparová, K. 2011, CQG, 28, 155017 [Google Scholar]
- Wilson, D. B. 1984, Nature, 312, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Zanotti, O., Rezzolla, L., & Font, J. A. 2003, MNRAS, 341, 832 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Stationary distribution of mass across the meridional section of the equilibrium non-magnetised torus in Kerr metric (a = 0.3; the case of a purely hydrodynamical torus). The top panel shows the shape and the density structure in the poloidal coordinates as defined in the HARM code (Gammie et al. 2003), and the same configuration is drawn for Boyer-Lindquist coordinates in the bottom panel. See the text for details. |
| In the text | |
 |
Fig. 2 Schematic graph of the angular momentum radial profile of the material inside the accretion torus. At the inner edge (Rin = 4.5GM / c2) of the matter configuration the angular momentum is equal to the Keplerian value, l = lK(Rin). The relativistic Keplerian angular momentum distribution first decreases with the radius, passes through a minimum, and then grows ∝ R1 / 2 asymptotically at large radii. The constant value, l = const., corresponds to the marginally stable configuration, which has been often discussed in the context of geometrically thick discs. The radially growing profile (q > 0) improves the stability of the accretion flow. |
| In the text | |
 |
Fig. 3 Torus mass, Md(t), relative to the black-hole mass as a function of time. The initial rapid accretion rate results in a drop of Md that becomes partially stabilised during the subsequent evolution. Time is given in dimensionless units of GM / c3. The orbital period is close to its Keplerian value near the inner edge, i.e. about Δt(R) ≃ 100 for the material near R = Rin. Top panel: the case of spin a = 0.1 is shown for different values of magnetisation parameters β = 3 (dashed), β = 80 (dotted), and β → ∞ (i.e. a non-magnetized case; solid line). Bottom panel: as above, but for a = 0.9. |
| In the text | |
 |
Fig. 4 Time evolution of density levels in four snapshots of the poloidal section (x,y) across the accretion torus (x = 0 is the symmetry axis). This example starts from the critical equilibrium configuration, which is perturbed at the initial moment of time. At this moment the Keplerian orbital time at the inner cusp, R = 5 GM / c2, corresponds to TKep = 70 GM / c3. Subsequently, accretion across the inner edge takes place onto the black hole (the outer horizon is at the left side of the panel). This process proceeds in an oscillatory manner, interchanging the phases of fast and diminishing accretion rate. The plasma magnetization parameter is set to β = 25 (sub-equipartion pressure of the magnetic field), the black-hole spin a = 0.1 (slow rotation of the black hole) in this example. The same colour scale as in Fig. 1. Geometrized units are used, where the length is scaled with respect to the gravitational radius, GM / c2, and time is scaled by GM / c3. |
| In the text | |
 |
Fig. 5 Md(t), mass of the torus, normalised with respect to the starting mass at the initial moment of the simulation, Md(0), is plotted as a function of time for different values of q = 0.6 (dotted), 0.8 (dot-dashed), 1.0 (dashed), 1.1 (solid). Top panel: a = 0.3; bottom panel: a = 0.9. For small q and small a the torus is unstable and its mass becomes quickly accreted onto the black hole, whereas higher values of the slope of the angular moment distribution and fast spin of the black hole tend to stabilise the system against the initial perturbation (accretion stops at a certain moment). |
| In the text | |
 |
Fig. 6 Top panel: time to accrete half of the total mass of the torus as a function of q (plasma parameter β = 3). In agreement with the graph of Md(t) in Fig. 5 we notice a higher rate of accretion (shorter accretion half-time) for lower values of q. Bottom panel: the dependence of accretion half-time on the plasma magnetization parameter β is shown; the power-law index of the angular moment radial profile is set to a fixed value q = 1.1. |
| In the text | |
 |
Fig. 7 Oscillation of the torus centre R = Rc (top panel; radius is expressed in geometrized units GM / c2 on the vertical axis), and of the central density ρ = ρc (bottom panel); density is relative to its peak value at the centre, ρc = ρ(Rc). The solid line is for a non-magnetized case (β ≫ 1), the dotted line denotes the magnetized configuration (β = 3). |
| In the text | |
 |
Fig. 8 Central mass density for the fixed angular momentum a = 0.5 of the black hole and varying index of the angular momentum profile of matter in the torus: q = 0.9, 1.0, and 1.1. Vanishing magnetisation (β ≫ 1) in this example. |
| In the text | |
 |
Fig. 9 Evolution of the characteristic radii during the process of mass transfer from the
accretion torus onto the black hole. Left panel: the mean radius
R = Rcusp(t) of the
cusp (i.e. the inner edge of the critical overflowing configuration) as a function
of the mass accreted from the torus onto the black hole, computed by integrating
|
| In the text | |
 |
Fig. 10 Oscillation frequency of the torus as a function of the black-hole dimensionless spin a from the numerical simulation (assuming 0 ≤ a ≤ 1, q = 1). Different runs differ from each other by the radial position of the centre of the accretion torus, and therefore the oscillation frequency also varies. The functional dependence agrees with the radial epicyclic mode. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.